Производная функции — определение и геометрический смысл
Производная функции – что это такое? Как раз и навсегда понять и узнавать производную функцию. Производная – это понятие применимое к какой-либо функции и означает оно ни что иное как быстроту изменения функции (величины y) при изменении величины x, то есть другими словами – производная – это скорость с которой изменяется функция при изменении аргумента.
Такая зависимость – скорость изменения функции от аргумента также может быть описана функцией. Соответственно, возможны и первая, и вторая производные, если функция достаточна изменчива и непрерывна, чтобы позволить это. Давайте разберем это подробнее.
Содержание
Понятие производной
Если мы возьмем на графике любые две точки, например точки с координатами и . Тогда – это приращение аргумента, а – приращение функции. Приращение аргумента кратко обозначается , а приращение функции .
Определение производной
Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
На графике это означает, что точка с координатой стремится к точке с координатой .
Производная обозначается также как функция, только сверху ставится штрих – вот так
Итак, производная функции:
Замечание: Если вы встречаете такое выражение “производная f(x)” или “производная f” – это все равно что производная функции y(x). Функцию можно обозначать любой буквой, наиболее часто встречаются следующие обозначения функции – f(x), y(x), g(x).
Геометрический смысл производной
Проведем через точки A и B прямую и обратим внимание на то, что отношение это тангенс угла α. При стремлении к нулю, точка B приближается к точке A и наша прямая становится касательной к графику функции в точке A, а значение производной – это будет тангенс угла наклона касательной с осью Ox.
Обратите внимание, что в нашем примере , а , производная будет отрицательна, то как при делении отрицательного числа на положительное, мы получим отрицательное число.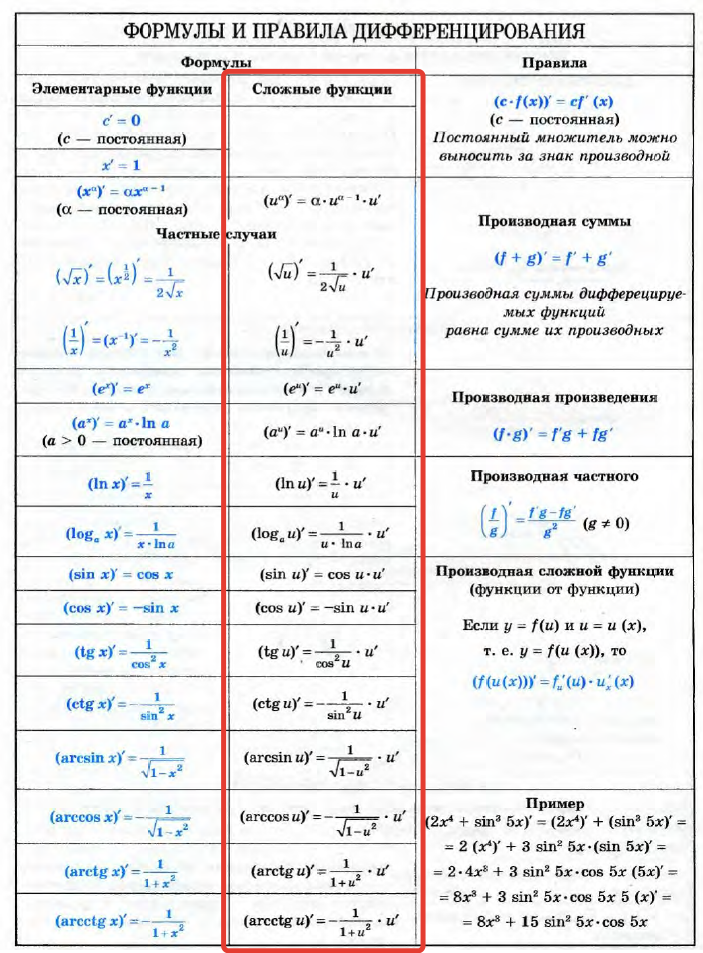
Подробнее поговорим об этом в теме “Знак производной”. Однако уже понятно, что если функция убывает, то значение производной на всем участке убывания будет отрицательным. Самостоятельно вы можете проверить – каким будет значение производной, если функция возрастает, а также в точках максимума и минимума функции.
Существование производной
Производная существует не для любых функций, есть определенные критерии, при которых возможно существование производной:
- Функция задана и непрерывна.
- Предел существует и конечен.
Если предел не существует, то это, как правило, связано с тем, что в точке, в которой ищется производная, нельзя провести касательную к графику функции. Или касательная образует с осью угол 900. В этом случае производная обращается в бесконечность.
Пример: дана функция . Найдем производную этой функции:
.
В точке производная будет обращаться в бесконечность, то есть .
Сейчас уже не строят графики функций, чтобы определить значение производной, для ее нахождения применяются таблица производных элементарных функций и правила дифференцирования. А пока решим несколько несложных примеров на понятия приращения функции и приращения аргумента.
Примеры на приращение функции и аргумента
Пример 1
Найдите приращение функции для функции , если , =2.
Решение: Понятно что начальное значение аргумента равно 2, а конечное значение 2,5. Найдем значение функции в этих двух точках
и .
Тогда
.
Пример 2
Дана функция . Найдите приращение при и .
Решение:
.
Ответ:
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2.
Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits.
Rules of differentiationЗадачи для самостоятельной работыРешения задачТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1.
Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.
3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1).
Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.
Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1.
Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2.
Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1.
Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1.
Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.
5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1).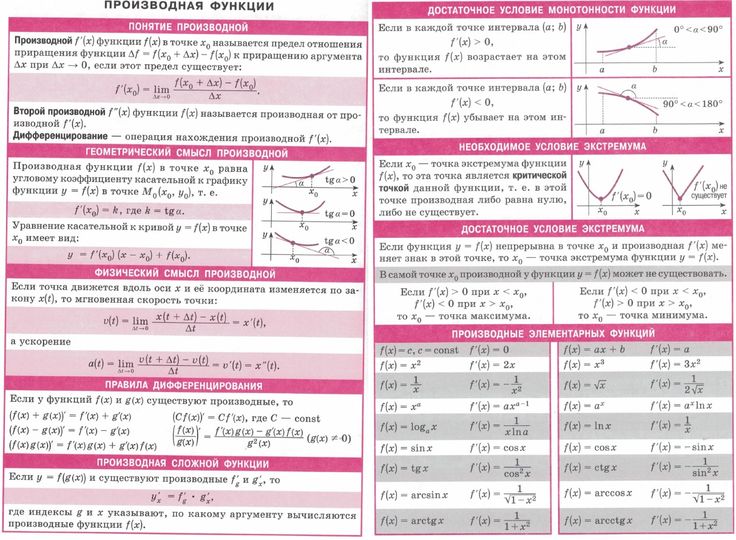
Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)Производная функция Excel
Рассмотрим функцию:
f(x)=x⁢sin(x2)+1
Аналитические производные от f(x) до четвертого порядка:
f'(x)=sin(x2)+2⁢x2⁢cos(x2)
f»(x)=6⁢x⁢cos(x2)-4⁢x3⁢sin(x2)
f»'(x)=6⁢cos(x2)-8⁢x4⁢cos(x2)-24⁢x2⁢sin(x2)
f»»(x)=16⁢x5⁢sin(x2)-80⁢x3⁢cos(x2)-60⁢x⁢sin(x2)
Мы вычисляем численные производные при x = 0 92)+1 2 =ПРОИЗВОДНАЯ(A1,X1,0) 3 =ПРОИЗВОДНАЯ(A1,X1,0,2) 4 =ПРОИЗВОДНАЯ(A1,X1,0,3) 5 =ПРОИЗВОДНАЯ(A1,X1,0,4)
⇒
| А | Б | |
| 1 | 1 | 1 |
| 2 | 3. 18603E-15 | 0 |
| 3 | 0 | 0 |
| 4 | 6 | 6 |
| 5 | 1.27896E-15 | 0 |
При
х=1| А | |
| 6 | =ПРОИЗВОДНАЯ(A1,X1,1) |
| 7 | =ПРОИЗВОДНАЯ(A1,X1,1,2) |
| 8 | =ПРОИЗВОДНАЯ(A1,X1,1,3) |
| 9 | =ПРОИЗВОДНАЯ(A1,X1,1,4) |
⇒
.
| А | Б | |
| 6 | 1.922075597 | 1.922075597 |
| 7 | -0,124070104 | -0,124070104 |
| 8 | -21.27590825 | -21.27590825 |
| 9 | -80.24890792 | 80.24890780 |
Формула производной — производная функции, примеры решений и важные вопросы и ответы
Производные — это основной инструмент, используемый в вычислениях.
Производная измеряет крутизну графика данной функции в некоторой конкретной точке графика. Таким образом, производная также измеряется как наклон. Это означает, что это отношение изменения значения функции к изменению независимой переменной. Например, если независимой переменной является время, мы часто думаем об этом соотношении как о скорости изменения, подобной скорости.
В этой статье мы обсудим, что такое производная в математике, формулы дифференциального исчисления, основные формулы дифференцирования.
Что такое дериватив?
Давайте узнаем, что такое производная. Производная функции — одно из основных понятий вычислительной математики. Вместе с интегралом производная занимает центральное место в исчислении. Процесс нахождения производной называется дифференцированием. Обратная операция для дифференцирования известна как интегрирование. В этой статье мы обсудим формулу производной с примерами.
Что означает производная?
Вот что значит производная.
Производная функции в данной точке характеризует скорость изменения функции в этой точке. Мы можем оценить скорость изменения, вычислив отношение изменения функции Δy к изменению независимой переменной Δx.
При определении производной предельным значением этого отношения считается Δx → 0. Применим более строгую формулировку.
Как найти производную функции?
Теперь, как найти производные функции (любой)
Предположим, что y = f(x), мы обычно используем формулу наклона:
Наклон равен изменению Y/ изменению X, которое можно записать как Δy/ Δx
[Изображение будет загружено в ближайшее время]
И (из диаграммы, приведенной выше) мы видим, что:
| Значение переменной 30 x00034 x | до | x+Δx | ||||||||
Значение переменных y с | F (x) | F (x) | F (x) 9003 | F (x) 9003 | 9003 9. 20639.2039.2039.2039.2039.20639.20639.20639.2063. | . |
Если f — функция с действительным знаком, а a — любая точка в ее области определения, для которой f определена, то говорят, что f(x) дифференцируема в точке x=a, если производная в a точка функции f'(a) существует в каждой точке своей области определения, она определяется как
f'(a) = \[\frac{f(x_{0} + Δx) — f(x_{0})}{Δx}\]
Учитывая, что указанный выше предел существует и что f'( а) представляет производную в точке а функции f(x). Известно, что это первый принцип производной.
Область определения функции f'(a) определяется наличием ее пределов. Производная обозначается как \[\frac{d}{dx}\] f(x) = D(f(x))
Пусть y = f(x), тогда производная функции f(x) может быть дается как
\[\frac{d}{dx}\] f(x) в a или \[\frac{df}{dx}\] в a
Это известно как производная от y по x.
Кроме того, производная функции f по x при x = a задается как:
Производная в точке функции f(x) означает скорость изменения функции f(x) по отношению к x при точку, лежащую в его области определения. Чтобы любая данная функция была дифференцируемой в любой точке, предположим, что x = a в своей области определения, тогда она должна быть непрерывной в этой конкретной данной точке, но наоборот не всегда верно.
Так находят производные функции.
Шаги для нахождения производной функции:
Шаги для нахождения производной функции f(x) в точке x\[_{0}\] следующие:
Сформируйте разностное частное \[\frac{f(x_{0} + Δx) — f(x_{0})}{Δx}\]
Упростите частное, сократив Δx, если возможно;
Найдите производные в математике:
Рассмотрим функции f и g как две вещественные функции, такие, что дифференцирование этих функций определено в общей области, затем давайте обсудим операции, которые можно выполнить по функциям,
1) Сумма производных: | Сумма производных функции f и функции всегда равна сумме производной функции f и функции. |
2) Разность Производные: | Разность производных функции f и функции g равна производной разности функций f и g. \[\frac{d}{dx}\] [f(x)-g(x)] = \[\frac{d}{dx}\] f(x) -\[\frac{d} {dx}\] g(x) Теперь предположим, что f(x) = u и g(x) = v, тогда (u-v)’ = u’-v’ |
3) Цепное правило Дифференцирование: | Вот две функции f(x) и g(x), формула цепного правила: x ) |
4) Производная произведения двух функций: | Производная произведения двух функций может быть решена по правилу произведения, \[\frac{d}{dx}\] [f(x).g(x)] = g(x) \[\frac{d}{dx}\] f(x) +f(x ) \[\frac{d}{dx}\] g(x) Теперь предположим, что f(x) = u и g(x) = v, тогда (uv)’ = u’v+v’u Это правило также известно как правило ЛЕЙБНИЦА для дифференцирования произведения любых двух функций. |
\[\frac{d}{dx}\] [f(x)+g(x)] = \[\frac{d}{dx}\] f(x) +\[\frac{d}{dx }\] g(x) Теперь предположим, что f(x) = u и g(x) = v, тогда (u+v)’ = u’+v’