Производная из корня: Обучение — учебные курсы и тесты

6. Кратность корня и производная многочлена.

Определение 1. Корень многочлена имеет кратность если и , . Корни кратности 1 называют простыми, остальными кратными.

Для того чтобы узнать, кратен корень или нет, бывает полезным понятие производной многочлена. Если рассматривать многочлен с числовыми коэффициентами как функцию, то это понятие совпадает с обычной производной, определяемой в анализе. Следовательно, все свойства производной сохраняются у производной многочлена.

Теорема 1. Простой корень многочлена не является корнем его производной; кратный корень кратности является корнем производной, и кратность его в производной равна .

Теорема 2. Для того чтобы число было корнем кратности многочлена необходимо и достаточно, чтобы и .

Всякий многочлен можно представить в виде

,

т.

е. разложить его по степеням линейного двучлена . Такое разложение однозначно и дается формулой Тейлора

.

ПРИМЕРЫ:

1. Найти кратность корня в многочлене , .

Решение: Для решения задачи воспользуемся схемой Горнера:

									– первый
									– второй
									– третий
									– четвертый

Искомая кратность равна .

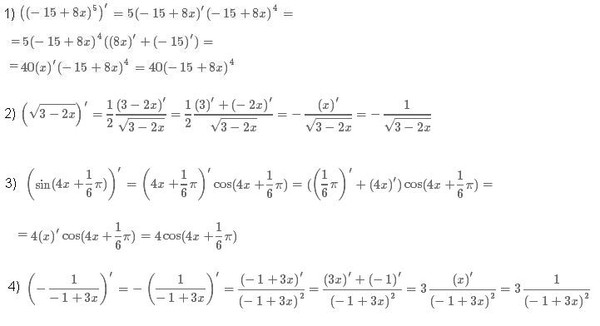
2. Найти при каких и многочлен делится на .

Решение: Условие задачи означает, что – является корнем кратности не меньшей , что равносильно утверждению .

Найдем : , значения многочлена и его производной при : , , откуда , .

Определение 1. Дробно-рациональной функцией называется отношение (частное) пары многочленов и , где . Краткая запись .

Одна и та же дробь может быть представлена в виде частного различных пар многочленов. Если НОД =1, то – несократимая запись. Такая запись существует у каждой дроби и она единственна, если многочлен нормирован.

Определение 2. Дробь называется правильной, если степень ее числителя меньше степени знаменателя.

Определение 3. Комплексная простейшая дробь – это дробь с несократимой записью , где , а .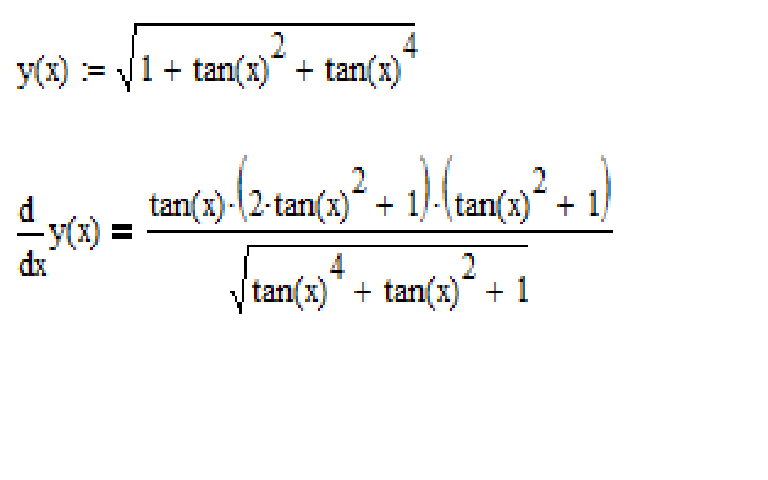

Определение 4. Вещественная простейшая дробь – это дробь с несократимой записью одного из двух типов: , , где , , .

Теорема 1. Всякая правильная дробь представима в виде суммы простейших комплексных дробей; всякая правильная вещественная дробь представима в виде суммы простейших вещественных дробей.

Один из способов разложения дроби на простейшие дает формула Лагранжа. Эта формула применима к дробям , если не имеет кратных корней и при разложении на вещественные простейшие имеет только вещественные корни. Если , при , то . Значение производной можно вычислять по формуле .

Для дроби формула Лагранжа не применима. В этом случае можно получить требуемое, разложив многочлен по степеням многочлена .

ПРИМЕРЫ:

1. Разложить на простейшие комплексные дроби.

Решение: Заметим, что знаменатель не имеет кратных корней, его корни , , , – корни четвертой степени из ; . По формуле Лагранжа:

2. Разложить на вещественные простейшие дроби.

Решение: У знаменателя все корни просты и вещественны, следовательно, можно применить формулу Лагранжа:

3. Разложить на простейшие вещественные дроби.

Решение: Для решения задачи используем схему Горнера:

4. Разложить на простейшие вещественные дроби.

Решение:

Заметим, что дискриминант отрицателен. Введем обозначения: ; . Разделим многочлен на многочлен с остатком:

, т.е. , где , . Теперь разделим на : , т.е. , где , . Таким образом, .

5. Разложить на простейшие комплексные дроби.

Решение: Воспользуемся видом разложения дроби на простейшие:

.

Для нахождения коэффициентов и домножим это равенство на : . При получаем . Теперь продифференцируем полученное уравнение: . При получаем .

Теперь так же находим коэффициенты , , . Домножаем сначала на : . При : . После дифференцирования:

, при : . Еще раз дифференцируем: , : .

Итак, .

6. Разложить на простейшие вещественные дроби.

Решение: Заметим, что в разложении будет единственное слагаемое со знаменателем, имеющим корень . Найдем сначала его:

, домножаем на : и при получаем .

Теперь находим разность

. Разложим числитель по степеням : . Тогда .

«Решаем с помощью производной»

Производная широко применяется при решении ряда задач элементарной математики. Из всего круга таких задач выделим те, при решении которых используется теорема Лагранжа и ее следствия. К ним относятся задачи на доказательство тождеств, неравенств, вывод формул тригонометрии, разложение алгебраических выражений на множители, решение уравнений, неравенств, систем уравнений, уравнений с параметрами. При этом можно указать общие методы решения и некоторые частные приемы.

Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что <Рисунок1>.

Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].

Следствие 2. Если функции и непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.

Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.

Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.

Теорему Лагранжа можно применять:

— при доказательстве неравенств, в частности – числовых неравенств;

— при исследовании вопроса о корнях многочлена или уравнения;

— при решении уравнений.

В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа <Рисунок1>, c (a;b) и оценивается f’(c), а, следовательно, и выражение <Рисунок2>, что позволяет доказать рассматриваемое неравенство или решить вопрос о корнях многочлена, уравнения.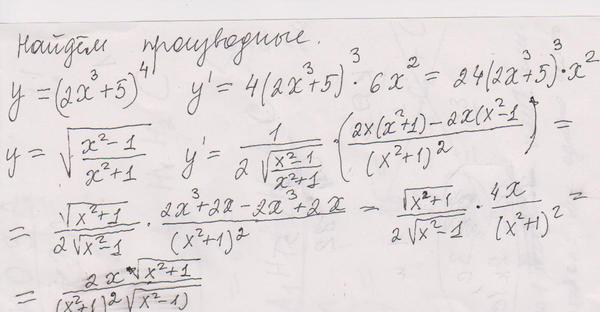

Пример 1. Доказать, что <Рисунок3>.

Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), <Рисунок4>. Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и <Рисунок5>, где 0,6<c<0,8. Имеем <Рисунок6>, т.е. <Рисунок7>. Оценим число<Рисунок8>. Так как 0,6<c<0,8, то 0,36<1-c²<0,64 и 0,6<<Рисунок9><0,8, следовательно <Рисунок10>. Тогда <Рисунок11> и окончательно <Рисунок3>.

Пример 2. Доказать, что e^x>=ex.

Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=e^x-ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b<1 – выполняется условие теоремы на отрезке [b;1] и, следовательно, существует внутренняя точка соответствующего отрезка, такая, что <Рисунок12>, т. е. <Рисунок13>. Так как c>1 при b>1, то e^c>e и, следовательно, e^c-e>0. Тогда <Рисунок14>, а значит e^b-eb>0, т.е. e^b>eb для любого b>1. Таким образом доказано, что e^x>=ex при x>=1.

Если b<1, то <Рисунок15>, т.е. с<1, тогда e^c<e и e^c-e<0. Учитывая, что b-1<0, из равенства <Рисунок13>, следует, что e^b-eb>0, т.е. e^b>eb.

Итак, доказано, что неравенство e^x>=ex верно при любом действительном х. В частности, при x=c+1 получим e^c+1>=e(c+1), т.е. e^c>=c+1, где с – любое действительное число.

Пример 3. Доказать, что уравнение <Рисунок16> не имеет действительных положительных корней.

Решение. Пусть b – любое положительное число. Рассмотрим функцию f(x)= <Рисунок17>, непрерывную на отрезке [a;b] и имеющую производную <Рисунок18> на интервале (0;b). По теореме Лагранжа имеем <Рисунок19>, 0<c<b, т.е. <Рисунок20>. А так как при любом с>0 e^c>c+1 (доказано в примере 2), то e^c-c>1 и, следовательно, <Рисунок21>. Отсюда получим <Рисунок22>, а значит <Рисунок23> для любого b>0. Таким образом, <Рисунок24> при x>0, т.е. <Рисунок25>, следовательно, равенство <Рисунок16> не выполняется ни при каком x>0. А, значит, уравнение <Рисунок16> не имеет действительных положительных корней.

Пример 4. Доказать, что на промежутке (0, 2) имеется не более двух различных действительных корней уравнения <Рисунок26>.

Решение. Предположим, что уравнение имеет не менее трех различных действительных корней х₁, х₂, х₃, принадлежащих промежутку (0,2), и пусть x₁<x₂<x₃. Тогда они являются нулями функции <Рисунок27>, т.е. f(x₁)=f(x₂)=f(x₃)=0. На каждом из отрезков [x₁;x₂], [x₂;x₃] для функции f(x) выполняются условия теоремы Лагранжа, следовательно, существуют числа c₁ и с₂ из интервалов (х₁;х₂), (х₂;х₃) соответственно, такие, что <Рисунок28> и <Рисунок29>. А так как f(x₁)=f(x₂)=f(x₃)=0, то f’(c₁)=0 и f’(c₂)=0, причем с₁с₂.

Найдем производную f’(x):

<Рисунок30>. Так как <Рисунок31> для любых х, то уравнение f’(x)=0 имеет единственный корень x=, принадлежащий промежутку (0, 2). Пришли к противоречию, так как с₁ и с₂ (с₁с₂) являются корнями уравнения f’(x)=0, тем самым доказано, что уравнение <Рисунок26> имеет на промежутке (0,2) не более двух различных действительных корней.

Пример 5. Решить уравнение x⁹-9x⁵+63x-55=0.

Решение. Легко заметить, что число х₁=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х₂, отличный от х₁. Числа х₁ и х₂ являются нулями функции f(x)=x⁹-9x⁵+63x-55 и, следовательно, f(x₁)=f(x₂)=0. Применим терему Лагранжа к функции f(x) на отрезке [x₁;x₂], если x₁<x₂ или на отрезке [x₂;x₁], если x₁>x₂. Следовательно, найдется такая внутренняя точка с этого отрезка, что будет выполняться <Рисунок32>. Учитывая, что f(x₁)=f(x₂)=0, получим f’(с)=0, т.е. число с – корень уравнения f’(x)=0. Но производная f’(x)=9x⁸-45x⁴+63, т.е. f’(x)=9(x⁴-2,5)²+6,75 положительна для любых х, а значит уравнение f’(x)=0 не имеет корней. Полученное противоречие доказывает, что найденный корень х₁=1 является единственным корнем уравнения x⁹-9x⁵+63x-55=0.

Пример 6.

Определить число критических точек функции y=(x²-1)(x²-8х)(x-9).

Решение. Так как степень многочлена f(x)= (x²-1)(x²-8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней. Применим теорему Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках [-1;0], [0;1], [1;8], [8;9] и при этом учтем, что f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся внутренние точки х₁, х₂, х₃, х₄ соответственно, такие, что <Рисунок33>, <Рисунок34>, <Рисунок35>, <Рисунок36>, т.е. f’(x₁)=0, f’(x₂)=0, f’(x₃)=0, f’(x₄)=0. А учитывая, что x₁, х₂, х₃, х₄ – различные корни многочлена f’(x) четвертой степени, делаем вывод, что других корней, отличных от полученных, нет и, следовательно, функция y=(x²-1)(x²-8х)(x-9) имеет четыре критические точки.

Условие монотонности функции можно применять:

— при решении неравенств;

— при доказательстве неравенств с переменной;

— при доказательстве числовых неравенств;

— при исследовании вопроса о количестве корней уравнения;

— в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.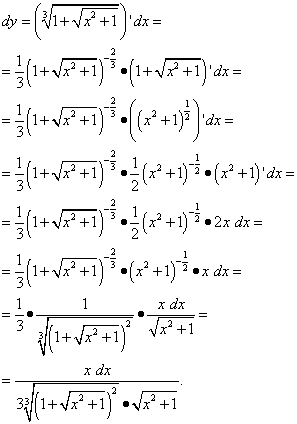

Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.

Пример 7. Доказать, что 3xcosx<sinx+sin2x, если 0<x<<Рисунок37>.

Решение. Докажем, что, если 0<x<<Рисунок37>, то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке <Рисунок38>функцию f(x)=tgx-3x+2sinx. Ее производная <Рисунок39> при <Рисунок40> принимает положительные значения, следовательно, функция f(x) возрастает на промежутке <Рисунок38>и на нем f(x)>f(0).

Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0.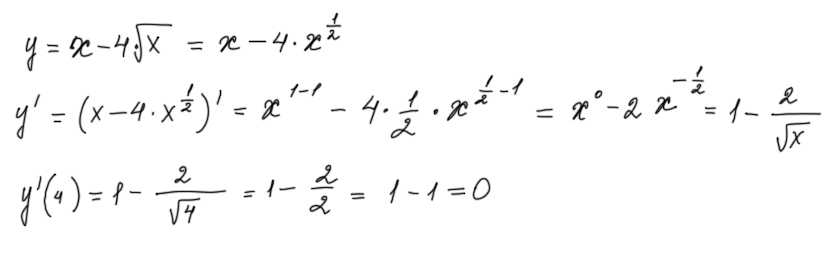 А так как на промежутке <Рисунок38> cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано, что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если 0<x<<Рисунок37>.

Пример 8. Доказать, что

1) <Рисунок41> и <Рисунок42>, если 0<x₁<x₂<=e;

2) <Рисунок43>и <Рисунок44>, если e<=x₁<x₂.

Решение. Рассмотрим непрерывную на промежутке (0;+) функцию <Рисунок45>. Так как ее производная <Рисунок46> равна нулю при х=е, а при 0<x<e f’(x)>0 и f’(x)<0 при x>e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+) - убывает. Тогда для любых значений х₁ и х₂ таких, что 0<x₁<x₂<=e, будет выполняться неравенство f(x₁)<f(x₂), то есть <Рисунок47>.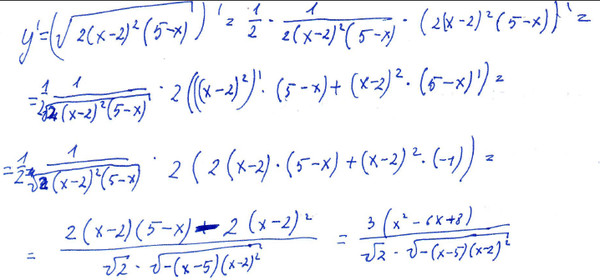 Запишем его в виде <Рисунок48>, <Рисунок49>. Учитывая, что функция ln t возрастающая, получим <Рисунок50>. А если обе части неравенства <Рисунок47> умножить на произведение x₁x₂>0, то получим x₂lnx₁<x₁lnx₂, далее <Рисунок51>, откуда и будем иметь <Рисунок52>.

Если же e<=x₁<x₂, то f(x₁)>f(x₂), то есть <Рисунок47>, откуда и получим <Рисунок53>и <Рисунок54>.

Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.

Пример 9. Сравнить (сtg48°)^tg48° и (сtg50°)^tg50°.

Решение. Заметим, что сtg48°=сtg<Рисунок55>, tg48°=tg<Рисунок55>, ctg50°=ctg<Рисунок55>, tg50°=tg<Рисунок55>, а также, что <Рисунок57>.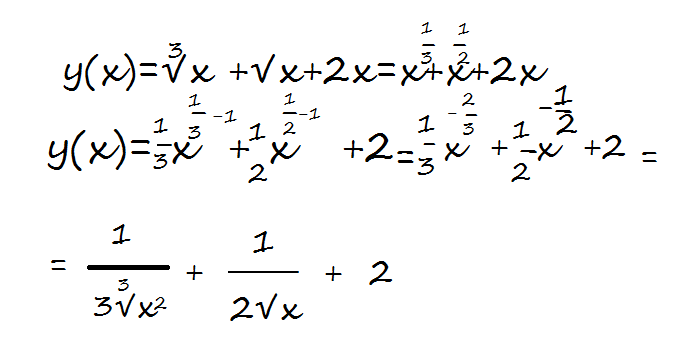 Взяв <Рисунок58>, <Рисунок59> и учитывая, что <Рисунок53>, если 0<x₁<x₂<=e, получим <Рисунок60>, т.е. (сtg48°)^tg48° > (сtg50°)^tg50°.

Пример 10. Доказать, что 2006 ²⁰⁰⁷>2007 ²⁰⁰⁶.

Решение. Воспользуемся неравенством x₁^x2>x₂^x1, если e<=x₁<x₂. Положив х₁=2006 и х₂=2007, имеем e<2006<2007, следовательно, 2006 ²⁰⁰⁷>2007 ²⁰⁰⁶.

Пример 11.

Определить число действительных корней уравнения 2х³-24х-19=0.

Решение. Функция f(x)= 2х³-24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x²-24=6(x-2)(x+2).

При x<-2 и x>2 f’(x)>0, а при –2<x<2 f’(x)<0. Следовательно, на промежутках (-:-2],[2;+) функция возрастает, а на промежутке [-2;2] – убывает. Вычислим значения функции в точках х=-3, х=-2, х=2, х=5. Имеем f(-3)=-1<0, f(-2)=13>0, f(2)=-51<0, f(5)=111>0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х³-24х-19=0 имеет три действительных корня, которые находятся на промежутках  (-3;-2), (-2;2), (2;5).

Остальные следствия теоремы Лагранжа можно применять:

— при доказательстве тождеств, в частности при выводе формул элементарной математики;

— при упрощении выражений;

— при разложении алгебраических выражений на множители.

При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.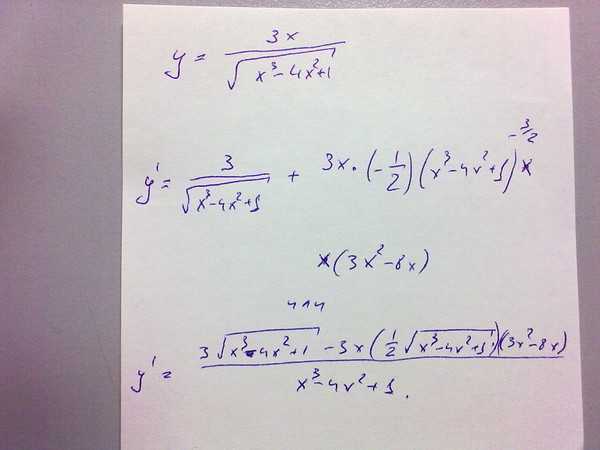 е. имеет вид f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x), и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту постоянную находят, положив х равным некоторому значению х₁.

Пример 12. Вывести формулу <Рисунок61>.

Решение. Функция f(x)= <Рисунок62> непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin²0-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим <Рисунок62>=0, или <Рисунок61>.

Пример 13. Доказать, что arctgx=arcsin<Рисунок63> при x<0.

Решение. Рассмотрим две непрерывные на промежутке (-;0] функции f(x)=arctgx и g(x)=arcsin<Рисунок64>, тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.

<Рисунок65>, <Рисунок66>. Так как при x<0 |x|=-x, то <Рисунок67> и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin<Рисунок69>, то есть <Рисунок68> Итак, получим arctgx=arcsin<Рисунок63> при x<0.

Пример 14. Доказать тождество

<Рисунок70>

Решение. Заметим, что <Рисунок71>, <Рисунок72> для любого действительного х и функции <Рисунок73>, <Рисунок74> непрерывны на всей числовой прямой. Имеем <Рисунок75>,

<Рисунок76>.

1) Рассмотрим функцию F(x)=f(x)+g(x), x (-;-1) (0;1).

F(x)= <Рисунок77>, а F’(x)=f’(x)+g’(x)= <Рисунок78>. Если x (-;-1), то |х²-1|=х²-1, |х|=-х и F’(x)=0. Если x (0;1), то |х²-1|=-(х²-1), |х|=х и F’(x)=0. На основании условия постоянства функции F(x)=c, то есть <Рисунок79>. На каждом из рассматриваемых промежутков определим с, положив, например, х=<Рисунок80> и x=<Рисунок81>.

<Рисунок82>, cледовательно, с=.

<Рисунок83>, следовательно, с=0. Имеем: <Рисунок84> при x (-;-1), <Рисунок85> при x (0;1).

2) Рассмотрим функцию G(x)=f(x)-g(x), x (-1;0) (1; +).

<Рисунок86>, <Рисунок87>.

Если x (-1;0), то |х²-1|=-(х²-1), |x|=-x и G’(x)=0.

Если x (1; +), то |х²-1|=х²-1, |x|=x и G’(x)=0. Тогда на указанных промежутках функция G(x) постоянна, т.е. <Рисунок88>. Положим x=<Рисунок80> и x=<Рисунок81>, получим <Рисунок89>, следовательно, с=; <Рисунок90>, тогда с=0.

Имеем: <Рисунок91> при x (-1;0), <Рисунок92> при x (1;+ ).

3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.

f(-1)=arccos(-1)=, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=+g(x), то есть <Рисунок93>. <Рисунок94>, <Рисунок95>, следовательно, при х=0 f(x)=-g(x), то есть <Рисунок96>. f(1)=arccos1=0, g(1)=arcsin0=0, следовательно, при х= 1 f(x)=g(x), то есть <Рисунок97>.

Таким образом, данное тождество доказано для всех действительных х.

Пример 15. Разложить на множители выражение

y²(x-z)+x²(z-y)+z²(y-x).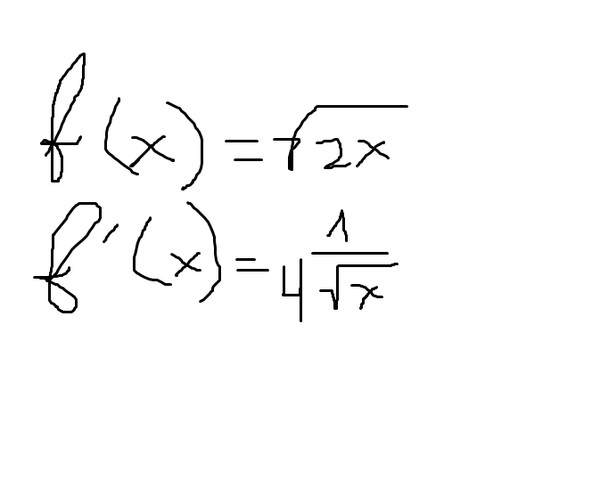

Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y²(x-z)+x²(z-y)+z²(y-x).

Найдем f’(x).

f’(x)=y²+2x(z-y)-z²=y²-z²-2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).

Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.

g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x²).

Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y²(x-z)+x²(z-y)+z²(y-x)=(y-z)((y+z)x-x²)+c.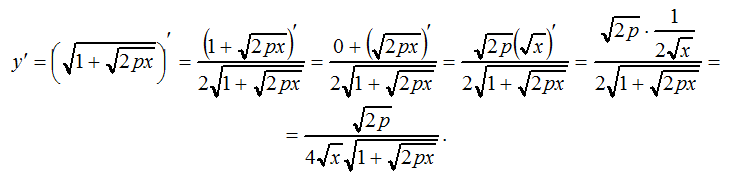 Найдем с, полагая в этом равенстве, например, х=0. Имеем yz²-zy²=c. Тогда f(x)=g(x)+yz²-zy², то есть

f(x)=(y-z)((y+z)x-x²)+yz²-zy²=(y-z)(xy+xz-x²)-yz(y-z)=(y-z)(xy-x²+xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).

Итак, y²(x-z)+x²(z-y)+z²(y-x)=(y-z)(y-x)(x-z).

Рисунки

исчисление — производная квадратного корня

спросил 10 лет, 6 месяцев назад

Изменено 1 год, 1 месяц назад

Просмотрено 305 тысяч раз

$\begingroup$

Какой будет производная квадратных корней? Например, если у меня есть $2 \sqrt{x}$ или $\sqrt{x}$.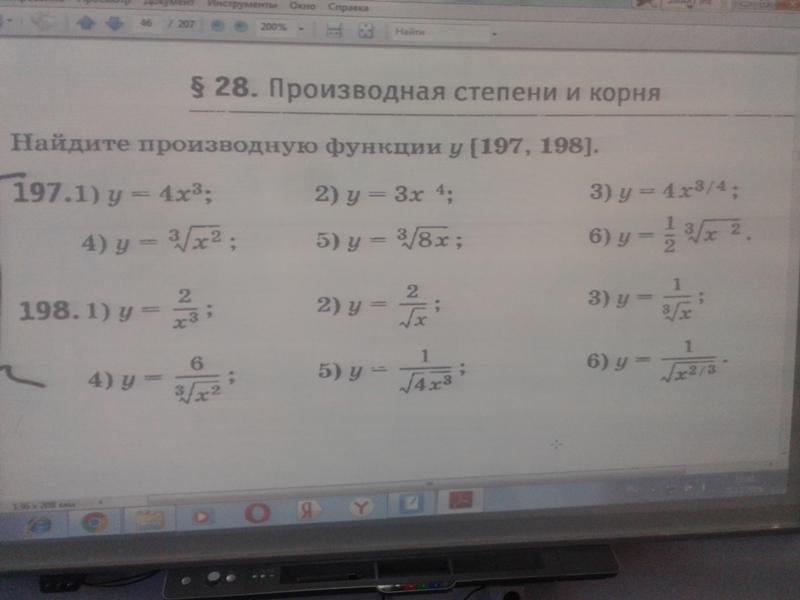 2.$$

Это сумма подобластей, добавленных с каждой стороны квадрата (оранжевые области на рисунке выше). Последний член в приведенном выше уравнении очень мал, и им можно пренебречь. Таким образом:

$$dx=2*d\sqrt x * \sqrt x$$

$$\frac{dx}{d\sqrt x}=2 * \sqrt x$$

$$\frac{ d\sqrt x}{dx}=\frac{1}{2*\sqrt x}$$

(Чтобы перейти от второго шага к последнему, переверните дроби в обеих частях уравнения.)

Артикул: 9{-1/2} •1 =\frac{d}{dx}\sqrt{x}$ в заключение $\frac{1}{2\sqrt{x}}$

$\endgroup$

2

Видео-вопрос: Нахождение производной корневой функции с помощью предельного определения производных

Стенограмма видео

Определите производную функции 𝑓 из 𝑥, равной квадратному корню из двух 𝑥 минус 16, используя определение производной.

Давайте сначала вспомним определение производной: 𝑓 простое число 𝑥 равно пределу, когда ℎ приближается к нулю числа 𝑓 числа 𝑥, добавить ℎ минус 𝑓 числа 𝑥 над ℎ.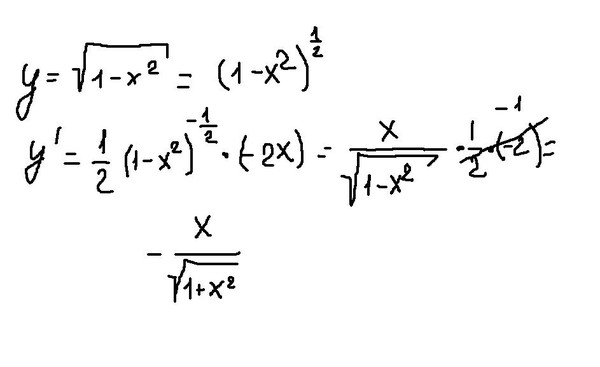 Помните, что чтобы получить 𝑓 из 𝑥 добавить ℎ, мы просто заменим 𝑥 на 𝑥 добавить ℎ в 𝑓 из 𝑥. Это дает нам 𝑓 из 𝑥 добавить ℎ равно квадратному корню из двух, умноженному на 𝑥 добавить ℎ минус 16. Затем мы можем раскрыть эти скобки, чтобы получить, что 𝑓 из 𝑥 плюс ℎ равно квадратному корню из двух 𝑥 плюс два ℎ минус 16.

Теперь сделаем эту замену в определении производной. Теперь, отсюда, на самом деле есть небольшая хитрость, которую мы используем, когда пытаемся найти производную корневой функции по определению. Это то, что мы часто делаем, когда имеем дело с корнями, и это умножение на сопряжение. Помните, сопряжение — это когда мы меняем знак в середине двух терминов. Но мы также должны умножить знаменатель на то же самое. Таким образом, мы, по сути, просто умножаем то, что у нас было, на единицу и, следовательно, технически ничего не меняем.

Начнем с перемножения числителей. Мы можем думать об этом так же, как если бы нам нужно было перемножить две скобки, содержащие алгебраические термины. Мы можем начать с умножения квадратного корня из двух 𝑥 прибавить два ℎ минус 16 с квадратным корнем из двух 𝑥 добавить два ℎ минус 16. Для этого вспомним, что квадратный корень из 𝑎, умноженный на квадратный корень из 𝑎, просто дает мы 𝑎. Таким образом, умножение этих двух членов вместе дает нам то, что мы имеем внутри квадратного корня: два 𝑥 добавить два ℎ минус 16. То же самое применимо, когда мы умножаем квадратный корень из двух 𝑥 минус 16 на квадратный корень из двух 𝑥 минус 16. Но на этот раз у нас есть минус перед одним из терминов. Поэтому нам нужно помнить об этом. Используя те же правила, что и раньше, это дает нам отрицательные два 𝑥 минус 16.

Теперь мы также можем умножить на минус квадратный корень из двух 𝑥 минус 16 на квадратный корень из двух 𝑥 добавить два ℎ минус 16. Мы можем просто написать их рядом, чтобы показать, что мы их перемножили. Это на самом деле не упрощает дальше этого. И, наконец, нам нужно умножить квадратный корень из двух 𝑥, добавить два ℎ минус 16 с квадратным корнем из двух 𝑥 минус 16.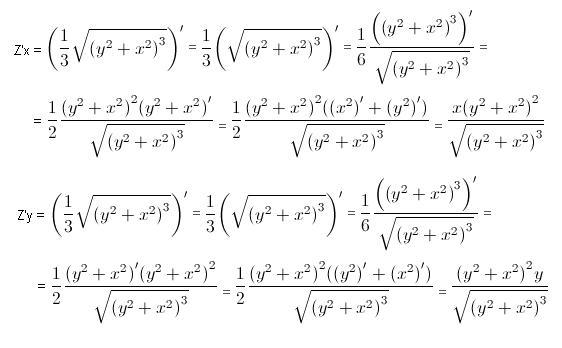 Когда мы это сделаем, мы увидим, что эти два члена на самом деле сокращаются. Итак, наш числитель просто два 𝑥 добавить два ℎ минус 16 минус два 𝑥 минус 16.

Теперь перемножим знаменатели. Мы можем просто записать это как ℎ, умноженное на квадратный корень из двух 𝑥 добавить два ℎ минус 16 добавить квадратный корень из двух 𝑥 минус 16. Давайте упростим числитель, расширив эту скобку, умножив ее на отрицательную единицу. Обратите внимание, что минус 16 становится плюсом 16. Отсюда упростим числитель. Два 𝑥 отменяются с отрицательными двумя 𝑥, а отрицательные 16 отменяются с добавлением 16. Таким образом, у нас осталось только два ℎ.

И теперь мы замечаем, что здесь мы можем что-то сократить в числителе и знаменателе. У нас есть ℎ как в числителе, так и в знаменателе. А так как ℎ приближается к нулю, а не равно нулю, то это нормально. И поскольку ℎ в знаменателе умножается на все в знаменателе, мы можем отменить это. Итак, давайте теперь применим предел, когда ℎ приближается к нулю.