Производная котангенс: Производная котангенса (ctgx)’

x*y*cos(z)

Подробнее про Производная функции.

Указанные выше примеры содержат также:

• модуль или абсолютное значение: absolute(x) или |x|
• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
• другие тригонометрические и гиперболические функции:
  секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x)
• функции округления:
  в меньшую сторону floor(x), в большую сторону ceiling(x)
• знак числа:
  sign(x)
• для теории вероятности:
  функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x)
• Факториал от x:
  x! или factorial(x)
• Гамма-функция gamma(x)
• Функция Ламберта LambertW(x)
• Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)

Правила ввода

Можно делать следующие операции

2*x

— умножение

3/x

— деление

x^2

— возведение в квадрат

x^3

— возведение в куб

x^5

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

Действительные числа

вводить в виде 7. 5, не 7,5

Постоянные

pi

— число Пи

e

— основание натурального логарифма

i

— комплексное число

oo

— символ бесконечности

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Все школьные темы по для 10 класса | Wika

Loading

Навигация по разделам

• Введение
• Делимость чисел
• Векторы, действия с векторами
• Квадратные уравнения
• Преобразование тригонометрических выражений
• Тригонометрия
• Тригонометрические уравнения
• Комплексные числа
• Производная и её применение
• Дифференциальное исчисление
• Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
• Тригонометрические функции
• Комбинаторика и вероятность
• Числовые функции
• Производная
• Треугольник Паскаля
• Синус и косинус. Тангенс и котангенс. Свойства и графики тригонометрических функций
• Математический анализ
• Вероятность
• Тригонометрическая форма записи комплексного числа

Введение

Правила умножения натуральных чисел

Делимость чисел

Какие признаки делимости чисел существуют

Какие числа называют составными в математике

Векторы, действия с векторами

Понятие числовых прямых в алгебре

Квадратные уравнения

Что нужно знать о квадратных уравнениях— основные сведения

Преобразование тригонометрических выражений

Как решать тригонометрические уравнения, сводящиеся к квадратным — примеры

Что такое формула двойного аргумента — какие формулы бывают

Тригонометрия

Четная или нечетная функция арккотангенс

Однородные тригонометрические уравнения первого и второго порядка

Тригонометрические уравнения

Как решить простейшее тригонометрическое уравнение — 10 класс

Комплексные числа

Основные сведения о координатной плоскости

Подробное решение задачи с комплексными числами

Основные сведения о комплексных числах, их применение

Производная и её применение

Вывод уравнения касательной к графику функции

Нахождение уравнения касательной к функции

Дифференциальное исчисление

Как можно дифференцировать сложную функцию, теория и примеры

Таблица основных формул дифференцирования

Соотношения между сторонами и углами треугольника.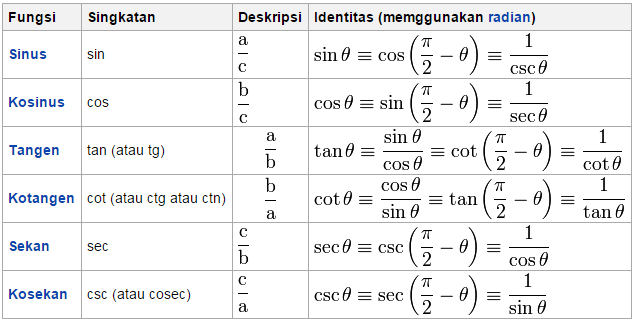

Тригонометрические тождества

Тригонометрические функции

Тригонометрические функции числового аргумента

Синус и косинус

Свойства функции y=cos(x) и построение графика

Основные сведения о решении уравнения У sin Х

Комбинаторика и вероятность

Основные сведения о факториалах, примеры решения задач

Объяснение и решение формулы бинома Ньютона простыми словами

Числовые функции

Обратная функция

Производная

Область значения функции

Понятие предела функции на бесконечности

Треугольник Паскаля

Основные сведения о треугольнике Паскаля — применение в математике

Синус и косинус. Тангенс и котангенс. Свойства и графики тригонометрических функций

Четность и нечетность функции

Функция y = tgx

Определение числовой окружности в математике

Математический анализ

Основные сведения о монотонности функции

Вероятность

Основные сведения о наступлении вероятности противоположного события

Тригонометрическая форма записи комплексного числа

Какая форма записи комплексного числа называется тригонометрической

Производные от Sec, Csc и Cot: расчет

Говорить о тригонометрических функциях все равно, что говорить о фильме или сериале. Вы сразу придумываете имена главных героев шоу! Но как насчет некоторых второстепенных персонажей? Они так же важны, как и другие персонажи истории, просто у них меньше экранного времени.

Сказав это, наверное, когда вы говорите о тригонометрических функциях, на ум приходят функции синуса и косинуса, а может быть, и функция тангенса. Но всего у нас шесть тригонометрических функций! Пришло время уделить немного экранного времени функциям секанса, косеканса и котангенса.

Функция секанса, а также функции косеканса и котангенса вместе известны как обратные функции , потому что они обратны основным тригонометрическим функциям. Здесь вы узнаете, как найти производную каждого из них.

Производная функции секущей сек

Функция секанса является обратной функцией косинуса.

Функция секанса обозначается как

\[\sec{x}\]

и является обратной величиной функция косинуса , то есть

\[\sec{x}=\frac{1}{\cos{x}}.\]

Чтобы найти производную функции секущей, вы можете использовать производную косинуса функция и факторное правило. Начните с записи функции секущей в терминах функции косинуса, то есть

\[\sec{x}=\frac{1}{\cos{x}}.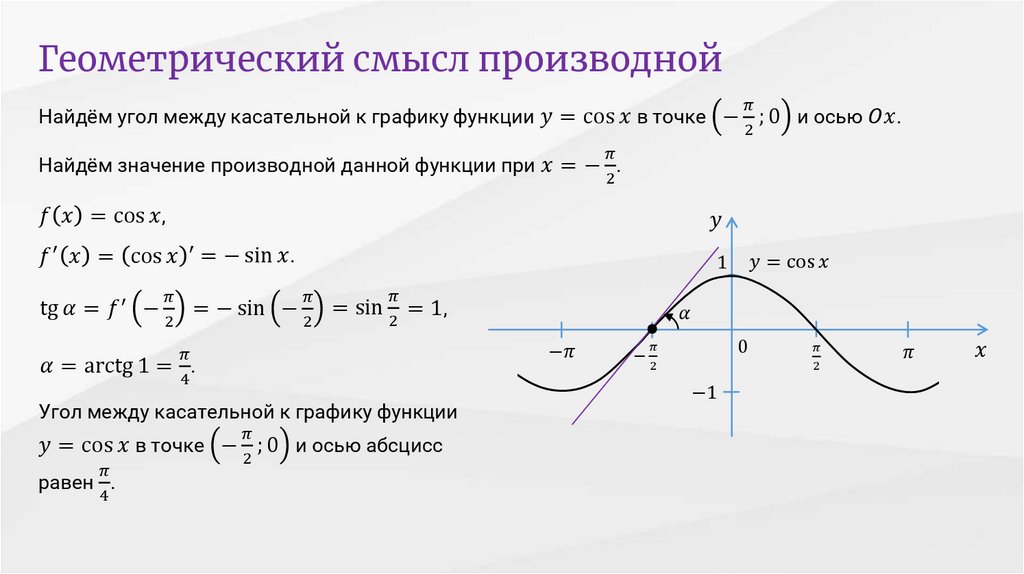 2{x}}. \конец{выравнивание}\] 92{x}} \\ &= \left( \frac{1}{\cos{x}} \right) \left(\frac{\sin{x}}{\cos{x}} \right). \end{align}\]

На последнем шаге вы можете снова переписать обратную величину косинуса как секанс, а также использовать тригонометрическое тождество

\[\frac{\sin{x}}{\ cos{x}}=\tan{x},\]

получение

\[ \frac{\mathrm{d}}{\mathrm{d}x}\sec{x} = (\sec{x} )(\tan{x}).\]

Вышеприведенное выражение обычно встречается в таблицах производных, просто написанных без круглых скобок. Это дает вам формулу для производной секущей функции.

Производная функции секущей равна

\[ \frac{\mathrm{d}}{\mathrm{d}x}\sec{x} = \sec{x}\,\tan{x}.\ ]

Производная функции котангенса cot

Пришло время перейти к функции котангенса, которая является обратной функцией тангенса.

Функция котангенса обозначается как

\[\cot{x}\]

и является обратной величиной функции тангенса , , которая равна

\[\cot{x}=\frac{1 }{\тан{х}}. \]

Одной из особенностей функций тангенса и котангенса является то, что они также могут быть записаны как рациональные функции с использованием функций синуса и косинуса, как показано на одном из шагов, необходимых для нахождения производной функции секанса. Для функции тангенса вы можете написать

\[\tan{x}=\frac{\sin{x}}{\cos{x}}.\]

Поскольку функция котангенса является обратной функцией тангенса , вы также можете найти функцию котангенса, записанную как рациональную функцию, используя функции синуса и косинуса, то есть

\[\begin{align} \cot{x} &= \frac{1}{\tan{x}} \\ &= \frac{1}{\frac{\sin{x}}{\cos {Икс}}}. \end{align}\]

Используя свойства дробей, вы можете записать это как

\[\cot{x}=\frac{\cos{x}}{\sin{x}},\]

это означает, что функция котангенса также может быть записана как частное функции косинуса и функции синуса.

Вы можете использовать приведенное выше тождество, чтобы найти производную функции котангенса. Поскольку это частное двух функций, вам нужно будет использовать правило отношения, поэтому 92{x}. \]

Производная функции косеканса csc

Наконец, вы также найдете обратную функцию синуса.

Функция косеканса обозначается как

\[\csc{x}\]

и является обратной величиной функции синуса , то есть

\[\csc{x}=\frac{1 }{\sin{x}}.\]

Вы можете найти производную функции косеканса точно так же, как и с функцией секанса. Начните с записи функции косеканса через функцию синуса, 92{x}} \\ &= -\left(\frac{1}{\sin{x}} \right) \left(\frac{\cos{x}}{\sin{x}} \right) .\end{align}\]

Наконец, перепишем обратное выражение и воспользуемся функцией котангенса, так что

\[\frac{\mathrm{d}}{\mathrm{d}x}\csc{x} = — (\csc{x})(\cot{x}).\]

И снова вы, скорее всего, обнаружите, что формула написана без круглых скобок.

Производная функции косеканса равна

\[\frac{\mathrm{d}}{\mathrm{d}x}\csc{x}=-\csc{x}\,\cot{x}. \]

Производная функции арксеканса

Вы видели, что функция секанса является обратной величиной функции косинуса. {-1}{x},\]

, где вы должны иметь в виду, что \(-1\) — это , а не показатель степени, он используется для обозначения обратной функции.

Не забывайте, что обратное число , а не , то же самое, что обратное число .

Всякий раз, когда вы говорите об обратных функциях, вы должны быть осторожны с их доменом. Для функции арксеканса вы должны учитывать, что выходы функции секанса таковы, что\[ |\sec{x}| \geq 1, \]

, поэтому областью определения функции арксеканса будут все числа, абсолютное значение которых больше или равно \(1\), то есть

\[ (-\infty,-1] \cup [1,\infty).\]

Кроме того, поскольку функция секанса является периодической функцией, можно получить один и тот же результат на двух разных входах. Чтобы убедиться, что арксеканс является функцией, этот диапазон должен быть ограничен, и обычно его выходы находятся между \(0\) и \(\pi\), за исключением \(\frac{\pi {2}\), поэтому

\[ 0 \leq \mathrm{arcsec}{\, x} \leq \pi, \text{where,}\, \mathrm{arcsec}{\, x} \neq \frac{\pi}{2}. \pi/_2\), за исключением \(0 \). это 92,\]

, поэтому цепное правило говорит вам, что

\[ f'(x)= \frac{\mathrm{d}}{\mathrm{d}u}\sec{u} \frac{\mathrm {d}u}{\mathrm{d}x}.\]

Используя правило степени, вы получаете

\[ \frac{\mathrm{d}u}{\mathrm{d}x} = 4x ,\]

, поэтому

\[f'(x)=\left(\frac{\mathrm{d}}{\mathrm{d}u} \sec{u} \right) (4x), \]

Теперь используйте производную функции секанса, что даст вам

\[ f'(x) = (\sec{u}\,\tan{u}) (4x).\]

Наконец, подставьте обратно \ (u\) и переставить, то есть 92}.\]

Вы также можете использовать правило произведения для нахождения производных обратных тригонометрических функций!

Найдите производную от

\[ g(x) = x\cot{x}.\]

Решение:

Здесь вам нужно будет использовать правило произведения, то есть

\[ g’ (x) = \ left (\ frac {\ mathrm {d}} {\ mathrm {d} x} x \ right) \ cot {x} + x \ left ( \ frac {\ mathrm {d}} {\ mathrm {d}x}\cot{x} \right). \]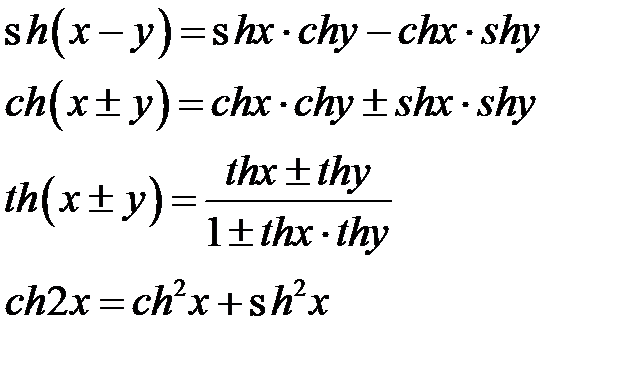

Затем используйте степенное правило и производную функции котангенса, так что 9{\csc{х}}\csc{х}\,\кроватка{х}. \end{align}\]

Производные sec, csc и cot — Основные выводы

• Функции секанса, косеканса и котангенса вместе известны как обратные тригонометрические функции.
  • Функция секанса является обратной функцией косинуса, \[\sec{x}=\frac{1}{\cos{x}}.\]
  • Функция косеканса является обратной функцией синуса, \ [\csc{x}=\frac{1}{\sin{x}}.\]
  • Функция котангенса является обратной величиной функции тангенса, \[\cot{x}=\frac{1}{\ тан{х}}.\] 92{x}.\]
• Обратные тригонометрические функции, также известные как аркус-функции, являются обратными функциями тригонометрических функций. Обратные тригонометрические функции , а не такие же, как обратные тригонометрические функции.
• Производные обратных тригонометрических функций могут быть получены с помощью неявного дифференцирования и некоторых тригонометрических тождеств.

  No related posts.