Производная от e 2 x: Найти производную y’ = f'(x) = e^(2*x) (e в степени (2 умножить на х))

px, em, rem и другие

В этом очерке я постараюсь не только рассказать о различных единицах измерения, но и построить общую картину – что и когда выбирать.

Пиксель px – это самая базовая, абсолютная и окончательная единица измерения.

Количество пикселей задаётся в настройках разрешения экрана, один px – это как раз один такой пиксель на экране. Все значения браузер в итоге пересчитает в пиксели.

Пиксели могут быть дробными, например размер можно задать в 16.5px. Это совершенно нормально, браузер сам использует дробные пиксели для внутренних вычислений. К примеру, есть элемент шириной в 100px, его нужно разделить на три части – волей-неволей появляются 33.333...px. При окончательном отображении дробные пиксели, конечно же, округляются и становятся целыми.

Для мобильных устройств, у которых много пикселей на экране, но сам экран маленький, чтобы обеспечить читаемость, браузер автоматически применяет масштабирование.

Достоинства

• Главное достоинство пикселя – чёткость и понятность

Недостатки

• Другие единицы измерения – в некотором смысле «мощнее», они являются относительными и позволяют устанавливать соотношения между различными размерами

Существуют также «производные» от пикселя единицы измерения: mm, cm, pt и pc, но они давно отправились на свалку истории.

Вот, если интересно, их значения:

• 1mm (мм) = 3.8px
• 1cm (см) = 38px
• 1pt (типографский пункт) = 4/3 px
• 1pc (типографская пика) = 16px

Так как браузер пересчитывает эти значения в пиксели, то смысла в их употреблении нет.

В реальной жизни сантиметр – это эталон длины, одна сотая метра. А пиксель может быть разным, в зависимости от экрана.

Но в формулах выше под пикселем понимается «сферический пиксель в вакууме», точка на «стандартизованном экране», характеристики которого описаны в спецификации.

Поэтому ни о каком соответствии cm реальному сантиметру здесь нет и речи. Это полностью синтетическая и производная единица измерения, которая не нужна.

1em – текущий размер шрифта.

Можно брать любые пропорции от текущего шрифта: 2em, 0.5em и т.п.

Размеры в em – относительные, они определяются по текущему контексту.

Например, давайте сравним px с em на таком примере:

<div>
  Страусы
  <div>Живут также в Африке</div>
</div>

24 пикселей – и в Африке 24 пикселей, поэтому размер шрифта в <div>

одинаков.

А вот аналогичный пример с em вместо px:

<div>
  Страусы
  <div>Живут также в Африке</div>
</div>

Так как значение в em высчитывается относительно текущего шрифта, то вложенная строка в 1. 5 раза больше, чем первая.

Выходит, размеры, заданные в em, будут уменьшаться или увеличиваться вместе со шрифтом. С учётом того, что размер шрифта обычно определяется в родителе, и может быть изменён ровно в одном месте, это бывает очень удобно.

Что такое «размер шрифта»? Это вовсе не «размер самой большой буквы в нём», как можно было бы подумать.

Размер шрифта – это некоторая «условная единица», которая встроена в шрифт.

Она обычно чуть больше, чем расстояние от верха самой большой буквы до низа самой маленькой. То есть, предполагается, что в эту высоту помещается любая буква или их сочетание. Но при этом «хвосты» букв, таких как

р, g могут заходить за это значение, то есть вылезать снизу. Поэтому обычно высоту строки делают чуть больше, чем размер шрифта.

В спецификации указаны также единицы ex и ch, которые означают размер символа "x" и размер символа "0".

Эти размеры присутствуют в шрифте всегда, даже если по коду этих символов в шрифте находятся другие значения, а не именно буква "x" и ноль "0". В этом случае они носят более условный характер.

Эти единицы используются чрезвычайно редко, так как «размер шрифта» em обычно вполне подходит.

Проценты %, как и em – относительные единицы.

Когда мы говорим «процент», то возникает вопрос – «Процент от чего?»

Как правило, процент будет от значения свойства родителя с тем же названием, но не всегда.

Это очень важная особенность процентов, про которую, увы, часто забывают.

Отличный источник информации по этой теме – стандарт, Visual formatting model details.

Вот пример с %, он выглядит в точности так же, как с em:

<div>
  Страусы
  <div>Живут также в Африке</div>
</div>

В примере выше процент берётся от размера шрифта родителя.

А вот примеры-исключения, в которых % берётся не так:

margin-left

При установке свойства margin-left в %, процент берётся от ширины родительского блока, а вовсе не от его margin-left.

line-height

При установке свойства line-height

в %, процент берётся от текущего размера шрифта, а вовсе не от line-height родителя. Детали по line-height и размеру шрифта вы также можете найти в статье Свойства font-size и line-height.

width/height

Для width/height обычно процент от ширины/высоты родителя, но при position:fixed, процент берётся от ширины/высоты окна (а не родителя и не документа). Кроме того, иногда % требует соблюдения дополнительных условий, за примером – обратитесь к главе Особенности свойства height в %.

Итак, мы рассмотрели:

• px – абсолютные, чёткие, понятные, не зависящие ни от чего.
• em – относительно размера шрифта.
• % – относительно такого же свойства родителя (а может и не родителя, а может и не такого же – см. примеры выше).

Может быть, пора уже остановиться, может этого достаточно?

Э-э, нет! Не все вещи делаются удобно.

Вернёмся к теме шрифтов. Бывают задачи, когда мы хотим сделать на странице большие кнопки «Шрифт больше» и «Шрифт меньше». При нажатии на них будет срабатывать JavaScript, который будет увеличивать или уменьшать шрифт.

Вообще-то это можно сделать без JavaScript, в браузере обычно есть горячие клавиши для масштабирования вроде Ctrl++, но они работают слишком тупо – берут и увеличивают всю страницу, вместе с изображениями и другими элементами, которые масштабировать как раз не надо. А если надо увеличить только шрифт, потому что посетитель хочет комфортнее читать?

Какую единицу использовать для задания шрифтов? Наверно не px, ведь значения в px абсолютны, если менять, то во всех стилевых правилах. Вполне возможна ситуация, когда мы в одном правиле размер поменяли, а другое забыли.

Следующие кандидаты – em и %.

Разницы между ними здесь нет, так как при задании font-size в процентах, эти проценты берутся от font-size родителя, то есть ведут себя так же, как и em.

Вроде бы, использовать можно, однако есть проблема.

Попробуем использовать этот подход для <li>.

Протестируем на таком списке:

<ul>
<li>Собака
  <ul>
  <li>бывает
    <ul>
    <li>кусачей
      <ul>
      <li>только
        <ul>
        <li>от жизни
          <ul>
          <li>собачей</li>
          </ul>
        </li>
        </ul>
      </li>
      </ul>
    </li>
    </ul>
  </li>
  </ul>
</li>
</ul>

Пока это обычный вложенный список.

Теперь уменьшим размер шрифта до 0.8em, вот что получится:

<style>
  li {
    font-size: 0.8em;
  }
</style>
<ul>
<li>Собака
  <ul>
  <li>бывает
    <ul>
    <li>кусачей
      <ul>
      <li>только
        <ul>
        <li>от жизни
          <ul>
          <li>собачей</li>
          </ul>
        </li>
        </ul>
      </li>
      </ul>
    </li>
    </ul>
  </li>
  </ul>
</li>
</ul>

Проблема очевидна. Хотели, как лучше, а получилось… Мелковато. Каждый вложенный <li> получил размер шрифта 0.8 от родителя, в итоге уменьшившись до нечитаемого состояния. Это не совсем то, чего мы бы здесь хотели.

Можно уменьшить размер шрифта только на одном «корневом элементе»… Или воспользоваться единицей

rem, которая, можно сказать, специально придумана для таких случаев!

Единица rem задаёт размер относительно размера шрифта элемента <html>.

Как правило, браузеры ставят этому элементу некоторый «разумный» (reasonable) размер по умолчанию, который мы, конечно, можем переопределить и использовать rem для задания шрифтов внутри относительно него:

<style>
  html {
    font-size: 14px;
  }
  li {
    font-size: 0.8rem;
  }
</style>
<div><button>Кликните, чтобы увеличить размер шрифта</button></div>
<img src="https://js.cx/clipart/angry_dog. png">
<ul>
<li>Собака
  <ul>
  <li>бывает
    <ul>
    <li>кусачей
      <ul>
      <li>только
        <ul>
        <li>от жизни
          <ul>
          <li>собачей</li>
          </ul>
        </li>
        </ul>
      </li>
      </ul>
    </li>
    </ul>
  </li>
  </ul>
</li>
</ul>
<script>
let html = document.documentElement;
up.onclick = function() {
  // при помощи JS увеличить размер шрифта html на 2px
  html.style.fontSize = parseInt(getComputedStyle(html, '').fontSize) + 2 + 'px';
};
</script>

Получилось удобное масштабирование для шрифтов, не влияющее на другие элементы.

Элементы, размер которых задан в rem, не зависят друг от друга и от контекста – и этим похожи на px, а с другой стороны они все заданы относительно размера шрифта <html>.

Единица rem не поддерживается в IE8-.

Во всех современных браузерах, исключая IE8-, поддерживаются новые единицы из черновика стандарта CSS Values and Units 3:

• vw – 1% ширины окна
• vh – 1% высоты окна
• vmin – наименьшее из (vw, vh), в IE9 обозначается vm
• vmax – наибольшее из (vw, vh)

Эти значения были созданы, в первую очередь, для поддержки мобильных устройств.

Их основное преимущество – в том, что любые размеры, которые в них заданы, автоматически масштабируются при изменении размеров окна.

Этот текст написан с размером `5vh`.

Вы сможете легко увидеть, как работает vh, если поменяете высоту окна браузера. Текст выше будет расти/уменьшаться.

Мы рассмотрели единицы измерения:

• px – абсолютные пиксели, к которым привязаны и потому не нужны mm, cm, pt и pc. Используется для максимально конкретного и точного задания размеров.
• em – задаёт размер относительно шрифта родителя, можно относительно конкретных символов: "x"(ex) и "0"(ch), используется там, где нужно упростить масштабирование компоненты.
• rem – задаёт размер относительно шрифта <html>, используется для удобства глобального масштабирования: элементы которые планируется масштабировать, задаются в rem, а JS меняет шрифт у <html>.
• % – относительно такого же свойства родителя (как правило, но не всегда), используется для ширин, высот и так далее, без него никуда, но надо знать, относительно чего он считает проценты.
• vw, vh, vmin, vmax – относительно размера экрана.

-2x?

Производная от e к x относительно переменной x равна e ^-2x . Обозначается d/dx (e ^-2x ). Это скорость изменения показательной функции e, и она всегда равна самой показательной функции.

Производная е

^-2x формула

Формула производной е куба х равна показательной функции е, то есть;

d/dx (ex) = e ^-2x

Как доказать производную от e

^-2x ?

Существует множество способов получения производных e ^-2x . Следовательно, мы можем доказать производную e ^-2x , используя;

1. Первый принцип

2. Правило продукта

3. Частное правило

Производная от e

^-2x по первому принципу

Производная функции по первому принципу относится к нахождению общего выражения для наклона кривой с помощью алгебры. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна

f(x)=lim f(x+h)-f(x)/h

Доказательство производной e

^-2x по первому принципу

Чтобы доказать производную e по первому принципу, замените f (х) по эл. f(x)=lim _h→0 f(x+h)-f(x)/h

f(x) = lim e ^-2(x+h) — e ^-2x /h

Кроме того,

f(x) = lim e ^-2x .e ^-2h — e ^-2x /h

Принимая e ^-2x общее as;

f(x) = lim e ^-2x (e ^-2h — 1)/h

Еще больше упрощения,

f(x) = -e ^-2x .lim (e ^-2h — 1)/-h

Когда h приближается к нулю,

f(x) = -2e ^-2x lim (e ⁰ — 1)/-2h

f(x) = -2e ^-2x f(0)

Следовательно,

f(x ) = -2e ^-2x

Следовательно, производная от e ^-x также может быть рассчитана с использованием первого принципа.

Производное от e

^-2x по правилу произведения

Производную от e можно вычислить с помощью правила произведения, поскольку функция косинуса может быть записана как комбинация двух функций. Правило произведения производных определяется как;

[uv] = u. v +u.v

Доказательство производной e

^-2x по правилу произведения

Чтобы доказать производную e по правилу произведения, предположим, что

f(x) = 1. e ^-2x

Используя правило дифференцирования произведения,

f(x) = (e ^{-2x 9-2x, мы можем записать это,}

f(x) = e ^-2x /1 = u/v

Предположим, что u = e ^-2x и v = 1. Теперь по правилу частных,

f (x) = (vu — uv)/v ²

f(x) = [d/dx(e ^-2x ) — e ^-2x .d/dx(1)] / (1) ²

= [-2e ^-2x ] / 1

= -e ^-2x

Следовательно, мы получили производную от e ^-2x , используя правило дифференцирования.

Как найти производную от e

^-2x с помощью калькулятора?

Самый простой способ вычислить производную e — использовать онлайн-инструмент. Для этого вы можете воспользоваться нашим калькулятором производных. Здесь мы предлагаем вам пошаговый способ расчета производных с помощью этого инструмента.

1. Запишите функцию как e ^-2x в поле ввода функции. На этом шаге вам необходимо указать входное значение в виде функции, так как вы должны вычислить производную e ^-2x .

2. Теперь выберите переменную, по которой вы хотите дифференцировать e ^-2x . Здесь вы должны выбрать х.

3. Выберите, сколько раз вы хотите отличить e ^-2x от x. На этом шаге вы можете выбрать 2 для второй производной, 3 для третьей производной и так далее.

4. Нажмите кнопку расчета. После этого шага вы получите производную от e ^-2x в течение нескольких секунд.

92x

Производная e2x является второй производной функции ex2x. Скорость изменения функции называется скоростью изменения. Это не отрицательное число, и его можно вычислить. Чтобы найти производную от e2x, воспользуемся цепным правилом. Используя цепное правило, мы можем вычислить f (x) = 2e2x. Затем мы можем использовать значение e2x для вычисления f (x).

Функция может иметь дифференцируемое значение, но это не означает, что она постоянна. Вы можете вычислить производную от e2x, разделив ex на e. В этом случае скорость изменения e2x равна числу изменений функции. Когда вы пытаетесь найти производную функции, вы должны знать первую производную функции и вторую производную функции.

Затем вам нужно найти n-ю производную от e2x. Это то же самое, что найти первую производную, но есть дополнительный шаг. Чтобы определить n-й член функции, нужно сначала найти ее первую производную. Для этого нужно определить его вторую производную. Также можно получить третью и четвертую производные функции. Четвертая производная такая же, как и первая, поэтому вам нужно вычислить ее несколько раз.

Когда дело доходит до нахождения производной e2x, вам нужно знать, как вычислить n-й член. Первая производная является константой, а производная e2x является ее следующей производной. Второй член является производной переменной, а не константой. Он имеет измеримое значение. Затем вы можете использовать его, чтобы найти n-й член e2x. 92x

Производная от e2x представляет собой наклон графика. Это обобщение наклона экспоненциальной функции. Он говорит нам, насколько функция изменяется в определенный момент. Обратное значение экспоненциальной функции такое же, как обращение синуса или арксинуса. Касательная линия к графику и есть график. Два термина e2x одинаковы.

Производная функции — это наклон между двумя точками. Наклон графика в точке является его производной. Его обратным является синус арксинкса. Обратной показательной функции является натуральный логарифм по основанию. Его производная представляет собой натуральный логарифм исходной функции. Это самый фундаментальный предел функции. Итак, мы можем получить значение e2x, используя определение e2x.

Производная от e2x является производной от e2x. Это наклон между двумя точками. Его обратным является натуральный логарифм основания.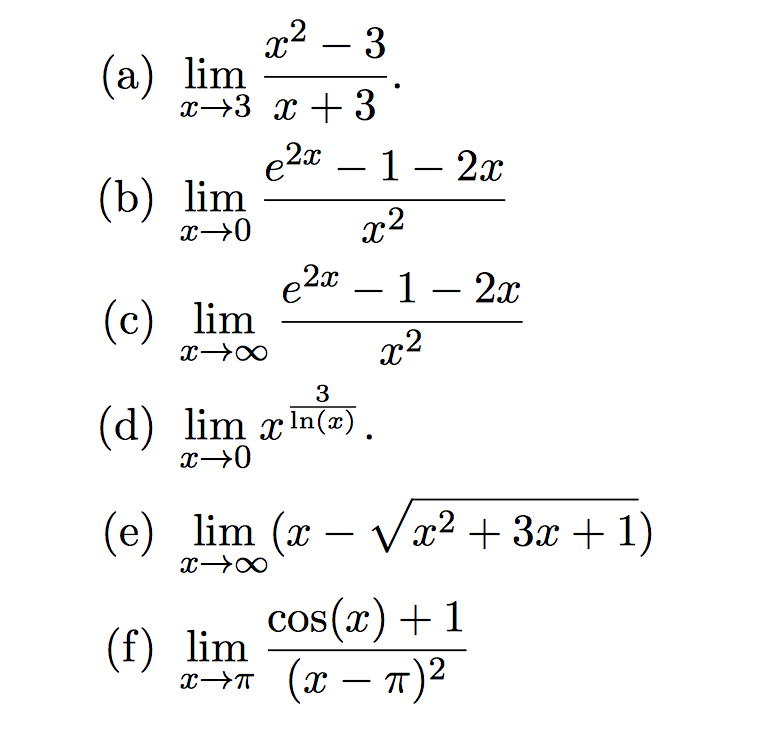 Инверсия e2x — это арксинус в точке. В общем случае отношение e2x/e2x является предельным значением функции. Если график бесконечен, значение e2x/e2nx бесконечно.

Производная e2x является полезным инструментом для количественного анализа. Он говорит о скорости изменения исходной функции. Его можно использовать для моделирования скорости изменений. Это также демонстрирует чувствительность выхода к исходной функции. Вторая производная от e2x полезна в математических моделях. Затем значение e2x меняется в зависимости от начального параметра. Поэтому полезно изучать e2x так же, как и e2x. 92x

Производная от e2x — это скорость изменения функции. Это значение известно как наклон e2x. Цепное правило используется для расчета наклона. Эту функцию можно записать в виде f(x) = e2x. Решение: f(x) = 2e2x. Мы используем термин e2x для обозначения второй производной функции.

N-я производная от e2x — это скорость, с которой e2x изменяется по отношению к x. Это также известно как n-я производная от e2x. Чтобы найти n-ю производную e2x, мы должны найти первую, вторую, третью и четвертую производные e2x. Чтобы найти конкретную производную e2x, нам нужно знать, как вычисляются первая и вторая производные.

N-я производная от e2x получается дифференцированием e2x n раз. Сначала нам нужно найти первую производную e2x. Затем нам нужно найти вторую производную, а затем третью. Четвертая производная e2x получается путем нахождения n-й производной по времени от e2x. Нам нужно найти n-ю производную e2x много раз, чтобы найти n-ю производную e2x. Как только мы поймем тренд, мы сможем легко вычислить n-ю производную e2x и решить уравнение для e2x.

После определения n-й производной от e2x мы должны найти n-ю производную от e2 x. Например, если e2x увеличивается на определенное количество секунд каждую секунду, мы могли бы найти более высокое значение e2x, взяв n-е время. После вычисления n-й производной от e2X мы должны определить, насколько сильно произошло изменение. 92x

Получив n-ю производную от e2x, мы должны найти n-ю производную от e2 n в заданной точке. Это известно как n-я производная от e2X. Это то же самое, что и n-я производная от упр. n-я производная от e2x такая же, как и n-я производная. Это означает, что e2x совпадает с e2x.

N-я производная e2x является касательной. Его можно определить с помощью правила произведения. n-я производная от e2 — это касательная, которая является касательной к e2x. Его можно получить, вычислив e2x, разделив его на n-ю степень e2x. n-я производная — это n-я степень оси e2x.

n-я производная e2x является n-й степенью e-значения x. Это n-я производная от e2x. Это умножение двух функций. Энная степень e2x обратна e2x. Следовательно, n-я степень e2x в графе является n-м членом второй степени.

Энная степень e2x является произведением двух экспоненциальных функций. N-я степень e2 — это n-я степень e2. Другими словами, n-я степень e2x может быть определена как сумма первых трех степеней e2x. Энная степень — это энная степень числа e2x. n-я степень является основанием e2x. N-я степень e2x является основанием исходной функции.

No related posts.