100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Ежегодно Институт образовательных технологий при Открытом университете Великобритании публикует доклад о десяти самых важных трендах в образовании.
По мнению авторов исследования, эти тенденции уже заметны и в будущем могут серьёзно повлиять на мировую систему образования, поэтому заслуживают пристального внимания.
Как эти тренды будут реализованы на постсоветском пространстве и какой отклик они найдут у учащихся? Об этом на международной образовательной конференции Global Impact Conference рассказала Диана Королёва, заведующая лабораторией инноваций в образовании при российской Высшей школе экономики.
Тренд 1. Гибридное обучение
В чём суть. Учащиеся чередуют очные занятия с онлайн-уроками.
Проблемы, выявленные ВШЭ:
- Не везде есть соответствующая инфраструктура.
- Учителя не умеют работать в онлайн-форматах.
Чтобы применять гибридное обучение, должна поменяться методика преподавания. Педагогам нужно будет научиться управлять вниманием учеников и по-новому выстраивать занятия.
Лекцию по видеосвязи нельзя считать гибридным обучением. Это должна быть не просто цифровизация, когда мы переносим обычные классные занятия в онлайн-формат, а трансформация всего образовательного процесса. Иначе на уроках будет «говорящая голова» учителя по видео и зевающие ученики.
Тренд 2. Образовательные курсы вместо поступления в вузы
В чём суть. Сегодня не все готовы инвестировать в университетское образование. Вместо этого люди всё чаще выбирают краткосрочные курсы, которые позволяют им быстро получить новые знания, чтобы трудоустроиться или повысить свою квалификацию. Это уже давно распространено в программировании, юриспруденции или психологии. Такая тенденция будет распространяться и на другие сферы.
Проблемы:
- Курсы не смогут заменить долгосрочное образование.
- Выбор курсов большой, поэтому сложно найти нужный, полезный и тот, который впечатлит работодателя.
- Не все умеют планировать своё время. Есть вероятность начать несколько разных курсов и не закончить ни один.
Тренд 3. Совмещение учёбы с практикой
В чём суть. Студенты учатся и одновременно работают на предприятиях или в компаниях по их специализации, чтобы не отставать от всё время меняющихся технологий.
Проблемы:
- В исследовании ВШЭ отмечается, что не все педагоги готовы к такому формату. Одно дело прочитать теоретическую лекцию и спокойно уйти домой, другое – быть постоянно на связи со студентами и менять подход к образованию.
- Не у всех работодателей есть желание учить студентов. Чаще этот тренд распространён в сфере IT – там, где компании знают, что студенты пойдут работать именно к ним.
Тренд 4. Обучение с помощью инфлюенсеров
В чём суть. В последнее время многие блогеры и инфлюенсеры стали предлагать образовательный контент.
Это могут быть подкасты о маркетинге или видео в Youtube о законах физики. Они размывают грань между обучением и развлечением, что очень нравится людям.
Проблема: качество такого контента не всегда высокое.
Перспективы: если талантливые учителя научатся использовать соцсети и инструменты инфлюенсеров, они смогут привлечь к себе больше учащихся, сделать процесс обучения доступным и интересным для нового поколения. Это повысит статус учителя, к которому сейчас ученики не всегда относятся с уважением и восхищением, предположили в ВШЭ.
Тренд 5. Индивидуальные образовательные программы
В чём суть. Учащийся сам планирует свою образовательную траекторию – ставит себе цель, выбирает для её достижения дисциплины из списка, в какой последовательности их изучать и с каким темпом, даёт оценку своим результатам.
Это часто практикуется в вузах, но применимо и в школах. К примеру, детям могут на выбор дать задания разной сложности, проекты под их интересы, элективы или темы для изучения (какое произведение из выбранных хотите прочесть?), чтобы лучше раскрыть потенциал и талант ребёнка.
Проблема: когда каждый студент формирует свою уникальную траекторию, сложнее сравнивать уровень знаний учащихся и оценивать их.
Тренд 6. Повышение психологической грамотности учащихся
В чём суть. В школах и вузах вводятся предметы или темы, которые повышают психологическую грамотность учеников, обучают их основам самодиагностики и самопомощи, а также рассказывают, где и когда можно получить помощь.
Проблемы:
- обращение к психологу у нас до сих пор считается чем-то постыдным;
- низкое качество подготовки школьных психологов;
- отсутствие какой-либо психологической помощи учителям.
Тренд 7. Учёт домашней среды во время обучения
В чём суть. При выстраивании образовательного процесса учитель задумывается о том, как обстоят дела в семье ученика, с какими проблемами он сталкивается дома, чему его там учат.
Например, если он знает, что у ребёнка нет родителя, а на уроке будет обсуждаться тема семьи, учитель может скорректировать урок таким образом, чтобы ребёнку было более комфортно.
Или педагог, зная что ученик испытывает дома какую-то проблему (например, плохие отношения с родителями), может затронуть подобную тему на уроке, чтобы помочь ребёнку справиться с ней.
Проблемы:
- нельзя сделать этот процесс персонализированным, учителя могут видеть только общую картину своего класса;
- такие методы обучения должны быть выполнены профессионально, иначе это психологически небезопасно;
- активное вмешательство школы в семейное пространство может навредить отношениям между учениками, родителями и учителями;
- у учеников может появиться чувство, что за ними следят или нарушают их личные границы.
Тренд 8. Совместный просмотр видео
В чём суть. Учащиеся вместе смотрят видео, участвуют в его обсуждении, делятся мнениями, отвечают на вопросы. Это позволяет развить образную грамотность учащегося и развить его коммуникативные навыки.
Возможен и такой формат, когда фильм предлагают посмотреть заранее, в удобное для учащегося время, а потом собраться вместе и обсудить.
Проблемы:
- Ученик при таком подходе остаётся пассивным. Для развития творческих навыков и критического мышления полезнее будет совместное создание видео или подбор видеоматериалов учеником, считают в ВШЭ.
- Ученики часто отвлекаются, поэтому для учёбы удобнее смотреть короткие видео под конкретные цели.
- Не все учителя могут правильно использовать кинопросмотр и выстраивать диалог для обсуждения увиденного.
Тренд 9. Обсуждение острых тем и своих эмоций
В чём суть. Когда учитель на уроках обсуждает с учащимися деликатные темы, вроде социального неравенства, дискриминации, школьной травли, ученики могут открыто говорить о своих чувствах. Вместе с педагогом они стараются исследовать и критически осмысливать эти негативные эмоции, чтобы потом корректировать своё поведение.
Проблемы:
- Дети у нас не привыкли делиться эмоциями, раскрываться перед учителем и другими детьми, и подобного рода обсуждения могут делать их достаточно уязвимым в коллективе.
- Без специальной подготовки обсуждение тем социального неравенства, угнетения и так далее может носить популистский характер и выражать личное мнение педагога, без реальной педагогической составляющей и психологической помощи ученикам, отмечается в докладе ВШЭ.
Тренд 10. Обучение во время прогулок
В чём суть. Родители всё больше обеспокоены тем, что их дети ведут сидячий образ жизни и мало общаются со сверстниками. Поэтому приобретают актуальность прогулки на воздухе, походы и экскурсии вместо обычных занятий в классе.
Проблема: подходит не для всех предметов. Если это урок экологии или истории искусства, то это работает. Но в остальных случаях практически не применяется.
Выводы: в сфере образования стали появляться тренды, которые нацелены на улучшение психологического здоровья учеников и решение социальных конфликтов. На постсоветском пространстве это не очень развито, и есть множество проблем, которые нужно решить, чтобы внедрить такие новшества.
По мнению экспертов из ВШЭ, развитие получат гибридное обучение, совмещение учёбы и практики, всевозможные курсы и проектирование собственного образовательного пути.
Источник: https://informburo.kz
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Математическая сцена — Функции 2 — Урок 5
Математическая сцена — Функции 2 — Урок 5 — Вторая производная| 2009 Расмус Эф и Джанн Сак | Функции 2 |
Урок 5
Если мы продифференцируем функцию, а затем
продифференцировав производную, мы получим то, что называется второй производной.
Если исходная функция называется f(x), мы находим f(x)
а затем продифференцируйте f(x) . Результат записывается f(x) .
Пример 1
Найдите вторую производную из следующих функций:
а) f(x) = х 3 + х 2 + х + 1
f(x) = 3x 2 + 2x + 1
f(x) = 6x + 2
б) f(x) = х 4 + х 3 + х 1 + 1
f(x) = 4x 3 + 3x 2 x 2
f(x) = 12x 2 + 6x + 2x 3
в) f (х) = грех х
f(x) = cos x
f(x) = sin x
г) f(x) = cos x
f(x) = sin x
f(x) = cos x
д) f(x) = e x
f(x) = e x
f(x) = e x
е) f(x) = ln x
f(x) = 1/x = x 1
f(x) = x 2
Если мы определим функцию f(t) как положение
объект в момент времени t мы получаем следующие определения в физике.
f(t) — положение объект по истечении времени t.
f(t) дает нам скорость объекта в момент времени t.
f(t) дает ускорение тела в момент времени t.
Скорость – это мера изменение положения в единицу времени. Ускорение является мерой изменения по скорости в единицу времени.
Если f(t) измеряется в метров и t в секундах, тогда f(t) измеряется в м /с, а f(t) в м /с 2 .
Пример 2
Когда стрела выпущена вертикально в воздух, мы
можно найти функцию h(t), которая определяет высоту стрелки над землей в точке
время т. Эта функция зависит от различных факторов, таких как прочность
стрелок и тип лука и стрелы.
Следующая функция дает высоту h кончика стрелки в
метров, t секунд после выстрела из лука.
h(t) = 4,9t 2 + 24,5t + 2,4.
а) Найти время, за которое стрела упадет на землю.
Представьте себе систему координат с высотой h на
по вертикальной оси (y) и время t по горизонтальной оси (x).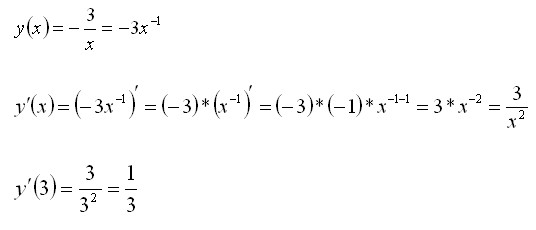 Представьте, что стрелок стоит у истока системы, а наводка
стрелы выходит из лука на высоте 2,4 м. Стрелка идет вверх и снова опускается, достигая земли когда высота h равна 0. Для решения задачи нужно найти, когда высота функция h(t) = 0. Мы можем сделать это с помощью калькулятора или квадратичная формула. |
Значение t ≈ 0 не совсем точно, так как мы начинаем измерять
момент, когда стрела находится на высоте 2,4 м.
Другое значение t говорит нам, что стрелка
ударяется о землю через 5 секунд.
б) Теперь рассчитаем высоту, на которую достигает стрелка.
Стрела замедляется, когда она поднимается и достигает максимальной высоты, когда скорость равна нулю. h(t) дает скорость в момент времени t. Итак, мы нужно найти h(t) и решить уравнение h(t) = 0,
h(t) = 9,8t + 24,5 = 0
9,8т = 24,5
t = 24,5 / 9,8 = 2,5 с
Мы
сделать вывод, что стрелка достигает максимальной высоты через 2,5 секунды.
Сейчас мы
можно использовать формулу для h(t), чтобы найти максимальную высоту.
ч(2,5) = 4,92,5 2 + 24,52,5 + 2,4 = 33,025 м
Стрела достигает высоты 33 м .
в) Теперь найдем ускорение, снова дифференцируя.
h(t) = 9,8t + 24,5
h(t) = 9,8 м/с 2
Это очень важно результат, значение, которое дает ускорение из-за гравитационного поля Земля. Отрицательное значение связано с тем, что стрелка замедляется.
Давайте посмотрим, что
информацию, которую вторая производная дает нам о графике функции.
первая производная говорит нам о наклоне графика. Если производная
положительный наклон увеличивается, если отрицательный наклон уменьшается.
Вторая производная говорит нам, как изменяется наклон. Если вторая производная
положительный, это означает, что наклон графика увеличивается, если отрицательный наклон
уменьшается.
При изменении знака второй производной с положительного на отрицательный
означает, что градиент перестает увеличиваться и начинает уменьшаться.
Другими словами,
график меняется с выпуклого (изгибающегося вверх) на вогнутого (изгибающегося вниз).
Обратное происходит, когда вторая производная изменяется с отрицательной на
положительный. Точка, в которой изменяется изгиб кривой, называется точкой
флексия. Когда непрерывная функция изменяется между положительной и
отрицательный, он должен пройти через ноль, поэтому в точке перегиба второй
производная равна нулю. Если вы попытаетесь провести касательную в точке перегиба, вы
обнаружит, что он разрезает граф.
Подведение итогов:
Когда вторая производная
положительно, градиент графика увеличивается, а кривая изгибается вверх,
является выпуклым. .
Когда вторая производная отрицательна, градиент графика уменьшается
и кривая изгибается вниз, является вогнутой.
Производная от
функция f(x) = e x f(x) = e x а вторая производная f(x) = e x .
Вторая производная всегда положительна, поэтому график всегда
выпуклый.
См. диаграмму ниже.
Функция g(x) = ln x определяется только для х больше нуля. Производная равна g(x) = 1/x = x 1 а вторая производная g(x) = x 2 = 1/х 2 . Секунда производная всегда отрицательна, поэтому график изгибается вниз или становится вогнутым. схема показывает.
f(x) = e х является выпуклым.
f(x) положительный
(+).
г(х) = ln x вогнуто.
г(х) отрицательно
().
Пример 3
Найдите первое и второе
производные функций f(x) = x 2 + 4x + 3 и g(x) = x 2 +
4x 3.
f(x) = x 2 + 4x + 3 g(x) = х 2 + 4х 3
f(x) = 2x + 4 г(х) = 2х + 4
f(x) = 2 г (х) = 2
f(x) положительно, поэтому график функции f(x) выпуклый. g(x) отрицательна, поэтому график g(x) вогнут.
Используйте производную для найти вершину каждой функции. Вершина возникает, когда градиент тангенс равен нулю, поэтому:
f(x) = 2x + 4 = 0 г(х) = 2х + 4 = 0
2x = 4 2x = 4
х = 2 Икс = 2
f(2) = (2) 2 + 4(2) + 3 = 1 г(2) = 2 2 + 42 3 = 1
График f(x) выпукла и поэтому имеет точку минимума (2, 1).
График функции g(x) вогнут и, следовательно, имеет точку максимума (2, 1). Графики показаны ниже.
Пример 4
Найдите первое и второе
производные функции f(x) = x 3 3x 2 + 4, максимальное и минимальное количество баллов и точка
перегибы (если они есть).
Затем найдите уравнение касательной в точке
сгибания.
f(x) = x 3 3x 2 + 4
f(x) = 3x 2 6x
f(x) = 3x 2 6х = 3х(х 2) = 0
х = 0 или 2
Теперь посмотрим, как знаки производной меняются вокруг нулей:
f(1) = 3(1) 2 6(1) = 3 + 6 = 9 (+)
ж(1) = 31 2 61 = 3 ()
ж(3) = 33 2 63 = 9 (+)
Мы сделать то же самое для второй производной:
f(x) = 6x 6 = 0
6x = 6
x = 1
ж(0) = 60 6 = 6 ()
f(2) = 62 6 = 6 (+)
Объединив всю эту информацию, мы можем сделать следующую таблицу:
График вогнутый, когда x меньше 1, что показано изогнутой вниз кривой. График выпуклый, когда x больше 1, показанной кривой, изгибающейся вверх. Мы видим, что там является максимумом при x = 0 , минимумом при x = 2 и точкой перегиба когда х = 1,
Теперь мы можем вычислить
координаты этих точек.
f(0) = 0 3 30 2 + 4 = 4 Максимальная точка = (0, 4)
f(2) = 2 3 32 2 + 4 = 0 Минимальная точка = (2, 0)
f(1) = 1 3 31 2 + 4 = 2 Точка перегиба = (1, 2)
Теперь, чтобы найти уравнение касательной в точке перегиба.
Общее уравнение
касательной к функции f(x) в точке ( a, b ) есть y =
f(a)(x a) + b. В этом случае (a, b) является точкой перегиба, (1, 2).
Мы уже обнаружили, что f(1) = 3, поэтому нам просто нужно положить это
информацию в уравнение касательной.
у = 3(х 1) + 2
= 3x + 3 + 2
= 3x + 5
Уравнение касательной в точке перегиба находится у = 3х + 5,
Мы можем проверить работу по рисование графика f(x) и тангенса на графическом калькуляторе. Обратите внимание, как касательная пересекает график в точке перегиба.
Попрактикуйтесь в этих методах, затем попробуйте
Тест 5 по функциям 2.