производная анализ
задан 16 Дек ’12 23:17
Валентин
9●3●11
50% принятых
изменен 17 Дек ’12 12:27
ХэшКод
55●2●5
Вопрос был закрыт. Причина — «Домашнее задание». Закрывший - ХэшКод 17 Дек ’12 12:26
старыеновыеценные
|
Можно сначала упростить функцию,а потом дифференцировать. ссылка отвечен 17 Дек ’12 23:57 ASailyan изменен 18 Дек ’12 0:48 |
|
Сначала берёте производную от того, что внутри корня, умножаете на производную корня, и всё это произведение умножаете на производную всей функции (берётся как производная степенной функции). ссылка отвечен 16 Дек ’12 23:22 {2}} }$$ссылка отвечен 16 Дек ’12 23:48 Dikaz изменен 17 Дек ’12 0:08 |
Если вы не нашли ответ, задайте вопрос.
Исчисление. Я пытаюсь доказать производную от $\sqrt{x}$ с помощью геометрии.
$\begingroup$
Я пытаюсь доказать производную от $\sqrt{x}$ с помощью геометрии.
На данный момент я создал квадрат с площадью $x$ и длинами сторон $\sqrt{x}$. 2$ со сторонами x. Следовательно, ваша 92$, поскольку он оценивается как слишком маленький,
2$ со сторонами x. Следовательно, ваша 92$, поскольку он оценивается как слишком маленький,
$dx = 2(\sqrt{x})(d\sqrt{x}) \ подразумевает \frac{d\sqrt{x}}{dx} = \frac{1 }{2\sqrt{x}}$,
, то есть то, что вы хотели найти в первую очередь — производную от $\sqrt{x}$ по x.
Надеюсь, это поможет!
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Доказательство производной квадратного корня
- Математические сомнения
- Дифференциальное исчисление
- Дифференциация
- Правила
- Квадратный корень
$x$ — это переменная, и ее квадратный корень записывается как $\sqrt{x}$. Производная квадратного корня из $x$ по $x$ записывается в дифференциальном исчислении следующим образом.
$\dfrac{d}{dx}{(\sqrt{x})}$
Express Производная функции в предельной операции
Согласно определению производной, дифференцирование $\sqrt{x}$ с относительно $x$ можно записать в форме предельной операции.
$\dfrac{d}{dx}{\sqrt{x}}$ $\,=\,$ $\displaystyle \large \lim_{\Delta x \,\to \, 0}{\normalsize \dfrac {\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}}$
Теперь возьмем $\Delta x = h$ и преобразуем уравнение в терминах $h$ из $\Delta x $.
$\implies$ $\dfrac{d}{dx}{\sqrt{x}}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\sqrt{x+h}-\sqrt{x}}{h}}$
Теперь вычислим дифференцирование квадратного корня из $x$ по $x$ по первому принципу.
Оценка предела методом прямой подстановки
Предел алгебраической функции в радикальной форме может быть оценен методом прямой подстановки.
$\implies$ $\dfrac{d}{dx}{\sqrt{x}}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\sqrt{x+h}-\sqrt{x}}{h}}$
$=\,\,\,$ $\dfrac{\sqrt{x+0}-\sqrt{x}}{0}$
$=\,\,\,$ $\dfrac{\sqrt {x}-\sqrt{x}}{0}$
$=\,\,\,$ $\dfrac{0}{0}$
Подсчитано, что предел алгебраической функции не определен. Таким образом, найти производную квадратного корня из $x$ прямым методом пределов подстанции невозможно. Значит, надо считать по другому методу.
Оценка предела методом рационализации
Функция имеет радикальную форму. Итак, попробуем оценить его методом рационализации, рационализируя функцию в числителе сопряженной ей функцией.
$\dfrac{d}{dx}{\sqrt{x}}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\ sqrt{x+h}-\sqrt{x}}{h}}$ $\times$ $1$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\sqrt{x+h}-\sqrt{x}}{h}}$ $\times$ $\dfrac{\sqrt{x+h}+\sqrt{x}}{ \sqrt{x+h}+\sqrt{x}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{{ (\sqrt{x+h}-\sqrt{x})}{(\sqrt{x+h}+\sqrt{x})}}{h \times (\sqrt{x+h}+\sqrt{ x})}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{{(\sqrt{x+h}) }^2-{(\sqrt{x})}^2}{ч \times (\sqrt{x+h}+\sqrt{x})}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{x+h-x}{h \times (\sqrt{x+h} +\sqrt{x})}}$
$=\,\,\,$ $\require{cancel} \displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\ cancel{x}+h-\cancel{x}}{h \times (\sqrt{x+h}+\sqrt{x})}}$
$=\,\,\,$ $\displaystyle \ большой \lim_{h \,\to \, 0}{\normalsize \dfrac{h}{h \times (\sqrt{x+h}+\sqrt{x})}}$
$=\,\ ,\,$ $\require{cancel} \displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{\cancel{h}}{\cancel{h} \times (\sqrt{ х+ч}+\sqrt{х})}}$
$\implies$ $\dfrac{d}{dx}{\sqrt{x}}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to \, 0}{\normalsize \dfrac{1}{\sqrt{x+h}+\sqrt{x}}}$
Оцените предел методом прямой подстановки
Теперь оцените предел алгебраической функции, когда $h$ приближается к $0$, прямым методом метод замещения.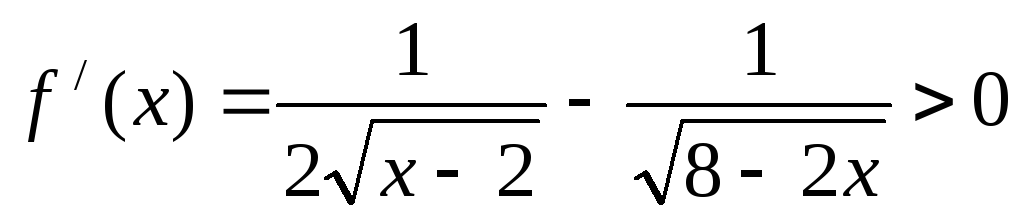

 2}}-1$%
2}}-1$%