ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 23.  x, sin x, cos x x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
Таблица производных. Доказательство формул
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y=C(C)’=0 Степенная функция y=xp (xp)’=p·xp-1 | Показательная функция y=ax (ax)’=ax·ln a В частности, при a=e имеем y=ex (ex)’=ex |
Логарифмическая функция (logax)’=1x·ln a В частности, при a=e имеем y=ln x (ln x)’=1x | Тригонометрические функции (sin x)’=cos x(cos x)’=-sin x(tgx)’=1cos2x(ctgx)’=-1sin2x |
Обратные тригонометрические функции (arcsin x)’=11-x2(arccos x)’=-11-x2(arctg x)’=11+x2(arcctg x)’=-11+x2 | Гиперболические функции (shx)’=chx(chx)’=shx(thx)’=1ch3x(cthx)’=-1sh3x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x0=x, где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f(x)=C. Составим запись предела отношения приращения функции к приращению аргумента при ∆x→0:
lim∆x→0∆f(x)∆x=lim∆x→0C-C∆x=lim∆x→00∆x=0
Обратите внимание, что под знак предела попадает выражение 0∆x. Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f(x)=C равна нулю на всей области определения.
Пример 1Даны постоянные функции:
f1(x)=3,f2(x)=a, a∈R,f3(x)=4.13722,f4(x)=0,f5(x)=-87
Необходимо найти их производные.
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f1′(x)=(3)’=0,f2′(x)=(a)’=0, a∈R,f3′(x)=4.13722’=0,f4′(x)=0’=0,f5′(x)=-87’=0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (xp)’=p·xp-1, где показатель степени p является любым действительным числом.
Доказательство 2Приведем доказательство формулы, когда показатель степени – натуральное число: p=1, 2, 3, …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
(xp)’=lim∆x→0=∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x+∆x)p-xp=Cp0+xp+Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+. ..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
Таким образом:
(xp)’=lim∆x→0∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x==lim∆x→0(Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p)∆x==lim∆x→0(Cp1·xp-1+Cp2·xp-2·∆x+…+Cpp-1·x·(∆x)p-2+Cpp·(∆x)p-1)==Cp1·xp-1+0+0+…+0=p!1!·(p-1)!·xp-1=p·xp-1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x>0. Тогда: xp>0. Логарифмируем равенство y=xp по основанию e и применим свойство логарифма:
y=xpln y=ln xpln y=p·ln x
На данном этапе получили неявно заданную функцию.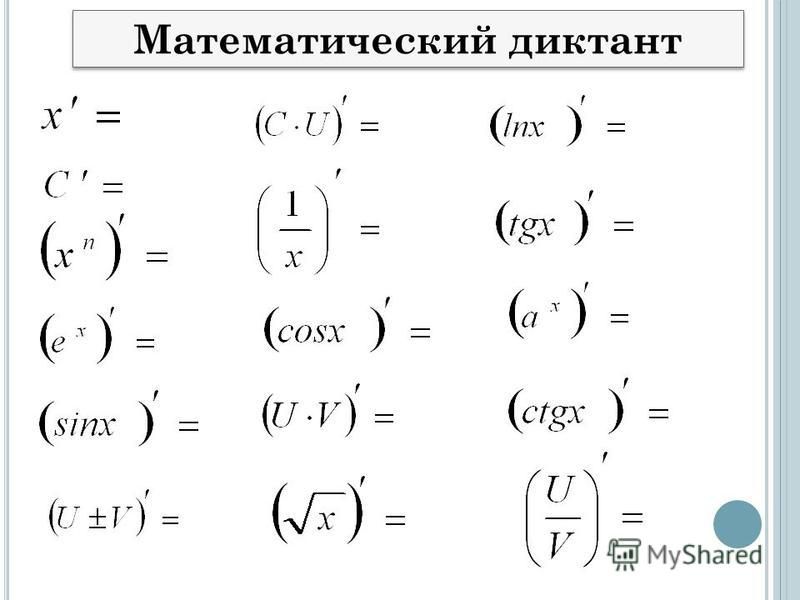 Определим ее производную:
Определим ее производную:
(ln y)’=(p·ln x)1y·y’=p·1x⇒y’=p·yx=p·xpx=p·xp-1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x<0, причем является четной: y(x)=-y((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Тогда xp<0 и возможно составить доказательство, используя логарифмическую производную.
Если p есть нечетное число, тогда степенная функция определена и при x<0, причем является нечетной: y(x)=-y(-x)=-(-x)p. Тогда xp<0, а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y'(x)=(-(-x)p)’=-((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, при отрицательных x верно равенство (-x)p-1=xp-1.
Итак, мы доказали формулу производной степенной функции при любом действительном p.
Пример 2Даны функции:
f1(x)=1×23,f2(x)=x2-14,f3(x)=1xlog712
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y=xp, опираясь на свойства степени, а затем используем формулу:
f1(x)=1×23=x-23⇒f1′(x)=-23·x-23-1=-23·x-53f2′(x)=x2-14=2-14·x2-14-1=2-14·x2-54f3(x)=1xlog712=x-log712⇒f3′(x)=-log712·x-log712-1=-log712·x-log712-log77=-log712·x-log784
Производная показательной функции
Доказательство 4Выведем формулу производной, взяв за основу определение:
(ax)’=lim∆x→0ax+∆x-ax∆x=lim∆x→0ax(a∆x-1)∆x=ax·lim∆x→0a∆x-1∆x=00
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z=a∆x-1 (z→0 при ∆x→0). В таком случае a∆x=z+1⇒∆x=loga(z+1)=ln(z+1)ln a. Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(ax)’=ax·lim∆x→0a∆x-1∆x=ax·ln a·lim∆x→011z·ln(z+1)==ax·ln a·lim∆x→01ln(z+1)1z=ax·ln a·1lnlim∆x→0(z+1)1z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(ax)’=ax·ln a·1lnlimz→0(z+1)1z=ax·ln a·1ln e=ax·ln a
Пример 3Даны показательные функции:
f1(x)=23x,f2(x)=53x,f3(x)=1(e)x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f1′(x)=23x’=23x·ln23=23x·(ln 2-ln 3)f2′(x)=53x’=53x·ln 513=13·53x·ln 5f3′(x)=1(e)x’=1ex’=1ex·ln1e=1ex·ln e-1=-1ex
Производная логарифмической функции
Доказательство 5Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
(logax)’=lim∆x→0loga(x+∆x)-logax∆x=lim∆x→0logax+∆xx∆x==lim∆x→01∆x·loga1+∆xx=lim∆x→0loga1+∆xx1∆x==lim∆x→0loga1+∆xx1∆x·xx=lim∆x→01x·loga1+∆xxx∆x==1x·logalim∆x→01+∆xxx∆x=1x·logae=1x·ln eln a=1x·ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim∆x→01+∆xxx∆x=e является верным в соответствии со вторым замечательным пределом.
Пример 4Заданы логарифмические функции:
f1(x)=logln3 x,f2(x)=ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f1′(x)=(logln3 x)’=1x·ln(ln 3);f2′(x)=(ln x)’=1x·ln e=1x
Итак, производная натурального логарифма есть единица, деленная на x.
Производные тригонометрических функций
Доказательство 6Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x
Формула разности синусов позволит нам произвести следующие действия:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x==lim∆x→02·sin x+∆x-x2·cosx+∆x+x2∆x==lim∆x→0sin ∆x2·cosx+∆x2∆x2==cosx+02·lim∆x→0sin ∆x2∆x2
Наконец, используем первый замечательный предел:
sin’ x=cos x+02·lim∆x→0sin∆x2∆x2=cos x
Итак, производной функции sin x будет cos x.
Совершенно также докажем формулу производной косинуса:
cos’ x=lim∆x→0cos (x+∆x)-cos x∆x==lim∆x→0-2·sin x+∆x-x2·sinx+∆x+x2∆x==-lim∆x→0sin∆x2·sinx+∆x2∆x2==-sinx+02·lim∆x→0sin∆x2∆x2=-sin x
Т. е. производной функции cos x будет –sin x.
е. производной функции cos x будет –sin x.
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
tg’x=sin xcos x’=sin’ x·cos x-sin x·cos’ xcos2 x==cos x·cos x-sin x·(-sin x)cos2 x=sin2 x+cos2 xcos2 x=1cos2 xctg’x=cos xsin x’=cos’x·sin x-cos x·sin’xsin2 x==-sin x·sin x-cos x·cos xsin2 x=-sin2 x+cos2 xsin2 x=-1sin2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex—e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch3x=ch3x-sh3xch3x=1ch3xcth’x=chxshx’=ch’x·shx-chx·sh’xsh3x=sh3x-ch3xsh3x=-1sh3x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Множественное правило констант — формула, доказательство, примеры, применение
Множественное правило констант — это общее правило, которое используется в исчислении, когда операция применяется к функции, умноженной на константу. У нас есть разные постоянные множественные правила для дифференцирования, пределов и интегрирования в исчислении. Общее утверждение правила кратности констант заключается в том, что когда операция (дифференцирование, пределы или интегрирование) применяется к произведению константы и функции, тогда оно равно произведению константы и операции, примененной к функции.
Далее в этой статье мы подробно изучим концепцию постоянного кратного правила дифференцирования, пределов и интегрирования. Мы поймем их формулы, доказательство постоянного кратного правила и его применение с помощью решенных примеров для лучшего понимания.
| 1. | Что такое постоянное множественное правило? |
| 2. | Формула постоянного множественного правила |
| 3. | Доказательство постоянного множественного правила |
| 4. | Применение постоянного множественного правила |
| 5. | Часто задаваемые вопросы о постоянном множественном правиле |
Что такое постоянное множественное правило?
Правило постоянного множителя в исчислении используется для трех операций, а именно интегрирования, ограничения и дифференцирования. Общее утверждение постоянного кратного правила для трех операций:
- Множественное правило дифференцирования констант : оно гласит, что производная произведения константы на функцию f(x) равна произведению константы на производную функции f(x).

- Множественное правило пределов констант : Оно гласит, что предел констант, умноженный на функцию f(x), равен произведению константы на предел функции.
- Константа Множественное правило интегрирования : Это правило гласит, что интеграл от произведения константы на функцию f(x) равен произведению константы на интеграл от функции f(x).
Мы применяем эти правила для упрощения математических задач. Давайте теперь разберемся с их формулами в следующем разделе.
Формула постоянного множественного правила
В этом разделе мы напишем формулы для постоянного кратного правила пределов, дифференцирования и интегрирования. Рассмотрим константу k и функцию f(x), тогда искомые формулы будут следующими:
- Константа Множественное правило дифференцирования: d(k f(x))/dx = k d(f((x))/dx
- Постоянное множественное правило пределов: lim x→a k f(x) = k lim x→a f(x)
- Константа Множественное правило интегрирования: ∫k f(x) dx = k ∫f(x) dx
Доказательство постоянного множественного правила
Теперь, когда мы знаем формулы кратных констант для дифференцирования, интегрирования и пределов, мы докажем эти формулы, используя различные формулы и свойства производных, интегралов и пределов. Сначала выведем формулу постоянного кратного правила дифференцирования.
Сначала выведем формулу постоянного кратного правила дифференцирования.
Правило дифференцирования констант кратных
Правило кратных констант производных утверждает, что производная произведения константы на функцию f(x) равна произведению константы на производную функции f(x) . Чтобы доказать эту формулу, воспользуемся первым принципом дифференцирования, т. е. определением пределов. Мы докажем формулу постоянного кратного правила d(k f(x))/dx = k d(f((x))/dx, используя следующие формулы:
- f'(x) = lim h→0 [f(x+h) — f(x)] / h — (1)
- Правило пределов продукта: lim x→a [ f(x) × g(x) ] = lim x→a f(x) × lim x→a g(x)
- Предел константы: lim x→a k = k
Предположим, что h(x) = k f(x). Используя приведенные выше формулы, мы имеем
LHS = h'(x)
= d(k f(x))/dx
= lim h→0 [k f(x+h) — k f(x)] / ч
= lim ч→0 {k [f(x+h) — f(x)] / h } — [Вычитая общий множитель k]
= lim h→0 {k × [f(x+h) — f (x)] / h }
= lim h→0 k × lim h→0 [f(x+h) — f(x)]/h
= k × lim h→0 [f(x+h) — f(x)] / h — [Используя предел постоянной формулы lim x→a k = k]
= k × f'(x) — [ Используя (1)]
= k d[f(x)]/dx
= RHS
Таким образом, мы доказали постоянное кратное правило дифференцирования.
Постоянное кратное правило пределов
Чтобы доказать формулу постоянного кратного правила для пределов, заданного lim x→a k f(x) = k lim x→a f(x), воспользуемся формулой для предела произведения функций и формулы для постоянной функции, заданной
- Правило пределов произведения: lim x→a [ f(x) × g(x) ] = lim x→a f(x) × lim x→a g(x)
- Предел константы: lim x→a к = к
Используя приведенные выше формулы, мы имеем
LHS = lim x→a k f(x)
= lim x→a [k × f(x)]
= lim x→a k × lim x→a f(x) — [Используя правило пределов произведения]
= k × lim x→a f(x) — [Предел константы равен самой константе ]
= k lim x→a f(x)
= RHS
Таким образом, мы доказали формулу правила постоянного кратного для пределов.
Постоянное кратное правило для интегралов
В этом разделе мы докажем формулу постоянного кратного правила интегрирования, заданного выражением ∫k f(x) dx = k ∫f(x) dx, используя метод интегрирования по частям. . Он используется для определения интеграла от произведения функций. Его формула имеет вид Чтобы доказать правило кратности констант для интегралов, предположим, что g(x) = k и h(x) = f(x). Тогда имеем
. Он используется для определения интеграла от произведения функций. Его формула имеет вид Чтобы доказать правило кратности констант для интегралов, предположим, что g(x) = k и h(x) = f(x). Тогда имеем
∫kf(x) dx = k × ∫f(x) dx — ∫[(k)’ × ∫f(x) dx] dx
= k ∫f(x) dx — ∫[0 × ∫f(x) dx] dx — [Поскольку производная константы всегда равна нулю]
= k ∫f(x) dx — 0
= k ∫f(x)
= RHS
Таким образом, мы вывели и доказали формулу постоянного кратного правила интегрирования.
Применение постоянного множественного правила
Теперь, когда мы поняли формулы и вывод правила постоянного кратного числа, давайте решим несколько примеров, основанных на концепции, чтобы понять ее применение. Рассмотрим функцию f(x) = x 2 + 3x — 4 и k = 5. Теперь примените формулу правила множителя констант, чтобы найти производную, интеграл и предел k f(x).
Применение правила постоянного кратного для производных
Теперь воспользуемся правилом постоянного кратного, чтобы найти производную kf(x) = 5 [x 2 + 3x — 4] = 5x 2 + 15x — 20 an проверить результат с помощью правила мощности. По правилу постоянного кратного имеем
По правилу постоянного кратного имеем
d(kf(x))/dx = d[5 (x 2 + 3x — 4)]/dx
= 5 d[x 2 + 3x — 4]/dx — [Использование постоянного кратного правила]
= 5 × (2x + 3) — [Использование степенного правила]
= 10x + 15
Чтобы проверить результат, продифференцируем kf(x) = 5x 2 + 15x — 20, используя степенное правило дифференцирования:
Проверка: d(kf(x))/dx
= d(5x 2 + 15x — 20)/dx
= 10x + 15
Таким образом, мы применили правило постоянного кратного дифференцирования и проверили результат.
Применение постоянного множественного правила пределов
Теперь найдем предел функции kf(x) = 5 [x 2 + 3x — 4], где k = 5 и f(x) = x 2 + 3x — 4, когда x стремится к 3, используя правило постоянного кратного для пределов, и проверяем результат, взяв предел функции kf(x) = 5x 2 + 15x — 20, где x стремится к 3. Итак, мы есть
lim x→3 k f(x) = lim x→3 5 [x 2 + 3x — 4]
= 5 lim x→3 [x 2 + 3x — 4] — [Использование постоянного кратного правила для пределов]
= 5 × (3 2 + 3(3) — 4)
= 5 × ( 9 + 9 — 4)
= 5 × 14
= 70
Теперь для проверки результата найдем предел функции kf(x) = 5x 2 + 15x — 20 при стремлении x к 3.
Проверка: lim x→3 k f(x)
= lim x→3 (5x 2 + 15x — 20)
= 5(3) 8 + 1 — 20
= 5 × 9 + 15 × 3 — 20
= 45 + 45 — 20
= 90 — 20
= 70
Таким образом, мы поняли применение правила постоянного кратного для пределов.
Применение постоянного кратного правила интегрирования
В этом разделе мы вычислим интеграл от kf(x) = 5 [x 2 + 3x — 4], используя постоянное кратное правило интегралов, и проверим результат, вычислив интеграл от kf(x) = 5x 2 + 15x — 20 с использованием степенного правила интегрирования. Итак, у нас
∫kf(x) dx = ∫5 [x 2 + 3x — 4] dx
= 5 ∫(x 2 + 3x — 4) dx
= 5 [x 909227 3 3x 2 /2 — 4x] + C
= 5x 3 /3 + 15x 2 /2 — 20x + C — (1)
Теперь для проверки результата найдем интеграл от kf(x) = 5x 2 + 15x — 20 с использованием степенного правила интегрирования.
∫kf(x) dx = ∫[5x 2 + 15x — 20] dx
= ∫5x 2 dx + ∫15x dx — ∫20 dx
= 5x 3 /3 + 15x 2 /2 — 20x + C — (2)
Из (1) и (2) мы проверили правило постоянного кратного интегрирования.
Важные примечания о постоянном кратном правиле
- Постоянное кратное правило используется в исчислении для трех операций, а именно интегрирования, ограничения и дифференцирования.
- Постоянное множественное правило дифференцирования: d(k f(x))/dx = k d(f((x))/dx
- Постоянное множественное правило пределов: lim x→a k f(x) = k lim x→a f(x)
- Постоянное множественное правило интегрирования: ∫k f(x) dx = k ∫f(x) dx
☛ Похожие темы:
- Интеграл от log x
- Производное от xlnx
- Антилог стол
Часто задаваемые вопросы о постоянном множественном правиле
Что такое постоянное кратное правило в исчислении?
Правило умножения констант — это общее правило, которое используется в вычислениях, когда операция применяется к функции, умноженной на константу. Общее утверждение правила кратности констант заключается в том, что когда операция (дифференцирование, пределы или интегрирование) применяется к произведению константы и функции, тогда оно равно произведению константы и операции, примененной к функции.
Общее утверждение правила кратности констант заключается в том, что когда операция (дифференцирование, пределы или интегрирование) применяется к произведению константы и функции, тогда оно равно произведению константы и операции, примененной к функции.
Что такое постоянные формулы множественных правил?
Общие формулы для постоянного кратного правила дифференцирования, пределов и интегрирования:
- Постоянное кратное правило дифференцирования: d(k f(x))/dx = k d(f((x))/dx
- Постоянное множественное правило пределов: lim x→a k f(x) = k lim x→a f(x)
- Постоянное множественное правило интегрирования: ∫k f(x) dx = k ∫f(x) dx
Когда использовать постоянное множественное правило?
Мы можем использовать правило кратности констант, когда операция применяется к функции, умноженной на константу. Например, чтобы найти производную функции, умноженной на константу, мы используем формулу d(k f(x))/dx = k d(f((x))/dx.
Как использовать правило кратности констант?
Мы можем использовать постоянное кратное правило, применяя формулы для нахождения производных, интегралов и пределов
- Постоянное кратное правило дифференцирования: d(k f(x))/dx = k d(f((x)) / дх
- Постоянное множественное правило пределов: lim x→a k f(x) = k lim x→a f(x)
- Постоянное множественное правило интегрирования: ∫k f(x) dx = k ∫f(x) dx
Что такое постоянное кратное правило для производных?
Правило множителя констант для производных утверждает, что производная произведения константы на функцию f(x) равна произведению константы на производную функции f(x). Чтобы применить это правило, мы можем использовать формулу d(k f(x))/dx = k d(f((x))/dx.
Как доказать постоянное кратное правило для производных?
Мы можем доказать правило кратности констант для производных, используя первый принцип дифференцирования. Мы можем использовать следующие формулы, чтобы доказать правило кратных констант для производных: )
Производная постоянной функции
Производная постоянной функции Понять значение производной непросто, а вот уметь брать производные несложно. Лучший способ научиться этому, очевидно, через практику.
Лучший способ научиться этому, очевидно, через практику.
Следующая таблица содержит несколько функций $$f(x)$$ в первом столбце и ее производные $$f ‘(x)$$ во втором. Посмотри на него и попробуй завершить:
| $$f (х)$$ | $$f'(x)$$ |
| $$1$$ | $$0$$ |
| $$5$$ | $$0$$ |
| $230$$ | $$0$$ |
| $0,76$$ | $$0$$ |
| $$А$$ | $$0$$ |
| $$N$$ | ? |
| $$3 млрд$$ | ? |
Решение: $$$ \begin{array} {ll} f(x)=N & f'(x)=0 \\ f(x)=3B & f'(x)=0\end{ массив}$$$
Обратите внимание, что во всех случаях производная равна нулю.

