Определение модуль числа: Модуль числа — урок. Математика, 6 класс.

Содержание

Модуль числа | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная 🙂 Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.

Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.

Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному (без знака!).
Например,

Обратите внимание: модуль числа всегда неотрицателен:

Определение модуля

Вот оно:

От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.

Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 🙂

Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,

В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.

Геометрическая интерпретация модуля

Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа.

Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.

Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.

Вообще, если имеются два числа, a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A
до точки B.)

Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).

Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.

Перейдём к неравенствам. Решим неравенство: .

Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.

Ответ: (-11; -3).

Другой пример. Решим неравенство: |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно 7. Отметим эти точки на числовой прямой.
Ответ: .

График функции

Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.

Корень из квадрата

Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что

Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .

Примеры заданий ЕГЭ

1. Найдите значение выражения: при .

Заметим, что при . Следовательно, значение нашего выражения равно: .

2. Найдите значение выражения: при .

Действуем аналогично:

В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.

Читайте также: Уравнения с модулем

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Модуль числа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 07.04.2023

Что такое модуль действительного числа: определение, примеры, график, интерпретация

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

Определение модуля числа
Геометрическая интерпретация модуля
График функции с модулем
Пример задачи

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е. |0| = 0.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т. е. |a| = OA.

|-4| = |4| = 4

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

y = x при x>0
y = -x при x<0
y=0 при x=0
область определения: (−∞;+∞)
область значений: [0;+∞).
в точке x=0 график “ломается”.

Пример задачи

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:
Согласно приведенному выше определению:

|3| = 3
|-7| = 7
|12,4| = 12,4
|-0,87| = 0,87

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Развлечение с модульной арифметикой – BetterExplained

Недавно один читатель предложил мне написать о модульной арифметике (также известной как «вычисление остатка»). Я не особо задумывался об этом, но понял, что модуль чрезвычайно мощный: он должен быть в нашем умственном наборе инструментов рядом со сложением и умножением.

Вместо того, чтобы бить вас по лицу формулами, давайте рассмотрим идею, которой мы тонко владели годами. Есть хорошая статья о модульной арифметике, которая вдохновила меня на этот пост.

Нечетное, четное и трехчетное

Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:

Четное: делится на 2 (0, 2, 4, 6). ..)
Нечетное: не делится на 2 (1, 3, 5, 7…)

Почему это различие важно? Это начало абстракции — мы замечаем свойств числа (например, четность или нечетность), а не только само число («37»).

Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить отношения между набирает цифр, а не конкретных. Например, мы можем создать такие правила:

Четный x Четный = Четный
Нечетное x Нечетное = Нечетное
Четное x Нечетное = Четное

Эти правила являются общими — они работают на уровне свойств. (Интуитивно у меня есть химическая аналогия, что «четность» — это молекула, которой обладают некоторые числа, и ее нельзя удалить путем умножения.)

Но четность/нечетность — это очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:

«Три» означает, что число делится на 3 (0, 3, 6, 9…)
«Тродд» означает, что вы , а не делитесь на 3 (1, 2, 4, 5, 7, 8…)

Странно, но работает. Вы заметите несколько вещей: есть два типа throdd. Такое число, как «4», на 1 меньше, чем тричетырнадцать (остаток 1), а число 5 — на два (остаток 2).

Быть «три-семь» — это еще одно свойство числа. Возможно, это не так полезно сразу, как чет/нечет, но оно есть: мы можем создавать правила, такие как «три семь х тривен = тривен» и так далее.

Но это сходит с ума. Мы не можем все время составлять новые слова.

Ввод по модулю

Операция по модулю (сокращенно «mod» или «%» во многих языках программирования) — это остаток при делении.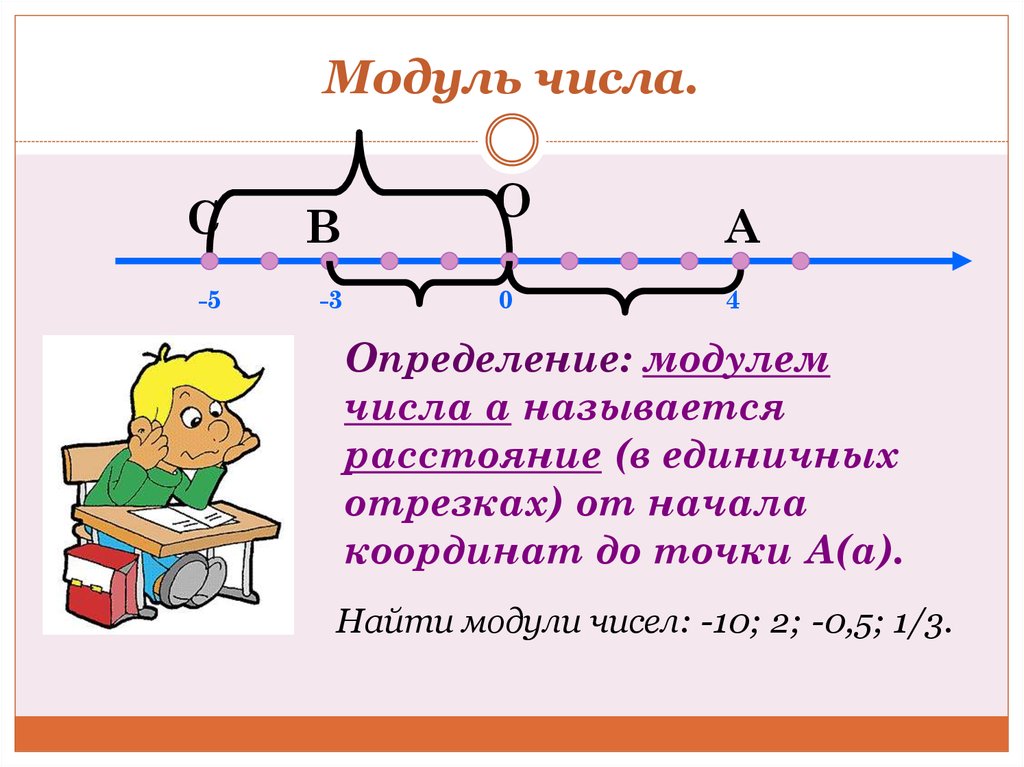 Например, «5 mod 3 = 2», что означает, что 2 – это остаток при делении 5 на 3.

Преобразуя повседневные термины в математические выражения, «четное число» – это число, в котором «0 mod 2», т. е. имеет остаток 0 при делении на 2. Нечетное число равно «1 mod 2» (имеет остаток 1).

Почему это круто? Итак, наши «четные/нечетные» правила становятся такими:

Четный x Четный = 0 x 0 = 0 [четный]
Нечетное x Нечетное = 1 x 1 = 1 [нечетное]
Четный x Нечетный = 0 x 1 = 0 [четный]

Круто, да? Довольно легко разобраться — мы преобразовали «свойства» в настоящие уравнения и нашли несколько новых фактов.

Сколько будет четное x четное x нечетное x нечетное? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, что если умножить где-нибудь на , то весь результат будет равен нулю… Я имею в виду даже :).

Математика часов

Коварная особенность модульной математики заключается в том, что мы уже использовали ее для учета времени — иногда называемую «арифметикой часов».

Например: сейчас 7:00 (утра/вечера не имеет значения). Где будет часовая стрелка через 7 часов?

Хром. 7 + 7 = 14, но мы не можем показать «14:00» на часах. Значит, должно быть 2. Мы рассуждаем интуитивно и в математических терминах:

(7 + 7) по модулю 12 = (14) по модулю 12 = 2 по модулю 12 [2 — это остаток от деления 14 на 12]

Уравнение «14 mod 12 = 2 mod 12» означает, что «14 часов» и «2 часа» выглядят одинаково на 12-часовых часах. Они конгруэнтны , обозначены тройным знаком равенства: 14 ≡ 2 по модулю 12.

Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?

Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Таким образом, часы переведутся на 1 час вперед, в 9:00.

(8 + 25) по модулю 12 ≡ (8) по модулю 12 + (25) по модулю 12 ≡ (8) по модулю 12 + (1) по модулю 12 ≡ 9мод 12

Вы интуитивно преобразовали 25 в 1 и прибавили это к 8.

Забавное свойство: математика просто работает

Используя часы в качестве аналогии, мы можем выяснить, «просто работают» ли правила модульной арифметики (они работают).

Сложение/Вычитание

Допустим, два раза на наших часах выглядят одинаково («2:00» и «14:00»). Если мы добавим к ним одинаковые «x» часов, что произойдет?

Ну меняют на столько же на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба будут показывать 7:00.

Почему? Ну, нас никогда не волновали лишние «12:00», которые таскал с собой 14-й. Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.

Умножение

Труднее понять, остается ли умножение неизменным. Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?

Посмотрим — что получится, если умножить на 3?

Ну, 2 часа * 3 ≡ 6 часов. Но что такое «14:00» * 3?

Помните, 14 = 12 + 2. Таким образом, мы можем сказать

14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12

Первую часть (12 * 3) можно игнорировать! «12-часовое переполнение», которое носит с собой 14, просто повторяется несколько раз. Но кого это волнует? Мы все равно игнорируем переполнение.

При умножении важен только остаток, который равен 2 часам в 14:00 и 2:00. Интуитивно я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе части модульного отношения и получить тот же результат). Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.

Использование модульной арифметики

Теперь самое интересное — чем полезна модульная арифметика?

Простые расчеты времени

Мы делаем это интуитивно, но неплохо дать этому название. Ваш рейс прибывает в 15:00. Задержка на 14 часов. В какое время он приземлится?

Ну, 14 ≡ 2 mod 12. Поэтому я думаю об этом как о «2 часах и переключении утра/вечера», поэтому я знаю, что это будет «3 + 2 = 5 утра».

Это немного сложнее, чем простой оператор по модулю, но принцип тот же.

Размещение предметов в случайных группах

Предположим, у вас есть люди, которые купили билеты в кино с номером подтверждения. Вы хотите разделить их на 2 группы.

Чем ты занимаешься? «Шансы здесь, четы там». Вам не нужно знать, сколько билетов было выдано (первая половина, вторая половина), каждый может определить свою группу мгновенно (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.

Нужно 3 группы? Разделите на 3 и возьмите остаток (он же мод 3). У вас будут группы «0», «1» и «2».

В программировании по модулю вы можете разместить элементы в хеш-таблице: если в вашей таблице N записей, преобразуйте ключ элемента в число, выполните mod N и поместите элемент в это ведро (возможно, сохраняя связанный список там). По мере увеличения размера вашей хэш-таблицы вы можете пересчитать модуль для ключей.

Выбор случайного предмета

В реальной жизни я использую модуль. Действительно. У нас есть 4 человека, играющих в игру, и нужно выбрать кого-то, кто пойдет первым. Сыграй в мини-игру мод N! Дайте людям цифры 0, 1, 2 и 3.

Теперь все кричат «раз, два, три, стрелять!» и высовывает случайное количество пальцев. Сложите их и разделите на 4 — тот, кто точно наберет остаток, ходит первым. (Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, так как 11 по модулю 4 = 3).

Это быстро и работает.

Выполнение задач в цикле

Предположим, задачи должны выполняться по определенному расписанию:

Задача A выполняется 3 раза в час
Задача B выполняется 6 раз в час
Задача C выполняется 1 раз в час

Как вы храните эту информацию и составляете расписание? В одну сторону:

Таймер, работающий каждую минуту (отслеживайте минуты как «n»)
3x/час означает один раз каждые 60/3 = 20 минут. Итак, задача A запускается всякий раз, когда «n % 20 == 0»
Задача B запускается всякий раз, когда «n % 10 == 0»
Задача C запускается всякий раз, когда «n % 60 == 0»

О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, запустите его, когда «n mod 60 == 1» (по-прежнему один раз в час, но не так, как C1).

Мысленно я вижу цикл, который хочу «поразить» с различными интервалами, поэтому вставляю мод. Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).

Точно так же при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n % 100 == 0){ print… }.

Это очень гибкий и простой способ запуска элементов по расписанию. На самом деле, это способ ответить на проверку вменяемости FizzBuzz. Если в вашем batbelt нет операции по модулю, вопрос становится намного сложнее.

Нахождение свойств чисел

Предположим, я сказал вам следующее:

a = (47 * 2 * 3)

Что вы можете сделать быстро? Что ж, «а» должно быть четным, так как оно равно чему-то, что включает умножение на 2.

Если бы я также сказал вам:

а = (39 * 7)

Ты бы отказался. Не потому, что вы «знаете», что два продукта разные, а потому, что один явно четный, а другой нечетный. Есть проблема: а не может быть одним и тем же числом в обоих, начиная с 9.Свойства 0017 не соответствуют .

Такие вещи, как «четный», «три» и «mod n», являются более общими свойствами, чем отдельные числа, и мы можем проверить их согласованность. Таким образом, мы можем использовать модуль, чтобы выяснить, согласуются ли числа, не зная, что они собой представляют!

Если я скажу вам это:

3a + 5b = 8
3а + б = 2

Можно ли решить эти уравнения с целыми числами? Давайте посмотрим:

3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3 или b ≡ 1 mod 3
3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3

Противоречие, молодцы! Б не может быть одновременно «1 по модулю 3» и «2 по модулю 3» — это так же абсурдно, как быть четным и нечетным одновременно!

Но есть одна загвоздка: числа вроде «1,5» не четные и не нечетные — они не целые! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .

Потому что на самом деле мы можем решить это уравнение:

(3а + 5б) – (3а +б) = 8 – 2
4b = 6
б = 1,5
3а + 1,5 = 2, поэтому 3а = 0,5 и а = 1/6

Не соблазняйтесь силой модуля! Знайте его пределы: это относится к целым числам.

Криптография

Игра с числами имеет очень важное применение в криптографии. Это слишком много, чтобы охватить здесь, но модуль используется в обмене ключами Диффи-Хеллмана — используется при настройке SSL-соединений для шифрования веб-трафика.

Простой английский

Компьютерщики любят использовать технические слова в обычном контексте. Вы можете услышать «X такое же, как Y по модулю Z», что примерно означает «Игнорируя Z, X и Y одинаковы».

Например:

b и B идентичны, капитализация по модулю
iTouch и iPad идентичны по модулю размера 😉

Вперед и вверх

Странно думать о «полезности» оператора по модулю — это все равно, что кто-то спрашивает, почему экспоненты полезны. В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.

В общем, я вижу несколько общих вариантов использования:

Редуктор диапазона: возьмите ввод, мод N, и у вас есть число от 0 до N-1.
Назначение группы: возьмите ввод, мод N, и вы пометите его как группу от 0 до N-1. Эта группа может быть согласована любым количеством сторон — например, разные серверы, которые знают N = 20, могут договориться о том, к какой группе принадлежит ID=57.
Вывод свойств: обрабатывать числа в соответствии со свойствами (четные, тричетные и т. д.) и разрабатывать принципы, полученные на уровне свойств

Я уверен, что я пропустил еще десятки применений — не стесняйтесь комментировать ниже. Удачной математики!

Другие сообщения из этой серии

Методы сложения чисел от 1 до 100
Переосмысление арифметики: визуальное руководство
Quick Insight: интуитивное значение подразделения
Краткий обзор: вычитание отрицательных чисел
Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
Развлечение с модульной арифметикой
Учимся считать (как избежать проблемы с забором)
Причудливое введение в системы счисления
Еще один взгляд на простые числа
Интуиция для золотого сечения
Различные интерпретации числа ноль

Основы конгруэнтности

Основная история: Триллион треугольников

Мы говорим, что целые числа a и b «конгруэнтны по модулю n », если их разница кратна и . Например, 17 и 5 равны. по модулю 3, потому что 17 — 5 = 12 = 4⋅3, а 184 и 51 конгруэнтны по модулю 19, поскольку 184 — 51 = 133 = 7⋅19. Мы часто пишем это как 17 ≡ 5 mod 3 или 184 ≡ 51 mod 19. Выражение -8 ≡ 10 mod 9 произносится «отрицательное 8 сравнимо с 10 по модулю 9» или иногда «минус 8 соответствует 10 по модулю 9».

Знакомое использование модульной арифметики — всякий раз, когда мы конвертируем от 12 до 24 часов. Мы знаем, что 14:00 и 14:00 обозначают то же время с 14 ≡ 2 mod 12.

Хотя используется реже, мы можем расширить это определение до рациональное число. Рациональные числа 1/2 и 13/2 конгруэнтны по модулю 3, потому что 13/2 — 1/2 = 6 = 2⋅3.

Назовем площадь прямоугольного треугольника с рациональными сторонами «конгруэнтное число» может сбивать с толку, потому что использование «конгруэнтного» почти не имеет ничего общего со стандартом использование «конгруэнтного», как описано выше. Если бы терминология была изобрели сегодня, мы бы назвали это как-то иначе.

Даже математики находите это сбивающим с толку: утверждение «5 — конгруэнтное число» вызывает реакцию «конгруэнтно чему?»

Но есть один способ связи этих терминов, который мы сейчас объясним.

Если n конгруэнтное число, то есть если это площадь прямоугольного треугольника с рациональные стороны, то существует рациональный квадрат a ² , такой что а ² — n и a ² + n также являются квадратами.

Чтобы убедиться в этом, предположим, что x, y, и z рациональные стороны прямоугольного треугольника, площадь которого равна и . Мы знаем из базовой геометрии (теорема Пифагора), что x ² + y ² = z ² , а также из условия площади, что xy = 2 n . Это означает

(x+y) ² = x ² + 2xy +y ² = z ² + 4n &nbsp &nbsp и &nbsp &nbsp (x-y) ² = x ² — 2xy +y ² = z ² — 4н .