Производная синус квадрат: Производная sin^2 x

Производная синуса угла равна косинусу того же угла

Дана простейшая функция тригонометрии у = Sin(х), она дифференцируема в каждой своей точке из всей области определения. Необходимо доказать, что производная синуса любого аргумента равна косинусу того же угла, то есть у’ = Cos(х).

Доказательство основывается на определении производной функции

Зададим х (произвольное) в некоторой малой окрестности Δх конкретной точки х₀. Покажем значение функции в ней и в точке х, чтобы найти приращение заданной функции. Если Δх ― приращение аргумента, то новый аргумент — это х₀+Δx = х, значение данной функции при заданном значении аргумента у(х) равно Sin(х₀+Δx), значение функции в конкретной точке у(х₀) тоже известно.

Теперь имеем Δу= Sin(х₀+Δх)-Sin(х₀) ― полученное приращение функции.

По формуле синуса суммы двух неодинаковых углов будем преобразовывать разность Δу.

Δу = Sin(х₀)·Cos(Δх)+Cos(х₀)·Sin(Δx) минус Sin(х₀) = (Cos(Δx)-1)·Sin(х₀)+Cos(х₀)·Sin(Δх).

Выполнили перестановку слагаемых, сгруппировали первое с третьим Sin(х₀), вынесли общий множитель — синус — за скобки. Получили в выражении разность Cos(Δх)-1. Осталось сменить знак перед скобкой и в скобках. Зная, чему равно 1-Cos(Δх), сделаем замену и получим упрощенное выражение Δу, которое затем разделим на Δх.
Δу/Δх будет иметь вид: Cos(х₀)·Sin(Δх)/Δх-2·Sin²(0,5·Δх)·Sin(х₀)/Δх. Это и есть отношение приращения функции к допущенному приращению аргумента.

Осталось найти предел полученного нами отношения lim при Δх, стремящегося к нулю.

Известно, что предел Sin(Δх)/Δx равен 1, при данном условии. А выражение 2·Sin²(0,5·Δх)/Δх в полученном частном подведем преобразованиями к произведению, содержащему в качестве множителя первый замечательный предел: числитель и знеменатель дроби разделим на 2, квадрат синуса заменим произведением. Вот так:
(Sin(0,5·Δx)/(0,5· Δx))·Sin(Δx/2).
Предел этого выражения при Δх, стремящемся к нулю, будет равен числу ноль (1 умножить на 0). Выходит, что предел отношения Δy/Δх равен Cos(х₀)·1-0, это и есть Cos(х₀), выражение, которое не зависит от Δх, стремящегося к 0. Отсюда следует вывод: производная синуса любого угла х равна косинусу х, запишем так: у’ = Cos(х).

Полученная формула занесена в известную таблицу производных, где собраны все элементарные функции

При решении задач, где встречается производная синуса, можно пользоваться правилами дифференцирования и готовыми формулами из таблицы. Например: найти производную простейшей функции у=3·Sin(х)-15. Воспользуемся элементарными правилами дифференцирования, выноса числового множителя за знак производной, и вычисления производной постоянного числа (она равна нулю). Применим табличное значение производной синуса угла х, равное Cos(х). Получаем ответ: y’ = 3·Cos(x)-O. Эта производная, в свою очередь, тоже является элементарной функцией у = З·Cos(х).

Производная синуса в квадрате от любого аргумента

При вычислении данного выражения (Sin²(х))’ необходимо вспомнить, как дифференцируется сложная функция. Итак, у = Sin²(х) ― является степенной функцией, так как синус в квадрате. Аргументом ее является тоже тригонометрическая функция,^{сложный аргумент. Результат в этом случае равен произведению, первый множитель которого производная квадрата данного сложного аргумента, а второй ― производная от синуса. Вот как выглядит правило дифференцирования функции от функции: (u(v(х)))’ равна (u(v(х)))’·(v(х))’. Выражение v(х) ― сложный аргумент (внутренняя функция). Если дана функция «игрек равен синусу в квадрате х», то производная этой сложной функции будет у’ = 2·Sin(х)·Cos(x). В произведении первый удвоенный множитель ― производная известной степенной функции, а Cos(х) ― производная синуса, аргумента сложной квадратичной функции. Окончательный результат можно преобразовать, воспользовавшись тригонометрической формулой синуса двойного угла. Ответ: производная равна Sin(2·x). Эта формула легко запоминается, ею часто пользуются как табличной.}

Производная синуса угла равна косинусу того же угла

Дана простейшая функция тригонометрии у = Sin(х), она дифференцируема в каждой своей точке из всей области определения. Необходимо доказать, что производная синуса любого аргумента равна косинусу того же угла, то есть у’ = Cos(х).

Доказательство основывается на определении производной функции

Зададим х (произвольное) в некоторой малой окрестности Δх конкретной точки х₀. Покажем значение функции в ней и в точке х, чтобы найти приращение заданной функции. Если Δх ― приращение аргумента, то новый аргумент — это х₀+Δx = х, значение данной функции при заданном значении аргумента у(х) равно Sin(х₀+Δx), значение функции в конкретной точке у(х₀) тоже известно.

Теперь имеем Δу= Sin(х₀+Δх)-Sin(х₀) ― полученное приращение функции.

По формуле синуса суммы двух неодинаковых углов будем преобразовывать разность Δу.

Δу = Sin(х₀)·Cos(Δх)+Cos(х₀)·Sin(Δx) минус Sin(х₀) = (Cos(Δx)-1)·Sin(х₀)+Cos(х₀)·Sin(Δх).

Выполнили перестановку слагаемых, сгруппировали первое с третьим Sin(х₀), вынесли общий множитель — синус — за скобки. Получили в выражении разность Cos(Δх)-1. Осталось сменить знак перед скобкой и в скобках. Зная, чему равно 1-Cos(Δх), сделаем замену и получим упрощенное выражение Δу, которое затем разделим на Δх.
Δу/Δх будет иметь вид: Cos(х₀)·Sin(Δх)/Δх-2·Sin²(0,5·Δх)·Sin(х₀)/Δх. Это и есть отношение приращения функции к допущенному приращению аргумента.

Осталось найти предел полученного нами отношения lim при Δх, стремящегося к нулю.

Известно, что предел Sin(Δх)/Δx равен 1, при данном условии. А выражение 2·Sin²(0,5·Δх)/Δх в полученном частном подведем преобразованиями к произведению, содержащему в качестве множителя первый замечательный предел: числитель и знеменатель дроби разделим на 2, квадрат синуса заменим произведением. Вот так:

(Sin(0,5·Δx)/(0,5· Δx))·Sin(Δx/2).
Предел этого выражения при Δх, стремящемся к нулю, будет равен числу ноль (1 умножить на 0). Выходит, что предел отношения Δy/Δх равен Cos(х₀)·1-0, это и есть Cos(х₀), выражение, которое не зависит от Δх, стремящегося к 0. Отсюда следует вывод: производная синуса любого угла х равна косинусу х, запишем так: у’ = Cos(х).

Полученная формула занесена в известную таблицу производных, где собраны все элементарные функции

При решении задач, где встречается производная синуса, можно пользоваться правилами дифференцирования и готовыми формулами из таблицы. Например: найти производную простейшей функции у=3·Sin(х)-15. Воспользуемся элементарными правилами дифференцирования, выноса числового множителя за знак производной, и вычисления производной постоянного числа (она равна нулю). Применим табличное значение производной синуса угла х, равное Cos(х). Получаем ответ: y’ = 3·Cos(x)-O. Эта производная, в свою очередь, тоже является элементарной функцией у = З·Cos(х).

Производная синуса в квадрате от любого аргумента

При вычислении данного выражения (Sin²(х))’ необходимо вспомнить, как дифференцируется сложная функция. Итак, у = Sin²(х) ― является степенной функцией, так как синус в квадрате.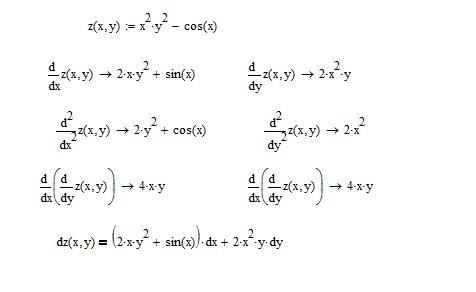 Аргументом ее является тоже тригонометрическая функция,^{сложный аргумент. Результат в этом случае равен произведению, первый множитель которого производная квадрата данного сложного аргумента, а второй ― производная от синуса. Вот как выглядит правило дифференцирования функции от функции: (u(v(х)))’ равна (u(v(х)))’·(v(х))’. Выражение v(х) ― сложный аргумент (внутренняя функция). Если дана функция «игрек равен синусу в квадрате х», то производная этой сложной функции будет у’ = 2·Sin(х)·Cos(x). В произведении первый удвоенный множитель ― производная известной степенной функции, а Cos(х) ― производная синуса, аргумента сложной квадратичной функции. Окончательный результат можно преобразовать, воспользовавшись тригонометрической формулой синуса двойного угла. Ответ: производная равна Sin(2·x). Эта формула легко запоминается, ею часто пользуются как табличной.}

2}x}}{{\Delta x}} \\ \frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\left[ {\sin\left({x+\Deltax}\right) +\sinx}\right]\left[ {\sin\left({x+\Deltax}\right) -\sinx}\right ]}}{{\Delta x}} \\ \end{gathered} \]

Используя формулу из тригонометрии \[\sin A – \sin B = 2\cos \left( {\frac{{A + B }}{2}} \right)\sin \left( {\frac{{A – B}}{2}} \right)\]
\[\begin{gathered}\frac{{dy}}{{ dx}} = \mathop {\lim}\limits_{\Delta x \to 0} \frac{{\left[ {\sin \left({x + \Delta x} \right) + \sin x} \right ] \ left [ {2 \ cos \ left ( {\ frac {{x + \ Delta x + x}} {2}} \ right) \ sin \ left ( {\ frac {{x + \ Delta x — x} }{2}} \right)} \right]}}{{\Delta x}} \\ \frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\Delta x \to 0} \left[ {\sin\left({x + \Delta x} \right) + \sinx} \right] \times\frac{{\cos\left( {\frac{{2x +\Delta x) }}{2}} \right)\sin \left( {\frac{{\Delta x}}{2}} \right)}}{{\frac{{\Delta x}}{2}}} \ \ \frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\Delta x \to 0} \lef t [ {\ sin \ left ({x + \ Delta x} \ right) + \ sin x} \ right] \ times \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ cos \ left ( { \frac{{2x + \Delta x}}{2}} \right)\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \left( {\frac{{\Delta x}}{2}} \right)}}{{\frac{{\Delta x}}{2}}} \\ \frac{{dy}}{{dx}} = \left[ {\sin\ влево( {x + 0} \right) + \sin x} \right]\cos \left( {\frac{{2x + 0}}{2}} \right)\left( 1 \right) \\ \ frac{{dy}}{{dx}} = 2\sin x\cos x \\ \end{gathered} \] 92}x = 2\sin x\cos x$$, получаем

\[\begin{gathered}\frac{{dy}}{{dx}} = 2\sin \sqrt {x – 1} \cos \ sqrt {x – 1} \frac{d}{{dx}}\sqrt {x – 1} \\ \frac{{dy}}{{dx}} = 2\sin \sqrt {x – 1} \cos \sqrt {x – 1} \frac{1}{{2\sqrt {x – 1} }}\frac{d}{{dx}}\left( {x – 1} \right) \\ \frac{ {dy}}{{dx}} = \frac{{\sin\sqrt {x – 1} \cos \sqrt {x – 1} }}{{\sqrt {x – 1}}} \\ \end{ собрал} \]

⇐ Производная косеканса ⇒ Производная квадрата косинуса ⇒

Производная квадратного корня из X

В тригонометрическом дифференцировании большинство примеров основано на функции синуса квадратного корня.