Лучший ответ по мнению автора
| |||||||||||||||||
09.15
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Сестра нашла 27 грибов, а брат — .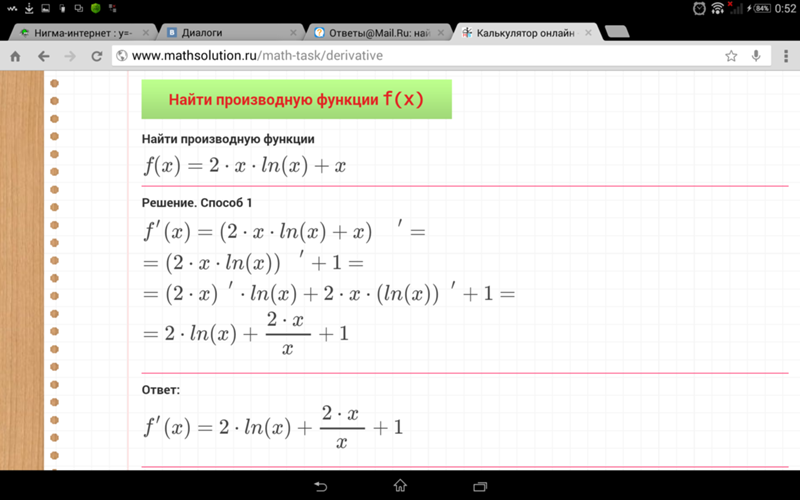
Среди этих грибов было 3 несъедобных. Сколько всего съедобных грибов нашли дети? Заполни пропуск. Реши задачу разными способами.
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
в зале на шести скамейках сидят 18 учеников . Сколько учеников на трех скамейках, если на каждой скамейке помещается одно и тоже число учеников
подберите значение переменной и решите задачу. на одной из остановок Том купил для себя 2 рыболовных крючка и заплатил х $. сколько стоит один такой крючок ,3 крючка и 5 крючков
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
Пользуйтесь нашим приложением
Производная от ln(2x) — DerivativeIt
Производная от ln(2x) равна 1/x
Как рассчитать производную от ln(2x)
вычисление производной от ln(2x).
Первый метод заключается в использовании цепного правила для производных.
Второй метод заключается в использовании свойств журналов для записи ln(2x) в форму, которая дифференцируема без необходимости использования цепного правила.
Нахождение производной от ln(2x) с помощью цепного правила
Цепное правило полезно для нахождения производной выражения, которое можно было бы дифференцировать, если бы оно было выражено в x, но в форме другого выражения, которое также могло бы быть дифференцированным, если бы он стоял сам по себе.
В этом случае:
- Мы знаем, как дифференцировать 2x (ответ 2)
- Мы знаем, как дифференцировать ln(x) (ответ 1/x)
Это означает, что цепное правило позволит нам провести дифференцирование функции ln(2x).
Чтобы выполнить дифференцирование, цепное правило говорит, что мы должны дифференцировать выражение, как если бы оно было выражено только в терминах x, если мы затем умножаем этот результат на производную того, чем на самом деле выражено выражение (в данном случае производная от 2x).
Использование цепного правила для нахождения производной от ln(2x)
ln(2x) представляет собой стандартную логарифмическую функцию ln(x), за исключением того, что она не имеет x в качестве аргумента, вместо этого она имеет другой функция х (2х).
Вызовем функцию в аргументе g(x), что означает:
g(x) = 2x
Отсюда следует, что:
ln(2x) = ln(g(x))
Итак если функция f(x) = ln(x) и функция g(x) = 2x, то функция ln(2x) может быть записана как составная функция.
f(x) = ln(x)
f(g(x)) = ln(g(x)) (но g(x) = 2x)
f(g(x)) = ln(2x) )
Определим эту составную функцию как F(x):
F(x) = f(g(x)) = ln(2x)
Мы можем найти производную от ln(2x) (F'(x)) с помощью цепного правила.
Цепное правило:
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(g(x))
Тогда производная от (x) есть F'(x) = f'(g(x)).
g'(x)
Теперь мы можем просто подставить f(x) и g(x) в цепное правило. Но прежде чем мы это сделаем, просто вспомним производную натурального логарифма.
Производная ln(x) по x равна (1/x)
Производная ln(s) по s равна (1/s)
Аналогичным образом производная ln(2x) по 2x равна (1/2x).
Мы будем использовать этот факт как часть цепного правила, чтобы найти производную ln(2x) относительно x .
Как найти производную от ln(2x) с помощью цепного правила: Определение правила Используя цепное правило, мы находим, что производная от ln(2x) равна 1/x Наконец, небольшое замечание по синтаксису и обозначениям: ln(2x) иногда записывается в приведенных ниже формах (с производной согласно приведенным выше расчетам). Top Tip Можно обобщить производную выражения в виде ln(ax) (где a — постоянное значение): Производная ln(ax) = 1 /x (независимо от значения константы, производная ln(ax) всегда равна 1/x) Поскольку ln — натуральный логарифм, применяются обычные свойства логарифма. Свойство произведения бревен утверждает, что ln(xy) = ln(x) + ln(y). Другими словами, получение журнала продукта равно суммированию журналов каждого члена продукта. Поскольку 2x является произведением 2 и x, мы можем использовать свойства логарифмов, чтобы переписать ln(2x): f(x) = ln(2x) = ln(2) + ln(x) Как найти производную от ln(2x), используя свойство произведения бревен Правило произведения для дифференцирования утверждает, что производная от f(x). Правило произведения: 6 6 = f'(g(x)).(2) g(x) = 2x ⇒ g'(x) = 2 = (1/2x).2 f (g(x)) = ln(2x) ⇒ f'(g(x)) = 1/2x
(Производная ln(2x) по 2x равна (1/2x)) = 1/x 
Просто имейте в виду, что не все приведенные ниже формы математически правильны. LN2X ► Производная LN2X = 1/x LN 2x ► Производное LN 2x = 1/x LN 2x 99696969696969696969696969696969696969696969696 гг. /x Нахождение производной от ln(2x) с использованием свойств логарифма
= 0 + ln(x) ln2 — константа, производная от константы равна 0 = 1/x Вторая производная от ln(2x) 92x с использованием правила произведения
g(x) равна f'(x)g(x) + f(x).g'(x)
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(x).g(x) 9004
Тогда производная F(x) равна F'(x) = f'(x)g(x) + f(x)g'(x)
Сначала пусть F(x) = ln 2 (x)
Тогда помните, что ln 2 (x) равно ln(x).ln(x)
Итак, F(x) = ln(x)ln(x)
Установив f( x) и g(x), поскольку ln(x) означает, что F(x) = f(x).g(x), и мы можем применить правило произведения, чтобы найти F'(x) (вспоминая, что производная ln( x) равно 1/x)
| F'(x) | = f'(x)g(x) + f(x)g'(x) | Определение правила продукта |
| = f'(x)ln(x) + ln(x)g'(x) | f(x) = g(x) = ln(x) 92x с использованием цепного правила Цепное правило полезно для нахождения производной функции, которую можно было бы дифференцировать, если бы она была по x, но она представлена в виде другого выражения, которое также можно было бы дифференцировать, если бы оно стояло само по себе . |
