1.2.3 Синус, косинус, тангенс и котангенс числа
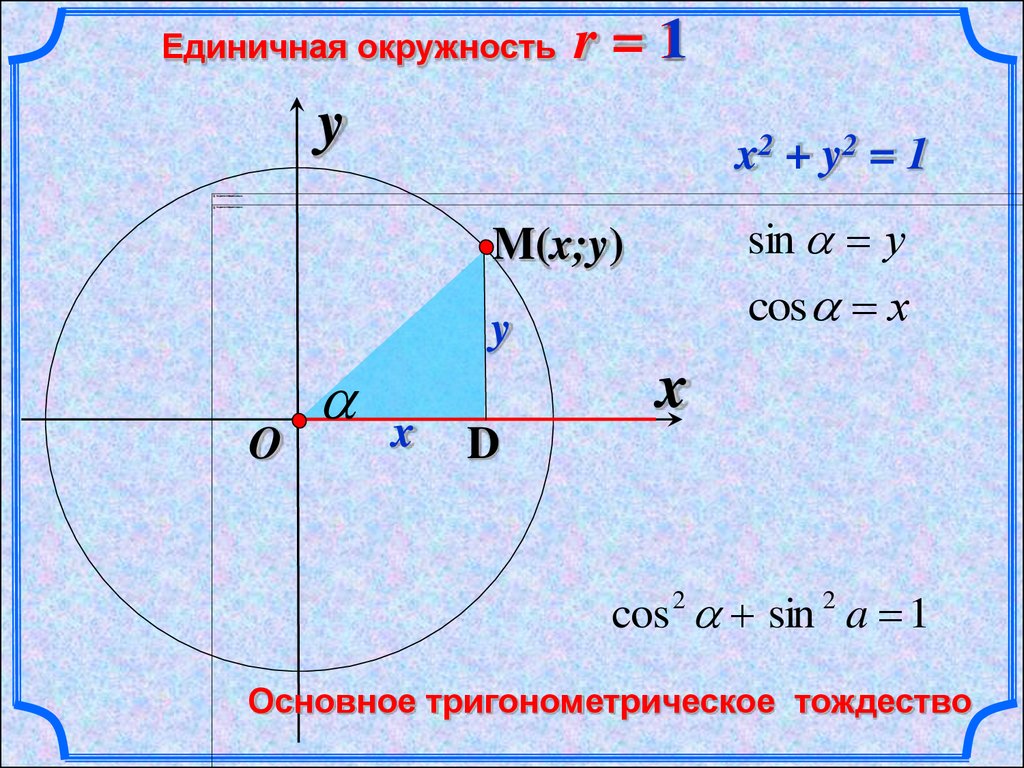
Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус. Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.
Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол
Решение. За начало отсчета принимаем точку Р0. Угол, равный нулю радиан совпадает с данной точкой.
Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Рπ/6.
Чтобы получить угол π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка — π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.
Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.
3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.
Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.
Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.
Отсюда можно сделать вывод, что:
Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.
Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.
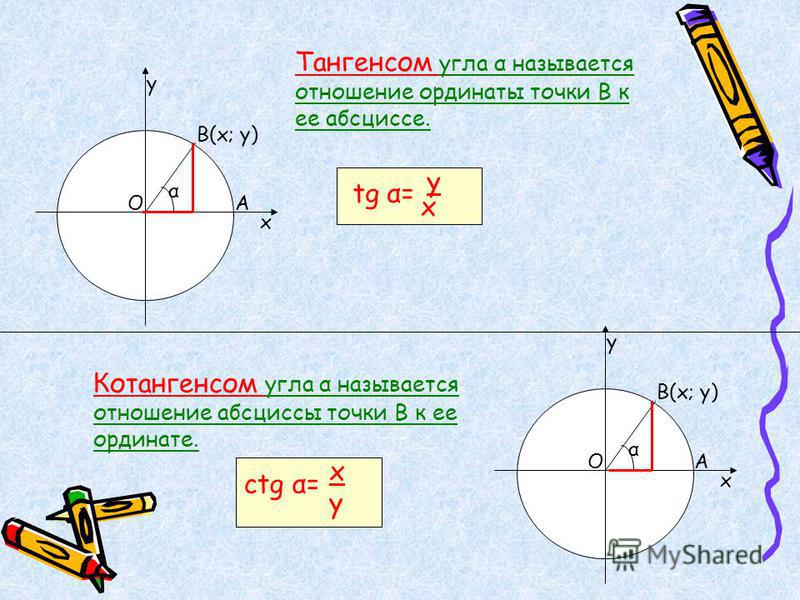
Тангенс некоторого числа — это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.
Котангенс некоторого числа — это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.
Синус и косинус имеют период, равный 6,28. Тангенс и котангенс имеет период, равный 3,14.
 2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)
2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)- Вконтакте
- Сайт
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒
· Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (AB/OB). · Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе (ОА/OB). · Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету (AB/OA). · Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету (ОА/AB).
Значения тригонометрических функций. Значения тригонометрических функций для некоторых углов.
Значения косинуса и синуса на окружности.
Свойства тригонометрических функций Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или основному тригонометрическому тождеству, имеем: Деля это уравнение на квадрат косинуса и синуса соответственно, имеем далее: Формулы приведения: sin (90° — α) = cos α cos (90° — α) = sin α sin (180° — α) = sin α cos(180° — α) = — cos α Чётность и нечетность функций. Чётная функция— функция y = f ( x ) называется чётной, если область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство f (- x ) = f ( x ) Нечётная функция— функция, область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство f(- x) = — f( x) Косинус — единственная чётная функция. Теоремы Теорема о площади треугольника:
Дано: ∆ АВС, АВ= с, ВС = a, СА = b , h — высота Доказать: S = ½ ab sin C Доказательство: Введём систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S = ½ ah , где h – высота треугольника. Но h равна ординате точки А, т.е. h = b sin C (т.к. sin C = h / b) => S = ½ ab sin C Ч.
Теорема синусов:
Дано: ∆АВС АВ= с, ВС= а, СА= b Доказать : a/ sinA = b/ sin B = c/ sinC Доказательство: По теореме о площади треугольника S= ½ ab sinC, S = ½ bc sinA, S= ½ ac sinB. Из первых двух равенств получаем ½ ab sinC = ½ bc sinA, ½ ab sinC = ½ bc sinA │ : ½ b a sinC = c sinA │: sinA sinC a/sinA = c/sinC Точно также из второго и третьего равенства получаем ½ bc sinA = ½ ac sinB │: ½ c b sinA = a sinB │: sinA sinB b/sinB = a/sinA Так как a/sinA = c/sinC и b/sinB = a/sinA, то a/sinA= b/sinB= c/sinC. Ч.т.д. Замечание: Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. a/sinA= b/sinB= c/sinC= 2R Дано: R – радиус описанной окружности, ВС = a, BA1 — диаметр Доказать: BC/sinA = 2R (BC=2R sinA) Доказательство: Проведем диаметр ВА1. Рассмотрим ∆А1ВС, ∟С — прямоугольный => ВС=ВА1×sinA1. Если т.А1 лежит на дуге ВАС, то ∟А1=∟А, если на дуге BDC, то ∟A1= 180° — ∟A. И в том, и в другом случае sinA1 = sinA => BC= BA1*sinA, BC= 2R sinA или BC/sinA= 2R. Ч.т.д.
Теорема косинусов:
Дано: Доказать: a2 = b2 + c2 − 2bc cosα Доказательство: Введем систему координат с началом в точке А. Точка В имеет координаты (с; 0), а точка С(b cosA; b sinA). По формуле расстояния между двумя точками d2 = (x2 – x1)2 + (y2 – y1)2 получаем: ВС2 = a2 = (b cosA – c)2 +(bsinА- 0) 2, a 2= b2cos2A — 2bc cosA + c2 + b2 sin2A, a2= b2 (cos2A + sin2A) + c2— 2bc cosA, a2= b2+ c2 – 2bc cosA. Ч. ⇐ Предыдущая123Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с. |
Вопрос Видео: Использование коэффициента синуса для нахождения котангенса угла
Стенограмма видео
Найдите раскладушку 𝜃, учитывая, что грех 𝜃 равен трем пятым, где 𝜃 находится между 90 и 180 градусами.
Итак, мы пытаемся найти кроватку 𝜃. А используя триггерные тождества, мы знаем несколько вещей. Мы знаем, что кроватка 𝜃 равна косинусу 𝜃, деленному на грех 𝜃, что на самом деле то же самое, что кроватка 𝜃 равна единице больше тангенса 𝜃, потому что тангенс 𝜃 равен греху 𝜃 разделить на кос 𝜃. Поэтому, когда вы берете единицу, деленную на это, она просто переворачивает ее, косинус над синусом. Теперь это не будет очень полезно, потому что мы знаем синус, однако у нас нет никакой информации о косинусе. Поэтому мы не хотим их использовать.
Теперь наше второе уравнение: кроватка в квадрате 𝜃 плюс один равно csc в квадрате 𝜃. А csc 𝜃 равно единице над sin 𝜃, а синус нам известен. Таким образом, осталась бы только раскладушка в квадрате 𝜃, и мы могли бы возвести корень и найти только раскладушку из 𝜃.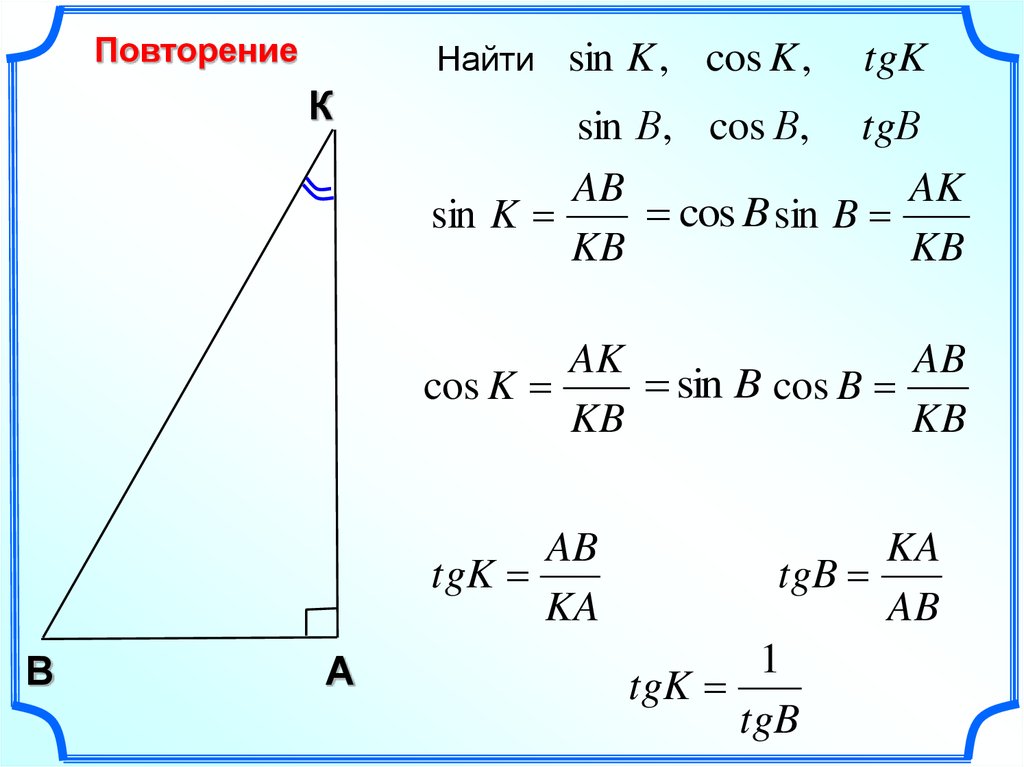 Итак, давайте продолжим и воспользуемся этим уравнением.
Итак, давайте продолжим и воспользуемся этим уравнением.
Итак, как мы сказали, мы можем заменить csc 𝜃 на единицу над грехом 𝜃. И тогда, конечно, мы должны привести его в квадрат. Итак, теперь давайте заменим sin числа 𝜃 на три пятых, так что это означает, что внутри скобок у нас есть единица, разделенная на три пятых. Теперь один равен одному на один, поэтому, если мы берем один на один и делим на три пятых, это означает, что мы на самом деле закончим умножением на обратное значение знаменателя. По сути, мы переворачиваем нижнюю часть дроби. А теперь умножаем прямо. Итак, один раз пять — пять, а один раз три — три. Таким образом, мы получаем пять третей. А если возвести пять третей в квадрат, то пять в квадрате будет 25, а три в квадрате — девять.
Итак, теперь нашим следующим шагом будет выделение раскладушки в квадрате 𝜃. Итак, давайте вычтем один с обеих сторон. Те, что слева, сокращаются, но справа, двадцать пять девятых минус один, мы можем сделать из одного девять больше девяти, потому что это эквивалентно единице. Теперь, когда мы вычитаем дроби, мы вычитаем числители и сохраняем знаменатели. Итак, у нас есть кроватка в квадрате 𝜃 равна шестнадцати девятым. Теперь, чтобы найти котангенс, нам нужно извлечь квадратный корень из обеих сторон. Таким образом, квадратный корень из 16 равен четырем, а квадратный корень из девяти равен трем. Таким образом, детская кроватка 𝜃 равна четырем третям.
Теперь, когда мы вычитаем дроби, мы вычитаем числители и сохраняем знаменатели. Итак, у нас есть кроватка в квадрате 𝜃 равна шестнадцати девятым. Теперь, чтобы найти котангенс, нам нужно извлечь квадратный корень из обеих сторон. Таким образом, квадратный корень из 16 равен четырем, а квадратный корень из девяти равен трем. Таким образом, детская кроватка 𝜃 равна четырем третям.
Теперь это также дает нам другую информацию, что 𝜃 находится между 90 градусами и 180 градусами. Итак, глядя на наш график здесь, у нас есть ноль градусов, затем 90, 180, 270. И затем, на самом деле, когда мы делаем целый круг, мы получаем 360 градусов, что точно такое же, как ноль градусов. Итак, он говорит, что 𝜃 находится между 90 и 180, значит, 𝜃 здесь. Теперь мы находим котангенс, и важно знать, что мы смотрим на график, 𝑥 представляет косинус 𝜃, а 𝑦 представляет грех 𝜃. А котангенс равен cos 𝜃, деленному на sin 𝜃. Итак, мы смотрим на это только для того, чтобы решить, положительно это или отрицательно, четыре трети.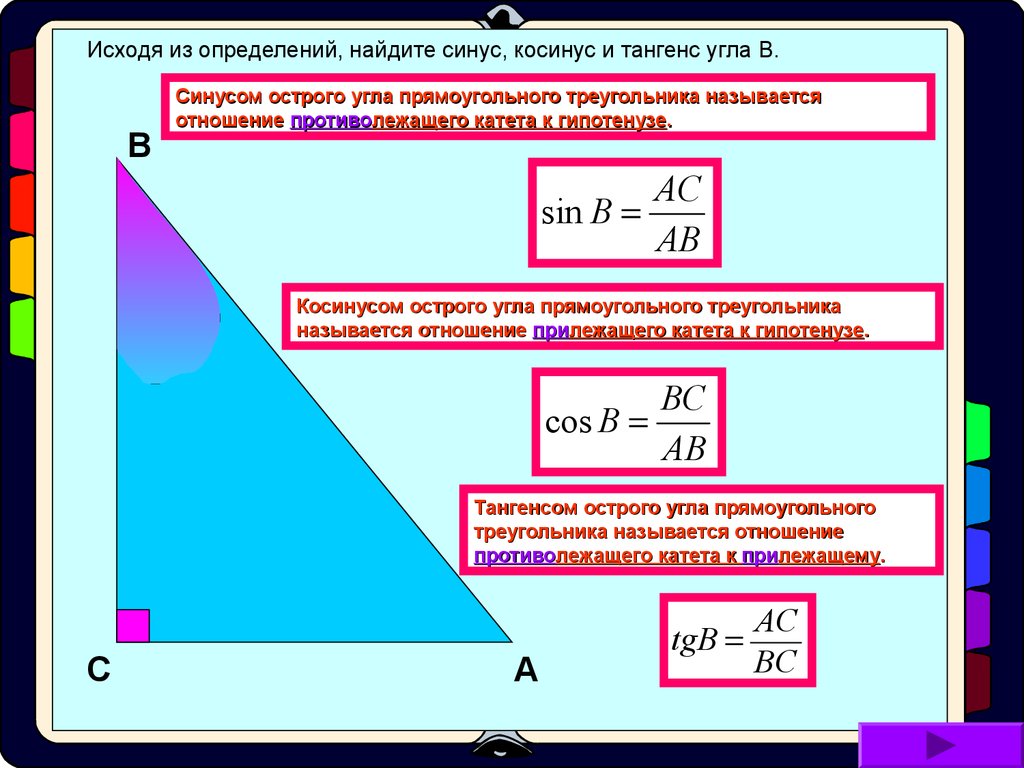
Итак, во втором квадранте из всех четырех квадрантов мы рассматриваем второй квадрант для 𝜃, потому что мы находимся между 90 и 180 градусами. Здесь мы видим, что 𝑦 положительно, но 𝑥 будет отрицательным. Это означает, что синус положительный, а косинус отрицательный. А минус разделить на плюс — это минус. Поэтому нам нужно сделать наши четыре трети отрицательными четырьмя третями из-за того, где находится 𝜃.
Итак, котангенс числа 𝜃 равен отрицательным четырем третям.
Тригонометрическая функция (круговая функция) — Статистика Как сделать
Содержание (щелкните, чтобы перейти к этому разделу):
- Что такое тригонометрическая функция?
- Общие типы тригонометрических функций
- Функция косеканса: csc(x),
- Функция косинуса: cos(x),
- Котангенс Функция: cot(x),
- Синусоидальная функция: sin(x),
- Функция секанса: сек(х),
- Tan Функция: tan(x).

- Обратная тригонометрическая функция
- Обратный синус (Arcsin)
- Функция арккосинуса
- Функция арктангенса
- Арктический секанс
- Архаичные и необычные триггерные функции
- Экскосеканс: csc(x)
- Функция экссеканса
- Функция гаверсина
- Функция Versine
- Общие типы тригонометрических функций
- Производная тригонометрической функции
- Формулы двойного угла
- Интегралы триггерных функций
- Тригонометрические тождества
- Единичный круг
Тригонометрическая функция , также называемая круговой функцией , является функцией угла.
Посмотрите видео с введением в тригонометрические функции или прочитайте ниже:
Тригонометрические функции: синус, косинус, тангенс, косеканс, секанс и котангенс
Посмотрите это видео на YouTube.
Функция косинуса ( cos(x) ) является периодической функцией, что означает, что она повторяется через равные промежутки времени.
Он широко используется в физике и геометрии и фактически был разработан — наряду с функцией синуса — в период Средневековья. Они использовались в период Гупта в индийской астрономии и занимают важное место в исламских математических документах 9 века.
Функция косинуса сокращается до cos , которая, кажется, возникла в математике 16-го века.
Одним из способов определения функции косинуса является прямоугольный треугольник. Представьте себе прямоугольный треугольник с углом A. Косинус треугольника A, сокращенно cos A, будет отношением прилежащей стороны к гипотенузе. На изображении ниже это будет b/h.
Существует только одна проблема с определением функции косинуса с помощью прямоугольного треугольника. Он работает только для угла между θ и π/2 радиан — между 0 и 90 градусами. Однако есть и другой способ определения косинуса, который позволяет использовать угол как положительное или отрицательное действительное число.
Определение тригонометрической функции с помощью единичного круга
На изображении ниже показан единичный круг с отмеченными на нем шестью тригонометрическими функциями. Как видите, cos θ можно определить как значение координаты x точки A.
Обратите внимание, что это определение совпадает с нашим старым определением для 0 ≤ θ ≤ π/2.
Также обратите внимание, что, поскольку для каждой точки P(x,y) на единичной окружности x 2 + y 2 = 1, мы можем написать тождество Пифагора для sin и cos также:
cos 2 + sin 2 = 1.
В начало
Функция котангенса , cot(x), является тригонометрической функцией — функцией углов. Это периодическая функция, повторяющаяся с периодом π.
Обозначение
Хотя обычно используется обозначение cot(x) , функция иногда обозначается как ctg(x) .
Формулу также можно записать так:
- Обратная функция тангенса: y = 1 / tan(x) или, что то же самое,
- В виде соотношения: y = cos(x) / sin(x),
- Как логарифмическая производная функции синуса: cot(x) = (log(sinx))′.
Где cos(x) — функция косинуса, а sin(x) — функция синуса.
График функции котангенса
Функция котангенса является нечетной функцией . «Странный» здесь не значит «необычный»! Это означает, что функция симметрична относительно начала координат. Это означает, что для каждой точки (x, y) на графике функции существует также точка (−x, −y). На графике зеленым цветом показаны симметричные точки (-1, -0,642) и (1, 0,642). Весь график состоит из ряда таких симметричных точек.
Особенности графика: касательные, корни, домен и диапазон
Некоторые наблюдения о вертикальных касательных графика, домен и диапазон и корни (нули):
- График имеет вертикальный тангенс везде sin(x) = 0.
 Они встречаются в каждом целом кратном π.
Они встречаются в каждом целом кратном π. - Область определения функции котангенса представляет собой все действительные числа, кроме: 0, ±π, ± 2π, ±3π …. При этих значениях sin(x) = 0, что делает знаменатель в уравнении (cos(x)/sin(x)) равным нулю (т. е. деление на ноль не допускается, поэтому функция в этих точках не определена).
- Диапазон функции котангенса представляет собой набор всех действительных чисел (-∞, ∞).
- корня (нули) функции котангенса находятся там, где график пересекает ось x. Они возникают там, где x = 0 (другими словами, когда значение косинуса равно нулю). Корни на приведенном выше графике находятся в ±π/2 и ±3π/2. Другой способ заявить это состоит в том, что корни находятся в каждом нечетном полуцелом кратном π.
Вернуться к началу
Функция гаверсинуса ( «половина синуса ») — тригонометрическая функция, чаще всего определяемая как:
гаверсин A = sin 2 ( A / 2).
Или, что то же самое:
hav A = ½(1 – cos A ).
Где :
- «А» — угол.
- sin = функция синуса.
- cos = функция косинуса.
Что делает функция гаверсина?
Функция гаверсинуса вычисляет расстояние по окружности d от двух точек снаружи сферы.
Расширяя это использование от сферической геометрии до реальной жизни, его можно использовать для определения расстояния путешествия (на земном шаре) с использованием широты и долготы.
Название «хаверсин», по-видимому, произошло от слов половина + версина; Версинус, одна из менее распространенных тригонометрических функций, в два раза больше гаверсинуса.
Историческое использование
Использование функции гаверсинуса исторически «…ограничивалось моряками и профессиональными [человеческими] компьютерами» (Hall, 1914). Он использовался как из-за его краткости (моряк хотел самых быстрых расчетов), так и из-за его точности (в течение сотен лет Морской альманах был библией мореплавателя и славился своей высокой точностью).
Сегодня функция гаверсинуса вышла из моды, ее заменили синус и косинус (гаверсинус можно записать в терминах функции синуса). Функция действительно всплывает время от времени. Например, функция гаверсинуса в компьютерном языке «R» использует широту и долготу для строк таблицы.
Вернуться к началу
Функция тангенса — популярная тригонометрическая функция; Это периодическая функция, которая повторяется каждые π периодов.
В виде формулы функция тангенса представляет собой частное (деление) функций синуса и косинуса: равно нулю из-за проблемы с делением на ноль. Работает большинство действительных чисел, за исключением x = π2 + целое число, кратное π. Следовательно, эти значения не находятся в домене.
Обозначение:
D = {x ∈ ℝ: x ≠ π/2 + nπ для n = 0, ±1, ±2,…}
Где:
- ℝ множество вещественные числа.
- ∈ = «находится в [наборе]».
Функция тангенса не ограничена, что означает, что диапазон стремится к бесконечности (она имеет вертикальные тангенсы в каждом периоде). Записанный в нотации диапазон равен:
Записанный в нотации диапазон равен:
R = (-∞, ∞)
График касательной функции
График представляет собой нечетную функцию, которая не имеет ничего общего с нечетными числами: «нечетный ” здесь означает, что он симметричен относительно начала координат.
График функции тангенса не проходит тест на горизонтальную линию, что говорит нам о том, что это не функция взаимно однозначного соответствия.
При работе с функцией тангенса в исчислении вы обычно ограничиваете домен, что означает, что вы будете использовать границу для ваших значений x. Приведенный ниже график имеет домен, ограниченный от -1 до 1.
Этот график напоминает «правильную» функцию (а не сильно колеблющуюся), что значительно упрощает работу с ним в вычислениях. Например, вы можете вычислить интеграл с такой ограниченной областью, что было бы невозможно, если бы область включала множество вертикальных асимптот, показанных на большем графике в разделе выше.
Производная tan(x) равна sec 2 .
В дополнение к приведенному выше примеру (и доказательству), второй рабочий пример см. в разделе: Правило частного (Tan x).
Вернуться к началу
Обратные тригонометрические функции буквально являются обратными тригонометрическими функциями. Вы можете думать о них как о противоположностях; В некотором смысле эти две функции «отменяют» друг друга.
Функция обратного синуса (Arcsin) , y = arcsin x, является обратной функцией синуса.
Функция синуса (красный) и функция обратного синуса (синий).
Однако, в отличие от функции синуса, которая имеет область значений от -π/2 до π/2, обратная функция имеет очень маленькую область значений: от -1 до 1.
Другие свойства функции обратного синуса :
- Диапазон составляет от -π/2 до π/2,
- Это нечетная функция (что означает, что она симметрична относительно начала координат),
- Arcsin x является возрастающей функцией : движется вверх слева направо.

Дополнительная информация: Определение функции арксинуса и примеры.
Эта функция, обозначаемая как arccos x, является обратной функцией косинуса.
Функция косинуса (красный) и арккосинуса (синий).
Свойства arccos x:
- Домен : [-1, 1],
- Диапазон от 0 до π,
- Эта функция не имеет симметрии (это ни нечетная, ни четная функция),
- Arccos x представляет собой убывающую функцию : она движется вниз слева направо.
В начало
Функция арктангенса, arctan x, является обратной функцией тангенса.
Функция арктангенса (зеленый) и функция тангенса (синий).
Свойства arctan x:
- Домен равен [-∞, ∞],
- Диапазон составляет от -π/2 до π/2,
- Это нечетная функция (симметрично относительно начала координат),
- Arccos x представляет собой возрастающую функцию , перемещающуюся вверх слева направо.

Вернуться к началу
Функция обратного косинуса , обозначаемая как arccos x или cos -1 x*, является обратной функцией косинуса. В тригонометрии арккосинус дает угол верхней половины единичной окружности.
*Обратите внимание, что верхний индекс -1 — это , а не показатель степени, это просто обозначение для обозначения инверсии. Поэтому стало обычным использовать arccos вместо sin 9.0130 -1 , чтобы избежать путаницы с показателями степени.
График функции арккосинуса
График функции арккосинуса — это просто функция косинуса, отраженная по диагональной линии y = x.
График cos x (красный) и функции арккосинуса arccos x (синий).
Домен и диапазон
Область определения функции арккосинуса [-1, to 1]. Диапазон равен [0, π].
Почему домен ограничен [-1, 1]?
Может показаться странным, что инверсия определена только для очень узкой области. Это связано с тем, что функция косинуса является функцией «многие к одному», что означает, что более одного входа дают один и тот же результат. Это создает проблемы с созданием инверсий, когда домен равен бесконечности; было бы неясно, какой член диапазона сопоставляется с каким членом домена.
Это связано с тем, что функция косинуса является функцией «многие к одному», что означает, что более одного входа дают один и тот же результат. Это создает проблемы с созданием инверсий, когда домен равен бесконечности; было бы неясно, какой член диапазона сопоставляется с каким членом домена.
По сути, у вас будет проблема, когда каждый вход сопоставляется с несколькими выходами. Если вы помните определение функции, это нарушает правило «один уникальный выход»; Функция арккосинуса не была бы функцией без этой ограниченной области.
На приведенном ниже графике показано, как будет выглядеть арккосинус, если немного выйти за пределы допустимого диапазона.
Допустимый диапазон [-1, 1] показан внутри желтого прямоугольника. Если вы выходите за пределы этой области, это не функция из-за нескольких выходов на один вход. Например, обе черные точки отображают от 0,9 до0110
Ссылки
График cos(x) и cos -1 x создан с помощью Desmos. com
com
Oldham, K. et al. (2008). Атлас функций. Спрингер.
Янг, К. (2017). Предварительный расчет. Уайли.
Вернуться к началу
Функция арксеканса (сек -1 ( x ) или arcsec( x )) является обратной функцией ограниченного секанса.
График функции арксеканс.Домен и область значений функции арксеканса
Область определения функции арксеканса равна [∞, -1) ∪ (1, ∞]. На английском языке это означает, что область определения состоит из двух отдельных частей. В графике существует разрыв между -1 и 1.
Если вы не знакомы с обозначениями, символ ∪ представляет собой «объединение», которое просто говорит вам, что две части вместе равны всему домену. Круглые скобки обозначают открытый интервал, а квадратные скобки — закрытый интервал. Вместе несоответствующие ( и ] называются полузакрытым интервалом (или полуоткрытым).
Диапазон функции арксеканса (показан на графике выше) от 0 до π. В обозначениях это:
0 ≤ x ≤ π.
Примечание об ограничении домена
График функции секущей.
Большинство текстов ограничивают домен приведенным выше определением, но некоторые авторы с этим не согласны. Разногласие связано с тем, что функция секущей определяется как sec(x) = 1/cos(x). Эта функция не определена везде, где происходит деление на ноль: существует вертикальная асимптота для каждого нечетного числа, кратного π/2 (например, π/5, 3π). Следовательно, чтобы получить взаимно-однозначную функцию, необходимо ограничить область определения до [0, π/2) ∪ (π/2,π], поскольку только взаимно-однозначные функции имеют обратные функции9.0005
В некоторых текстах вместо этого вы можете встретить домен [0, π/2) ∪ [3π/2).
Вернуться к началу
Триггерные функции и их производные:
| Триггерная функция | Производная |
| Синусоидальная функция: sin(x) | d/dx (sin x) = cos x |
| Функция косинуса: cos(x) | d/dx (cos x) = – sin x |
| Функция загара: загар(х) | d/dx (тангенс х) = сек 2 х |
| Функция секанса: сек(х) | d/dx (сек x) = сек x тангенс x |
| Функция косеканса: csc(x) | d/dx (csc x) = -csc x кроватка x |
| Функция котангенса: cot(x) | d/dx (раскладушка x) = – csc 2 x |
Использование определения производной тригонометрической функции
Вас могут попросить (особенно в начале исчисления) найти производную тригонометрической функции, используя определение производной вместо таблицы. Когда вы используете определение производной, вы на самом деле работаете над доказательством. Другими словами, если вы хотите доказать, что одна функция является производной от другой, вы почти всегда будете начинать с определения производной и заканчивать производной тригонометрической функции.
Когда вы используете определение производной, вы на самом деле работаете над доказательством. Другими словами, если вы хотите доказать, что одна функция является производной от другой, вы почти всегда будете начинать с определения производной и заканчивать производной тригонометрической функции.
Пример задачи
В. Найдите производную тригонометрической функции (sin x), используя определение производной (другими словами, докажите, что d/dx sin x = cos x:
Шаг 1: Вставьте функцию sin x в определение производной:
Шаг 2: Используйте тригонометрическое тождество sin(a + b) = sin a * cos B + cos a * sin B чтобы переписать определение шага 1:
шага 3: Используйте алгебру , чтобы переписать формулу шага 2:
= – sin x* (0) + cos x * (1) = cos x
Вот и все!
Совет: Вы можете использовать точно такую же технику для разработки доказательства любой тригонометрической функции. Начните с определения производной и найдите подходящие триггерные функции.
Начните с определения производной и найдите подходящие триггерные функции.
Наверх.
Версина на единичной окружности (круг радиусом один).
Функция versine (или versine e) является менее распространенной тригонометрической функцией. Он равен удвоенному гаверсину (название «гаверсин», по-видимому, произошло от слов половина + версин).
Функция имеет наклон с плавным переходом в начале и в конце функции (SPIE называет функцию «плавным профилем»):
График функции версуса,
Устаревшая функция
Функция versine в значительной степени устарела и в настоящее время считается в основном «исторической» функцией, редко используемой, за исключением случайных упоминаний в литературе. Когда-то эта функция была популярна, особенно в навигации, из-за ее полезности при поиске определенных сегментов линии. Однако даже эти ссылки в основном были связаны с более популярной функцией гаверсинуса, которая определяется в терминах версинуса следующим образом:
гаверсинус = ½версинус (x).
Ее также можно определить по-другому (используя немного алгебры) через гаверсинус: используется в теории управления (изучение поведения динамических систем) и обработке сигналов.
Функция также была определена как:
vers(x) = 1 – cos(x)
Или та же функция в другом обозначении:
cosC(t) = 1 − cos(t)
Вернуться к началу
Содержание:
- Синусная формула двойного угла
- Формула двойного угла Cos
- Формула двойного угла загара
Формулы двойного угла называются «двойными» углами, потому что они включают тригонометрические функции двойных углов, такие как sin 2x или cos 2x. Другими словами, когда мы используем формулу, мы удваиваем угол. Эти формулы позволяют переписать выражение с двойным углом, например sin 2x и cos 2θ, в выражение с одним углом. Это означает, что вместо того, чтобы работать со сложным выражением, вы можете преобразовать его в более простое. Помимо их способности помогать нам упрощать и решать уравнения, они могут проверять тождества и необходимы для некоторых аспектов исчисления, связанных с аналитической геометрией [1].
Помимо их способности помогать нам упрощать и решать уравнения, они могут проверять тождества и необходимы для некоторых аспектов исчисления, связанных с аналитической геометрией [1].
Список формул двойного угла
Формула двойного угла для синуса:
Косинус имеет три формы формулы двойного угла. Каждая выводится из теоремы Пифагора, поэтому вам нужно знать только одну (остальные можно вывести из формулы и теоремы Пифагора) [2]. Тем не менее, один может подойти для формата конкретной задачи, чем другие. Например, если в уравнении много синусов, используйте первую форму; Выберите тот, который приводит к меньшему количеству вычислений для вас:
Пример
Пример вопроса: Умножьте и упростите следующее выражение:
cos 4 θ – sin 4 θ.
Шаг 1: Разложите выражение на множители:
Вопрос требует, чтобы мы разложили на множители, поэтому давайте сделаем это сначала, чтобы привести его к «формуле двойного угла» в удобном формате:
Шаг 2: Упростить:
- Используйте основное тригонометрическое тождество cos 2 x + sin 2 x = 1 для замены левой части:
- Используйте первую формулу двойного угла cos, чтобы заменить правую часть формулы:
Решение cos 2θ.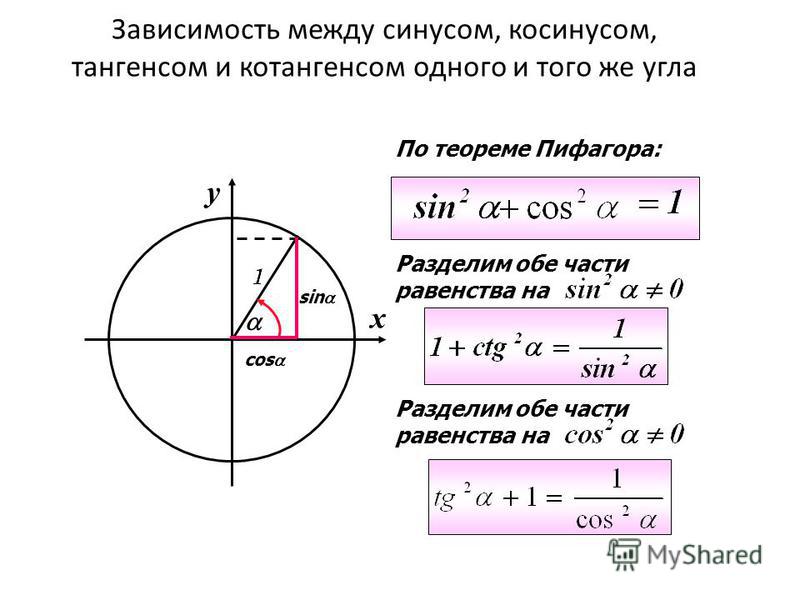
Формулы двойного угла: ссылки
[1] Формулы двойного угла и формулы половинного угла. Получено 11 июля 2021 г. с: https://www.math.utah.edu/lectures/math2060/2-5PostNotes.pdf
[2] Джойс, Д. (1996). Краткое изложение тригонометрических тождеств. Получено 11 июля 2021 г. с: https://www2.clarku.edu/faculty/djoyce/trig/identities.html
Интегралы для шести основных тригонометрических функций:
- ∫ sin(x) dx = -cos(x) + C dx
- ∫ cos(x) dx = sin(x) + C dx
- ∫ tan(x) dx = ln |sec(x)| + С дх
- ∫ кроватка(х) dx = ln |sin(x)| + С дх
- ∫ sec(x) dx = ln |sec(x) + tan(x)| + С дх
- ∫ csc(x) dx = ln |csc(x) – cot(x)| + С дх
Вернуться к началу
Тригонометрическая функция: триггерные тождества
Вам необходимо ознакомиться с тригонометрических тождества (или хотя бы знать, где их искать). Тригонометрия — это курс на целый семестр (иногда два!), поэтому здесь невозможно поставить всех тождеств.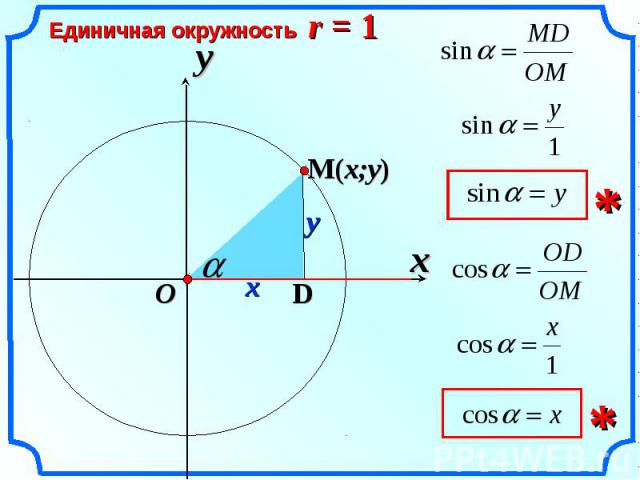 Но некоторые тождества проявляются в исчислении гораздо чаще, чем другие. Это тригонометрические тождества, которые вы будете использовать снова и снова.
Но некоторые тождества проявляются в исчислении гораздо чаще, чем другие. Это тригонометрические тождества, которые вы будете использовать снова и снова.
Взаимные тождества
Это говорит вам о том, что взаимные функции sec, csc и cot являются обратными функциями косинуса, синуса и тангенса.
Тождества тангенса и котангенса
Эти тождества говорят вам, что:
- Тангенс функции есть отношение синуса к косинусу,
- Раскладушка есть соотношение cos и sin.
Другие тригонометрические тождества
Первое тождество на самом деле просто версия теоремы Пифагора.
Приведенные выше тригонометрические тождества будут снова и снова использоваться на ваших занятиях. Они особенно пригодятся, когда дело доходит до вычисления производных или упрощения функций.
Например, если у вас есть sin 2 и cos 2 , близкие друг к другу в функции, вы можете отменить их, используя тригонометрическое тождество. Если у вас есть беспорядочно выглядящая функция с sin/cos/-cos 2 /sec и другими компонентами, поищите способы преобразования в sin или cos, используя приведенные выше тригонометрические тождества.
Если у вас есть беспорядочно выглядящая функция с sin/cos/-cos 2 /sec и другими компонентами, поищите способы преобразования в sin или cos, используя приведенные выше тригонометрические тождества.
Другие типы тригонометрических функций
Существуют десятки других возможных типов тригонометрических функций, таких как арккосинус, арктангенс и арксинус, но на самом деле вы будете редко или никогда не будете их использовать. Думаю, что за пять семестров курса вычислений в колледже я использовал более редкие тригонометрические функции только один или два раза. Вы, вероятно, никогда не увидите их в тесте (они могут быть заданы как «сложная» домашняя задача по тригонометрической функции). если они — это на тесте, ваш инструктор предоставит (или должен) список менее известных тригонометрических тождеств. Если вы знаете (и можете использовать) приведенные выше идентификаторы, у вас должно быть все готово для вашего класса.
Вернуться к началу
Единичный круг часто используется для определения тригонометрической функции, такой как версина.
Единичный круг имеет радиус 1 с центром в начале координат (0, 0) декартовой плоскости. Многие тригонометрические функции определяются в терминах единичной окружности, включая функцию синуса, функцию косинуса и функцию тангенса. Вот почему триггерные функции иногда называют «круговыми».
Единичный круг с радианами и градусами
Следующий единичный круг помечен градусами (полный оборот = 360°) и радианами (один оборот = 2π радиан), а также их соответствующими координатами на декартовой плоскости.
Единичная окружность, наложенная на ось x-y [2].
Эти координаты используются для нахождения шести общих тригонометрических значений:
- Координата x представляет собой косинус этого угла,
- Координата Y представляет собой синус этого угла.
Например, cos(30°) = √3/2 и sin(30° = ½).
Любая тригонометрическая функция может быть получена из этих двух соотношений.
Тригонометрическая функция: ссылки
Изображение круга единиц измерения: Jim. belk, CC BY-SA 1.0 , через Wikimedia Commons
belk, CC BY-SA 1.0 , через Wikimedia Commons
Графический калькулятор Desmos.
ДеЖарнетт, Н. Касательная функция. Получено 6 декабря 2019 г. с: https://faculty.math.illinois.edu/~ndejarne/teaching/MA115SP2014/Lecturetopics/LectureOutline14_Tangent_Inverse_Trig.pdf
Дешанг, Ю. (2016). Тригонометрические функции и комплексные числа: в математических олимпиадах и олимпиадах. Всемирная научная издательская компания. Эрдейи, А.; Магнус, В .; Оберхеттингер, Ф.; и Трикоми, Ф.Г. Высшие трансцендентальные функции, Vol. 1. Нью-Йорк: Кригер, с. 6, 1981.
Фишетти, Т. Майор, Э. и Форте, Р. (2017). Р: Предиктивный анализ. Packt Publishing Ltd.
Градштейн И. С., Рыжик И. М. Таблицы интегралов, рядов и произведений, 6-е изд. Сан-Диего, Калифорния: Academic Press, 2000.
Холл, В. (1914). Современная навигация: Учебник навигации и морской астрономии, адаптированный к курсу для кадетов Королевского флота. Университетское учебное издательство.
Корн, Г. и Корн, Т. (2013). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Курьерская корпорация.
Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Курьерская корпорация.
Ларсон, Р. и Эдвардс, Б. (2017). Исчисление. Cengage Learning.
Раздел 5.5 Обратные тригонометрические функции и их графики. Получено 4 мая 2020 г. с: http://www.math.wustl.edu/~freiwald/131inversetrig.pdf
Маор, Э. (2003). Справочник фактов о файловом исчислении. Издание информационной базы.
SPIE — Международное общество оптической инженерии, 1995. Интеллектуальные структуры и материалы: промышленное и коммерческое применение технологий интеллектуальных структур, том 2447 — Интеллектуальные материалы
Пенья, Дж. Сохраняющие форму альтернативы рациональной модели Безье. Получено 11 ноября 2019 г. из: Сохраняющие форму альтернативы рациональной модели Безье
Raaijmakers, S. (2009). Полиномиальное изучение языка. Проверено 19 ноября., 2019 г. из: https://pure.uvt.nl/ws/portalfiles/portal/1154994/Proefschrift_Stephan_Raaijmakers_011209.




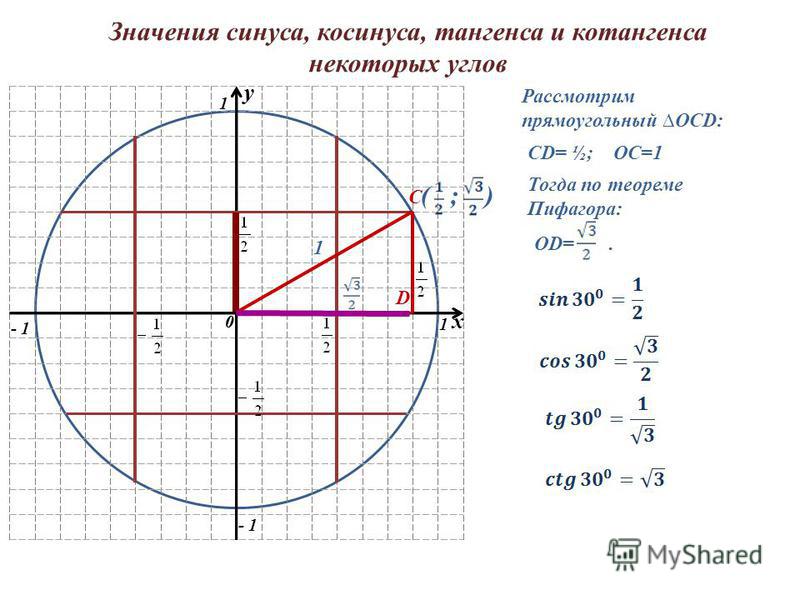
 т.д.
т.д.
 a 2 = b2 + c2 − 2bc cosα .
a 2 = b2 + c2 − 2bc cosα .
 т.д.
т.д. )
)
 Они встречаются в каждом целом кратном π.
Они встречаются в каждом целом кратном π.