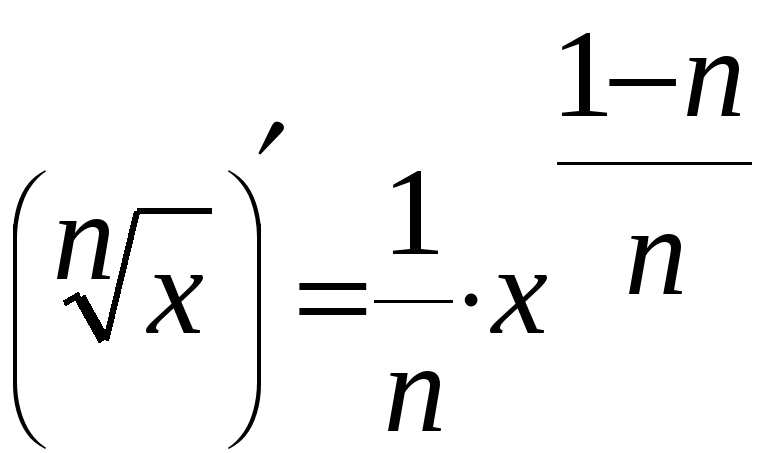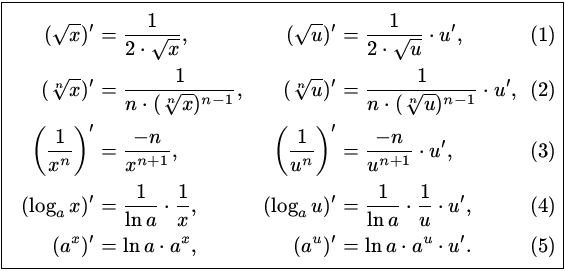Разработка урока ( 2*45 мин.) в 10 классе с профильным изучением математики по теме: «Применение производной к решению математических задач практического содержания.» Останькович Татьяна Эдгаровна- учитель высшей категории. Цель: формирование практических навыков применения теоретических знаний и общеучебных компетенций учащихся. Задачи: · познавательный аспект- расширение общего кругозора школьников, стимулирование познавательной деятельности, умение находить и обрабатывать информацию; · учебный аспект- активизация мыслительной деятельности учащихся при решении задач прикладного характера, алгоритмизация деятельности; ·
воспитательный
аспект- развитие умения работать в команде, активно слушать,
уважать чужое мнение, формировать потребности в самовыражении и научном
творчестве. Математические задачи с практическим содержанием – это такие задачи, которые связаны с применением математики в технике, химии, экономике, медицине, экологии, а так же в быту. Мы рассмотрим задачи, которые можно решить с помощью производной . Эти задачи не совсем обычны как по форме изложения, так и по применяемым методам решения. Одним из важнейших понятий математического анализа является производная функции. Производная характеризует скорость изменения функции по отношению к изменению независимой переменной. В геометрии производная характеризует крутизну графика, в механике – скорость неравномерного прямолинейного движения, в биологии – скорость размножения колонии микроорганизмов, в экономике – отзывчивость производственной функции (выход продукта на единицу затрат), в химии – скорость химической реакции. В приложениях математики к
решению конкретных задач приходится иметь дело с величинами, числовые значения
которых получены путем измерений и, следовательно, точное их значение
неизвестно. Среди многих задач, решаемых с помощью производной, наиболее важной является задача нахождения экстремума функции и связанная с ней задача нахождения наибольшего (наименьшего) значения соответствующих функций. Рассмотрим некоторые из них. ( Образцы задач может приводить как сам учитель, так и заранее подготовленные ученики). Задача №1 Докажите, что уравнение 3×5 – 25×3 + 60x + 15 = 0 имеет только один действительный корень. Решение: Рассмотрим функцию f(x) = 3×5 – 25×3 + 60x + 15 = 0 и найдем её интервалы
монотонности. Имеем: f’(x) = 15×4 – 75×2 + 60 = 15(x + 2)(x + 1)(x — 1)(x — 2). Производная f’(x) обращается в нуль в четырех точках: -2, -1, 1, 2. Эти точки разбивают числовую прямую на пять промежутков: (- ∞; -2), (-2; -1), (-1; 1), (1; 2), (2; +∞). На каждом из указанных промежутков производная сохраняет постоянный знак. Отсюда заключаем, что на каждом из этих промежутков функция y = f(x) монотонна, т.е. или возрастает или убывает. Тогда график функции на каждом из указанных промежутков может пересекать ось абсцисс не более∞ чем в одной точке. Это значит, что функция y = f(x) на каждом из рассматриваемых промежутков может иметь не более одного корня, причем корни функции могут быть в тех и только тех промежутках, на концах которых функция имеет разные по знаку значения. Имеем lim f(x) = — ∞, f(- 2) < 0, f(- 1) < 0, f(1) > 0, f(2) > 0, lim f(x) = +∞ x → — ∞ x → +∞
f(1) > 0, f(2) > 0, lim f(x) = +∞ x → + ∞ Так как f(x) имеет
различные знаки только на концах промежутка (-1; 1), то заданное уравнение
имеет лишь один действительный корень, лежащий внутри этого интервала. Задача №2. При извержении вулкана камни горной породы выбрасываются перпенди- кулярно вверх с начальной скоростью 120 м/ с. Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь? Решение: Вещество выбрасывается перпендикулярно вверх. Высота камня h, функция времени- h(t) = Vо t -1/2gt2 .Откуда следует: h(t)= v(t)= vо–gt. Следовательно, 0= 120-9,8t и t≈13 сек. Тогда h=745м, т.е. камни горной породы достигают уровня 720 м от края вулкана.
Задача №3. Нагруженные сани движутся по горизонтальной поверхности под действием силы F, приложенной к центру тяжести. Какой угол α должна составлять линия действия силы F с горизонтом, чтобы равномерное движение саней происходило под действием наименьшей силы? Коэффициент трения саней о снег равен к. Решение: Разложим силу F на горизонтальную и вертикальную составляющие. Сила нормального движения саней и вертикальной составляющей силы F:N=P-F sinα, поэтому сила трения F тр =kN= =k(P-Fsinα). Fx=Fтр., то есть Fcosα=k (P-Fsinα). Далее находим силу как функцию угла α: F(α)= kP/(ksinα+cosα). F′(α) =kP(sinα-kcosα)/(ksinα+cosα)2. Тогда F′(α)=0 при k=tgα. Определим знак второй производной в этой точке…
Из решения этой задачи можно сделать практический вывод: когда необходимо везти на санях груз по дороге с большим коэффициентом трения, нужно тянуть сани за короткую веревку. Если же коэффициент трения мал, веревка должна быть длинной.
Задача№4. Расход горючего легкового автомобиля (литр на 100 км) в зависимости от скорости х км/ч при движении на четвертой передачи приблизительно описывается функцией f(x)=0,0017х-0,18х+10,2; х>30. При какой скорости расход горючего будет наименьший? Найдите этот расход. Решение: Исследуем расход горючего с помощью производной: f′(х)=0,0034х-0,18.Тогда f′(х)=0 при х≈53. Определим знак второй производной в критической точке: f′′(х)=0,0034>0, следовательно, рас- ход горючего при скорости 53
км/ч будет наименьшим.
Задача№5. Оборот предприятия за истекший год описывается через функцию U(t)=0,15t2 – 2t2 + 200, где t –месяцы, U-миллионы. Исследуйте оборот предприятия. Решение. Исследуем оборот предприятия с помощью производной:U′(t)=0,45t2 — 4t U′′(t)=0,9t-4 U″′(t)=0,9. Момент наименьшего оборота при U(t)=0, т.е.при t=8,9.Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U(t)=0 следует t=4,4.Так как U″′(t)>0, то на пятом месяце имеется сильное снижение оборота. Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение. Так, например, по решению предложенной задачи можно сделать выводы: 1.В начале исследуемого периода у предприятия было снижение оборота; 2.Предприятие пыталось выйти из этого состояния и для этого использовало определенные средства. На пятом месяце ( точка перегиба) что-то было предпринято и предприятие стало выходить из кризиса, а
на девятом месяце стало набирать обороты.
Задачи из биологии и химии Биологический смысл производной. Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у=p(t). Пусть ∆t-промежуток времени от некоторого начального значения t до t+∆t. Тогда у+∆у=p(t+∆t)- новое значение численности популяции, соответствующее моменту t+∆t, а ∆y+p(t+∆t)-p(t)-изменение числа особей организмов. Химический смысл производной. Пусть дана функция m=m(t),где m-количество некоторого вещества, вступившего в химическую реакцию в момент времени t. Приращению времени ∆t будет соответствовать приращение ∆m величины m. Отношение ∆m/∆t- есть средняя скорость химической реакции за промежуток времени ∆t. Предел этого отношения при стремлении t∆ к нулю- есть скорость химической реакции в данный момент времени .
Р а с с м о т р и м н е с к о л ь к о з а д а ч
Задача №6. Зависимость между количеством х вещества, получаемого в результате некоторой химической реакции и временем t выражается уравнением
Х=А(1+е)
Определите скорость химической реакции в момент времени t.
Задача №7. Закон накопления сухой биомассы у винограда сорта Шалса определяется уравнением y=0,003x-0,0004x , где x- число дней от распускания почек, y-накопление биомассы в кг на 1 куст. Равенство отражает зависимость величин x и y как средний результат массовых наблюдений. Выясните, как изменится сухая биомасса при изменении от 50 до 60 дней.
Задача №8. Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, уменьшения температуры тела, изменении пульса или других физиологических показателей. степень реакции зависит от назначенного лекарства, его дозы. Предположим, что Х обозначает дозу назначенного лекарства, У — функция степени реакции. У=f(x)=x2(a-x) ,где а — некоторая положительная постоянная. При каком значении Х реакция максимальна? Решение: 0<x<а. Значит f′(x)=2ax-3×2 . Тогда
f′(x)=0 при x=⅔ а. В этой точке f″(⅔ а)= -2а<0, то х=⅔-а — тот уровень
дозы, который дает максимальную реакцию. Точки перегиба важны в биохимии, так как они определяют условия, при которых некоторая величина, например скорость процесса, наиболее ( или наименее) чувствительна к каким-либо воздействиям.
Предлагается творческое задание (при наличии времени на уроке, если имеем в наличии сдвоенные уроки. Если такая возможность отсутствует, творческое задание выполняется дома). Задача №9. За последние 10 лет численность грызунов в городе Н выросла в 5 рази достигла 1 миллиона особей: по одной крысе на каждого жителя. За год одна пара крыс способна воспроизвести 50 штук себе подобных. По словам эпидемиологов, крысы являются переносчиками многих болезней – чумы, бешенства, энцефалита. Составьте задачу по приведенным данным и решите её.
Задача №10. Зависимость суточного удой У в литрах от возраста коров Х в годах определяется уравнением У(х)=
-9,3+6,86х-0,49х , где х>2.Найдите возраст дойных коров, при котором
суточный удой будет наибольшим. Подведение итогов.
|
trig derivatives worksheet — Google Suche
AlleBilderBücherVideosMapsNewsShopping
Suchoptionen
Bilder
Alle anzeigen
Alle anzeigen
[PDF] Trig Derivatives Worksheet #1
mryangteacher.weebly.com › uploads › trig_derivatives_ws_1
Trig Рабочий лист №1 по производным… Нахождение производной тригонометрической функции. Упражнения 39-54, найдите производную тригонометрической функции.
[PDF] Дифференциация — Тригонометрические функции — Kuta Software
cdn.kutasoftware.com › Рабочие листы › Calc › 03 — Цепное правило с триггером
Рабочий лист от Kuta Software LLC. Программное обеспечение Kuta — Бесконечное исчисление … Дифференциация — Тригонометрические функции. Дифференцируйте каждую функцию по …
[PDF] Исчисление 1. Рабочий лист для наставника 4. Производные тригонометрических. ..
..
Исчисление 1 Репетитор — Рабочий лист 4 – Производные тригонометрических функций … Производная функции, умноженная на константу, является константой.
[PDF] Производные тригонометрических функций. Математические задания. Найдите производные тригонометрических функций: = 4 sin. + 5 соед. = грех, потому что. = 2 сек + тангенс.
Исчисление I. Производные триггерных функций (практические задачи)
tutorial.math.lamar.edu › calci › difftrigfcns
16.11.2022 · Вот набор практических задач для сопровождения раздела «Производные триггерных функций» глава «Производные» заметок для Пола …
Рабочий лист II | Superprof
www.superprof.co.uk › … › Исчисление › Производные
Bewertung 4,0
(2)
92 — 4}.Урок Рабочий лист: Дифференцирование тригонометрических функций — Nagwa
www.nagwa.com › рабочие листы
В этом рабочем листе мы потренируемся находить производные тригонометрических функций и применять к ним правила дифференцирования.
[DOC] Производные тригонометрических функций
www.cbsd.org › cms › lib › Centricity › Domain › Trig Derivatives Notes Производные тригонометрических функций. Для каждого уравнения найти. 1. 2. 3. 4. 5. 6. Исчисление AP Имя AB. Рабочий лист триггерных производных.
[PDF] Исчисление 1 Рабочий лист №16 Производные тригонометрических функций …
2.files.edl.io › …
22.09.2010 · Страница 1. |. +. |. +. +. +. +. +. + +. Т.+. Т.+. +. +. +. Т.+. |. +. |. ||. |. = ||. ||. ||. +. +. ||. ||. ||. ||. ||. ||. знак равно = ||.
Ähnliche Fragen
Что такое 6 триггерных производных?
Что такое 12 триггерных функций?
Что такое 7 триггерных функций?
Калькуляторточек разрыва — Googlesuche
AlleBilderVideosBücherMapsNewShopping
suchoptionen
Онлайн-калькулятор разрыва — Wolfram|Alpha
www.wolframalpha.com › калькуляторы › прерывание. ..
..
Больше, чем просто онлайн-инструмент для изучения непрерывности функций. Wolfram|Alpha — отличный инструмент для поиска неоднородностей функции.
Калькулятор непрерывности функций — Symbolab
www.symbolab.com › … › Функции › Функции
Бесплатный калькулятор разрыва функции — шаг за шагом определите, является ли функция разрывной.
Калькулятор разрывов — Math34.pro
math34.pro › разрывы
Калькулятор находит разрывы функции с пошаговым решением. Разрыв — это точка, в которой математическая функция не является непрерывной.
Ähnliche Fragen
Как найти точки разрыва?
Как найти разрыв в TI 84 Plus CE?
Как определить виды разрыва функции в точке?
Как избавиться от точки разрыва?
Калькулятор непрерывности — AllMath
www.allmath.com › Калькулятор непрерывности
Калькулятор непрерывности определяет, является ли функция непрерывной или прерывистой. Этот непрерывный калькулятор находит результат шагами за пару секунд.
Этот непрерывный калькулятор находит результат шагами за пару секунд.
Найти точку разрыва и сказать, устранимая она или нет
www.youtube.com › смотреть
29.09.2016 · Ваш браузер не может воспроизвести это видео. Учить больше. Переключить камеру.
Dauer: 1:46
Прислан: 29.09.2016
Нахождение разрывов рациональных функций — YouTube
www.youtube.com › смотреть
22.05.2011 · http://www.gdawgenterpriseshowes найти разрывы рационального …
Дауэр: 17:19
Прислан: 22.05.2011
Нахождение непрерывности на вашем графическом калькуляторе [Calc] — YouTube
www.youtube.com › смотреть
18.03.2020 · Поиск непрерывности в графическом калькуляторе [Calc] … Точка, бесконечность и скачок разрыва …
Дауэр: 3:19
Прислан: 18.03.2020
Разрывы рациональных функций, дыры и вертикальные асимптоты
www.youtube.com › смотреть
11.11.2015 · Разрывы рациональных функций, дыры и вертикальные асимптоты .




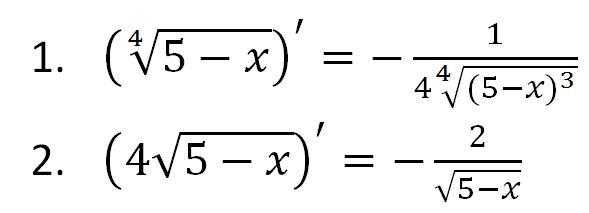
 Сани будут двигаться равномерно при
условии компенсации горизонтальных сил:
Сани будут двигаться равномерно при
условии компенсации горизонтальных сил: