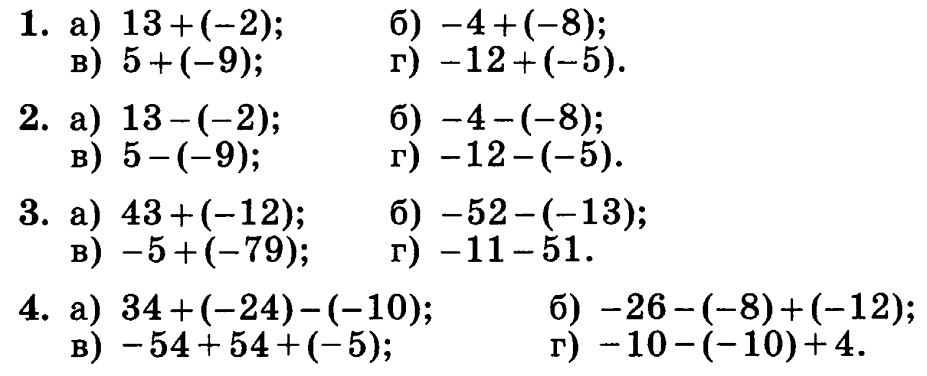* : (- ) | * + | * — | * : | * + (- ) | — 4 | — : (- ) | + | — | — : | — + (- ) | — 4 | — 6 | 0 | — 2 | 4 | 1 | 5 | — 3 | 3 | — 1 | — 5 | — 4 |
т | к | н | д | а | а | я | р | н | и | о | о | — 5 | — 4 | — 3 | — 2 | — 1 | 0 | 1 | 2 | 3 | 4 | 5 |
к | о | о | р | д | и | н | а | т | н | а | я | — 2 | 2 | 1 | — 1 | 3 |
м | я | р | я | а | п | 2 | 1 | 0 | — 1 | — 2 | |
п | р | я | м | а | я | 3,7 | 5,6 | ||||
— 1,8 | — 4,5 | 5 | |||||||||
— 7,4 | — 0,8 | — 8 | — 4 | 4 | |||||||
— 2,78 | — 4,5 | 3,57 | |||||||||
6,8 | 4 | 9,5 |
Положительные и отрицательные числа. 6-й класс
Цель: закрепить умения и навыки в действиях с положительными и отрицательными числами.
Задачи:
- Повторить понятия положительных и отрицательных чисел; закрепить навыки выполнения действий с положительными и отрицательными числами.
- Способствовать воспитанию интереса к предмету через нетрадиционную форму проведения урока.
- Развивать логическую смекалку, творческое мышление.
Тип урока: урок повторения и закрепления знаний учащихся с использованием ИТ.
Формы организации учебной деятельности: коллективная, индивидуальная.
Оборудование: компьютер, проектор, презентация PowerPoint, набор индивидуальных карточек (приложение 1, приложение 2), аудиофайлы с музыкой.
Я рада видеть каждого из вас
И пусть весна прохладой в окна дышит
Нам будет здесь уютно, ведь наш класс
Друг друга любит, чувствует и слышит.
– Сегодня в нашей школе открыт научно-исследовательский институт. На месте кабинетов организованны лаборатории, а все учащиеся школы его научные сотрудники. В кабинете математики открыта лаборатория № 1. Заведующей лабораторией назначили меня. И сегодня мы с вами повторим, обобщим и систематизируем знания, полученные вами на предыдущих занятиях.
– Для работы мне понадобятся помощники – старшие научные сотрудники – которые будут помогать мне в течение урока. Это Рината и Ирина.
– А теперь в ваших журналах наблюдения – рабочих тетрадях – запишем число, классная работа, тема исследования: «Положительные и отрицательные числа».
II. Устная работа.– В нашу лабораторию поступило сообщение.
«В архиве нашего института произошел сбой системы. Потерялись многие сведения. Чтобы их восстановить, нужны специалисты в области положительных и отрицательных чисел. Помогите»
– Мы с вами уже изучили положительные и отрицательные числа, много действий умеем с ними делать. Мы в какой-то мере являемся специалистами в этой области, как вы думаете? {Да}
– Поможем? {Да}
– Раз мы будем помогать восстанавливать утраченные сведения, то мы должны пройти испытания: все ли готовы совершить эту важную миссию.
– Ответим на несколько вопросов.
- Скажите пожалуйста какое перед нами число? {Число – 32}
- Как называется это число? {Это число отрицательное}
- А где расположено это число на координатной прямой? {Это число на координатной прямой расположено слева от нуля}
- А какие числа называются отрицательными? {Отрицательными числами называются числа, которые расположены на координатной прямой слева от нуля}
- Мы говорим о координатной прямой.
 А какая прямая называется координатной? {Координатной прямой называется прямая, на которой есть начало отсчета, единичный отрезок и направление}
А какая прямая называется координатной? {Координатной прямой называется прямая, на которой есть начало отсчета, единичный отрезок и направление} - Назовите два целых соседних с данным числа. {– 31 и – 33}
- А какое число будет противоположно данному? {Число 32}
- А какие числа называются противоположными? {Противоположными называются числа, которые отличаются друг от друга только знаками}
- Чему равен модуль данного числа? {Модуль данного числа равен 32}
- А что называется модулем числа? {Модулем числа называется расстояние от начала отсчета до точки на координатной прямой}
– Ну что ж с заданием все справились. Значит, можем продолжить восстанавливать потерянные сведения.
III. Задания на сравнение чисел и выполнение действий с модулями чисел.– Выполним следующее задание: Расставьте синие числа в порядке возрастания, а красные – в порядке убывания.
| 2,3 | 0,1 | 5 | |
| — 7 | — 8 | — 3,5 | |
| — 4,2 | 1,4 |
– А теперь проверим, что у вас получилось. {Синие: — 8; — 7; — 4,2; — 3,5; ; ; Красные: ; 5; ; 2,3; 1,4; 0,1}
– Молодцы. С этим заданием вы справились.
– Теперь возьмите желтые листы. На них вы видите схему, по которой нужно найти значение выражения. I вариант выполняет первое задание, II вариант выполняет второе задание. А так как мы все сотрудники одной лаборатории, то и ответ вы найдете вместе.
– Проверим ваши ответы. {Ответ: 28}
IV.
Историческая справка.– Сейчас сядьте поудобнее, можно немножко расслабится, подготовится к следующим серьезным заданиям и прослушать небольшую историческую справку.
Понятие об отрицательных числах возникло в практике очень давно, причем при решении таких заданий, где из меньшего числа приходилось вычитать большее число. Египтяне, вавилоняне, а также древние греки не знали отрицательных чисел и для производства вычислений математики того времени пользовались счетной доской. А так как знаков «плюс» и «минус» не существовало, то они на этой доске положительные числа отмечали красными счетными палочками, а отрицательные – синими. И отрицательные числа долгое время назывались словами, которые означали долг, недостача, а положительные трактовались как имущество.
Древнегреческий ученый Диофант вообще не признавал отрицательных чисел, и если при решении у него получался отрицательный корень, то он отбрасывал его как недоступный.
Совершенно по-другому относились к отрицательным числам древнеиндийские математики: они признавали существование отрицательных чисел, но относились к ним с некоторым недоверием, считая их своеобразными, не совсем реальными.
Не одобряли их долго и европейцы, потому что истолкование имущество – долг вызывало недоумение и сомнение. Действительно, можно складывать и вычитать имущество – долг, а как умножать и делить? Это было непонятно и нереально.
Всеобщее признание отрицательные числа получили в первой половине XIX века. Была создана теория, по которой мы сейчас и изучаем отрицательные числа.
– Скажите, пожалуйста, а эти определения отрицательных и положительных чисел как имущество и долг сейчас в нашем современном мире просматриваются? Как вы думаете? {Ответы учащихся}
– Ну вот, мы восстановили еще немного информации об отрицательных числах.
V. Практические задания.– Все научно-исследовательские институты решают задачи, которые потом применяются на практике. Сейчас мы тоже решим несколько задач, в которых увидим, где применяются отрицательные числа.
Задача 1. Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха – 35°С в гнезде температура не ниже 14°С. На сколько температура в гнезде выше температуры воздуха?
Даже при температуре воздуха – 35°С в гнезде температура не ниже 14°С. На сколько температура в гнезде выше температуры воздуха?
Решение.
Чтобы определить на сколько температура в гнезде больше, чем температура воздуха, нужно от 14 отнять – 35.
1) 14 – (- 35) = 14 + 35 = 49°С – температура в гнезде больше.
Ответ: на 49°С.
Задача 2. Шмели выдерживают температуру до – 7,8°С, пчелы – выше этой на 1,4°С. Какую температуру выдерживают пчелы?
Решение.
Чтобы найти на какую температуру выдерживают пчелы, нужно к числу – 7,8 прибавить число 1,4.
1) – 7,8 + 1,4 = — (7,8 – 1,4) = — 6,4 °С выдерживают пчелы.
Ответ: — 6,4°С.
– Молодцы. С этим заданием вы тоже справились.
VI. Релаксация.– Как и у каждого учреждения у нас перерыв.
– Сядьте посвободнее, закройте глаза, расслабьтесь. На улице весна. Ярче светит солнышко.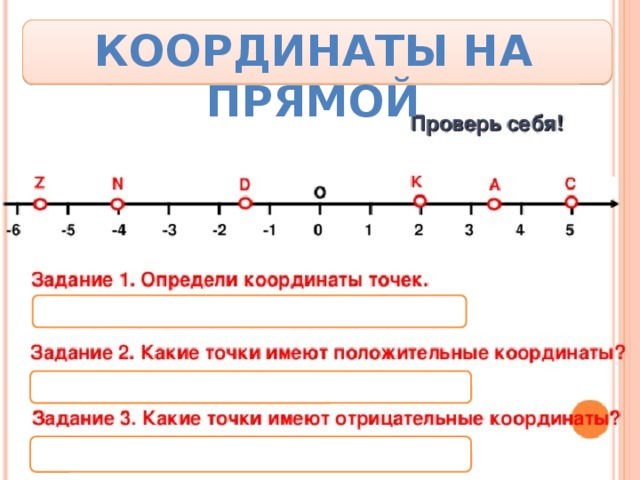 Звенит капель. Побежали ручейки и стали появляться проталины. На проталинах робко выглядывает и тянется к солнышку зеленая трава. С юга потянулись стаи птиц. Лучик солнца скользит по вашим лицам. От этого вам тепло и уютно, вы чувствуете себя отдохнувшими и полными свежих сил и энергии.
Звенит капель. Побежали ручейки и стали появляться проталины. На проталинах робко выглядывает и тянется к солнышку зеленая трава. С юга потянулись стаи птиц. Лучик солнца скользит по вашим лицам. От этого вам тепло и уютно, вы чувствуете себя отдохнувшими и полными свежих сил и энергии.
– А теперь откройте глаза. Перерыв окончен.
VII. Тестовая работа.– Пока вы отдыхали, я узнала, что руководство НИИ решило провести тестирование научных сотрудников.
– Перед вами лежат бланки с тестами. Подпишите их. В этом тестовом задании вам нужно выбрать правильный вариант ответа и обвести его кружочком.
– Все готовы? Тогда начинаем.
| Фамилия, имя _____________ Класс 6 Вариант 1 |
Фамилия, имя _____________ Класс 6 Вариант 2 |
|
|
– Время закончилось. Я попрошу старших научных сотрудников собрать бланки с тестами.
– Вот и закончился рабочий день в нашем научно-исследовательском институте. Мы помогли восстановить потерянные сведения о положительных и отрицательных числах.
– Придете вы сегодня домой, к своим родителям и что вы скажете? Продолжите, пожалуйста, фразу: «Сегодня на уроке математики я …»
– А я сегодня, когда приду домой скажу своим родственникам, что сегодня на уроке математики я еще раз убедилась какие у меня замечательные, дружные, умные ученики.
– А сегодня у нас урок закончился. Спасибо. До свидания.
Отрицательные числа
Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в EmailEmailПоделиться в FlipboardFlipboardРабочие листы
Печатные формы
Головоломки
Футболки
Футболки
Go Sheet 3 Ad0 Worksheet 3000 Free Math!Основные математические рабочие листы
Рабочие листы с дробями
Словесные задачи
Другие рабочие листы
Измерения и преобразования
Образцы и головоломки
Цвет по номеру
Holiday & Seasonal
Раннее обучение
ПЕЧАТИ
Калькуляторы
Математические листы по классу
.
 время! Начиная со сложения и вычитания отрицательных чисел, постепенно переходите к умножению и делению отрицательных чисел, умножению многозначных отрицательных чисел и делению отрицательных чисел в длинное число.
время! Начиная со сложения и вычитания отрицательных чисел, постепенно переходите к умножению и делению отрицательных чисел, умножению многозначных отрицательных чисел и делению отрицательных чисел в длинное число.Сложение и вычитание отрицательных чисел
36 рабочих листов с отрицательными числами
Рабочие листы для сложения и вычитания отрицательных чисел.
Сложение и вычитание
Умножение и деление малых отрицательных чисел
16 рабочих листов с отрицательными числами
Рабочие листы в этом разделе знакомят с отрицательными целыми числами в математических задачах на умножение и деление. Все задачи имеют дело с меньшими целыми числами, которые можно решить без многоразрядного умножения или деления в длинную сторону.
Факты об умножении и делении
Многозначное умножение с отрицательными числами
16 рабочих листов с отрицательными числами
Если вы освоили базовое умножение с отрицательными целыми числами, эти рабочие листы для многозначного умножения дадут вам больше навыков работы с отрицательными числами. тщательный тест.
тщательный тест.
Многозначное умножение
Длинное деление с отрицательными числами
16 Отрицательные числа Рабочие листы
Готовы следить за чистотой знаков? Эти листы с длинным делением имеют отрицательные делители и отрицательные частные (или и то, и другое!). Некоторые задачи на отрицательное деление включают остатки.
Длинное деление
Решение математических задач с отрицательными числами
Отрицательные числа — это математическая тема, которая обычно начинается в 6-м классе и вводится как часть стандарта Common Core на этом уровне.
Отрицательные числа появляются в различных ситуациях в прикладной математике. Часто вы будете видеть отрицательные числа непосредственно в измерениях, например, при измерении высоты над или под уровнем моря, температуры выше или ниже точки замерзания или в финансовых приложениях с положительными и отрицательными суммами денег. Более частое, но и более абстрактное применение отрицательных чисел связано с темпами изменений. Вы также столкнетесь с отрицательными значениями в геометрии при построении графика в различных квадрантах на координатной плоскости. И, конечно же, по мере того, как вы углубляетесь в алгебру и более сложную геометрию, отрицательные числа играют все более важную роль.
Более частое, но и более абстрактное применение отрицательных чисел связано с темпами изменений. Вы также столкнетесь с отрицательными значениями в геометрии при построении графика в различных квадрантах на координатной плоскости. И, конечно же, по мере того, как вы углубляетесь в алгебру и более сложную геометрию, отрицательные числа играют все более важную роль.
Дети поздних начальных классов должны уметь рассуждать об отрицательных целых числах на числовой прямой, и обычно это хорошее место для начала изучения основных математических операций с отрицательными числами. Это также хороший способ начать визуализировать, как работают правила для чисел со знаком. Два важных момента, которые необходимо усвоить, заключаются в том, что вычитание отрицательного числа — это то же самое, что и сложение, и что умножение двух отрицательных чисел дает положительное произведение. Большинство других способов поведения отрицательных чисел в обычных математических операциях кажутся простыми и интуитивно понятными, но запоминание этих двух правил даст вашим школьникам хороший старт. Дополнительные сведения о правилах управления знаками с отрицательными числами для различных операций см. на соответствующих страницах рабочего листа для полного обсуждения и советов.
Дополнительные сведения о правилах управления знаками с отрицательными числами для различных операций см. на соответствующих страницах рабочего листа для полного обсуждения и советов.
Рабочие листы на этой странице знакомят с сложением и вычитанием отрицательных чисел, а также с умножением и делением отрицательных чисел. Начальные наборы имеют дело с небольшими целыми числами, прежде чем перейти к многозначному умножению и длинному делению с отрицательными числами. Независимо от того, на каком этапе изучения отрицательных чисел вы находитесь, эти рабочие листы дадут вашим ученикам много практики, когда им нужно будет освоить эту часто негативную тему!
KS2 Негативы | Сложение и вычитание отрицательных чисел
KS1 (5-7 лет)KS2 (7-11 лет)11+ (7-11 лет)KS3 (11-14 лет)GCSE (14-17 лет)ИспанскийESLGamesCup of TeaPSHE
- Домашний
- KS2
- KS2 Математика
- Отрицательные числа (6 класс)
Температура -13 o . Если он увеличится на 39 o , то будет 26 o .
Если он увеличится на 39 o , то будет 26 o .
В KS2 Maths дети начнут понимать отрицательные или отрицательные числа. В шестом классе дети должны уверенно считать отрицательные числа вверх и вниз и заполнять пропуски в числовой последовательности. Они также должны уметь решать задачи на сложение и вычитание с отрицательными числами, а теперь им будут даваться задачи с двузначными и трехзначными отрицательными числами.
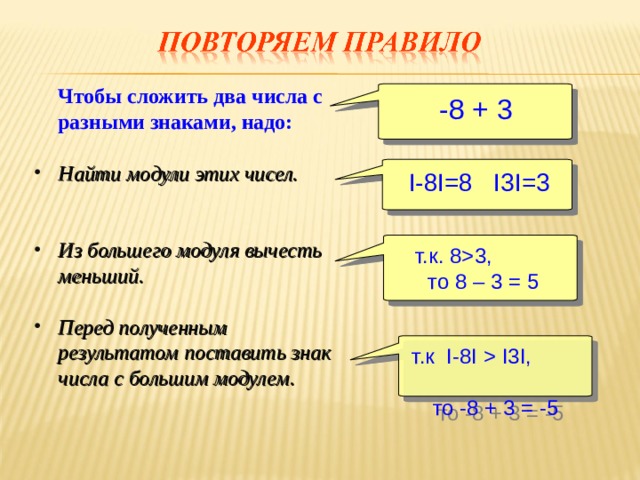
Отрицательные или минусовые числа — это целые числа ниже нуля. Вы можете задаться вопросом, где на земле может быть использовано отрицательное число. Примером использования отрицательных чисел может быть измерение температуры. Если она холоднее точки замерзания воды (0 o С), мы говорим, что это минусовая температура. Сложение и вычитание могут быть сложными с отрицательными числами. Один из методов, который может помочь, — переставить проблему. Например:
14 — 8 = 6, значит 6 — 14 = -8 С практикой все становится проще!
Пройдите этот тест, чтобы проверить свои навыки сложения и вычитания с отрицательными числами.
1.
Температура 6 o . Если выпадет 18 o какая сейчас температура?
24 O
-24 O
-8 O
-12 O
2.
Какой номер является следующим числом в следующей последовательности? 10, 5, 0, -5
10
-1
-10
-15
3.
Температура -28 o . Если она поднимется 13 o какая сейчас температура?
-41 O
-15 O
15 O
41 O
4.
Какое из этих заявлений является правдой?
-33 > -3
-29 > -28
-7 > -17
-44 > -34
5.
Температура -15 o . Если выпадет 8 или какая сейчас температура?
23 o
-7 o
-23 o
7 o
4
0 Какое из этих утверждений верно?
-1 < -58
-23 < -1
2 < -99
-15 < -20
7.
Какое из этих чисел наименьшее?
-1
-28
-15
8.
Какое из этих чисел больше?
2
-35
-3
-14
9.
Какие числа пропущены в этой последовательности? -33, -35, ___, -39, -41, ___?
-36 и -43
-37 и -42
-37 и -43
-37 и -40
10.
Температура -13 o
. Если она поднимется 39 o какая сейчас температура?26 или
39 или
13 или
-26 или
Сегодня у вас есть 15 бесплатных вопросов. Чтобы получить неограниченный доступ ко всем викторинам, играм и многому другому, вам необходимо подписаться.
Если вы хотите сразу подписаться, посетите нашу страницу Присоединяйтесь к нам.
Или осмотрите веб-сайт и начните с нашей домашней страницы.
Мы используем файлы cookie, чтобы сделать ваш опыт работы с нашим веб-сайтом лучше.

 задание), разноцветные треугольники с цифрами (см. задание), «лента времени» (см. задание), учебники.
задание), разноцветные треугольники с цифрами (см. задание), «лента времени» (см. задание), учебники. Необходимо собрать фигурки в соответствующие корзинки. Цель: развитие внимательности и быстроты реакции. Задание выполняют у доски два человека на скорость). Соберите в корзинки яблоки (кубики и т.д.) так, чтобы пары попали в правильные корзинки.
Необходимо собрать фигурки в соответствующие корзинки. Цель: развитие внимательности и быстроты реакции. Задание выполняют у доски два человека на скорость). Соберите в корзинки яблоки (кубики и т.д.) так, чтобы пары попали в правильные корзинки.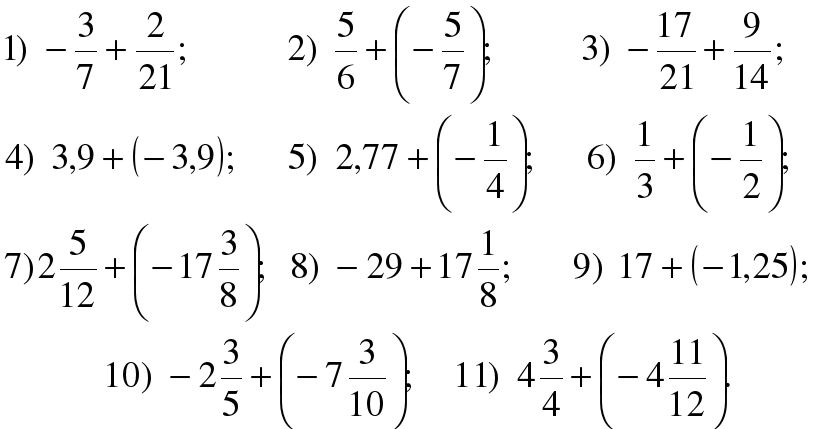 Найдите числа, которые спрятались за звездочками, учитывая, что за * и ** скрыты разные числа, но за одной (* или **) – числа одинаковые.
Найдите числа, которые спрятались за звездочками, учитывая, что за * и ** скрыты разные числа, но за одной (* или **) – числа одинаковые. Например, 15 – 30 = — 15, 24 – 39 = — 15, 18 – 33 = — 15 и т.д.
Например, 15 – 30 = — 15, 24 – 39 = — 15, 18 – 33 = — 15 и т.д.


 Выполнение заданий
Выполнение заданий


 Справа от нее расположена цифра 9,5.
Справа от нее расположена цифра 9,5. А какая прямая называется координатной? {Координатной прямой называется прямая, на которой есть начало отсчета, единичный отрезок и направление}
А какая прямая называется координатной? {Координатной прямой называется прямая, на которой есть начало отсчета, единичный отрезок и направление}