Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
12.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
помогите срочно контрольная!!!
Решено
Осевое сечение цилиндра — квадрат, диагональ которого 4 см, Найти площадь полной поверхности цилиндра
Решено
Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов.
2. Найдите площадь полной поверхности цилиндра.
Решено
в треугольнике ABC угол А=45…
Пользуйтесь нашим приложением
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| Оценить интеграл | интеграл от cos(2x) относительно x | ||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная sinx Доказательство
- Математические сомнения
- Дифференциальное исчисление
- Дифференциация
- Правила
- Тригонометрические функции
Производная функции sin по переменной равна косинусу.
Если $x$ представляет собой переменную, то функция синуса записывается как $\sin{x}$. Следовательно, дифференцирование $\sin{x}$ по $x$ равно $\cos{x}$, и это можно доказать математически из первого принципа.
Метод для начинающих
В этом методе дифференцирование синусоидальной функции выводится математически с использованием в основном тригонометрических тождеств.
Запись производной функции в предельной форме
Согласно определению производной, производная функции по $x$ записывается в следующей форме предельной операции.
$\dfrac{d}{dx}{\, f(x)}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{ f(x+h)-f(x)}{h}}$
Возьмем $f{(x)} = \sin{x}$, тогда $f{(x+h)} = \sin{(x+h)}$. На основе этой информации можно начать доказательство дифференцирования $\sin{x}$ по $x$, выводимое из первого принципа.
$\implies \dfrac{d}{dx}{\, (\sin{x})}$ $\,=\,$ $\displaystyle \large \lim_{h \,\to\, 0}{ \normalsize \dfrac{\sin{(x+h)}-\sin{x}}{h}}$
Упростите тригонометрическое выражение
Первый член тригонометрического выражения в числителе есть грех суммы двух углов и его можно расширить с помощью тождества суммы углов функции греха.
Теперь сосредоточьтесь на упрощении тригонометрического выражения.
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\sin{x}\cos{h}+\cos{x} \sin{h}-\sin{x}}{h}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac {\sin{x}\cos{h}-\sin{x}+\cos{x}\sin{h}}{h}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\sin{x}{(\cos{h}-1)}+\cos{x}\sin{h}}{h}} $
$ = \, \, \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sin {x} {(- (1- \ cos {h }))}+\cos{x}\sin{h}}{h}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{-\sin{x}{(1-\cos{h}) }+\cos{x}\sin{h}}{h}}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \ Bigg[ \dfrac{-\sin{x}{(1-\cos{h})}}{h}+\dfrac{\cos{x}\sin{h}}{h}\Bigg]}$
$=\,\,\,$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{{(-\sin{x})}{(1-\cos{ h})}}{h}}$ $+$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\cos{x}\sin{h}}{h} }$
Ввод операции ограничения выражен в виде $h$.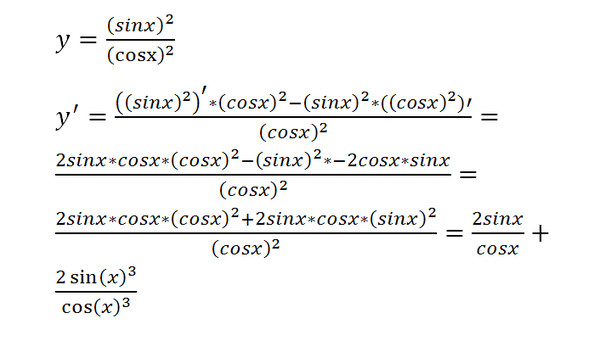
Таким образом, $-\sin{x}$ и $\cos{x}$ становятся константами, и их можно записать отдельно по множественному константному правилу пределов.
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{1-\cos{h }}{h}}$ $+$ $\cos{x} \times \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\sin{h}}{h}} $
Вычисление пределов тригонометрических функций
Согласно пределам формул тригонометрических функций предел отношения $\sin{h}$ к $h$ при стремлении $h$ к нулю равен единице.
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{1-\cos{h }}{h}}$ $+$ $\cos{x} \times 1$
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{1-\cos{h }}{h}}$ $+$ $\cos{x}$
Теперь вычислим предел тригонометрической функции при приближении $h$ к $0$ методом прямой подстановки.
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{1-\cos{( 0)}}{0}}$ $+$ $\cos{x}$
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \ ,\to\, 0}{\normalsize \dfrac{1-1}{0}}$ $+$ $\cos{x}$
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{0}{0}}$ $+$ $\cos{x}$
В этом случае невозможно определить предел функции.
Итак, попробуем вычислить эту тригонометрическую функцию другим методом.
$=\,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{1-\cos{h }}{h}}$ $+$ $\cos{x}$
Используйте степень тригонометрического тождества, чтобы представить числитель в квадратной форме. 9092{\Big(\dfrac{h}{2}\Big)}}{\dfrac{h}{2}}}$ $+$ $\cos{x}$
$=\,\,\, $ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\sin{\Big(\dfrac{h}{2}\Big )} \times \sin{\Big(\dfrac{h}{2}\Big)}}{\dfrac{h}{2}}}$ $+$ $\cos{x}$
$=\ ,\,\,$ ${(-\sin{x})} \displaystyle \large \lim_{h \,\to\, 0}{\normalsize \Bigg[\sin{\Big(\dfrac{h}) {2}\Big)} \times \dfrac{\sin{\Big(\dfrac{h}{2}\Big)}}{\dfrac{h}{2}}\Bigg]}$ $+$ $ \cos{x}$
Теперь воспользуемся степенным правилом пределов для вычисления предела произведения двух функций как произведения их пределов.
$=\,\,\,$ ${(-\sin{x})}\Bigg[\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \sin{\Big( \dfrac{h}{2}\Big)}}$ $\times$ $\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \dfrac{\sin{\Big(\dfrac{ h}{2}\Big)}}{\dfrac{h}{2}}\Bigg]}$ $+$ $\cos{x}$
Если $h \to 0$, то $\dfrac{ h}{2} \to \dfrac{0}{2}$.
Следовательно, $\dfrac{h}{2} \to 0$. Доказано, что если $h$ стремится к нулю, то $\dfrac{h}{2}$ также стремится к нулю.
$=\,\,\,$ ${(-\sin{x})}\Bigg[\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \sin{\Big( \dfrac{h}{2}\Big)}}$ $\times$ $\displaystyle \large \lim_{\frac{h}{2} \,\to\, 0}{\normalsize \dfrac{\sin {\Big(\dfrac{h}{2}\Big)}}{\dfrac{h}{2}}\Bigg]}$ $+$ $\cos{x}$
Возьмем $w = \dfrac{h}{2}$ и преобразуем эту вторую известковую функцию в $w$.
$=\,\,\,$ ${(-\sin{x})}\Bigg[\displaystyle \large \lim_{h \,\to\, 0}{\normalsize \sin{\Big( \dfrac{h}{2}\Big)}}$ $\times$ $\displaystyle \large \lim_{w \,\to\, 0}{\normalsize \dfrac{\sin{w}}{w} \Bigg]}$ $+$ $\cos{x}$
Согласно пределу $\dfrac{\sin{x}{x}$ при приближении $x$ к нулевому правилу, предел тригонометрической функции равен единице .
$=\,\,\,$ ${(-\sin{x})}\Bigg[\sin{\Big(\dfrac{0}{2}\Big)} \times 1 \Bigg]$ $+$ $\cos{x}$
$=\,\,\,$ ${(-\sin{x})}\Bigg[\sin{\Big(\dfrac{0}{2}\Big)}\Bigg]$ $+$ $\cos{x}$
$=\,\,\,$ ${(-\sin{x})}\Big[\sin{(0)}\Big]$ $+$ $\cos{ x}$
Согласно тригонометрии точное значение синуса нуля градусов равно нулю.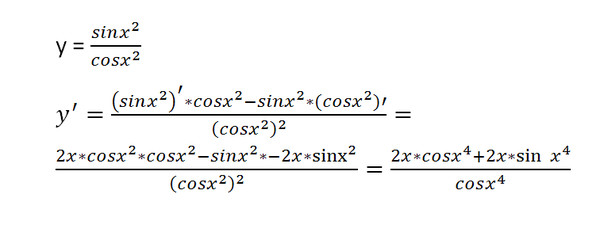
$=\,\,\,$ ${(-\sin{x})}{(0)}$ $+$ $\cos{x}$
$=\,\,\,$ $ {(-\sin{x})} \times 0$ $+$ $\cos{x}$
$=\,\,\, 0 + \cos{x}$
$\следовательно \,\ ,\,\,\,\, \dfrac{d}{dx}{\, (\sin{x})} \,=\, \cos{x}$
Расширенный метод
Это еще один метод, в котором используется только одно тригонометрическое тождество для упрощения тригонометрического выражения через функции sin.
Экспресс Дифференцирование функции в предельной форме
Согласно определению производной дифференцирование функции по $x$ записывается в следующей форме предельной операции.
$\dfrac{d}{dx}{\, f(x)}$ $\,=\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \ dfrac{f(x+\Delta x)-f(x)}{\Delta x}}$
Возьмем $f{(x)} = \sin{x}$, тогда $f{(x+\Delta x)} = \sin{(x+\Delta x)}$. Теперь доказательство производной от $\sin{x}$ по $x$ можно начать по первому принципу.
$\ подразумевает \dfrac{d}{dx}{\, (\sin{x})}$ $\,=\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0 }{\normalsize \dfrac{\sin{(x+\Delta x)}-\sin{x}}{\Delta x}}$
Использовать правило преобразования разности для произведения
Использовать разность для идентичности произведения функций sin для объединить разность двух синусоидальных функций в числителе функции.
$ = \,\,\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{2\cos{\Bigg[\dfrac{x+\Delta x +x}{2}\Bigg]}\sin{\Bigg[\dfrac{x+\Delta x-x}{2}\Bigg]}}{\Delta x}}$
$= \,\,\,$ $\require{cancel} \displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{2\cos{\Bigg[\dfrac{2x+\Delta x}{2}\Bigg ]}\sin{\Bigg[\dfrac{\cancel{x}+\Delta x-\cancel{x}}{2}\Bigg]}}{\Delta x}}$
$= \,\, \, $ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{2\cos{\Bigg[\dfrac{2x+\Delta x}{2}\Bigg]} \sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\Delta x}}$
Упростить всю функцию
Число $2$ умножает числитель и делит знаменатель. Итак, переместите число $2$ в знаменатель.
$ = \,\,\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{\cos{\Bigg[\dfrac{2x+\Delta x} {2}\Bigg]}\sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}}$
Теперь разделите эту функцию как произведение двух функций.
$ = \,\,\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \Bigg(\cos{\Bigg[\dfrac{2x+\Delta x} {2}\Bigg]} \times \dfrac{\sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}\Bigg)}$
Примените правило пределов произведения, чтобы найти предел функции по произведению их пределов.
$ = \,\,\,$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \cos{\Bigg[\dfrac{2x+\Delta x}{2} \Bigg]}}$ $\times$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{\sin{\Bigg[\dfrac{\Delta x}{2 }\Bigg]}}{\dfrac{\Delta x}{2}}}$
Вычислить предел функции
Теперь сначала найдем предел функции cos методом прямой подстановки.
$= \,\,\,$ $\cos{\Bigg[\dfrac{2x+0}{2}\Bigg]}$ $\times$ $\displaystyle \large \lim_{\Delta x \, \to\, 0}{\normalsize \dfrac{\sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}}$
$ = \,\,\,$ $\cos{\Bigg[\dfrac{2x}{2}\Bigg]}$ $\times$ $\displaystyle \large \lim_{\Delta x \,\to\, 0 }{\normalsize \dfrac{\sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}}$
$= \,\, \,$ $\require{cancel} \cos{\Bigg[\dfrac{\cancel{2}x}{\cancel{2}}\Bigg]}$ $\times$ $\displaystyle \large \lim_{\ Delta x \,\to\, 0}{\normalsize \dfrac{\sin{\Sin{\Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}} $
$= \,\,\,$ $\cos{x}$ $\times$ $\displaystyle \large \lim_{\Delta x \,\to\, 0}{\normalsize \dfrac{\sin{ \Bigg[\dfrac{\Delta x}{2}\Bigg]}}{\dfrac{\Delta x}{2}}}$
Предел функции, в котором участвует функция sin, аналогичен предел sinx/x, когда x приближается к правилу 0, но входное значение немного отличается.