Производная: определение и основные формулы. 11 класс
Похожие презентации:
Неопределенный интеграл. Основные понятия и определения
Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций
Производная. Основные теоремы о производных. Формулы дифференцирования функций. (Лекция 5)
Производные элементарных функций. 11 класс
Устные упражнения. Определение производной. (10 класс)
Определение производной
Производная показательной функции. 11 класс
Определение производной
Непосредственное вычисление производных. Табличное дифференцирование. Общее определение производной. (Семинар 7)
Определение производной
1. Дистанционный урок «Производная: определение и основные формулы »
алгебра и начала анализа11 класс
2. Содержание:
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

13.
Цели и задачи
Определение производной
Физический смысл производной
Правила дифференцирования
Основные формулы производных
Примеры взятия производных
Производные элементарных функций
Производная сложной функции
Задания для закрепления материала
Задания для самоанализа
Ответы
Домашнее задание
Основная литература
3. Цели и задачи
Цель: познакомиться с одним из важных элементовматематического анализа – производной: ее
определением, физическим смыслом, а также
освоить аппарат нахождения производной различных
функций.
Задачи:
1.
2.
3.
Знать определение производной;
Знать и уметь применять правила
дифференцирования;
Знать и уметь применять формулы для
вычисления производных элементарных
функций.
Определение производной
y
x = x — x0
x = x0 + x
y=f(x)
В
f(x)
приращение аргумента
f
f(x0)
А
f = f(x) – f(x0)
f(x) = f(x0) + f
приращение функции
x
O
x0
x
f f(x0 + x) – f(x0)
— = ———————
x
x
x
разностное
отношение
Производной функции f в точке x0
называется число, к которому
стремится разностное отношение
при x 0.

f f(x0 + x) – f(x0)
f´(x0)= lim — = ———————
при x 0 x
x
Физический смысл производной
x
Если тело движется по прямой и за время t
его координата изменяется на x, то
t t(x0 + x) – t(x0) — средняя скорость
Vср( t) = — = ——————— движения тела за t
x
x
Таким образом, физический смысл
производной – это мгновенная скорость
Правила дифференцирования
Если функция y = f(x) имеет производную, то она называется
дифференцируемой; операция нахождения производной
функции называется дифференцированием.
Пусть f(x) , g(x) – дифференцируемые функции, С – постоянная.
(c f ( x)) c f ( x)
( f ( x) g ( x)) f ( x) g ( x)
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
f ( x) f ( x) g ( x) f ( x) g ( x)
2
g ( x)
g ( x)
Основные формулы производных
x 1
c 0
n 1
x n x
n
x 2
kx b n kx b
n
n 1
1
k
x
Примеры взятия производной
8 0
0
5x 5
5
x 6x
x
8
x 7 x
x
6
7
x5
100
3, 4 x 3, 4
100 x99
100
100 x 101
52 5 32 5 x 3
x x
2
2
1
5
3 4
3
3
4
4 3x 4 x 4 5
x
4 x
Производные элементарных функций
1
ln x
x
log a x
1
x ln a
sin
x
cos x
cos
x
sin x
tgx
1
2
cos x
1
ctgx 2
sin x
x
e e
x
x
a a ln a
x
Производная сложной функции
Пусть f(x) , g(x) – дифференцируемые функции.
 Тогда:
Тогда:f g x
f g x g x
Пример:
sin 4x
5
cos 4 x
3x
2
5
2
5
2
sin 4 x 3x 4 x 3x
5
3x 20 x 6 x
2
4
Задания для закрепления материала
Найдите производные, используя образцы.
5
4
4
Образец:(2 x) 2; (5 x 1) 5; (3x ) 3 5 x 15 x
(4 x) ….
(6 x 2) …..
(3 2 x) …..
(2 x 4 ) ……….
(3×6 ) ………..
Образец:y 3e x ; y 3e x
f ( x) e3 x 1; f ( x) e3 x 1 (3x 1) 3e3 x 1
y 5e x ; y ……..
y e2 x ; y ……….
y 3e4 x ; y 3(e4 x ) …………… …………
y 0,5e6 x 2 ; y 0,5 (e6 x 2 ) 0,5 e………… (…………) ……………….. ……………….
Образец: y 52 x 1;
y 52 x 1 ln 5 (2 x 1) 2ln 5 52 x 1
y 63 2 x ; y ……… ln… (………..) …………………..
y 5 23 x ; y …………………………………………………….
Образец:f ( x)
x2 2x ;
f ( x) ( x 2 ) (2 x ) 2 x 2 x ln 2
f ( x) 2 x4 4x ; f ( x) (.
 …..) (…..) …………………………………………………………
…..) (…..) …………………………………………………………y 3×6 52 x 1; y ……………………………………………………………..
y 4 x5 2 63 2 x ; y ……………………………………………………………..
14. Для каждой из функций, графики которых изображены в верхнем ряду, найдите график ее производной.
Задания для самоанализаЗадание 1. Найдите производные функций:
1. f x 3 x 5
2. f x 4 x 5 x 9 x
2
3
3 x
3. f x
x 3
2
5 7
4. f x 2 3
x
x x
5. f x x 4
1
1
6. f x
2 4x
3x 2 x
Задание 2. Найдите производные функций:
2. f x x 5 x x x
2
3 x
3. f x 3
x
2
2 x 5
4. f x
x 1
5. f x
x 4
3
2
x 2
1 1 2
6. f x 4 x
2 x
English Русский Правила
Производная функции. Формулы и правила дифференцирования .
Тема урока : Производная функции. Формулы и правила дифференцирования .
Формулы и правила дифференцирования .
Конспект урока
Производные — это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным отношением называется отношение разности значения функции к разности значений переменной.
После закрепления знаний по таблице производной, приступаем к изучению теорем дифференцирования.
Теорема 1. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:
Теорема 2. Производная произведения двух функций равна:
Теорема 3. Производная частного двух функций равна:
Приложение 1
Ранее мы рассматривали производные отдельных функций. Здесь мы рассмотрим правила дифференцирования, то есть правила дифференцирования суммы, разности, произведения и частного отдельных функций. Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Производная суммы
Дано: ; .
Существует ; .
Доказать, что существует производная от суммы заданных функций и она вычисляется по следующему правилу:
Доказательство
Пусть задана функция , требуется найти .
По стандартному алгоритму требуется найти отношение :
При получаем:
Что и требовалось доказать.Так, производная от суммы функций равна сумме производных этих функций.Аналогично производная разности функций равна разности производных:
Пример
1. .
2. Найти значение производной функции в точке :
;
Производная произведения
Дано: ; .
Существует ; .
Доказать, что существует производная от произведения и вычисляется она по правилу:
Доказательство .Нужно использовать разностное отношение по стандартному алгоритму нахождения производной. Это разностное отношение можно проиллюстрировать. Пусть есть прямоугольник со сторонами ; . Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
Рис. 1. Разностное соотношениеПлощадь любого прямоугольника (старого, нового, их разности) мы можем посчитать.Составим разностное соотношение. Пусть , ищем :
При :
А первое слагаемое стремится к нулю, так как стремится к нулю.
Так, производная произведения функций:
Что и требовалось доказать.Рассмотрим важное следствие. Пусть , константа. Согласно правилу:
Так, постоянный множитель можно вынести за знак производной.
Производная степенной функции
Производная степенной функции:
Рассмотрим частные случаи:
;
Найдем эту производную по правилу произведения:
С другой стороны:
И так далее. Поэтому угадывается формула:
– мы принимаем ее без доказательства.
Производная частного
Дано: ; .
Существуют ; .
При этом , а значит, существует дробь .
Доказать, что существует производная частного и вычисляется по формуле:
Доказательство
Представим .
Тогда по формуле производной произведения:
С другой стороны:
Из этих двух выражений получаем уравнение:
Умножим все уравнение на :
Что и требовалось доказать.
Решение примеров
Пример
.
.
Домашнее задание: Итоговые тесты по теме «Производная функции»
1. Найдите производную функции y(х) = x4+ 3x3 + 4.
1) 4x3 + 9x2 + 4
2) 4x3 + 9x2 + 4x
3) 4x2 + 3x2 + 4
4) 4x3 + 9x2
2. Производная функции F(x) = cos(4x) равна:
1) -4sin(4x)
2) 4cos(- 4x)
3) 4xsin(4x)
4) 4xcos(- 4x)
3. Найдите значение производной функции
при х=1
Найдите значение производной функции
при х=1
1) 0,5
2) -1
3) -0,5
4) 1
4. Вычислите значение производной функции в точке .
1) | 16 | 2) | 64 | 3) | – 16 | 4) | – 64 |
5. Найдите производную функции .
1) | 3) | ||
2) | 4) |
6. Найдите производную функции
1) | 3) | ||
2) | 4) |
Просмотр содержимого документа
«Тема урока : Производная функции.
 Формулы и правила дифференцирования .»
Формулы и правила дифференцирования .»
Тема урока : Производная функции. Формулы и правила дифференцирования .
Конспект урока
Производные — это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным отношением называется отношение разности значения функции к разности значений переменной.
После закрепления знаний по таблице производной, приступаем к изучению теорем дифференцирования.
Теорема 1. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:
Теорема 2. Производная произведения двух функций равна:
Теорема 3. Производная частного двух функций равна:
Приложение 1
Ранее мы рассматривали производные отдельных функций. Здесь мы рассмотрим правила дифференцирования, то есть правила дифференцирования суммы, разности, произведения и частного отдельных функций.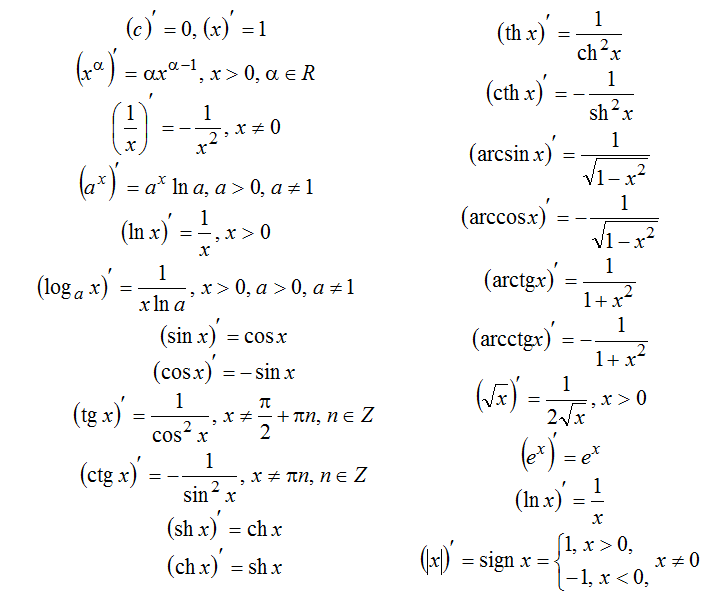 Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Производная суммы
Дано: ; .
Существует ; .
Доказать, что существует производная от суммы заданных функций и она вычисляется по следующему правилу:
Доказательство
Пусть задана функция , требуется найти .
По стандартному алгоритму требуется найти отношение :
При получаем:
Что и требовалось доказать.Так, производная от суммы функций равна сумме производных этих функций.Аналогично производная разности функций равна разности производных:
Пример
1. .
2. Найти значение производной функции в точке :
;
Производная произведения
Дано: ; .
Существует ; .
Доказать, что существует производная от произведения и вычисляется она по правилу:
Доказательство .Нужно использовать разностное отношение по стандартному алгоритму нахождения производной. Это разностное отношение можно проиллюстрировать. Пусть есть прямоугольник со сторонами ; . Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
Это разностное отношение можно проиллюстрировать. Пусть есть прямоугольник со сторонами ; . Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
При :
А первое слагаемое стремится к нулю, так как стремится к нулю.
Так, производная произведения функций:
Что и требовалось доказать.Рассмотрим важное следствие. Пусть , константа. Согласно правилу:
Так, постоянный множитель можно вынести за знак производной.
Производная степенной функции
Производная степенной функции:
Рассмотрим частные случаи:
;
Найдем эту производную по правилу произведения:
С другой стороны:
И так далее. Поэтому угадывается формула:
Поэтому угадывается формула:
– мы принимаем ее без доказательства.
Производная частного
Дано: ; .
Существуют ; .
При этом , а значит, существует дробь .
Доказать, что существует производная частного и вычисляется по формуле:
Доказательство
Представим .
Тогда по формуле производной произведения:
С другой стороны:
Из этих двух выражений получаем уравнение:
Умножим все уравнение на :
Что и требовалось доказать.
Решение примеров
Пример
.
.
Домашнее задание: Итоговые тесты по теме «Производная функции»
1. Найдите производную функции y(х) = x4+ 3x3 + 4.
1) 4x3 + 9x2 + 4
2) 4x3 + 9x2 + 4x
3) 4x2 + 3x2 + 4
4) 4x3 + 9x2
2. Производная функции F(x) = cos(4x) равна:
Производная функции F(x) = cos(4x) равна:
1) -4sin(4x)
2) 4cos(- 4x)
3) 4xsin(4x)
4) 4xcos(- 4x)
3. Найдите значение производной функции
при х=1
1) 0,5
2) -1
3) -0,5
4) 1
4. Вычислите значение производной функции в точке .
1) | 16 | 2) | 64 | 3) | – 16 | 4) | – 64 |
5. Найдите производную функции .
1) | 3) | ||
2) | 4) |
6. Найдите производную функции
1) | 3) | ||
2) | 4) |
Формулы для первой производной функции
y является функцией y = y(x)
C = константа, производная (y’) константы равна 0
у = С => у’ = 0
Пример: у = 5, у’ = 0
Если y является функцией типа y = x n формула производной:
y = x n => y’ = nx n-1
Пример: y = x 3 y’ = 3x 3-1 = 3x 2
y = x -3 y’ = -3x -4
Из верхней формулы мы можем сказать для производной y’ функции y = x = x 1 , что:
если y = x, то y’=1
y = f 1 (x) + f 2 (x) + f 3 (x) . ..=>
..=>
y’ = f’ 1 (x) + f’ 2 ( х) + f’ 3 (х) …
Эта формула представляет собой производную функции, являющейся суммой функций.
Пример: если у нас есть две функции f(x) = x 2 + x + 1 и
г (х) = х 5 + 7 и y = f(x) + g(x), тогда y’ = f'(x) + g'(x) =>
y’ = (x 2 + x + 1)’ + (x 5 + 7)’ = 2x 1 + 1 + 0 + 5x 4 + 0 = 5x 4 + 2x + 1
Если функция кратна двум функциям, производная определяется как:
y = f(x).g(x) => y’ = f'(x)g(x) + f(x)g'(x)
Если f(x) = C(C — константа) и y = f(x)g(x)
y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + С.д'(х) = С.д'(х)
y = Cf(x) => y’ = Cf'(x)
В разделе задачи есть примеры следующих формул.
| г = |
| г’ = |
|
у = ln х => у’ = 1 / х
у = е х => у’ = е х
у = грех х => у’ = потому что х
у = потому что х => у’ = -sin х
y = tan x => y’ = 1 / cos 2 x
y = кроватка x => y’ = — 1 / sin 2 x
| у = арксинус х | => | г’ = |
|
| y = arccos x | => | г’ = |
|
| у = арктангенс х | => | г’ = |
|
| у = дуга x | => | г’ = |
|
Когда функция является функцией функции: u = u(x)
y = f(u) => y’ = f'(u). u’
u’
Пример: пусть y = sin(x 2 )
Здесь u = x 2 , f(u) = sin(u), производные f'(u) = cos(u), u’ = 2x
y’ = (sin(u))’⋅u’ = cos(x 2 )⋅2x = 2⋅x⋅cos(x 2 )
Задачи на производные
1) f(x) = 10x + 4y. Чему равна первая производная f'(x) = ?
Решение: Мы можем использовать формулу для производной функции, которая является суммой
функции
f(x) = f 1 (x) + f 2 (x), f 1 (x) = 10x, f 2 (x) = 4y
для функции f 2 (x) = 4y, y является константой, поскольку аргумент f 2 (x) равен x
поэтому f’ 2 (x) = (4y)’ = 0. Следовательно, производная функция f(x): f'(x) = 10 + 0 = 10.
| 2) Вычислите производную f(x) = |
|
Решение: У нас есть две функции: h(x) = x 10 и g(x) = 4,15 + cos x
. Функция f(x) равна h(x), деленной на g(x). h'(x) = 10x 9 g'(x) = 0 — sin x = -sin x
Функция f(x) равна h(x), деленной на g(x). h'(x) = 10x 9 g'(x) = 0 — sin x = -sin x
| f'(х) = |
|
| f'(x) = |
| = |
3) f(x) = ln(sinx). чему равна производная функции f(x)?
Калькулятор производныхПодробнее о производных на математическом форумеРегистрация на форуме
Производная формула функции. Стандартное обозначение, производное от некоторых… | Фикри Мульяна Сетиаван | Упрощенная математика Стандартное обозначение, производное от некоторых… | Фикри Мульяна Сетиаван | Упрощенная математикаИсчисление для всехСтандартное обозначение, производная некоторых общих функций и цепное правило дифференцированияКак я объяснял в предыдущей статье, основная тема производных/дифференциалов заключается в том, насколько быстро происходит изменение. И — как вы знаете — скорость изменения представлена градиентом функции на графике . То есть чем больше градиент функции, тем быстрее изменяется значение функции. В предыдущей статье мы видели, что градиент функции в точке может быть выражен как f’(x). f’(x) также показывает скорость изменения функции f(x). f’(x) — это то, что мы назвали производной/дифференцированием f(x). Прежде чем перейти к следующему обсуждению, следует знать, что существует специальное обозначение, которым можно заменить приведенную выше формулу для производной. 4. Производная f(x) = ln xИз приведенного выше расчета мы знаем, что производная ln x равна 1/x. С помощью приведенной выше формулы нам очень легко вычислить производную функции. Например, легко вычислить производную x². А как насчет производной от (x+3)²? Это легко, нам просто нужно расширить его, вычислив (x+3)(x+3) как обычно. А как насчет производной от (x+3)⁵⁶? Вы все еще хотите расширить его? Нет, вы потратите слишком много времени. К счастью, у нас есть цепное правило, чтобы решить эту проблему. Вот утверждение, которое я процитировал с сайта khanacademy.org :
Итак, цепное правило можно использовать для получения составной функции. |

 x (e — константа, известная как число Эйлера ) и f(x) = ln x. 9Икс.
x (e — константа, известная как число Эйлера ) и f(x) = ln x. 9Икс.