Математический анализ. Продолжение курса
Математический анализ. Продолжение курса
ОглавлениеПРЕДИСЛОВИЕГлава 1. ЧИСЛОВЫЕ РЯДЫ § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА 2. Критерий Коши сходимости ряда. § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 2. Признаки сравнения. 3. Признаки Даламбера и Коши. 4. Интегральный признак Коши—Маклорена. 5. Признак Раабе. 6. Отсутствие универсального ряда сравнения. § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ 2. О перестановке членов условно сходящегося ряда. 3. О перестановке членов абсолютно сходящегося ряда. § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 2. Связь между сходимостью бесконечных произведений и рядов. 3. Разложение функции sin x в бесконечное произведение. § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ 1. Метод Чезаро (метод средних арифметических). 2. Метод суммирования Пуассона—Абеля. § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ Глава 2.  ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ§ 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве. 3. Равномерная сходимость на множестве. 4. Критерий Коши равномерной сходимости последовательности (ряда). § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ 2. Почленное дифференцирование. 3. Сходимость в среднем. § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ 2. Непрерывность суммы степенного ряда. 3. Почленное интегрирование и почленное дифференцирование степенного ряда. § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ 2. Разложение некоторых элементарных функций в ряд Тейлора. 3. Элементарные представления о функциях кемплексной переменной.  4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами. Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА 2. Условия существования двойного интеграла для прямоугольника. 3. Определение и условия существования двойного интеграла для произвольной области. 4. Общее определение двойного интеграла. § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ 2. Случай произвольной области. § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Два признака сходимости несобственных интегралов от неотрицательных функций. 3. Несобственные интегралы от знакопеременных функций. 4. Главное значение кратных несобственных интегралов. Глава 4.  n. n.3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора. 4. Инварианты линейного оператора. Дивергенция и ротор. 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе. § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА 3. Некоторые другие формулы векторного анализа. 4. Заключительные замечания. § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА 2. Формула Остроградского—Гаусса. 3. Формула Стокса. § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ 2. Выражение объема через поверхностный интеграл. ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ 2. Билинейные формы. 3. Полилинейные формы. 4. Знакопеременные полилинейные формы. 5. Внешнее произведение знакопеременных форм.  6. Свойства внешнего произведения знакопеременных форм. 7. Базис в пространстве знакопеременных форм. § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 2. Внешний дифференциал. § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ 2. Свойства отображения. § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 2. Дифференцируемые цепи. 3. Формула Стокса. 4. Примеры. Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ 2. Критерий Коши равномерного стремления функции к предельной. 3. Применения понятия равномерного стремления к предельной функции. § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Случай, когда пределы интегрирования зависят от параметра. § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Несобственные интегралы второго рода, зависящие от параметра. § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ § 5. 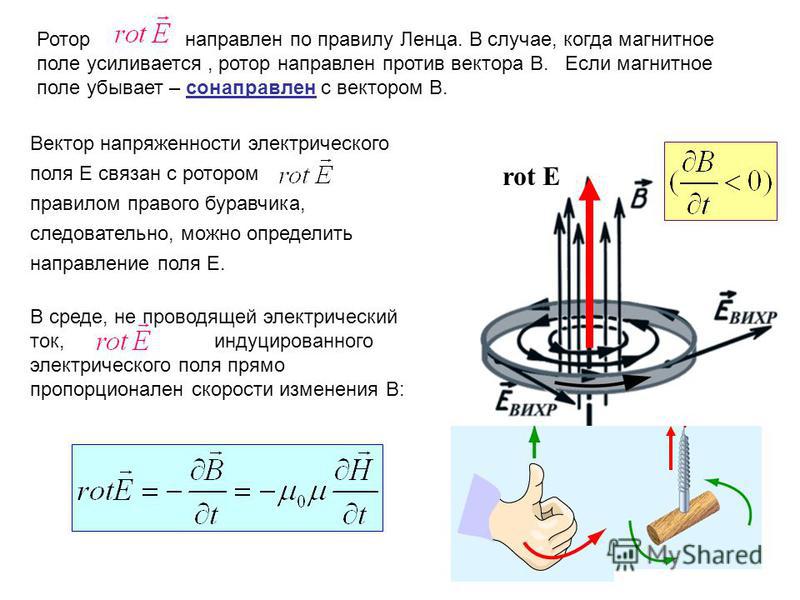 ИНТЕГРАЛЫ ЭЙЛЕРА ИНТЕГРАЛЫ ЭЙЛЕРА3. Связь между эйлеровыми интегралами. 4. Примеры. § 6. ФОРМУЛА СТИРЛИНГА § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ 2. Несобственные кратные интегралы, зависящие от параметра. Глава 8. РЯДЫ ФУРЬЕ § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ 2. Понятие об общем ряде Фурье. § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ 2. Доказательство замкнутости тригонометрической системы. 3. Следствия замкнутости тригонометрической системы. § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье. 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье. § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ 2. Выражение для частичной суммы тригонометрического ряда Фурье.  3. Вспомогательные предложения. 4. Принцип локализации. 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера. 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции. 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических. 8. Заключительные замечания. § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ 2. Модуль непрерывности и классы Гёльдера для функции N переменных. 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье. Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ 2. Основная теорема. Формула обращения. 3. Примеры. § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ |
2. Градиент, дивергенция, ротор
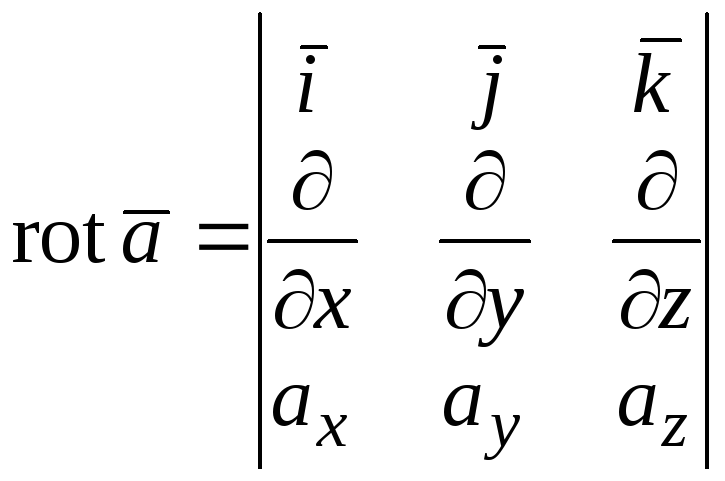 В декартовой системе
координат задание скалярного поля
эквивалентно заданию функции трех
переменных u(М)
= u(x,y,z).
Примерами скалярных полей могут служить
поле температур данного тела, поле
атмосферного давления и т.д. Пусть
функция u(x, y, z)
является непрерывно дифференцируемой
в области V.
В каждой точке этой области определен
вектор, проекциями которого на оси
координат являются значения частных
производных функции u(x,y,z):
В декартовой системе
координат задание скалярного поля
эквивалентно заданию функции трех
переменных u(М)
= u(x,y,z).
Примерами скалярных полей могут служить
поле температур данного тела, поле
атмосферного давления и т.д. Пусть
функция u(x, y, z)
является непрерывно дифференцируемой
в области V.
В каждой точке этой области определен
вектор, проекциями которого на оси
координат являются значения частных
производных функции u(x,y,z):Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М.
Если
каждой точке М некоторой области V поставлен в соответствие определенный
вектор
,
то говорят, что в этой области задано
векторное поле. В декартовой системе
координат задание векторного поля
равносильно заданию трех скалярных
функций:P(x,y,z), Q(x,y,z)
и R(x,y,z)
– проекций этого вектора на оси координат.
Вектор
в этом случае записывается в виде
В декартовой системе
координат задание векторного поля
равносильно заданию трех скалярных
функций:P(x,y,z), Q(x,y,z)
и R(x,y,z)
– проекций этого вектора на оси координат.
Вектор
в этом случае записывается в виде
а функции P(x,y,z), Q(x,y,z) и R(x,y
Ротором (вихрем) векторного поля называется вектор
Все
рассмотренные величины полей: grad u,
div
иrot
вычисляются с помощью частного
дифференцирования скалярного поляu и компонентов P, Q, R векторного поля. Таким образом, мы имеем дело с
дифференциальными операциями первого
порядка. Наряду с ними можно рассмотреть
дифференциальные операции второго
порядка:grad
div
,rot
rot
иdiv
grad u.
Рассмотрим последнюю операцию:
Таким образом, мы имеем дело с
дифференциальными операциями первого
порядка. Наряду с ними можно рассмотреть
дифференциальные операции второго
порядка:grad
div
,rot
rot
иdiv
grad u.
Рассмотрим последнюю операцию:
Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
Максимумом (минимумом) функции называется такое значениеэтой функции, которое больше (меньше) всех ее значений, принимаемой данной функцией в точках некоторой окрестности точкиМаксимум или минимум функцииназывается экстремумом этой функции, точка, в которой достигается экстремум, называется точкой экстремума:
а) Необходимый признак экстремума: в точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует . Точки, в которых частные производные первого порядка равна нулю, либо не существуют, называются критическими;
б) Достаточный признак экстремума: если точка – критическая точка функциии,,,, тогда:
1) если , то функция имеет экстремум в точке, а именно максимум, если, и минимум, если;
2) если , то экстремума в точкенет;
3)
если
,
то вопрос о наличии экстремума в точкетребует дополнительного исследования.
Пример 3.1. Исследовать на экстремум функцию .
а) Найдем критические точки:
Таким образом, имеем две критические точки и. Находим.
В точке , т.е. в этой точке экстремума нет. В точкеи, следовательно, в этой точке функция имеет локальный минимум:.
Идея ротора векторного поля
Расходимость и ротор векторного поля векторное поле — это два векторных оператора, основные свойства которых можно понять геометрически, рассматривая векторное поле как поток жидкости или газа. Расхождение обсуждается на сопутствующей странице. Здесь мы даем обзор основных свойств завихрения, которые можно интуитивно понять из потока жидкости.
Завиток векторного поля отражает идею того, как жидкость
может вращаться. Представьте, что приведенное ниже векторное поле $\dlvf$ представляет
поток жидкости. Векторное поле указывает на то, что жидкость циркулирует
вокруг центральной оси.
Загрузка апплета
Вращающееся векторное поле. Если векторное поле интерпретировать как скорость потока жидкости, кажется, что жидкость течет по кругу. С исходной точки графика (т. е. до того, как вы повернете его с помощью мыши), кажется, что жидкость циркулирует против часовой стрелки. Если вы повернете график, вы можете увидеть точки, плавающие вдоль оси вращения. Эти точки представляют собой вектора нулевой длины, поскольку скорость там равна нулю.
Дополнительная информация об апплете.
Эта макроскопическая циркуляция жидкости по кругу (т.е.
вращение вы можете легко увидеть на графике выше) на самом деле это не то, что
меры по завивке. Но оказывается, что это векторное поле также имеет
завиток, который мы могли бы назвать «микроскопическим кровообращением». Тестировать
для завихрения представьте, что вы погружаете в поток жидкости маленькую сферу,
и вы фиксируете центр сферы в какой-то точке так, чтобы сфера
не может следовать за жидкостью вокруг. Хотя вы фиксируете центр
сферы, вы позволяете сфере вращаться в любом направлении вокруг своей
Центральная точка. Вращение такой сферы показано на
ниже апплет.
Вращение
сфера измеряет ротор векторного поля $\dlvf$ в точке
центр сферы. (Сфера должна быть действительно
действительно маленький, потому что, помните, завиток равен микроскопический тираж.)
Хотя вы фиксируете центр
сферы, вы позволяете сфере вращаться в любом направлении вокруг своей
Центральная точка. Вращение такой сферы показано на
ниже апплет.
Вращение
сфера измеряет ротор векторного поля $\dlvf$ в точке
центр сферы. (Сфера должна быть действительно
действительно маленький, потому что, помните, завиток равен микроскопический тираж.)
Загрузка апплета
Сфера, вращаемая вращающимся векторным полем. Сфера погружена во вращающуюся жидкость, скорость которой определяется векторным полем. Середина сферы привязана к точке (первоначально в начале координат), но ей разрешено вращаться вместе с жидкостью. Вращение сферы жидкостью указывает на завихренность векторного поля. Вы можете перемещать точку, в которой закреплена сфера, перетаскивая ее мышью.
Дополнительная информация об апплете.
Векторное поле $\dlvf$ определяет как в каком направлении сфера вращается, а скорость , с которой она вращается. Мы
задайте ротор $\dlvf$, обозначаемый как $\curl \dlvf$, вектором, который
точек вдоль оси вращения и длина которых соответствует
скорость вращения.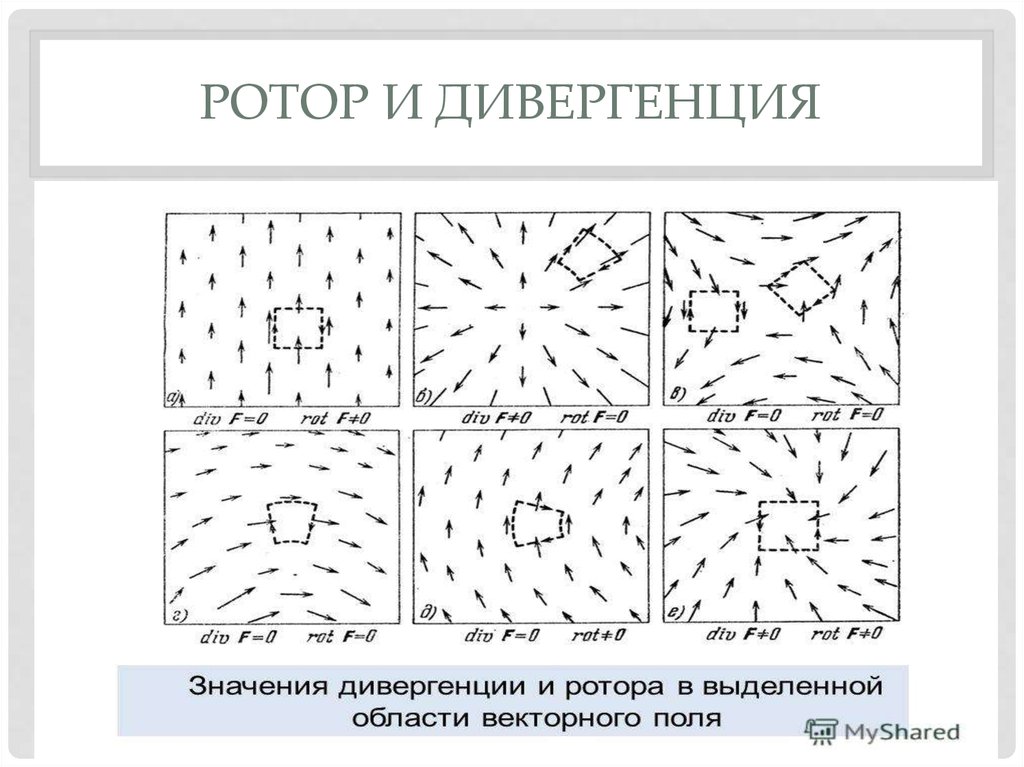 (Поскольку завиток является вектором, он сильно отличается от
из дивергенции, которая является скаляром.)
(Поскольку завиток является вектором, он сильно отличается от
из дивергенции, которая является скаляром.)
Мы можем нарисовать вектор, соответствующий $\curl \dlvf$, следующим образом. Сделаем длину вектора $\curl \dlvf$ пропорциональной скорость вращения шара. Направление $\curl\dlvf$ указывает на ось вращения, но нам нужно укажите, в каком направлении вдоль этой оси должен указывать вектор. Мы (произвольно?) установим направление вектора завитка, используя следующее «правило правой руки». Чтобы увидеть, где $\curl \dlvf$ должен указать, согнуть пальцы правой руки в направлении сферы вращается; ваш большой палец будет указывать в направлении $\curl \dlvf$. В нашем примере $\curl \dlvf$ отображается как зеленая стрелка.
Загрузка апплета
Вращающаяся сфера, указывающая на наличие завитка. Зеленая стрелка вдоль оси вращения сферы — это завиток векторного поля. Вы можете вращать
график, чтобы лучше видеть зеленую стрелку. Длина стрелки соответствует скорости вращения, а направление стрелки определяется правилом правой руки. Вы можете перемещать точку, в которой закреплена сфера, перетаскивая ее мышью. В этом примере завиток постоянен во всем векторном поле, поэтому зеленая стрелка и вращение сферы остаются неизменными при перемещении сферы.
Вы можете перемещать точку, в которой закреплена сфера, перетаскивая ее мышью. В этом примере завиток постоянен во всем векторном поле, поэтому зеленая стрелка и вращение сферы остаются неизменными при перемещении сферы.
Дополнительная информация об апплете.
Для этого конкретного векторного поля оказывается, что $\curl \dlvf$ не меняется с положением (это, конечно, неверно в общий). Например, если мы переместим сферу в другое место, она будет вращаться в том же направлении с той же скоростью. Обратите внимание, как сфера вращается одинаково, если вы переместите сферу в другое место в приведенных выше апплетах. (Дополнительную информацию см. на странице апплета.)
Завиток представляет собой трехмерный вектор, и каждый из его трех
компонентов оказывается комбинацией производных вектора
поле $\dlvf$. Вы можете прочитать о том, что можно использовать одни и те же вращающиеся сферы, чтобы получить представление о компонентах
вектор $\curl\dlvf$. Формула для компонентов завитка может
поначалу кажутся уродливыми, и некоторые умные обозначения
может помочь вам вспомнить формулу. Когда у вас есть формула,
вычисление ротора векторного поля является простым делом, как показано на
этот пример.
Когда у вас есть формула,
вычисление ротора векторного поля является простым делом, как показано на
этот пример.
Не дайте себя ввести в заблуждение
Презентация идеи завитка с помощью изображений сопровождается важное предупреждение. Нужно помнить, что картинки могут быть обманчивы. В частности, можно ошибочно подумать, что завиток возникает из-за макроскопическая циркуляция векторного поля, которую легко заметить на приведенных выше картинках. Предупреждаем, что это предположение далеко не правда! Если вы думаете, что можете запутаться между микроскопическая циркуляция локона и макроскопическая циркуляция что можно наблюдать на картинке, мы призываем вас проверить некоторые тонкости о завитке, которые могут вам помочь действительно понимаю завиток.
Stream Hidden Forms — Ротор (EatbrainLP009) от EATBRAIN
Stream Hidden Forms — Ротор (EatbrainLP009) от EATBRAIN | Слушайте онлайн бесплатно на SoundCloudJavaScript отключен
Вам необходимо включить JavaScript для использования SoundCloud
Покажите мне, как его включить
опубликовано //художник
Скрытые формы
//этикетка
facebook. com/Eatbra1n
twitter.com/eatbra1n
// Дата выпуска
Битпорт Искл. 07.10.19и по всему миру — 21.10.19
Много времени прошло с того первого момента ДИВЕРГЕНЦИИ, когда человек пожертвовал радостями своего существования ради общего блага. Там, где когда-то стоял человек, теперь осталось огромное дерево, возвышающееся над деревней своим невероятным размером. В течение многих лет магия его ветвей защищала тех, кто был внизу, от вреда, но время стерло его ствол, и обереги, которые он проецировал, теперь грозили рухнуть под натиском духов, которые давно бросились на границу. Одна-единственная жизнь, казалось, не могла сдерживать зло всю вечность. Этот факт был известен совету деревни внизу, и, когда великое дерево начало исчезать из мира, они привели в действие следующий план.
В глубине одной из высоких гор, окружавших деревню, каждый ее житель неустанно трудился, вырубая и вытаскивая каменные кости земли из грандиозного зала, который они строили. В его центре усердно трудились самые искусные ремесленники деревни, надписывая лицо огромного обелиска рунами и символами на языке, которого никто из них не знал.
com/Eatbra1n
twitter.com/eatbra1n
// Дата выпуска
Битпорт Искл. 07.10.19и по всему миру — 21.10.19
Много времени прошло с того первого момента ДИВЕРГЕНЦИИ, когда человек пожертвовал радостями своего существования ради общего блага. Там, где когда-то стоял человек, теперь осталось огромное дерево, возвышающееся над деревней своим невероятным размером. В течение многих лет магия его ветвей защищала тех, кто был внизу, от вреда, но время стерло его ствол, и обереги, которые он проецировал, теперь грозили рухнуть под натиском духов, которые давно бросились на границу. Одна-единственная жизнь, казалось, не могла сдерживать зло всю вечность. Этот факт был известен совету деревни внизу, и, когда великое дерево начало исчезать из мира, они привели в действие следующий план.
В глубине одной из высоких гор, окружавших деревню, каждый ее житель неустанно трудился, вырубая и вытаскивая каменные кости земли из грандиозного зала, который они строили. В его центре усердно трудились самые искусные ремесленники деревни, надписывая лицо огромного обелиска рунами и символами на языке, которого никто из них не знал. Ночью и днем деревня трудилась, пока при последнем ударе кирки они не услышали самый зловещий звук. По долине пронесся болезненный стон, за которым последовал оглушительный удар того, что могло быть всего лишь падением огромного дерева. Жители спрятались в пещере, с ужасом наблюдая, как духи зла начали порхать над потолком над ними. Тем не менее, поскольку все казалось потерянным, каждый дух, вошедший в комнату, был вырван вниз, его сущность была привязана к огромному обелиску, который поймал их лица в карикатурах агонии на своей поверхности. Хотя поток духов казался бесконечным, вскоре каждый из них оказался в такой же каменной тюрьме, когда диссонирующие завывания этих созданий зла растворились в небытии в его земном бытии. При этом зрелище село радовалось, вспоминая того, кто многим пожертвовал ради них. Хотя жизнь не могла сдержать поток ДИВЕРГЕНЦИИ, камень свяжет ее с неизбежной формой.
EATBRAIN, их девятый LP со вторым релизом в их серии DIVERGENCE, включающей 16 треков от многих звуковых лидеров огромной орды лейбла.
Ночью и днем деревня трудилась, пока при последнем ударе кирки они не услышали самый зловещий звук. По долине пронесся болезненный стон, за которым последовал оглушительный удар того, что могло быть всего лишь падением огромного дерева. Жители спрятались в пещере, с ужасом наблюдая, как духи зла начали порхать над потолком над ними. Тем не менее, поскольку все казалось потерянным, каждый дух, вошедший в комнату, был вырван вниз, его сущность была привязана к огромному обелиску, который поймал их лица в карикатурах агонии на своей поверхности. Хотя поток духов казался бесконечным, вскоре каждый из них оказался в такой же каменной тюрьме, когда диссонирующие завывания этих созданий зла растворились в небытии в его земном бытии. При этом зрелище село радовалось, вспоминая того, кто многим пожертвовал ради них. Хотя жизнь не могла сдержать поток ДИВЕРГЕНЦИИ, камень свяжет ее с неизбежной формой.
EATBRAIN, их девятый LP со вторым релизом в их серии DIVERGENCE, включающей 16 треков от многих звуковых лидеров огромной орды лейбла.

