08. ПРОИЗВОДНАЯ и ИНТЕГРАЛ — Физика это просто!!! 2016
Теперь пора познакомиться с математикой, которая поможет вам быстро и просто решать задачи механики. И не только механики. Можно безо всякого преувеличения заметить, что производные и интегралы используются при описании физических моделей реального мира во всех разделах физики. Итак, вернемся к рассмотренным в параграфах 3, 4, 5 понятиям пути, скорости и ускорения. Рассмотрим подробнее соотношения между координатами материальной точки, ее скоростью и ускорением в каждый момент времени. Ограничимся, для начала, случаем одномерного движения. Нарисуем произвольный график зависимости скорости V(t) материальной точки от времени t. Рисунок 6 В произвольный момент времени t1 мгновенная скорость V1 = V(t1). Запомним два утверждения: 1) Тангенс угла наклона касательной к графику V(t) в точке (в момент времени) t1 равен по величине значению ускорения а(t1) материальной точки в этот момент времени t1. 2) Площадь под кривой V(t) от t1 до t2 равна по величине пути, пройденному материальной точкой за время от момента t1 до момента t2 со скоростью, описываемой функцией V(t).
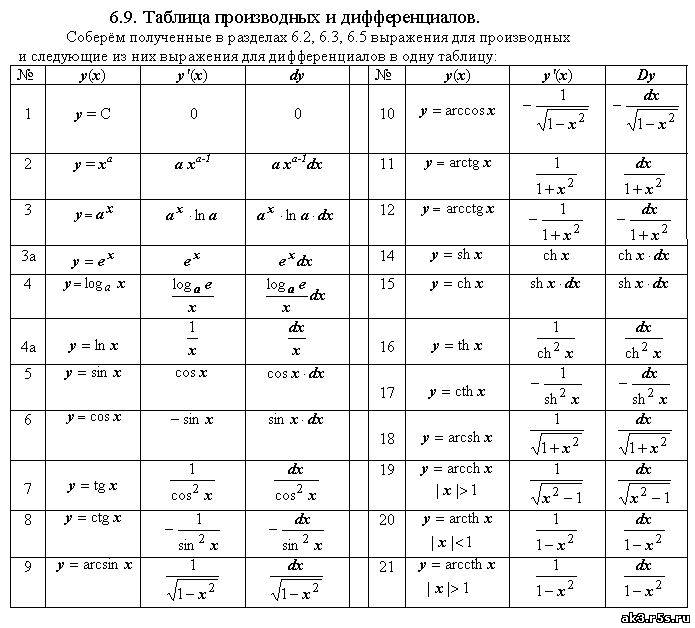
Строго математически это можно записать: 1. — «ускорение» есть первая производная функции скорости по времени. Просто запомните! Тангенс угла наклона касательной к функции f(t) в точке t есть значение первой производной этой функции в этой точке t ! Для нас с вами в данный момент, не вдаваясь в «глубины» дифференциального исчисления, важно следующее: · Для любой функции скорости материальной точки от времени V(t) существует функция a(t), которая определяет ускорение нашей материальной точки в любой момент времени t, в который определена функция скорости V(t). Как мы помним, «вычисление производной» в математике называется операцией «дифференцирования», или «операцией взятия производной» (видимо, по аналогии «взятия крепости»). Для некоторых функций эта операция по своей сложности, действительно, сравнима со взятием укрепленной крепости или покорением неприступной вершины. Но, к счастью, в курсе средней школы производные большинства функций можно просто брать из готовых таблиц. Либо, вообще, в интернет-сервисах. Например, http://www.webmath.ru/web.php или http://www.wolframalpha.com/. Просто задаете функцию — получаете производную! Напомним основные правила дифференцирования:
Приведем таблицу производных простейших функций:
2. Математически, определенный интеграл – это разность значения первообразной в конечной точке отрезка t2 минус значение первообразной в начальной точке отрезка t1. Он равен величине площади под кривой. На рисунке 2 эта площадь закрашена серым цветом. где X1,2(t1,t2) – перемещение, совершенное материальной точкой от момента времени t1 до момента времени t2. !!! Заметим, что формула (32) вычисляет именно «перемещение», потому что пройденный путь — это всегда положительная величина. Мы прошли километр в одну сторону, затем километр в обратную — в результате, пройденный путь равен двум километрам, а перемещение равно нулю. Мы никуда не переместились, вернувшись в исходную точку. Пройденный путь будет равен перемещению, только если мы движемся все время в одну сторону по прямой. По формуле (32) мы вычисляем перемещение, как разность координат в конечный момент времени и в начальный момент времени. Для нас важно запомнить: Первое. Неопределенный интеграл (так называемая «первообразная») какой-либо функции f(t) — это такая функция, продифференцировав которую мы получим обратно саму функцию f(t). В математике первообразную функции часто обозначают заглавной буквой, например, для функции f(t)первообразную можно обозначить F(t). Второе. Если мы интегрируем функцию скорости V(t) от точки t1 до точки t2, то интегралом будет перемещение X(t2) – X(t1). Резюме: · Если мы знаем функцию зависимости координаты X(t) точки от времени t, то, найдя производную этой функции по времени t (обозначим эту производную V(t)), мы получим функцию зависимости мгновенной скорости точки от времени. · Если мы далее продифференцируем полученную функцию скорости V(t) по времени t, то получим «первую производную» скорости по времени — функцию a(t) — функцию зависимости мгновенного ускорения от времени. Причем, все это чистая математика. Более того, в большинстве случаев функции можно брать прямо из специальных таблиц производных. А что, если мы продифференцируем функцию a(t)? В результате (в общем случае) мы получим некую функцию зависимости мгновенного изменения ускорения от времени. Это будет функция, которая позволит нам видеть, как сильно в каждый момент времени меняется ускорение движения нашей точки. В принципе, можно долго продолжать эти операции последовательного дифференцирования. И, заметьте, все время мы будем получать функции, которые наделены физическим смыслом. К счастью, в рамках школьной программы мы ограничимся равноускоренным движением. A(t) = const. А производная от константы всегда равна нулю! И, соответственно, дальше, хоть задифференцируйся, будет A'(t) = … = A»…‘(t) = 0. Все последующие производные будут равны нулю. |
И, что самое приятное, мы можем в подавляющем большинстве случаев очень просто найти одну функцию из другой. И наоборот.
Площадь под кривой, заданной функцией V(t) на отрезке от t1 до t2 есть значение «определенного интеграла» этой функции на отрезке [t1;t2]. Про первообразную функции мы уже знаем. 
Определенный интеграл на каком-либо отрезке области определения функции f(t) – это, по сути, разница значений первообразной этой функции F(t) в конечной и начальной точках отрезка.
Т.е. таким движением, при котором значение ускорения не изменяется. Оно равно некоторой «константе» (постоянной величине, не изменяющейся с течением времени).5.12. Производная интеграла, зависящего от параметра
Пусть в определенном интеграле пределы интегрирования и подынтегральная функция зависят от некоторого параметра , т.е. интеграл имеет вид
.
Требуется найти производную интеграла по этому параметру . Будем считать, что функции , — дифференцируемые функции по .
Рассмотрим отдельно
три случая, когда в интеграле зависят
от параметра либо подынтегральная
функция, либо какой-то из пределов
интегрирования.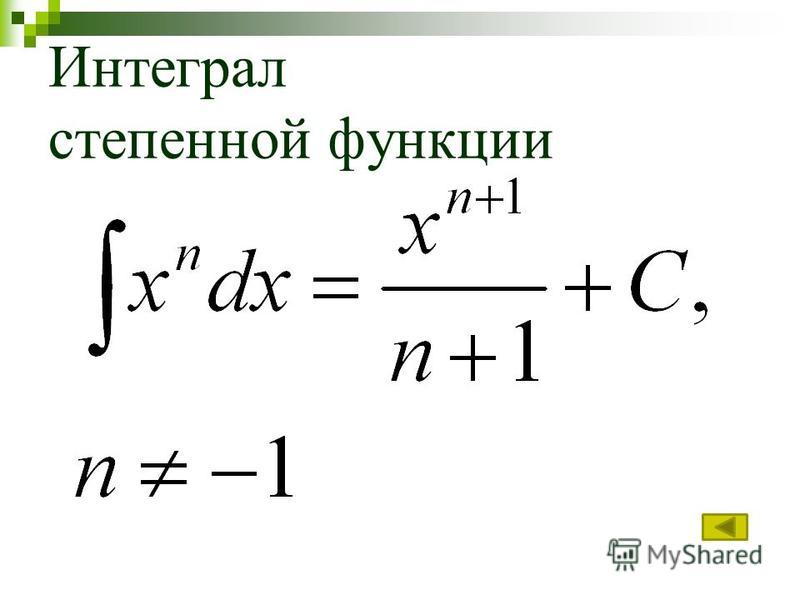
1. Пусть .
Найдем
Используем теорему Лагранжа о конечном приращении функции, запишем
, где .
Тогда . Следовательно,
.
Пример 5.17. Найти , если .
.
Пусть от параметра зависит верхний предел интегрирования, т. е.
. Найдем
.
По теореме о среднем
, где .
Тогда . Следовательно,
.
Если верхний предел интегрирования сложная функция , то производная интеграла найдется как производная сложной функции, т. е.
.
В практических задачах нередко требуется найти производную по x от интеграла . В этом интеграле x под интегралом – это переменная интегрирования, а верхний предел x является фактически параметром. Поэтому
.
3. Если от параметра зависит только нижний предел интегрирования, то переставим верхний и нижний предел интегрирования и получим
.
Используем формулы дифференцирования сложной функции нескольких переменных, получим производную интеграла, зависящего от параметра в общем случае или
.
Данная формула называется формулой Лейбница.
Пример 5.18. Найти , если .
Находим
.
Пример 5.19. Найти рекуррентное соотношение для вычисления интеграла , зависящего от параметра.
Данный интеграл называется гамма-функцией. Он часто используется в математической статистике и других прикладных разделах высшей математики.
Найдем .
При применим интегрирование по частям. Получим
,
так как .
Таким образом
.
Получим формулу для нахождения при n целом. Так .как. , то , , и т. д.
Глава 6. Двойные интегралы
6.1. Определение двойного интеграла
Двойные интегралы
являются обобщением понятием определенного
интеграла на случай функции двух
переменных.
Рис. 75 | Пусть некоторая функция двух переменных непрерывная и ограниченная в некоторой области D плоскости Оxy. Пусть область D ограничена конечным числом непрерывных линий, уравнения которых имеют вид или . С помощью таких же произвольно выбранных непрерывных линий разобьем область D на n элементарных областей , , площади которых равны , (рис. 75). |
Назовем диаметром элементарной области наибольшее расстояние между точками этой области. В каждой элементарной области выберем произвольно точку и вычислим значение функции .
Составим сумму , которая называется интегральной.
Двойным интегралом
от функции по области D называется предел интегральной суммы
при неограниченном увеличении числа n элементарных областей и стремление к
нулю наибольшего их диаметра
,
т.
3 \ right) \ mathrm dt} \ right)
$$ 9{3}х \справа)\sin х
$
Итак, сначала я вычисляю примитив, а затем вывожу его. Но я не знаю, как интегрировать. Должен ли я использовать метод «замены»? Я пытался, но потом меня заблокировали…
- исчисление
- интеграция
$\endgroup$
$\begingroup$
Я так понял из комментариев, что вы пока не совсем довольны ответами. Вот почему я пробую это (с небольшой задержкой). Заметьте, ничего нового в этом ответе нет… 93) \cos x.$$
Надеюсь, это поможет вам.
$\endgroup$
0
Разница между производной и интегралом
Автор: Admin
Производная и интеграл
Дифференцирование и интегрирование — две фундаментальные операции в исчислении.
Они имеют множество приложений в нескольких областях, таких как математика, инженерия и физика. И производная, и интеграл обсуждают поведение функции или поведение интересующего нас физического объекта.
Что такое производная?
Предположим, что y=ƒ(x) и x 0 находится в области ƒ. Мгновенной скоростью изменения ƒ называется at x 0 при условии, что этот предел существует конечно. Этот предел также называется производной от at и обозначается через ƒ(x).
Значение производной функции f в произвольной точке x в области определения функции определяется выражением lim Δ x→∞ [ƒ(x+Δx) − ƒ(x)]/Δx. Это обозначается любым из следующих выражений: y, ƒ(x), ƒ, dƒ(x)/dx, dƒ/dx, D x y.
Для функций с несколькими переменными мы определяем частную производную. Частная производная функции с несколькими переменными — это ее производная по одной из этих переменных при условии, что остальные переменные являются константами.
Символ частной производной ∂.
Геометрически производную функции можно интерпретировать как наклон кривой функции ƒ(x).
Что такое интеграл?
Интеграция или антидифференциация — это процесс, обратный дифференцировке. Другими словами, это процесс нахождения исходной функции, когда задана производная функции. Таким образом, интеграл или первообразная функции ƒ(x), если ƒ(x)= F (x), может быть определена как функция F (x), для всех x в области ƒ (x).
Выражение ∫ƒ(x) dx обозначает производную функции ƒ(x). Если ƒ(x)= F (x), то ∫ƒ(x) dx = F (x)+C, где C – константа, ∫ƒ(x) dx называется неопределенным интегралом от ƒ( Икс).
Для любой функции ƒ, которая не обязательно неотрицательна и определена на интервале [a,b], a ∫ b ƒ(x) dx называется определенным интегралом ƒ на [a,b] .
Определенный интеграл a ∫ b ƒ(x) dx функции ƒ(x) можно геометрически интерпретировать как площадь области, ограниченной кривой ƒ(x), осью x и линиями x=a и x=b.