Функция может быть полностью упрощенной или нет, это не имеет значения, так как калькулятор сначала упростит функцию, если это необходимо, прежде чем вычислить ее производную.
Однажды действующая функция уже предоставлен, вам нужно просто нажать кнопку «Рассчитать», подождать несколько секунд, и вам будут представлены все этапы расчета.
Дифференцирование — это основной инструмент, используемый в Calculus (наряду с интегрированием), и это важнейшая операция, которая широко используется в более продвинутой математике.
Как вычислить производную функции?
Процесс вычисления производной функции называется дифференциация и заключается в определении мгновенной скорости изменения точки, в каждой точке области функции.
Что такое мгновенная скорость изменения функции? Что ж, давайте начнем с определения скорость изменения : Рассмотрим функцию \(f\) и предположим, что у нас есть две точки, \(x_0\) и \(x_1\). В точке \(x_0\) функция имеет значение \(f(x_0)\), а в точке \(x_1\) функция принимает значение \(f(x_1)\)
Тогда изменение f определяется как \(\Delta y = f(x_1) — f(x_0)\) (которое также называется изменением y). Также изменение x определяется как \(\Delta x = x_1 — x_0)\). Простыми словами, \(\Delta x\) — это изменение x, а \(\Delta y\) — это изменение значения функции, вызванное изменением x.
Графически:
Производная формула
Так, если \(\Delta x\) представляет изменение x, а\(\Delta y\) представляет изменение значения функции, обусловленное изменением x, то соответствующее скорость изменения это:
\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]
Итак, какова же тогда будет мгновенная скорость изменения? Это соответствует анализу того, что произойдет, если \(\Delta x\) станет очень маленьким.
Можно ожидать, что \(\Delta y\) также станет маленьким, но что произойдет со скоростью между \(\Delta y\) и \(\Delta x\)?
Итак, в данном контексте мгновенная скорость изменения определяется как
\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]
Итак, говоря простым языком, мы задаем фиксированное значение \(x_0\) и вычисляем скорость изменения для значений \(x_1\), которые все ближе и ближе к \(x_0\). Используя эту идею о мгновенной скорости изменения, мы можем дать следующую формулу для производной в точке \(x_0\).
\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) — f(x_0)}{x_1 — x_0} \]
Если указанный выше предел существует, то мы говорим, что функция f дифференцируема на \(x_0\).
Также мы будем говорить, что функция дифференцируема на множестве A, если функция дифференцируема в каждой точке этого множества.
Шаги для использования формулы производной
- Шаг 1: Четко определите функцию f, которую вы хотите дифференцировать
- Шаг 2: Убедитесь, что вы максимально упростили f, иначе нахождение требуемого предела может быть неоправданно усложнено
- Шаг 3: Решите, будете ли вы работать с общей точкой x0, или вы задаете конкретную числовую точку для x0
- Шаг 4: Исходя из определения функции, используйте формулу \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) — f(x_0)}{x_1 — x_0} \).
То есть, подставьте значения x0 и x1 в f и посмотрите, как алгебраически выглядит формула - Шаг 5: Упростите все, что можно, ДО того, как взять лимит
- Шаг 6: Иногда проще задать x1 = x0 + h, а затем вычислить предел, когда h сходится к 0
То есть, подставьте значения x0 и x1 в f и посмотрите, как алгебраически выглядит формулаОбратите внимание, что шаг 6 — это шаг, который некоторым людям нравится по умолчанию. Действительно, альтернативная формула производной, которая может показаться более простой для целей упрощения, такова:
\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) — f(x_0)}{h} \]
это формула, которую вы можете найти в своем учебнике, вместо другой.
Правила производных
Вычисление производной по формуле может показаться чертовски трудоемким занятием. И действительно, это может быть трудоемким процессом, если мы решим каждый процесс дифференцирования проводить по формуле производной.
К счастью, существует ряд функций (а именно полиномы , Тригонометрические функции ), для которых мы точно знаем их производные.
Кроме того, у нас есть
правила дифференциации
которые позволяют нам найти производную функции, которая является
Составная функция
и/или комбинацию элементарных функций (для которых известна их производная), в терминах элементарных производных.
Каковы этапы вычисления производной?
- Шаг 1: Определите функцию f, которую вы хотите дифференцировать. Упростите как можно больше перед вычислением ее производной
- Шаг 2: Определите, должны ли вы использовать формулу производной или нет
- Шаг 3: Если вы должны использовать формулу производной, используйте \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) — f(x_0)}{x_1 — x_0} \), или вы можете использовать \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) — f(x_0)}{h} \), если это кажется более простым подходом
- Шаг 4: Если вам не требуется использовать формулу производной, вы можете воспользоваться основными правилами дифференцирования: Линейность, Правило Продукта , Правило Квоты и Правило Цепи , что поможет вам свести вычисление производной к использованию основных известных производных
Часто бывает так, что функция, которую вы пытаетесь
найти производную
for не является простой функцией, а представляет собой базовую комбинацию нескольких простых функций.
Например, функция
\[f(x) = x + \cos(x) + \sin(x)\]
не является элементарной функцией сама по себе, но является составной функцией трех элементарных функций, \(x\), \(\sin x\) и \(\cos x\).
Применение деривативов
Можно подумать: «Ну, производные связаны с пределами, а это супертеоретически, поэтому они не должны иметь слишком много применений», но вы будете совершенно неправы. Магия производных заключается в том, что они, по сути, представляют собой скорость изменения функций, которые могут представлять различные типы процессов.
Именно поэтому дифференциация позволяет изучить процесс изменения и сравнить изменяющиеся переменные, что имеет широкое применение.
2\right)\)
Таким образом, мы получаем следующий график для функции на интервале \([-5, 5]\):
Пример: калькулятор производных
Найдите производную от \( f(x) = \displaystyle \frac{4}{x}\). Определена ли она везде? Постройте график.
Отвечать: Функция, для которой требуется производная, — \(\displaystyle f(x)=\frac{4}{x}\).
Дальнейшее упрощение не требуется, поэтому мы можем перейти непосредственно к вычислению его производной:
\( \displaystyle \frac{d}{dx}\left(\frac{4}{x}\right)\)
Using the Power Rule for a polynomial term with negative exponent: \(\frac{d}{dx}\left( \frac{4}{x} \right) = -\frac{4}{x^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle -\frac{4}{x^2}\)
Графически:
Подробнее о производных и функциях
Функции являются чрезвычайно важными конструкциями в математике.
Вам необходимо уметь
упростить функцию
обычно в качестве преамбулы других, более специализированных вычислений. Существуют специальные типы функций, которые позволяют выполнять конкретные операции, например, то, что вы делаете с
Полиномиальные операции
.
Интересно, что многие важные элементы, такие как нахождение координат вершина параболы которые можно вывести хитрым способом, используя геометрические аргументы, можно тривиально получить с помощью дифференцирования.
производная калькулятор dy/dx APK (Android App)
Калькулятор производных позволяет вычислять математические функции путем дифференцирования.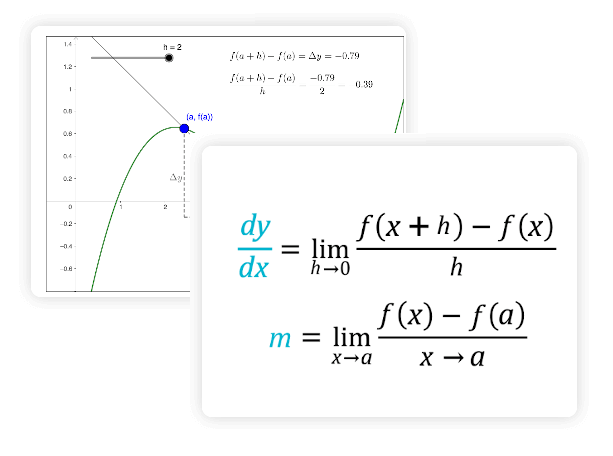
Это приложение для решения производных дает вам подробное пошаговое решение деривации. Таким образом, вы можете легко понять реализацию производной формулы dy/dx.
Приложение для решения производных помогает быстро решить расчет производных. Вам не нужно вручную вычислять производную, когда у вас есть это приложение калькулятора производных уравнений. Вставьте вопрос с правильными значениями, нажмите кнопку расчета. Получите точное решение с помощью графика и графиков с помощью этого Калькулятора производных с шагами.
Мы создали этот калькулятор дифференцирования с использованием новейших методов нахождения производных. Именно поэтому, это экономит много вашего времени. Вы можете решить свое задание и сложные уравнения вывод. Если у вас мало времени и вы ищете хорошее работающее приложение Derivative Solution App! Попробуйте этот бесплатный калькулятор производных и получите точные результаты.
Преимущества математического решателя производных
Этот калькулятор производного исчисления прост в использовании.
Вот несколько простых шагов для учителей и студентов исчисления. Так что каждый может легко использовать этот производный калькулятор.
Новички: Используя дифференциальный калькулятор для решения функции, любой новичок в дифференцировании может получить некоторую практику, которая позже спасет их в сезоне тестов и экзаменов.
Учащиеся старших курсов: те, кто уже разбирается в производных, могут по-прежнему использовать этот решатель производных. Они могут использовать его для решения своих заданий или научиться оценивать любой сложный вопрос вывода.
Учителя: Да, даже учителям будет полезно это производное приложение-решение. Его можно использовать для проверки назначений или устранения любой двусмысленности, когда вы зашли в тупик при дифференциации с помощью этого калькулятора dy/dx.
Все, кто хочет учиться: те, кто не учится и не преподает в каком-либо институте, но просто хочет изучать производные, потому что они находят это интересным (да, многие люди любят математику).
Они могут легко выучить формулу производной и ее реализацию с помощью этого калькулятора исчисления с шагами.
Точно так же авторы статей по математике могут решать здесь примеры вычисления производных, которые они хотят добавить в свои публикации.
Возможности калькулятора производных
— Хорошо для студентов и преподавателей исчисления.
— Реализация формулы с шагами.
— Плавный работающий решатель производных.
— Поддерживает почти все устройства.
— Очень легкое приложение калькулятора производных.
— Быстрый расчет производной с графиком и графиками.
— Легко найти производную функции.
— Сделайте неограниченный расчет производной бесплатно.
b>Множественное дифференцирование
Вы можете дифференцировать одну и ту же функцию для первой, второй, третьей, четвертой и пятой производных. Все, что вам нужно сделать, это ввести число в помеченном поле производной.
Пошаговое решение
Калькулятор дифференцирования производной T дает вам полное решение, содержащее все этапы вывода.