Произвольный четырехугольник выпуклый: Выпуклый четырехугольник

Содержание

Выпуклый четырехугольник

Определения

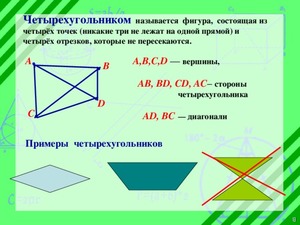
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Диагональ четырехугольника – отрезок, соединяющий любые две несоседние вершины.

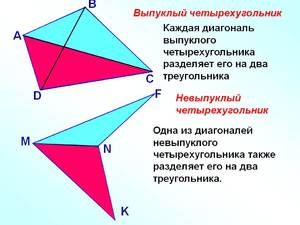
Различают выпуклые и невыпуклые четырехугольники.

Четырехугольник называется выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону.

В школьном курсе рассматриваются только выпуклые четырехугольники. Поэтому далее “выпуклый четырехугольник” будем сокращенно называть “четырехугольник”.

Теорема

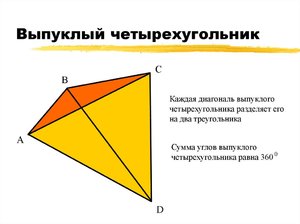
Сумма внутренних углов любого четырехугольника равна $360^\circ$.

Доказательство

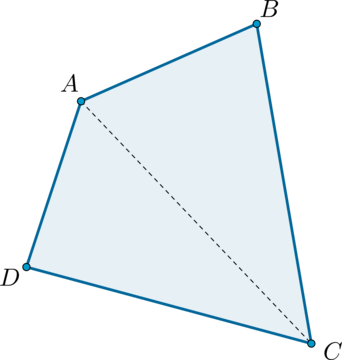
Рассмотрим четырехугольник $ABCD$ и проведем его диагональ $AC$. Она разбила четырехугольник на два треугольника. Сумма углов любого треугольника равна $180^\circ$, следовательно:

\[\begin{multline*} 360^\circ=180^\circ+180^\circ=(\angle DAC+\angle D+\angle ACD) + (\angle CAB+\angle B+\angle ACB)=\\ =\angle D+\angle B +(\angle DAC+\angle CAB)+(\angle ACD+\angle ACB)=\angle D+\angle B+\angle A+\angle C \end{multline*}\]

Теорема Вариньона

Выпуклый четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом.

Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Средняя линия треугольника”.

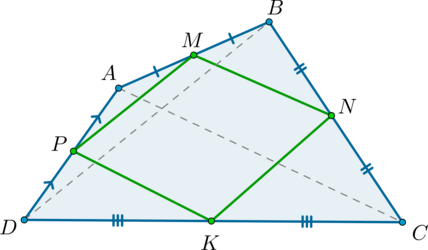
Проведем диагонали четырехугольника $ABCD$. Рассмотрим $\triangle ABC$: $MN$ – средняя линия этого треугольника, следовательно, $MN\parallel AC$.

Рассмотрим $\triangle ADC$: $PK$ – средняя линия этого треугольника, следовательно, $PK\parallel AC$.

Таким образом, $MN\parallel AC\parallel PK$.

Аналогичным образом доказывается, что $MP\parallel BD\parallel NK$.

Следовательно, по определению $MNKP$ – параллелограмм.

Теорема

Если в четырехугольнике $ABCD$ диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон равны: \[AB^2+CD^2=BC^2+AD^2\]

Доказательство

По теореме Пифагора:

\[\begin{aligned} &AB^2=x^2+a^2\\ &CD^2=b^2+y^2\\ &BC^2=x^2+b^2\\ &AD^2=a^2+y^2 \end{aligned}\]

Из равенств видно, что $AB^2+CD^2=x^2+a^2+y^2+b^2=BC^2+AD^2$

Замечание

Все известные четырехугольники, изучаемые в школьной программе, подчиняются следующей схеме:

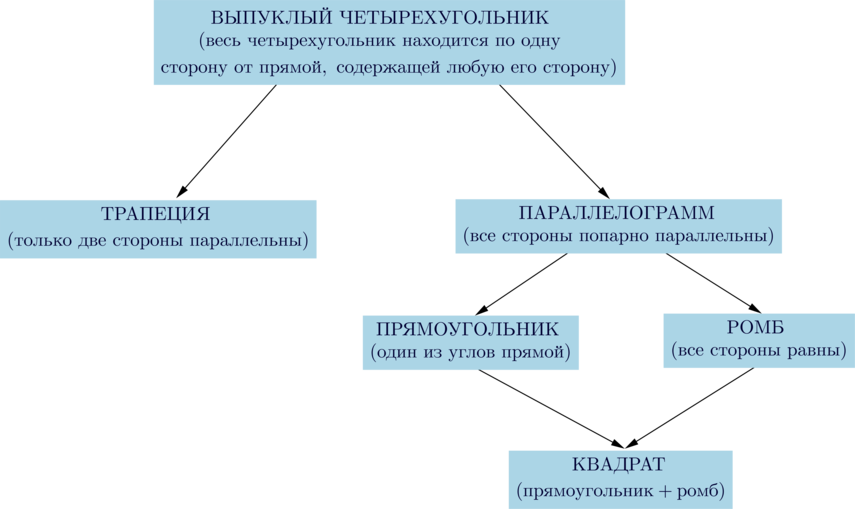
Таким образом, любой четырехугольник из этой схемы обладает свойствами всех предыдущих четырехугольников, из которых он следует.

Например, прямоугольник обладает свойствами параллелограмма и произвольного выпуклого четырехугольника; квадрат обладает свойствами прямоугольника, параллелограмма, выпуклого четырехугольника.

Геометрия. Урок 4. Четырехугольники — ЁП

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

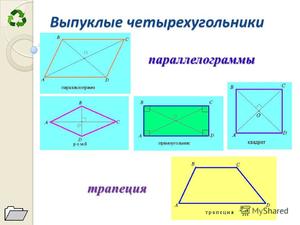
Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

Противолежащие стороны равны.
Противоположные углы равны.
Диагонали точкой пересечения делятся пополам.
Сумма углов, прилежащих к одной стороне, равна 180 ° .
Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

Параллелограмм: площадь параллелограмма равна произведению основания на высоту

S = a ⋅ h a = b ⋅ h b

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Параллелограмм: площадь параллелограмма равна произведению двух сторон на синус угла между ними

S = a ⋅ b ⋅ sin α

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Параллелограмм: площадь равна полупроизведению диагоналей на синус угла между ними

S = 1 2 ⋅ d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

Диагонали пересекаются под прямым углом.
Диагонали являются биссектрисами углов, из которых выходят.
Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

Ромб: площадь ромба равна произведению основания на высоту

S = a ⋅ h

Как произведение стороны ромба на высоту ромба.

Ромб: площадь ромба равна произведению сторон на синус угла между ними

S = a 2 ⋅ sin α

Как квадрат стороны ромба на синус угла между двумя сторонами.

Ромб: площадь ромба равна полупроизведению диагоналей

S = 1 2 ⋅ d 1 ⋅ d 2

Как полупроизведение диагоналей ромба.

Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .

Свойства прямоугольника:

Диагонали прямоугольника равны.
Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

Прямоугольник: площадь прямоугольника равна произведению сторон

S = a ⋅ b

Как произведение двух смежных (соседних) сторон прямоугольника.

Прямоугольник: площадь равна полупроизведению диагоналей на синус угла между дими

S = 1 2 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

Сохраняет свойства ромба.
Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

Квадрат: площадь квадрата равна квадрату стороны

S = a 2

Как квадрат стороны.

Квадрат: площадь квадрата равна половине квадрата диагонали

S = d 2 2

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.

B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна 180 ° .

∠ A + ∠ B = 180 °

∠ C + ∠ D = 180 °

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Трапеция: площадь трапеции равна произведению полусуммы оснований на высоту

S = a + b 2 ⋅ h = m ⋅ h

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Трапеция: площадь трапеции равна полупроизведению диагоналей на синус угла между ними

S = 1 2 d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Модуль геометрия: задания, связанные с четырехугольниками

Скачать домашнее задание к уроку 4.

Понятие выпуклого четырехугольника, его свойства и признаки

Выпуклый четырехугольник — это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Как видно, определение довольно легко запоминающееся.

Выпуклый четырехугольник

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

параллелограмм;
квадрат;
прямоугольник;
трапеция;
ромб.

Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция. Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка [AB]. Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым

. Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

Это интересно: титульный лист проекта — образец, как правильно оформляется?

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам. Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.

Итак, известны основные признаки и свойства:

сумма углов четырехугольника равна 360 градусам;
диагонали фигур пересекаются в одной точке.

Далее рассмотрим каждый четырехугольник по отдельности.

Прямоугольник. Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название — прямоугольник.

Квадрат, тот же параллелограмм, но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция — очень интересная фигура. Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб — не менее интересная фигура. Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Виды выпуклых четырехугольников

Четырёхугольники, виды и свойства / math5school.ru


	Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна:
	Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника:

Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны; S_ABCD= 2S_MNPQ.
	Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP²+ NQ²+ RS ²= ¼(AB²+BC²+CD²+AD²+AC²+BD²). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: S_ABCD= MP·NQ·sinβ.


Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.

	Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника:
	Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения:

	Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°: ∠A+∠C=∠B+∠D=180°. Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
	Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Радиус окружности, описанной около четырёхугольника: Площадь вписанного четырёхугольника:
	Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов. У вписанного четырёхугольника любые два связанных угла равны.
	Если четырёхугольник одновременно является описанным и вписанным, то его площадь: Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:

	Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны: AB\|\|CD, BC\|\|AD. У параллелограмма противолежащие стороны равны и противолежащие углы равны: AB=CD, BC=AD; ∠A=∠C, ∠B=∠D. Сумма любых двух соседних углов параллелограмма равна 180°: ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.
	Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: AO=OC; BO=OD. Каждая диагональ делит параллелограмм на два равных треугольника: ∠ABC=∠CDA; ∠ABD=∠CDB. Две диагонали параллелограмма делят его на четыре равновеликих треугольника: S_ΔABO=S_ΔBCO=S_ΔCDO=S_ΔADO. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: e²+f²= a²+b²+a²+b²= 2(a²+b²).
Признаки параллелограмма: Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм. Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм. Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм. Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.
	Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне: h_a= b·sin γ; h_b= a·sin γ. Площадь параллелограмма можно определить: через его сторону и высоту, проведённую к ней: S = ah_a= bh_b; через две его стороны и угол между ними: S = ab·sin γ.

	Ромбом называется параллелограмм, у которого все стороны равны: AB=BC=CD=AD. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов: AC⊥BD; ∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.
	В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности, вписанной в ромб, можно вычислить: через высоту ромба: через диагонали ромба и сторону: через отрезки, на которые делит сторону ромба точка касания: Площадь ромба можно определить: через диагонали: через сторону и угол ромба: через сторону и высоту: через сторону и радиус вписанной окружности:

	Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°.
	Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка: AC=BD; AO=BO=CO=DO. Площадь прямоугольника можно определить: через его стороны: S = ab; через диагонали и угол между ними: S = ½d²·sin γ.
	Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали: BD = 2R.

	Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, AB=BC=CD=AD.
	Диагонали квадрата равны и перпендикулярны. Сторона и диагональ квадрата связаны соотношениями: Площадь квадрата:
	У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей. Радиус описанной окружности: Радиус вписанной окружности:

	Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны: AD\|\|BC. Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
	Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: AK=KB; CL=LD. Средняя линия трапеции параллельна её основаниям и равна их полусумме: KL\|\|AD; KL\|\|BC; KL = ½(AD+BC).
	При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ: ΔAED∼ΔBEC, k=AD/BC. Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ: ΔAОD∼ΔCОВ, k=AD/BC. Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: S_ΔABO= S_ΔCDO.
	Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон: O∈KL; E∈KL. Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности: RS\|\|AD; RS\|\|BC; RS = ½(AD–BC).
	В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон: AD+BC=AB+CD. Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции. В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств: Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом: ∠AOB=∠COD=90°. Радиус вписанной в трапецию окружности можно определить: через отрезки, на которые делится боковая сторона точкой касания:
	Равнобокой называется трапеция, у которой боковые стороны равны: AB=CD. У равнобокой трапеции: диагонали равны: AC=BD; углы при основании равны: ∠A=∠D, ∠B=∠C; сумма противолежащих углов равна 180?: ∠A+∠C=∠B+∠D=180°. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая. Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².
	Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
	Площадь трапеции можно определить: через полусумму оснований (первую среднюю линию) и высоту: через диагонали и угол между ними:


Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон. Дельтоид может быть выпуклым или невыпуклым. Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом. В любом дельтоиде углы между соседними неравными сторонами равны. Площадь любого дельтоида можно определить: через его диагонали: через две соседние неравные стороны и угол между ними: S = ab·sin α .

В любой выпуклый дельтоид можно вписать окружность. Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида. Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.
	Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°. Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:

	Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом. Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий: для сторон четырёхугольника верно: a²+c² = b²+d²; для площади четырёхугольника верно: S = ½ef; параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.
	Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности: a²+c² = b²+d² = 4R².
	Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны: ac = bd. Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения:

Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)

Виды четырехугольников:
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны
Ромб — это параллелограмм, у которого все стороны равны.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Квадрат — это прямоугольник, у которого все стороны равны.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Свойства произвольных четырехугольников:
Сумма внутренних углов четырехугольника равна 360^o

что это такое, каковы его свойства и чему равна сумма его уголов

Если на плоскости имеются четыре точки, из которых никакие три не принадлежит одной прямой, то их можно попарно соединить отрезками. В результате получится фигура с четырьмя углами, содержащая две диагонали, при пересечении которых получится выпуклый четырехугольник.

Виды

Существует несколько видов фигур с четырьмя углами, но не все они являются выпуклыми. Слева рисунок отображает выпуклый четырехугольник, все его внутренние точки находятся в одной полуплоскости относительно прямой l, на которой лежит сторона AD. Для среднего данное условие выполняется, но его нельзя считать выпуклым, потому что его стороны пересекаются. Такие четырехугольники называются самопересекающимися. Правый тоже не является выпуклым, так как две его точки B и C лежат в разных полуплоскостях относительно разбиения прямой l.

На основании вышесказанного дадим определение. Выпуклым четырехугольником называется фигура, состоящая из четырех точек и четырех отрезков, которые последовательно их соединяют. Главное условие: никакие три точки не должны одновременно лежать на одной прямой, а соединяющие отрезки пересекаться.

Виды выпуклых четырехугольников:

прямоугольник;
параллелограмм;
трапеция;
ромб;
квадрат.

Перечисленные отношения между множествами фигур упрощают доказательства теорем (предложений, выражающих свойства). Например, если теорема доказана для параллелограмма (будет ли параллелограмм выпуклым? и т.д.), то она будет верна и для любого соответствующего подмножества фигур. Если же доказана более общая теорема для выпуклого четырехугольника, то она будет верна и для параллелограмма, и для трапеции.

Свойства

Главные признаки:

сумма углов — 360 градусов;
диагонали могут пересекаться в одной точке.

Если сумма углов равна 360, это следствие более общего случая – четырехугольника, не имеющего пересекающихся отрезков. Но для выпуклого обычно проводят отдельное и очень простое доказательство. Если внутри выпуклого четырехугольника провести диагональ, то она разобьет его на два треугольника. Как известно, сумма углов в треугольнике равна 180. Сложив все получившиеся углы, получаем величину 360.

Если взять средние точки всех сторон произвольного выпуклого четырехугольника и построить на них новый, то он окажется параллелограммом (Теорема Вариньона).

Доказательство на следующем фото. Выпуклый четырёхугольник ABCD имеет на каждой из сторон точку, делящую эту сторону пополам. Рассмотрим отрезок FG. Это средняя линия треугольника DAB, параллельная диагонали DB. Это следует из подобия треугольников DAB и FAG.

Аналогично проводятся рассуждения для треугольников DBC и EHC. Из чего следует параллельность DB и EH. Поскольку отрезки FG и EH параллельны диагонали DB, то и сами параллельны.

Аналогично доказывается, что отрезки FE и GH параллельны. Так как противолежащие стороны EFGH попарно параллельны, значит, это параллелограмм.

Обратите внимание! Теорема Вариньона справедлива для всех четырехугольников, невыпуклых и самопересекающихся. Если взять середины диагоналей, то можно построить еще два параллелограмма. Центры всех трех параллелограммов окажутся на одной прямой.

Если выпуклый четырёхугольник имеет свойство взаимной перпендикулярности своих диагоналей, то суммы квадратов его противоположных сторон у него равны. Это доказывается при помощи теоремы Пифагора, как показано на следующем чертеже:

Квадрат каждой из сторон выражается через сумму квадратов отрезков диагоналей, ограниченных вершинами и точкой пересечения. Для удобства мы обозначаем их малыми буквами латинского алфавита, совпадающими с названием вершин. Затем выписываем выражения для сумм квадратов противолежащих сторон:

В правой части каждого из выражений стоит одна и та же сумма слагаемых. Следовательно, равны и правые части между собой, что доказывает теорема.

Вписанные и описанные

Часто требуется проверить, не лежат ли вершины четырехугольника на окружности, или существует ли окружность, вписанная в 4-угольник. Центр описанной окружности находится в точке пересечения срединных перпендикуляров к сторонам, а центр вписанной – на пересечении биссектрис внутренних углов.

Если сумма противоположных углов составляет 180, то рядом с ними можно описать окружность, другими словами, существует окружность, на которой лежат все вершины четырехугольника. Его называют вписанным (подразумевается, что в окружность). Верно и обратное утверждение, то есть выраженное в теореме условие необходимое и достаточное.

Расчет площади

Площадь, которую имеет любой выпуклый четырёхугольник, равна половине произведения длин диагоналей на синус угла между ними. Докажем это правило.

Здесь опять поможет теорема Вариньона (мы имеем “большой” параллелограмм, о котором сразу не было сказано). Проведем прямые, параллельные диагоналям, через вершины A, B, C, D исходного прямоугольника. Мы получим параллелограмм EFGH. Его площадь равна сумме площадей параллелограммов AFBO, BGCO, CHDO, DEAO. Но каждый из перечисленных делится своей диагональю на пару треугольников с равными площадями. С другой стороны, в силу параллельности диагоналей ADCD сторонам внешнего параллелограмма, мы можем применить формулу площади:

Полезное видео

Подведем итоги

Фигуру, состоящую из четырех углов, можно часто увидеть в обычной жизни, такую форму обычно имеют земельные участки, здания, параллелограммы служат для построения векторных базисов на плоскости. Не случайно 4-угольники хорошо изучены и установлено большое число свойств, связанных с ними.

Вконтакте

Одноклассники

Facebook

Мой мир

Twitter

Выпуклый четырехугольник | Треугольники

Что такое выпуклый четырехугольник? Чем он отличается от четырехугольника, который не является выпуклым?

Определение.

Четырехугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Другими словами, четырехугольник — выпуклый, если он лежит по одну сторону от каждой прямой, содержащей две его соседние вершины.

Например, четырехугольник ABCD является выпуклым.

Он лежит в одной полуплоскости относительно любой из прямых, проходящих через его стороны.

Четырехугольник FKMN не является выпуклым.

Прямые, проходящие его стороны FK и MK, разбивают FKMN на части, лежащие относительно этих прямых в разных полуплоскостях ( то есть по разные стороны от прямых).

Четырехугольники

Выпуклые и вогнутые четырехугольники — A Plus Topper

Выпуклый четырехугольник: Четырехугольник называется выпуклым четырехугольником, если отрезок прямой, соединяющий любые две вершины четырехугольника, находится в одной области.
На рисунке ABCD — выпуклый четырехугольник, потому что AB, BC, CD, DA, AC, BD находятся в той же области четырехугольника.
В выпуклом четырехугольнике каждый угол меньше 180 °.

Вогнутый четырехугольник: Четырехугольник называется вогнутым четырехугольником, если хотя бы один отрезок прямой, соединяющий вершины, не является частью той же области четырехугольника.
То есть любой отрезок линии, соединяющий две внутренние точки, выходит за пределы фигуры. В вогнутом четырехугольнике по крайней мере один угол является углом отражения, то есть углом больше 180 °. На рисунке ABCD представляет собой вогнутый четырехугольник, поскольку линия, соединяющая вершины A и C, выходит за пределы области четырехугольника.

Свойство суммы углов четырехугольника

Сумма всех углов четырехугольника равна 360 ° или четырем прямым углам.
Нарисуйте четырехугольник ABCD с одной из диагоналей AC.

Диагональ AC делит четырехугольник на два треугольника, т. Е. ΔADC и ΔABC.
Ясно, что ∠l + ∠2 = ∠A
и ∠3 + ∠4 = ∠C… (1)
Мы знаем, что сумма углов треугольника равна 180 °.
∴ In ΔABC, ∠1 + ∠3 + ∠B = 180 °
In ΔADC, ∠2 + ∠4 + ∠D = 180 °
Сумма углов четырехугольника
= Сумма углов ΔABC и ΔADC
∴ (∠1 + ∠3 + ∠B) + (∠2 + ∠4 + ∠D) = 180 ° + 180 °
или ∠1 + ∠3 + ∠B + ∠2 + ∠4 + ∠D = 360 °
или (∠1 + ∠2) + ∠B + (∠3 + ∠4) + ∠D = 360 °
или ∠A + ∠B + ∠C + ∠D = 360 ° (используя 1)
Следовательно, сумма углов четырехугольника равна 360 °.

Пример 1: Углы четырехугольника находятся в соотношении 1: 2: 1: 2. Найдите размер каждого угла.
Решение: Пусть первый угол четырехугольника равен x.
Здесь второй угол = 2x
третий угол = x
четвертый угол = 2x
Сумма всех углов четырехугольника = 360 °
∴ x + 2x + x + 2x = 360 °
6x = 360 °
x = 60 °
∴ Первый угол = x = 60 °
Второй угол = 2x = 2 × 60 ° = 120 °
Третий угол = x = 60 °
Четвертый угол = 2x = 120 °.

Интерполяция с использованием произвольного четырехугольника

Plasma Simulations by Example book discount

В предыдущей статье о методе частиц в ячейках (PIC) мы представили концепцию рассеивания данных по сетке. Метод PIC в значительной степени зависит от интерполяции данных между частицами и сеткой. Во-первых, операция рассеяния используется для вычисления плотности заряда, который затем передается в решатель Пуассона. Вычисленное электрическое поле, которое хранится в узлах сетки, впоследствии собирается обратно в положения частиц для расчета их ускорения.

Интерполяция сетки

Метод интерполяции, который мы использовали в этом примере, основан на линейном взвешивании по площади. Есть и другие альтернативы (см., Например, [1]). Некоторые из них, например метод ближайшей точки, менее точны. Другие используют схему второго или более высокого порядка для повышения точности. Описанный здесь линейный метод предлагает хороший компромисс между точностью и вычислительными затратами. Это метод, который используется во всех наших кодах.

Эта схема интерполяции кратко представлена ниже на Рисунке 1.Мы хотим интерполировать некоторую величину, существующую в позиции, обозначенной большим красным кружком, на четыре узла сетки. Для этого мы делим ячейку на четыре части (или восемь в 3D). Доля, которая должна быть внесена в каждый узел, просто задается отношением площади, диагонально противоположной от узла, к общей площади ячейки, \ (w_i = A_i / A \) (в 3D вы должны использовать объемные отношения). Чтобы помочь вам визуализировать это, на рисунке 1 узлы заштрихованы цветом, соответствующим доле площади, которая попадает на них.

2d linear area interpolation used to scatter data to grid

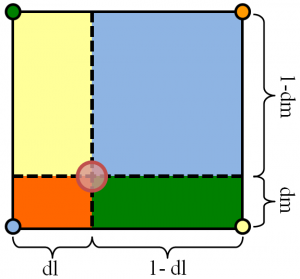Рис. 1. Вычислительная ячейка разделена, и часть, соответствующая диагональной области, нанесена на каждый узел.

При выполнении этого вычисления помогает работать в логических (или естественных) координатах . Это координаты, которые определяют положение в ячейке как долю расстояния ячейки по соответствующему измерению. В этой статье мы помечаем эти координаты как \ (l = [0,1] \) и \ (m = [0,1] \). Значение нуля соответствует левому или нижнему краю, а значение 1 соответствует правому или верхнему краю.Для декартовой системы, такой как та, которая используется в примере кода PIC, мы можем легко получить эти координаты как \ (i_f = (x-x_0) / \ Delta x \) и \ (l = i_f- \ text {int} (i_f ) \) (индекс «f» был добавлен, чтобы указать, что \ (i_f \) является числом с плавающей запятой, а не целым числом). В логических координатах общая площадь равна единице, и поэтому нам просто нужно умножить значение, которое нужно рассеять, на соответствующую площадь сечения. Соответствующие длины показаны на рисунке 1. Чтобы собрать данные от сетки до частицы, мы просто умножаем значение в каждом узле на противоположную область и складываем вклады вместе, \ (n_x = w_1n_1 + w_2n_2 + w_3n_3 + w_4n_4 \).

Функция отображения для произвольного четырехугольника

Вышеупомянутый метод работает, но у него есть один серьезный недостаток: как написано, он полезен только для прямоугольных ячеек. Но часто мы предпочитаем использовать клетки неправильной формы. Даже если мы не используем метод конечных элементов, мы можем захотеть использовать такой метод, как конечный объем вместе с ячейками разреза, чтобы аппроксимировать границу поверхности. Или мы можем захотеть использовать структурированную сетку по фигуре. Эти методы дадут нам ячейки сетки, которые больше не являются прямолинейными, а являются произвольными четырехугольниками.Конечно, вы можете получить разные формы, такие как треугольники или трехмерные клинья, в зависимости от вашей установки, но здесь для простоты мы рассматриваем только двухмерные четырехугольники. В [2] есть хороший обзор различных типов клеток.

Чтобы выполнить интерполяцию на произвольном квадрате, нам нужно получить функцию отображения, как показано на рисунке 2. Наша цель — придумать такие функции, как \ ((x, y) = f (l, m) \), где \ (l = [0,1] \) и \ (m = [0,1] \) описывает все точечное пространство, заключенное в четырехугольник.Кроме того, мы хотим, чтобы \ (f (0,0) = (x_1, y_1) \), \ (f (1,0) = (x_2, y_2) \) и так далее соответствовали вершинам многоугольника. Эта функция, которую еще предстоит определить, формирует карту, которая позволяет нам преобразовать квад из набора физических координат в логическое пространство координат. В логических координатах многоугольник трансформируется в квадрат независимо от его физической формы. Как только логические координаты получены, мы выполняем операции разброса и сбора, как описано в предыдущем абзаце.

mapping of physical coordinates to logical ones for polygon interpolation

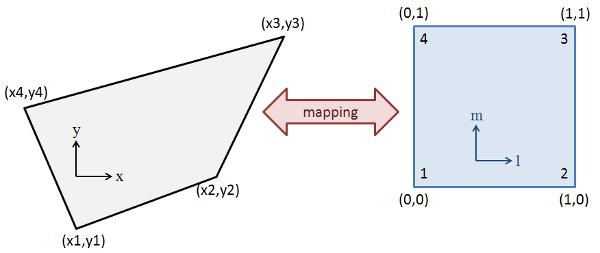Рисунок 2.Функция отображения позволяет нам представить четырехугольник произвольной формы в виде квадрата.

Теперь остается найти карту. Для этого мы предполагаем, что функция билинейного отображения [2] задана как
$$ x = \ alpha_1 + \ alpha_2 l + \ alpha_3 m + \ alpha_4 lm $$
и
$$ y = \ beta_1 + \ beta_2 l + \ beta_3 m + \ beta_4 lm $$
Далее мы используем эти выражения для определения четырех коэффициентов:
$$ \ left [\ begin {array} {c} x_1 \\ x_2 \\ x_3 \\ x_4 \ end {array } \ right] = \ left [\ begin {array} {cccc} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \ end {array} \ right] \ left [\ begin {array} {c} \ alpha_1 \\\ alpha_2 \\\ alpha_3 \\\ alpha_4 \ end {array} \ right] $$
Коэффициенты в матрице взяты из рисунка 2.Например, для узла «1» мы имеем (l, m) = (0,0). Аналогичное выражение написано и для бета-версии. Мы можем легко найти коэффициенты, инвертируя матрицу:
$$ \ left [\ begin {array} {c} \ alpha_1 \\\ alpha_2 \\\ alpha_3 \\\ alpha_4 \ end {array} \ right] = \ left [\ begin {array} {cccc} 1 & 0 & 0 & 0 \\ — 1 & 1 & 0 & 0 \\ — 1 & 0 & 0 & 1 \\ 1 & -1 & 1 & -1 \ end {array} \ right] \ left [\ begin {array} {c} x_1 \\ x_2 \ \ x_3 \\ x_4 \ end {array} \ right] $$

Используя синтаксис Matlab, мы можем написать

% создать наш многоугольник
px = [-1, 8, 13, -4];
py = [-1, 3, 11, 8];

% вычислить коэффициенты
A = [1 0 0 0; 1 1 0 0; 1 1 1 1; 1 0 1 0];
AI = inv (A);
a = AI * px ';
б = AI * py ';

Теперь у нас есть отображение, чтобы перейти от логического мира к физическому.Чтобы получить обратное отображение, нам нужно решить
$$ \ begin {array} {rcl} x & = & \ alpha_1 + \ alpha_2l + \ alpha_3m + \ alpha_4 lm \\ y & = & \ beta_1 + \ beta_2l + \ beta_3m + \ beta_4 lm \ end {array} $$
Обратите внимание, что эта система больше не является линейной, однако ее довольно легко решить аналитически. Сначала вы можете получить
$$ l = \ left (\ dfrac {x- \ alpha_1- \ alpha_3 m} {\ alpha_2 + \ alpha_4 m} \ right) $$
, которое затем можно подставить во второе выражение (это как они говорят, «упражнение оставлено для читателя»), чтобы получить
$$ (\ alpha_4 \ beta_3 — \ alpha_3 \ beta_4) m ^ 2 + (\ alpha_4 \ beta_1- \ alpha_1 \ beta_4 + \ alpha_2 \ beta_3 — \ alpha_3 \ beta_2 + x \ beta_4 — y \ alpha_4) m + (\ alpha_2 \ beta_1 — \ alpha_1 \ beta_2 + x \ beta_2 — y \ alpha_2) = 0 $$
Это просто квадратное уравнение с тремя коэффициентами, задаваемыми членами в скобках и с физическим решением \ (m = (-b + \ sqrt {b ^ 2-4ac}) / 2a \).2-4ac)) / (2a) det = sqrt (bb * bb — 4 * aa * cc); m = (-bb + det) / (2 * аа); % вычислить l l = (x-a (1) -a (3) * m) / (a (2) + a (4) * m); конец

Пример 1: Выбор случайных точек в четырехугольнике

Теперь у нас есть все необходимое, чтобы повеселиться. Первый пример показывает, как выбирать случайные точки, которые находятся в заданном квадрате. Любая точка, расположенная внутри многоугольника, будет иметь естественные координаты в диапазоне от 0 до 1. Следовательно, нам просто нужно выбрать две случайные естественные координаты и преобразовать их с помощью функции отображения.Код приведен ниже. Настоящая часть — это часть цикла, а вторая половина — это просто код для создания графика. Вы получите график, аналогичный изображенному на Рисунке 3, однако фактическое расположение точек будет отличаться. Обратите внимание, что все точки расположены внутри границ многоугольника.

% отображает случайные точки внутри многоугольника
функция [] = plot_points_in_poly (px, py, a, b)

    % выбрать случайную логическую координату и преобразовать в физическую
    для i = 1: 100
л = ранд ();
м = ранд ();
x (i) = a (1) + a (2) * l + a (3) * m + a (4) * l * m;
y (i) = b (1) + b (2) * l + b (3) * m + b (4) * l * m;
    конец

    %участок
    фигура 1);
    откладывать;
    сюжет ([px px (1)], [py py (1)]);
    Оставайтесь на линии;
    сюжет (x, y, 'x');
конец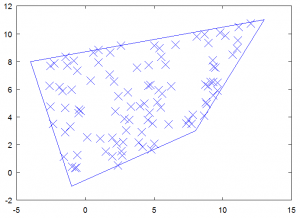

Рисунок 3.Участок из 100 случайных точек, расположенных внутри многоугольника.

Пример 2: Определение того, находится ли точка внутри или снаружи четырехугольника

Первый пример показал, как перейти от логических координат к физическим. Второй пример обратный. В этом примере мы выбираем 200 точек, случайно распределенных в ограничивающей рамке многоугольника, и определяем, находятся ли они внутри или за пределами многоугольника. Для этого мы используем тот факт, что точка внутри многоугольника будет иметь обе естественные координаты в диапазоне от 0 до 1.Хотя здесь мы просто помечаем местоположение узла, вариант этого метода можно использовать в неструктурированном коде для поиска ячейки, содержащей частицу. Координата \ (m> 1 \) указывает, что следующая поисковая ячейка должна быть той, которая разделяет край \ (m = 1 \) (что бы это ни значило физически, зависит от отображения). Это намного быстрее, чем перебирать ячейки одну за другой. Запустив приведенный ниже код, вы получите график, аналогичный показанному на рис. 4

% выбирает случайные точки и раскрашивает их в зависимости от внутренних или внешних
функция [] = plot_internal_and_external_points (px, py, a, b)

    %Ограничительная рамка
    x0 = мин (пикс.);
    lx = max (px) -min (px);
    y0 = min (py);
    ly = max (py) -min (py);

    % преобразовать случайные физические координаты в логические
    для i = 1: 200

  % выберите случайную точку в ограничивающей рамке
х (я) = х0 + рандом () * lx;
y (i) = y0 + rand () * ly;

% вычислить логические координаты
[l, m] = XtoL (x (i), y (i), a, b);

% это точка вне квадратика?
если (m <0 || m> 1 || l <0 || l> 1)
type (i) = 1;
еще
type (i) = 0;
конец
    конец

    %участок
    фигура 2);
    откладывать;
    сюжет ([px px (1)], [py py (1)]);
    Оставайтесь на линии;
    разброс (x, y, 4, type, 'x');
конец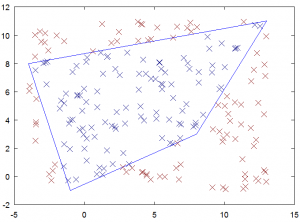

points classified as internal or external to a polygon

Рисунок 4.Точки выбираются случайным образом в ограничивающей рамке многоугольника и классифицируются по их местоположению.

Пример 3: Данные о рассеянии по узлам многоугольника

Далее мы рассмотрим кое-что, что действительно может использоваться в методе PIC: операцию разброса. Здесь мы выбираем 100 случайных точек внутри многоугольника и разбрасываем значение «1» для каждой точки. По сути, это подсчитывает количество точек в многоугольнике. Учитывая большое количество выборок и хороший генератор случайных чисел, мы должны получить значение 25 на каждом узле.В приведенном ниже коде мы масштабируем эти данные так, чтобы ожидаемое значение на каждом узле было 10 (это было сделано для целей визуализации). Когда я запустил приведенный ниже код, я получил:
9.8026 9.6121 9.8507 10.7346
Эти значения в сумме дают 40, как и ожидалось. На рисунке 5 эти данные показаны графически с размером круга, соответствующего значению узла. Если бы плотность была неоднородной, мы бы увидели круги разных размеров.

% разбросов до четырех узлов сетки
функция [] = scatter_data (px, py, a, b)

    %в этом
    с = [0 0 0 0];

    % выбрать случайную логическую координату и преобразовать в физическую
    для i = 1: 100

 % случайная точка внутри квадрата
л = ранд ();
м = ранд ();

Учитывается% депозита, обратите внимание: l, m = [0: 1].В реальной 2d сетке
% индекс, который нам сначала нужно вычесть из интеграла
% индекс ячейки, чтобы получить расстояние между ячейкой, dl = l - (int) l;
dl = l;
dm = m;

с (1) + = (1-дл) * (1-дм);
с (2) + = dl * (1-дм);
с (3) + = dl * dm;
с (4) + = (1-дл) * дм;
    конец

    % данных шкалы, равномерное распределение = 10
    с = 40 * (с / я);

    %вывод
    disp (c);

    %участок
    рисунок (3);
    откладывать;
    сюжет ([px px (1)], [py py (1)]);
    Оставайтесь на линии;
    разброс (px, py, c, [1 0 0], 'o');
конец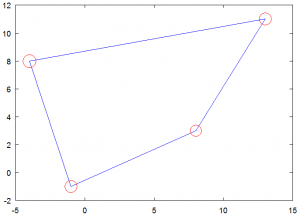

Рис. 5. Счетчики частиц, отобранных внутри многоугольника, разбросаны по узлам многоугольника, что приводит к равномерному распределению.

Пример 4: Сбор данных из узлов многоугольника на частицу

И, наконец, обратное предыдущему примеру. Здесь мы интерполируем данные из узлов сетки в положение частицы. Это аналогично сбору компонентов электрического поля перед оценкой ускорения. В этом примере мы устанавливаем значения [1,2,3,4] для вершин многоугольника. Чтобы лучше проиллюстрировать эту интерполяцию, мы построим равномерную сетку 30 × 15 и интерполируем значения многоугольника на точки сетки.Мы делаем это только для точек, расположенных внутри многоугольника. 2D-сетка позволяет нам визуализировать результаты как контурное наводнение. Пример начинается с построения сетки. Затем он проходит через узлы сетки и выполняет расчет, используя положение каждого узла сетки. Результат показан на рисунке 6.

% интерполирует данные из вершин многоугольника в сетку
функция [] = gather_data (px, py, a, b)

    %Ограничительная рамка
    x0 = мин (пикс.);
    lx = max (px) -min (px);
    y0 = min (py);
    ly = max (py) -min (py);

    % установите интервал таким образом, чтобы у нас была сетка 30x30 (т.е.е. 29 ячеек)
    ni = 30;
    nj = 15;

    dx = lx / (ni-1);
    dy = ly / (nj-1);

    % позиций узлов (для построения)
    для i = 1: ni
 х (я) = х0 + (я-1) * dx;
    конец
    для j = 1: nj
 y (j) = y0 + (j-1) * dy;
    конец

    % значений узлов
    c = [1 2 3 4];

    val = нули (nj, ni);

    для i = 1: ni
для j = 1: nj
             % преобразовать в логические координаты
[l m] = XtoL (x (i), y (j), a, b);

% оцениваем только если мы внутри
если (l> 0 && l <= 1 && m> = 0 && m <= 1)

                 % снова, если бы у нас было несколько ячеек, мы бы установили dl = l - (int) l
dl = l;
dm = m;

val (j, i) = (1-dl) * (1-dm) * c (1) +...
дл * (1-дм) * с (2) + ...
dl * dm * c (3) + ...
(1-дл) * дм * с (4);
             конец
        конец
    конец

    %участок
    рисунок (4);
    откладывать;
    contourf (x, y, val);
    Оставайтесь на линии;
    plot ([px px (1)], [py py (1)], 'w', 'LineWidth', 4);
конец

Рис. 6. Значения узлов, интерполированные из четырехугольника на сетку.

Полный исходный код

Вы можете получить полный исходный код здесь: interpolate2d.m.

Кстати, этот код был протестирован с использованием Octave 3.2.4, а не Matlab, так как копии последнего у меня нет. Octave - это бесплатный эмулятор Matlab с открытым исходным кодом, который можно загрузить с octave.org или как пакет Cygwin. Версия Cygwin новее (версия 3.6.2 на момент написания), но поскольку для нее требуется несколько дополнительных шагов, таких как (1) установка Cygwin и (2) установка XWin, я использовал старую (и довольно глючную) предварительно собранную версию Windows из Сайт Octave.

Список литературы

[1] Бердсолл, К. К., Лэнгдон, А. Б., «Физика плазмы с помощью компьютерного моделирования», Институт физики, 2000 г.

[2] Хьюз, Т.Дж. Р., «Метод конечных элементов», Dover Publications, 2000

Подпишитесь на рассылку новостей и следите за нами в Twitter. Отправьте нам письмо по электронной почте, если у вас возникнут вопросы. .

Определение, свойства, типы, формулы, примечания

Классы
Класс 1–3
Класс 4–5
Класс 6–10
Класс 11–12

КОНКУРЕНТНЫЙ ЭКЗАМЕН
BNAT 000 000 NC Книги
Книги NCERT для класса 5
Книги NCERT для класса 6
Книги NCERT для класса 7
Книги NCERT для класса 8
Книги NCERT для класса 9
Книги NCERT для класса 10
Книги NCERT для класса 11
Книги NCERT для класса 12
NCERT Exemplar
NCERT Exemplar Class 8
NCERT Exemplar Class 9
NCERT Exemplar Class 10
NCERT Exemplar Class 11
NCERT 9000 9000
NCERT Exemplar Class
Решения RS Aggarwal, класс 12
Решения RS Aggarwal, класс 11
Решения RS Aggarwal, класс 10
90 003 Решения RS Aggarwal класса 9
Решения RS Aggarwal класса 8
Решения RS Aggarwal класса 7
Решения RS Aggarwal класса 6
Решения RD Sharma
RD Sharma Class 6 Решения
Решения RD Sharma
Решения RD Sharma Class 8
Решения RD Sharma Class 9
Решения RD Sharma Class 10
Решения RD Sharma Class 11
Решения RD Sharma Class 12
PHYSICS
Механика
Оптика
Термодинамика Электромагнетизм
ХИМИЯ
Органическая химия
Неорганическая химия
Периодическая таблица
MATHS
Теорема Пифагора
0004
000300030004
9000
Простые числа
Взаимосвязи и функции
Последовательности и серии
Таблицы умножения
Детерминанты и матрицы
Прибыль и убыток
Полиномиальные уравнения
Деление фракций
000
000
000
000
000
000 Microology
000
000 Microology
000 BIOG3000
FORMULAS
Математические формулы
Алгебраические формулы
Тригонометрические формулы
Геометрические формулы
КАЛЬКУЛЯТОРЫ
Математические калькуляторы
0003000 PBS4000
000300030002 Примеры калькуляторов химии
Класс 6
Образцы документов CBSE для класса 7
Образцы документов CBSE для класса 8
Образцы документов CBSE для класса 9
Образцы документов CBSE для класса 10
Образцы документов CBSE для класса 11
Образцы документов CBSE чел для класса 12
CBSE Контрольный документ за предыдущий год
CBSE Контрольный документ за предыдущий год Класс 10
Контрольный документ за предыдущий год CBSE, класс 12
HC Verma Solutions
HC Verma Solutions Class 11 Physics
Решения HC Verma, класс 12, физика
Решения Лакмира Сингха
Решения Лакмира Сингха, класс 9
Решения Лакмира Сингха, класс 10
Решения Лакмира Сингха, класс 8
Заметки CBSE
CBSE Notes
Примечания CBSE класса 7
Примечания CBSE класса 8
Примечания CBSE класса 9
Примечания CBSE класса 10
Примечания CBSE класса 11
Примечания CBSE класса 12
Примечания к редакции CBSE
Примечания к редакции
CBSE Class
Примечания к редакции класса 10 CBSE
Примечания к редакции класса 11 CBSE 9000 4
Примечания к редакции класса 12 CBSE
Дополнительные вопросы CBSE
Дополнительные вопросы по математике класса 8 CBSE
Дополнительные вопросы по науке 8 класса CBSE
Дополнительные вопросы по математике класса 9 CBSE
Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
Дополнительные вопросы по науке, класс 10 по CBSE
CBSE, класс
, класс 3
, класс 4
, класс 5
, класс 6
, класс 7
, класс 8
, класс 9 Класс 10
Класс 11
Класс 12
Учебные решения
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения для биологии класса 11
Решения NCERT для математики класса 11
9 0003 NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions For Class 12
NCERT Solutions For Класс 12 по физике
Решения NCERT для химии класса 12
Решения NCERT для класса 12 по биологии
Решения NCERT для класса 12 по математике
Решения NCERT Класс 12 Бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
Решения NCERT, класс 12 Экономика
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solutions For Класс 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для социальных наук класса 6
Решения NCERT для класса 6 Английский
Решения NCERT для класса 7
Решения NCERT для класса 7 Математика
Решения NCERT для класса 7 Наука
Решения NCERT для класса 7 по социальным наукам
Решения NCERT для класса 7 Английский
Решения NCERT для класса 8
Решения NCERT для класса 8 Математика
Решения NCERT для класса 8 Science
Решения NCERT для социальных наук 8 класса
Решение NCERT ns для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для социальных наук класса 9
Решения NCERT для математики класса 9
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для Математика класса 9 Глава 2
Решения NCERT для математики класса 9 Глава 3
Решения NCERT для математики класса 9 Глава 4
Решения NCERT
для математики класса 9 Глава 5
Решения NCERT для математики класса 9 Глава 6
Решения NCERT для Математика класса 9 Глава 7
Решения NCERT для математики класса 9 Глава 8
Решения NCERT
для математики класса 9 Глава 9
Решения NCERT
для математики класса 9 Глава 10
Решения NCERT для математики класса 9 Глава 11
Решения NCERT для Математика класса 9 Глава 12
Решения NCERT для математики класса 9 Глава 13
Решения
NCERT для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9
Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для класса 9 Наука Глава 3
Решения NCERT для Науки Класса 9 Глава 4
Решения NCERT для Науки Класса 9 Глава 5
Решения NCERT для Науки Класса 9 Глава 6
Решения NCERT для Науки Класса 9 Глава 7
Решения NCERT для Класса 9 Наука Глава 8
Решения NCERT для Науки Класса 9 Глава 9
Решения NCERT для Науки Класса 9 Глава 10
Решения NCERT для Науки Класса 9 Глава 12
Решения NCERT для Науки Класса 9 Глава 11
Решения NCERT для Класса 9 Наука Глава 13
Решения NCERT для класса 9 Наука Глава 14
Решения NCERT для класса 9 по науке Глава 15
Решения NCERT для класса 10
Решения NCERT для класса 10 по социальным наукам
Решения NCERT для математики класса 10
Решения NCERT для математики класса 10 Глава 1
Решения NCERT для математики класса 10 Глава 2
Решения NCERT для математики класса 10 Глава 3
Решения NCERT для математики класса 10 Глава 4
Решения NCERT для математики класса 10 Глава 5
Решения NCERT для математики класса 10 Глава 6
Решения NCERT для математики класса 10 Глава 7
Решения NCERT для математики класса 10 Глава 8
Решения NCERT для математики класса 10 Глава 9
Решения NCERT
для математики класса 10 Глава 10
Решения
NCERT для математики класса 10 Глава 11
Решения NCERT для математики класса 10 Глава 12
Решения NCERT для математики класса 10 Глава 13
NCERT Sol Решения NCERT для математики класса 10 Глава 14
Решения NCERT для математики класса 10 Глава 15
Решения NCERT для науки класса 10
Решения NCERT для науки класса 10 Глава 1
Решения NCERT для науки класса 10 Глава 2
Решения NCERT для науки 10 класса, глава 3
Решения NCERT для науки 10 класса, глава 4
Решения NCERT для науки класса 10 Глава 5
Решения NCERT для науки класса 10 Глава 6
Решения NCERT для науки класса 10 Глава 7
Решения NCERT для науки 10 класса, глава 8
Решения NCERT для науки класса 10 Глава 9
Решения NCERT для науки класса 10 Глава 10
.
Урок Середины четырехугольника - это вершины параллелограмма
Урок Середины четырехугольника - это вершины параллелограмма.

Этот урок (Середины четырехугольника являются вершинами параллелограмма) создал ikleyn (32805) : View Source, Show
About ikleyn :
Середины четырехугольника - вершины параллелограмма

Теорема
В произвольном выпуклом четырехугольнике середины его сторон являются вершинами параллелограмма.Докажи.

Проба
Пусть ABCD будет произвольным выпуклым четырехугольником ( Рисунок 1 ),
и пусть точки E , F , G и H будут серединами его
сторон AB , BC , CD и AD соответственно.
Нам нужно доказать, что четырехугольник EFGH является параллелограммом.
Нарисуйте диагонали AC и BD в четырехугольнике ABCD ( Рисунок 2 ).
Сегмент HG является сегментом средней точки в треугольнике ACD .
Следовательно, отрезок HG параллелен стороне AC треугольника
ACD в соответствии с уроком Отрезок прямой, соединяющий середины
двух сторон треугольника (в рамках темы Треугольники схемы раздел
Геометрия на этом сайте).

Рисунок 1 . К теореме

Рисунок 2 . К доказательству теоремы
Сегмент EF - это сегмент средней точки в треугольнике ABC . Следовательно, отрезок EF параллелен стороне AC треугольника ABC .
Поскольку сегменты HG и EF параллельны диагонали AC , они параллельны друг другу.
Точно так же сегмент GF является сегментом средней точки в треугольнике DCB . Следовательно, сегмент GF параллелен стороне DB треугольника DCB .
Отрезок HE - это сегмент средней точки в треугольнике ABD . Следовательно, сегмент HE параллелен стороне DB треугольника ABD .
Поскольку сегменты GF и HE параллельны диагонали DB , они параллельны друг другу.
Таким образом, мы доказали, что в четырехугольнике EFGH противоположные стороны HG и EF , HE и GF попарно параллельны.
Следовательно, четырехугольник EFGH является параллелограммом. Теорема доказана.
Мои другие уроки по параллелограммам на этом сайте:
- В параллелограмме каждая диагональ делит его на два конгруэнтных треугольника.
- Свойства сторон параллелограмма
- Свойства сторон параллелограммов
- Свойства диагоналей параллелограммов
- Противоположные углы параллелограмма
- Последовательные углы параллелограмма
- Длина диагоналей параллелограмма
- Замечательные сложные задачи на параллелограммах
- КАК решать задачи о мерах сторон параллелограмма - Примеры
- КАК решать задачи об углах параллелограммов - Примеры
- СВОЙСТВА ПАРАЛЛЕЛОГРАММ
Для навигации по всем темам / урокам Онлайн-учебника по геометрии используйте этот файл / ссылку ГЕОМЕТРИЯ - ВАШ ОНЛАЙН-УЧЕБНИК.
К этому уроку обращались 23049 раз.

.
No related posts.

Выпуклый четырехугольник

Геометрия. Урок 4. Четырехугольники — ЁП

Понятие выпуклого четырехугольника, его свойства и признаки

Выпуклый четырехугольник

Основные свойства и виды

Является ли параллелограмм выпуклым четырехугольником?

Свойство диагоналей выпуклого четырехугольника

Другие свойства и признаки выпуклости четырехугольника

Четырёхугольники, виды и свойства / math5school.ru

Виды четырехугольников:

Свойства произвольных четырехугольников:

что это такое, каковы его свойства и чему равна сумма его уголов

Виды

Свойства

Вписанные и описанные

Расчет площади

Полезное видео

Подведем итоги

Выпуклый четырехугольник | Треугольники

Выпуклые и вогнутые четырехугольники — A Plus Topper

Свойство суммы углов четырехугольника

Интерполяция с использованием произвольного четырехугольника

Интерполяция сетки

Функция отображения для произвольного четырехугольника

Пример 1: Выбор случайных точек в четырехугольнике

Пример 2: Определение того, находится ли точка внутри или снаружи четырехугольника

Пример 3: Данные о рассеянии по узлам многоугольника

Пример 4: Сбор данных из узлов многоугольника на частицу

Полный исходный код

Список литературы

Определение, свойства, типы, формулы, примечания

Урок Середины четырехугольника - это вершины параллелограмма

Середины четырехугольника - вершины параллелограмма

Добавить комментарий Отменить ответ