|
Пропорция, пропорционирование
ПРОПОРЦИОНИРОВАНИЕ (от лат. Proportio — «соотношение, соразмерность частей«) — разновидность трансформации, способ установления определенных отношений частей формы. Пропорциями называются размерные соотношения элементов или частей формы между собой, а также между различными объектами. Пропорция — это гармонизация формы художественного произведения, пропорциональность ее эстетическое качество. Соразмерность частей образует красоту формы. Мы признаем определенные пропорциональные отношения в построении фигуры человека, его окружения, архитектуры, как нечто должное. Эмоциональное начало художественного творчества проверяется точной наукой.Выдающиеся мастера былых эпох постоянно стремились проверить алгеброй гармонию, впрочем, математика античности, средневековья и Возрождения была лишена сухости и абстрактности. Пропорция — равенство двух или более отношений. Например, математическое выражение 1:2 = 3:6 называют пропорцией, поскольку его левая и правая части равны между собой. Наименьшее число в таких отношениях именуют модулем, его, как правило, избирают в качестве единицы измерения. Среди множества возможных пропорций существует единственное решение, в котором уравниваются не только отношения частей формы, но всех частей между собой и отношение каждой части к целому. Такая пропорция называется «божественной«, или «золотой серединой» (лат. aurea mediocritas). В искусстве способ пропорционирования используют в качестве основного средства гармонизации формы художественного произведения, поскольку гармония, в отличие от красоты, подлежит геометрическому и математического анализу. Когда мы знакомимся с историей искусства, любуемся совершенными произведениями, например античной статуей или храмом, картинами Леонардо да Винчи, Рафаэля, Энгра, то нас поражает удивительная гармония, присущая им, которая во многом определяется таким эстетическим качеством, как пропорциональность целого и деталей. Сравнивая предметы, окружающие нас, по величине, высоте, ширине, объему мы можем сказать, что одни из них длинные, а другие короткие, высокие и низкие,широкие и узкие, большие и маленькие и т. д. Устанавливая соотношение между предметами и между частями формы отдельного предмета, мы выясняем их пропорциональные характеристики. Поиск пропорций в изображении фигуры человека является сложной задачей.Обратимся к истории, посмотрев, как решали ее художники разных эпох и разных культур.
Египтяне пользовались и специальными сетками-таблицами, которые наносили на поверхность каменной плиты или стены для создания рельефа или росписи. На сохранившихся и дошедших до нас памятниках можно видеть, что горизонтальные и вертикальные линии делят рисунок в определенных местах, что соответствует членению фигур на части. Были установлены также определенные размеры для изображения сидящих фигур и изображения разных богов в соответствии с их иерархическим старшинством (одни должны быть выше, другие немного ниже ). Детей изображали как взрослых, но значительно меньшими по размеру. Художнику необходимо было знать установленные каноном нормы и научиться вписывать в них изображения, пользуясь сеткой-таблицей. Единая система обучения и строгое соблюдение выработанных норм позволяли выполнять части одного произведения разными мастерами. Когда такие части составляли в единую композицию, то они точно сходились и не было нарушения пропорций.Изучение математических отношений,заложенных в пропорциях египетскихп ирамид, а также исследования архитектора И. П. Шмелева,посвященные личности зодчего Хеси-Ра (егип. Hesi-Ra —»Отмеченный солнцем«), жреца бога Гора и главного архитектора фараона Джосера (ок. 2800—2700 гг. до н. э.), позволили установить, что египтяне пользовались отношениями чисел: 1:3, 2:3,4:3.
Исследования пропорций пирамид подтверждают, что канон пропорций египетской архитектуры включал числа 3:4:5 (стороны «египетского священного треугольника»), а также диагональ «двусмежного квадрата«, равную √5. Пифагор, обобщая данные, которые он отчасти почерпнул в Египте, ввел в созданную им теорию гармонии понятия пентатоники ( греч. pente — «пять» и tonos— «натяжение, напряжение») — пяти ступеней октавы (ряда из восьмиступеней) и пентахорда (греч. chorde — «струна»). Пифагор использовал средние пропорциональные числа: арифметическое c=(a+b)/2, геометрическое c=√ab, гармоническое c=2ab/a+b, а также наиболее сложную музыкальную пропорцию a:(a+b/2)=(2ab/a+b):b или 12:9=8:6. Созвучие квинты музыкального звукоряда построено на отношении чисел 2:3. Известно также, что Иерусалимский храм, возведенный в 1010 г. до н. э., имел план сотношением сторон 1:3. Исследования пифагорейцев позволили разделить смысл понятий «соразмерность«и «пропорциональность«. Так открытое Пифагором свойствоколебания струн, длина которых выражена отношениями простых целых чисел,создавать полнозвучные аккорды, легло в основу понятия гармонии Абсолюта,» С глубокой древности человека волновали идеи уподобления своих творений прекрасным проявлениям природы, преображения хаоса в космос, числовые закономерности, которые лежат в основе устройства Вселенной. Древние эллины воспринимали пространство исключительно оптически: целостным и непрерывным, а в архитектуре использовали целые числа ирациональные приемы, основанные на кратных отношениях, хотя и вводили оптические поправки, нюансирование, придававшие отношениям величин дробность и легкую «неправильность«. Вся история учения о пропорциях связана с поисками законов гармонии и красоты. В ДревнейГреции систему идеальных пропорций человеческой фигуры создал скульптор Поликлет в V векедо н. э. Его теоретическое сочинение на эту тему называлось «Канон», а выражением в скульптуре этой системы явилась его статуя « Дорифор», что означает копьеносец. Мастер изобразил атлета-юношу, победителя в соревнованиях по метанию копья, в момент, когда после одержанной победы он совершает круг почета по стадиону и его приветствуют восторженные зрители. Пропорция, или «аналогия«, как ее называли греки, есть соответствие между частями и целым по отношению к части(модулю), принятой за исходную величину. Соотнесение симметрии с метрическим строем, а пропорциональности — с ритмическим рядом величин составляет сущность «Канона» древнегреческого скульптора Поликлета, который также связан с правилом золотого сечения. Открытие пропорций, полагают, принадлежит к заслугам древневосточной математики, античная же традиция связывает его с именем выдающегося философа и математика Пифагора, жившего в VI веке до н. э. Универсальный принцип гармонии и красоты в
Расстояние от бровей до основания носа определяет величину ушей. В действительности редко встречаются у людей такие идеальные пропорции, но знать их необходимо, чтобы видеть отклонения от нормы и лучше понимать индивидуальные пропорции живой натуры. Знакомство с золотым сечением сыграло немалую роль в работе античных архитекторов, скульпторов и живописцев. Древнегреческие строители при расчете зданий пользовались эпиморными отношениями, в которых, в отличие от простых кратных (1:2, 1:3, 1:4), превышение большей части равняется одной доле меньшей (греч. epi — «сверх, над»;morion, moros — «часть, член, частица»). Например: 2:3, 3:4, 8:9. Эллины не дробили единицу, считая ее наименьшей из возможных величин, и использовали её в качестве модуля. Поэтому пропорции древнегреческих храмов, в частности отношения количества колонн на переднем и боковых фасадах, следуют эпиморной формуле: n:(n+1). Эту и производные закономерности древние греки обозначали словом «ana-logia» — соответствие, правильное соотношение, расчет (дословно: «вновь-отношение»). 
Древнеримский оратор и писатель Цицерон (106—43 гг. до н. э.), переводя сочинения древнегреческого философа Платона на латинский язык, сделал со слова аналогия «кальку» (лат. Pro-portio — «вновь-отношение») и стал автором термина, который пережил многие столетия и существует до сих пор. Однако содержание этого термина много сложнее его буквального прочтения: пропорции есть не отношения величин между собой, а их уравнивание, в чем и заключается математический смысл понятия гармонии. Древнегреческому поэту Иону (ок. 490—422 гг. до н. э.) с о. Хиос приписывают философское сочинение «Триагма» (греч. triagma — «троичность») о господстве численных отношений троичности. Трехчастное деление свойственно композиции античной архитектуры. В философии Платона (427—347 гг. до н. э.) понятие пропорции связывается с явлением симметрии (греч. Syn-metria — «соразмерность»), поскольку Бог сотворил мир из четырех элементов (огня, земли, воды и воздуха), а «тело космоса упорядочено благодаря пропорции» этих элементов. В учении Платона о гармонии сохраняется пифагорейская традиция, которая восходит к учению древнеегипетских жрецов. Пропорциональность — более сложное качество, оно отражает целостность сложносочиненной формы, т. е. закономерную взаимосвязанность всех ее частей и внутренних членений. Именно такое понимание легло в основу средневековой эстетики. В частности, в сочинениях Боэция (480—524), «последнего римлянина» и неоплатоника, квадривиум (единство четырех наук) рассматривается согласно пифагорейской традиции.
Древнеримский архитектор Витрувий (I в. до н. э.), который канонизировал композиционные приемы античной архитектуры, понимал симметрию («соразмерность«) как метрический строй (равномерные членения формы, на котором основан канон), а пропорцию считал ритмической организацией элементов композиции. Витрувий дополняет «Канон Поликлета «идеальными размерами частей мужской фигуры: длина ладони — 1/10 высоты фигуры, размер головы — 1/8, стопы — 1/6,локтя — 1/4, ширина груди — 1/4. Причем эти размеры приведены не в разделеProportio, а в разделе Symmetria, в котором автор оперирует исключительно кратными величинами. Пропорции, согласно теории Витрувия, —результат приведения всех размеров к нужному масштабу (уменьшению или увеличению относительно роста человека). Они являются практическим инструментом архитектора и скульптора. Важное значение в теории Витрувия имеет понятие модуса (лат. modus — «протяжение, предел, положение«), или лада, — согласованности всех частей формы на основе какого-либо элемента (чаще всего модуля). Модальность, или ладовость, придает пропорциональному строю эмоциональную окраску, тональность. Витрувий и его последователи, создатели архитектурной теории Классицизма, выделяли три основных модуса: дорический, ионический и коринфский.
Далее к системе математического расчета пропорций прилагается эвритмия (греч.eurhythmia — «стройность, ритмичность«) — система нюансирования оптических поправок. Она создает «приятную внешность и подобающий вид» (лат. venusta species et commoduscue aspectus). Примечательно еще одно определение Витрувия: пропорция — это то, «чтокажется гармоничным» (т. е. математическая закономерность с поправками на особенность зрительного восприятия). Согласно одной из концепций, в античном искусстве существовало два течения, условно называемые «симметрическим» и «эвритмическим«. Они могут быть соотнесены саполлоновским и дионисийским началами в искусстве либо с «классическим» и»современным» стилями (такие формулировки встречаются у античных авторов). Модуль в истории архитектуры также не является постоянной величиной. Основным модулем всегда был «фут» (греч. pous — «стопа, нога»). Его размер в разное время ив разных областях античного мира колебался в пределах 0,295—0,310 м. Длина восточной части наоса и ширина главного фасада Парфенона в Афинах равняется ста греческим футам. Эта исходная мера заложена в пропорциях многих классических сооружений: храма Посейдона в Пестуме, Гефестейона в Афинах, базилики Максенция и Константина и огромного Пантеона в Риме. Создается впечатление, что эта мера была неписанным правилом, хотя она не имела символического значения, не сказывалась на внешнем облике здания или прочности его конструкции. В то же время римляне, которые оперировали в своей архитектуре кратными числами, в качестве модуля избирали 5/2 каких-либо единиц линейной меры: локтей или футов. Эту странность можно объяснить тем, что при любых построениях на основе золотого сечения отношение 5:2 дает удобные производные (чаще получался модуль, равный 5 римским футам, или 1,55 м). По канону Витрувия, модуль четырех колонного фасада здания (за модуль принимали нижний диаметр колонны) равняется 1/27 его ширины, шести колонного — 1/42 части. В эпоху Итальянского Возрождения Дж. Виньола делил модуль на разное количествопарт (итал. parte — «часть»), архитектор А. Палладио — на минуты(лат. minuta — «мелочь«). Л. Б. Альберти в качестве модуля использовал одну шестую роста фигуры человека. В Средневековье система пропорционирования была проще. Типичная схема центрических храмов заключалась в том, что всю постройку вписывали в квадрат со стороной в 100 традиционных футов. Для базилик удлиненного плана длину храма устанавливали по диагонали квадрата, построенного на ширине главного фасада. Такая схема восходит к системе, принятой в ранней античности. В большинстве случаев у храмов разных типов высота вместе с куполом равняется длине нефа (с апсидой либо без апсиды). В византийских иконах, мозаиках и фресках наблюдался отказ от античного принципа антропометрии и поиска наиболее гармоничных природных пропорций. Средневековый способ пропорционирования можно назвать плоскостной, или планиметрической, схематизацией. В техническом аспекте он имел явные преимущества, поскольку позволял даже неумелым мастерам легко пользоваться общепринятой схемой. Однако происхождение этих схем объясняется не стремлением демократизировать искусство, а особенным пониманием изобразительного пространства. Объем физических тел и физическое пространство в средневековом изобразительном искусстве обесценивались, они не имели принципиального значения, поэтому объемные и пространственные факторы не могли играть существенной роли в системе пропорционирования изображений.
Отсюда типичная округлость голов, получаемая с помощью циркуля, свойственная в равной степени иконописным образам Св. Петра и Павла, Андрея, Св. Николая, Ильи и других. Подобный канон сохраняется в произведениях Джотто, Чимабуэ, даже при ракурсных изображениях и перспективном сокращении фигур вертикальные размеры «трех кругов» остаются при этом неизменными. Согласно концепции «соответствий» и утверждению Августина Блаженного (354—430; Отцы Церкви), Ноев ковчег имел отношения сторон 300:50:30 локтей, таковы же должны быть пропорции идеальной человеческой фигуры — рост, ширина и толщина должны соотноситься как 30:5:3 (так называемый августиновский канон). Средневековая теория пропорций (в отличие от свода технических правил изображения) неотрывна от метафизического понимания формы и пространства. Эта теория, как отмечал Э. Панофский, не была связана с потребностями изобразительного искусства. Даже более того, «как только подобная связь возникала, теория пропорций вырождалась в свод практических правил,терявший всякую связь с гармонической космологией«. Характерно, что средневековые авторы, изучая трактат Витрувия, многое из него заимствовали, но полностью игнорировали рассуждения о пропорциях. В средневековой арабской эстетике пропорциональность также не входит в число двадцати категорий прекрасного. Только в эпоху Итальянского Возрождения метафизика и техника пропорционирования снова соединяются. Гармоничные пропорции фигуры человека, здания, статуи рассматривали как непременное условие создания произведения искусства — отражения предустановленной Божественной красоты. При этом метафизическое толкование прекрасного весьма неустойчивым образом соединялось с рациональными приемами пропорционирования. Ренессансные ученые-гуманисты по-новому прочли Витрувия, а затем через арабские переводы — сочинения Аристотеля и Платона. В симметрии спиральной раковины наутилуса увидели образ Вселенной и численный ряд Фибоначчи. В результате древнегреческая «соразмерность«(греч. Symmetria) обрела метафизический смысл. Гравюра А. Дюрера «Адам и Ева«(1504) родилась в результате штудий пропорций фигуры человека по трактату Витрувия, в которых голова составляет 1/8 высоты фигуры. Однако в отличие от своих предшественников Дюрер использовал не один, а три канона пропорций фигуры (1:9,1:8, 1:7) в зависимости от характера изображаемого персонажа. Л. Б. Альберти в трактате «Десять книг о зодчестве» (1444—1450) не удовлетворяется цитированием Витрувия, а изобретает собственные отношения и модули. Монах-францисканец Л. Пачьоли разрабатывает собственную теорию математической гармонии. В 1487 г. он опубликовал трактат «Сумма арифметики и геометрии«. Основная идея, которая волновала рациональномыслящих художников, заключалась в том, каким образом согласовать прекрасные пропорции природного объекта, поддающиеся математическому анализу, с пропорциями изображения этого объекта на плоскости бумаги, холста или в массиве мраморного блока. Эта двойственность объясняет путаность многих рассуждений Леонардо да Винчи и противоречия в трактате А. Дюрера «О пропорциях человеческого тела» (1528). Художникам требовался не абсолютный канон красоты, а система относительных пропорций, которая позволяла бы сохранять гармоничные отношения частей,увеличивая или уменьшая композицию в требуемом масштабе. Тогда-то, возможно впервые, была осознана главная идея искусства пропорционирования: не вычислять, а создавать впечатление гармонии, когда большое кажется не столь огромным, а малое — не таким малым. Другими словами, пропорционирование было поставлено в зависимость не только от конструкциии абсолютных размеров объекта, но и от масштаба —зрительной оценки величины. Масштабное или, что то же самое, пространственное понимание пропорций не было известно ни древним эллинам, ни средневековым мастерам. Однако примечательно, что в эпоху Возрождения наиболее консервативным мыслителем оказался гениальноодаренный Леонардо да Винчи. Он настойчиво продолжал искать гармонию пропорций исключительно в природе, т. е. в конструкции природного объекта, например в анатомическом строении тела человека, расширяя сферу наблюдений и пытаясь вывести некие усредненные, идеальные данные. Отчасти этим можно объяснить тот факт, что Леонардо не удалось обобщить собранные им сведения в единую систему. Подобная задача попросту не имеет решения, даже с учетом «оптических поправок«.
Сознавая связь методики пропорционирования с вопросами симметрии, масштабности, перспективы, движения и ритма, Дюрер прибегал к геометризации,так называемой «кубической системе«, наглядно иллюстрирующей эти связи. Именно такое, динамичное, пропорционирование привлекало художников Маньеризма и Барокко XVI—XVIII вв. Мастера Классицизма, напротив, оставались приверженцами античной теории симметрии рациональных пропорций. На фреске Рафаэля «Афинская школа» наскрижали рядом с фигурой Пифагора изображена «пифагорова диаграмма«— символ античной теории гармонии. Своеобразно, но аналогично западноевропейской, складывалась система пропорционирования в древнерусском искусстве. Как древние египтяне, а затем эллины, русские зодчие использовали мерный шнур, который называли «золотым поясом«. Его длина составляла четыре греческих фута (123—124 см). Существовали и деревянные «мери́ла» с делениями. Их применение обеспечивало взаимосвязь рядов гармонически связанных величин. При первом знакомстве с древнерусскими мерами длины удивляет наличие не одной, а нескольких, именно шести, са́женей (от сягать — протягивать руку), к тому же выраженных дробными числами.
Предполагают, что эта система мер заимствована южными славянами через Византию из Древней Греции. Ее построение осуществлялось в так называемых»вавилонах» — геометрическом подобии форм, связанных антропоморфными отношениями. Если вписать в подобный «вавилон«древнерусские меры длины, то мы получим фигуру, несколько отличную, но в принципе сходную с египетской системой диагоналей. А при наложении этой системы на окружность с вписанной в нее фигурой человека увидим совпадение с ренессансной системой пропорций по канону Леонардо да Винчи. Даже с первого взгляда очевидна общность древнерусских мер длины и западноевропейской системы пропорционирования. Слово «сажень» означает то же, что по-гречески «орги́йя» (расстояние между простертыми руками; от греч. orego — «простирать»). Мерная сажень соответствует греческой оргийе, или 6 футам, что составляет сторону квадрата в системе пропорционирования человеческой фигуры, предложенной Витрувием. Этот же размер равняется 24 палестам (древнегреческая мера длины в четыре пальца). Диаметр вписанной окружности (по схеме Витрувия) представляет собой «косую» оргийю, или 30 палестов. Разница двух оргий равняется 6 палестам (по византийской системе мер), или одному «локтю». Отношение длины распростертых рук к диаметру окружности в рисунке Леонардо да Винчи при любом росте человека дает «золотое число». Расстояние между распростертыми руками служило главной единицей мер в течение всего Средневековья как на Западе, так и на Востоке Европы.Великая косая сажень относится к мерной как диагональ к стороне квадрата (√ 2:1). «Сажень без чети» (четверти) является диагональю половины этого же квадрата и т. д. Второй взаимосвязанный ряд величин образуется делением каждой сажени пополам: полусажень, локоть (1:4 сажени), пядь (1:8 сажени). Отношение мерной сажени (176,4) к сажени без чети (197,21) равно 0,9:1; прямой сажени (152,76) к мерной (176,4) равно 5:6; косой сажени (216) к великой косой (249,46) равно 7:8. Таким образом, независимо от размеров здания, применением этой шкалы величин в древнерусской архитектуре возникали отношения, совпадающие с теми, которые использовал А. Палладио в Италии, и числами ряда Фибоначчи (1:1:2:3:5:8). Вторым эталоном был мерный шнур «сока́рь» (греч.sokarion — «сильный«) длиной в 10 оргий (иногда в 12). В древнерусской архитектуре за модуль принимали длину бревна «венца» либо кирпич. Квадратная клеть — основной элемент деревянной постройки — требовала проверки правильности прямых углов. Эту операцию осуществляли с помощью мерного шнура размером в диагональ квадрата (обе диагонали должны быть равны). Таким образом возникало сразу два модуля — ме́рная сажень (сторона квадрата) и великая косая сажень (диагональ квадрата). Далее на диагонали строили новый квадрат. Так без вычислений получали удвоенную площадь. Все остальные производные связаны отношениями квадратов различных величин и их диагоналей. Эту систему и называли на Руси «вавилонами«. Древнерусскую систему диагоналей переносили в вертикальную плоскость, размечая таким образом пропорции стен, оконных и дверных проемов, которые также оказывались антропоморфными. Принципы пропорционирования перенесли в каменное зодчество, поэтому стены русских крепостей и башен также часто соответствуют отношениям квадрата и его диагонали. Таким образом, очевидно, что строители разных стран и эпох прибегали к аналогичным системам пропорционирования, связанным антропоморфными отношениями. Отсюда, в частности, символическое значение изображений вавилонов в качестве знаков «строительной мудрости» наподобие западноевропейских. Как на Западе, так и на Востоке пропорции мужской фигуры следовали квадрату «золотого числа» (2,618034 — полный рост, отношения нижней к верхней части, т. е. длины ног и таза к торсу и голове: 1,618:1). В начале XX в. русский архитектор И. В. Жолтовский (1867—1959), поклонник творчества А. Палладио, предложил использовать «удвоенную третью величину», прибавив ее к классическому ряду: 1; 0,618; 0,382; 0,236; 0,472 (0,236×2 = 0,472). Производным метода численного пропорционирования является прием гармонизации величин, основанный на «правиле прямого угла«. В геометрии существует аксиома о том, что диагонали подобных прямоугольников (разновеликих, но с равными отношениями сторон) будут (в зависимости от пространственного положения прямоугольников) либо параллельными, либо перпендикулярными. Использование этой аксиомы позволяет без вычислений добиваться сложнейшего «всепроникающего подобия» целого и множества разновеликих деталей. Архитекторы до сих пор пользуются «правилом прямого угла» и «обратным методом«. Вначале строят с помощью рейсшины ряд параллельных и перпендикулярных диагоналей, а затем на них — прямоугольники необходимого размера: фасады, проемы, членения стен. Отношения сторон этих прямоугольников будут равны, что обеспечивает подобие целого и деталей. Эта музыка отношений величин складывается в гармоничное звучание, получившее наименование «гармонического резонанса» (от лат. resonare — «звучать в ответ, откликаться«). Когда мы созерцаем произведение классического искусства, входим в здание классической архитектуры (не обязательно в храм), невольно замирает дыхание, учащается пульс. В этом состоянии умеряется резкость движений и суета. Наш организм от природы настроен на «золотые» ритмические отношения, и когда он попадает в пространство, организованное на тех же основаниях — пропорциях, симметрии и ритме гармонических интервалов, тогда (вначале на физиологическом, а затем на уровнях эстетического и художественного сознания) возникает явление «гармонического резонанса«, обладающее громадной силой воздействия. В этом случае даже простая строительная конструкция или пространство заурядного пейзажа, независимо от идеологического содержания, преображается в художественно-образную целостность, имеющую власть над человеком. Возникает ощущение величия, значительности, рождается чувство возвышенного (независимо от размеров воспринимаемого объекта). Такова сила антропометрических пропорций. С переходом в 1795 г. от античной системы гармонично связанных мер на искусственную метрическую систему эффект гармонического резонанса стал невозможен. Современная архитектура чужда человеку прежде всегопропорционально. И человек всегда будет к ней равнодушен. Более того: продолжительное пребывание в урбанистической среде неклассической архитектурынебезопасно с психологической точки зрения. Одним из первых эту опасность осознал французский архитектор Ле Корбюзье. Убедившись на собственном опыте в изъянах индустриального метода изготовленияархитектурных деталей на основе единой метрической системы мер, Ле Корбюзье в 1945—1948 гг. создал инструмент пропорционирования, «настроенный» на шкалу «золотых отрезков«. Причем на эту идею его натолкнуло правило прямого угла.
Вначале французский архитектор попытался совместить правило прямого угла, которое он исследовал в классической архитектуре и живописи, с античной системой парных мер. Затем Ле Корбюзье разработал две шкалы гармонично возрастающих величин в пропорции золотого сечения. Основой «красного ряда» величин послужила величина 108 см (условное расстояние от уровня земли до пуповины человека), а второго, «синего ряда» — удвоенная величина: рост человека с поднятой рукой — 216 см. Существенно, что условность исходных величин не влияет на гармонию пропорций(согласно «Канону» Поликлета, идеальная высота фигуры равна 261,8 см — квадрат золотого числа, в древнерусском вавилоне — 176,4 см). Однако изобретение Ле Корбюзье не оправдало возложенных на него надежд. В индустриальном мире удобнее пользоваться метрической системой кратных отношений, чем «золотой шкалой» с множеством мер. Ле Корбюзье разрабатывал свой модулор, изучая классическую архитектуру. Однако и архитекторов Классицизма подстерегала неудача, когда они подменяли иррациональное пропорционирование простыми метрическими отношениями величин. Так, К. Росси, создавая Театральную улицу вПетербурге, взял за основу композицию улицы Уффици во Флоренции (Дж. Вазари, 1559—1565), но применил не иррациональные, а простые кратные отношения величин: длина улицы 220 м, ширина и высота 22 м. В результате возникает ощущение стесненности и монотонности. |
shedevrs.ru
Пропорции и пропорционирование — Композиция в технике
Пропорции и пропорционирование
Категория:
Композиция в технике
Пропорции и пропорционирование
Среди всех «классических» средств композиции на первое место следует поставить пропорции—как по степени важности того качества, которое достигается с их помощью (пропорциональность), так и с точки зрения их возможностей при организации формы. В самом деле, размерные отношения элементов формы — это та основа, на которой строится вся композиция. Как бы ни были хороши детали изделия сами по себе, но если всю его объемно-пространственную структуру не объединяет четкая пропорциональная система, трудно рассчитывать на целостность формы.
О пропорциях как средстве гармонизации формы написано, пожалуй, больше, чем обо всех других, вместе взятых. Исследованию пропорций посвящали свои труды ученые, зодчие и художники античности и эпохи Ренессанса (Витру-вий, Палладио, Виньола, Серлио и многие другие). В наше время изучением пропорций занимались Э. Мессель, Д. Хэмбидж, М. Гика, крупные советские архитекторы и искусствоведы И. В. Жолтовский, А. Г. Габричевский, И. Б. Михайловский, Б. М. Михайлов, JI. Н. Павлов.
Притягательная сила пропорций—в непосредственном эффекте гармонизации, который связан с умелым, целенаправленным пропорционированием.
Знали силу этого средства и в совершенстве владели им многие мастера-ремесленники— эти инженеры и дизайнеры своего времени, создававшие прекрасные станки, машины, часы, светильники, мебель. Формы вещей XIV—XV вв. и более позднего времени нередко поражают совершенством своих пропорций. Однако мир техники так изменился, что использовать давно сложившиеся приемы и методы пропорционирования в современном художественном конструировании почти невозможно.
К сожалению, в работах, посвященных пропорционированию станков, машин, приборов, мало анализируется объективная сторона гармоничных размерных отношений, не указываются приемы пропорционирования станка или прибора со сложной объемно-пространственной структурой, где крайне трудно использовать существующие методы. Пропорционирование в технике нельзя сводить к механическому заимствованию классических приемов пропорционирования в архитектуре или прославлению «золотого сечения» на все случаи жизни. Пропорции лишь тогда приобретают действенную силу, когда проектировщик подходит к ним от самой сущности вещи, а не навязывает форме произвольно выбранную пропорциональную схему. Вспомним диалог Сократа и оружейника Пистия. Философ спрашивает оружейника: «Как получается, что ты продаешь больше панцирей, чем другие мастера, хотя делаешь их не более прочными и не более роскошными?» — «Потому, что я делаю их пропорциональными».— «Но ведь бывают непропорциональные фигуры. Как же ты можешь делать «пропорциональные» панцири для «непропорциональных» фигур?» — «А я их подгоняю. Панцирь по мерке и есть панцирь пропорциональный». Какая глубоко материалистическая связь красоты и пользы в этом анализе!
От формального использования пропорций предостерегали еще ученые и зодчие эпохи Возрождения. В частности, Леон-Батиста Альберти писал: «Красота есть строгая соразмерная гармония (курсив наш — Ю. С.) всех частей, объединяемых тем, чему они принадлежат,— такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже… Украшение есть как бы некий вторичный свет красоты или, так сказать, ее дополнение. … Красота, как нечто присущее и прирожденное телу, разлита по всему телу в той мере, в какой оно прекрасно, а украшение скорее имеет природу присоединяемого, чем прирожденного» [8, с. 178]. Это утверждение можно в полной мере отнести и к современной технике.
Различия методов пропорционирования в технике и архитектуре определяются прежде всего разной степенью обусловленности формы конструкцией. Если в классической архитектуре заранее разработанная система пропорций иногда могла служить своего рода основой композиции сооружения, во многом предопределяя его конструкцию, то в технике это почти невозможно. Немыслимо пропор-ционировать станок раньше, чем определится его кинематика и хотя бы в общем виде будет выбрана конструктивная схема.
По мере уточнения конструкции расчетом, проработки узлов и деталей у проектировщиков появляется возможность яснее представить себе форму и уточнить размерные отношения главных элементов объемно-пространственной структуры *. Таким образом, на стадии инженерной отработки конструкции параллельно идет и художественно-конструкторская отработка формы, и в результате пропорции станка оказываются во многом производными от его инженерной компоновки. Именно поэтому пропорциональный строй, соразмерность частей и целого служат важной проверкой технического совершенства конструкции. Можно принять за аксиому, что чем точнее учтены в конструкции истинные усилия, чем логичнее она в целом и деталях, чем большую роль играет расчет в определении важнейших размерных отношений несущей основы станка, тем больше шансов на то, что станок окажется и гармонически соразмерным. Все, что конструктивно нелогично, заведомо непропорционально.
Если же, пренебрегая инженерной стороной, дизайнер рисует форму только ради «красивых» пропорций, неизбежно возникают конструктивно неоправданные пустоты за кожухами, увеличиваются габариты и масса станка.
Итак, пропорции во многом складываются объективно—они связаны с основой конструкции, и от этого нельзя абстрагироваться .
Существует два основных подхода к пропорционированию различных промышленных изделий. Первый строится на относительной свободе проектировщика в выборе пропорций, когда он может задавать пропорции, идя от формы к конструкции, например при проектировании мебели, некоторых бытовых приборов, оборудования и т. п. Иного подхода требуют изделия со сложной объемно-пространственной структурой, размерные отношения которых определяются конструкцией. Здесь необходимо вовремя корректировать пропорциональный строй формы как в целом, так и в отдельных ее элементах.
Правда, это разграничение в известной мере условно. Над каким бы изделием ни работал проектировщик, он должен ясно представлять себе не только всю важность пропорций как средства гармонизации вещи, но и диапазон своих возможностей.
Остановимся на важных особенностях пропорционирования, имеющих непосредственное отношение к технике. В общем виде они состоят в том, что методы пропорционирования различны для разных объемно-пространственных структур.
М. Гика писал; «Когда мы имеем дело, например в архитектуре, с анализом объемов, то глаз в основном довольствуется восприятием или оценкой отношений между площадями. Это происходит оттого, что наш орган зрения, несмотря на его стереоскопическую приспособленность, учитывает прежде всего площади или профили. Архитектурные сооружения чаще всего преломляются в нашем зрении как плоские поверхности (площади), характеризуемые своими осями или вертикальными планами симметрии». Это справедливо и для многих технических структур.
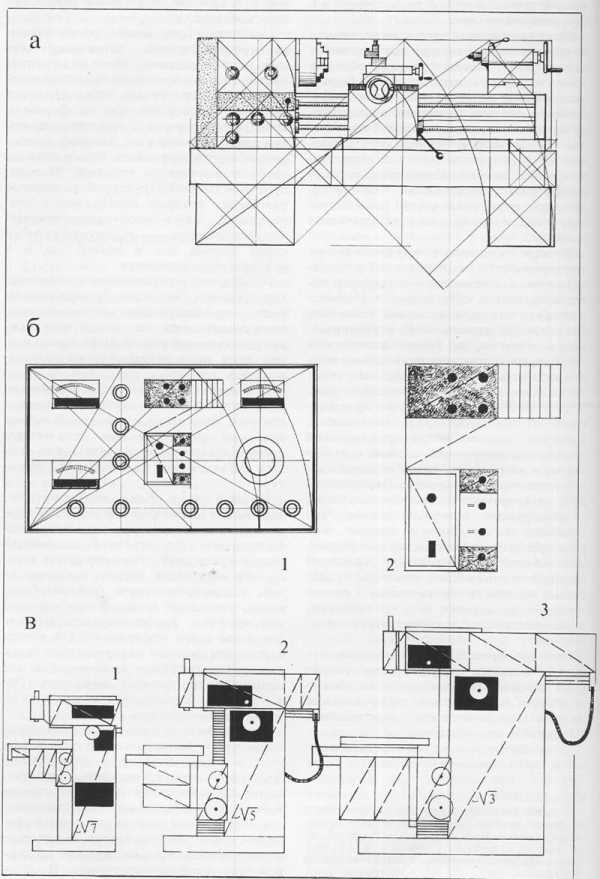
Как правило, в качестве методических примеров по пропорционированию в технике и берут изделия с относительно простыми геометрическими формами, легко поддающимися пропорционированию. Таковы, например, приближающиеся к плоскости панели различных приборов и пультов управления, к которым вполне применимы классические приемы и методы пропорционирования. На деталях 1 и 2 на рис. 59, б показан такой пример организации панели прибора с помощью пропорционирования. Токарный станок лаконичной, геометрически четкой формы также поддается традиционному приему пропорционирования (рис. 59,а), так как мы улавливаем в его форме единую, сопоставимую в своих размерах систему плоскостей. С небольшой натяжкой этим путем можно про-порционировать и те токарные, винторезные, шлифовальные, фрезерные станки, объемно-пространственную структуру которых можно представить как ряд относительно легко воспринимаемых условных планов. Именно такой эффективный метод пропорционирования применен в решении гаммы фрезерных станков (см. модели 1—3 на рис. 59, в, где приведена только часть всей гаммы)*.
Сложная же объемно-пространственная структура иного изделия не укладывается в простые геометрические схемы.
В этих случаях трудно уловить отношения между площадями, о которых говорит М. Гика, так как вместо простых объемов и крупных плоскостей, зрительно легко сопоставимых, перед нами целые комплексы технических элементов — разнообразных валов и валиков, шпинделей и муфт, органов управления и т. д. Можно ли вообще пропорционировать такие структуры? Не только можно, но еще более необходимо, чем простейшие, так как тут диспропорциональность — это почти хаос. Однако пропорционированию подобных структур должно предшествовать такое упорядочение всех элементов, которое позволяет достигнуть определенного уровня начальной целостности. По сути дела, речь должна идти о первоначальной пространственной организации сложной многоэлементной системы, организации, которую нужно провести уже на начальной стадии конструкторской разработки — компоновки станка или машины.
Собственно пропорционирование будет вторым этапом организации системы, когда и начнут уточняться с точки зрения гармонизации формы основные размерные отношения между визуально автономными, пространственно обособленными группами элементов.
Рассмотрим некоторые приемы такой композиционной группировки элементов сложной объемно-пространственной структуры.
Один из приемов заключается в том, чтобы небольшими сдвижками, перемещениями элементов или групп элементов, воспринимаемых как совокупность, создать более четкую систему горизонтальных и вертикальных членений.
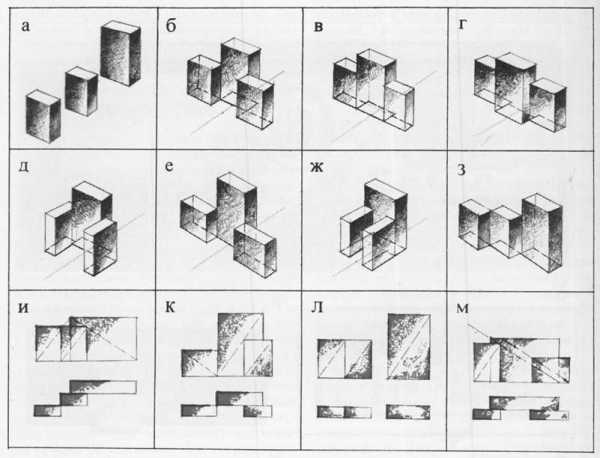
Условные модели структуры показаны на рис. 60, а. Элементы 1—8 на поз. I не организованы, композиционные связи между ними отсутствуют—такую «структуру» пропорционировать практически невозможно. Благодаря группировке элементов путем относительно небольших перемещений структура уже организуется (поз. II). Здесь использованы активные горизонтали по верху элементов 6—8 и по низу элементов 3—5.
На поз. III организация достигается с помощью горизонтальных и вертикальных членений: нижняя линия элемента 7 и верхние — элементов 6 и 8 образуют единую горизонталь. Такая же горизонталь проходит по нижней линии элементов 3—5. Начинают читаться и вертикальные «окна», образуемые элементами 6, 3 и 7; 4, 7 и 8 (цветные схемы).
Организующим началом группировки элементов на поз. IV являются три вертикальных пространственных «окна» и одно горизонтальное.
На поз. V, как и на поз. II, преобладают четкие горизонтальные членения, хотя элементы сгруппированы по-своему. Заметим, что в ходе такой организации конкретных объектов важно проследить и за конфигурациями пустот.
Условные модели сложной объемно-пространственной структуры, близкие к станочным формам, показаны на рис. 60, б. Поз. I—неорганизованная верхняя часть модели плохо воспринимается, так как глаз не улавливает композиционных связей элементов. На поз. II—IV— модели, с которыми уже проведена предварительная работа по организации связей между элементами формы. После такой предварительной группировки и анализа применительно к конкретной конструкции можно приступить к про-порционированию, т. е. к уточнению размерных отношений между группами и элементами внутри каждой группы. По сути дела пропорционирование является следующим шагом в организации сложной структуры.
Особенно велика организующая роль горизонтальных членений. Даже в том случае, когда единые горизонтали местами прерываются, они зрительно хорошо прослеживаются в форме, что и позволяет использовать их как весьма активное средство организации элементов в общности. Прием «завязки горизонталями» в технике служит одним из способов пропорционирования—ведь именно активные членения делят форму на легко сопоставимые по размерам части. Организующая роль горизонтальных членений увеличивается по мере возрастания их активности, подчеркиваемой глубиной падающих теней, цветом, тоном и т. п. Сильные членения с активной светотенью образуются перепадом плоскостей. Случайная сбивка таких членений, их нечеткость ломают весь пропорциональный строй, нарушая целостность формы.
Другим приемом организации элементов в общности является корректировка их размеров в пределах, допускаемых конструкцией, а также изменения в характере связей (местоположении элементов, цветовых и тональных соотношениях и т. п.). Прием такой корректировки применим в тех случаях, когда отсутствует возможность введения сквозных членений и визуальной общности элементов приходится добиваться небольшими местными сдвигами, нюансными перемещениями. Композиционно связывать элементы помогает здесь акцентирование местных осей в отдельных группах, активизация местных симметричных включений в структуру. Естественно, что упорядочение формы конкретного изделия связано с различными трудностями — конструкция не кубики, которые можно с легкостью менять местами. Однако важен принцип: в сложных условиях инженерной компоновки необходимо сначала упорядочить форму, а затем постепенно выявлять избранный пропорциональный строй.
Как видим, пропорции тесно связаны с характером взаимоотношений элементов формы — их пространственным расположением, соподчиненностью в композиции. Упорядочение формы в качестве начальной фазы пропорционирования в работе проектировщика имеет большое значение. Без этого невозможно подступиться к пропорционированию сложной технической структуры. Каждое конкретное изделие подсказывает свои приемы. Так, организация панели управления станком имеет свою специфику — многочисленные органы управления зачастую почти не поддаются никаким произвольным сдвижкам, так как связаны с технической структурой станка. Что-то существенно изменить на панели трудно, а в то же время расположение маховичков, рукояток, кнопок, других элементов скорее случайно, нежели системно, и выглядит почти хаотично. Если все это не организовать в систему, то подобные панели управления будут противоречить тем функциональным и эстетическим критериям, которые предъявляются сегодня к станкам, машинам, приборным комплексам высокого класса. Кроме чисто композиционных недостатков, уже с эргономических позиций неприемлемо визуально асистемное расположение различных органов управления. Как же поступить? Исходная ситуация порой кажется безвыходной. И действительно— здесь мы имеем дело со сложной композиционной задачей. Речь идет о необходимости упорядочить элементы при условии, что изменить их расположение почти невозможно. Мы рассматриваем этот вопрос в разделе о пропорциях потому, что весьма своеобразные приемы такой визуальной организации более всего эффективны, если искусственно создаваемые конфигурации, объединяющие все элементы и отдельные их группы, связаны четкой системой размерных отношений, т. е. определенным образом спро-порционированы.
Тут-то и вырабатываются различные приемы группировки разрозненных элементов— придание группам значения визуально автономных, но крепко спаянных сообществ, которые, композицией-но осмысленно, а не случайно соотносясь друг с другом, позволяют приступить к их пропорциональному упорядочению.
Этот метод постепенного упорядочения технической структуры дает эффективные результаты. Он очень гибок в отношении начальных факторов, реалистичен в достижении высокого качества художественно-конструкторской разработки. На рис. 61, а — и показан ряд приемов подобной организации органов управления станком. В цветной рамке (рис. 61, б) исходная и явно неблагоприятная ситуация в расположении органов управления на панели. Модель а—один из конечных вариантов упорядочения такой структуры. Модели в — и показывают ход поиска приема организации. Как видим, принцип поиска сходен с тем, что был намечен на условных моделях (см.рис. 60, а). Однако здесь мы исходим из частичной или даже полной невозможности свободного перемещения элементов. Визуальная организация панели осуществляется только путем «графического» объединения, обособления, акцентирования групп элементов. Тот или иной прием строится на использовании «сетки» разъемов, разности фактур поверхности участков, объединения групп с помощью небольших приливов литья и т. д. Такое упорядочение может предшествовать следующему этапу — собственно пропорционированию как своего рода дальнейшему уточнению избранной схемы.
Попытаемся теперь установить наиболее типичные закономерности в проявлении связей между характером соподчинения и пропорциями в симметричных формах.
На рис. 62, а—три элемента: два малых и один большой, подобный им по пропорциям. Наметим ряд композиционных построений — пространственных вариаций расположения этих элементов. В каждой из простейших композиций свои особенности соподчинения элементов. На рис. 62, б заданные объемы создают симметричную композицию, которую в архитектуре назвали бы композицией с неглубоким курдонером. В принципе к ней близки композиции на рис. 62, дне, где также развивается активно подчеркнутая ось симметрии и организуется пространство перед центральным объемом. Композицию на рис. 62, ж как будто тоже следовало бы отнести к этому ряду построений, однако расстояние между фланкирующими объемами здесь так сократилось, что пространство между ними играет уже менее активную роль.
Интересно проследить, в какой из композиций на рис. 62, б—г активнее проявляется симметрия и как это связано с расположением главного и фланкирующих элементов. Ведь с подобными сочетаниями мы постоянно сталкиваемся в технике.
В композиции на рис. 62, в лицевые плоскости всех трех объемов совпадают и, следовательно, ось симметрии выявляется только в силуэте (если условно отбросить линии примыкания боковых объемов к центральному). Активизация оси симметрии или ее большая нейтрализация могут быть достигнуты изменением пропорций боковых объемов. При уменьшении их высоты симметрия становится более активной, при увеличении высоты и ее приближении к высоте центрального объема активность симметрии падает.
Правда, в обоих случаях изменения происходят в ограниченных пределах. При значительном же снижении высоты фланкирующих объемов они перестают выполнять свою композиционную роль, а центральный объем уже не доминирует, теряя необходимую для подчеркнутой симметрии поддержку боковых элементов. При значительном увеличении высоты боковых объемов и ее приближении к центральному силуэт становится невыразительным и вялым.
Композиция на 62, г активнее, чем на рис. 62, в,— в ней сильнее звучит ось симметрии. Боковые объемы, отойдя на задний план, открыли сверху донизу вертикали центрального элемента. Кроме силуэта, которым в основном обозначалась ось симметрии на рис. 62, в, теперь она подчеркнута и пространством. Но особенно характерно это для композиции на рис. 62, б: здесь симметрия развивается и усиливается благодаря глубине пространства, образованного вышедшими вперед весьма активными вертикалями фланкирующих объемов. Их боковые стенки играют роль своеобразных шор, углубляющих пространство и тем остро подчеркивающих ось. Степень соподчи-ненности элементов в таких композициях в значительной мере зависит от активности симметрии.
Итак, наиболее активно проявляется соподчиненность в композиции на рис. 62, б. Однако эта зависимость интересует нас не сама по себе, но прежде всего тем, как соподчиненность связана с пропорциями каждой из этих простейших композиций.
Сравним композиции на рис. 62, б и д. Разница лишь в расположении фланкирующих объемов: в одном случае торцами вперед (рис. 62, д), в другом—лицевыми плоскостями параллельно лицевой плоскости центрального объема (рис. 62, б).
И все же, несмотря на близость принципа пространственной организации обеих композиций, разница между ними несомненна. Ось симметрии более активна в композиции на рис. 62, д, что объясняется несколькими причинами.
Главная в том, что при общих вертикальных пропорциях обеих композиций «вертикальность» на рис. 62, д проявляется гораздо резче. Фланкирующие торцы вытянулись, а весь строй вертикалей стал более насыщенным. У композиции на рис. 62, б подобие лицевых плоскостей фланкирующих и центрального объемов не столь сильно активизирует эту ось, так как наряду с действительной осью мы прочитываем как бы второстепенные оси, проходящие по каждому из боковых объемов. Проявление симметрии у модели на рис. 62, д усиливается тем, что боковые объемы резко отличаются от центрального, а глубина запада больше, чем у модели на рис. 62, б.
Если расположить фланкирующие объемы горизонтально, то влияние оси симметрии снова усилится (рис. 62, е), уже как следствие противопоставления горизонталей и вертикалей. Стоит при прочих неизменных условиях сильно удлинить горизонтально расположенные объемы, чтобы в определенный момент центральный объем не смог их композиционно сдержать,— эффект симметрии ослабеет, и композиция как целостность перестанет существовать*.
Однако прием фланкирования основного объема не во всех случаях приводит к активизации оси симметрии, и решающую роль здесь играют пропорции. Форма на рис. 62, ж, например, где фланкирующие объемы сближены настолько, что пространство между ними теряет роль организующего начала— утрачивает активную симметрию, свойственную формам на рис. 62, б, д.
Таким образом, пропорции целого и отдельных его частей могут оказывать непосредственное влияние на многие проявления композиции, в данном случае на соподчиненность и эффект симметрии.
В ходе разработки станков, машин, приборов дизайнеру часто приходится либо усиливать эффект симметрии, либо нейтрализовать его. В этих случаях и необходимо использовать влияние пропорций частей на образуемое ими целое. Иногда пропорционирование понимают лишь как нахождение «красивых» размерных отношений. В действительности пропорционирование является одним из сильных средств гармонизации формы в целом.
Рассмотрим теперь роль пропорций в асимметричных композициях. На рис. 62, з—асимметричная композиция, которую можно охарактеризовать как динамичную, поскольку в ней хорошо выражено движение в сторону большего объема. Здесь можно говорить об определенном композиционном эффекте, связанном с положенной в основу формы закономерностью размерных отношений— с параллельными диагоналями подобных фигур большого и двух малых объемов. Пусть эти диагонали никак не выявлены—мы подсознательно прочитываем их. Если хоть немного изменить отношения сторон большего объема, непараллельность малых и больших диагоналей сразу даст себя знать, и нам захочется либо восстановить утраченную закономерность композиции, либо развить новую.
Гармония отнюдь не означает, что такое подобие обязательно. Она лишь означает, что размерные отношения между элементами должны быть не случайными, а закономерными. Пропорционирование в технике непосредственно связано с достижением целостности огромного множества разнообразных асимметричных форм. Неточно найденные пропорции какого-либо важного в такой композиции элемента нарушают и ее равновесие.
Если, не изменяя отношений сторон, изменить абсолютные размеры большего элемента и положить его длинной стороной на плоскость, как показано на рис. 62, и, характер восприятия композиции изменится. В поисках закономерного глаз уже не ищет параллельности диагоналей, так как непараллельность слишком очевидна, но находит закономерность в том, что диагонали малых элементов перпендикулярны идущей к ним навстречу диагонали большего.
Можно спорить о степени этой способности через пропорции улавливать закономерность строения формы, но несомненно, что она в какой-то мере присуща каждому человеку, а тем более проектировщику.
В моделях на рис. 62, к, л, м закономерности существуют при индивидуальности пропорций каждой из композиций.
На примерах простейших композиций мы убедились в том, что соподчинение элементов, а следовательно, и целостность во многом обусловлены наличием той или иной закономерности в размерных отношениях между элементами формы.
Как же проявляются эти закономерности? Что делает пропорции таким мощным средством организации формы, выдвигая их на первое место среди остальных? Ряд исследователей указывает на магическую организующую силу геометрического подобия отрезков и фигур. Именно геометрическое подобие, пронизывая объемно-пространственную структуру, переводит ее из случайной общности элементов в общность, построенную на закономерности, в строгую систему композиционно связанных элементов. Едва ли можно переоценить значение этой закономерности.
Особенности пропорционирования многих промышленных изделий зависят и от того, какими средствами пользуется проектировщик, чтобы усилить воздействие пропорциональной закономерности, лежащей в основе композиции изделия. Это может быть, например, тоновой контраст или нюанс, определенная светотеневая структура и т. п. Если теперь вернуться к общей схеме формы токарного станка на рис. 59, а и глубже проанализировать возможности использования различных приемов визуальной организации пропорций с доведением ее до уровня системы, то можно использовать, например, приемы, показанные на рис. 63, а — в. Модель 1 (рис. 63, а) — начало пропорциональной организации станка. Здесь еще как бы только отыскивается ее принцип. Введение активных темных элементов 2 помогает обострить восприятие размерных отношений в композиции этого станка.
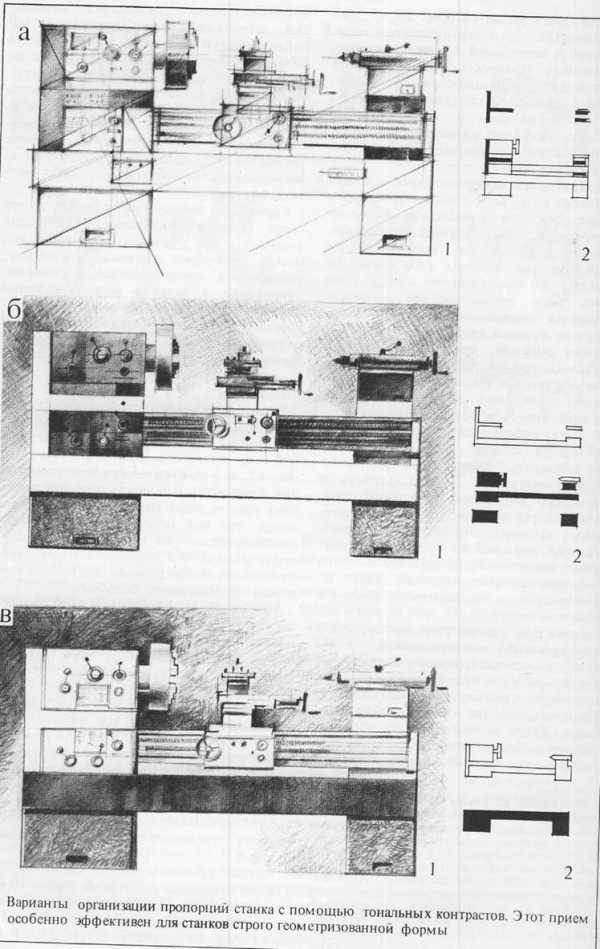
Модель 1 на рис. 63, б отличается иным пропорциональным строем. Визуально он гораздо активнее: контраст светлого и темного активизировал и восприятие всех размерных отношений элементов. Распределение светлого в данном случае — это особый прием достижения целостности (см. модели 2) — «захват», «рама», «обойма»… Как видим, светлое здесь играет решающую роль в пропорциональной организации формы.
Модели 1 и 2 на рис. 63, в совсем не похожи по пропорциям на предыдущие. Здесь композиция строится на четком противопоставлении темного основания светлой верхней части.
Один и тот же станок, но совершенно разное выражение пропорций, а отсюда и разное восприятие самого станка. Заметим, что достигается это всякий раз достаточно простыми средствами. Какой вариант лучше? Все зависит от задачи — от того, как хотелось бы нам выразить объективную основу пропорций. Главное, чтобы во всех вариантах принцип организации формы находил ясное проявление.
Если приборный комплекс или какая-нибудь установка членятся горизонталями в определенной системе размерных отношений, то воздействие пропорционального строя можно активно усиливать подчеркиванием с помощью заглублений мест разъема отдельных блоков, выделением блоков по тону окраски или одновременно тем и другим. Для пропорционального строя формы небезразлично, что и как располагается и на плоскостях блоков. Так, в данном случае пропорциональные членения и средства их активизации должны быть увязаны с тем, как скомпонованы элементы каждой панели. Ряды ручек и шкал могут поддержать выявленную систему членений, но в иных случаях могут и сбить ее, и тогда придется поработать над компоновкой этих элементов. Композиция сложных панелей во многом зависит даже от нюансов в расположении элементов. Подчас при небольших, вполне возможных корректировочных смещениях одних по отношению к другим появляются визуально активные организующие оси, которые могут способствовать пропорци-онированию всей панели.
Проблема пропорционирования в технике связана с исключительным разнообразием самих форм. Среди них немало столь сложных по своей структуре, что начинает казаться вообще невозможным целенаправленное упорядочение размерных отношений. Именно в подобных случаях легко упустить из виду саму задачу пропорционирования в процессе художественно-конструкторской разработки, однако для любой технической структуры необходимо найти прием достижения гармоничных размерных отношений ее основных элементов или групп мелких элементов, визуально объединенных между собой. В противном случае в конце концов выявятся серьезные диспропорции либо вообще хаотичность формы.
Реклама:
Читать далее:
Масштаб и масштабность
Статьи по теме:
pereosnastka.ru
Отношения и пропорции
Отношение двух чисел
Определение 1
Отношением двух чисел является их частное.
Пример 1
отношение $18$ к $3$ может быть записано как:
$18\div 3=\frac{18}{3}=6$.
отношение $5$ к $15$ может быть записано как:
$5\div 15=\frac{5}{15}=\frac{1}{3}$.
С помощью отношения двух чисел можно показать:
- во сколько раз одно число превышает другое;
- какую часть представляет одно число от другого.
При составлении отношения двух чисел в знаменателе дроби записывают то число, с которым проводится сравнение.
Чаще всего такое число следует после слов «по сравнению с …» или предлога «к …».
Вспомним основное свойство дроби и применим его к отношению:
Замечание 1
При умножении или делении обоих членов отношения на одно и то же число, отличное от нуля, получаем отношение, которое равно исходному.
Рассмотрим пример, который иллюстрирует использование понятия отношения двух чисел.
Пример 2
Количество осадков в предыдущем месяце составляло $195$ мм, а в текущем месяце – $780$ мм. Во сколько раз увеличилось количество осадков в текущем месяце по сравнению с предыдущим месяцем?
Решение.
Составим отношение количества осадков в текущем месяце к количеству осадков в предыдущем месяце:
$\frac{780}{195}=\frac{780\div 5}{195\div 5}=\frac{156\div 3}{39\div 3}=\frac{52}{13}=4$.
Ответ: количество осадков в текущем месяце в $4$ раза больше, чем в предыдущем.
Пример 3
Найти сколько раз число $1 \frac{1}{2}$ содержится в числе $13 \frac{1}{2}$.
Решение.
$13 \frac{1}{2}\div 1 \frac{1}{2}=\frac{27}{2}\div \frac{3}{2}=\frac{27}{2} \cdot \frac{2}{3}=\frac{27}{3}=9$.
Ответ: $9$ раз.
Понятие пропорции
Определение 2
Пропорцией называется равенство двух отношений:
$a\div b=c\div d$
или
$\frac{a}{b}=\frac{c}{d}$.
Пример 4
$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,
$\frac{8}{2}=\frac{36}{9}$, $\frac{10}{40}=\frac{9}{36}$, $\frac{15}{75}=\frac{1}{5}$.
В пропорции $\frac{a}{b}=\frac{c}{d}$ (или $a:b = с\div d$) числа a и d называются крайними членами пропорции, а числа $b$ и $c$ – средними членами пропорции.
Правильную пропорцию можно преобразовать следующим образом:
Замечание 2
Произведение крайних членов правильной пропорции равно произведению средних членов:
$a \cdot d=b \cdot c$.
Данное утверждение является основным свойством пропорции.
Справедливо и обратное утверждение:
Замечание 3
Если произведение крайних членов пропорции равно произведению ее средних членов, то пропорция правильная.
Замечание 4
Если в правильной пропорции переставить средние члены или крайние члены, то пропорции, которые получатся, также будут правильными.
Пример 5
$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,
$\frac{2}{8}=\frac{9}{36}$, $\frac{40}{10}=\frac{36}{9}$, $\frac{75}{15}=\frac{5}{1}$.
С помощью данного свойства легко из пропорции найти неизвестный член, если известны остальные три:
$a=\frac{b \cdot c}{d}$; $b=\frac{a \cdot d}{c}$; $c=\frac{a \cdot d}{b}$; $d=\frac{b \cdot c}{a}$.
Пример 6
$\frac{6}{a}=\frac{16}{8}$;
$6 \cdot 8=16 \cdot a$;
$16 \cdot a=6 \cdot 8$;
$16 \cdot a=48$;
$a=\frac{48}{16}$;
$a=3$.
Пример 7
$\frac{a}{21}=\frac{8}{24}$;
$a \cdot 24=21 \cdot 8$;
$a \cdot 24=168$;
$a=\frac{168}{24}$;
$a=7$.
Пример 8
Для пошива $7$ платьев понадобилось $21,7$ м шелка. Сколько нужно метров такого же шелка, чтобы пошить $18$ платьев?
Решение.
Пусть $x$ м – количество шелка, необходимого для пошива $18$ платьев. Тогда, по условию:
$7$ платьев – $21,7$ м;
$18$ платьев – $x$ м.
Составим пропорцию:
$\frac{7}{18}=\frac{21,7}{x}$.
Воспользуемся правилом нахождения неизвестного члена пропорции:
$d=\frac{b \cdot c}{a}$;
$x=\frac{18 \cdot 21,7}{7}$;
$x=18 \cdot 3,1$;
$x=55,8$.
Ответ: для пошива 18 платьев понадобится 55,8 м шелка.
Пример 9
$3$ садовника обрезают в день $108$ деревьев. Сколько нужно садовников, чтобы обрезать $252$ дерева?
Решение.
Пусть $x$ – количество садовников, необходимое для обрезки $252$ деревьев.
Тогда, по условию:
$3$ садовника – $108$ деревьев;
$x$ садовников – $252$ дерева.
Составим пропорцию:
$\frac{3}{x}=\frac{108}{252}$.
Воспользуемся правилом нахождения неизвестного члена пропорции:
$b=\frac{a \cdot d}{c}$;
$x=\frac{3 \cdot 252}{108}$;
$x=\frac{252}{36}$;
$x=7$.
Ответ: для обрезки $252$ деревьев потребуется $7$ садовников.
Чаще всего свойства пропорции используют на практике в математических вычислениях в случаях, когда необходимо вычислить значение неизвестного члена пропорции, если известны значения трех остальных членов.
spravochnick.ru
Пропорция, Алгебраическая Пропорция
359. Для точного и близкого ознакомления с учением о соотношениях необходимо хорошо понимать принципы пропорции, одного из наиболее важных ответвлений в математике. В соотношениях мы сравниваем две величины, для того, чтобы найти их разность или частное одного при делении на другое. А в пропорции идёт сравнение двух соотношений. И это сравнение ограничено нахождением того, равны ли они. Мы не спрашиваем насколько одно соотношение больше или меньше другого, но только являются ли они одинаковыми. Поэтому числа 12, 6, 8, 4, называют пропорциональными, так как соотношение 12:6 равно соотношению 8:4.
360. Тогда пропорция — это равенство соотношений. Она является либо арифметической, либо геометрической. Арифметическая пропорция является равенством арифметических соотношений, а геометрическая пропорция — это равенство геометрических соотношений. Таким образом числа 6, 4, 10, 8 составляют арифметическую пропорцию, потому что разница между 6 и 4 такая же как и разница между 10 и 8. А числа 6, 2, 12, 4 находятся в геометрической пропорции, так как частное при делении 6 на 2, такое же как и частное при делении 12 на 4.
361. Надо быть внимательным и не смешивать понятия пропорция и соотношение. Эта осторожность ещё больше необходима, потому что в общих рассуждениях эти два термина используются неразборчиво, или ,пожалуй, пропорция используется вместо обоих понятий. Говорят, что расходы одного человека составляют большую пропорцию его прибыли, чем другого. Но, согласно только что даному определению, одна пропорция не может быть ни больше, ни меньше чем другая. Потому что равенство не признает степеней. Одно соотношение может быть больше или меньше другого. Соотношение 12:2 больше, чем соотношение 6:2 и меньше, чем соотношение 20:2. Но эта разница не применима к пропорции, когда этот термин применяется в своём формальном смысле. Часто используемая свободная трактовка этого слова может доста
www.math10.com
Понятие пропорции и пропорциональности
Пропорции в архитектуре служат средством упорядочения и установления закономерных взаимосвязей между всеми частями сооружения. Пропорция — это соотношение между архитектурным сооружением в целом, и его частями, — между отдельными частями и их элементами. Пропорция (от лат. слова «proportio») — означает соразмерность. Удачно найденные пропорции являются одним из существенных моментов, определяющих художественную ценность сооружения.
Существует мною теорий пропорций, но для практической работы они могут иметь лишь подобное значение.
Модульная система пропорций известна со времен античности и лежит в основе архитектурных ордеров, где за модуль принят радиус нижнего основания колонны. Можно отметить геометрическую пропорциональную систему (которая также называется иррациональной) и метод «подобия пропорций», разработанный немецким архитектором А.Тиршем в конце XIX в.
Наибольшее распространение получил метод пропорций, называемый «золотым сечением» (приближенные числовые значения этой теории 5:3). Метод этот известен со времен Леонардо да Винчи. Но наиболее полно значение «золотого сечения» было отмечено в конце XIX в.
При выведении пропорциональности этим методом исходят из того, что деление целого на 2 части пропорционально тогда, когда меньшая так относится к большей, как большая — к целому.
Из последних работ, посвященных проблеме пропорций, представляет интерес система «модулор» архитектора Ле Корбюзье.
В ней сделана попытка увязать размеры, выраженные в метрах с размерами человеческой фигуры. Взяв за основу рост человека высотой 183 см и высоту человека с поднятой рукой — 226 см, Ле Корбюзье создал шкалу измерений из двух рядов, расчленив эти размеры в отношениях «золотого сечения» («красная» и «синяя» шкала).
Принцип этой системы измерений таков, что каждый последующий член «синей» шкалы может быть получен удвоением предыдущего члена «красной» шкалы».
Достоинством этой системы является то, что все числовые величины согласуются с основными параметрами человека. Недостатком «модулора» является дробность величин, которая очень усложняет вычисление. На базе «модулора» Ле Корбюзье построил несколько архитектурных сооружений .
| Цвет в архитектурной композиции< Предыдущая | Следующая >Понятие о масштабе и масштабность |
|---|
xn--80aam4cn.xn--b1ad5aajzan.xn--p1ai
Понятие пропорции и пропорциональности » СтудИзба
ПОНЯТИЕ ПРОПОРЦИИ И ПРОПОРЦИОНАЛЬНОСТИ
Пропорции в архитектуре служат средством упорядочения и установления закономерных взаимосвязей между всеми частями сооружения. Пропорция — это соотношение между архитектурным сооружением в целом, и его частями, — между отдельными частями и их элементами. Пропорция (от лат. слова «proportio») — означает соразмерность. Удачно найденные пропорции являются одним из существенных моментов, определяющих художественную ценность сооружения.
Существует мною теорий пропорций, но для практической работы они могут иметь лишь подобное значение.
Модульная система пропорций известна со времен античности и лежит в основе архитектурных ордеров, где за модуль принят радиус нижнего основания колонны. Можно отметить геометрическую пропорциональную систему (которая также называется иррациональной) и метод «подобия пропорций», разработанный немецким архитектором А.Тиршем в конце XIX в.
Наибольшее распространение получил метод пропорций, называемый «золотым сечением» (приближенные числовые значения этой теории 5:3). Метод этот известен со времен Леонардо да Винчи. Но наиболее полно значение «золотого сечения» было отмечено в конце XIX в.
При выведении пропорциональности этим методом исходят из того, что деление целого на 2 части пропорционально тогда, когда меньшая так относится к большей, как большая — к целому.
Из последних работ, посвященных проблеме пропорций, представляет интерес система «модулор» архитектора Ле Корбюзье.
В ней сделана попытка увязать размеры, выраженные в метрах с размерами человеческой фигуры. Взяв за основу рост человека высотой 183 см и высоту человека с поднятой рукой — 226 см, Ле Корбюзье создал шкалу измерений из двух рядов, расчленив эти размеры в отношениях «золотого сечения» («красная» и «синяя» шкала).
Принцип этой системы измерений таков, что каждый последующий член «синей» шкалы может быть получен удвоением предыдущего члена «красной» шкалы».
Достоинством этой системы является то, что все числовые величины согласуются с основными параметрами человека. Недостатком «модулора» является дробность величин, которая очень усложняет вычисление. На базе «модулора» Ле Корбюзье построил несколько архитектурных сооружений .
studizba.com
Пропорция. Основное свойство пропорции. Прямо и обратно пропорциональные величины. Деление числа пропорционально данным числам.
Пропорция – это равенство двух отношений.
Основное свойство пропорции: произведение средних членов пропорции равно произведению крайних членов.
Прямо пропорциональные величины – величины, если при увеличении (уменьшении) одной величины, вторая увеличивается (уменьшается) во столько же раз.
Например, для зависимости S = v *t расстояние и время – прямо пропорциональные величины.
Обратно пропорциональные величины – величины, если при увеличении (уменьшении) одной величины, вторая уменьшается (увеличивается) во столько же раз.
Например, для зависимости S = v *t скорость и время – обратно пропорциональные величины.
Деление числа на части пропорционально данным числам: данное число разделить на сумму чисел, выражающих части, умножить на соответствующую часть.
Например, разделить число 12 на части пропорционально числам 1 и 3. . Ответ: 3 и 9. Для проверки сложить данные числа, их сумма должна быть равна исходному числу.
Проценты. Нахождение процента от числа и числа по процентам.
Процент — сотая часть числа ( % ).
Нахождение процента от числа: число разделить на 100, умножить на число, выражающее процент.
Нахождение числа по процентам: заданное число разделить на заданную величину процента, а результат умножить на 100.
Противоположные и взаимообратные числа.
Противоположные числа – числа, отличающиеся только знаком. Например, 17 и – 17.
Взаимообратные числа – числа, произведение которых равно 1. Например, 17 и .
Отрицательные числа, действия с ними.
Сравнение отрицательных чисел: чем больше модуль отрицательного числа, тем меньше число. Отрицательное число всегда меньше 0 и любого положительного числа.
Сложение отрицательных чисел: сложить модули чисел и поставить знак минус.
Сложение чисел с разными знаками: из большего модуля вычесть меньший и поставить знак числа с большим модулем.
Вычитание отрицательных чисел и чисел с разными знаками: вычитание заменить сложением, изменив при этом знак вычитаемого.
Умножение и деление отрицательных чисел и чисел с разными знаками: умножить/разделить модули, поставить знак в соответствии с правилом: если количество минусов нечётное, то поставить знак минус, если количество минусов чётное, то поставить знак плюс.
Иррациональные числа. Корень квадратный, корень n-ой степени. Арифметический квадратный корень.
Числа называются иррациональными, если их можно представить в виде бесконечной десятичной непериодической дроби.
Периодическая десятичная дробь – бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же последовательности. Например, 4,6753535353. Период записывают в скобочках 4, 67(53).
Чтобы перевести смешанную периодическую дробь в обыкновенную, нужно из числа, стоящего после запятой до второго периода, вычесть число, стоящее после запятой до первого периода, и эту разность сделать числителем, а в знаменатель записать цифру 9 столько раз, сколько цифр в периоде, со столькими нулями справа, сколько цифр между запятой и периодом, целую часть оставить той же.
Например, 1,4(37) = .
Корнем степени n из числа a называется число, которое при возведении в степень n равно числу a. Если n чётное, то число a должно быть неотрицательным.
Квадратным корнем из неотрицательного числа a называется число, которое при возведении в квадрат равно числу a.
Арифметическим квадратным корнем из неотрицательного числа a называется неотрицательное число, которое при возведении в квадрат равно числу a.
16. Дискриминант.
Теорема Виета.
Применяется для приведённого уравнения:
Если уравнение не приведённое, то
Линейные и квадратные уравнения.
Линейное уравнение – уравнение вида ax=b, где x – неизвестное, ,b – некоторые числа.
Квадратное уравнение – уравнение вида , где x – неизвестное, ,b,с – некоторые числа (коэффициенты уравнения).
Решение квадратных уравнений:
1 способ. Через дискриминант: , . Если D>0, то уравнение имеет 2 корня, если D=0, то уравнение имеет один корень , если D<0, то уравнение не имеет корней.
2 способ. Если b=2k, то .
3 способ. Теорема Виета.
Теорема Пифагора.
Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
, где a, b – катеты, c – гипотенуза.
! Катет всегда меньше гипотенузы.
Пифагоровы тройки: 3:4:5; 6:8:10; 5:12:13; 8:15:17.
Числовые промежутки.
(a,b) – промежуток не включает числа a и b.
[a,b] – промежуток включает числа a и b.
[a,b) – промежуток включает число a и не включает число b.
Рекомендуемые страницы:
lektsia.com

 Анализ изображений 11 деревянных панелей, найденных в 1912 г. в гробнице зодчего Хеси-Ра в Саккара, доказывает (
Анализ изображений 11 деревянных панелей, найденных в 1912 г. в гробнице зодчего Хеси-Ра в Саккара, доказывает (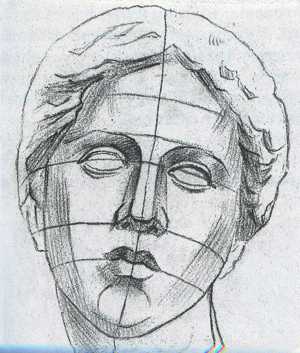 Античное искусство установило идеальные пропорции и для головы человека, согласно которым она по вертикали от темени до конца подбородка делится на две равные части линией глазных впадин. Каждую из этих половин можно, в свою очередь, разделить на две равные части: верхнюю — линией волос, а нижнюю —основанием носа. Получается четыре равные части. Расстояние между глазами принимается равным ширине крыльев носа.
Античное искусство установило идеальные пропорции и для головы человека, согласно которым она по вертикали от темени до конца подбородка делится на две равные части линией глазных впадин. Каждую из этих половин можно, в свою очередь, разделить на две равные части: верхнюю — линией волос, а нижнюю —основанием носа. Получается четыре равные части. Расстояние между глазами принимается равным ширине крыльев носа. Средокрестие представляет собой в плане квадрат Л. Б. Альберти в проекте западного фасада церкви Санта Мария Новелла во Флоренции (1458) применил оригинальный прием сочетания квадратуры и средневековой триангуляции: фасад вписан в три равных квадрата. В поперечном сечении по средокрестию многие базилики представляют собой квадрат, диагональ которого, поднятая в вертикальную плоскость, дает высоту барабана до основания купола. Другим модулем является диагональ подкупольного квадрата. Все вариации осуществляются в пределах одной схемы.
Средокрестие представляет собой в плане квадрат Л. Б. Альберти в проекте западного фасада церкви Санта Мария Новелла во Флоренции (1458) применил оригинальный прием сочетания квадратуры и средневековой триангуляции: фасад вписан в три равных квадрата. В поперечном сечении по средокрестию многие базилики представляют собой квадрат, диагональ которого, поднятая в вертикальную плоскость, дает высоту барабана до основания купола. Другим модулем является диагональ подкупольного квадрата. Все вариации осуществляются в пределах одной схемы. В «Учебнике афонских иконописцев» за единицу всех размеров фигуры принимается лик (в Италии — testa— «голова«). Длина лица укладывается девять раз в высоте фигуры (что отлично от античных пропорций) и,в частности, три раза в высоте торса. Лик делится на три равные части по высоте независимо от характера изображаемого персонажа: высота лба, носа и от основания носа до подбородка. Голова, по византийскому канону, строится в «схеме трех радиусов«.
В «Учебнике афонских иконописцев» за единицу всех размеров фигуры принимается лик (в Италии — testa— «голова«). Длина лица укладывается девять раз в высоте фигуры (что отлично от античных пропорций) и,в частности, три раза в высоте торса. Лик делится на три равные части по высоте независимо от характера изображаемого персонажа: высота лба, носа и от основания носа до подбородка. Голова, по византийскому канону, строится в «схеме трех радиусов«. Более перспективными оказались труды Дюрера и итальянских маньеристов последующей эпохи. Отказавшись от создания «идеальной фигуры«, тяготевшей над сознанием итальянцев, Дюрер разрабатывал пропорции «характерных типов«головы и фигуры человека, включая детские и гротескные, избегая, однако, как он сам писал, «прямого уродства«. Художник составил 26 серий «характерных рисунков«с вариациями пропорций.
Более перспективными оказались труды Дюрера и итальянских маньеристов последующей эпохи. Отказавшись от создания «идеальной фигуры«, тяготевшей над сознанием итальянцев, Дюрер разрабатывал пропорции «характерных типов«головы и фигуры человека, включая детские и гротескные, избегая, однако, как он сам писал, «прямого уродства«. Художник составил 26 серий «характерных рисунков«с вариациями пропорций.