Пропорции правило: Пропорции. Основное свойство пропорции — урок. Математика, 6 класс.

Электронный справочник по математике для школьников арифметика пропорции основное свойство пропорции производные пропорции свойства равных отношений

Справочник по математике

Арифметика

Пропорции и пропорциональная зависимость

Содержание

Пропорции, члены пропорции. Основное свойство пропорции

Производные пропорции

Свойства равных отношений

Пропорции, члены пропорции. Основное свойство пропорции

Частное от деления числа   a   на число   b   называют отношением числа   a   к числу   b.

Число   a   называют предыдущим членом отношения, число   b   – последующим членом отношения.

Пропорцией называют равенство двух отношений:

.

Иногда пропорцию записывают так:

a : b = c : d .

И в одной, и во второй формах записи пропорции числа   a   и   d   называют крайними членами пропорции, а числа   b   и   c   – средними членами пропорции.

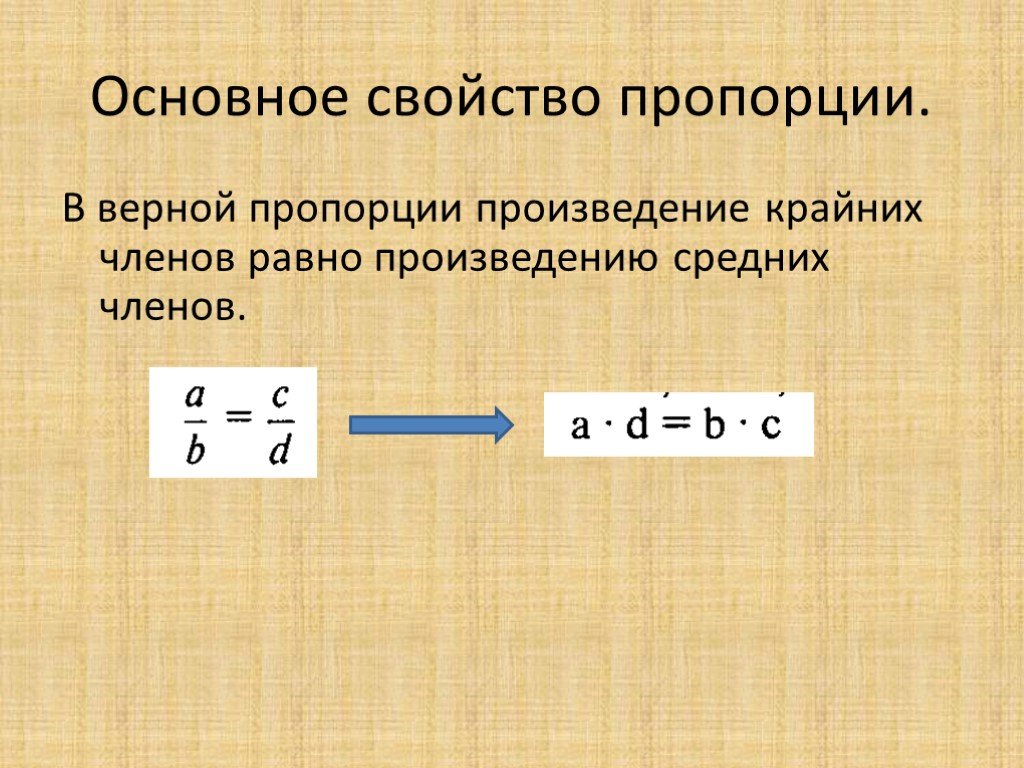
Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:

Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.

Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение   .

В результате получим:

что и требовалось доказать.

Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.

ПРИМЕР 1. Найти неизвестный член пропорции   x ,   если

РЕШЕНИЕ. Воспользовавшись основным свойством пропорции, получаем:

ОТВЕТ:   3,15 .

ПРИМЕР 2. Найти неизвестный член пропорции   x ,   если

РЕШЕНИЕ. Воспользовавшись основным свойством пропорции, получаем:

ОТВЕТ: .

Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если

.

то

Производные пропорции

Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если

,

то

	,
	,
	,
	,
	,

В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции

.

достаточно прибавить 1. В результате получаем,

что и требовалось.

ЗАМЕЧАНИЕ. Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.

Свойства равных отношений

Если выполнено соотношение

то выполнено и соотношение

где

k₁ ,  k₂ , … k_n

– произвольные числа, которые не могут все одновременно равняться нулю.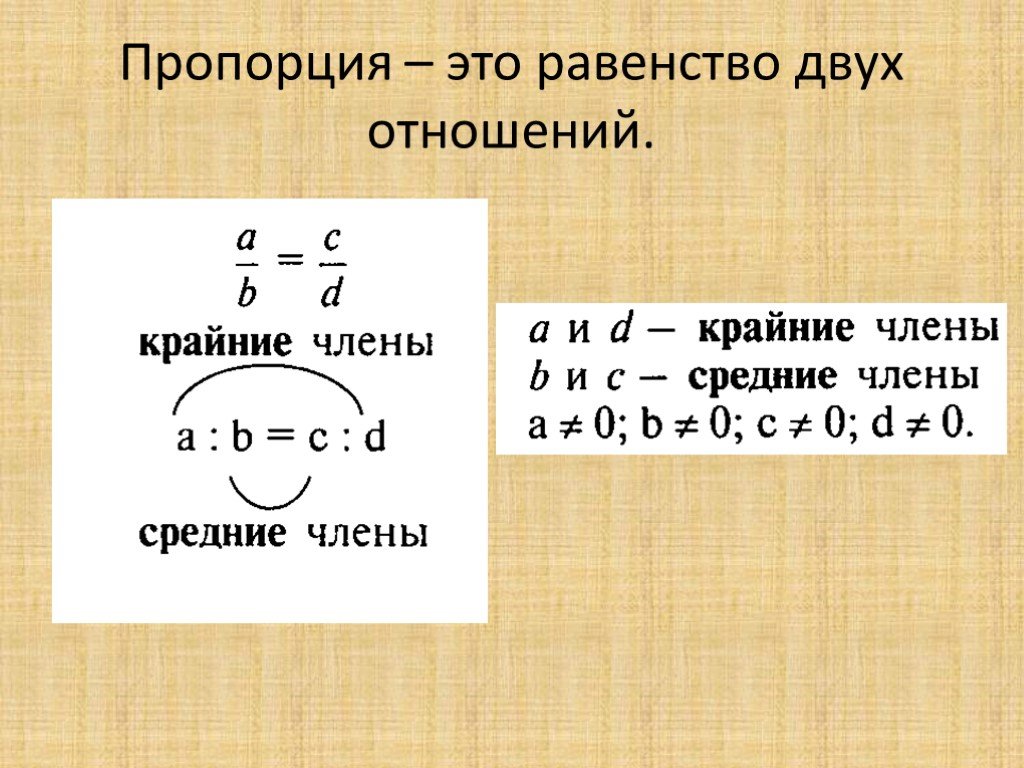

Раствор для штукатурки: пропорции, правила замешивания

28.12.2022

Строительство любого здания и сооружения не обходится без черновой отделки стен. Залогом качественного выполнения этого этапа работ и долговечности результата отделочных работ в целом является правильно замешанный раствор для штукатурки стен. Он служит основой для чистовой отделки. Если выравнивающий материал начнет трескаться, осыпаться или вздуваться, внешнее покрытие придется снимать и переделывать всё заново. Чтобы этого не произошло, цементно-песчаный раствор должен быть приготовлен из качественного сырья в нужных пропорциях. Они, в свою очередь, зависят от разных факторов, в том числе предназначения смеси, условий нанесения, выбора цемента и других.

Состав и особенности раствора

В состав штукатурного раствора входит три основных компонента: цемент – вяжущее вещество, песок – наполнитель и вода – растворитель. Чтобы добиться нужных характеристик и необходимой консистенции смеси, необходимо учесть особенности её приготовления.

Главное внимание надо обратить на следующие факторы:

1. Марка цемента и расшифровка к ней. Раствор для стен готовят на основе цемента М300 – М600. Для разных видов работ и определенных условий используется различные марки. Так, для выравнивания стен в сухом помещении подойдет М300, а с повышенной влажностью – М600.
2. В качестве основного наполнителя применяется песок. Для штукатурки подойдет и речной, и карьерный. Главное требование – максимальная чистота и минимальное количество глинистых примесей. Для укладки чернового слоя штукатурки рекомендуют песок крупной фракции – 2-4 мм. Среднефракционный с диаметром от 0,5 до 2 мм лучше подходит для финишного выравнивания. Предпочтительно купить очищенный и просеянный наполнитель, но в любом случае перед внесением его надо просеять.
3. Воду надо использовать чистую, без добавок и посторонних примесей, масел, химических и органических веществ, желательно не водопроводную.
4. Предназначение раствора. По своим характеристикам он делится на три вида:
   • Простой – для оштукатуривания стен, где не требуется высокого качества отделки, например, в чулане подсобке и т. п.
   • Улучшенный – в жилом, офисном, производственном помещении.
   • Высококачественный – материал для финишных отделочных работ, например, под покраску. Используется для покрытия стен в жилых домах, гостиницах, музеях, кафе, торговых центрах и т.д.

Нередко для выполнения определенных работ требуется штукатурный раствор с улучшенными техническими и эксплуатационными характеристиками: быстрое затвердевание, повышенная подвижность, влаго- и морозостойкость, устойчивость к грибку и плесени и другое. В таких случаях в смесь вводятся дополнительные ингредиенты:

• Алебастр (строительный гипс) – сокращает время застывания. Используют для выравнивания откосов, монтажа электропроводки, устранения дефектов поверхностей.
• Гипс – алебастр мелкой фракции, высыхание смеси не такое быстрое, поэтому раствор более пластичный. Подходит для отделки углов, потолков и труднодоступных мест.
• Известь в виде известкового молочка или теста. Придает материалу прочность, паропроницаемость, устойчивость к бактериям (плесени), влагостойкость и другие положительные качества. Препятствует растрескиванию. Хорошо подходит для выравнивания фасадов и внутренних поверхностей во влажном помещении.
• Клей ПВА – 5% от общего объема смеси. Повышает прочность, снижает растрескиваемость, улучшает адгезию.
• Жидкое мыло – добавление трех процентов от общей массы повышает пластичность.

Пропорции для цементно-песчаной штукатурки

Классическое, усредненное соотношение вяжущего и наполнителя цементно-песчаного раствора – 1:3-1:4. То есть на одно ведро цемента – 3-4 ведра песка. При этом марка полученного раствора зависит от этой характеристики цемента. Чем выше она у вяжущего компонента, тем, соответственно будет выше у готового продукта.

В зависимости от того, какие свойства должны быть у раствора и где он будет применяться, пропорции изменяются.

Универсальный состав для большинства работ без повышенных требований и особых условий применения смешивают, как правило, в соотношении 1:5. Воду добавляют постепенно для достижения нужной консистенции.

Жирный раствор для покрытия стен грунтом. Этот второй слой после набрызга (подготовки поверхности к нанесению смеси) приготавливают в пропорции 1:3.

Для третьего, накрывочного слоя отделки стен компоненты берут в соотношении 1:1. Смешанные цемент и песок разводят до густоты сметаны. Этот раствор наносят поверх грунта.

Приступая к приготовлению материала, надо знать, какая марка раствора Вам потребуется, от этого будет зависеть рецептура. По данному критерию можно использовать следующую таблицу:

Марка цемента	Марка раствора (пропорции цемент: песок)
	М100	М75	М50
М600	1:4,5	1:6	—
М500	1:4	1:5	—
М400	1:3	1:4	1:6
М300	1:2,5	1:3	1:4,5
М200	—	1:2,5	1:3,5

 

Растворы марок, применяющихся для наиболее распространенных в индивидуальном строительстве видов работ:

• М10 – М50 – для оштукатуривания поверхностей;
• М50 – М200 – для укладки;
• М 150 и М200 – для устройства фундамента и стяжки.

Дополнительные компоненты для штукатурки

Для улучшения качества и придания раствору дополнительных свойств смеси в него в процессе приготовления вносят специальные модифицирующие добавки, которые можно купить в магазине.

1. Пластификаторы. Повышают подвижность материала, Не дают влаге впитываться в поверхность и испаряться, увеличивают объем смеси и не позволяют ей расслаиваться.
2. Замедлители затвердения. Необходимость в них возникает, когда надо продлить срок жидкого состояния смеси, например, если в него надо добавить гипс. В магазинах продаются также ускорители схватывания.
3. Противоморозные добавки замедляют замерзание жидкости. Это надо для того, чтобы вода в растворе не замерзла прежде, чем он наберет необходимую прочность приобретёт другие требуемые характеристики.
4. Армирующие присадки – это вещества и материалы, повышающие прочность цемента. С этой целью используются химические соединения или фибра – отходы металлургического, стекольного, целлюлозного производства, например, металлическая стружка. В растворе для штукатурки они выполняют функцию арматуры, смешиваясь с частицами компонентов и повышая прочностные характеристики.

В качестве присадок используют также некоторые стройматериалы, улучшающие поверхностные характеристики и внешний вид стен, придающие итоговому продукту специфические свойства:

• Кварцевый песок крупной фракции придает влагонепроницаемость, стойкость к воздействию кислот и щелочей, пропускает воздух.
• Мелкофракционный барит добавляют в тяжелый раствор для защиты стен рентгенкабинетов от радиации.
• Крошка из вспененного полистирола используется для создания теплоизоляционного слоя.
• Мраморная крошка повышает прочность, обеспечивает влагостойкость, устойчивость к перепадам температур и атмосферным явлениям. Придает эстетичный внешний вид, поэтому такой раствор нередко применяется для облицовочных работ, в том числе фасадных.
• Измельченная слюда защищает здание от воздействия солнечных лучей.
• Акрил, эпоксидная и полиуретановая смолы используется для повышения гидроизоляционных качеств.
• Жидкое стекло, каменная мука, кварцит. Предохраняют от агрессивного воздействия кислоты, что необходимо при отделке стен в лабораториях, цехах химической промышленности и т.д.

Технология приготовления раствора

Замесить раствор для штукатурки своими руками несложно. При этом следует строго соблюдать правило: готовую смесь надо использовать в течение часа, поэтому приготавливать надо именно то количество, которое может быть израсходовано в течение этого времени.

Приготовление раствора для штукатурки ведется в следующем порядке:

• Засыпать в емкость цемент и песок в нужной пропорции, тщательно перемешать компоненты мастерком, лопатой.
• Залить воду, замесить раствор. Для этого удобно воспользоваться строительным миксером, дрелью или шуруповёртом с насадкой. Работать надо на средней или малой скорости.
• При желании внести добавки.
• Проверить консистенцию на готовность. Она должна быть однородной, густоты сметаны. Проведите по поверхности мастерком, если остается борозда, материал готов к работе.

Есть и другой способ приготовления:

• залить воду в ёмкость;
• внести половину песка;
• засыпать весь цемент;
• размешать смесь;
• высыпать оставшийся наполнитель, ещё раз перемешать;
• проверить консистенцию, при необходимости добавить воды.

Готовая цементная смесь не должна ни налипать, ни стекать с мастерка, а свободно удерживаться на нем. Недопустимы прослойки жидкости.

Правила нанесения цементно-песчаной штукатурки

Основные правила проведения штукатурных работ предусматривают несколько этапов нанесения раствора.

1. Первый, очень ответственный этап – подготовка поверхности. Прежде всего с помощью лески, натянутой по диагоналям плоскости, определяется слой нанесения. Если он больше 2 см, смесь надо наносить за несколько подходов, если меньше – достаточно одного. Далее производится очистка от старых обоев, штукатурки и других ненадежных фрагментов. При наличии старого слоя краски, который трудно удалить, на нем надо сделать насечки шпателем для надежной сцепки раствора и стен. Нанесение покрытия большой толщины, до 5 см, требует армирования металлической сеткой. Для защиты от влажности и бактерий и надежной адгезии проводится грунтование. Если дефекты поверхности видны невооруженным глазом, перед нанесением состава надо установить маяки.
2. Следующий этап – обрызг (наброска). Густую смесь набирают на инструмент и набрасывают на поверхность. На маяки ставят правило и выравнивают покрытие снизу вверх. Оставляют для просушки на 2 часа. На бетонные и кирпичные стены кладут слой около 5 см, на деревянные – 8-9 см.
3. Грунт. Материал наносят широким шпателем с некоторым усилием. С помощью правила проверяют выравнивание плоскости. Устраняют дефекты: впадины заполняют раствором, бугорки удаляют смоченной в воде тёркой. Раствор должен сохнуть минимум 3 часа.
4. Накрывка. Раствор консистенции сметаны накладывают шпателем или небольшими порциями поливают на стены сверху вниз. Полностью выравнивают правилом. Через 8 часов немного увлажняют и зачищают.

При проведении отделочных работ для достижения лучшего результата надо соблюдать ряд правил:

• для тонкого слоя штукатурки нужен жидкий состав, для более толстого – густой;
• если на поверхности, предназначенной для оштукатуривания, есть трещины и шероховатости, её рекомендуется периодически обрызгивать водой из пульверизатора;
• участки, прилегающие к полу и потолку, обрабатывают последним;
• при выравнивании оштукатуренной зоны правило прикладывают острой частью к граням направляющих;
• выравнивание стен начинают с пола, постепенно двигаясь вверх, инструмент при этом надо двигать зигзагообразно;
• собранный при выравнивании состав сразу накладывают на верхние участки, чтобы он не успевал высохнуть;
• образующиеся в ходе отделочных работ пузыри и пустоты необходимо ликвидировать сразу, не дожидаясь высыхания;
• весь процесс выравнивания не должен продолжаться более 12 часов;
• если надо нанести несколько слоев, то следующий накладывается после высыхания предыдущего;
• оконные и дверные проемы штукатурят вровень с ними либо внахлест.

В компании «Правильный бетон» можно купить готовый цементный раствор, изготовленный на собственном производстве в соответствии с требованиями ГОСТ. Качество проверяется в заводской сертифицированной лаборатории. Предлагаем выгодные цены и доставку точно в срок, при необходимости – дополнительные услуги.

Правило 3: прямое и обратное

В сегодняшней статье мы будем работать над пропорциями . На этот раз мы рассмотрим способ решения прямой и обратной пропорции: правило 3 .

Что такое правило 3?

Правило 3 — это операция, которая помогает нам быстро решать как прямые, так и обратные пропорции словесных задач.

Чтобы использовать правило 3, нам нужны три значения: два пропорциональных друг другу и третье. Оттуда мы будем вычислить четвертое значение .

Прямое правило 3

Мы начнем с рассмотрения того, как применить его в случае прямой пропорции .

Мы поместим 3 значения (которые мы назовем «a» , «b» и «c» ) и неизвестное значение, которое мы хотим вычислить ( «x» ) в таблице. Далее применим следующую формулу:

В качестве примера решим следующую задачу:

По прибытии в отель персонал дал нам карту с указанием достопримечательностей города и сказал нам, что 5 сантиметров на карте соответствуют 600 метрам в действительности. Сегодня мы хотим отправиться в парк, который находится в 8 сантиметрах от отеля на карте. Как далеко от отеля парк?

Давайте составим таблицу с 3 значениями и неизвестным значением («x»), и мы найдем «x» по формуле , которую мы только что узнали.

Сантиметры на карте               Метры в реальности

 

Ответ:  Парк находится в 960 метрах от отеля.

Обратное правило 3

Теперь рассмотрим, как применить правило 3 в случае обратной пропорциональности .

Мы поместим 3 значения и неизвестное значение в таблицу , так же, как мы сделали в предыдущем случае, , а применим другую формулу:

Рассмотрим пример:

Вчера перевозили грузы со склада на порту. Сегодня 3 грузовика того же размера, что и вчера, должны будут совершить 6 рейсов, чтобы перевезти такое же количество товаров со склада в торговый центр. Сколько рейсов грузовики сделали вчера?

Помещаем значения в таблицу и Применить формулу для обратного правила 3 ​​:

Грузовики Требуется

Ответ: Вчера, 2 грузовики.

Что вы думаете об этом посте? Разве не легко применить правило 3 к пропорциональным задачам со словами!

Вы можете узнать больше о прямой и обратной пропорции из этого предыдущего поста в нашем блоге: Правило трех задач.

Помните, что с помощью Smartick вы сможете практиковать упражнения, задачи на пропорции и и многое другое! Попробуйте бесплатно!

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

Обратная пропорциональность: правило трех, обратное

использовать его для решения проблем.

Правило трех — способ решения проблем пропорциональности. Если мы имеем дело с прямой пропорциональностью, то применим прямое правило трех. Если мы имеем дело с обратной пропорциональностью, мы применяем правило трех обратных величин.

Давайте посмотрим, что такое обратная пропорциональность, чтобы мы могли узнать, как ее применять позже в этом посте.

Что такое обратная пропорциональность?

У нас есть 2 величины (А и В), и нам нужно наблюдать взаимосвязь между ними. Чтобы возникла обратная пропорциональность, мы должны убедиться, что выполняются два следующих правила:

1. Чем больше A, тем меньше B.
2. Что увеличивает одно, уменьшает другое. Это, например, если A удвоить, то B разделить пополам. Или, если B утроится, то A уменьшится на треть.

Это означает, что пропорция между двумя величинами обратная.

Например, в следующей таблице вы можете увидеть величины A и B:

Это обратная пропорция, потому что, пока A становится больше, B становится меньше, что именно и описывает Правило 1.

Кроме того, когда A удваивается, B уменьшается вдвое (во второй строке таблицы мы видим, что A стоит 2, а B — 12). Когда A утроится (от 1 до 3), значение B падает с 24 до 8, что составляет одну треть от 24. Глядя на последнюю строку, если A стоит 4, B уменьшается до 6, что составляет одну четверть от 24. сколько он стоил, когда A был равен 1. В результате правило 2 было выполнено.

 

Как использовать обратное правило трех?

Обратное правило трех используется в задачах, где известны три из четырех пропорциональных чисел, а нужно решить четвертое число.

Сначала нам нужно связать А с Б. Затем мы записываем следующую пару чисел, которые нам нужно связать.

C — значение величины A, а X, значение, которое мы ищем, — значение величины B.

Как решить задачу с обратным правилом трех?

На ферме 20 уткам требуется 10 дней, чтобы съесть оставшуюся для них пищу. За сколько времени 40 уток съедят один и тот же корм?

Во-первых, мы должны определить, является ли пропорциональность прямой или обратной:

На 20 уток уходит 10 дней. 40 уток… потребуется ли им больше или меньше времени, чтобы съесть еду?

Если количество уток увеличивается, то количество дней, на которые хватит корма, уменьшается, и можно подумать, что если уток будет в два раза больше, то они съедят корм в два раза быстрее. Так что это обратная пропорциональность.

Теперь применим обратное правило трех:

5 дней потребуется , чтобы 40 уток съели всю еду.

3 маляра покрасят дом за 12 дней. За какое время 9 маляров выполнят ту же работу?

Во-первых, нам нужно определить, какой это вид пропорциональности.

На 3 маляров уходит 12 дней. 9 маляров… им потребуется больше или меньше времени, чтобы выполнить работу?

Так как маляров больше, работа будет завершена быстрее, и разумно предположить, что с тройным количеством маляров работа будет выполнена за треть времени. Следовательно, это обратная пропорциональность.

Теперь нам просто нужно применить правило трех, обратное:

Требуется 4 дня для покраски дома 9 малярами.

Если вы хотите продолжать изучать и практиковать элементарную математику в соответствии с вашим уровнем, зарегистрируйтесь в Smartick и попробуйте бесплатно.