Простейшие тригонометрические уравнения и неравенства: Методическое пособие для студентов. Решение тригонометрических уравнений и неравенств.

Содержание

Примеры решения простейших тригонометрических неравенств

Часть 2.

Начало здесь.

Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические уравнения (часть III).

Кстати, для сдающих ЕГЭ по математике, – умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Примеры решения простейших тригонометрических неравенств

Пример 1.

Решить неравенство: tgx<1.

Решение:

Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.

Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1. Для этого мы ~~мысленно~~ соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.

Заметим, кстати, что дуга $(\frac{3\pi}{2}+2\pi n;\frac{9\pi}{4}+2\pi n),\;n\in Z$ повторяет дугу $(\frac{\pi}{2}+2\pi n;\frac{5\pi}{4}+2\pi n)$

равно через пол круга, то есть через $\pi$ (период функции y=tgx

– это $\pi$ ).

Все подходящие значения можно записать в виде следующего двойного неравенства:

$\frac{\pi}{2}+\pi n<x<\frac{5\pi}{4}+\pi n,\;n\in Z$

или так

$x\in (\frac{\pi}{2}+\pi n;\frac{5\pi}{4}+\pi n),\;n\in Z.$

Пример 2.

Решить неравенство: $tgx\geq -\sqrt3.$

Решение:

Отмечаем на оси тангенсов $-\sqrt3$ . Указываем все значения тангенса, большие или равные $-\sqrt3$

– выше $-\sqrt3$ (включая саму точку).

«Транслируем» отмеченные точки оси тангенсов на тригонометрический круг.

Все подходящие значения можно записать в виде следующего двойного неравенства:

$\frac{2\pi}{3}+\pi n\leq x<\frac{3\pi}{2}+\pi n,\;n\in Z$

или такого (разницы – никакой):

$-\frac{\pi}{3}+\pi n\leq x<\frac{\pi}{2}+\pi n,\;n\in Z.$

Пример 3.

Решить неравенство: $ctgx\geq \frac{\sqrt3}{3}.$

Решение:

Отмечаем на оси котангенсов $\frac{\sqrt3}{3}$ . Указываем все значения котангенса, большие или равные $\frac{\sqrt3}{3}$ – правее $\frac{\sqrt3}{3}$

(включая саму точку).

«Транслируем» отмеченные точки оси котангенсов на тригонометрический круг:

Все подходящие значения можно записать в виде следующего двойного неравенства:

$\pi n<x\leq \frac{\pi}{3}+\pi n,\;n\in Z.$

Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки $\pm \frac{\pi}{2}+2\pi n,\;\in Z$

(значение тангенса в этих точках не определено)?

А, решая тригонометрическое неравенство с котангенсом, – мы не включаем в ответ точки $\pi+\pi n,\;\in Z$ (значение котангенса в этих точках не определено).

Пример 4.

Решить неравенство: $ctgx\leq 2.$

Решение:

лор

$arcctg2+\pi n\leq x<\pi +\pi n,\;n\in Z.$

Проверьте себя

Помните, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например, задание 2).

1. Решить неравенство: $tgx\geq -1.$

Ответ: + показать

$[-\frac{\pi}{4}+\pi n;\frac{\pi}{2}+\pi n),\; n\in Z$

2. Решить неравенство: $ctgx\leq -\frac{1}{\sqrt3}.$

Ответ: + показать

$[\frac{2\pi}{3}+\pi n;\pi+\pi n),\; n\in Z$

3. Решить неравенство:

Ответ: + показать

$(-\frac{\pi}{2}+\pi n;arctg3+\pi n),\; n\in Z$

Если у вас есть вопросы, – пожалуйста, – пишите в комментариях!

Простейшие тригонометрические уравнения и неравенства(10 класс)

Инфоурок › Алгебра ›Конспекты›Простейшие тригонометрические уравнения и неравенства(10 класс)

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Приложение 1.pptx

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Выбранный для просмотра документ Приложение 2.docx

Выбранный для просмотра документ Простейшие тригонометрические уравнения и неравенства.docx

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: 167926

Оставьте свой комментарий

Простейшие тригонометрические уравнения и неравенства. Подведение итогов

Здравствуйте!

Сегодня мы подводим итоги раздела, посвященного решению простейших тригонометрических уравнений и неравенств.

Давайте повторим определения и свойства обратных тригонометрических функций: арксинуса, арккосинуса, арктангенса и арккотангенса:

Запомнить, как строится на тригонометрическом круге множество решений простейшего уравнения, поможет интерактивная модель. Обратите внимание на особые случаи, когда решение уравнения можно записать, используя значения табличных углов.

Посмотрите разбор решения нескольких типов простых тригонометрических уравнений, включая простой случай сведения к квадратному, в этом плейлисте:

С помощью интерактивной модели можно увидеть, как множество решений простейшего тригонометрического неравенства изменяется в динамике на круге и на графике соответствующей функции.

Повторяем задачи к разделу. Напомним, что тренажеры с пошаговым решением и задачи для самостоятельной работы ждут подписчиков в Библиотеке.

Начать тренировку

Мы научились решать простейшие тригонометрические уравнения и неравенства. Но задача №13 варианта КИМ ЕГЭ содержит, как правило, более сложное уравнение. И для этих уравнений существуют свои методы и приемы решений. Какие? Об этом мы узнаем на следующей неделе.

Следите за обновлениями на сайте и подписывайтесь на наш канал в Ютьюбе и группу Вконтакте!

Лекция 18. Простейшие тригонометрические неравенства. — Студопедия

Неравенство, в котором неизвестная переменная находится под знаком тригонометрической функции, называется тригонометрическим неравенством.

К простейшим тригонометрически неравенствам относятся следующие 16 неравенств:
sinx>a, sinx≥a, sinx<a, sinx≤a,
cosx>a, cosx≥a, cosx<a, cosx≤a,
tanx>a, tanx≥a, tanx<a, tanx≤a,
cotx>a, cotx≥a, cotx<a, cotx≤a.
Здесь x является неизвестной переменной, a может быть любым действительным числом.

Неравенства вида sinx>a, sinx≥a, sinx<a, sinx≤a

Неравенство sinx>a

При |a|≥1 неравенство sinx>a не имеет решений: x∈∅

При a<−1 решением неравенства sinx>a является любое действительное число: x∈R

При −1≤a<1 решение неравенства sinx>a выражается в виде
arcsina+2πn<x<π−arcsina+2πn,n∈Z (рис.1).

Неравенство sinx≥a

При a>1 неравенство sinx≥a не имеет решений: x∈∅

При a≤−1 решением неравенства sinx≥a является любое действительное число: x∈R

Случай a=1 x=π/2+2πn,n∈Z

При −1<a<1 решение нестрогого неравенства sinx≥a включает граничные углы и имеет вид arcsina+2πn≤x≤π−arcsina+2πn,n∈Z (рис.1).

Неравенство sinx<a

При a>1 решением неравенства sinx<a является любое действительное число: x∈R

При a≤−1 у неравенства sinx<a решений нет: x∈∅

При −1<a≤1 решение неравенства sinx<a лежит в интервале
−π−arcsina+2πn<x<arcsina+2πn,n∈Z (рис.2).

Неравенство sinx≤a

При a≥1 решением неравенства sinx≤a является любое действительное число: x∈R

При a<−1 неравенство sinx≤a решений не имеет: x∈∅

Случай a=−1 x=−π/2+2πn,n∈Z

При −1<a<1 решение нестрогого неравенства sinx≤a находится в интервале
−π−arcsina+2πn≤x≤arcsina+2πn,n∈Z (рис.2).

Неравенства вида cosx>a, cosx≥a, cosx<a, cosx≤a

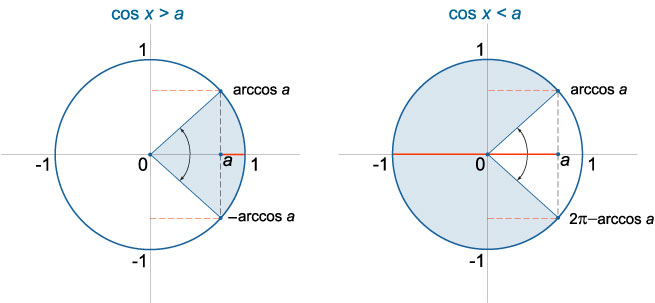
Неравенство cosx>a

При a≥1 неравенство cosx>a не имеет решений: x∈∅

При a<−1 решением неравенства cosx>a является любое действительное число: x∈R

При −1≤a<1 решение неравенства cosx>a имеет вид
−arccosa+2πn<x<arccosa+2πn,n∈Z (рис.3).

Неравенство cosx≥a

При a>1 неравенство cosx≥a не имеет решений: x∈∅

При a≤−1 решением неравенства cosx≥a является любое действительное число: x∈R

Случай a=1 x=2πn,n∈Z

При −1<a<1 решение нестрогого неравенства cosx≥a выражается формулой
−arccosa+2πn≤x≤arccosa+2πn,n∈Z (рис.3).

Неравенство cosx<a

При a>1 неравенство cosx<a справедливо при любом действительном значении x: x∈R

При a≤−1 неравенство cosx<a не имеет решений: x∈∅

При −1<a≤1 решение неравенства cosx<a записывается в виде
arccosa+2πn<x<2π−arccosa+2πn,n∈Z (рис.4).

Неравенство cosx≤a

При a≥1 решением неравенства cosx≤a является любое действительное число: x∈R

При a<−1 неравенство cosx≤a не имеет решений: x∈∅

Случай a=−1 x=π+2πn,n∈Z

При −1<a<1 решение нестрогого неравенства cosx≤a записывается как
arccosa+2πn≤x≤2π−arccosa+2πn,n∈Z (рис.4).

Неравенства вида tanx>a, tanx≥a, tanx<a, tanx≤a

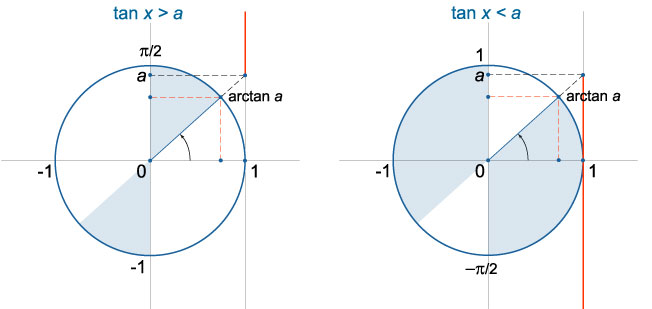
Неравенство tanx>a

При любом действительном значении a решение строгого неравенства tanx>a имеет вид arctana+πn<x<π/2+πn,n∈Z (рис.5).

Неравенство tanx≥a

Для любого значения a решение неравенства tanx≥a выражается в виде
arctana+πn≤x<π/2+πn,n∈Z (рис.5).

Неравенство tanx<a

Для любого значения a решение неравенства tanx<a записывается в виде
−π/2+πn<x<arctana+πn,n∈Z (рис.6).

Неравенство tanx≤a

При любом a неравенство tanx≤a имеет следующее решение:
−π/2+πn<x≤arctana+πn,n∈Z (рис.6).

Неравенства вида cotx>a, cotx≥a, cotx<a, cotx≤a

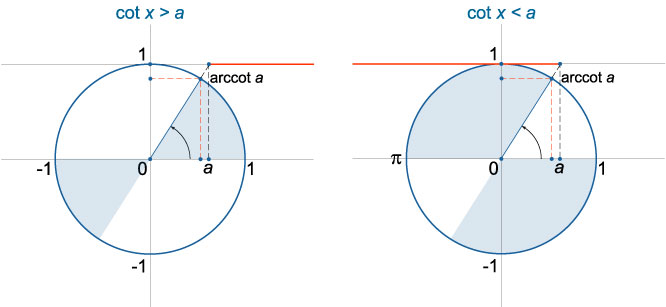
Неравенство cotx>a

При любом a решение неравенства cotx>a имеет вид
πn<x<arccot a+πn,n∈Z (рис.7).

Неравенство cotx≥a

Нестрогое неравенство cotx≥a имеет аналогичное решение
πn<x≤arccot a+πn,n∈Z (рис.7).

Неравенство cotx<a

Для любого значения a решение неравенства cotx<a лежит в открытом интервале arccot a+πn<x<π+πn,n∈Z (рис.8).

Неравенство cotx≤a

При любом a решение нестрогого неравенства cotx≤a находится в полуоткрытом интервале
arccot a+πn≤x<π+πn,n∈Z (рис.8).

Формулы для решения простейших тригонометрических уравнений

Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться в тригонометрическом круге.

Все тригонометрические уравнения, какими они не были – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.

Вы просто обязаны уметь решать уравнения вида

$sin\:x=a,\;cos\:x=a,\;tg\:x=a,\;ctg\:x=a.$

Формулы–алгоритмы будут разбросаны по трем статьям,

здесь же они собраны все вместе =>

+ показать

Давайте разбираться. В этой статье мы рассмотрим решение уравнения вида $cos\:x=a$ . Решение остальных типов простейших уравнений смотрим здесь: часть 2 ( $sin\:x=a$ ), часть 3 ( $tg\:x=a$ , $ctg\:x=a$ )

Уравнение вида $\LARGE cos\:x=a$

Решим уравнение $cos\:x=\frac{1}{2}.$

Мы должны подобрать такие значения аргумента , то есть такие значения углов, косинус которых равнялся бы $\frac{1}{2}$ .

Смотрим на тригонометрический круг, на оси косинусов находим $\frac{1}{2}$ :

Выстраиваем через эту точку вертикаль, получаем две точки на круге:

Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен $\frac{1}{2}$ . Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.

На координатной прямой подходящие нам точки располагаются так:

$\frac{1}{2}$

А с графической точки зрения решение уравнения $cos\:x=\frac{1}{2}$ выглядело бы так:

Как все точки взять в ответ?

Нам поможет счетчик . Возьмем $n\in Z$ , то есть $n=...-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;...$

Решением уравнения $cos\:x=\frac{1}{2}$ будет

$x=\pm\frac{\pi}{3}+2\pi n,\;n\in Z$

Возьмите, поперебирайте различные значения подставьте в вышеуказанную формулу.

Вы получите как раз точки $\pm\frac{\pi}{3}$ при n=0 ,

$\frac{7\pi}{3},\;\frac{5\pi}{3}$ при n=1 ,

$\frac{13\pi}{3},\;\frac{11\pi}{3}$ при n=2 и т.д.

То что нам нужно!

Если бы мы решали, например, уравнение $cos\:x=-\frac{\sqrt2}{2}$ , то решением бы было

$cos\:x=-\frac{\sqrt2}{2}$

$x=\pm\frac{3\pi}{4}+2\pi n,\;n\in Z$ .

Я думаю, вы уже увидели общий принцип формирования ответа.

Давайте дадим формулу, которой можно руководствоваться, решая уравнения

$cos\:x=a$ , где – из $[-1;\:1]$

(в противном случае, когда – не из $[-1;\;1]$ – решений нет)

Но вам формула будет понятна, если вы уже знакомы с понятием «арккосинус».

$x=\pm arccos\:a +2\pi n, \;n\in Z.$

Если нам попадается уравнение с нетабличным значением косинуса, вроде этого $cos\:x=0,3$ , то решение будет следующее:

$x=\pm arccos\:0,3+2\pi n,\;n\in Z.$

Частные случаи решения уравнения $cos\:x=a$

1) $cos\:x=0$

Мы должны бы записать так:

$x=\pm\frac{\pi}{2}+2\pi n,n\in Z$ .

Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик $\pi n$ ):

$x=\frac{\pi}{2}+\pi n,\;n\in Z.$

2) $cos\:x=1$

У нас только одна серия корней:

$x=0+2\pi n,n\in Z,$ то есть $x=2\pi n,n\in Z.$

3) $cos\:x=-1$

Аналогично решению примера 2, решение такое: $x=\pi+2\pi n,\;n\in Z.$

§3 Решение простейших тригонометрических уравнений. Алгебра и начала математического анализа, 10 класс: уроки, тесты, задания.

1.	Тригонометрическое уравнение вида cosx=a Сложность: лёгкое	2
2.	Решение уравнения cos x=a Сложность: лёгкое	1
3.	Тригонометрическое уравнение вида sinx=a Сложность: лёгкое	2
4.	Уравнение (cos) Сложность: лёгкое	1
5.	Уравнение (sin) Сложность: лёгкое	1
6.	Уравнения и выражения Сложность: лёгкое	1
7.	Тригонометрическое уравнение вида ctgx=a Сложность: лёгкое	2
8.	Решение уравнения sin x=a Сложность: лёгкое	1
9.	Тригонометрическое уравнение вида tgx=a Сложность: лёгкое	2
10.	Решение уравнения tg x=a. Сложность: лёгкое	1
11.	Решение уравнения вида sin x=a Сложность: среднее	2
12.	Решение уравнения вида cos x/a=b Сложность: среднее	2
13.	Решение уравнения вида sin bx=a Сложность: среднее	2
14.	Тригонометрическое уравнение вида sin5x=a Сложность: среднее	3
15.	Нахождение корней уравнения tg x =а, используя график Сложность: сложное	10
16.	Решение уравнения ctg x=a Сложность: сложное	3

математических упражнений и математических задач: тригонометрические уравнения и неравенства

Решите тригонометрические уравнения:

Решите тригонометрические неравенства:

Вас также может заинтересовать:

— Тригонометрия

— Тригонометрические функции

— Линейные уравнения и неравенства

— Системы уравнений и неравенств

— Квадратные уравнения и неравенства

— Иррациональные уравнения и неравенства

— Экспоненциальные уравнения и неравенства

— Логарифмические уравнения и неравенства

— Комбинаторные уравнения и неравенства

— Комплексные числа и уравнения

— Матричные уравнения

— Задачи со словами в уравнениях

— Проблемы со словами неравенства

Решение простых (и средней сложности) триггерных уравнений

Purplemath

При решении тригонометрических уравнений используются как исходные углы, так и тригонометрические тождества, которые вы запомнили, а также большая часть изученной вами алгебры. Будьте готовы к тому, что для решения этих уравнений потребуется думать .

Далее предполагается, что вы хорошо разбираетесь в значениях триггерного отношения в первом квадранте, как работает единичный круг, соотношение между радианами и градусами и как выглядят кривые различных триггерных функций на минимум по первому периоду.Если вы не уверены в себе, вернитесь и сначала просмотрите эти темы.

MathHelp.com

Решить sin ( x ) + 2 = 3 в интервале 0 ° & leq; x <360 °

Как и в случае с линейными уравнениями, я сначала выделю член, содержащий переменную:

sin ( x ) + 2 = 3

sin ( x ) = 1

Теперь я буду использовать запомненные углы отсчета, чтобы получить окончательный ответ.

Примечание. В инструкциях указан интервал в градусах, что означает, что я должен давать свой ответ в градусах. Да, синус в первом периоде принимает значение 1 на π / 2 радиан, но это не тот тип угловой меры, который им нужен, и использование этого в качестве моего ответа, вероятно, приведет к тому, что я, по крайней мере, потеряю несколько моментов по этому вопросу.

Итак, в градусах мой ответ:

Решить tan ² (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 °

Есть соблазн быстро вспомнить, что тангенс 60 ° включает в себя квадратный корень из 3, и получить ответ, но это уравнение на самом деле не имеет решения.Я вижу это, когда замедляюсь и делаю шаги. Мой первый шаг:

Может ли любой квадрат (касательной или любой другой триггерной функции) быть отрицательным ? Нет! Итак, мой ответ:

Решить в интервале 0 ° & leq; x <360 °

Левая часть этого уравнения множится.Я привык делать такой простой факторинг:

2 л ² + 3 л = 0

л (2 л + 3) = 0

… и затем решить каждый из факторов. То же самое и здесь. Чтобы решить уравнение, которое они мне дали, я начну с факторинга:

Я занимался алгеброй; то есть, я сделал факторинг, а затем решил каждое из двух уравнений, связанных с факторами.Это создало два триггерных уравнения. Итак, теперь я могу сделать триггер; а именно решение этих двух результирующих тригонометрических уравнений, используя то, что я запомнил о косинусной волне. Из первого уравнения я получаю:

Из второго уравнения я получаю:

Соединяя эти два набора решений вместе, я получаю решение для исходного уравнения как:

x = 30 °, 90 °, 270 °, 330 °

Решить sin ² (θ) — sin (θ) = 2 на интервале 0 & leq; θ <2π

Во-первых, перенесу все по одну сторону от знака «равно»:

sin ² (θ) — sin (θ) — 2 = 0

Это уравнение является «квадратичным по синусу»; то есть форма уравнения представляет собой формат квадратного уравнения:

В случае уравнения, которое они хотят, чтобы я решил, X = sin (θ), a = 1, b = –1 и c = –2.

Поскольку это квадратная форма, я могу применить некоторые методы квадратного уравнения. В случае этого уравнения я могу разложить на множители квадратичный:

sin ² (θ) — sin (θ) — 2 = 0

(грех (θ) — 2) (грех (θ) + 1) = 0

Первый фактор дает мне соответствующее тригонометрическое уравнение:

Но синус никогда не превышает 1, поэтому это уравнение не разрешимо; у него нет решения.

Другой фактор дает мне второе связанное тригонометрическое уравнение:

грех (θ) + 1 = 0

sin (θ) = –1

θ = (3/2) π

Тогда мой ответ:

(Если вы выполняете решения только для степеней в своем классе, значение решения, указанное выше, равно «270 °».)

Решите cos ² (α) + cos (α) = sin ² (α) на интервале 0 ° & leq; x <360 °

Я могу использовать триггерное тождество, чтобы получить квадратичный косинус:

cos ² (α) + cos (α) = sin ² (α)

cos ² (α) + cos (α) = 1 — cos ² (α)

2cos ² (α) + cos (α) — 1 = 0

(2cos (α) — 1) (cos (α) + 1) = 0

cos (α) = 1/2, cos (α) = –1

Первое тригонометрическое уравнение, cos (α) = 1/2, дает мне α = 60 ° и α = 300 °.Второе уравнение дает мне α = 180 °. Итак, мое полное решение:

Решить sin (β) = sin (2β) на интервале 0 ° & leq; β <360 °

Я могу использовать обозначение с двумя углами в правой части, а также переставлять и упрощать; тогда я фактор:

sin (β) = 2sin (β) cos (β)

sin (β) — 2sin (β) cos (β) = 0

sin (β) (1-2cos (β)) = 0

sin (β) = 0, cos (β) = 1/2

Синусоидальная волна (из первого триггерного уравнения) равна нулю при 0 °, 180 ° и 360 °.Но в исходном упражнении 360 ° не включены, поэтому последнее значение решения не учитывается в данном конкретном случае.

Косинус (из второго триггерного уравнения) равен 1/2 при 60 ° и, следовательно, также при 360 ° — 60 ° = 300 °. Итак, полное решение:

β = 0 °, 60 °, 180 °, 300 °

Решите sin ( x ) + cos ( x ) = 1 на интервале 0 ° & leq; x <360 °

Хм… Я действительно ничего здесь не вижу. Было бы неплохо, если бы одно из этих триггерных выражений было возведено в квадрат …

Хорошо, почему бы мне не возвести обе стороны в квадрат и посмотреть, что произойдет?

(sin ( x ) + cos ( x )) ² = (1) ²

sin ² ( x ) + 2sin ( x ) cos ( x ) + cos ² ( x ) = 1

[sin ² ( x + cos ² ( x )] + 2sin ( x ) cos ( x ) = 1

1 + 2sin ( x ) cos ( x ) = 1

2sin ( x ) cos ( x ) = 0

sin ( x ) cos ( x ) = 0

Ха; пойди и посчитай: я возведен в квадрат и получил то, с чем мог бы работать .Ницца!

Из последней строки выше либо синус равен нулю, либо косинус равен нулю, поэтому мое решение выглядит следующим образом:

x = 0 °, 90 °, 180 °, 270 °

Однако (и это важно!), Чтобы получить это решение, я построил квадрат, а возведение в квадрат — это «необратимый» процесс.

(Почему? Если вы возведете что-то в квадрат, вы не сможете просто извлечь квадратный корень, чтобы вернуться к тому, с чего начали, потому что возведение в квадрат могло где-то изменить знак.)

Итак, чтобы быть уверенным в своих результатах, мне нужно проверить свои ответы в исходном уравнении , чтобы убедиться, что я случайно не создал решения, которые на самом деле не учитываются. Подключив обратно, вижу:

sin (0 °) + cos (0 °) = 0 + 1 = 1

… поэтому решение « x = 0 °» работает

sin (90 °) + cos (90 °) = 1 + 0 = 1

…поэтому решение « x = 90 °» тоже работает

sin (180 °) + cos (180 °) = 0 + (–1) = –1

… ну ладно, значит « x = 180 °» НЕ работает

sin (270 °) + cos (270 °) = (–1) + 0 = –1

… так что « x = 270 °» тоже не работает,

Хорошо, что я проверил свои решения, потому что два из них на самом деле не работают.Они были созданы путем возведения в квадрат.

Мое фактическое решение :

Примечание: в приведенном выше примере я мог бы остановиться на этой строке:

… и использовал тождество с двойным углом для синуса, наоборот, вместо того, чтобы делить 2 в предпоследней строке в моих вычислениях. Ответ был бы таким же, но мне нужно было бы учесть интервал решения:

2sin ( x ) cos ( x ) = sin (2 x ) = 0

Тогда 2 x = 0 °, 180 °, 360 °, 540 ° и т. Д., И разделение 2 из x даст мне x = 0 °, 90 °, 180 °, 270 °, это то же самое почти решение, что и раньше.После выполнения необходимой проверки (из-за возведения в квадрат) и отбрасывания посторонних решений мой окончательный ответ был бы таким же, как и раньше.

Трюк с возведением в квадрат в последнем примере, приведенном выше, встречается нечасто, но если все остальное не работает, возможно, стоит попробовать. Имейте это в виду для следующего теста.

URL: https: // www.purplemath.com/modules/solvtrig.htm

PPT — Глава 5 Обратные тригонометрические функции; Тригонометрические уравнения и неравенства PowerPoint Presentation

Глава 5 Обратные тригонометрические функции; тригонометрические уравнения и неравенства 5.1 Обратный синус, косинус и тангенс Подход

5.1 Обратный синус, косинус и тангенс • Функция обратного синуса • Функция обратного косинуса • Функция обратного тангенса

Функция обратного синуса

Нахождение точного значения sin-1 x • Пример. Найдите точное значение sin-1 (√3 / 2) • Решение: y = sin-1 (√3 / 2) эквивалентно sin y = √3 / 2.Найдите значение y, которое находится между –p / 2 и p / 2 на единичной окружности. • Ответ — p / 3.

Функция обратного косинуса

Нахождение точного значения cos-1x • Пример: Найдите точное значение cos-1 ½. • Решение: • y = cos-1 ½ эквивалентно cos y = ½. Мы находим значение y на единичном круге между 0 и p, для которого это верно. • Ответ — p / 3.

Функция обратной касательной

Графики функций tan и tan-1

Нахождение точного значения tan-1 x • Пример: найти точное значение tan-1 (-1 / √3).• Решение: • Y = tan-1 (-1 / √3) эквивалентно tan y = -1 / √3. Найдите значение y на единичной окружности между –p / 2 и p / 2, для которого это верно. • Ответ –p / 6.

5.2 Функции обратного котангенса, секанса и косеканса • Определение функций обратного котангенса, секанса и косеканса • Расчет с помощью калькулятора

Домены для котангенса, секанса и косеканса

, Секанс и косеканс

Нахождение точного значения arccot (-1) • Пример: найдите точное значение arccot (-1) • Решение: • y = arccot (-1) эквивалентно cot у = -1.Найдите значение y на единичной окружности между 0 и p, при котором это верно. • Ответ: 3p / 4

Идентичности

5.3 Тригонометрические уравнения: алгебраический подход • Введение • Решение тригонометрических уравнений с использованием алгебраического подхода

Поиск уравнения • Решение простого синуса • все решения в единичном круге для sin x = 1 / √2. • Решение: • Используйте единичный круг, чтобы определить, что одно решение — x = p / 4.• Видно, что другая точка на окружности с желаемой высотой равна x = 3p / 4.

Предложения по решению тригонометрических уравнений

Точные решения с использованием факторинга • Пример: Найдите все решения в [0, 2p] для 2 sin2x + sin x = 0 • Решение: • 2 sin2x + sin x = 0 • sin x (2 sin x + 1) = 0 • sin x = 0 или sin x = -1/2 • Найдите эти значения на единичной окружности. • Решения: x = 0, p, 7p / 6 и 11p / 6.

Точные решения с использованием идентичностей и факторинга • Пример: найти все решения для sin 2x = sin x, 0  x  2p.• Решение: • sin 2x = sin x • 2 sin x cos x = sin x • 2 sin x cos x — sin x = 0 • sin x (2 cos x — 1) = 0 • sin x = 0 или cos x = ½ • Из единичного круга находим 4 решения: x = 0, p / 3, p и 5p / 3.

5.4 Тригонометрические уравнения и неравенства: Подход с использованием графического калькулятора • Решение тригонометрических уравнений с помощью графического калькулятора • Решение тригонометрических неравенств с использованием графического калькулятора

Решения с использованием графического калькулятора • Пример: (x / 2) и y2 = 0.2x — 0,5 больше [-4p, 4p]. • Используйте команду ПЕРЕСЕЧЕНИЕ, чтобы найти, что x = 5,1609 — это пересечение. • Используйте команду ZOOM, чтобы обнаружить, что в третьем квадранте нет пересечения.

Решение с использованием графического калькулятора • Пример: Найдите все действительные решения (с точностью до четырех знаков после запятой), чтобы tan (x / 2) = 5x — x2 по [0, 3p]. • График y = tan (x / 2) и y = 5x — x2 над 0X3p и -10Y10. • Используйте команду ПЕРЕСЕЧЕНИЕ, чтобы найти три решения: x = 0,0000, 2,8292, 5,1272

Система тригонометрических уравнений — Учебный материал для IIT JEE

В предыдущих разделах мы уже узнали, как решать тригонометрические уравнения с одной переменной.Но вы, должно быть, видели в газетах прошлого года различные вопросы, касающиеся более чем одной переменной. Есть несколько стандартных шаблонов вопросов по тригонометрическим уравнениям с более чем одной переменной, которые всегда задаются на большинстве конкурсных экзаменов.

Когда вы освоитесь и у вас будет прочный фундамент тригонометрических уравнений с одной переменной, эта тема не будет для вас очень сложной. Хотя не существует установленного способа решения всех проблем, но, пройдя различные возможные пути, вы наверняка сможете справиться с проблемами IIT JEE.

Пожалуйста, ознакомьтесь с перечисленными ниже приемами и стандартными шагами по решению таких проблем. Эти советы помогут решить большинство проблем:

(1) Если возможно, сократите уравнение в терминах какой-либо одной переменной, предпочтительно x. Затем решите уравнение, как раньше, в случае одной переменной.

(2) Попробуйте вывести линейные / алгебраические одновременные уравнения из данных тригонометрических уравнений и решить их как алгебраические совместные уравнения.

(3) Иногда от вас могут потребоваться определенные замены. Было бы полезно, если бы в системе было всего две тригонометрические функции.

Иллюстрация: Решите для общих x, y,

sin (x - y) = 2 sin x sin y, где x и y - два острых угла прямоугольного треугольника.

Решение: Поскольку дано, что x и y являются двумя острыми углами прямоугольного треугольника, мы делаем замену y = π / 2 - x в первом уравнении и преобразуем его следующим образом: -

sin (2x - π / 2) = 2 sin x sin (π / 2 - x)

⇒ - sin (π / 2 - 2x) = 2sin x cos x

⇒ –cos 2x = sin 2x

⇒ tan 2x = –1 = tan (-π / 4)

⇒ 2x = n π - π / 4, где n = 0, ± 1, ± 2, ………

или, x = nπ / 2 - π / 8, где n = 0, ± 1, ± 2, ………

y = nπ / 2 - 5π / 8, где n = 0, ± 1, ± 2, ………

Следовательно, решение равно {nπ / 2 + π / 8, 5π / 8 - πn / 2}.

Иллюстрация: Учитывая, что sin x (cos y + 2sin y) - cos x (2cos y - sin y) = 0, найдите значение tan (x + y).

Решение: sin x (cos y + 2sin y) - cos x (2cos y - sin y) = 0

Избавимся от скобок:

sin x * cos y + 2sin x * sin y - 2cos x * cos y + cos x * sin y = 0

Переставьте термины:

sin x * cos y + cos x * sin y - 2cos x * cos y + 2sin x * sin y = 0

Фактор -2 из 3-го и 4-го семестра:

sin x * cos y + cos x * sin y - 2 (cos x * cos y - sin x * sin y) = 0

Используйте тождество sin (A + B) = sin A * cos B + cos A * sin B, чтобы переписать первые два члена:

sin (x + y) - 2 (cos x * cos y - sin x * sin y) = 0

Используйте тождество cos (A + B) = cos A * cos B - sinA * sin B, чтобы переписать два члена в круглых скобках.Следовательно, уравнение сводится к
грех (х + у) - 2 * соз (х + у) = 0

Разделить на cos (x + y)

{sin (x + y)} / {cos (x + y)} - {2 * cos (x + y)} / {cos (x + y)} = 0

Используя тождество tan A = sin A / cos A, чтобы переписать начальные члены и после упрощения, мы получаем

загар (x + y) - 2 = 0

, что дает tan (x + y) = 2.

Посмотрите это видео, чтобы получить дополнительную информацию

Иллюстрация: Решите систему уравнений

sin ² x + sin ² y = 1/2.

х - у = 4π / 3

Решение: Преобразуем первое уравнение системы -

1/2 (1 - cos 2x) + 1/2 (1 - cos 2y) = ½

cos 2x + cos 2y = 1 и

2 cos (x + y). Cos (x - y) = 1

Отсюда ясно, что система -

cos (x + y) cos (x - y) = 1/2 …… (1)

x - y = 4π / 3 …… (2)

имеет то же решение, что и исходная система, т.е.е. системы эквивалентны.

Итак, из уравнений (1) и (2) имеем

cos (x + y) cos (4π / 3) = 1/2 или cos (x + y) = –1

х + у = 2nπ ± π

Следовательно, у нас есть два линейных уравнения относительно x и y

х + у = 2n π ± π, n ∈ I

х - у = 4π / 3

x = nπ + 2π / 3 ± π / 2 …… (а)

Принимая знак + ve (а)

х = (п +7/6) π

= kπ, k = (n +7/6) и y = kπ - 4π / 3

Принимая отрицательный знак (а)

х = nπ + π / 6

y = nπ + π / 6-4π / 3

= п π - 7π / 6.

Общее решение системы уравнений дается выражениями (kπ, kπ - 4π / 3) и (nπ + π / 6, nπ -7π / 2), где k = n + 7/6, n ∈ I

Итак, это решения исходной системы.

Примечание: В предыдущих примерах мы записали отношения между неизвестными x, и набор решений системы был выражен только одним интегральным параметром, например n, k и т. д. Но в практических приложениях иногда может потребоваться выразить общее решение в терминах двух интегральных параметров при решении системы уравнений с двумя переменными.

Часто вы обнаружите, что введение новой переменной эффективно помогает уравнению. Введение новых переменных может применяться в тех случаях, когда система содержит только две тригонометрические функции, или может быть приведена к такому виду. Давайте посмотрим на иллюстрацию.

Иллюстрация: Решите систему

sin x + cos y = 1 ……… (1)
cos 2x - cos 2y = 1 ……… (2)
Решение: Мы можем преобразовать уравнение (2), положив cos 2x = 1 - 2sin ² x и cos 2y = 2 cos ² y –1
cos 2x - cos 2y = 1 - 2 sin ² x + 1 - 2 cos ² y = 1
⇒ sin ² x + cos ² y = 1/2
и следовательно наша система
sin x + cos y = 1 ……… (3)
sin ² x + cos ² y = 1/2 ……… (4)
что эквивалентно исходной системе.
Для простоты положим sin x = y, cos y = v [note → u ∈ [–1, 1] и v ∈ [–1, 1] и, следовательно,
u + v = 1 ………… (5)
u ² + v ² = 1/2 ………… (6)

, решая (5) и (6), получаем,

и = грех х = 1/2

v = cos y = ½

Следовательно, общее решение данной системы уравнений дается

x = mπ + (–1) m π / 6, m ∈ I

y = 2nπ + π / 3, n ∈ I

Решение различных пар, образованных из этих значений x и y, является в точности набором всего решения исходной системы.

Примечание: Как мы можем решить уравнение, если члены на двух сторонах (левая и правая) уравнения имеют разную природу, например тригонометрический и алгебраический?

Задачи этого типа могут быть решены с помощью метода неравенства. Этот метод используется для проверки того, имеет ли уравнение какое-либо реальное решение или нет, рекомендуется выполнить следующие шаги.

Шаг I: Пусть y = каждая сторона уравнения, т.е.разбейте уравнение на две части.

Шаг II: Найдите неравенство для y, взяв левую часть уравнения, а также правую часть уравнения. Если существует какое-либо значение y, удовлетворяющее обоим неравенствам, тогда будет реальное решение, в противном случае реального решения не будет.

Иллюстрация: Покажите, что уравнение

2 cos ² (x / 2) sin ² x = x ² + x ^-2 для 0

Решение: Это проблема, при которой LHS находится в тригонометрической форме, а RHS - в алгебраической. Поэтому воспользуемся методом неравенства.

Пусть y = 2 cos ² (x / 2) sin ² x ……… (1)

и y = x ² + x ^-2 ……… (2)

из (1), y = 2 cos ² x / 2 sin ² x

= (1 + cos x) sin ² x

= (число <2) × (число <1)

<2 [? для 0

и.е. у <2 ……… (3)

из (2), y = x ² + x ^-2

A.M. > Г.

(x ² + x ^-2) / 2 ≥ √ (x ². X ^-2)

x ² + x ²> 2

т.е. y> 2 ……… (4)

Ни одно значение y не может быть получено одновременно, удовлетворяющее (3) и (4), поскольку y не может быть больше или меньше 2 одновременно.

⇒ реального решения уравнения не существует.

Примечание: Некоторые проблемы можно решить с помощью графиков. Номер точки пересечения равен номеру решения.

Иллюстрация: Найдите количество корней уравнения tan x = x + 1 между –π / 2 и 2 π.

Решение: Опять же, это проблема тригонометрической формы на LHS и алгебраической формы на RHS.

Это можно решить, построив график

Пусть y = tan x

у = х + 1

Количество точек пересечения равно двум, что означает, что количество решений равно 2.
Примечание: на обеих иллюстрациях мы использовали два разных способа решения. Мы выбираем графический метод, если отслеживать легче, в противном случае мы выбираем метод неравенства.

Обзор важных моментов

Поскольку тригонометрические функции являются периодическими функциями, решения тригонометрических уравнений могут быть обобщены с помощью периодичности тригонометрических функций. Решение, состоящее из всех возможных решений тригонометрического уравнения, называется его общим решением.

Мы используем следующие формулы для решения тригонометрических уравнений:

sin θ = sinα и cosθ = cosα ⇒ θ = 2nπ + α
sinθ = 0 ⇒ θ = nπ
cosθ = 0 ⇒ θ = (2n + 1) π / 2
tanθ = 0 ⇒ θ = nπ
sinθ = sinα ⇒ θ = nπ + (–1) nα, где α ∈ [–π / 2, π / 2]
cosθ = cosα ⇒ θ = 2nπ ± α, где α ∈ [0, π]
tanθ = tanα ⇒ θ = nπ + α, где α ∈ (–π / 2, π / 2)
sin2θ = sin2α, cos2θ = cos2α, tan2θ = tan2α ⇒ θ = nπ ± α
sinθ = 1 ⇒ θ = (4n + 1) π / 2
sinθ = –1 ⇒ θ = (4n — 1) π / 2
sinθ = –1 ⇒ θ = (2n + 1) π / 2
| sinθ | = 1 ⇒ θ = 2nπ
cosθ = 1 ⇒ θ = (2n + 1) π
| cosθ | = 1 ⇒ θ = nπ

Примечание: Везде в этой главе n принимается как целое число, если не указано иное.

Следует дать общее решение, если только решение не требуется в указанном интервале или диапазоне.

За главное значение угла принимается

α. Численно наименьший угол называется главным значением.

Примечания:

При решении тригонометрического уравнения следует избегать возведения уравнения в квадрат на любом этапе, насколько это возможно, и, если это неизбежно, проверьте решение на наличие посторонних значений.

Никогда не отменяйте условия, содержащие неизвестные термины с двух сторон, которые есть в продукте.Это может привести к потере подлинного решения.

Иногда решение уравнения может привести к более чем одному множеству решений. Эти наборы решений могут быть непересекающимися, перекрывающимися или наложенными. Если наборы решений перекрываются, мы пытаемся переписать решение таким образом, чтобы общие решения включались только в один из наборов решений. Если одно из набора решений оказывается подмножеством другого, чем мы опускаем подмножество из окончательного набора решений.

Иллюстрация: Число решений пары уравнений 2 sin2θ — cos 2θ = 0 и 2cos2θ — 3 sin θ = 0 в интервале [0, 2π] равно

(а) 0

(б) 1

(в) 2

(г) 4

Решение: Учитывая первое уравнение 2 sin2θ — cos 2θ = 0

Это дает sin2θ = ¼

Также второе уравнение: 2cos2θ — 3 sin θ = 0

Следовательно, это означает 2cos2θ = 3 sin θ.

, что дает sin θ = 1/2.

Следовательно, два решения существуют в интервале [0, 2π].

Связанные ресурсы

Чтобы узнать больше, купите учебные материалы по Тригонометрия , включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также найдите дополнительные учебные материалы по математике здесь .

Особенности курса

731 Видео-лекции
Примечания к редакции
Документы за предыдущий год
Интеллектуальная карта
Планировщик учебы
Решения NCERT
Обсуждение Форум
Тестовая бумага с видео-решением

Примеры решения простейших тригонометрических неравенств

Часть 2.

Примеры решения простейших тригонометрических неравенств

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Проверьте себя

Простейшие тригонометрические уравнения и неравенства(10 класс)

Оставьте свой комментарий

Простейшие тригонометрические уравнения и неравенства. Подведение итогов

Здравствуйте!

Лекция 18. Простейшие тригонометрические неравенства. — Студопедия

Формулы для решения простейших тригонометрических уравнений

здесь же они собраны все вместе =>

Уравнение вида <img decoding="async" src="/800/600/https/egemaximum.ru/wp-content/ql-cache/quicklatex.com-1ccfc9b659e27fd7ed936f663b894b6c_l3.svg" alt="\LARGE cos\:x=a" title="Rendered by QuickLaTeX.com" />

§3 Решение простейших тригонометрических уравнений. Алгебра и начала математического анализа, 10 класс: уроки, тесты, задания.

математических упражнений и математических задач: тригонометрические уравнения и неравенства

Решение простых (и средней сложности) триггерных уравнений

Purplemath

MathHelp.com

Решить sin ( x ) + 2 = 3 в интервале 0 ° & leq; x <360 °

Решить tan 2 (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 °

Решить в интервале 0 ° & leq; x <360 °

Решить sin 2 (θ) — sin (θ) = 2 на интервале 0 & leq; θ <2π

Решите cos 2 (α) + cos (α) = sin 2 (α) на интервале 0 ° & leq; x <360 °

Решить sin (β) = sin (2β) на интервале 0 ° & leq; β <360 °

Решите sin ( x ) + cos ( x ) = 1 на интервале 0 ° & leq; x <360 °

PPT — Глава 5 Обратные тригонометрические функции; Тригонометрические уравнения и неравенства PowerPoint Presentation

Система тригонометрических уравнений — Учебный материал для IIT JEE

Обзор важных моментов

Связанные ресурсы

Особенности курса

Добавить комментарий Отменить ответ

Уравнение вида $\LARGE cos\:x=a$

Решить tan ² (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 °

Решить sin ² (θ) — sin (θ) = 2 на интервале 0 & leq; θ <2π

Решите cos ² (α) + cos (α) = sin ² (α) на интервале 0 ° & leq; x <360 °