Двойные интегралы в полярных координатах: теория и примеры
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ:
.
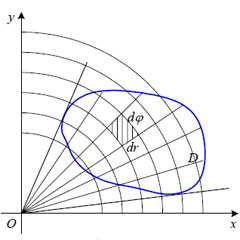
Что представляет собой элемент площади dxdy,
выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D
на участки линиями окружности r = const и лучами
φ = const. Рассмотрим один частичный участок
(заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы
dxdy = rdrdφ,
а двойной интеграл в полярных координатах записывается так:
.
Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ, а внутренний — по радиусу r.
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D.
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D, область ограничена линией r = r(φ).
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:
.
Случай второй
Полюс O находится на границе области интегрирования D, ограниченного линией r = r(φ), но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:
.
Случай третий
Полюс O находится на границе области интегрирования D, ограниченного линией r = r(φ), и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы α и β. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:
.
Случай четвёртый
Полюс O находится вне области интегрирования D.
Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы α и β, а область D ограничивают линии r = r1(φ) и r = r2(φ). Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β, а внутреннего интеграла — r1(φ) и r2(φ). Переход к повторным интегралам осуществляется следующим образом:
.
Пример 1. Вычислить в полярных координатах двойной интеграл
,
Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.

Выразим подынтегральную функцию как функцию полярных переменных:
.
Данные в условии линии, ограничивающие D, приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:
.
Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x², а сверху — прямой y = 1. Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части.
Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области
полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1,
в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и
параболы: (1; 1) и (−1; 1). В
первой точке полярный угол составляет ,
во второй точке он составляет .
Поэтому в первой области
Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1: или . Найдём уравнение параболы y = x² в полярной системе координат:
Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:

Пример 3. Вычислить в полярных координатах двойной интеграл
,
где область D ограничена линией окружности .
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a. В этом легко убедиться, преобразовав её уравнение следующим образом:.
Линия окружности касается оси Oy, поэтому полярный угол в области интегрирования меняется от до . Подставим и в уравнение окружности и получим
Напишем подынтегральную функцию в полярных координатах:
.
Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:

В полученном выражении второе слагаемое равно нулю, так как и sinπ, и sin(−π
Пример 5. Вычислить в полярных координатах двойной интеграл
,
где область D ограничена линиями и .
Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:
.
Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:
.
В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:

Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
Двойной интеграл в полярных координатах
Алгоритм вычисления двойных интегралов при переходе к полярным координатам детально приведен как в настоящей статье, так и предыдущих публикациях с теорией. Для перехода к полярным координатам нужно найти якобиан, который несколько раз здесь повторим. Дальше сами уравнения кривых, которые ограничивают область интегрирования следует также перевести в полярные координаты. В теории все хорошо описано и выглядит понятным, однако на практике во многих студентов возникают трудности и немало вопросов, поэтому внимательно пересмотрите приведенные дальше решения.
Пример 2.1 Вычислить двойной интеграл, используя полярные координаты:
Решение: Построим область интегрирования ограниченную кривыми
-3≤x≤3
Эти кривые записываем из пределов интегрирования, внимательно пересмотрите в каких пределах изменяются «икс» и «игрек».
Нижний предел по оси «игреков» приведем к каноническому виду
x2+y2=9.
Получили уравнение круга с центром в точке O(0;0) и радиусом 3 (нижняя половина).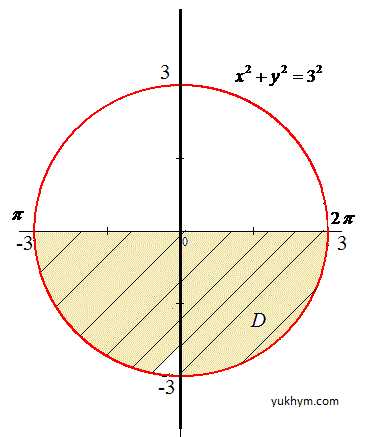
Перейдем к полярной системе координат с помощью превращения координат:
найдем якобиан перехода:
Найдем подынтегральную функцию в полярных координатах:
Внимательно пересмотрите формулы двойного синуса, косинуса и им подобных.
Они достаточно часто встречаются при упрощении подынтегральных функций, все сделано умышленно для того, чтобы Вы без проблем могли интегрировать.
Запишем пределы интегрирования в полярной системе координат:
0≤r≤3, π≤φ≤2 π.
Вычислим двойной интеграл:
Поскольку переменные разделены, то интегрирование не тяжелое, достаточно воспользоваться табличными интегралами и подставить пределы.
Пример 2.2 Найти двойной интеграл, используя полярные координаты:
Решение: Из интеграла выписываем область интегрирования
0≤x≤1
Она ограничена прямыми, которые совпадают с-осями координат
, y2=12-x2,x2+y2=12 — дуга круга в I четверти.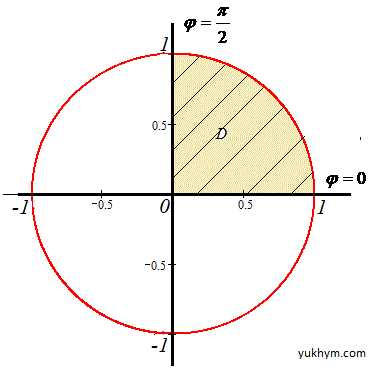
Получили круг с центром в точке O(0;0) и радиусом r=1 (верхняя половина).
Якобиан перехода к ПСК I=r.
Запишем подынтегральную функцию в полярной системе координат:
Для круговых областей не трудно записать пределы интегрирования при переходе к полярной системе координат:
0≤r≤1, 0≤φ≤π/2.
Находим двойной интеграл: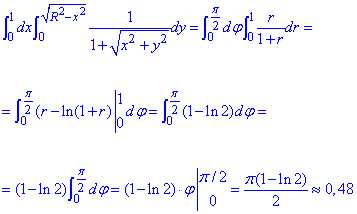
В результате интегрирования в ответе получили выражение которое содержит логарифм двойки, и число Пи.
Пример 2.3 Вычислить значение двойного интеграла, перейдя к полярным координатам:
Решение: Выпишем область интегрирования, которая ограничена кривыми
— 2≤x≤2,
По «игреку» имеем ограничения ветками круга , y2=4-x2, x2+y2=22 с центром в начале координат O(0;0) и радиусом 2.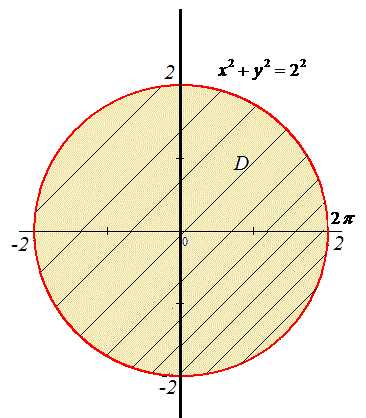
Перейдем к полярной системе координат:
якобиан переходу: I=r.
С учетом формул перехода подынтегральная функция в полярной системе координат примет вид корневой зависимости:
Пределы интегрирования в ПСК следующие:
0≤r≤2, 0≤φ≤2π.
Переходим от двойного интеграла в декартовых координатах к двойному в полярных координатах и находим его значение:
Интеграл равен 16π/3.
Пример 2.4 Найти двойной интеграл, используя полярные координаты:
D: {x2+y2=π2/9; x2+y2=π2/4}.
Решение: Выпишем область интегрирования ограниченную кривыми
Первая кривая x2+y2=π2/9 — круг с центром в начале координат O(0;0) и радиусом π/3;
второе уравнение описывает x2+y2=π2/4 — больший круг с центром в той же точке O(0;0) и радиусом π/2.
Область между кругами образует кольцо, по которому выполняем интегрирование.
Найдем подынтегральную функцию в полярной СК:
Круги в полярной системе координат можно задать радиусами и центрами:
, отсюда r= π/3;
, имеем r= π/2.
Пределы интегрирования в полярной системе координат следующие:
π/3≤r≤π/2, 0≤φ≤2π.
Выполняем вычисление двойного интеграла: 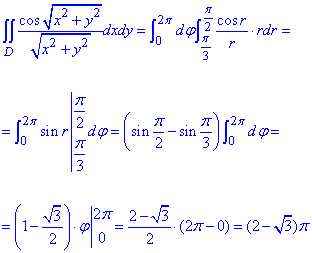
Переход к полярной СК значительно упрощает вычисление интегралов для круговых и кольцевых областей.
Пример 2.5 Найти двойной интеграл, используя полярные координаты:
D: {x2+y2— 2y=0; x2+y2— 4y=0}.
Решение: На основе предыдущих примеров делаем вывод, что область интегрирования, ограниченная x2+(y-1)2=1 — кругом с центром в точке O(0;1) и радиусом 1;
Вторая кривая x2+(y-2)2=2- круг с центром в точке O(0;2) и радиусом 2.
Графически они формируют следующую область интегрирования. 
Переходим к полярной системе координат с помощью якобиана перехода I=r.
Дальше записываем кривые в полярной системе координат:
расставляем корректные пределы интегрирования:
2sin(φ)≤r≤4sin(φ), 0≤φ≤2π.
Вычисляем двойной интеграл в полярной СК: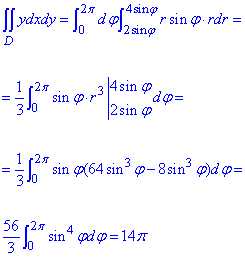
Нахождение двойных интегралов не тяжелое занятие, если часто самостоятельно практиковать и иметь перед собой таблицу основных интегралов.
Все остальные манипуляции не тяжелые и их Вы повсюду в математике выполняете.
Дальше рассмотрим еще несколько примеров на вычисление двойных интегралов в полярных координатах.
yukhym.com
Переход к полярным координатам в двойном интеграле.
Важнейшимчастным случаем криволинейных координат являются полярные координаты (r,φ). Они связаны с прямоугольными координатами формулами: , . Якобиан преобразования в этом случае , а формула перехода к полярным координатам в двойном интеграле имеет вид:
(4)
Переходить к полярным координатам удобно в тех случаях, когда область интегрирования есть круг, кольцо или их часть, а так же в случае, когда подынтегральная функция имеет вид . В полярных координатах выражение . Границей круга является окружность и ее уравнение в полярных координатах принимает вид: r=R. Тогда область D — круг в полярной системе координат на плоскости Оrφ переходит в прямоугольную область Ω, которая задается неравенствами : (рис.17а,б).
Интегрирование в полярных координатах проводится по координатным линиям r=const и φ
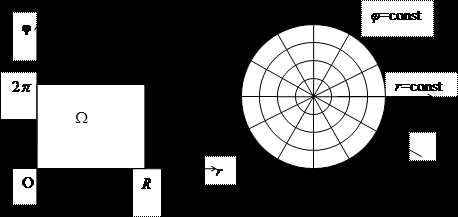 | |||
Рис.17а Рис.17б Рис.18
Пусть область D расположена между лучами φ=α и φ=β, где α< β, и ограничена линиями и , где и любой луч, выходящий из полюса φ=const ( ) пересекает ее границу не более чем в
двух точках (простая область относительно r) (рис.19).Тогда двойной интеграл сводится к повторному по формуле:
Рис.19 Рис.20
(5)
Пусть область D расположена между окружностями r=а и r=b, где а< b и ограничена линиями и , где и любая окружность радиуса r=const ( ) пересекает границу области не более чем в двух точках (правильная относительно φ) (рис.20). В этом случае двойной интеграл сводится к повторному по формуле:
6)
Пример 1. Вычислить двойной интеграл , где область D ограничена окружностью .
Решение: Как уже говорилось выше, если интегрирование ведется по кругу, то уравнение его границы в полярных координатах имеет вид r=1, а на плоскости Оrφ область Ω является прямоугольником . Осталось записать в полярных координатах подынтегральную функцию: . Вычисляем интеграл
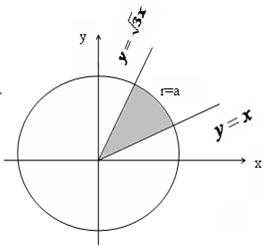 Пример 2. Вычислить , если область D ограничена окружностью , лежащей в первой четверти, и прямыми y=x и .
Пример 2. Вычислить , если область D ограничена окружностью , лежащей в первой четверти, и прямыми y=x и .
Решение: Область D изображена на рис.21. Переведем ее границы в полярные координаты: уравнение окружности имеет вид r=a , а отрезки прямых y=x являются лучами и . Проводя лучи φ=const , определяем, что координата r изменяется от 0 до а. Тогда по формуле (5) получаем:
Рис.21
Пример 3. В двойном интеграле перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена кривой .
Решение: Чтобы построить область D, приведем уравнение кривой к каноническому виду, для чего выделяем полный квадрат по переменной х: , . Получаем уравнение окружности с центром на оси Ох в точке х=а, у=0, радиуса а, при этом окружность касается оси Оу (рис.22а,б).
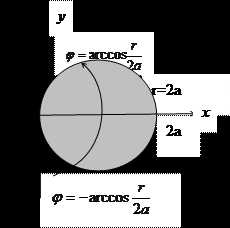 | |||
Рис.22а Рис.22б
Переведем границу области D в полярные координаты, для этого удобнее воспользоваться уравнением окружности в виде : или . Область D находится между лучами и и проводя
лучи при , определяем, что координата r изменяется от 0 в начале координат до значения радиуса на окружности, т.е. до значения (рис.22а). Тогда по формуле (5) расставляем пределы интегрирования:
Чтобы расставить пределы интегрирования в другом порядке, определим границы изменения координаты r. Для этого проведем координатные линии r=const, пересекающие область D, и определим окружности, которые касаются нашей области. Очевидно, что это будут линии r=0 и r=2а, так что r изменяется в пределах от 0 до а (рис.22б).
Для нахождения границ изменения переменной φ уравнение окружности разрешим относительно φ: или . Для нижней ветви окружности берется знак «-», а для верхней ветви – знак «+». Теперь по координатным линиям r=const, которые пересекают область D, определяем границы изменения φ: от значения на нижней ветви окружности до значения на верхней ветви окружности. В результате по формуле (6) получаем:
Пример 4. В двойном интеграле перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена линиями
Решение: Кривая является уравнением окружности с центром в точке (0,1): . При выбирается верхняя половина круга – это и будет область D . Переведем границы области в полярные координаты, при этом уравнение окружности имеет вид . Если из него выразить φ, получаем для правой ветки окружности и — для левой. Прямая y=1 в полярных координатах имеет уравнение или и для отрезков прямых, лежащих в первой и во второй четверти соответственно. Нанесем координатные линии φ=const, откуда определяем, что область D расположена между лучами и , а радиус изменяется от значения на отрезке прямой y=1 до значения на дуге окружности (рис.23а). Тогда получаем:
.
Рис.23а Рис.23б
Проведем линии r=const и определяем, что область заключена между координатными линиями r=1 и r=2, а координатная линия проходит через точки (±1,1), в которых пересекаются границы области — окружность и прямая (рис.23б). Поэтому D необходимо разбить на две простые области относительно φ: и и пределы интегрирования в двойном интеграле расставляются так:
Замечание: В некоторых случаях, если область интегрирования в двойном интеграле ограничена окружностью , удобнее делать замену . При такой замене осуществляется параллельный перенос системы координат в центр окружности, а якобиан преобразования при этом не изменяется, т.е. J=r (предлагается убедиться в этом самостоятельно). В частности, если в примере 4 ввести замену , то уравнение окружности преобразуется к виду r=1, а область интегрирования Ω в координатах Оrφ становится прямоугольной: .
Пример 5. Вычислить интеграл , где область D – лежащая в первой четверти часть эллиптического кольца .
Замечание: В случае, когда область интегрирования в двойном интеграле является эллипс или его часть, то вводят обобщенные полярные или
эллиптические координаты . При этом J=abr (проверить самостоятельно), а выражение преобразуется в выражение .
Решение: Перейдем к эллиптическим координатам, при этом границы эллиптического кольца принимают вид r=1 и r=2, а вся область расположена между лучами φ=0 и . Поэтому интеграл вычисляем следующим образом:
infopedia.su
18. Замена переменных в двойном интеграле
Пусть функции осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости на область S плоскости . Тогда существует обратное непрерывно дифференцируемое отображение , области S на область P, если якобиан преобразования
=.
Величины U и V можно рассматривать как прямоугольные координаты для точек области P и в то же время как Криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат U и V сохраняет постоянное значение, образуют Координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть есть дифференцируемое преобразование области P из плоскости на область S Из плоскости . Тогда справедливо равенство
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
(2.6)
Преобразуют полярные координаты точки в декартовы координаты этой точки и переводят область (или область ) на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам:
Фиксируя в последних формулах И, получим координатные линии из разных семейств: окружность с центром в точке И луч, исходящий из точки .
Якобиан преобразования
И формула (2.5) принимает вид:
(2.7)
Рекомендация. К полярным координатам целесообразно переходить, когда в подынтегральное выражение или в уравнения границы области интегрирования входит комбинация .
В некоторых случаях при вычислении двойного интеграла удобно перейти от декартовых координат к Эллиптическим полярным Координатам по формулам
, (2.8)
— постоянные, . Тогда
, (2.9)
Пример 6. Записать в полярной системе координат область S , заданную в декартовой системе координат неравенством (круг радиуса R с центром в точке ).
Ñ Перейдем от декартовых координат X, Y к полярным по формулам , . Подставим X и Y в исходное неравенство, получим: или . На координату j дополнительных ограничений не накладывается, поэтому (или ).
В полярной системе координат круг записывается неравенствами: . #
Пример 7. Записать в полярной системе координат область S — часть круга, ограниченную линиями , , (), — постоянные, .
Ñ Изобразим область S (рис. 14.9). Запишем заданные линии в полярных координатах, которые связаны с декартовыми формулами , : 1)Þ ;
2) Þ, ;
3)Þ.
Область переходит в область
.
В полярной системе координат заданная область определяется системой неравенств: . #
Пример 8. Вычислить двойной интеграл , S — множество точек, удовлетворяющих неравенству .
Ñ Границей области является линия или — окружность радиуса 2 с центром в точке (Рис. 14.10).
Рис. 14.10
Наличие в уравнении границы комбинации наводит на мысль, что для вычисления двойного интеграла удобно перейти к полярным координатам по формулам , , . Уравнение границы переходит в уравнение или . Отсюда r=0 (соответствует полюсу O) и — уравнение окружности. Так как всегда (по смыслу r), то из следует , отсюда получаем (этот же результат можно усмотреть из рисунка). Итак, в полярных координатах область интегрирования есть . Тогда по формуле (2.7)
. #
Пример 9. Вычислить , где .
Ñ Область D ограничена линиями: – эллипс с полуосями A и B, – эллипс с полуосями и , Y=0 – прямая (ось Ox), – прямая (рис. 14.11).
Рис.14.11
Анализ границы области указывает на целесообразность перехода к Эллиптическим полярным координатам по формулам (2.8), (2.9): , . Уравнения границы области в координатах будут: 1), 2) , 3) ,
4) . Итак, область интегрирования в координатах есть
. Тогда
. #
Задачи для самостоятельного решения
Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования в порядке: внешнее – по j, внутреннее — по r:
27. D – область, ограниченная окружностями , и прямыми , .
28. D — область, являющаяся общей частью двух кругов и .
29. D — меньший из двух сегментов, на которые прямая рассекает круг .
30. D — внутренняя часть правой петли лемнискаты Бернулли .
31. D:.
32. D: .Указание. Перейти к эллиптическим полярным координатам.
33. D — область, ограниченная линией . Указание. Перейти к эллиптическим полярным координатам.
34. . 35. . 36. .
С помощью перехода к полярным координатам вычислить интегралы:
37. . 38. .
39. . 40. , D — часть кольца ,
, . 41. .
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42. .
43. — область, ограниченная линией .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Лекции кратные интегралы, двойной интеграл 2
Скачать с Depositfiles
Двойной интеграл в полярных координатах.
В полярных координатах точка M однозначно определяется полярным углом φ (0 ≤ φ <2π или –π < φ π) и полярным радиусом r (r≥0). Для начала координат O радиус r = 0, а полярный угол не определен.
Пусть декартова полуось Ox совпадает с полярным лучом.
Декартовы координаты выражаются через полярные по формулам
(14)
Полярные координаты выражаются через декартовы:
. (15)

Пусть область D в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10).
Якобиан в данном случае равен:
Тогда интеграл (2) преобразуется в двойной интеграл в полярных координатах по формуле
(16)
Двойной интеграл (16) вычисляется переходом к повторному интегралу в полярных координатах. Пусть область Dr имеет вид
Dr = { (r, φ ) : α ≤ φ ≤ β, r1(φ) ≤ r≤ r2 (φ)},
где лучи φ = α и φ = β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
(17)
Замечание. При расстановке пределов интегрирования в повторном интеграле нужно учесть, что изменение полярного угла определяется поворотом луча, исходящего из начала O вокруг него против хода часовой стрелки, а изменение полярного радиуса определяется движением точки вдоль луча в сторону его возрастания.
Рисунок 5
Примеры. 1). Расставить пределы интегрирования в повторном интеграле в полярных координатах
где Dr полукруг из рисунка 5.
Решение. Все точки этого полукруга будут охвачены, если луч Оl будет поворачиваться от  до φ = 0 против хода часовой стрелки. Значит,
до φ = 0 против хода часовой стрелки. Значит,  . Пусть теперь луч Оl имеет полярный угол
. Пусть теперь луч Оl имеет полярный угол  . Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус r изменяется от 0 до координаты r=2cosφ точки M. Значит,
. Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус r изменяется от 0 до координаты r=2cosφ точки M. Значит,
0 ≤ r ≤ 2cos φ. Таким образом, Dr = {(r, φ):  , 0 ≤ r ≤ 2 cos φ} . Следовательно,
, 0 ≤ r ≤ 2 cos φ} . Следовательно,
2) Вычислить 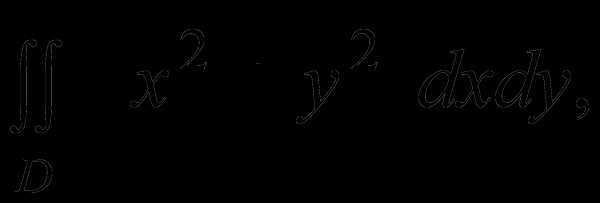 где D = {(x, y): x2 + y22x ≤ 0, y≤ 0} .
где D = {(x, y): x2 + y22x ≤ 0, y≤ 0} .
Решение. Подставим в уравнение окружности x2 +y22x = 0 полярные координаты (9) и преобразуем: r22 rcosφ = 0  r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤ 0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим:
r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤ 0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим:
Вычисление площади фигуры.
Площадь плоской фигуры вычисляется по формуле 
Пример. Вычислить площадь фигуры, ограниченной линиями
Решение. Данная фигура D расположена в вертикальной полосе 0 ≤ x ≤ 2, а в ней ограничена снизу параболой y = x2, сверху прямой y = 4 (рис. 6). По формуле (5) имеем
.
Вычисление объема цилиндрического тела.
Если f (x,y) ≥ 0 в ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по формуле V = 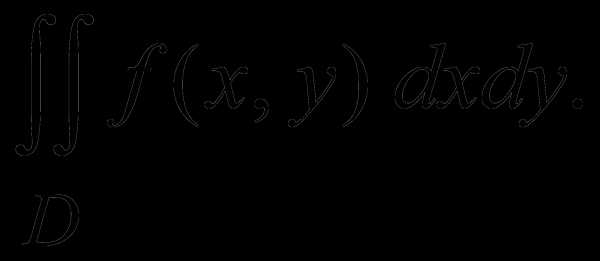
Пример. Найти объем тела, ограниченного поверхностями
z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. x2 + y2 = 4 это круговой цилиндр радиуса 2, ось которого совпадает с Оy. z = x2 + y2 параболоид, который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4 . z=0 координатная плоскость xOy. Таким образом, тело ограничено сверху параболоидом
z = x2 + y2 , снизу кругом D , с боков цилиндрической поверхностью x2 + y2 = 4. Так как данное тело цилиндрическое и
z = x2 + y2 ≥ 0, то для вычисления его объема можно использовать формулу
где D ={ (x, y) : x2 + y2 ≤ 4, z = 0 } круг в плоскости xOy. Для вычисления этого интеграла перейдем к полярным координатам. При этом круг Dпреобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }. По формуле (17) получим


greleon.ru
Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах
Преобразование
двойного интеграла от прямоугольных
координат 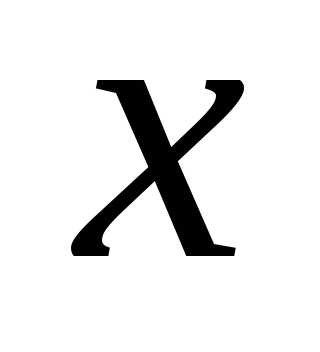 ,
, к полярным координатам
к полярным координатам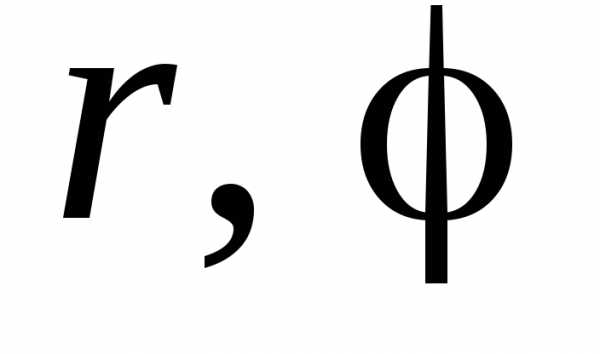 ,
связанных с прямоугольными координатами
соотношениями,,
осуществляется по формуле
,
связанных с прямоугольными координатами
соотношениями,,
осуществляется по формуле
.
Если
область интегрирования  ограничена двумя лучами
ограничена двумя лучами ,
, (
(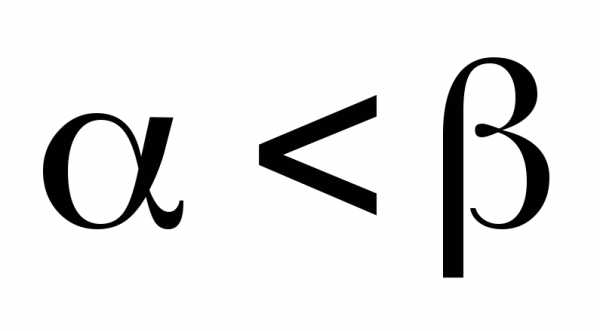 ),
выходящими из полюса, и двумя кривыми
),
выходящими из полюса, и двумя кривыми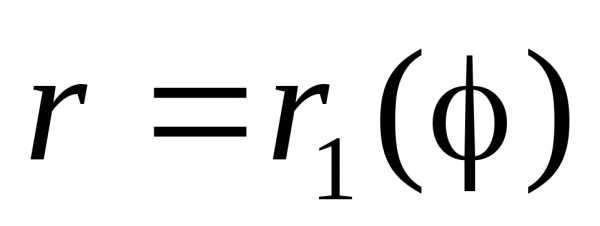 и
и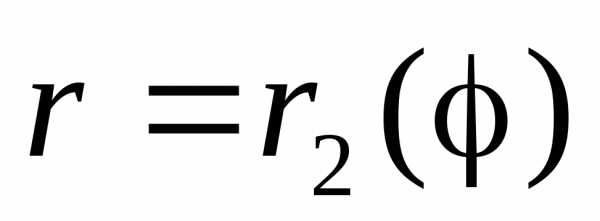 ,
то двойной интеграл вычисляют по формуле
,
то двойной интеграл вычисляют по формуле
.
Пример
1.3. Вычислить
площадь фигуры, ограниченной данными
линиями:
,, ,
, .
.
Решение. Для
вычисления площади области  воспользуемся формулой:
воспользуемся формулой: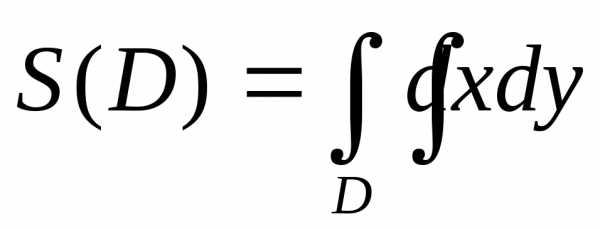 .
.
рис. 1.5 | Изобразим
область , , , . Перейдем к полярным координатам: , . В
полярной системе координат область |

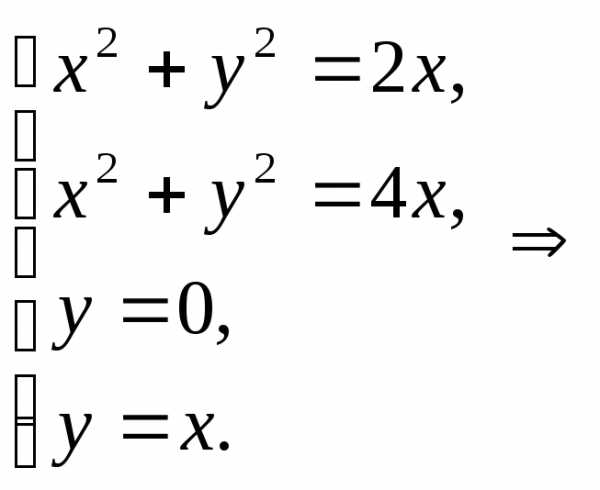
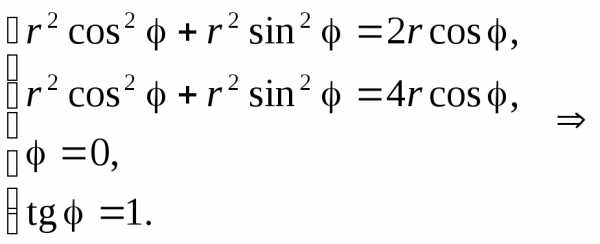

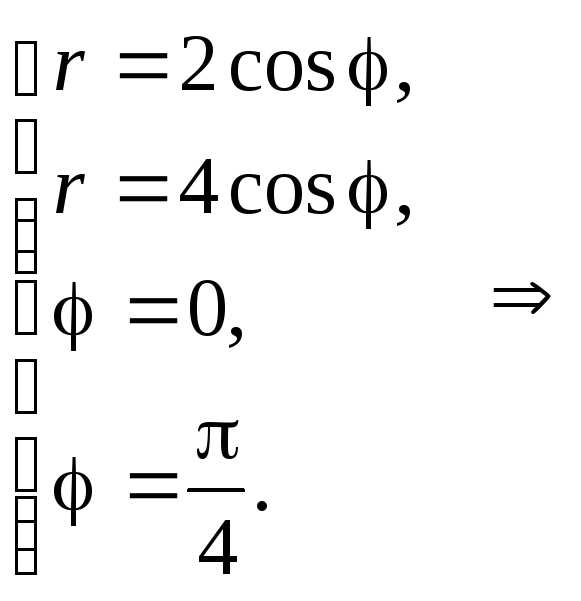
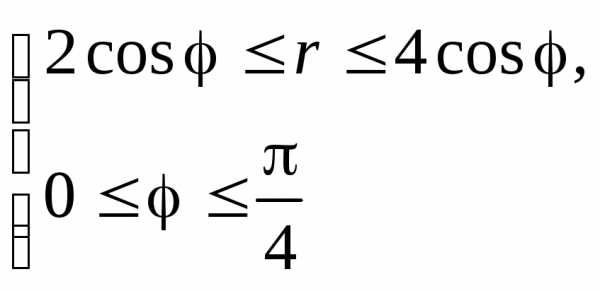 .
.
.
1.2. Тройные интегралы
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.
В декартовых координатах тройной интеграл обычно записывают так:
.
Если
,
то тройной интеграл по области численно равен объему тела
численно равен объему тела :
:
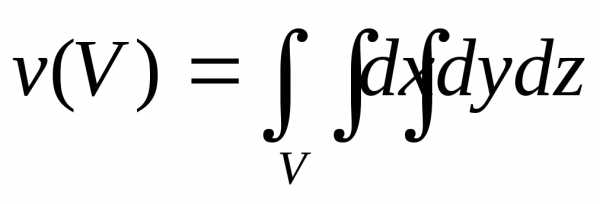 .
.
Вычисление тройного интеграла
Пусть
область интегрирования
ограничена снизу и сверху соответственно
однозначными непрерывными поверхностями,,
причем проекция области на координатную плоскость
на координатную плоскость есть плоская область
есть плоская область (рис. 1.6).
(рис. 1.6).
.
Пример
1.4. Вычислить
,
где —
тело, ограниченное плоскостями:
—
тело, ограниченное плоскостями:
рис. 1.7 | , Решение. Областью интегрирования является
пирамида (рис. 1.7). Проекция области
|
рис. 1.8 | Расставляя
пределы интегрирования для треугольника |
.
Тройной интеграл в цилиндрических координатах
При
переходе от декартовых координат  к цилиндрическим координатам
к цилиндрическим координатам (рис. 1.9), связанных с
(рис. 1.9), связанных с соотношениями,,
соотношениями,, ,
причем
,
причем
рис. 1.9 | , ,, тройной интеграл преобразуется: . Пример
1.5. Вычислить
объем тела, ограниченного поверхностями:
,, Решение. Искомый
объем тела |
рис. 1.10 | Областью
интегрирования является часть цилиндра,
ограниченного снизу плоскостью Перейдем к цилиндрическим координатам. ,,. Приаппликаты точек, удовлетворяют неравенству или в цилиндрических координатах: . |
Область  ,
ограниченная кривой,
примет вид,
или
,
ограниченная кривой,
примет вид,
или ,
при этом полярный угол .
В итоге имеем
,
при этом полярный угол .
В итоге имеем
.
2. Элементы теории поля
Напомним предварительно способы вычисления криволинейных и поверхностных интегралов.
Вычисление
криволинейного интеграла по координатам
от функций, определенных на кривой  ,
сводится к вычислению определенного
интеграла вида
,
сводится к вычислению определенного
интеграла вида
, | (2.1) |
если
кривая  задана параметрическии
задана параметрическии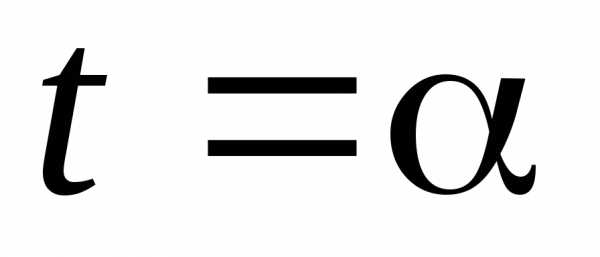 соответствует начальной точке кривой
соответствует начальной точке кривой ,
а
,
а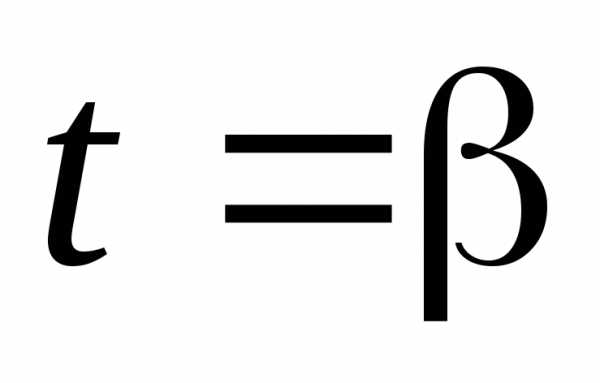 — ее конечной точке.
— ее конечной точке.
Вычисление
поверхностного интеграла от функции
,
определенной на двусторонней поверхности ,
сводится к вычислению двойного интеграла,
например, вида
,
сводится к вычислению двойного интеграла,
например, вида
, | (2.2) |
если
поверхность  ,
заданная уравнением,
однозначно проецируется на плоскость
,
заданная уравнением,
однозначно проецируется на плоскость в область
в область .
Здесь
.
Здесь — угол между единичным вектором нормали
— угол между единичным вектором нормали к поверхности
к поверхности и осью
и осью :
:
| (2.3) |
Требуемая
условиями задачи сторона поверхности  определяется выбором соответствующего
знака в формуле (2.3).
определяется выбором соответствующего
знака в формуле (2.3).
Определение
2.1. Векторным полем  называется
векторная функция точки
называется
векторная функция точки 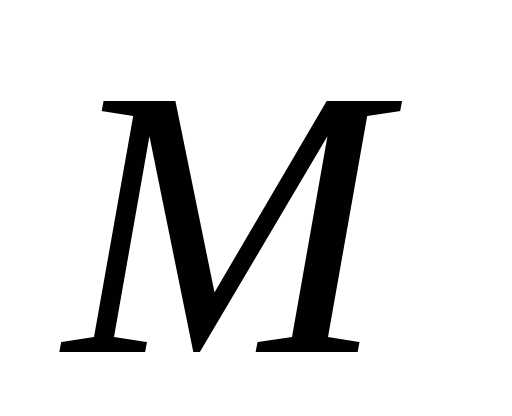 вместе с областью ее определения:
вместе с областью ее определения:
.
Векторное
поле 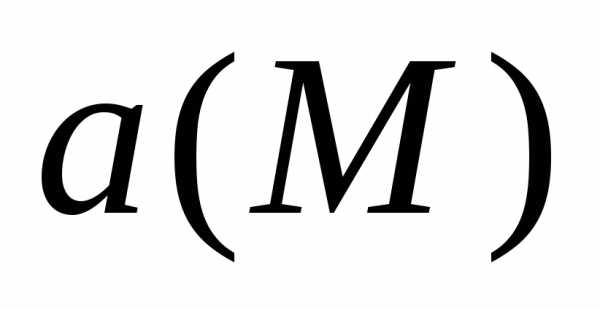 характеризуется скалярной величиной
–дивергенцией:
характеризуется скалярной величиной
–дивергенцией:
(2.4) |
и векторной величиной – ротором:
. | (2.5) |
Определение
2.2. Потоком векторного
поля  через
поверхность
через
поверхность  называется
поверхностный интеграл:
называется
поверхностный интеграл:
, | (2.6) |
где 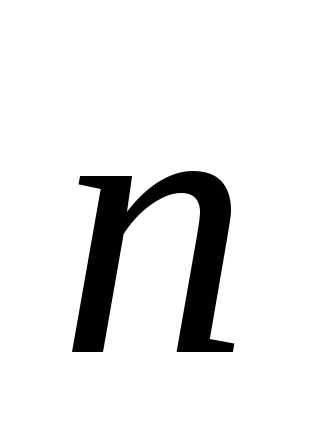 —
единичный вектор нормали к выбранной
стороне поверхности
—
единичный вектор нормали к выбранной
стороне поверхности ,
а
,
а — скалярное произведение векторов
— скалярное произведение векторов и
и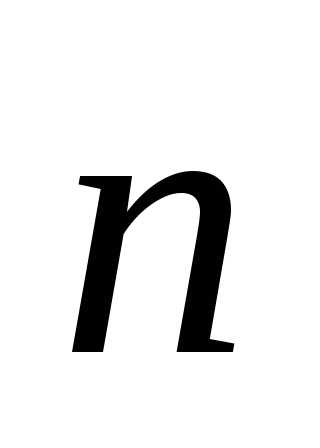 .
.
Определение 2.3. Циркуляцией векторного поля
по замкнутой кривой называется криволинейный интеграл
, | (2.7) |
где .
Формула
Остроградского-Гаусса устанавливает связь между потоком
векторного поля  через замкнутую поверхность
через замкнутую поверхность  и дивергенцией поля:
и дивергенцией поля:
, | (2.8) |
где  — тело, ограниченное поверхностью
— тело, ограниченное поверхностью  .
.
Формула
Стокса устанавливает связь между циркуляцией
векторного поля  и его ротором:
и его ротором:
, | (2.9) |
где  — поверхность, ограниченная замкнутым
контуром
— поверхность, ограниченная замкнутым
контуром  ,
а
,
а 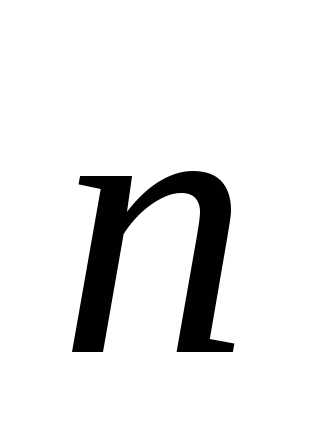 — единичный вектор нормали к этой
поверхности. Направление нормали должно
быть согласовано с направлением обхода
контура
— единичный вектор нормали к этой
поверхности. Направление нормали должно
быть согласовано с направлением обхода
контура  .
.
Пример 2.1. Вычислить поверхностный интеграл
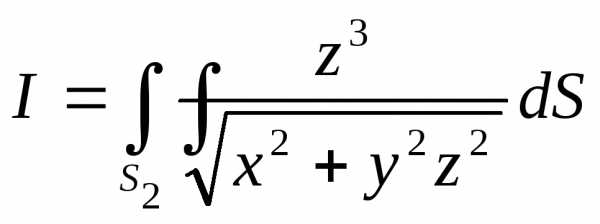 ,
,
где 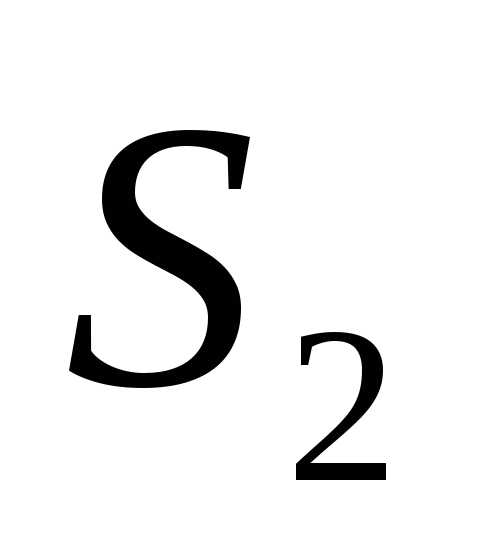 — внешняя часть конуса(),
отсекаемая плоскостью
— внешняя часть конуса(),
отсекаемая плоскостью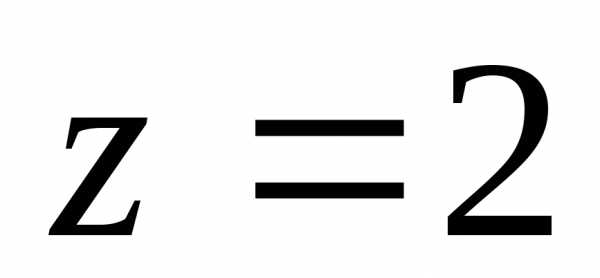 (рис 2.1).
(рис 2.1).
Решение. Поверхность 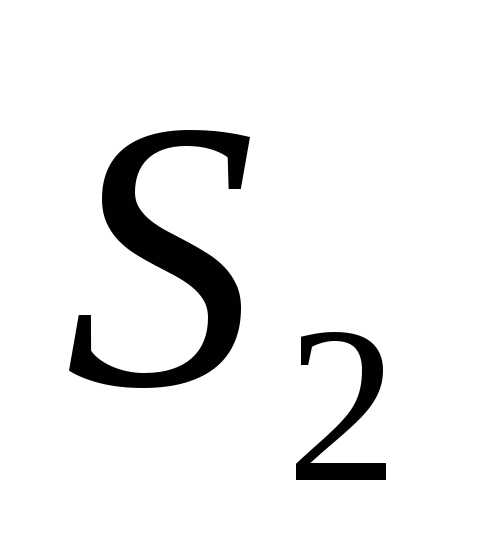 однозначно проецируется в область
однозначно проецируется в область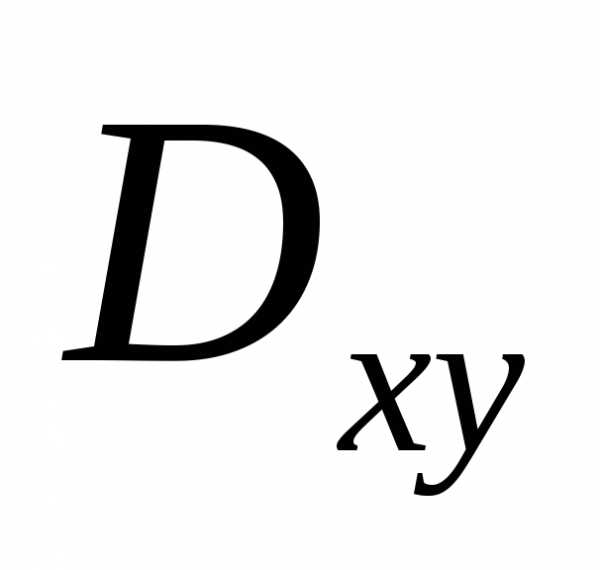 плоскости
плоскости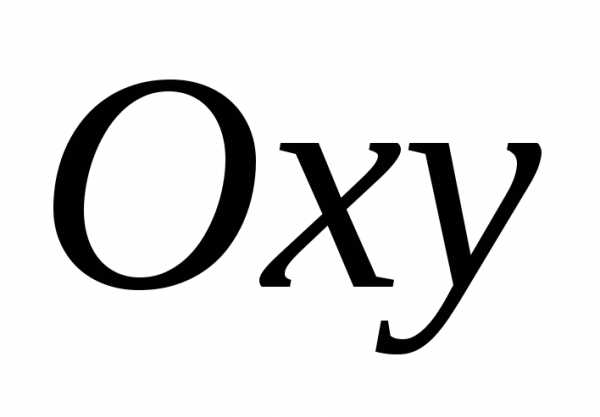 ,
и интеграл вычисляется по формуле (2.2).
,
и интеграл вычисляется по формуле (2.2).
.
Область 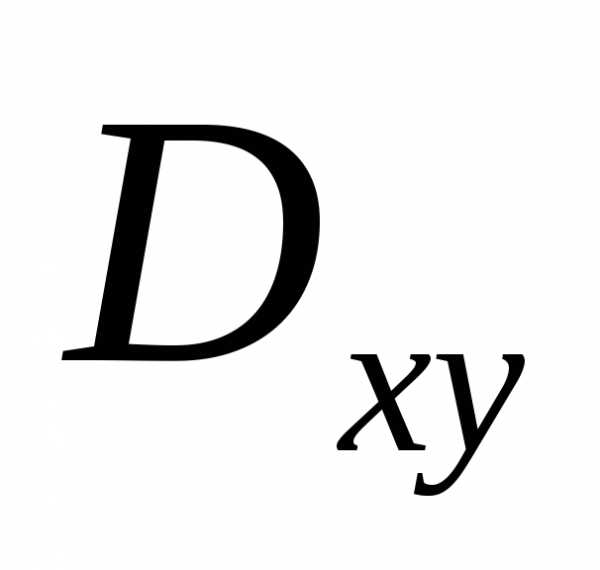 есть круг.
Поэтому в последнем интеграле переходим
к полярным координатам, при этом,:
есть круг.
Поэтому в последнем интеграле переходим
к полярным координатам, при этом,:
.
Пример 2.2. Найти дивергенцию и ротор векторного поля .
Решение. По формуле (2.4) получаем
.
Ротор данного векторного поля находим по формуле (2.5)
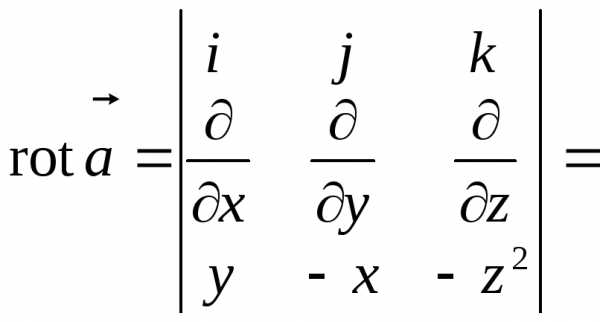
.
Пример
2.3. Найти поток векторного поля
через часть плоскости :,
расположенную в первом октанте (нормаль
образует острый угол с осью
:,
расположенную в первом октанте (нормаль
образует острый угол с осью ).
).
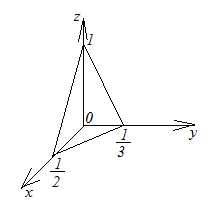
рис. 2.3 | Решение. В силу формулы (2.6) . Изобразим
часть плоскости (рис. 2.3). Вектор нормали к плоскости имеет координаты: , единичный вектор нормали |
рис. 2.4 | . . , , откуда, следовательно, |
,
где 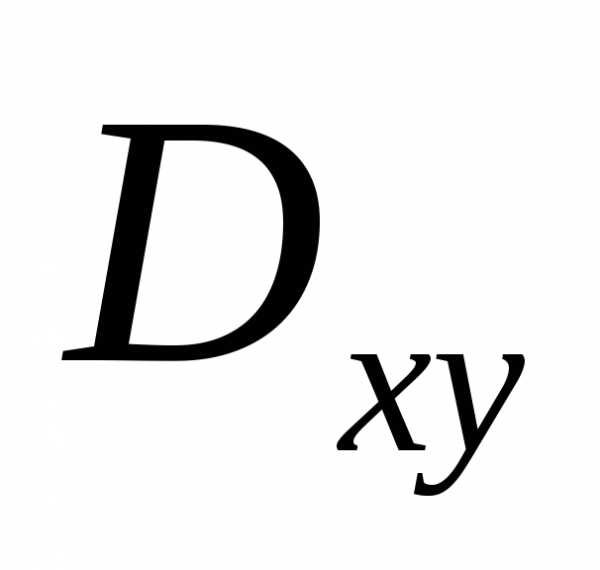 — проекция плоскости
— проекция плоскости на
на (рис. 2.4).
(рис. 2.4).
.
Пример
2.4. Вычислить
поток векторного поля
через замкнутую поверхность ,
образованную плоскостью
,
образованную плоскостью и частью конуса(
и частью конуса( )
(рис. 2.2).
)
(рис. 2.2).
Решение. Воспользуемся формулой Остроградского-Гаусса (2.8)
.
Найдем
дивергенцию векторного поля  по формуле (2.4):
по формуле (2.4):
.
,
где 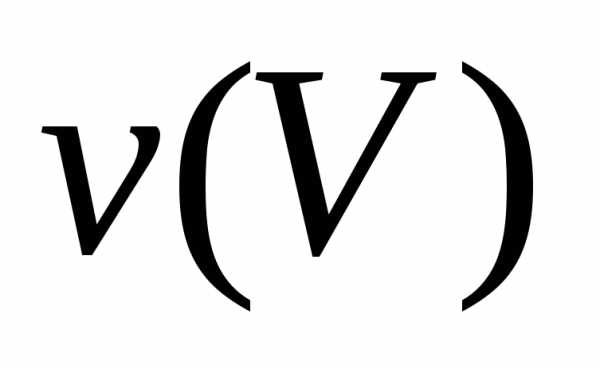 — объем конуса, по которому ведется
интегрирование. Воспользуемся известной
формулой для вычисления объема конуса
— объем конуса, по которому ведется
интегрирование. Воспользуемся известной
формулой для вычисления объема конуса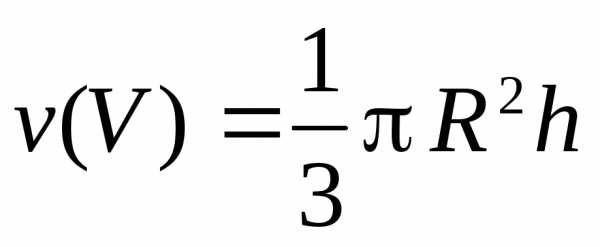 (
(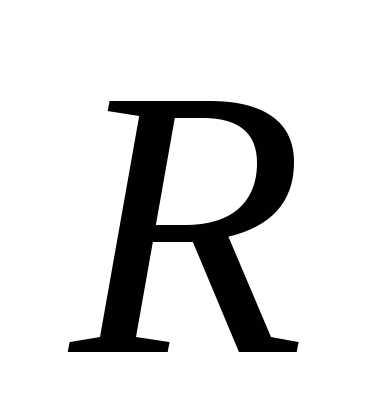 — радиус основания конуса,
— радиус основания конуса,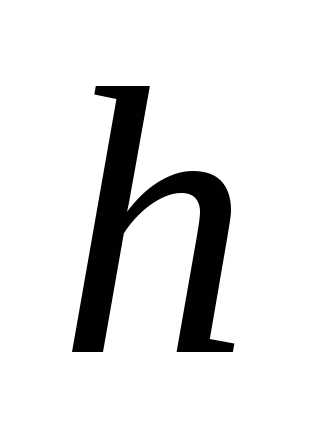 — его высота). В нашем случае получаем.
Окончательно получаем
— его высота). В нашем случае получаем.
Окончательно получаем
.
Пример
2.5. Вычислить
циркуляцию векторного поля
по контуру  ,
образованному пересечением поверхностей
,
образованному пересечением поверхностей  и(
и(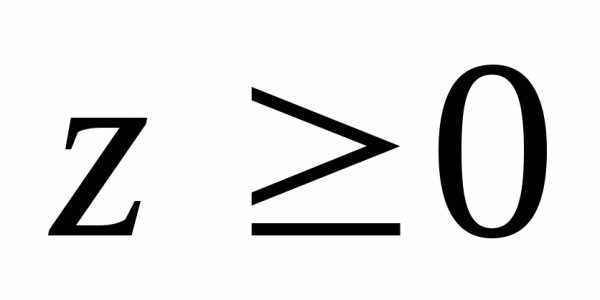 ).
Проверить результат по формуле Стокса.
).
Проверить результат по формуле Стокса.
Решение. Пересечением
указанных поверхностей является
окружность
, (рис. 2.1). Направление обхода выбирается
обычно так, чтобы ограниченная им область
оставалась слева. Запишем параметрические
уравнения контура
(рис. 2.1). Направление обхода выбирается
обычно так, чтобы ограниченная им область
оставалась слева. Запишем параметрические
уравнения контура  :
:
| (2.10) |
причем
параметр  изменяется от
изменяется от до
до .
По формуле (2.7) с учетом (2.1) и (2.10) получаем
.
По формуле (2.7) с учетом (2.1) и (2.10) получаем
.
Применим
теперь формулу Стокса (2.9). В качестве
поверхности  ,
натянутой на контур
,
натянутой на контур  ,
можно взять часть плоскости
,
можно взять часть плоскости  .
Направление нормали
.
Направление нормали к
этой поверхности согласуется с
направлением обхода контура
к
этой поверхности согласуется с
направлением обхода контура  .
Ротор данного векторного поля вычислен
в примере 2.2:
.
Поэтому искомая циркуляция
.
Ротор данного векторного поля вычислен
в примере 2.2:
.
Поэтому искомая циркуляция
,
где  — площадь области
— площадь области .
. — круг радиуса
— круг радиуса ,
откуда
,
откуда
.
В итоге получаем
.
studfiles.net
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам / Двойной интеграл / 3dstroyproekt.ru
Смысл этих задач — научиться быстро определять параметры $a,\;b,\;\varphi _1 (x),\;\varphi _2 (x),\;c,\;d,\;\psi _1 (y),\;\psi _2 (y)$ { в декартовых координатах } и $\varphi _0 ,\;\varphi _2 ,\;r_1 (\varphi ),\;r_2 (\varphi )$ { в полярных координатах } , необходимые для перехода от двойного интеграла к повторному.
Примеры:
Пример 1
Пусть область $D=\left[{ x\leqslant 0,\;y\leqslant 0,\;x^2+y^2\leqslant 4 }\right]\cup \left[{ x\geqslant 0,\;x^2+y^2\leqslant -2y }\right]$. Представить двойной интеграл по области $\mathbf { \textit { D } } $ в виде повторных. Перейти к полярным координатам. Решение:
Область изображена на рисунке. Для левой части $D-2\leqslant x\leqslant 0;\quad -\sqrt { 4-x^2 } \leqslant y\leqslant 0$; для правой — $0\leqslant x\leqslant 1,\;-1-\sqrt { 1-x^2 } \leqslant y\leqslant -1+\sqrt { 1-x^2 } $ уравнение правой полуокружности после выделения полных квадратов принимает вид $x^2+(y+1)^2=1$, поэтому
$$ I=\iint\limits_D { f(x,y)dxdy } =\int\limits_ { -2 } ^0 { dx\int\limits_ { -\sqrt { 4-x^2 } } ^0 { f(x,y)dy } } +\int\limits_0^1 { dx\int\limits_ { -1-\sqrt { 1-x^2 } } ^ { -1+\sqrt { 1-x^2 } } { f(x,y)dy } } . $$
$\mathbf { \textit { D } } $ можно также oписать неравенствами $-2\leqslant y\leqslant 0,\;-\sqrt { 4-y^2 } \leqslant x\leqslant \sqrt { -2y-y^2 } $, поэтому $I=\iint\limits_D { f(x,y)dxdy } =\int\limits_ { -2 } ^0 { dy\int\limits_ { -\sqrt { 4-y^2 } } ^ { \sqrt { -2y-y^2 } } { f(x,y)dx } } $. В полярных координатах уравнение левой четверти окружности имеет вид $r=2$ для $\pi \leqslant \varphi \leqslant 3\pi /2$ { можно взять и отрезок $-\pi \leqslant \varphi \leqslant -\pi /2$ } , правой полуокружности $r=-2\sin \varphi $ для $3\pi /2\leqslant \varphi \leqslant 2\pi $ { можно взять и отрезок $-\pi /2\leqslant \varphi \leqslant 0$ } , поэтому $I=\iint\limits_D { f(x,y)dxdy } =\iint\limits_ { D_ { r,\varphi } } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\int\limits_\pi ^ { 3\pi /2 } { d\varphi \int\limits_0^2 { f(r\cos \varphi ,r\sin \varphi )rdr } } + \\ + \int\limits_ { 3\pi /2 } ^ { 2\pi } { d\varphi \int\limits_0^ { -2\sin \varphi } { f(r\cos \varphi ,r\sin \varphi )rdr } } $
Пример 2
Изменить порядок интегрирования, перейти к полярным координатам. 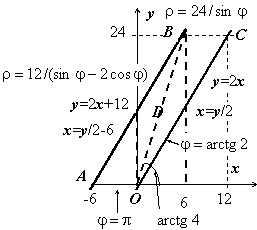 $I=\int\limits_ { -6 } ^0 { dx\int\limits_0^ { 2x+12 } { f(x,y)dy } } +\int\limits_0^6 { dx\int\limits_ { 2x } ^ { 2x+12 } { f(x,y)dy } } +\int\limits_6^ { 12 } { dx\int\limits_ { 2x } ^ { 24 } { f(x,y)dy } } $
$I=\int\limits_ { -6 } ^0 { dx\int\limits_0^ { 2x+12 } { f(x,y)dy } } +\int\limits_0^6 { dx\int\limits_ { 2x } ^ { 2x+12 } { f(x,y)dy } } +\int\limits_6^ { 12 } { dx\int\limits_ { 2x } ^ { 24 } { f(x,y)dy } } $
Решение:
Область $\mathbf { \textit { D } } $ — объединение трёх подобластей: $D=\left[{ -6\leqslant x\leqslant 0,\;0\leqslant y\leqslant 2x+12 }\right]\cup \left[{ 0\leqslant x\leqslant 6,\;2x\leqslant y\leqslant 2x+12 }\right]\cup\left[{ 6\leqslant x\leqslant 12,\;2x\leqslant y\leqslant 24 }\right]\cup $
На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. $\mathbf { \textit { D } } $ можно представить в виде $D=\left[{ 0\leqslant y\leqslant 24,\;y/2-6\leqslant x\leqslant y/2 }\right]$, поэтому $I=\int\limits_0^ { 24 } { dy\int\limits_ { y/2-6 } ^ { y/2 } { f(x,y)dx } } $. В полярных координатах $\mathbf { \textit { D } } $ представляется как объединение двух треугольников $\mathbf { \textit { OCB } } $и $\mathbf { \textit { OBA } } $. Уравнение прямой $\mathbf { \textit { ОС } } $: $\varphi =arctg2$ { можно получить и формально, перейдя к полярным координатам в её уравнении: $y=2x\Rightarrow \quad r\sin \varphi =2r\cos \varphi \Rightarrow tg\varphi =2$ } , прямой $\mathbf { \textit { ОВ } } $: $\varphi =arctg4$, прямой $\mathbf { \textit { СВ } } $: $y=24\Rightarrow r\sin \varphi =24\Rightarrow \quad r=24/\sin \varphi $, прямой $\mathbf { \textit { ОА } } $: $\varphi =\pi $, прямой $\mathbf { \textit { АВ } } $: $y=2x+12\Rightarrow r\sin \varphi =2r\cos \varphi +12\Rightarrow \quad r=\frac { 12 } { \sin \varphi -2\cos \varphi } $.
В результате $I=\iint\limits_D { f(x,y)dxdy } =\iint\limits_ { D_ { r,\varphi } } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\\ \quad =\int\limits_ { arctg2 } ^ { arctg4 } { d\varphi \int\limits_0^ { 24/\sin \varphi } { f(r\cos \varphi ,r\sin \varphi )rdr } } +\int\limits_ { arctg4 } ^\pi { d\varphi \int\limits_0^ { 12/(\sin \varphi -2\cos \varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdr } } $.
Пример 3
Вычислить двойной интеграл $\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } $, где область $D$ – квадрат со сторонами $x=0$, $x=1$, $y=2$, $y=3$. В повторном интеграле внутренний интеграл вначале вычислить по переменной $y$, а внешний – по $x$. Вычислить этот же интеграл, изменив порядок интегрирования.
Решение:
Вначале изобразим область интегрирования. Запишем заданный двойной интеграл через повторные: $\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 0 } ^ { 1 } { dx } \int\limits_ { 2 } ^ { 3 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dy } $.
Внутреннее { первое } интегрирование будем выполнять по переменной $y$ { при этом считаем, что $x$ – константа } , а внешнее { второе } – по переменной $x$:
$$\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 0 } ^ { 1 } { dx } \int\limits_ { 2 } ^ { 3 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dy } =$$
$$=\int\limits_ { 0 } ^ { 1 } { dx } \left[ 6x\int\limits_ { 2 } ^ { 3 } { { { y } ^ { 2 } } dy } -12 { { x } ^ { 2 } } \int\limits_ { 2 } ^ { 3 } { ydy }\right]=\int\limits_ { 0 } ^ { 1 } { \left( 6x\cdot \left. \frac { { { y } ^ { 3 } } } { 3 }\right|_ { 2 } ^ { 3 } -12 { { x } ^ { 2 } } \cdot \left. \frac { { { y } ^ { 2 } } } { 2 }\right|_ { 2 } ^ { 3 }\right)dx } =$$
$$=\int\limits_ { 0 } ^ { 1 } { \left[ 2x\left( { { 3 } ^ { 3 } } — { { 2 } ^ { 3 } }\right)-6 { { x } ^ { 2 } } \left( { { 3 } ^ { 2 } } — { { 2 } ^ { 2 } }\right) \right]dx } =\int\limits_ { 0 } ^ { 1 } { \left( 38x-30 { { x } ^ { 2 } }\right)dx } =$$
$$=\int\limits_ { 0 } ^ { 1 } { 38xdx } -\int\limits_ { 0 } ^ { 1 } { 30 { { x } ^ { 2 } } dx } =38\int\limits_ { 0 } ^ { 1 } { xdx } -30\int\limits_ { 0 } ^ { 1 } { { { x } ^ { 2 } } dx } =38\cdot \left. \frac { { { x } ^ { 2 } } } { 2 }\right|_ { 0 } ^ { 1 } -30\cdot \left. \frac { { { x } ^ { 3 } } } { 3 }\right|_ { 0 } ^ { 1 } =$$
$$=19\left( { { 1 } ^ { 2 } } — { { 0 } ^ { 2 } }\right)-10\left( { { 1 } ^ { 3 } } — { { 0 } ^ { 3 } }\right)=19-10=9$$
Вычислим теперь заданный по условию двойной интеграл, сменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$ { считая, что $y$ есть постоянной } , а внешнее – по переменной $y$:
$$\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 2 } ^ { 3 } { dy } \int\limits_ { 0 } ^ { 1 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dx } =$$
$$=\int\limits_ { 2 } ^ { 3 } { \left[ 6 { { y } ^ { 2 } } \int\limits_ { 0 } ^ { 1 } { xdx } -12y\int\limits_ { 0 } ^ { 1 } { { { x } ^ { 2 } } dx }\right]dy } =\int\limits_ { 2 } ^ { 3 } { \left[ 6 { { y } ^ { 2 } } \cdot \left. \frac { { { x } ^ { 2 } } } { 2 }\right|_ { 0 } ^ { 1 } -12y\cdot \left. \frac { { { x } ^ { 3 } } } { 3 }\right|_ { 0 } ^ { 1 }\right]dy } =$$
$$=\int\limits_ { 2 } ^ { 3 } { \left( 3 { { y } ^ { 2 } } -4y \right)dy } =\left. \left( 3\cdot \frac { { { y } ^ { 3 } } } { 3 } -4\cdot \frac { { { y } ^ { 2 } } } { 2 }\right) \right|_ { 2 } ^ { 3 } =27-8-2\left( 9-4 \right)=19-10=9$$
Пример 4
Вычислить двойной интеграл $\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } $, если область $D$ ограничена линиями $y= { { x } ^ { 2 } } $, $x=2$, $y=2x-1$. Вычислить этот же интеграл, изменив порядок интегрирования.
Решение:
Строим заданную область $D$. Вначале внутреннее интегрирование будем проводить по переменной $y$, а внешнее – по $x$: $$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { a } ^ { b } { dx } \int\limits_ { { { \phi } _ { 1 } } \left( x \right) } ^ { { { \phi } _ { 2 } } \left( x \right) } { \left( { { x } ^ { 2 } } +2y \right)dy } $$
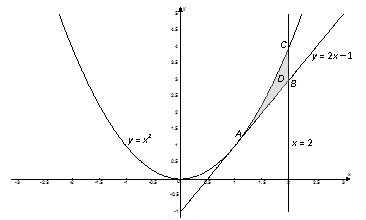
Контур области $D$ пересекается любой прямой, параллельной оси ординат, в двух точках.
Найдем пределы интегрирования. Переменная $x$ изменяется от абсциссы точки $A$ к абсциссе точек $B$ и $C$. Координаты точки $A$ найдем как координаты точки пересечения графиков функций $y= { { x } ^ { 2 } } $ и $y=2x-1$:
$$\left[ \begin { matrix } y= { { x } ^ { 2 } } , \\ y=2x-1 \\ \end { matrix }\right.\Rightarrow { { x } ^ { 2 } } =2x-1\Rightarrow { { x } ^ { 2 } } -2x+1=0\Rightarrow { { \left( x-1 \right) } ^ { 2 } } =0\Rightarrow { { x } _ { A } } =1$$
Так как точки $B$ и $C$ лежать на прямой $x=2$, то $ { { x } _ { B } } = { { x } _ { C } } =2$. Итак, $1\le x\le 2$. Далее на отрезке $\left[ 1;\ 2 \right]$ выбираем произвольную точку $x$, через нее проводим прямую, параллельную оси $Oy$, и на этой прямой рассмотрим отрезок $KL$, принадлежащий области $D$.
Область $D$ ограничена снизу прямой $y=2x-1$, а сверху – веткой параболы $y= { { x } ^ { 2 } } $. Переменная $y$ изменяется в заданной области $D$ от ее значения $2x-1$ на нижней части контура $ABC$ до ее значения $ { { x } ^ { 2 } } $ на верхней части этого контура.
Замечание. Уравнения линий, ограничивающих контур, должны быть разрешены относительно той переменной, относительно которой находится внутренний интеграл.
Таким образом, $2x-1\le y\le { { x } ^ { 2 } } $, а тогда область $D$ задается следующими неравенствами:
$$D:\left[ \begin { matrix } 1\le x\le 2, \\ 2x-1\le y\le { { x } ^ { 2 } } . \\ \end { matrix }\right.$$
Итак,
$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { 1 } ^ { 2 } { dx } \int\limits_ { 2x-1 } ^ { { { x } ^ { 2 } } } { \left( { { x } ^ { 2 } } +2y \right)dy } =\int\limits_ { 1 } ^ { 2 } { dx } \left. \left( { { x } ^ { 2 } } y+ { { y } ^ { 2 } }\right) \right|_ { 2x-1 } ^ { { { x } ^ { 2 } } } =$$
$$=\int\limits_ { 1 } ^ { 2 } { \left[ { { x } ^ { 2 } } \cdot { { x } ^ { 2 } } + { { \left( { { x } ^ { 2 } }\right) } ^ { 2 } } -\left( { { x } ^ { 2 } } \cdot \left( 2x-1 \right)+ { { \left( 2x-1 \right) } ^ { 2 } }\right) \right]dx } =$$
$$=\int\limits_ { 1 } ^ { 2 } { \left( 2 { { x } ^ { 4 } } -2 { { x } ^ { 3 } } -3 { { x } ^ { 2 } } +4x-1 \right)dx } =\left. \left( \frac { 2 { { x } ^ { 5 } } } { 5 } -\frac { { { x } ^ { 4 } } } { 2 } — { { x } ^ { 3 } } +2 { { x } ^ { 2 } } -x \right) \right|_ { 1 } ^ { 2 } =$$
$$=\frac { 64 } { 5 } -8-8+8-2-\left( \frac { 2 } { 5 } -\frac { 1 } { 2 } -1+2-1 \right)=\frac { 29 } { 10 } $$
Вычислим теперь рассматриваемый двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$, а внешнее – по $y$. То есть, перейдя к повторным интегралам, получим:
$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { c } ^ { d } { dy } \int\limits_ { { { \psi } _ { 1 } } \left( y \right) } ^ { { { \psi } _ { 2 } } \left( y \right) } { \left( { { x } ^ { 2 } } +2y \right)dx } $$ 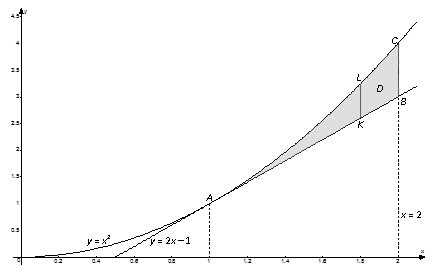 Из рисунка в области $D$ видно, что левая граница контура области – одна линия { положительная ветка параболы $y= { { x } ^ { 2 } } $), а его правая часть состоит из двух линий $AB$ { отрезок прямой $y=2x-1$) и $BC$ { отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ { { D } _ { 1 } } -ABF$ и $ { { D } _ { 2 } } -BCF$. Заданная область $D$ будет суммой областей $ { { D } _ { 1 } } $ и $ { { D } _ { 2 } } $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:
Из рисунка в области $D$ видно, что левая граница контура области – одна линия { положительная ветка параболы $y= { { x } ^ { 2 } } $), а его правая часть состоит из двух линий $AB$ { отрезок прямой $y=2x-1$) и $BC$ { отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ { { D } _ { 1 } } -ABF$ и $ { { D } _ { 2 } } -BCF$. Заданная область $D$ будет суммой областей $ { { D } _ { 1 } } $ и $ { { D } _ { 2 } } $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:
$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\iint\limits_ { { { D } _ { 1 } } } { \left( { { x } ^ { 2 } } +2y \right)dxdy } +\iint\limits_ { { { D } _ { 2 } } } { \left( { { x } ^ { 2 } } +2y \right)dxdy } $$
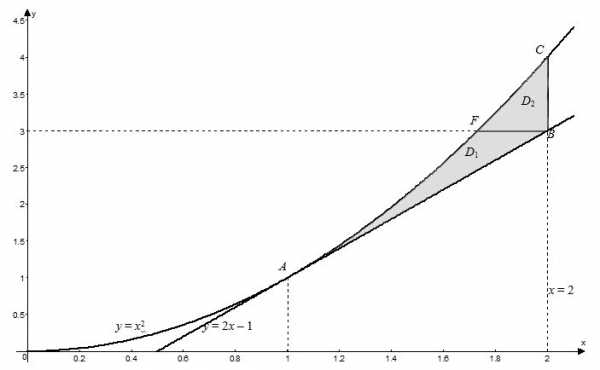
Поскольку в данном случае внутреннее интегрирование проводится по переменной $x$, то уравнения ограничивающих линий нужно разрешить относительно этой переменной:
$$AB:y=2x-1\Rightarrow x=\frac { y+1 } { 2 } ; \qquad AC:y= { { x } ^ { 2 } } \Rightarrow x=\sqrt { y } $$
Найдем пределы интегрирования для каждой из областей. В области $ { { D } _ { 1 } } $ переменная $y$ изменяется от ординаты точки $A$ до ординат точек $B$ и $F$. Точка $A$ принадлежит параболе $y= { { x } ^ { 2 } } $ и выше было найдено, что абсцисса этой точки $ { { x } _ { A } } =1$, тогда $ { { y } _ { A } } = { { 1 } ^ { 2 } } =1$. Точка $B$ – точка пересечения двух прямых $x=2$ и $y=2x-1$, а тогда $ { { y } _ { B } } =2\cdot 2-1=3$. Итак имеем, что $1\le y\le 3$. Переменная $x$ в области $ { { D } _ { 1 } } $ изменяется от ветки параболы $x=\sqrt { y } $ до прямой $x=\frac { y+1 } { 2 } $, то есть $ { { D } _ { 1 } } :\left[ \begin { matrix } 1\le y\le 3, \\ \sqrt { y } \le x\le \frac { y+1 } { 2 } . \\ \end { matrix }\right.$ Аналогично для области $ { { D } _ { 2 } } $ находим, что $ { { D } _ { 2 } } :\left[ \begin { matrix } 3\le y\le 4, \\ \sqrt { y } \le x\le 2. \\ \end { matrix }\right.$
Таким образом,
$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { 1 } ^ { 3 } { dy } \int\limits_ { \sqrt { y } } ^ { \frac { y+1 } { 2 } } { \left( { { x } ^ { 2 } } +2y \right)dx } +\int\limits_ { 3 } ^ { 4 } { dy } \int\limits_ { \sqrt { y } } ^ { 2 } { \left( { { x } ^ { 2 } } +2y \right)dx } =$$
$$=\int\limits_ { 1 } ^ { 3 } { \left. \left( \frac { { { x } ^ { 3 } } } { 3 } +2xy \right) \right|_ { \sqrt { y } } ^ { \frac { y+1 } { 2 } } dy } +\int\limits_ { 3 } ^ { 4 } { \left. \left( \frac { { { x } ^ { 3 } } } { 3 } +2xy \right) \right|_ { \sqrt { y } } ^ { 2 } dy } =$$
$$=\int\limits_ { 1 } ^ { 3 } { \left( \frac { { { \left( y+1 \right) } ^ { 3 } } } { 24 } + { { y } ^ { 2 } } +y-\frac { 7 } { 3 } { { y } ^ { \frac { 3 } { 2 } } }\right)dy } +\int\limits_ { 3 } ^ { 4 } { \left( \frac { 8 } { 3 } +4y-\frac { 7 } { 3 } { { y } ^ { \frac { 3 } { 2 } } }\right)dy } =$$
$$=\left. \left[ \frac { { { \left( y+1 \right) } ^ { 4 } } } { 96 } +\frac { { { y } ^ { 3 } } } { 3 } +\frac { { { y } ^ { 2 } } } { 2 } -\frac { 14 } { 15 } \sqrt { { { y } ^ { 5 } } }\right] \right|_ { 1 } ^ { 3 } +\left. \left[ \frac { 8y } { 3 } +2 { { y } ^ { 2 } } -\frac { 14 } { 15 } \sqrt { { { y } ^ { 5 } } }\right] \right|_ { 3 } ^ { 4 } =$$
$$=\left[ \frac { 8 } { 3 } +9+\frac { 9 } { 2 } -\frac { 42\sqrt { 3 } } { 5 } -\left( \frac { 1 } { 6 } +\frac { 1 } { 3 } +\frac { 1 } { 2 } -\frac { 14 } { 15 }\right) \right]+$$
$$+\left[ \frac { 32 } { 3 } +32-\frac { 448 } { 15 } -\left( 8+18-\frac { 42\sqrt { 3 } } { 5 }\right) \right]=\frac { 29 } { 10 } $$
Пример 5
Вычислить двойной интеграл (\iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dydx } ,) преобразовав его в полярные координаты. Область интегрирования (R) представляет собой сектор (0 \le \theta \le \large\frac { \pi } { 2 } \normalsize) круга радиусом (r = \sqrt 3.)
Решение: Область (R) в полярных координатах описывается множеством (R = \left[{ \left( { r,\theta }\right)|\;0 \le r \le \sqrt 3 ,0 \le \theta \le \large\frac { \pi } { 2 } \normalsize }\right]) (рисунок (4)). Применяя формулу $ { \iint\limits_R { f\left( { x,y }\right)dxdy } } = { \int\limits_\alpha ^\beta { \int\limits_ { a } ^ { b } { f\left( { r\cos \theta ,r\sin \theta }\right)rdrd\theta } } , } $ получаем $ { \iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dydx } } = { \int\limits_0^ { \frac { \pi } { 2 } } { \int\limits_0^ { \sqrt 3 } { { r^2 } \left( { { { \cos } ^2 } \theta + { { \sin } ^2 } \theta }\right)rdrd\theta } } } = { \int\limits_0^ { \frac { \pi } { 2 } } { d\theta } \int\limits_0^ { \sqrt 3 } { { r^3 } dr } } = { \left. \theta \right|_0^ { \frac { \pi } { 2 } } \cdot \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_0^ { \sqrt 3 } } = { \frac { \pi } { 2 } \cdot \frac { 9 } { 4 } = \frac { { 9\pi } } { 8 } . } $
Пример 6
Вычислить интеграл (\iint\limits_R { xydydx } ,) в котором область интегрирования (R) представляет собой кольцо, ограниченное окружностями ( { x^2 } + { y^2 } = 1) и ( { x^2 } + { y^2 } = 5.)
Решение:
В полярных координатах область интегрирования (R) является полярным прямоугольником: $R = \left( { \left( { r,\theta }\right)|\;1 \le r \le \sqrt 5 ,0 \le \theta \le 2\pi }\right).$

Тогда, используя формулу $ { \iint\limits_R { f\left( { x,y }\right)dxdy } } = { \int\limits_\alpha ^\beta { \int\limits_ { a } ^ { b } { f\left( { r\cos \theta ,r\sin \theta }\right)rdrd\theta } } , } $ находим значение интеграла $ { \iint\limits_R { xydydx } } = { \int\limits_0^ { 2\pi } { \int\limits_1^ { \sqrt 5 } { r\cos \theta r\sin \theta rdrd\theta } } } = { \int\limits_0^ { 2\pi } { \sin \theta \cos \theta d\theta } \int\limits_1^ { \sqrt 5 } { { r^3 } dr } } = { \frac { 1 } { 2 } \int\limits_0^ { 2\pi } { \sin 2\theta d\theta } \int\limits_1^ { \sqrt 5 } { { r^3 } dr } } = { \frac { 1 } { 2 } \left. { \left( { — \frac { { \cos 2\theta } } { 2 } }\right) }\right|_0^ { 2\pi } \cdot \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_1^ { \sqrt 5 } } = \\ = { \frac { 1 } { 4 } \left( { — \cos 4\pi + \cos 0 }\right) \cdot \frac { 1 } { 4 } \left( { 25 — 1 }\right) } = { \frac { 1 } { 4 } \left( { — 1 + 1 }\right) \cdot 6 = 0. } $
Пример 7
Найти интеграл (\iint\limits_R { \sin \theta drd\theta } ,) где область интегрирования (R) ограничена кардиоидой (r = 1 + \cos \theta ).
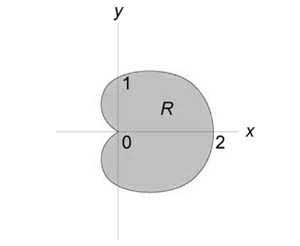
Решение:
Данный интеграл уже записан в полярных координатах. Выражая его через повторный интеграл, получаем: $\require { cancel } { \iint\limits_R { \sin \theta drd\theta } } = { \int\limits_0^ { 2\pi } { \int\limits_0^ { 1 + \cos \theta } { \sin \theta drd\theta } } } = { \int\limits_0^ { 2\pi } { \left[ { \int\limits_0^ { 1 + \cos \theta } { dr } }\right]\sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { \left[ { \left. r \right|_0^ { 1 + \cos \theta } }\right]\sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { \left( { 1 + \cos\theta }\right)\sin \theta d\theta } } = \\ = { \int\limits_0^ { 2\pi } { \left( { \sin \theta + \cos\theta \sin \theta }\right)d\theta } } = { \int\limits_0^ { 2\pi } { \sin \theta d\theta } + \int\limits_0^ { 2\pi } { \frac { { \sin 2\theta } } { 2 } d\theta } } = { \left. { \left( { — \cos \theta }\right) }\right|_0^ { 2\pi } + \frac { 1 } { 2 } \left. { \left( { — \frac { { \cos 2\theta } } { 2 } }\right) }\right|_0^ { 2\pi } } = { — \cos 2\pi + \cos 0 — \frac { 1 } { 4 } \cos 4\pi + \frac { 1 } { 4 } \cos 0 } = \\ = { -\cancel { 1 } + \cancel { 1 } — \cancel { \frac { 1 } { 4 } } + \cancel { \frac { 1 } { 4 } } = 0. } $
Пример 8
Вычислить интеграл (\iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dxdy } ) в круге ( { x^2 } + { y^2 } = 2x.)
Решение: Область интегрирования (R) показана на рисунке:
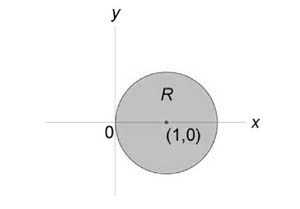
Преобразуем уравнение окружности следующим образом: $ { { x^2 } + { y^2 } = 2x, } \;\; { \Rightarrow { x^2 } — 2x + 1 + { y^2 } = 1, } \;\; { \Rightarrow { \left( { x — 1 }\right)^2 } + { y^2 } = 1. } $ Подставляя (x = r\cos \theta ,) (y = r\sin \theta ,) найдем уравнение окружности в полярных координатах. $ { { x^2 } + { y^2 } = 2x, } \;\; { \Rightarrow { r^2 } { \cos ^2 } \theta + { r^2 } { \sin^2 } \theta = 2r\cos \theta , } \;\; { \Rightarrow { r^2 } \left( { { { \cos } ^2 } \theta + { \sin^2 } \theta }\right) = 2r\cos \theta , } \;\; { \Rightarrow r = 2\cos \theta . } $ Образ (S) области интегрирования (R) показан на рисунке:
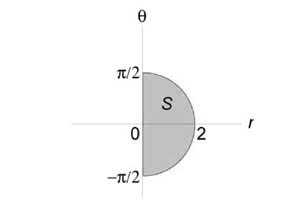
После перехода к полярным координатам вычисляем двойной интеграл. $ { \iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dxdy } } = { \iint\limits_S { \left( { { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta }\right)rdrd\theta } } = { \iint\limits_S { { r^3 } drd\theta } } = { \int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left[ { \int\limits_0^ { 2\cos \theta } { { r^3 } dr } }\right]d\theta } } = { 4\int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left[ { \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_0^ { 2\cos \theta } }\right]d\theta } } = { 4\int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { { { \cos } ^4 } \theta d\theta } } = \\ = { 4\int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { { { \left( { \frac { { 1 + \cos 2\theta } } { 2 } }\right) } ^2 } d\theta } } = { \int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { 1 + 2\cos 2\theta + { { \cos } ^2 } 2\theta }\right)d\theta } } = { \int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { 1 + 2\cos 2\theta + \frac { { 1 + \cos 4\theta } } { 2 } }\right)d\theta } } = { \int\limits_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { \frac { 3 } { 2 } + 2\cos 2\theta + \frac { 1 } { 2 } \cos 4\theta }\right)d\theta } } = \\ = { \left. { \left( { \frac { 3 } { 2 } \theta + \sin 2\theta + \frac { 1 } { 8 } \sin 4\theta }\right) }\right|_ { — \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } } = { \left( { \frac { 3 } { 2 } \cdot \frac { \pi } { 2 } + \sin \pi + \frac { 1 } { 8 } \sin 2\pi }\right) — \left( { — \frac { 3 } { 2 } \cdot \frac { \pi } { 2 } — \sin \pi — \frac { 1 } { 8 } \sin 2\pi }\right) } = { \frac { { 3\pi } } { 2 } . } $
Пример 9
Вычислить двойной интеграл (\iint\limits_R { \sin \sqrt { { x^2 } + { y^2 } } dxdy } ) посредством преобразования в полярные координаты. Область интегрирования (R) представляет собой круг ( { x^2 } + { y^2 } \le { \pi ^2 } .)
Решение:
Область интегрирования (R) представлена на рисунке: 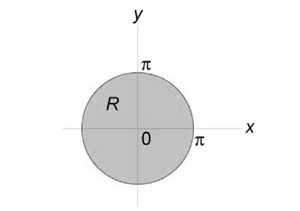
Образ (S) данной области описывается множеством (\left[{ S = \left( { r,\theta }\right)|\;0 \le r \le \pi ,0 \le \theta \le 2\pi }\right]) и показан на рисунке:
Запишем исходный двойной интеграл в полярных координатах. $ { I = \iint\limits_R { \sin \sqrt { { x^2 } + { y^2 } } dxdy } } = { \iint\limits_S { \sin \sqrt { { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta } rdrd\theta } } = { \iint\limits_S { r\sin rdrd\theta } } = { \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^\pi { r\sin rdr } } = { 2\pi \int\limits_0^\pi { r\sin rdr } . } $ Вычислим последний интеграл с помощью интегрирования по частям: $ { \int\limits_a^b { udv } } = { \left. { \left( { uv }\right) }\right|_a^b — \int\limits_a^b { vdu } . } $ Пусть (u = r,) (dv = \sin rdr.) Тогда (du = dr,\;\;v = \int { \sin rdr } = — \cos r). Следовательно, $ { I = 2\pi \int\limits_0^\pi { r\sin rdr } } = { 2\pi \left[ { \left. { \left( { — r\cos r }\right) }\right|_0^\pi — \int\limits_0^\pi { \left( { — \cos r }\right)dr } }\right] } = { 2\pi \left[ { \left. { \left( { — r\cos r }\right) }\right|_0^\pi + \int\limits_0^\pi { \cos rdr } }\right] } = \\ = { 2\pi \left[ { \left. { \left( { — r\cos r }\right) }\right|_0^\pi + \left. { \left( { \sin r }\right) }\right|_0^\pi }\right] } = { 2\pi \left. { \left( { \sin r — r\cos r }\right) }\right|_0^\pi } = { 2\pi \left[ { \left( { \sin \pi — \pi \cos \pi }\right) — \left( { \sin 0 — 0 \cdot \cos 0 }\right) }\right] } = { 2\pi \cdot \pi = 2 { \pi ^2 } . } $
3dstroyproekt.ru


 (рис. 1.5). Для этого преобразуем кривые:
(рис. 1.5). Для этого преобразуем кривые: .
. описывается уравнениями:
описывается уравнениями: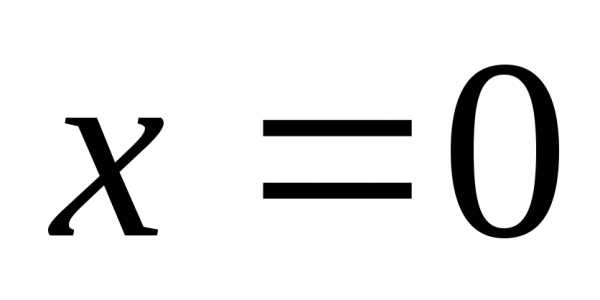 ,
,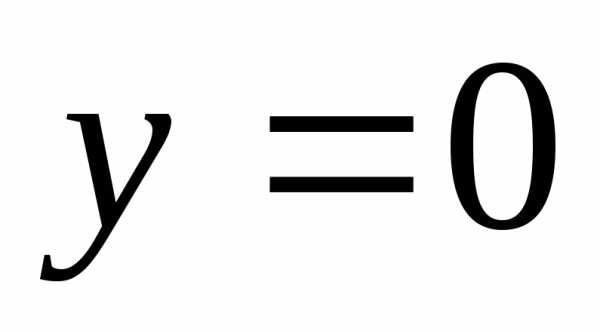 ,
,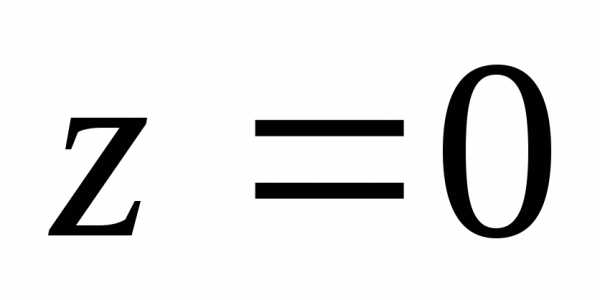 (
(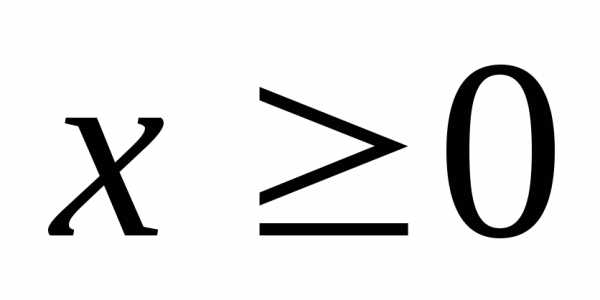 ,
,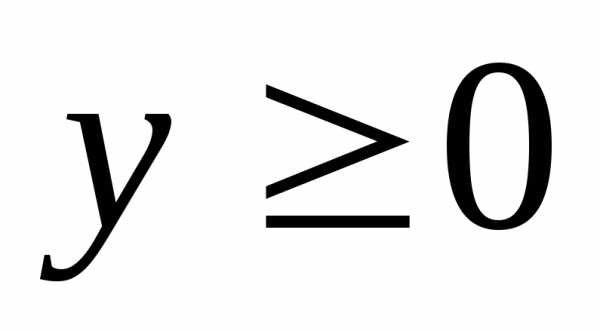 ,
,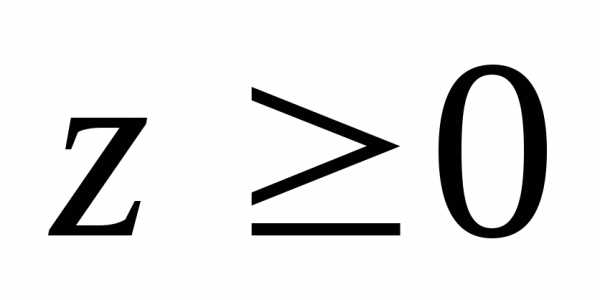 ).
). есть треугольник
есть треугольник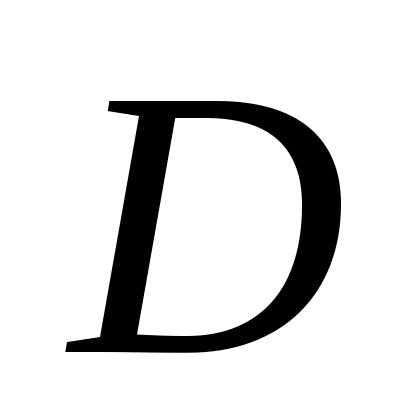 ,
ограниченный прямыми
,
ограниченный прямыми ,
,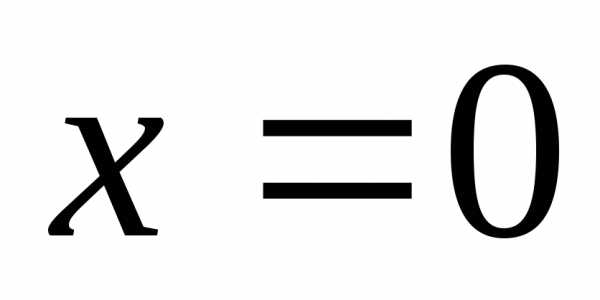 ,
,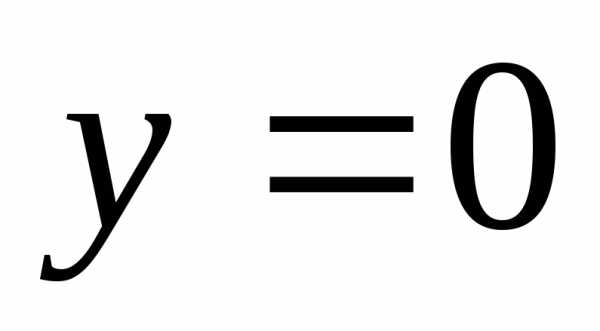 (рис. 1.8). Приаппликаты точекудовлетворяют неравенству,
поэтому
(рис. 1.8). Приаппликаты точекудовлетворяют неравенству,
поэтому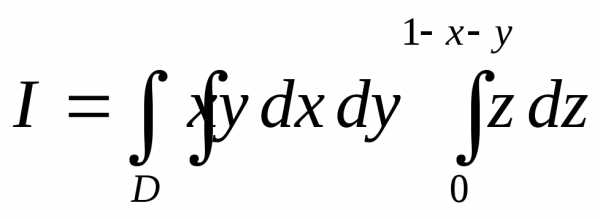 .
. ,
получим
,
получим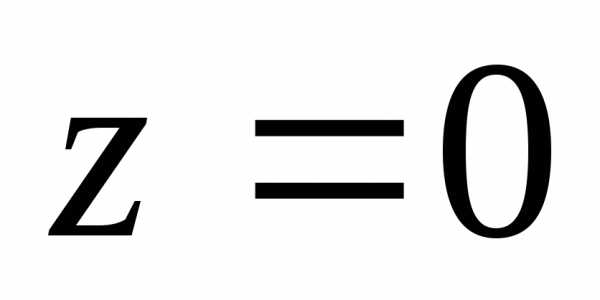 .
. равен
равен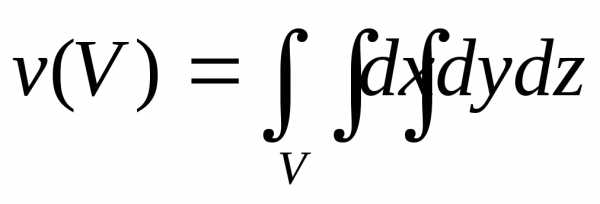 .
.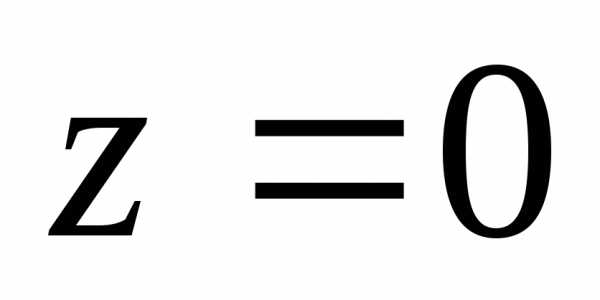 ,
а сверху плоскостью(рис. 1.10). Проекция области
,
а сверху плоскостью(рис. 1.10). Проекция области есть круг
есть круг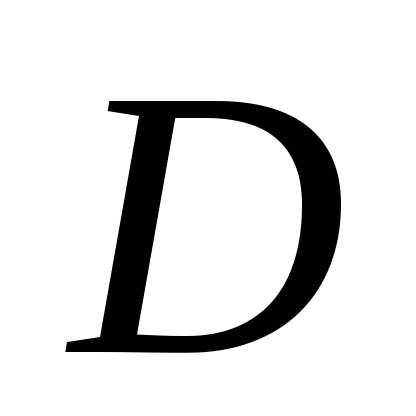 с центром в начале координат и единичном
радиусом.
с центром в начале координат и единичном
радиусом.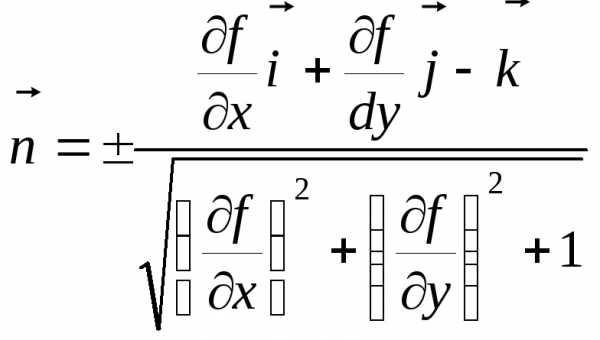 .
.
 :,
расположенную в первом октанте.
Уравнение данной плоскости в отрезках
имеет вид
:,
расположенную в первом октанте.
Уравнение данной плоскости в отрезках
имеет вид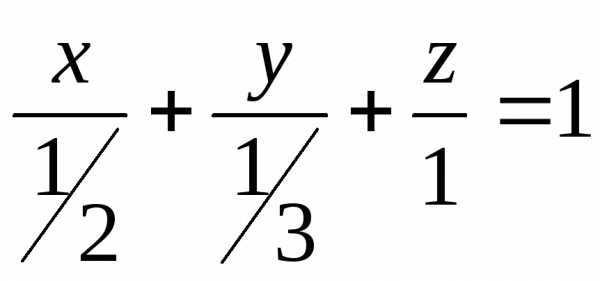
 откуда
откуда