Как проверить параллельность векторов
Содержание
- Координатная форма условия коллинеарности векторов
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- Примеры задач на коллинеарность векторов на плоскости
- Примеры задач на коллинеарность векторов в пространстве
- Общие сведения
- Критерии коллинеарности
- Сонаправленные вектора
- Противоположные отрезки
- Использование онлайн-калькулятора
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
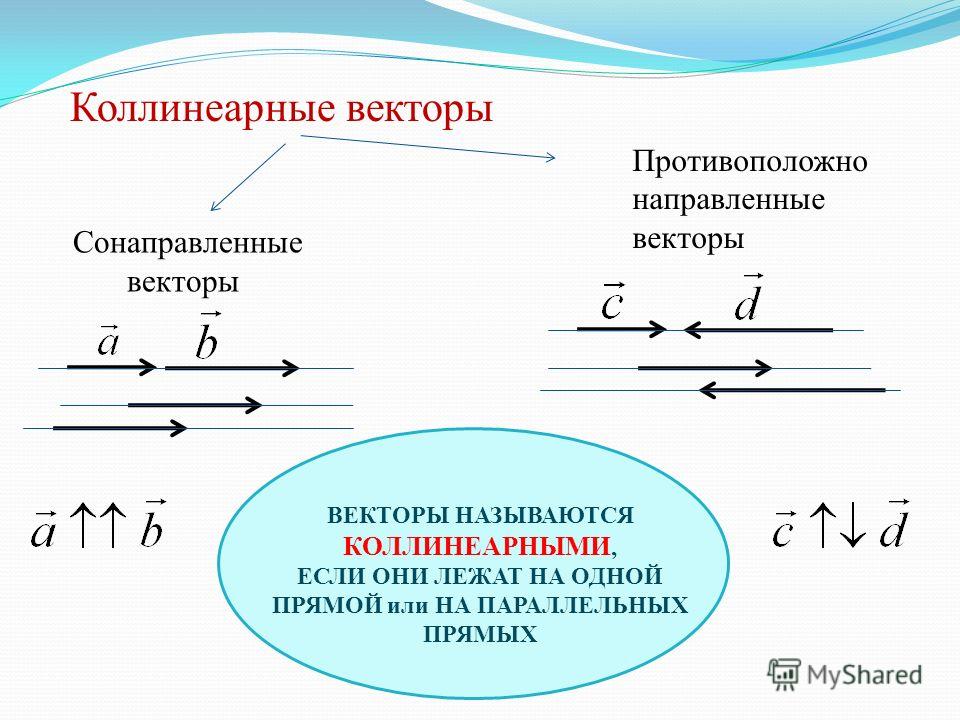
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .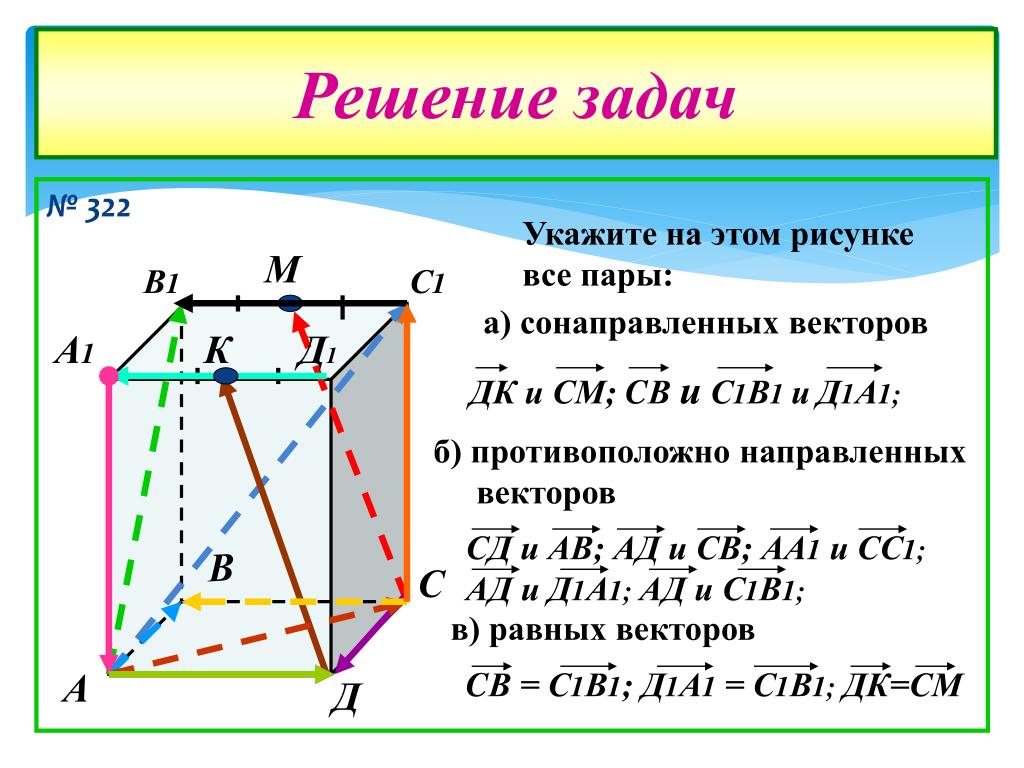
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1
Т. е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.
е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это a
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | .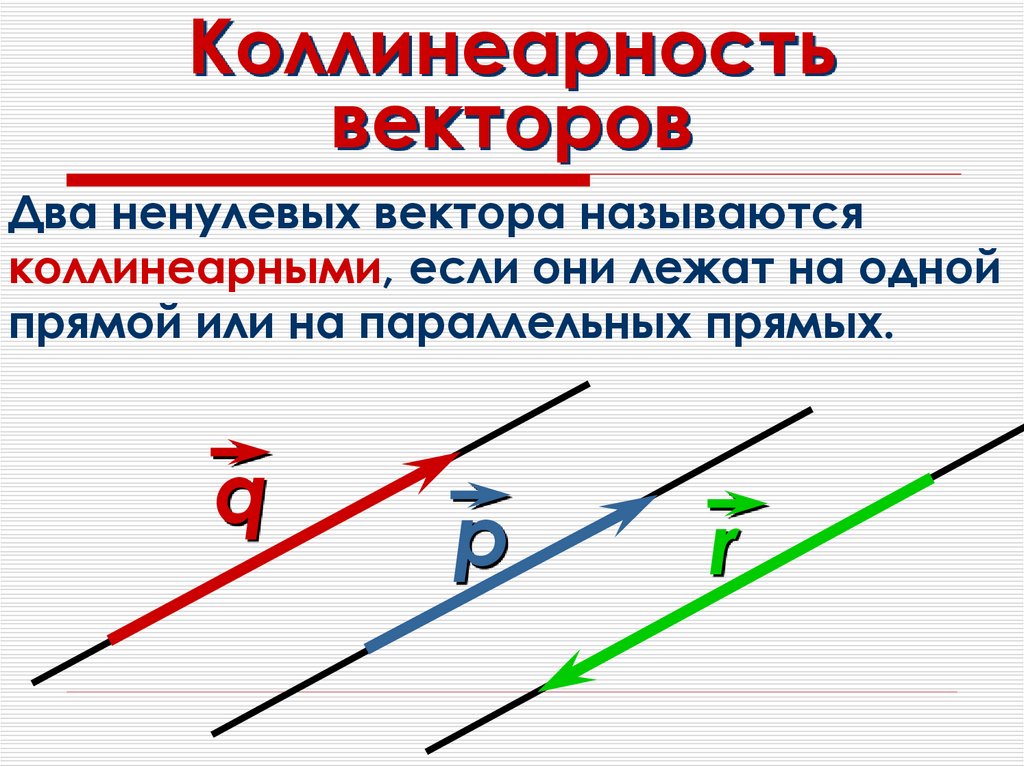 |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Общие сведения
Вектором называют направленный отрезок, который имеет начало и конец. Обозначают его либо большими буквами, либо маленькими, например, АБ или a. Над буквой ставится знак вектора — стрелка.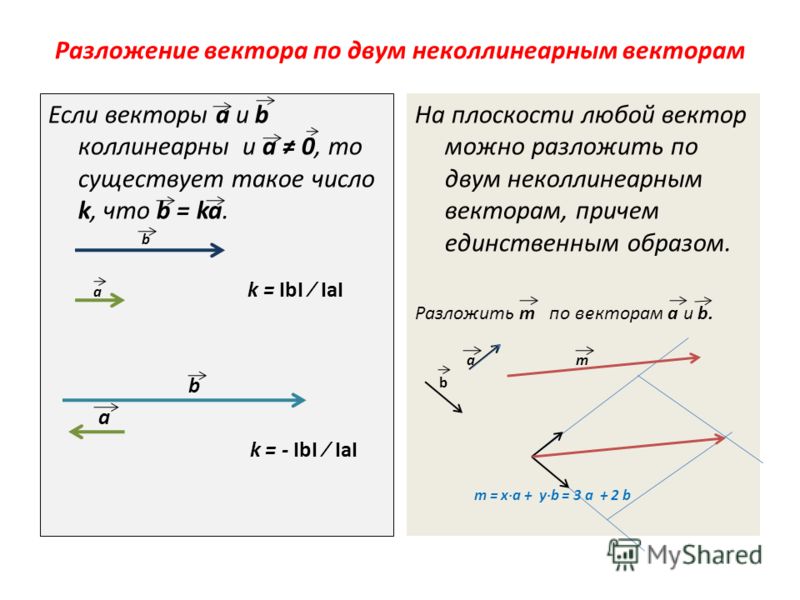 Любой отрезок характеризуется длиной, которую называют модулем. Если начало и конец прямой совпадают, то такой вектор носит название нулевой и обозначается в виде точки. При этом его модуль будет равняться нулю.
Любой отрезок характеризуется длиной, которую называют модулем. Если начало и конец прямой совпадают, то такой вектор носит название нулевой и обозначается в виде точки. При этом его модуль будет равняться нулю.
Для равенства векторов необходимо выполнение двух условий:
- модули отрезков должны быть равны;
- сравниваемые отрезки должны быть направлены в одну сторону.
Равные вектора могут быть совмещены параллельным переносом, при этом начало и конец отрезков должны совпадать. Если ограниченные линии не являются равными, но лежат на параллельных прямых, то их называют коллинеарными, то есть, по определению коллинеарных векторов, их направление для определения признака не является важным.
Коллинеарность является одним из признаков сонаправленности, но для выполнения последнего они должны ещё и совпадать по направлению. Наглядным понятием, объясняющим сонаправленность, является прямое движение транспорта или пешехода. Например, если рассматривать две траектории движения как векторы АБ и СД, лежащие на плоскости, при этом их лучи лежат в одной полуплоскости и перпендикулярны её границам, то их можно назвать сонаправленными.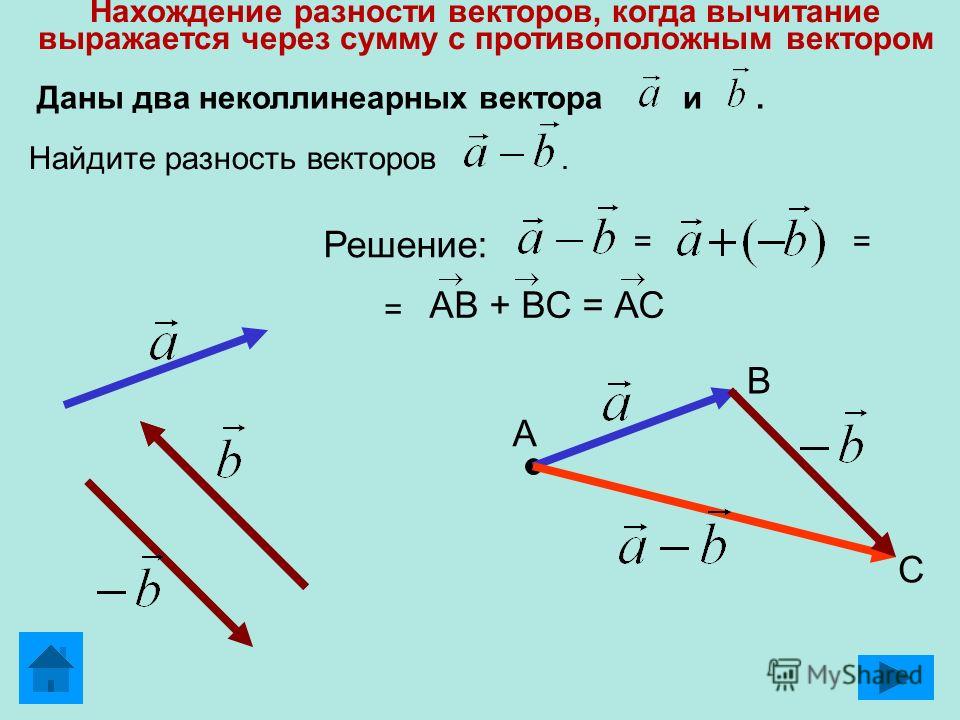
Поэтому параллельные отрезки будут направлены в одну сторону лишь тогда, когда их лучи находятся по одну сторону от прямой, соединяющей их начала. При этом если векторы коллинеарны, но не сонаправлены, то они будут являться противоположными.
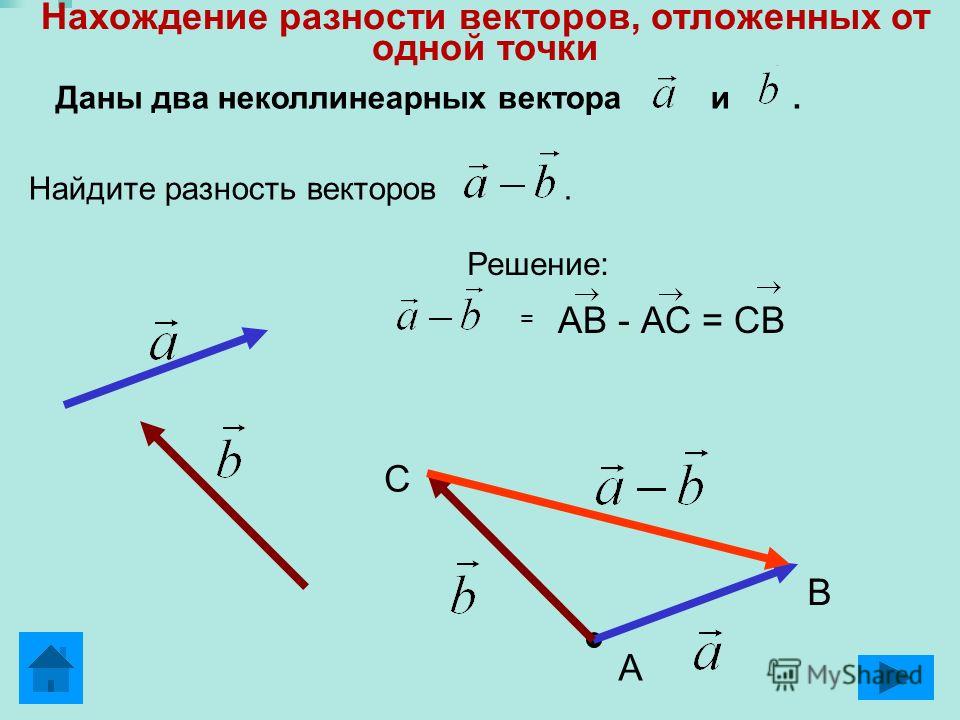
С векторами можно выполнять любые простейшие арифметические операции. При сложении используют правила параллелограмма и треугольника. Пусть есть два отрезка, имеющие общее начало. Для того чтобы найти их сумму, необходимо фигуру достроить до параллелограмма. Диагональ этой фигуры и будет искомой величиной. Когда же конец одного отрезка является началом другого, то, соединив свободные точки, можно получить треугольник. Новая прямая и будет являться вектором суммы. Следует отметить, что эти правила равнозначны друг другу. Вычитание отрезков находится аналогично.
Вектор можно и умножить на число, то есть длина отрезка увеличивается на значение множителя. Если в произведении стоит отрицательное число, то характеристика меняет направление.
Критерии коллинеарности
Теорема критерия коллинеарности представляет собой утверждение, которое сообщает, что если есть два не ортогональных отрезка, одинаковых по длине, a и b, то вектор a может быть выражен через формулу a || b = a = y * b. При этом y обозначает любое произвольное число. Есть и обратное утверждение: если вектор b умножить на число и получится отрезок a, то тогда a и b будут коллинеарными.
Эти два правила тождественны и называются критериями коллинеарности. Для их доказательства нужно знать правило арифметических действий с параллельными и перпендикулярными векторами, а также понимать основной базис. Заключается он в том, что если имеются три отрезка a, b и c, при этом верной является следующая комбинация a || b и a || c, то справедливо утверждать, что b || c.
Для того чтобы доказать свойство a || b = a = y * b, нужно воспользоваться определением коллинеарности. Из него следует, что если a || b, то отрезки могут быть сонаправлены или противоположно направлены. Таким образом, необходимо проверить утверждение для двух случаев:
Из него следует, что если a || b, то отрезки могут быть сонаправлены или противоположно направлены. Таким образом, необходимо проверить утверждение для двух случаев:
Если предположения окажутся верными, то можно будет сделать вывод о справедливости записи для других случаев. То есть к любым параллельным отрезкам можно применить равенство a = u * b. Этот критерий занимает важное место в геометрии наряду со свойствами перпендикулярности (ортогональности) прямых.
Сонаправленные вектора
Пусть a и b однонаправленные. Введём число y, равное отношению a на b. Так как длина вектора может быть только положительной, то и y = a /b > 0. Состояние вектора, когда он нулевой, является частным случаем и его можно не рассматривать, так как при этом получится равенство 0 = 0. Если длину b умножить на число, то получится новый вектор. Пусть это будет отрезок c, то есть с = y * b. Учитывая свойство коллинеарности, можно утверждать, что между c и b останется параллельность.
Учитывая свойство коллинеарности, можно утверждать, что между c и b останется параллельность.
По условию известно, что a || b. Исходя из транзитивности отрезков, можно заключить, что и c || b. Теперь необходимо установить их направление. Изначально a и b направлены в одну сторону. Ведённый множитель больше нуля. Это значит, что после умножения направление вектора не изменится, то есть c будет иметь то же направление что и b. Тогда получается, что a || b и c || b. Отсюда следует, что a || с.
Длина вектора c равняется |c| = |u| * |b|. Вместо u можно подставить a / b. В итоге получится |a| * |b| / |b| = |a|. Таким образом, два условия выполняются, и можно утверждать, что с = a. Получается, что для двух любых однонаправленных векторов будет выполняться правило a = u * b.
Противоположные отрезки
Пусть имеется два отрезка a и b, при этом их направления противоположны друг другу. Можно ввести переменную u, которая будет меньше нуля. Тогда справедливо записать u = — |a| / |b| 0, так как |m| ↑↑ |n|.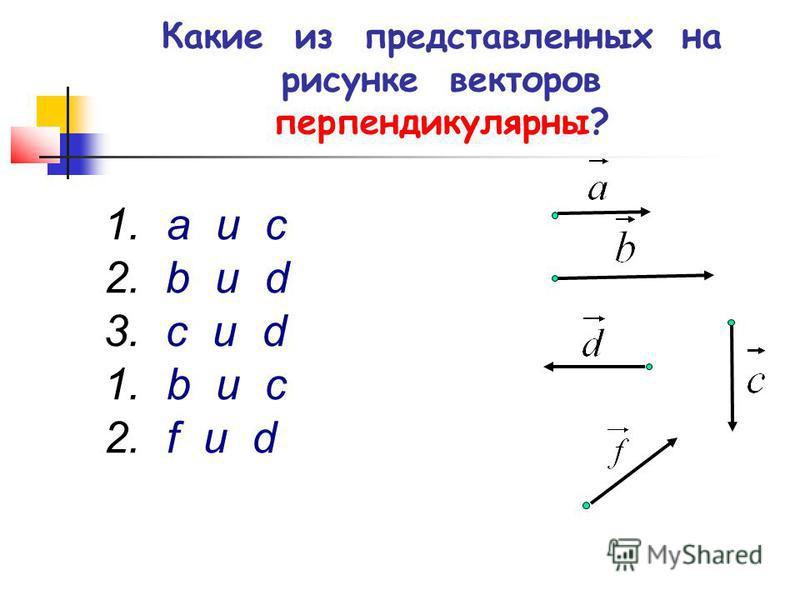 Отсюда u = 240 / 12 = 20.
Отсюда u = 240 / 12 = 20.
 Решение выполняют следующим образом. Если векторы коллинеарны, то будет существовать такое число, при котором будет верным равенство: c 1 = u * c 2. Иными словами, векторы коллинеарны если их координаты пропорциональны. Используя исходные данные, получим: c 1 = a + b = <1+1; 4+1; -2+(-1)>= <2; 5; -3>; c 2 = 4 * a + 2 * b = <4*1 + 2*1; 4*4 + 2*1; 4 * (-2) + 2 * (-1)>= <6; 18; -10>. В результате: 2/6 ≠ 5/18 ≠ -3/-10. Отсюда можно сделать вывод, что рассматриваемые отрезки не коллинеарны.
Решение выполняют следующим образом. Если векторы коллинеарны, то будет существовать такое число, при котором будет верным равенство: c 1 = u * c 2. Иными словами, векторы коллинеарны если их координаты пропорциональны. Используя исходные данные, получим: c 1 = a + b = <1+1; 4+1; -2+(-1)>= <2; 5; -3>; c 2 = 4 * a + 2 * b = <4*1 + 2*1; 4*4 + 2*1; 4 * (-2) + 2 * (-1)>= <6; 18; -10>. В результате: 2/6 ≠ 5/18 ≠ -3/-10. Отсюда можно сделать вывод, что рассматриваемые отрезки не коллинеарны.Использование онлайн-калькулятора
Решение простых заданий из школьного курса обычно не вызывает сложностей. Но на практике приходится сталкиваться со сложными выражениями. Для их вычисления нужно проявить усидчивость и при этом быть предельно внимательным. Кроме этого, расчёт занимает довольно много времени, а любая, казалось бы, незначительная оплошность, приведёт к неправильному решению.
Поэтому условие коллинеарности векторов удобно проверять на так называемых онлайн-калькуляторах. Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.
Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.
Для того чтобы выполнить на них математические операции, необходимо иметь доступ к интернету и установленный веб-обозреватель. Всё, что требуется от пользователя, это просто зайти на сайт и выбрать раздел, связанный с операциями над векторами. Затем в предложенную форму вести условие задания и запустить расчёт нажатием одной кнопки.
Из множества онлайн-расчётчиков, доступных в секторе рунета, можно выделить следующие:
- SolverBook — это простой на вид сайт, содержащий на своей странице приложение, позволяющее выполнять любые действия над отрезками, а также определять их вид. Кроме непосредственного предоставления ответа, сервис выдаёт пошаговое решение. При этом каждый этап будет детально расписан.
- O nlineMSchool — сайт помогает найти коллинеарные отрезки для любой сложности примеров.
 На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач.
На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач. - Kontrolnaya-rabota — отличительной его чертой является возможность отправления подробного решения на указанную электронную почту. Сайт умеет работать как с парой векторов, так и попарной системой.
Все указанные сервисы предоставляют доступ к услугам бесплатно и без регистрации. Воспользовавшись онлайн-калькуляторами, даже слабо подготовленный пользователь научится самостоятельно определять коллинеарность. Такие расчётчики будут полезны и учащимся, и инженерам.
404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
[PDF] Зам.
 Дир по УВР_______________ Утверждаю
Дир по УВР_______________ УтверждаюЗам.Дир по УВР_______________ Утверждаю №_____ Дата01/04/14 Предмет Геометрия Класс 10 Конспект урока геометрии для 10 класса «ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В
ПРОСТРАНСТВЕ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ» Цели урока: Изучить, что такое “вектор в пространстве», как определяются координаты, вектора, если известны координаты его начала и конца, научитесь решать задачи, связанные с вектором. Обобщить свои знания о векторах в координатах, узнаете о сложении векторов, вычитании векторов, умножении вектора на число, а также научитесь выполнять эти действия. Тип урока: Изучения нового материала. ХОД УРОКА 1. Организационный момент. Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения. 2. Этап актуализации. 3. Формирование новых понятий и способов действия.
ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением.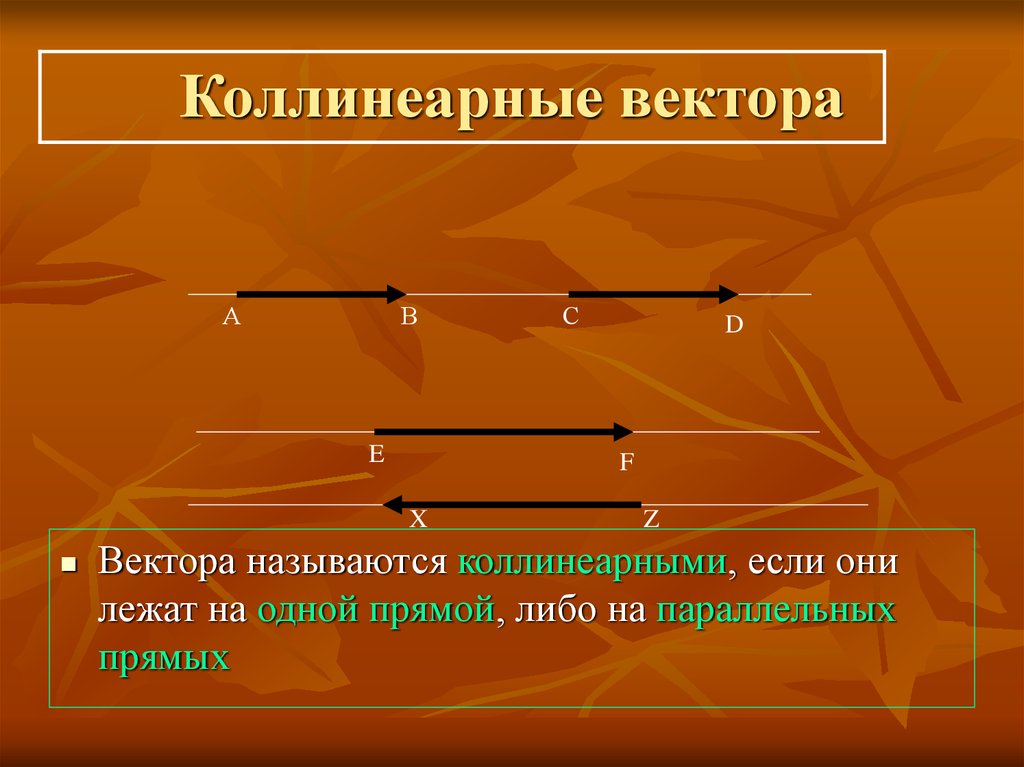 Вектор изображатеся направленным отрезком, длина которого равна длине вектора. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов. Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты. О п р е д е л е н и е . Координатами вектора ⃗⃗⃗⃗⃗ АВ, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1. Записывают такой вектор, указывая его координаты: ⃗⃗⃗⃗⃗ АВ (a1 а2, а3) или 𝑎 (a1 а2, а3). Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка ⃗⃗⃗⃗⃗ АВ, тогда а1 = 0 — 4 = -4, а2 = 6 — 0 = 6, а3 = 4 — 3 = 1. Значит, направленному отрезку ⃗⃗⃗⃗⃗ АВ соответствует вектор a⃗ (-4; 6; 1) (рис. 67). Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны.
Вектор изображатеся направленным отрезком, длина которого равна длине вектора. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов. Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты. О п р е д е л е н и е . Координатами вектора ⃗⃗⃗⃗⃗ АВ, начало которого точка A(x1,y1,z1), а конец — точка В(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1. Записывают такой вектор, указывая его координаты: ⃗⃗⃗⃗⃗ АВ (a1 а2, а3) или 𝑎 (a1 а2, а3). Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка ⃗⃗⃗⃗⃗ АВ, тогда а1 = 0 — 4 = -4, а2 = 6 — 0 = 6, а3 = 4 — 3 = 1. Значит, направленному отрезку ⃗⃗⃗⃗⃗ АВ соответствует вектор a⃗ (-4; 6; 1) (рис. 67). Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.
Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.
Длину вектора a⃗ (a1 а2, а3) можно выразить через его координаты. Отложим вектор a⃗ от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1 и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2 А второй катет Аz А = а3 и ОА2 = ОА2г + а32 = а12 + а22+ а32. Отсюда |a⃗ | = √𝑎12 + 𝑎22 + 𝑎32 Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю. Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называют коллинеарными. Коллинеарные векторы бывают сонаправлены (а ↑↑ b) или противоположно направлены (а ↑↓ b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой.
Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору. ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.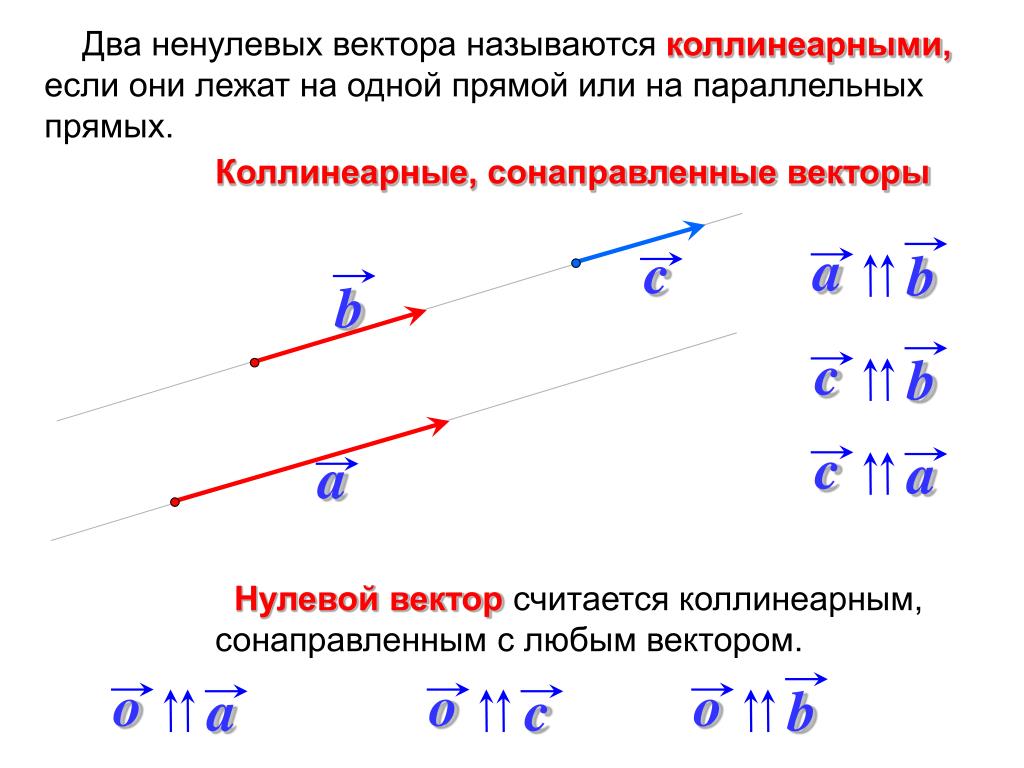 О п р е д е л е н и е . Суммой векторов a (a1 а2, а3) и b(b1 b2, b3) называется вектор а + b с координатами (а1 + b1; а2 + b2 ; а3 + b3) Для любых векторов а , b и с справедливы равенства: 1) а + b = b + а — переместительный закон сложения; 2) а + ( b + с ) = (а + b ) + с — сочетательный закон сложения. Чтобы доказать эти свойства, достаточно сравнить соответствующие координаты левой и правой частей каждого векторного равенства. Для любых трех точек А, В, С в пространстве имеет место векторное равенство ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ ВС = ⃗⃗⃗⃗⃗ АС . Действительно, для любых трех точек A(a1 а2, а3), B(b1 b2, b3), C(c1, с2, с3) ⃗⃗⃗⃗⃗ АВ (b1 – а1; b2 — а2; b3 — а3) и ⃗⃗⃗⃗⃗ ВС (с1 — bг; с2 — b2, с3 — b3). ⃗⃗⃗⃗⃗ (с1 – а1; с2 — а2; с3 — а3). Отсюда ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ ВС = АС Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника (рис. 69). Также применяется и правило параллелограмма. Оно часто используется в физике. Если ABCD — параллелограмм (рис. 70), то ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ 𝐴𝐷 = ⃗⃗⃗⃗⃗ АС .
О п р е д е л е н и е . Суммой векторов a (a1 а2, а3) и b(b1 b2, b3) называется вектор а + b с координатами (а1 + b1; а2 + b2 ; а3 + b3) Для любых векторов а , b и с справедливы равенства: 1) а + b = b + а — переместительный закон сложения; 2) а + ( b + с ) = (а + b ) + с — сочетательный закон сложения. Чтобы доказать эти свойства, достаточно сравнить соответствующие координаты левой и правой частей каждого векторного равенства. Для любых трех точек А, В, С в пространстве имеет место векторное равенство ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ ВС = ⃗⃗⃗⃗⃗ АС . Действительно, для любых трех точек A(a1 а2, а3), B(b1 b2, b3), C(c1, с2, с3) ⃗⃗⃗⃗⃗ АВ (b1 – а1; b2 — а2; b3 — а3) и ⃗⃗⃗⃗⃗ ВС (с1 — bг; с2 — b2, с3 — b3). ⃗⃗⃗⃗⃗ (с1 – а1; с2 — а2; с3 — а3). Отсюда ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ ВС = АС Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника (рис. 69). Также применяется и правило параллелограмма. Оно часто используется в физике. Если ABCD — параллелограмм (рис. 70), то ⃗⃗⃗⃗⃗ АВ + ⃗⃗⃗⃗⃗ 𝐴𝐷 = ⃗⃗⃗⃗⃗ АС . Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда АВ + ВС +CD + DE + EF = AF.
Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда АВ + ВС +CD + DE + EF = AF.
О п р е д е л е н и е . Два вектора, сумма которых равна нулевому вектору, называются противоположными. Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки. О п р е д е л е н и е . Разностью векторов а и b называется такой вектор с , который в сумме с вектором b дает вектор а . Если а (а 1 ; а2; а3) и b( b1; b2; b3), то а⃗ — ⃗⃗⃗ 𝑏 = с (а1 –b1; а2 — b2; а3 – b3). О п р е д е л е н и е . Произведением вектора 𝑎 (a 1 ; а2; a3) на число k называется вектор k а⃗ = (k а1; k а2; k а3). Из определения вытекают следующие свойства: 1) 2)
k ( 𝑎 + 𝑏⃗) = k 𝑎 + k 𝑏⃗, (т + n ) • а⃗ = т а⃗+ п а⃗ и равенство | k • а⃗ | = | k |•| а⃗ | (здесь k, т, п — числа).
Ненулевые векторы а и b коллинеарные тогда и только тогда, когда найдется такое число х, что выполняется равенство 𝑏⃗ = х а⃗ . При этом число х единственно. 4. Применение. Формирование умений и навыков. стр 72. №2,5. стр 74, №1,2,3,4,5,11,14. 5.Этап информации о домашнем задании. п.п.22,23. стр 72. №6,7. стр 74 № 8,10. 6.Подведение итогов урока.
При этом число х единственно. 4. Применение. Формирование умений и навыков. стр 72. №2,5. стр 74, №1,2,3,4,5,11,14. 5.Этап информации о домашнем задании. п.п.22,23. стр 72. №6,7. стр 74 № 8,10. 6.Подведение итогов урока.
Коллинеарные векторы
Навигация по странице:
- Коллинеарные векторы — определение
- Условие коллинеарности векторов
- Примеры задач
- плоские задачи
- пространственных задач
Онлайн-калькулятор для проверки коллинеарности векторов.
Онлайн упражнение. Коллинеарные векторы на плоскости.
Онлайн упражнение. Коллинеарные векторы в пространстве.
Определение.
Векторы, параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами (рис. 1).
| Рис. 1 |
Условие коллинеарности векторов
Два вектора коллинеарны, если выполняется любое из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условие коллинеарности векторов 2. Два вектора коллинеарны , если отношения их координат равны.
N.B. Условие 2 неверно, если один из компонентов вектора равен нулю.
Условие коллинеарности векторов 3. Два вектора коллинеарны , если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только к трехмерным (пространственным) задачам.
Доказательство условия коллинеарности 3
Пусть имеются два коллинеарных вектора a = {a x ; а и ; a z } и b = {na x ; нет и ; na z }. Находим их векторное произведение
| a × b = | и | к | к | = i (a y b z — a z b y ) — j (a x b z — a z b x ) + k (a x b y — a y b x ) = |
| а x | z | |||
| б х | б у | б z |
= I (A Y NA Z -A Z NA Y )- J (A x NA Z -A Z NA x )+77777. 77777777. 7777. 7. 277777777777777777777777777777771 гг. (a x na y — a y na x ) = 0 i + 0 j + 0 k = 0
77777777. 7777. 7. 277777777777777777777777777777771 гг. (a x na y — a y na x ) = 0 i + 0 j + 0 k = 0
Примеры задач
Примеры задач плоскости
Пример 1. Какой из векторов a = {1; 2}, б = {4; 8}, с = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты a равные нулю, то используем условие коллинеарности 2, что в случае плоской задачи для векторов a и b будет иметь вид:
| a x | = | . | |
| б х | б г |
Означает:
| Векторы a и b коллинеарны, потому что | 1 | = | 2 | . |
| 4 | 8 |
| Векторы а и с не коллинеарны, так как | 1 | ≠ | 2 | . |
| 5 | 9 |
| Векторы с и b не коллинеарны, так как | 5 | ≠ | 9 | . |
| 4 | 8 |
Пример 2. Докажите, что вектор a = {0; 3} и б = {0; 6} коллинеарны.
Решение: Поскольку компоненты вектора содержат ноль, то воспользовавшись условием коллинеарности 1, находим число n, для которого:
б = нет данных.
Для этого находим ненулевую компоненту вектора a в данном случае это a y . Если векторы коллинеарны, то
| n = | б г | = | 6 | = 2 |
| а у | 3 |
Рассчитать значение na:
па = {2 · 0; 2 · 3} = {0; 6}
Поскольку b = 2a, векторы a и b коллинеарны.
Пример 3. Найти значение n, при котором векторы a = {3; 2} и б = {9; n} коллинеарны.
Решение: Так как вектор не содержит компонентов равных нулю, то используем условие коллинеарности 2
| a x | = | . | |
| б х | б г |
Средства:
| 3 | = | 2 | . |
| 9 | п |
Решите это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: векторов a и b коллинеарны при n = 6,
Примеры пространственных задач
Пример 4. Какой из векторов a = {1; 2; 3}, б = {4; 8; 12}, с = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты a равные нулю, то используем условие коллинеарности 2, что в случае плоской задачи для векторов a и b будет иметь вид:
| a x | = | = | а г | . | |
| б х | б г | б г |
Средние значения:
| Векторы a и b коллинеарны, потому что | 1 | = | 2 | = | 3 | . |
| 4 | 8 | 12 |
| Векторы а и с не коллинеарны, так как | 1 | = | 2 | ≠ | 3 | . |
| 5 | 10 | 12 |
| Векторы с и b не коллинеарны, так как | 5 | = | 10 | ≠ | 12 | . |
| 4 | 8 | 12 |
Пример 5. Докажите, что вектор a = {0; 3; 1} и б = {0; 6; 2} коллинеарны.
Докажите, что вектор a = {0; 3; 1} и б = {0; 6; 2} коллинеарны.
Решение: Так как компоненты вектора содержат ноль, то воспользовавшись условием коллинеарности 1, находим число n, для которого:
b = na.
Для этого находим ненулевую компоненту вектора а в данном случае это и . Если векторы коллинеарны, то
| n = | б г | = | 6 | = 2 |
| а у | 3 |
Рассчитать значение na:
па = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Поскольку b = 2a, векторы a и b коллинеарны.
Пример 6. Найти значения n и m, при которых векторы a = {3; 2; m} и b = {9; н; 12} коллинеарны.
Решение: Так как вектор не содержит компонентов равных нулю, то используем условие коллинеарности 2
| a x | = | = | а г | . | |
| б х | б г | б г |
Средства:
| 3 | = | 2 | = | м |
| 9 | п | 12 |
Из этих соотношений получаем два уравнения:
| 3 | = | 2 |
| 9 | п |
| 3 | = | м |
| 9 | 12 |
Решите следующие уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| м = | 3 · 12 | = 4 |
| 9 |
Ответ: векторов a и b коллинеарны, когда n = 6 и m = 4.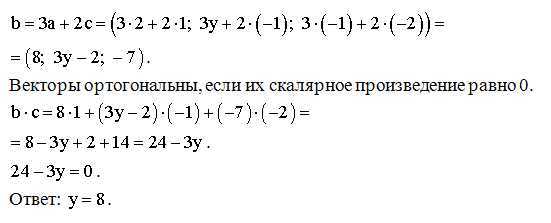
Векторы Определение векторов. Основная информация Компонентная форма вектора с начальной и конечной точками Длина вектора Направленные косинусы вектора Равные векторы Ортогональные векторы Коллинеарные векторы Компланарные векторы Угол между двумя векторами Векторная проекция Сложение и вычитание векторов Скалярно-векторное умножение Скалярное произведение двух векторов Перекрестное произведение двух векторов (векторное произведение) Скалярное тройное произведение (смешанный продукт) Линейно зависимые и линейно независимые векторы Разложение вектора по базису
Онлайн калькуляторы с векторами
Задания и упражнения с вектором 2D
Задания и упражнения с вектором 3D
Коллинеарные векторы — определения, условия, примеры
Коллинеарные векторы считаются одним из важных понятий в векторной алгебре. Когда два или более заданных вектора лежат вдоль одной и той же заданной прямой, то их можно рассматривать как коллинеарные векторы. Мы можем рассматривать два параллельных вектора как коллинеарные векторы, поскольку эти два вектора указывают точно в одном и том же направлении или в противоположном направлении.
Мы можем рассматривать два параллельных вектора как коллинеарные векторы, поскольку эти два вектора указывают точно в одном и том же направлении или в противоположном направлении.
В этой статье давайте узнаем о коллинеарных векторах, их определении, условиях коллинеарности векторов на решенных примерах.
| 1. | Что такое коллинеарные векторы? |
| 2. | Условия коллинеарных векторов |
| 3. | Часто задаваемые вопросы о коллинеарных векторах |
Что такое коллинеарные векторы?
Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем рассматривать любые два вектора как коллинеарные векторы тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.
Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.
На приведенной выше диаграмме векторы, параллельные одной прямой, коллинеарны друг другу, а пересекающиеся векторы неколлинеарны.
Условия коллинеарных векторов
Для того чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:
- Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует скаляр ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
- Условие 2. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
- Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору.
 Это условие применимо только к трехмерным или пространственным задачам.
Это условие применимо только к трехмерным или пространственным задачам.
Доказательство условия 3:
Рассмотрим два коллинеарных вектора \(\overrightarrow{a}\) = {\(a_{x}\),\(a_{y}\),\(a_{z}\ )} и \(\overrightarrow{b}\) = {n\(a_{x}\),n\(a_{y}\),n\(a_{z}\)}. Мы можем найти векторное произведение между ними как:
\(\overrightarrow{a}\) × \(\overrightarrow{b}\) = \(\left|\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
а_{х} и а_{у} и а_{г} \\
b_{x} и b_{y} и b_{z}
\end{массив}\right|\)
= i (\(a_{y}\)\(b_{z}\) — \(a_{z}\)\(b_{y}\)) — j (\(a_{x}\)\(b_{z}\) — \(a_{z}\)\(b_{x}\)) + k (\(a_{x}\)\(b_ {y}\) — \(a_{y}\)\(b_{x}\))
= i (\(a_{y}\)n\(a_{z}\) — \(a_{ z}\)n\(a_{y}\)) — j (\(a_{x}\)n\(a_{z}\) — \(a_{z}\)n\(a_{x} \)) + k (\(a_{x}\)n\(a_{y}\) — \(a_{y}\)n\(a_{x}\))
= 0i + 0j + 0k = \(\overrightarrow{0}\) [Поскольку разные компоненты одного и того же вектора перпендикулярны друг другу и, следовательно, их произведение равно 0. ]
]
Похожие статьи о коллинеарных векторах
Ознакомьтесь со следующими страницами, посвященными коллинеарному вектору
- Добавление калькулятора векторов
- Калькулятор угла между двумя векторами
- Обработка векторов, указанных в форме i-j
- Неравенство треугольников в векторах
- Вычитание двух векторов
Важные примечания о коллинеарных векторах
Вот несколько точек, которые следует помнить при изучении коллинеарных векторов
- Любые два данных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой .
- Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу.
Примеры коллинеарных векторов
Пример 1: Определите, являются ли заданные векторы коллинеарными векторами.
 \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).
\(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).Решение: Два вектора считаются коллинеарными, если отношения их соответствующих координат равны.
P 1 /Q 1 = 3/6 = 1/2
P 2 /Q 2 = 4/8 = 1/2
P 3 /Q 3 = 5/10 = 1/2
, так как P 1 /Q 1 = P 2 /Q 2 = P 3 /Q 3 , векторы \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.
Пример 2: Определите, являются ли заданные векторы коллинеарными векторами. \(\overrightarrow{P}\) = i + j + k, \(\overrightarrow{Q}\) = — i — j — k
Решение: Два вектора считаются коллинеарными векторами, если один вектор является скалярным кратным другого вектора.
Вектор Q = — i — j — k = — (i + j + k) = — (Вектор P)
⇒ Вектор Q является скалярным множителем вектора P.

Кроме того, поскольку P 1 /Q 1 = P 2 /Q 2 = P 3 /Q 3 = -1, векторы \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) могут быть рассматриваются как коллинеарные векторы.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о коллинеарных векторах
Что такое коллинеарные векторы?
Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.
Как узнать, является ли вектор коллинеарным?
Для того, чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:
- Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует число ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
- Условие 2. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
- Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.
Параллельные и коллинеарные векторы — одно и то же?
Да, параллельные и коллинеарные векторы — это одно и то же. Два вектора называются коллинеарными, если они имеют одинаковое направление, параллельны или антипараллельны. Два вектора параллельны, если они имеют одинаковое или противоположное направление.
Два вектора называются коллинеарными, если они имеют одинаковое направление, параллельны или антипараллельны. Два вектора параллельны, если они имеют одинаковое или противоположное направление.
Как доказать коллинеарность трех позиционных векторов?
Рассмотрим три отрезка PQ, QR и PR. Если PQ + QR = PR, то мы можем считать эти три точки коллинеарными. Три заданных сегмента линии могут быть переведены в соответствующие векторы PQ, QR и PR. Величины этих трех векторов равны длине трех отрезков, упомянутых здесь.
Приведите пример коллинеарных векторов
Рассмотрим два вектора \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10). Два вектора считаются коллинеарными, если отношения их координат равны.
P 1 /Q 1 = 3/6 = 1/2
P 2 /Q 2 = 4/8 = 1/2
Так как P 1 /Q 1 = P 2 /Q 2 = P 3 0 7 , 1 /Q 3 900 \overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.
Что такое неколлинеарные векторы?
Векторы считаются неколлинеарными, если они расположены в одной плоскости, но не действуют вдоль одной и той же линии действия.
Как найти коллинеарные векторы в трех измерениях?
Два вектора \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.
40 вопросов по машинному обучению (с решениями) для проверки Data Scientist
Введение
Машинное обучение — один из самых востребованных навыков в наши дни. Если вы специалист по обработке и анализу данных, вам нужно хорошо разбираться в машинном обучении. В рамках DataFest 2017 мы организовали различные тесты навыков, чтобы ученые, работающие с данными, могли оценить свои навыки. Эти тесты включали машинное обучение, глубокое обучение, проблемы временных рядов и вероятность. В этой статье будут представлены решения для теста на навыки машинного обучения. Если вы пропустили какой-либо из вышеперечисленных тестов навыков, вы все равно можете ознакомиться с вопросами и ответами в статьях, указанных выше.
Если вы пропустили какой-либо из вышеперечисленных тестов навыков, вы все равно можете ознакомиться с вопросами и ответами в статьях, указанных выше.
В тесте навыков машинного обучения зарегистрировалось более 1350 человек. Тест был разработан, чтобы проверить ваши концептуальные знания в области машинного обучения и подготовить вас к работе в отрасли. Если вы пропустили тест в реальном времени, вы все равно можете прочитать эту статью, чтобы узнать, как вы могли ответить правильно. Кроме того, ознакомьтесь с нашим онлайн-тренингом по машинному обучению.
Вот рейтинг всех участников теста машинного обучения.
Эти вопросы, наряду с сотнями других, являются частью нашего курса «Интервью с Ace Data Science». Это всеобъемлющее руководство с кучей ресурсов, которое поможет вам пройти интервью по науке о данных и получить роль своей мечты! А если вы только начинаете свой путь в науке о данных, ознакомьтесь с нашей самой полной программой для освоения машинного обучения 9. 0003
0003
- Сертифицированная программа AI & ML BlackBelt+
- Сертификационный курс по машинному обучению для начинающих
Общий балл
Ниже приведены баллы распределения, они помогут вам оценить вашу работу.
Вы можете просмотреть окончательные результаты здесь. В тесте на навыки машинного обучения приняли участие более 210 человек, и наивысший результат составил 36. Вот несколько статистических данных о распределении.
Средний балл: 19,36
Средний балл: 21
Очки режима: 27
Полезные ресурсы по обучению Mahchine
Основы машинного обучения для новичка
Глубокое обучение против машинного обучения — существенные различия, которые вам нужно знать!
Курс прикладного машинного обучения
Курс «Введение в науку о данных»
Курс интервью с Ace Data Science
Вопросы и решения по машинному обучению
Контекст вопроса
Функция F1 может принимать определенные значения: A, B, C, D, E и F и представляет собой оценку учащихся колледжа.
1) Какое из следующих утверждений верно в следующем случае?
A) Элемент F1 является примером номинальной переменной.
B) Функция F1 является примером порядковой переменной.
C) Не принадлежит ни к одной из перечисленных выше категорий.
D) Оба этих
Решение: (Б)
Порядковые переменные — это переменные, категории которых имеют некоторый порядок. Например, класс A следует рассматривать как более высокий класс, чем класс B.
2) Что из следующего является примером детерминированного алгоритма?
А) PCA
Б) K-средства
C) Ничего из вышеперечисленного
Решение: (A) Детерминированный алгоритм — это алгоритм, в котором выходные данные не меняются при различных запусках. PCA даст тот же результат, если мы запустим снова, но не k-средних.
3) [Верно или неверно] Корреляция Пирсона между двумя переменными равна нулю, но тем не менее их значения могут быть связаны друг с другом.
А) ИСТИНА
Б) ЛОЖЬ
Решение: (A)
Y = X 2. Обратите внимание, что они не только связаны, но и являются функцией друг друга, и корреляция Пирсона между ними равна 0,
4) Какое из следующих утверждений верно для градиентного приличия (GD) и стохастического градиентного приличия (SGD)?
- В GD и SGD вы итеративно обновляете набор параметров, чтобы минимизировать функцию ошибки.
- В SGD вам необходимо пройти через все образцы в вашем обучающем наборе для одного обновления параметра в каждой итерации.
- В GD вы либо используете все данные, либо подмножество обучающих данных для обновления параметра на каждой итерации.
A) Только 1
B) Только 2
C) Только 3
D) 1 и 2
E) 2 и 3
F) 1,2 и 3
Решение: (A) В SGD для каждой итерации вы выбираете пакет, который обычно содержит случайную выборку данных Но в случае GD каждая итерация содержит все обучающие наблюдения.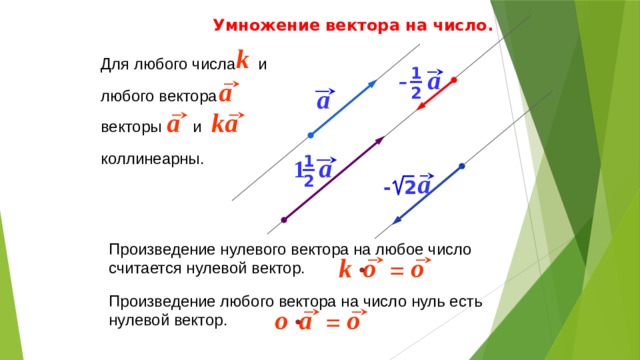
5) Увеличение какого из следующих гиперпараметров может привести к тому, что случайный лес будет соответствовать данным?
- Количество деревьев
- Глубина дерева
- Скорость обучения
A) Только 1
B) Только 2
C) Только 3
D) 1 и 2
E) 2 и 3
F) 1,2 и 3
6) Представьте, вы работаете с «Аналитикой Видхья» и хотите разработать алгоритм машинного обучения, предсказывающий количество просмотров статей.
Ваш анализ основан на таких функциях, как имя автора, количество статей, написанных одним и тем же автором в Analytics Vidhya в прошлом, и некоторых других функциях. Какой из следующих показателей оценки вы бы выбрали в этом случае?
Какой из следующих показателей оценки вы бы выбрали в этом случае?
- Среднеквадратическая ошибка
- Точность
- Очки F1
A) Только 1
B) Только 2
C) Только 3
D) 1 и 3
E) 2 и 3
F) 1 и 2
Решение: (A)
Можно подумать, что количество просмотров статей является непрерывной целевой переменной, которая подпадает под задачу регрессии. Таким образом, в качестве оценочной метрики будет использоваться среднеквадратическая ошибка.
7) Ниже приведены три изображения (1,2,3). Какой из следующих вариантов подходит для этих изображений?
A)
B)
C)
A) 1 – tanh, 2 – ReLU и 3 – функции активации SIGMOID.
B) 1 — SIGMOID, 2 — ReLU и 3 — функции активации tanh.
C) 1 — ReLU, 2 — tanh и 3 — функции активации SIGMOID.
D) 1 – это tanh, 2 – SIGMOID и 3 – функции активации ReLU.
Решение: (D)
Диапазон функции SIGMOID равен [0,1].
Диапазон функции tanh: [-1,1].
Диапазон функции RELU: [0, бесконечность].
Итак, вариант D — правильный ответ.
8) Ниже приведены 8 фактических значений целевой переменной в файле поезда.
[0,0,0,1,1,1,1,1]
Какова энтропия целевой переменной?
А) -(5/8 log(5/8) + 3/8 log(3/8))
B) 5/8 лог.(5/8) + 3/8 лог.(3/8)
C) 3/8 лог.(5/8) + 5/8 лог.(3/8)
D) 5/8 log(3/8) – 3/8 log(5/8)
Решение: (A) Формула для энтропии:
Таким образом, ответ A.
9) Допустим, вы работаете с категориальными признаками и не смотрели на распределение категориальной переменной в тестовых данных.
Вы хотите применить одно горячее кодирование (OHE) к категориальным функциям. С какими проблемами вы можете столкнуться, если примените OHE к категориальной переменной набора данных поезда?
С какими проблемами вы можете столкнуться, если примените OHE к категориальной переменной набора данных поезда?
A) Все категории категориальной переменной отсутствуют в тестовом наборе данных.
B) Частотное распределение категорий в поезде отличается от набора тестовых данных.
C) Обучение и тестирование всегда имеют одинаковое распределение.
D) Оба A и B
E) Ни один из этих
Решение: (D) Оба верны, OHE не сможет закодировать категории, которые присутствуют в тесте, но не в поезде, так что это может быть одна основных проблем при применении OHE. Проблема, указанная в варианте B, также верна, вам нужно быть более осторожным при применении OHE, если распределение частот не совпадает при обучении и тестировании.
10) Модель пропуска грамм — одна из лучших моделей, используемых в алгоритме Word2vec для встраивания слов. Какая из следующих моделей описывает модель пропуска грамма?
A) A
B) B
C) Обе A и B
D) Ни одна из этих
Решение: (B)
В алгоритме Word2vec используются обе модели (model1 и model2). Model1 представляет собой модель CBOW, где Model2 представляет модель Skip gram.
Model1 представляет собой модель CBOW, где Model2 представляет модель Skip gram.
11) Допустим, вы используете функцию активации X в скрытых слоях нейронной сети. На конкретном нейроне для любого заданного ввода вы получаете вывод как «-0,0001». Какую из следующих функций активации может представлять X?
А) РеЛУ
B) tanh
C) SIGMOID
D) Ни один из этих
Решение: (B) Функция представляет собой тангенс, потому что выходной диапазон этой функции находится между (-1,-1).
12) [True или False] Метрика оценки LogLoss может иметь отрицательные значения.
А) ИСТИНА
Б) ЛОЖЬ
Решение: (B) Потеря журнала не может иметь отрицательных значений.
13) Какое из следующих утверждений верно/верны в отношении ошибок «Тип-1» и «Тип-2»?
- Тип 1 известен как ложноположительный, а тип 2 известен как ложноотрицательный.

- Тип 1 известен как ложноотрицательный, а тип 2 известен как ложноположительный.
- Ошибка типа 1 возникает, когда мы отклоняем нулевую гипотезу, когда она на самом деле верна.
А) Только 1
B) Только 2
C) Только 3
D) 1 и 2
E) 1 и 3
F) 2 и 3
Решение: (E)
При проверке статистических гипотез ошибкой первого рода является неправильное отклонение истинной нулевой гипотезы («ложноположительный результат»), а ошибкой второго рода является неправильное сохранение ложной нулевой гипотезы («ложноотрицательный результат»).
14) Что из перечисленного ниже является одним из важных шагов предварительной обработки текста в проектах на основе НЛП?
- Стэмминг
- Удаление стоп-слов
- Стандартизация объекта
А) 1 и 2
B) 1 и 3
C) 2 и 3
D) 1,2 и 3
Решение: (D)
Выделение корней – это рудиментарный процесс удаления суффиксов («ing»), основанный на правилах. , «лы», «эс», «с» и т. д.) от слова.
, «лы», «эс», «с» и т. д.) от слова.
Стоп-слова — это те слова, которые не имеют отношения к контексту данных, например is/am/are.
Стандартизация объектов также является одним из хороших способов предварительной обработки текста.
15) Предположим, вы хотите спроецировать многомерные данные в более низкие измерения. Здесь используются два наиболее известных алгоритма уменьшения размерности — PCA и t-SNE. Допустим, вы применили оба алгоритма соответственно к данным «X» и получили наборы данных «X_projected_PCA», «X_projected_tSNE».
Какое из следующих утверждений верно для «X_projected_PCA» и «X_projected_tSNE»?
A) X_projected_PCA будет иметь интерпретацию в ближайшем соседнем пространстве.
B) X_projected_tSNE будет иметь интерпретацию в ближайшем соседнем пространстве.
C) Оба будут иметь интерпретацию в ближайшем соседнем пространстве.
D) Ни один из них не будет иметь интерпретации в ближайшем соседнем пространстве.
Решение: (B)
Алгоритм t-SNE рассматривает ближайшие соседние точки для уменьшения размерности данных. Итак, после использования t-SNE мы можем думать, что уменьшенные измерения будут иметь интерпретацию и в ближайшем соседнем пространстве. Но в случае с ПП это не так.
Контекст: 16-17Ниже приведены три диаграммы рассеяния для двух функций (изображения 1, 2 и 3 слева направо).
16) Какие из приведенных выше изображений являются примерами мультиколлинеарных объектов?
А) Особенности на изображении 1
B) Элементы на изображении 2
C) Элементы на изображении 3
D) Элементы на изображении 1 и 2
E) Элементы на изображении 2 и 3
F) Элементы на изображениях 3 и 1
Решение: (D)
На изображении 1 признаки имеют высокую положительную корреляцию, тогда как на изображении 2 имеется высокая отрицательная корреляция между признаками, поэтому на обоих изображениях парой признаков являются пример мультиколлинеарных признаков.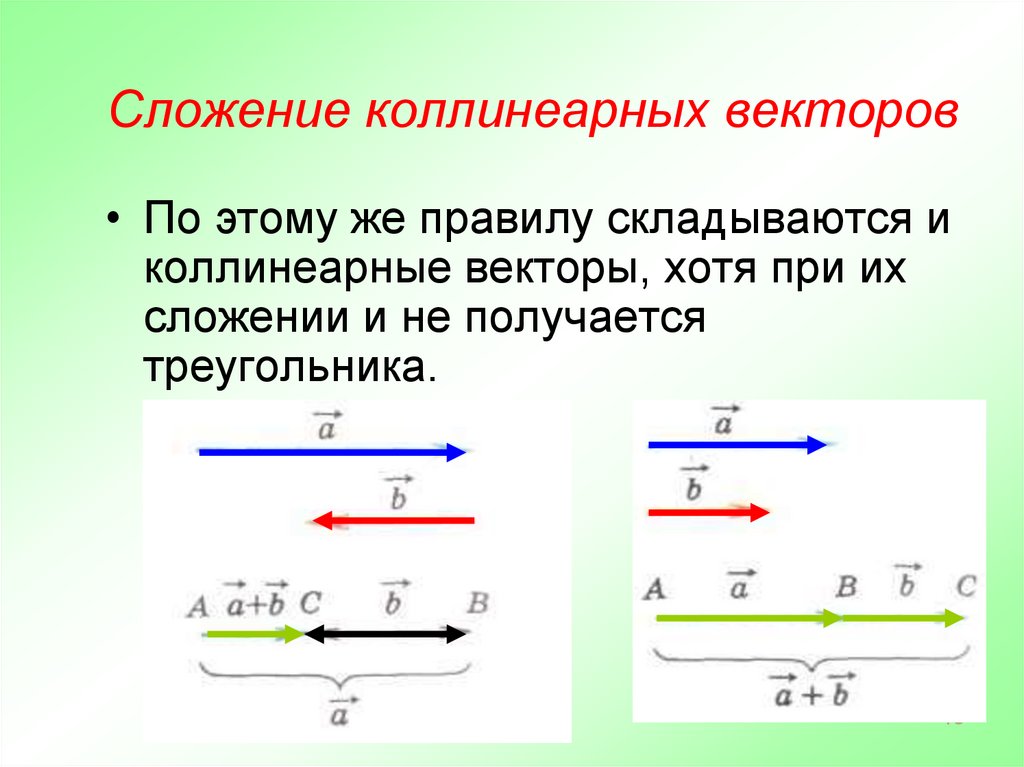
17) В предыдущем вопросе предположим, что вы определили мультиколлинеарные объекты. Какое из следующих действий вы бы выполнили следующим?
- Удалить обе коллинеарные переменные.
- Вместо удаления обеих переменных мы можем удалить только одну переменную.
- Удаление коррелированных переменных может привести к потере информации. Чтобы сохранить эти переменные, мы можем использовать модели регрессии со штрафом, такие как регрессия гребня или регрессия лассо.
А) Только 1
B) Только 2
C) Только 3
D) 1 или 3
E) 2 или 3
Решение: (E)
после удаления обеих функций невозможно функции, вы потеряете всю информацию, поэтому вам следует либо удалить единственную функцию, либо использовать алгоритм регуляризации, такой как L1 и L2.
18) Добавление неважной функции в модель линейной регрессии может привести к.
- Увеличение R-квадрата
- Уменьшение R-квадрата
А) Только 1 правильный
B) Верно только 2
C) Либо 1, либо 2
D) Ни один из этих
Решение: (A)
После добавления функции в пространство функций, независимо от того, является ли эта функция важной или неважной. R-квадрат всегда увеличивается.
19) Предположим, вам даны три переменные X, Y и Z. Коэффициенты корреляции Пирсона для (X, Y), (Y, Z) и (X, Z) равны C1, C2 и C3 соответственно.
Теперь вы прибавили 2 ко всем значениям X (т.е. новые значения становятся X+2), вычли 2 из всех значений Y (т.е. новые значения Y-2) и Z осталось прежним. Новые коэффициенты для (X,Y), (Y,Z) и (X,Z) задаются D1, D2 и D3 соответственно. Как значения D1, D2 и D3 связаны с C1, C2 и C3?
А) D1= C1, D2 < C2, D3 > C3
B) D1 = C1, D2 > C2, D3 > C3
C) D1 = C1, D2 > C2, D3 < C3
D) D1 = C1, D2 < C2, D3 < C3
E) D1 = C1, D2 = C2, D3 = C3
F) Невозможно определить
Решение: (E) Корреляция между признаками не изменится, если вы добавите или вычтете значение в признаках.
20) Представьте, что вы решаете задачу классификации с сильно несбалансированным классом. Наблюдается класс большинства 99% раз в тренировочных данных.
Ваша модель имеет точность 99 % после прогнозов на основе тестовых данных. Что из следующего верно в таком случае?
- Метрика точности не является хорошей идеей для проблем несбалансированного класса.
- Метрика точности — хорошая идея для проблем несбалансированного класса.
- Показатели точности и полноты хороши для задач несбалансированного класса.
- Показатели точности и полноты не годятся для задач с несбалансированным классом.
А) 1 и 3
B) 1 и 4
C) 2 и 3
D) 2 и 4
Решение: (A) См. вопрос № 4 из этой статьи.
21) При ансамблевом обучении вы агрегируете прогнозы для слабых учеников, так что ансамбль этих моделей дает лучший прогноз, чем прогноз отдельных моделей.
Какое из следующих утверждений верно для слабых учеников, используемых в ансамблевой модели?
- Обычно они не подходят.
- У них высокая предвзятость, поэтому они не могут решать сложные учебные задачи
- Обычно они переобуваются.
А) 1 и 2
B) 1 и 3
C) 2 и 3
D) Только 1
E) Только 2
F) Ничего из вышеперечисленного
конкретная часть проблемы. Таким образом, они обычно не переобучаются, что означает, что слабые ученики имеют низкую дисперсию и высокую предвзятость.
22) Какой из следующих вариантов верен для K-кратной перекрестной проверки?
- Увеличение K приведет к увеличению времени, необходимого для перекрестной проверки результата.
- Чем выше значение K, тем выше достоверность результатов перекрестной проверки по сравнению с более низким значением K.

- Если K=N, то это называется Перекрёстная проверка без исключения, где N — количество наблюдений.
А) 1 и 2 1, 2 и 3 будет ближе к общему набору данных) и больше времени выполнения (поскольку вы приближаетесь к предельному случаю: резюме «Оставить один-выход»). Нам также необходимо учитывать разницу между точностью k кратности при выборе k.
Контекст вопроса 23-24
Перекрестная проверка — важный шаг в машинном обучении для настройки гиперпараметров. Допустим, вы настраиваете гиперпараметр «max_depth» для GBM, выбирая его из 10 различных значений глубины (значения больше 2) для древовидной модели с использованием 5-кратной перекрестной проверки.
Время, затрачиваемое алгоритмом на обучение (на модели с max_depth 2) 4-кратного, составляет 10 секунд, а для прогнозирования оставшегося 1-кратного — 2 секунды.
Примечание. В уравнении игнорируйте аппаратные зависимости.
23) Какой из следующих вариантов верен для общего времени выполнения для 5-кратной перекрестной проверки с 10 различными значениями «max_depth»?
А) Менее 100 секунд
B) 100 – 300 секунд
C) 300 – 600 секунд
D) Больше или равно 600 секунд
C) Ничего из вышеперечисленного
D) Не могу оценить
: Решение (D) )
Каждая итерация для глубины «2» в 5-кратной перекрестной проверке будет занимать 10 секунд для обучения и 2 секунды для тестирования. Итак, 5 сгибов займут 12*5=60 секунд. Поскольку мы ищем более 10 значений глубины, алгоритм займет 60 * 10 = 600 секунд. Но обучение и тестирование модели на глубине больше 2 займет больше времени, чем на глубине «2», поэтому общее время будет больше 600.
24) В предыдущем вопросе, если вы обучаете один и тот же алгоритм для настройки двух гиперпараметров, скажите «max_depth» и «learning_rate».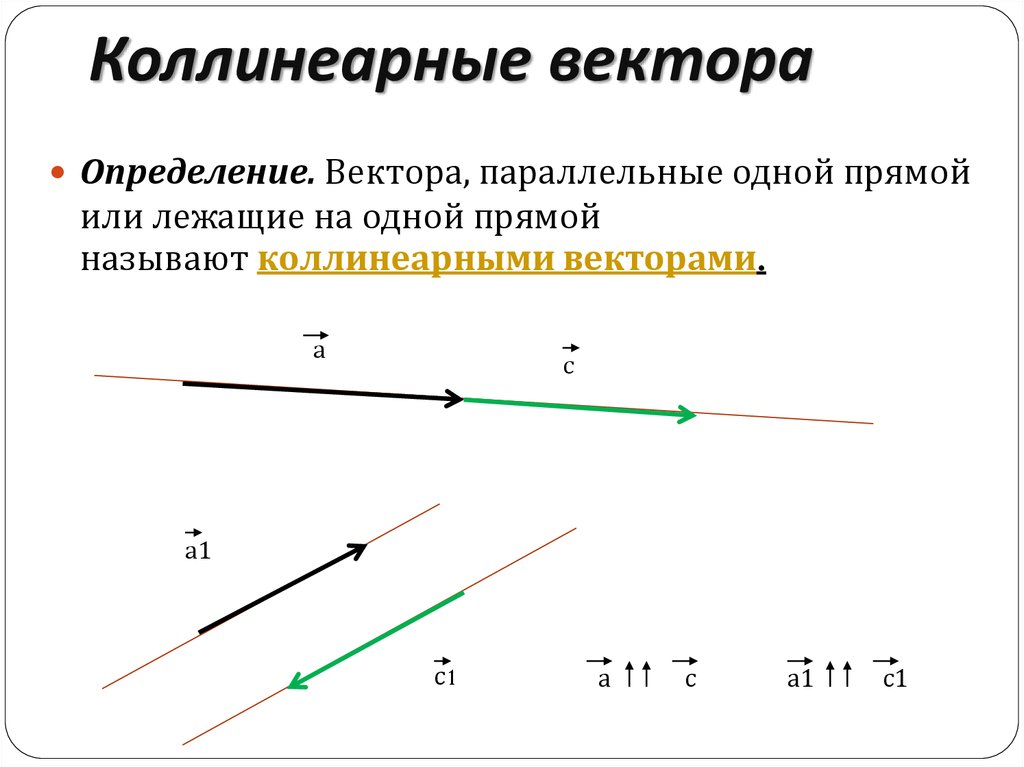
Вы хотите выбрать правильное значение для «max_depth» (из заданных 10 значений глубины) и скорости обучения (из заданных 5 различных скоростей обучения). В таких случаях, что из следующего будет представлять общее время?
A) 1000-1500 секунд
B) 1500-3000 секунд
C) Больше или равно 3000 секунд
D) Ничего из перечисленного
25) Ниже приведен сценарий для ошибки обучения TE и ошибки проверки VE для алгоритма машинного обучения M1. Вы хотите выбрать гиперпараметр (H) на основе TE и VE.
| Н | ТЭ | ВЭ |
| 1 | 105 | 90 |
| 2 | 200 | 85 |
| 3 | 250 | 96 |
| 4 | 105 | 85 |
| 5 | 300 | 100 |
Какое значение H вы выберете на основе приведенной выше таблицы?
А) 1
B) 2
C) 3
D) 4
E) 5
Решение: (D) Глядя на таблицу, вариант D кажется лучшим
26) Что бы вы сделали в ППШ, чтобы получить такую же проекцию, как у СВД?
A) Преобразование данных в нулевое среднее значение
B) Преобразование данных в нулевую медиану
C) Невозможно
D) Ничего из этого
Решение: (A) Когда данные имеют вектор с нулевым средним значением, PCA будет иметь те же проекции, что и SVD, в противном случае у вас есть сначала центрировать данные, прежде чем принимать SVD.
Контекст вопроса 27-28
Предположим, что существует алгоритм черного ящика, который использует обучающие данные с несколькими наблюдениями (t1, t2, t3,…….. tn) и новым наблюдением (q1). Черный ящик выводит ближайшего соседа q1 (скажем, ti) и соответствующую ему метку класса ci.
Вы также можете подумать, что этот алгоритм черного ящика такой же, как 1-NN (1-ближайший сосед).
27) Можно построить алгоритм классификации k-NN только на основе этого черного ящика.
Примечание. Где n (количество обучающих наблюдений) очень велико по сравнению с k.
ПРАВДА
B) ЛОЖЬ
Решение: (A)
На первом этапе вы передаете наблюдение (q1) в алгоритм черного ящика, чтобы этот алгоритм возвращал ближайшее наблюдение и его класс.
На втором этапе вы выбираете ближайшее наблюдение из данных поезда и снова вводите наблюдение (q1).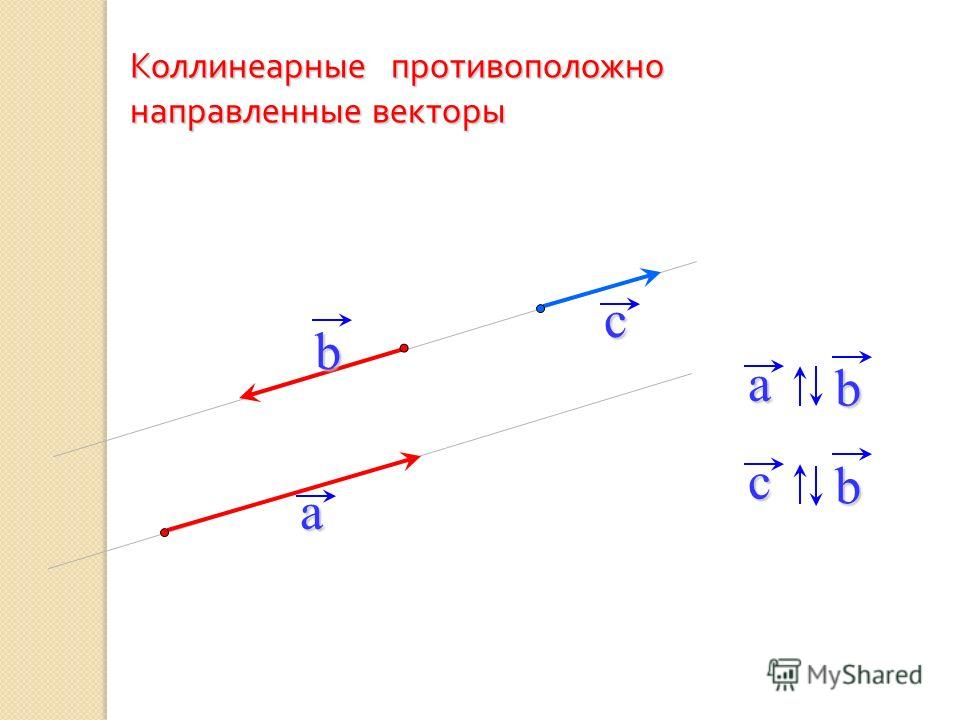 Алгоритм черного ящика снова вернет ближайшее наблюдение и его класс.
Алгоритм черного ящика снова вернет ближайшее наблюдение и его класс.
Вам нужно повторить эту процедуру k раз
28) Вместо использования черного ящика 1-NN мы хотим использовать алгоритм j-NN (j>1) в качестве черного ящика. Какой из следующих вариантов является правильным для нахождения k-NN с помощью j-NN?
- J должен быть правильным коэффициентом k
- Дж > k
- Невозможно
А) 1
B) 2
C) 3
Решение: (A) То же, что и в вопросе № 27
29) Предположим, вам дано 7 диаграмм рассеяния 1-7 (слева направо), и вы хотите сравнить коэффициенты корреляции Пирсона между переменными каждой диаграммы рассеяния.
Что из следующего в правильном порядке?
- 1<2<3<4
- 1>2>3 > 4
- 7<6<5<4
- 7>6>5>4
А) 1 и 3
B) 2 и 3
C) 1 и 4
D) 2 и 4
Решение: (B)
на изображениях с 1 по 4 корреляция уменьшается (абсолютное значение). Но от изображения 4 к 7 корреляция увеличивается, но значения отрицательные (например, 0, -0,3, -0,7, -0,99).
Но от изображения 4 к 7 корреляция увеличивается, но значения отрицательные (например, 0, -0,3, -0,7, -0,99).
30) Вы можете оценить производительность задачи классификации бинарных классов, используя различные показатели, такие как точность, потери журнала, F-Score. Допустим, вы используете функцию логарифмических потерь в качестве метрики оценки.
Какой из следующих вариантов является верным для интерпретации log-loss как показателя оценки?
-
Если классификатор уверен в неправильной классификации, то потеря журнала сильно накажет его. - Для конкретного наблюдения классификатор назначает очень маленькую вероятность для правильного класса, тогда соответствующий вклад в логарифмическую потерю будет очень большим.
- Чем меньше логарифмическая потеря, тем лучше модель.
А) 1 и 3
B) 2 и 3
C) 1 и 2
D) 1,2 и 3
Решение: (D) Варианты говорят сами за себя.
Контекстный вопрос 31-32
Ниже приведены пять образцов, приведенных в наборе данных.
Примечание. Визуальное расстояние между точками на изображении представляет собой фактическое расстояние.
31) Что из следующего является точностью перекрестной проверки с исключением одного для 3-NN (3-ближайшего соседа)?
А) 0
D) 0,4
C) 0,8
D) 1
Решение: (C)
Проверка. Рассматривайте каждую точку как точку перекрестной проверки, а затем найдите 3 точки, ближайшие к этой точке. Таким образом, если вы повторите эту процедуру для всех точек, вы получите правильную классификацию для всех положительных классов, указанных на рисунке выше, но отрицательный класс будет классифицирован неправильно. Следовательно, вы получите 80% точности.
32) Какое из следующих значений K будет иметь наименьшую точность перекрестной проверки при исключении одного?
А) 1NN
B) 3NN
C) 4NN
D) Все имеют одну и ту же ошибку:
Решение: (A) Каждая точка, которая всегда будет неправильно классифицирована в 1-NN, что означает, что вы получите 0% точность.
33) Предположим, вам даны приведенные ниже данные, и вы хотите применить модель логистической регрессии для их классификации по двум заданным классам.
Вы используете логистическую регрессию с регуляризацией L1.
Где C — параметр регуляризации, а w1 и w2 — коэффициенты x1 и x2.
Какой из следующих вариантов является правильным при увеличении значения C от нуля до очень большого значения?
А) Сначала w2 становится равным нулю, а затем w1 становится равным нулю.
B) Сначала w1 становится равным нулю, а затем w2 становится равным нулю
C) Оба значения становятся равными нулю одновременно
D) Оба не могут быть равны нулю даже при очень большом значении C
Решение: (B)
Глядя на изображение, мы видим, что даже при простом использовании x2 мы можем эффективно выполнять классификацию. Таким образом, сначала w1 станет равным 0. По мере увеличения параметра регуляризации w2 будет все больше и больше приближаться к 0.
По мере увеличения параметра регуляризации w2 будет все больше и больше приближаться к 0.
34) Предположим, у нас есть набор данных, который можно обучить со 100% точностью с помощью дерева решений глубины 6. Теперь рассмотрим пункты ниже и выберем вариант на основе этих пунктов.
Примечание. Все остальные гиперпараметры одинаковы и не влияют на другие факторы.
- Глубина 4 будет иметь высокое смещение и низкую дисперсию
- Глубина 4 будет иметь низкое смещение и низкую дисперсию
А) Только 1
B) Только 2
C) Оба 1 и 2
D) Ничего из вышеперечисленного
Решение: (A) данные. Таким образом, в случае недообучения у вас будет высокое смещение и низкая дисперсия.
35) Какой из следующих вариантов можно использовать для получения глобальных минимумов в алгоритме k-средних?
- Попробуйте запустить алгоритм для другой инициализации центроида
- Настройка числа итераций
- Узнать оптимальное количество кластеров
А) 2 и 3
B) 1 и 3
C) 1 и 2
D) Все вышеперечисленное
Решение: (D) Все параметры можно настроить для поиска глобальных минимумов.
36) Представьте, что вы работаете над проектом, который представляет собой задачу бинарной классификации. Вы обучили модель набору обучающих данных и получили приведенную ниже матрицу путаницы в наборе данных проверки.
Основываясь на приведенной выше матрице путаницы, выберите, какие варианты ниже дадут вам правильные прогнозы?
- Точность ~0,91
- Коэффициент ошибочной классификации ~ 0,91
- Частота ложных срабатываний составляет ~0,95
- Истинный положительный результат ~ 0,95
А) 1 и 3
B) 2 и 4
C) 1 и 4
D) 2 и 3
Решение: (C)
Точность (правильная классификация) равна (50+100)/165, что почти равно до 0,91.
Истинная положительная частота — это количество раз, когда вы правильно прогнозируете положительный класс, поэтому истинная положительная частота будет 100/105 = 0,95, также известная как «Чувствительность» или «Отзыв»
37) Для какого из следующих гиперпараметров большее значение лучше для алгоритма дерева решений?
- Количество образцов, используемых для разделения
- Глубина дерева
- Образцы листьев
А) 1 и 2
B) 2 и 3
C) 1 и 3
D) 1, 2 и 3
E) Затрудняюсь ответить
Решение: (E)
Для всех трех вариантов A, B и C, нет необходимости, чтобы при увеличении значения параметра производительность могла возрасти. Например, если у нас очень высокое значение глубины дерева, результирующее дерево может перекрыть данные и не будет хорошо обобщаться. С другой стороны, если у нас очень низкое значение, дерево может не соответствовать данным. Так что нельзя однозначно сказать, что «чем выше, тем лучше».
Например, если у нас очень высокое значение глубины дерева, результирующее дерево может перекрыть данные и не будет хорошо обобщаться. С другой стороны, если у нас очень низкое значение, дерево может не соответствовать данным. Так что нельзя однозначно сказать, что «чем выше, тем лучше».
Контекст 38-39
Представьте, что у вас есть изображение размером 28 * 28, и вы запускаете на нем нейронную сеть свертки 3 * 3 с глубиной ввода 3 и глубиной вывода 8.
Примечание. Шаг равен 1, и вы используете те же отступы.
38) Какова размерность выходной карты объектов при использовании заданных параметров.
А) 28 в ширину, 28 в высоту и 8 в глубину
B) 13 ширина, 13 высота и 8 глубина
C) 28 ширины, 13 высоты и 8 глубины
D) 13 ширины, 28 высоты и 8 глубины
Решение: (A) Формула для расчета выходного размера:
выходной размер = (N – F) /S + 1
, где N — размер ввода, F — размер фильтра, а S — шаг.
Прочитайте эту статью, чтобы лучше понять.
39) Каковы размеры выходной карты объектов при использовании следующих параметров.
А) ширина 28, высота 28 и глубина 8
B) 13 ширины, 13 высоты и 8 глубины
C) 28 ширины, 13 высоты и 8 глубины
D) 13 ширины, 28 высоты и 8 глубины
Решение: (B) То же, что и выше
40) Предположим, мы строили визуализацию для разных значений C (параметр Penalty) в алгоритме SVM. По какой-то причине мы забыли пометить значения C визуализациями. В этом случае, какой из следующих вариантов лучше всего объясняет значения C для изображений ниже (1,2,3 слева направо, поэтому значения C равны C1 для изображения 1, C2 для изображения 2 и C3 для изображения 3) в случае ядра rbf.
А) С1 = С2 = С3
B) C1 > C2 > C3
C) C1 < C2 < C3
D) Ничего из перечисленного
Решение: (C)
Штрафной параметр C условия ошибки.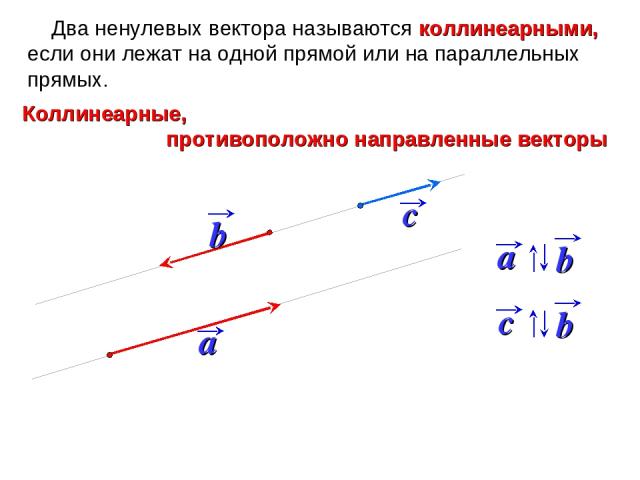


 На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач.
На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач.
 Это условие применимо только к трехмерным или пространственным задачам.
Это условие применимо только к трехмерным или пространственным задачам. \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).
\(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).

