Составить уравнение прямой онлайн по двум точкам или в пространстве
Пример решили: 43897 раз Сегодня решили: 0 раз
Введите координаты точки
Плоскость (2 координаты)
Пространство (3 координаты)
x1 y1 x2 y2
x1 y1 z1
x2 y2 z2
Составление уравнения прямой
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Данный онлайн-сервис поможет составить уравнение прямой в двухмерном или трехмерном пространстве.
Прямая – линия, путь которой равен расстоянию между двумя точками.
Через любые две несовпадающие точки можно провести прямую, притом только одну.
Две несовпадающие прямые на плоскости являются параллельными или пересекаются в одной точке.
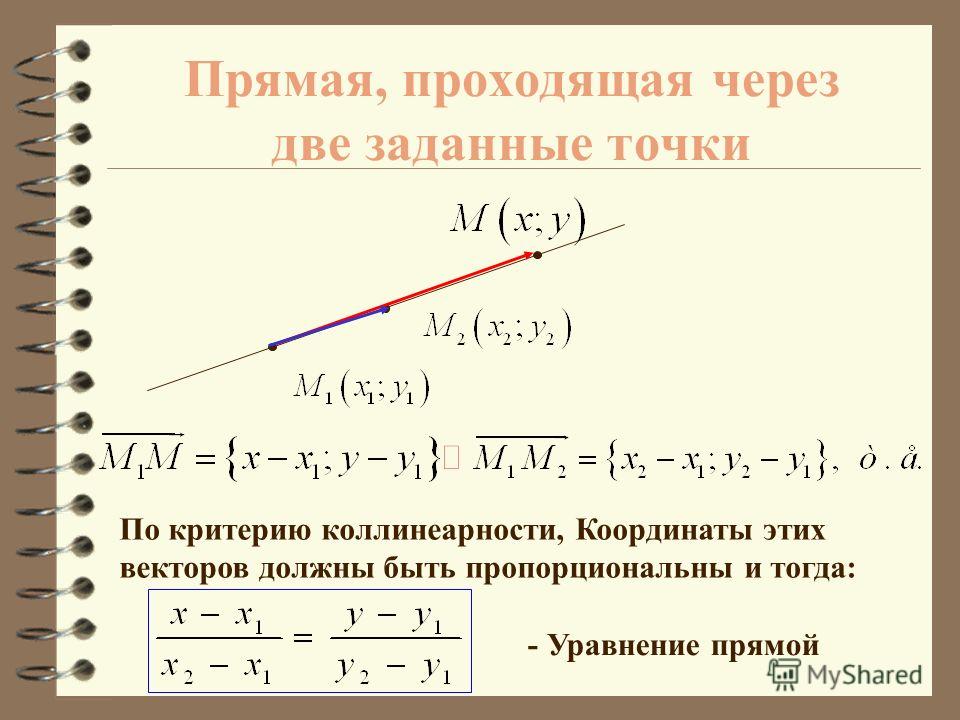
Уравнение прямой по двум точкам (на плоскости):
$$ {x-x_1 \over x_2 — x_1} = {y — y_1 \over y_2 — y_1}$$
Уравнение прямой в пространстве:
$$ {x-x_1 \over x_2 — x_1} = {y — y_1 \over y_2 — y_1} = {z — z_1 \over z_2 — z_1}$$
Примеры решений
- Составьте уравнение прямой на плоскости, проходящей через точки А(3;-4) и В(-6;12).
Посмотреть решениеРешение:
Запишем общее уравнение прямой на плоскости:
$$ \frac{(x-x1)}{(x2-x1)}= \frac{(y-y1)}{(y2-y1)} $$
По условию задачи получим значения:
$$ x1=3 $$
$$ x2=-6 $$
$$ y1=-4 $$
$$ y2=12 $$
Произведем подстановку:
$$ \frac{(x-3)}{(-6-3)} = \frac{(y+4)}{(12+4)} $$
$$ -\frac{(x-3)}{9}= \frac{(y+4)}{16} $$ – уравнение прямой.

Ответ:
$$ -\frac{(x-3)}{9}= \frac{(y+4)}{16} $$
- Составьте уравнение прямой в пространстве, которая проходит через точки М(2;-4;5) и К(4;12;-3).
Посмотреть решениеРешение:
Сначала записываем уравнение для прямой в пространстве в общем виде:
$$ \frac{(x-x1)}{(x2-x1)}= \frac{(y-y1)}{(y2-y1)}=\frac{(z-z1)}{(z2-z1)} $$
Запишем значения координат:
$$ x1=2 $$
$$ x2=4 $$
$$ y1=-4 $$
$$ y2=12 $$
$$ z1=5 $$
$$ z2=-3 $$
Произведем подстановку:
$$ \frac{(x-2)}{(4-2)}= \frac{(y+4)}{(12+4)}=\frac{(z-5)}{(-3-5)} $$
$$ \frac{(x-2)}{2}=\frac{(y+4)}{16}=-\frac{(z-5)}{8} $$ – уравнение прямой.
Ответ:
$$ \frac{(x-2)}{2}=\frac{(y+4)}{16}=-\frac{(z-5)}{8} $$
- Треугольник АВС имеет координаты вершин А(1;3), В(5;-1) и С(0;-4).
 Составьте уравнение прямой, на которой лежит медиана, выходящая из вершины С.
Составьте уравнение прямой, на которой лежит медиана, выходящая из вершины С.
Посмотреть решениеРешение:
Для того, чтобы составить уравнение прямой, необходимо найти координаты двух точек, через которые она проходит. Первая точка С(0;-4). Вторая точка М лежит на середине стороны АВ треугольника. Ее координаты находим по формуле:
$$ х=\frac{(х1+х2)}{2}, у=\frac{(у1+у2)}{2}$$, где А(х1;у1), В(х2;у2)
Подставим:
$$ х=\frac{(1+5)}{2}=3 $$
$$ у=\frac{(3-1)}{2}=1 $$
Координаты точки М(3;1).
Запишем уравнение прямой на плоскости в общем виде:
$$ \frac{(x-x1)}{(x2-x1)}=\frac{(y-y1)}{(y2-y1)} $$
Подставим в него значения:
$$ x1=0 $$
$$ x2=3 $$
$$ y1=-4 $$
$$ y2=1 $$
$$ \frac{(x-0)}{(3-0)}=\frac{(y+4)}{(1+4)} $$
$$ \frac{x}{3}=\frac{(y+4)}{5} $$ – уравнение прямой.

Ответ:
$$ \frac{x}{3}=\frac{(y+4)}{5} $$
Попробуйте другие сервисы
Нахождение расстояния между двумя точками
Составление уравнения плоскости
Нахождение расстояния от точки до плоскости
Написать нам
Оставить отзыв
Составить каноническое уравнение прямой онлайн. Общее уравнение прямой
Общее уравнение прямой:
Частные случаи общего уравнения прямой:
а) Если C = 0, уравнение (2) будет иметь вид
Ax + By = 0,
и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.
б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид
Ax + С = 0, или .
Уравнение не содержит переменной y , а определяемая этим уравнением прямая параллельна оси Oy .
в) Если в общем уравнении прямой (2) A
= 0, то это уравнение примет видBy + С = 0, или ;
уравнение не содержит переменной x , а определяемая им прямая параллельна оси Ox .
Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.
г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.
Это уравнение оси Ox .
д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.
Это уравнение оси Oy .
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Условие параллельности прямых. Условие перпендикулярности прямых.
l 1 l 2 l 1: A 1 x + B 1 y + C 1 = 0
l 2: A 2 x + B 2 y + C 2 = 0
S 2 S 1 Вектора S 1 и S 2 называются направляющими для своих прямых.
Угол между прямыми l 1 и l 2 определяется углом между направляющими векторами.
Теорема 1: cos угла между l 1 и l 2 = cos(l 1 ; l 2) =
Теорема 2: Для того, чтобы 2 прямые были равны необходимо и достаточно:
Теорема 3: чтобы 2 прямые были перпендикулярны необходимо и достаточно:
L 1 l 2 ó A 1 A 2 + B 1 B 2 = 0
Общее уравнение плоскости и его частные случаи. Уравнение плоскости в отрезках.
Общее уравнение плоскости:
Ax + By + Cz + D = 0
Частные случаи:
1. D=0 Ax+By+Cz = 0 – плоскость проходит через начало координат
2. С=0 Ax+By+D = 0 – плоскость || OZ
3. В=0 Ax+Cz+d = 0 – плоскость || OY
4. A=0 By+Cz+D = 0 – плоскость || OX
5. A=0 и D=0 By+Cz = 0 – плоскость проходит через OX
6. В=0 и D=0 Ax+Cz = 0 – плоскость проходит через OY
7. C=0 и D=0 Ax+By = 0 – плоскость проходит через OZ
Взаимное расположение плоскостей и прямых линий в пространстве:
1. Углом между прямыми в пространстве называется угол между их направляющими векторами.
Углом между прямыми в пространстве называется угол между их направляющими векторами.
Cos (l 1 ; l 2) = cos(S 1 ; S 2) = =
2. Углом между плоскостями определяется через угол между их нормальными векторами.
Cos (l 1 ; l 2) = cos(N 1 ; N 2) = =
3. Косинус угла между прямой и плоскостью можно найти через sin угла между направляющим вектором прямой и нормальным вектором плоскости.
4. 2 прямые || в пространстве, когда их || направляющие вектора
5. 2 плоскости || когда || нормальные вектора
6. Аналогично вводятся понятия перпендикулярности прямых и плоскостей.
Вопрос №14
Различные виды уравнения прямой линии на плоскости(уравнение прямой в отрезках, с угловым коэффициентом и др.)
Уравнение прямой в отрезках:
Допустим, что в общем уравнении прямой:
1. С = 0 Ах + Ву = 0 – прямая проходит через начало координат.
2. а = 0 Ву + С = 0 у =
3. в = 0 Ах + С = 0 х =
4. в=С=0 Ах = 0 х = 0
5. а=С=0 Ву = 0 у = 0
а=С=0 Ву = 0 у = 0
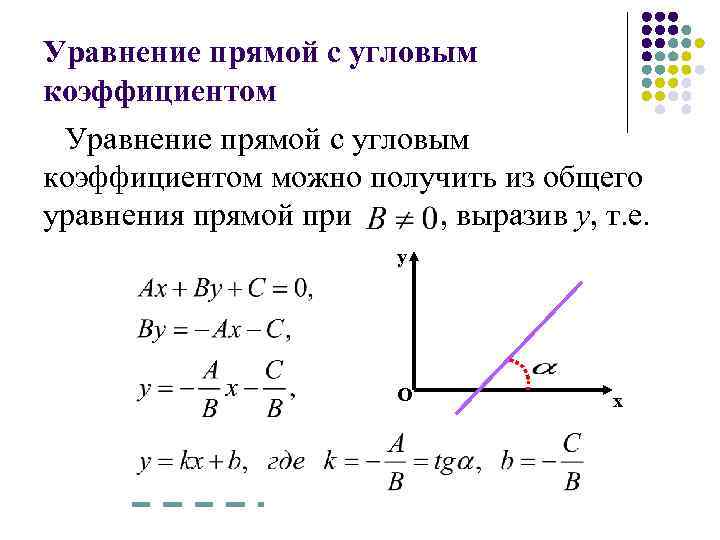
Уравнение прямой с угловым коэффициентом:
Любая прямая, не равная оси ОУ (В не=0), может быть записана в след. виде:
k = tgα α – угол между прямой и положительно направленной линией ОХ
b – точка пересечения прямой с осью ОУ
Док-во:
Ах+Ву+С = 0
Ву= -Ах-С |:В
Уравнение прямой по двум точкам:
Вопрос №16
Конечный предел функции в точке и при x→∞
Конечный предел в точке х 0:
Число А называется пределом функции y = f(x) при x→х 0 , если для любого Е > 0 существует б > 0 такое, что при х ≠x 0 , удовлетворяющее неравенству |х – х 0 |
Предел обозначается: = A
Конечный предел в точке +∞:
Число А называется пределом функции y = f(x) при x→ + ∞ , если для любого Е > 0 существует С > 0, такое что при x > C выполняется неравенство |f(x) — A|
Предел обозначается: = A
Конечный предел в точке -∞:
Число А называется пределом функции y = f(x) при x→-∞, если для любого Е
Уравнение линии
на плоскости.
Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.
Определение. Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию.
Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр
Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.
Уравнение прямой на плоскости.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А 2 + В 2 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
C = 0, А 0, В 0 – прямая проходит через начало координат
А = 0, В 0, С 0 { By + C = 0}- прямая параллельна оси Ох
В = 0, А 0, С 0 { Ax + C = 0} – прямая параллельна оси Оу
В = С = 0, А 0 – прямая совпадает с осью Оу
А = С = 0, В 0 – прямая совпадает с осью Ох
Уравнение прямой
может быть представлено в различном
виде в зависимости от каких – либо
заданных начальных условий.
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0.
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).
Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M 2 (x 2, y 2 , z 2), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
если
х 1
х 2
и х = х 1 ,
еслих 1
= х 2 .
Дробь
=k
называется угловым
коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и
обозначить
,
то полученное уравнение называетсяуравнением
прямой с угловым коэффициентом k .
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор ( 1 , 2), компоненты которого удовлетворяют условию А 1 + В 2 = 0 называется направляющим вектором прямой
Ах + Ву + С = 0.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Уравнение
искомой прямой будем искать в виде: Ax
+ By
+ C
= 0. В соответствии с определением,
коэффициенты должны удовлетворять
условиям:
В соответствии с определением,
коэффициенты должны удовлетворять
условиям:
1A + (-1)B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C/A = 0.
при х = 1, у = 2 получаем С/A = -3, т.е. искомое уравнение:
Уравнение прямой в отрезках.
Если
в общем уравнении прямой Ах + Ву + С = 0 С
0, то, разделив на –С, получим:
или
, где
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С
= 1,
,
а = -1,b
= 1.
Нормальное уравнение прямой.
Если
обе части уравнения Ах + Ву + С = 0 разделить
на число
,
которое называетсянормирующем
множителем ,
то получим
xcos + ysin — p = 0 –
нормальное уравнение прямой.
Знак нормирующего множителя надо выбирать так, чтобы С
р
– длина перпендикуляра, опущенного из
начала координат на прямую, а
— угол, образованный этим перпендикуляром
с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение
этой прямой в отрезках:
уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
; cos = 12/13; sin = -5/13; p = 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см 2 .
Уравнение
прямой имеет вид:
,
a
= b
= 1; ab/2
= 8; a
= 4; -4.
a = -4 не подходит по условию задачи.
Итого:
или х + у – 4 = 0.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение
прямой имеет вид:
,
где х 1
= у 1
= 0; x 2
= -2; y 2
= -3.
Угол между прямыми на плоскости.
Определение. Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми будет определяться как
.
Две прямые параллельны, если k 1 = k 2 .
Две прямые перпендикулярны, если k 1 = -1/k 2 .
Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты А 1 = А, В 1 = В. Если еще и С 1 = С, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
Уравнение прямой, проходящей через данную точку
перпендикулярно данной прямой.
Определение. Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b представляется уравнением:
Расстояние от
точки до прямой.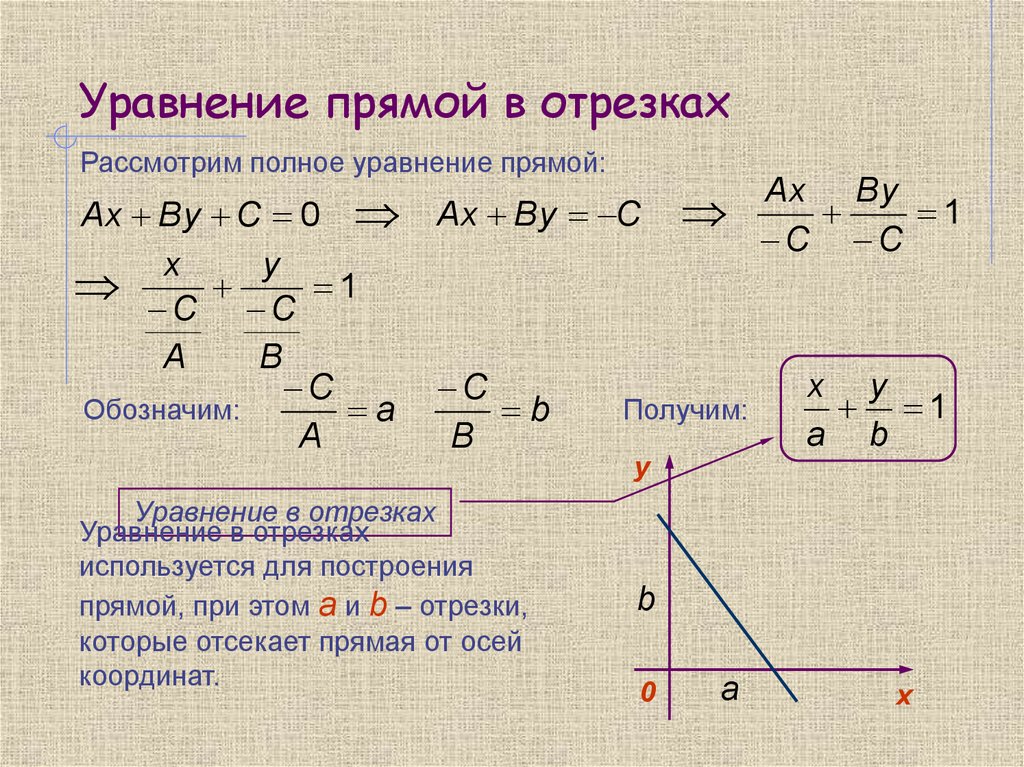
Теорема. Если задана точка М(х 0 , у 0 ), то расстояние до прямой Ах + Ву + С =0 определяется как
.
Доказательство. Пусть точка М 1 (х 1 , у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М 1:
Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,
то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
.
Теорема доказана.
Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
k 1
= -3; k 2
= 2 tg
=
;
= /4.
Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х +
6у – 3 = 0 перпендикулярны.
Находим: k 1 = 3/5, k 2 = -5/3, k 1 k 2 = -1, следовательно, прямые перпендикулярны.
Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Находим
уравнение стороны АВ:
;
4x
= 6y
– 6;
2x
– 3y
+ 3 = 0;
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k
=
.
Тогда y
=
.
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению:
откуда
b
= 17. Итого:
.
Ответ: 3x + 2y – 34 = 0.
Аналитическая геометрия в пространстве.
Уравнение линии в пространстве.
Уравнение прямой в пространстве по точке и
направляющему вектору.
Возьмем произвольную прямую и вектор (m, n, p), параллельный данной прямой. Вектор называетсянаправляющим вектором прямой.
На прямой возьмем две произвольные точки М 0 (x 0 , y 0 , z 0) и M(x, y, z).
z
M 1
Обозначим
радиус- векторы этих точек как
и
,
очевидно, что
— =
.
Т.к.
векторы
и
коллинеарны, то верно соотношение
=
t,
где t
– некоторый параметр.
Итого, можно записать: = + t.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой .
Это векторное уравнение может быть представлено в координатной форме:
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
.
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:
;
.
Отсюда получим: m: n: p = cos : cos : cos.
Числа m, n, p называются угловыми коэффициентами прямой. Т.к. — ненулевой вектор, тоm, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
Уравнение прямой в пространстве, проходящей
через
две точки.
Если на прямой в пространстве отметить две произвольные точки M 1 (x 1 , y 1 , z 1) и M 2 (x 2 , y 2 , z 2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
.
Кроме того, для точки М 1 можно записать:
.
Решая совместно эти уравнения, получим:
.
Это уравнение прямой, проходящей через две точки в пространстве.
Общие уравнения прямой в пространстве.
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.
Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:
+ D = 0, где
— нормаль плоскости; — радиус- вектор произвольной точки плоскости.
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы начнем изучать алгоритмы, связанные с геометрией. Дело в том, что олимпиадных задач по информатике, связанных с вычислительной геометрией, достаточно много и решение таких задач часто вызывают затруднения.
За несколько уроков мы рассмотрим ряд элементарных подзадач, на которые опирается решение большинства задач вычислительной геометрии.
На этом уроке мы составим программу для нахождения уравнения прямой , проходящей через заданные две точки . Для решения геометрических задач нам понадобятся некоторые знания из вычислительной геометрии. Часть урока мы посвятим знакомству с ними.
Сведения из вычислительной геометрии
Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач.
Исходными данными для таких задач могут быть множество точек на плоскости, набор отрезков, многоугольник (заданный например, списком своих вершин в порядке движения по часовой стрелке) и т.п.
Результатом может быть либо ответ на какой то вопрос (типа принадлежит ли точка отрезку, пересекаются ли два отрезка, …), либо какой-то геометрический объект (например, наименьший выпуклый многоугольник, соединяющий заданные точки, площадь многоугольника, и т. п.).
п.).
Мы будем рассматривать задачи вычислительной геометрии только на плоскости и только в декартовой системе координат.
Векторы и координаты
Чтобы применять методы вычислительной геометрии, необходимо геометрические образы перевести на язык чисел. Будем считать, что на плоскости задана декартова система координат, в которой направление поворота против часовой стрелки называется положительным.
Теперь геометрические объекты получают аналитическое выражение. Так, чтобы задать точку, достаточно указать её координаты: пару чисел (x; y). Отрезок можно задать, указав координаты его концов, прямую можно задать, указав координаты пары ее точек.
Но основным инструментом при решении задач у нас будут векторы. Напомню поэтому некоторые сведения о них.
Отрезок АВ , у которого точку А считают началом (точкой приложения), а точку В – концом, называют вектором АВ и обозначают либо , либо жирной строчной буквой, например а .
Для обозначения длины вектора (то есть длины соответствующего отрезка) будем пользоваться символом модуля (например, ).
Произвольный вектор будет иметь координаты, равные разности соответствующих координат его конца и начала:
,
здесь точки A и B имеют координаты соответственно.
Для вычислений мы будем использовать понятие ориентированного угла , то есть угла, учитывающего взаимное расположение векторов.
Ориентированный угол между векторами a и b положительный, если поворот от вектора a к вектору b совершается в положительном направлении (против часовой стрелки) и отрицательный – в другом случае. См рис.1а, рис.1б. Говорят также, что пара векторов a и b положительно (отрицательно) ориентирована.
Таким образом, величина ориентированного угла зависит от порядка перечисления векторов и может принимать значения в интервале .
Многие задачи вычислительной геометрии используют понятие векторного (косого или псевдоскалярного) произведений векторов.
Векторным произведением векторов a и b будем называть произведение длин этих векторов на синус угла между ними:
.
Векторное произведение векторов в координатах:
Выражение справа – определитель второго порядка:
В отличии от определения, которое дается в аналитической геометрии, это скаляр.
Знак векторного произведения определяет положение векторов друг относительно друга:
a и b положительно ориентирована.
Если величина , то пара векторов a и b отрицательно ориентирована.
Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда они коллинеарны (). Это значит, что они лежат на одной прямой или на параллельных прямых.
Рассмотрим несколько простейших задач, необходимых при решении более сложных.
Определим уравнение прямой по координатам двух точек.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки: с координатами (x1;y1) и с координатами (x2; y2). Соответственно вектор с началом в точке и концом в точке имеет координаты (x2-x1, y2-y1). Если P(x, y) – произвольная точка на нашей прямой, то координаты вектора равны (x-x1, y – y1).
С помощью векторного произведения условие коллинеарности векторов и можно записать так:
Т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
Последнее уравнение перепишем следующим образом:
ax + by + c = 0, (1)
c = x1(y1-y2) + y1(x2-x1)
Итак, прямую можно задать уравнением вида (1).
Задача 1. Заданы координаты двух точек. Найти её представление в виде ax + by + c = 0.
На этом уроке мы познакомились с некоторыми сведениями из вычислительной геометрии. Решили задачу по нахождению уравнения линии по координатам двух точек.
На следующем уроке составим программу для нахождения точки пересечения двух линий, заданных своими уравнениями.
Уравнение прямой проходящей через две точки. В статье » » я обещал вам разобрать второй способ решения представленных задач на нахождение производной, при данном графике функции и касательной к этому графику. Этот способ мы разберём в , не пропустите! Почему в следующей?
Дело в том, что там будет использоваться формула уравнения прямой. Конечно, можно было бы просто показать данную формулу и посоветовать вам её выучить. Но лучше объяснить – от куда она исходит (как выводится). Это необходимо! Если вы её забудете, то быстро восстановить её не представит труда. Ниже подробно всё изложено. Итак, у нас на координатной плоскости имеется две точки А (х 1 ;у 1) и В(х 2 ;у 2), через указанные точки проведена прямая:
Вот сама формула прямой:
*То есть при подстановке конкретных координат точек мы получим уравнение вида y=kx+b.
**Если данную формулу просто «зазубрить», то имеется большая вероятность запутаться с индексами при х . Кроме того, индексы могут обозначаться по разному, например:
Поэтому-то и важно понимать смысл.
Теперь вывод этой формулы. Всё очень просто!
Треугольники АВЕ и ACF подобны по острому углу (первый признак подобия прямоугольных треугольников). Из этого следует, что отношения соответственных элементов равны, то есть:
Теперь просто выражаем данные отрезки через разность координат точек:
Конечно, не будет никакой ошибки если вы запишите отношения элементов в другом порядке (главное соблюдать соответствие):
В результате получится одно и тоже уравнение прямой. Это всё!
То есть, как бы не были обозначены сами точки (и их координаты), понимая данную формулу вы всегда найдёте уравнение прямой.
Формулу можно вывести используя свойства векторов, но принцип вывода будет тот же, так как речь будет идти о пропорциональности их координат. В этом случае работает всё то же подобие прямоугольных треугольников. На мой взгляд описанный выше вывод более понятнее)).
Посмотреть вывод через координаты векторов >>>
Пусть на координатной плоскости построена прямая, проходящая через две заданные точки А(х 1 ;у 1) и В(х 2 ;у 2). Отметим на прямой произвольную точку С с координатами (x ; y ). Также обозначим два вектора:
Отметим на прямой произвольную точку С с координатами (x ; y ). Также обозначим два вектора:
Известно, что у векторов лежащих на параллельных прямых (либо на одной прямой), их соответствующие координаты пропорциональны, то есть:
— записываем равенство отношений соответствующих координат:
Рассмотрим пример:
Найти уравнение прямой, проходящей через две точки с координатами (2;5) и (7:3).
Можно даже не строить саму прямую. Применяем формулу:
Важно, чтобы вы уловили соответствие, при составлении соотношения. Вы не ошибётесь, если запишите:
Ответ: у=-2/5x+29/5 иди у=-0,4x+5,8
Для того, чтобы убедится, что полученное уравнение найдено верно, обязательно делайте проверку — подставьте в него координаты данных в условии точек. Должны получится верные равенства.
На этом всё. Надеюсь, материал был вам полезен.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
1. Уравнение прямой, проходящей через данную точку A (x 1 , y 1) в данном направлении, определяемом угловым коэффициентом k ,
y — y 1 = k (x — x 1). (1)
Это уравнение определяет пучок прямых, проходящих через точку A (x 1 , y 1), которая называется центром пучка.
2. Уравнение прямой, проходящей через две точки: A (x 1 , y 1) и B (x 2 , y 2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B . Если две прямые заданы уравнениями с угловым коэффициентом
y = k 1 x + B 1 ,
Калькулятор уклона
Что такое калькулятор уклона?
Калькулятор формулы уклона имеет большое значение как в математике, так и в физике. Это помогает найти градиент (наклон) линии, взяв в качестве входных данных две точки или линейные уравнения.
Это помогает найти градиент (наклон) линии, взяв в качестве входных данных две точки или линейные уравнения.
Помимо нахождения простого уклона, он также находит множество других характеристик наклона и линии. К ним относятся:
- Форма пересечения уклона
- Уклон, расстояние и угол в процентах
- 𝚫X и 𝚫Y
- График наклона
Что такое наклон линии?
Уклон в математике имеет то же значение, что и в английском, и это « Крутизна ». За исключением математики, мы используем слово «наклон» для обозначения крутизны линий и кривых.
Также известен как градиент, уклон и уклон. Примеры наклона в повседневной жизни включают крыши, горки и крутые горы.
Наклон может быть положительным, отрицательным, нулевым или неопределенным. Типы наклона зависят от их значений и знака со значением. Для быстрого обзора склон, который имеет
- положительный знак , затем положительный
- A отрицательный знак , тогда, конечно, отрицательный
- Горизонтальное значение означает, что оно равно нулю
Как найти наклон линии?
Если вам нужно найти склон быстро и без ошибок, вы можете использовать для этой цели искатель уклона. Но если вы хотите рассчитать это самостоятельно, продолжайте читать пример ниже.
Но если вы хотите рассчитать это самостоятельно, продолжайте читать пример ниже.
1. Наклон по двум точкам
Пример:
Найдите наклон линии, проходящей через точки (3,6) и (8,2).
Решение:
Шаг 1: Определите значения.
x 1 = 3
x 2 = 8
Y 1 = 6
Y 2 = 2
Шаг 2: Найдите разницу между очками.
𝚫Х = Х 2 — x 1
= 8 — 3
= 5
𝚫y = Y 2 — Y 1
= 2 — 6
= — 4
Шаг 3: Solve дробь 𝚫Y / 𝚫X.
м = 𝚫Y / 𝚫X
= -4 / 5
= -0,8
Следовательно, наклон линии равен -0,8 и имеет отрицательный характер.
2. Наклон с помощью уравнения линии
Наклон также можно найти, если у вас есть уравнение линии. Найдем наклон, используя линейное уравнение.
Найдем наклон, используя линейное уравнение.
Пример:
Найдите наклон линии в следующем уравнении прямой.
4y – 2x + 5 = 0
Решение:
Шаг 1: Оформите уравнение в виде y = mx + c
4y = 2x – 5
5 90 (2x – 5
5 90) /4
Шаг 2: Упростите правую часть уравнения.
y = 2x/4 – 5/4
y = 0,5x – 1,25
Теперь, когда у нас есть уравнение прямой линии, можно найти наклон, сравнив его с исходным уравнением, где м представляет уклон. Уклон (м) = 0,5
Наклон – это мера превышения заданных координатных точек x и y. Математически
Подъем над пробегом равен (y2 — y1)/(x2 — x1)
Что такое символ уклона?
Мера крутизны линии обозначается буквой «м «. Например,
м = подъем/разбег
Ссылки- Академия Хана.
 (н.д.). Что такое наклон линии? Академия Хана.
(н.д.). Что такое наклон линии? Академия Хана. - Learning, L. (nd). Как найти наклон линии? Люмен.
Создание линий соединения между двумя точками
Назад к результатам
Распечатать Делиться
Будьте первыми, кто получит обновления поддержки
Хотите знать о последних технических материалах и обновлениях программного обеспечения?
Получать уведомления
Наверх
Резюме
Приведенные инструкции описывают, как создать линии соединения между двумя точками в ArcMap. Например, электронная таблица данных сейсмических профилей обычно состоит из положений начальной и конечной точек, представляющих сейсмические профиля, которые должны быть сняты при съемке. В ArcMap можно сгенерировать набор линий из этих точек с помощью инструмента XY в линию.
В ArcMap можно сгенерировать набор линий из этих точек с помощью инструмента XY в линию.
Чтобы обеспечить точное расположение линий, сгенерированных в ArcMap, таблица атрибутов должна содержать широту и долготу объектов начальной и конечной точек, как показано в примере ниже.
Примечание : Обратитесь к разделу Как: вычислить широту и долготу для точечных объектов, чтобы получить инструкции по извлечению значений широты и долготы точечных слоев перед использованием инструмента XY к линии.
Процедура
Выполните следующие действия, чтобы создать линии соединения между двумя точками на карте.
- Вставьте данные XY в ArcMap.
- Выберите правильную систему координат и поля X и Y.
- Щелкните правой кнопкой мыши конкретный слой в таблице данных и выберите Показать данные XY .
- Выберите значения X и Y в полях X и Y.
- Щелкните Редактировать , чтобы определить правильную систему координат.

- Нажмите ОК дважды. Теперь точки добавляются на карту как слой в таблице содержания.
- Сохранить баллы навсегда.
- Щелкните правой кнопкой мыши слой событий и выберите Данные > Экспорт данных .
- Нажмите кнопку Обзор , чтобы выбрать местоположение и имя для нового файла.
- Установите тип файла как шейп-файл или класс пространственных объектов.
- Щелкните Сохранить и щелкните OK .
- Перейти к ArcToolbox > Инструменты управления данными > Функции > XY к линии .
- Используя новый шейп-файл или класс объектов, созданный на шаге 2, введите в Start X Field , Start Y Field , End X Field и End Y Field таблицы.
- Запустите инструмент XY в линию .
Дополнительная информация
- ArcMap: XY в линию
- ArcMap: создание новых линий из точек
- ArcMap: добавление данных координат x,y в виде слоя
- Как сделать: создать линии соединения между точкой и линией полигон из таблицы данных XY
- Как: Импорт данных XY в ArcMap и преобразование данных в шейп-файл или класс пространственных объектов в ArcMap 10.



 Составьте уравнение прямой, на которой лежит медиана, выходящая из вершины С.
Составьте уравнение прямой, на которой лежит медиана, выходящая из вершины С.
 (н.д.). Что такое наклон линии? Академия Хана.
(н.д.). Что такое наклон линии? Академия Хана.