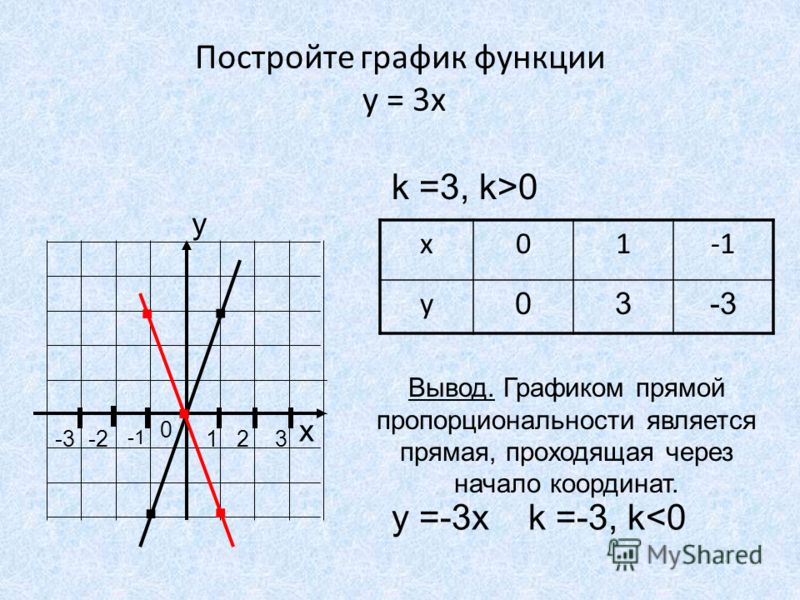
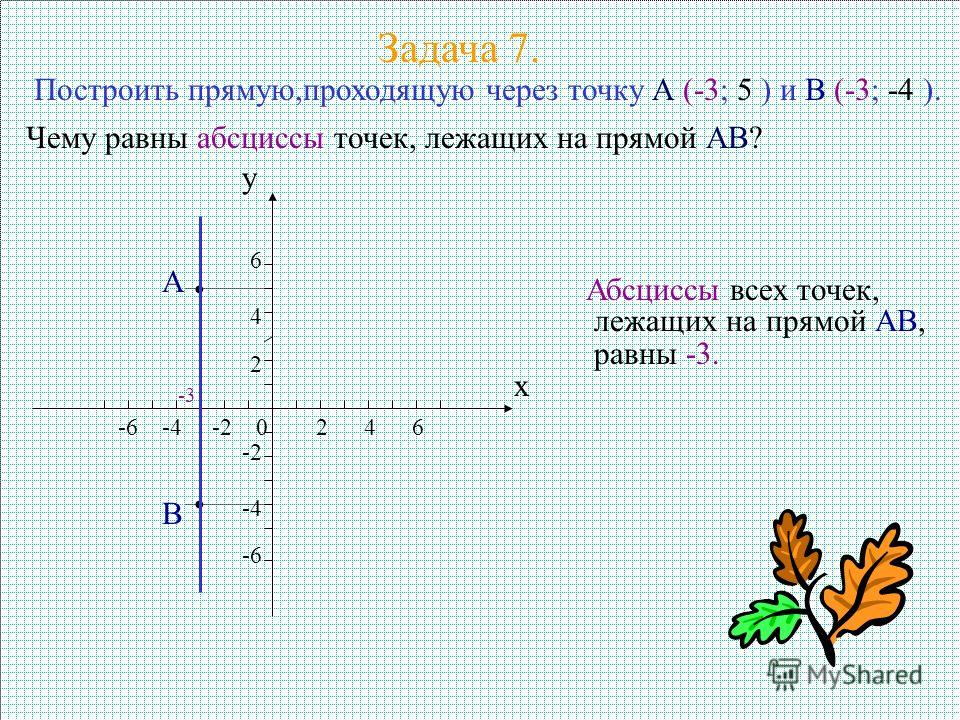
Наклон линии (крутизна)
Наклон линии (крутизна)
Предствим, что частица движется вдоль участка не вертикальной прямой из точки p1( x1,y1 ) к точке p1( x1,y1 ). Вертикальное изменение y2 – y1 называется подъемом, а горизонтальное изменение x2 – x1 — расстоянием.
ОПРЕДЕЛЕНИЕ
Если P(x1, y1) и P(x2, y2) есть точками на невертикальной прямой, тогда крутизна m прямой определяется как:
Не имеет значение, какая точка называется P1 и какая точка называется P2
Slope of P1P2
= (y2 — y1)/(x2 — x1)
= -(y1 — y2)/[-(x1 — x2)]
= (y1 — y2)/(x1 — x2) = Крутизна P1P2
Любые две различные точки на не вертикальной прямой могут быть использованы для расчета крутизны (наклона) прямой. Для измерения наклона, мы обычно двигаемся слева направо, когда измеряем дистанцию, пройденную горизонтально.
Для измерения наклона, мы обычно двигаемся слева направо, когда измеряем дистанцию, пройденную горизонтально.
Из-за этого, иногда понятие падения подменяется подъемом!
Пример
В каждой части найдите наклон линии, проходящей через
(A) (6, 2) и (9, 8)
(B) (2, 9) и (4, 3)
(C) (-2, 7) и (5, 7)
Решение:
Мы знаем, что наклон линии, проходящей через две точкиP1(x1, y1) иp1(x1, y1) , определяется как
m= (y2 — y1)/ (x2 — x1)
Отсюда
a) m= (8 — 2)/(9 — 6) = 6/3 = 2
На координатной плоскости xy
Подобным образом
b) m= (3 — 9)/(4 — 2) = -6/2 = -3
На координатной плоскости xy
Также
c) m= (7 -7)/[5 — (-2)] = 0/7 = 0
На координатной плоскости xy
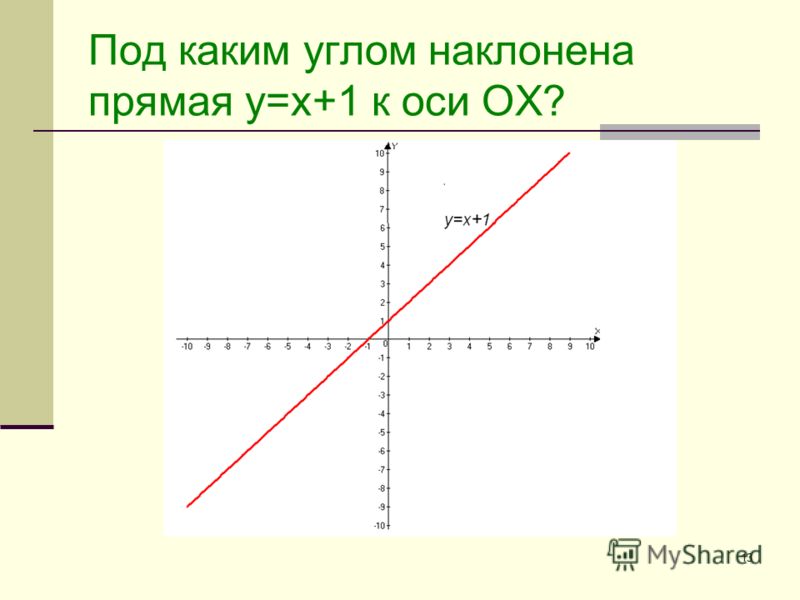
Определение (Угол наклона)
Для прямой L не параллельной к оси абсцисс, угол наклона есть наименьший углом φ, измеренный против часовой стрелки от направления положительная оси х к L.

Для прямой, параллельной оси x, мы берём φ = 0
Как показано на следующих рисунках.
Если m есть наклоном прямой, тогда
m = rise/run
= скорость изменения y относительно к x
ТЕОРЕМА
Для не вертикальной прямой наклон m и угол наклона φ связаны отношением
m = tan φ
Пример:
Найдите угол наклона для прямой с наклоном m = 1 и угол наклона для прямой с наклоном m = -1
Solution:
Если m=1 tan φ = 1, и поэтому φ = π/4 = 45°
Если m=-1 tan φ = -1, так как 0 φ = 3π/4 = 135°
Теорема
Пусть L1 и L2 есть прямыми с наклонами m1 и m2, соответственно
(a) Прямые параллельны тогда и только тогда m1 = m2
(b) Прямые параллельны тогда и только тогда m1m2 = -1
Доказательство: (a)
Если L1 и L2 не являются вертикальными прямыми, тогда их углы наклона φ1 и φ2 равны.
φ1 =φ2
Так,
m1 = tanφ1 = tanφ2 = m2
И наоборот, если два наклона линий равны, т.e.
M1 = M2
⇒ tan(φ1) = tan(φ
⇒ φ1 = φ2
То есть, прямые параллельны.
(b) Предположим, что φ12
Тогда, обращаясь к рисунку
m1 = tanφ1 = c/h
m2 = tanφ2 = -h/c
Доказательства обратного предлагается сделать в качестве упражнения.
TЕОРЕМА
Вертикальная прямая через (a, 0) и горизонтальная прямая через (0, b) представлены, соответственно, уравнением
x = a и y = b
ТЕОРЕМА
Прямая, проходящая через P1(x1, y1) и имеющая наклон m, выражается уравнением
y — y1 = m(x — x1)
ТЕОРЕМА
Прямая с пересечением оси y в b и наклоном m выражается уравнением
y = mx + b
Авиабилеты Nas Air: Абха-Джидда цена на прямой рейс, расписание самолетов
Укажите даты, чтобы найти дешевые билеты на самолёт
Откуда
Дата вылета
Дата возвращения
Пассажиры и класс 1 пассажир Эконом класс
Найти билеты
Джидда → Абха Nas Air
Цены на билеты Расписание самолетов
Цены на авиабилеты Nas Air из Абхи в Джидду
Найти авиабилеты Абха — Джидда Nas Air поможет UniTicket. uz. Мы сравниванием цены на рейсы по всему спектру предложений: на официальном сайте Nas Air, на сайтах наших партнеров, кассах аэропортов, что бы предложить вам дешевые билеты на самолет компании Nas Air от 394 973 сум.
uz. Мы сравниванием цены на рейсы по всему спектру предложений: на официальном сайте Nas Air, на сайтах наших партнеров, кассах аэропортов, что бы предложить вам дешевые билеты на самолет компании Nas Air от 394 973 сум.
В одну сторону Туда-обратно
Март 2023 Все месяцы
Пн
Вт
Ср
Чт
Пт
Сб
Вс
Цены на билеты из Абхи в Джидду (Саудовская Аравия) Nas Air туда и обратно. Укажите направление перелёта и календарь покажет самые дешевые авиабилеты в каждом месяце года.
Авиабилеты Nas Air Абха Джидда в одну сторону
Сортировка: На ближайшие датыСамые дешевые авиабилетыВремя в путиПрямые рейсы На ближайшие датыСамые дешевые авиабилетыВремя в путиПрямые рейсы
04.04.2023 Вторник
от 1 311 963 сум Kupi.com
Эконом Найден позавчера
1 пересадка
4 ч. 50 мин.
50 мин.
Найти
04.04.2023 Вторник
от 2 812 890 сум Aviakassa
Эконом Найден позавчера
2 пересадки 9 ч. 10 мин.
Найти04.04.2023 Вторник
от 393 516 сум Kupi.com
Эконом Найден позавчера
Без пересадок 1 ч. 15 мин.
Найти
*В цены включена стоимость: багажа, ручной клади, комиссии и сборы авиакомпании
Билеты на самолёт Nas Air Абха Джидда туда и обратно
Ниже представлены цены авиабилетов Абха Джидда на прямой рейс от авиакомпании Nas Air. Самый дешёвый билет на самолёт Абха Джидда стоит от 394 973 сум с отправлением 04 апреля 2023.
Сортировка: На ближайшие датыСамые дешевые авиабилетыДней пребыванияПрямые рейсы На ближайшие датыСамые дешевые авиабилетыДней пребыванияПрямые рейсы
Nas Air XY 426 Утренний рейс
туда
23. 03.23
05:45, Чт
03.23
05:45, Чт
прямой Пребывание 2 дня
обратно 25.03.23 03:50, Сб
Найти билеты от 1 597 958 сум
Nas Air XY 436 Вечерний рейс
туда 30.04.23 22:05, Вс
прямой Пребывание 8 дней
обратно 08.05.23 20:00, Пн
Найти билеты от 1 603 786 сум
Nas Air XY 436 Вечерний рейс
туда 24.03.23 22:05, Пт
прямой Пребывание 11 дней
обратно 04.04.23 14:45, Вт
Найти билеты от 1 603 786 сум
Nas Air XY 434 Дневной рейс
туда 21.03.23 15:00, Вт
прямой Пребывание 5 ч.
обратно 21.03.23 20:05, Вт
Найти билеты от 1 603 786 сум
Nas Air XY 426 Утренний рейс
туда 06.04.23 07:10, Чт
прямой Пребывание 5 дней
обратно 11.04.23 14:45, Вт
Найти билеты от 1 645 454 сум
Nas Air XY 436 Вечерний рейс
туда
22.
прямой Пребывание 8 дней
обратно 30.03.23 15:15, Чт
Найти билеты от 1 659 877 сум
Nas Air XY 436 Вечерний рейс
туда 27.04.23 22:05, Чт
прямой Пребывание 25 дней
обратно 22.05.23 20:00, Пн
Найти билеты от 1 856 708 сум
Nas Air XY 436 Вечерний рейс
туда 18.03.23 22:05, Сб
прямой Пребывание 1 день
обратно 19.03.23 20:05, Вс
Найти билеты от 1 888 469 сум
Nas Air XY 426 Утренний рейс
туда 20.04.23 07:10, Чт
прямой Пребывание 16 дней
обратно 06.05.23 05:05, Сб
Найти билеты от 2 018 864 сум
Nas Air XY 426 Утренний рейс
туда 04.04.23 07:10, Вт
прямой Пребывание 4 дня
обратно 08.04.23 05:05, Сб
Найти билеты от 2 044 943 сум
Nas Air XY 426 Утренний рейс
туда
31. 03.23
07:10, Пт
03.23
07:10, Пт
прямой Пребывание 1 день
обратно 01.04.23 05:05, Сб
Найти билеты от 2 044 943 сум
Nas Air XY 436 Вечерний рейс
туда 29.03.23 22:05, Ср
прямой Пребывание 2 дня
обратно 01.04.23 05:05, Сб
Найти билеты от 2 156 690 сум
Nas Air XY 436 Вечерний рейс
туда 25.04.23 22:05, Вт
прямой Пребывание 4 дня
обратно 29.04.23 20:00, Сб
Найти билеты от 2 212 490 сум
Nas Air XY 436 Вечерний рейс
туда 10.05.23 22:05, Ср
прямой Пребывание 6 дней
обратно 16.05.23 14:45, Вт
Найти билеты от 2 478 671 сум
Расписание самолётов Абха — Джидда Nas Air
Ознакомьтесь с подробным расписанием рейсов самолетов Абха Джидда на текущий год. Расписание меняется в зависимости от сезона года и дня недели, поэтому рекомендуем заранее проверять наличие авиарейсов на интересующие даты.
Более 2 рейсов каждый день, продолжительностью от 1ч. 15мин. Указано местное время вылета и прилета.
01:05 → 02:20
Nas Air XY436
AHB → JED
Пн Вт Ср Чт Пт Сб Вс
Узнать цену
08:40 → 09:55
Nas Air XY426
AHB → JED
Пн — Ср Чт — Сб —
Узнать цену
18:00 → 19:15
Nas Air XY434
AHB → JED
Пн Вт Ср Чт Пт Сб Вс
Узнать цену
Информация о рейсе
Самолеты Nas Air отправляются из Абхи с 01:50 до 23:45.
В неделю авиакомпания Nas Air осуществляет 5 прямых рейсов в Джидду: XY 432, XY 426, XY 860, XY 430, XY 434
Полеты производятся из 1 Аэропорт Абхи: Абха и прилетают в 1 аэропорт Джидды: Джидда.
Самый быстрый регулярный рейс от компании Nas Air XY 432 летит 01:15 мин. Вылетает в 01:50 из аэропорта Абха и прилетает в 03:05 в Джидда. Данный рейс осуществляется на современном лайнере Airbus A320.
Самый популярный аэропорт в Абхе из которого летают самолеты Nas Air: Абха (5 рейсов из данного аэропорта), а самый популярный аэропорт прилета в Джидде: Джидда (5 рейсов в данный аэропорт).
Самый быстрый
01:15
Самый ранний рейс
01:50
Самый поздний рейс
23:45
Время в пути
01:13 минут
Расстояние
529 км
Авиакомпании
Кроме Nas Air на маршруте Абха — Джидда летает 2 авиакомпании. Больше всех (13 рейсов в неделю) выполняет Saudia.
- Saudia (SV) — 13
- Flyadeal (F3) — 3
*Количество рейсов выполняемых а/к на данном маршруте.
Самолеты
Самолеты компании Nas Air, наиболее часто встречающиеся на направлении Абха — Джидда:
- Airbus A320 — 8
*Количество рейсов Nas Air Абха — Джидда выполняемых на данной модели самолета.
Аэропорты
Аэропорты, обслуживающие компанию Nas Air на авиасообщении Абха — Джидда:
Абха ~ 0.685 км.* от 470 986 сум
Джидда ~ 1.459 км.* от 470 986 сум
Авиакомпания FlyNas
FlyNas – крупнейший лоукостер Королевства Саудовская Аравия. Авиаперевозчик начал свою деятельность в 2007 году. Воздушный парк компании представлен более 30 бортами марки Airbus. Авиаперевозчик не входит ни в один из авиационных альянсов. Родная воздушная гавань – аэродром имени короля Абдул-Азиза (в 19 км от г. Джидда, Саудовская Аравия).
Все билеты Nas Air
Самолет Nas Air
Покупая билеты на самолет Абха — Джидда Nas Air, зайдите на UniTicket.uz и сравните стоимость, это займет 3 минуты, и вы гарантированно получите самые низкие цены.
Контакты Nas Air
Официальный сайт: https://www.flynas.com/en
Телефон: 966(114)349000
Адрес офиса:
Имеет в авиапарке 3 единиц техники
IATA код: XY
Акции на авиабилеты от Nas Air
Ниже представлены текущие акции и скидки на авиабилеты Абха — Джидда от компании Nas Air. Если нашли интересное предложение, не откладывайте с покупкой, цены меняются ежедневно.
Если нашли интересное предложение, не откладывайте с покупкой, цены меняются ежедневно.
Спецпредложений не найдено.
Чтобы начать поиск билетов, укажите даты.
Copyright © 2018-2023. Все права защищены. UniTicket.uz — часть HolidayPrice Inc., Поисковик №1 авиабилетов в Узбекистане. Правила использования.Политика конфиденциальности.
Прямая линия – Общая форма
Теперь, когда я рассмотрел все формы уравнений прямой линии (кроме одной), давайте посмотрим на общую форму уравнения прямой линии.
То есть какое уравнение представляет собой прямую линию? А какой не будет?
Могут быть всевозможные уравнения, например следующие:0019 = 4
Какое из этих чисел будет представлять собой прямую линию? А какой из них не будет?
Я утверждаю, что уравнение формы Ax + By + C = 0 будет представлять собой прямую линию. Здесь A , B , C — произвольные константы ( A и B не могут быть одновременно 0 ), а x и y — переменные (координаты которых представляют собой точки линия).
Вот доказательство (отчасти).
Предположим, что B ≠ 0 , тогда, разделив уравнение на B и переставив члены, мы получим
y = (-A/B)x + (-C/B)
Положив — A/B = m и -C/B = c , приведенное выше уравнение принимает вид
y = mx + c
Это выглядит знакомо.
Это линия наклона м и точка пересечения с осью Y c , как мы получили здесь. Следовательно, уравнение Ax + By + C = 0 представляет собой линию с наклоном -A/B и Y-пересечение -C/B .
В случае B = 0 уравнение Ax + By + C = 0 станет
x = -C/A
Это представляет собой линию, параллельную оси Y (поясняется здесь ).
Аналогично, если A = 0 , то уравнение Ax + By + C = 0 станет
y = -C/B
Это представляет собой линию, параллельную оси X (пояснение здесь).
В каждом случае уравнение Ax + By + C = 0 представляет собой прямую линию.
Но что, если бы мы не вывели эти уравнения раньше? Приведу еще одно доказательство.
Идея состоит в том, чтобы доказать, что любые три точки, взятые на кривой, представленной Ax + By + C = 0 , лежат на одной прямой. Потому что если они есть, то эта кривая не может быть ничем иным, как линией!
Пусть P(x 1 , y 1 ) и Q(x 2 , y 2 ) и R(x 3 , y 3 ) — любые три точки на кривой, уравнение которой Ax + By + C = 0 .
Тогда координаты этих трех точек должны удовлетворять уравнению. Получаем следующие три соотношения.
Ax 1 + By 1 + C = 0 … I
Ax 2 + By 2 + C = 0 … II
Ax 3 + By 3 + С = 0 … III
Теперь цель состоит в том, чтобы доказать, что если эти отношения выполняются, то точки должны быть коллинеарны. Попробуем это доказать.
Попробуем это доказать.
Вычитание I Из II, мы получаем
A (x 2 — x 1 ) = B (Y 2 — Y 1 )
(Y 2 )
(Y 2 — Y 23 — Y 2 — Y 2 — Y 2 — Y 2 — Y 2 — Y 2 — Y 2 — Y 2 )
(Y 2 ) )/(x 2 – x 1 ) = A/B … IV
Аналогично, вычитая II из III, получаем
(y 3 — Y 2 )/(x 3 — x 2 ) = A/B … V
от IV и V, мы получим
(Y 2 — Y 1 )/(x 2 — x 1 ) = (Y 3 — Y 2 )/(x 3 — x 2 )
. 1 (у 2 – у 3 ) + х 2 (у 3 – у 1 ) + х 3 2
123 — Y 2 ) = 0
Наконец, на разделение на 2, мы получаем
1/2 [x 1 (Y 2 — Y 3 ) + x 2 (Y 3 ) + x 2 (Y Y 3 — Y 1 ) + x 3 (Y 1 — Y 2 )] = 0
Это означает, что площадь треууурина PQR — 0 , это означает, что область треуугериата PQR составляет 0 10101010, PORION точки коллинеарны. (Мы уже делали что-то подобное ранее.)
(Мы уже делали что-то подобное ранее.)
Готово! Мы взяли три случайные точки на кривой и доказали, что эти три точки лежат на одной прямой. Это возможно только в том случае, если кривая является линией. Следовательно, уравнение Ax + By + C = 0 должен представлять линию.
Фу! Это может быть слишком сложным для вас. Прочтите еще раз, а затем еще раз. Все наладится. А пока вот вам симуляция, где вы можете увидеть график уравнения Ax + By + C = 0 .
Вы можете перетаскивать три ползунка и наблюдать за графиком — это всегда прямая линия (за исключением случаев, когда A и B равны 0 ). Также обратите внимание, что происходит, когда любой из A , B или C становится 0 . Заметили что-нибудь особенное?
- Любое уравнение вида Ax + By + C = 0 (т. е. линейное уравнение с одной или двумя переменными) будет представлять собой прямую линию на плоскости XY , где A и B должны не быть одновременно нулями.

Следующий урок расскажет о связи между двумя уравнениями, представляющими одну и ту же прямую. Увидимся там!
Уравнение прямой | Геометрия уравнений
Как найти уравнение прямой?
Мы уже знаем, как это сделать: зная градиент \(m\) и точку пересечения \(y\) \(c\), мы можем просто записать \[y=mx+c\] и мы сделали.
Но что, если мы не знаем \(y\)-перехвата? В этой статье мы рассмотрим несколько сценариев и некоторые связанные с ними методы решения этого вопроса.
Как найти уравнение по градиенту и точке на прямой?
В математике много раз мы знаем градиент прямой линии и координаты некоторой точки на линии и хотим найти ее уравнение. Когда мы дойдем до исчисления степеней, мы встретимся с очень распространенным примером задачи такого типа: как найти уравнение касательной к кривой?
А пока мы просто предположим, что нам известен градиент и точка на линии, и мы хотим найти уравнение этой линии.
Начнем с конкретного примера: Найдите уравнение линии с градиентом \(3\), проходящей через \((1,2)\).
Первый подход
Мы знаем, что прямая имеет уравнение \(y=mx+c\), и мы знаем, что \(m=3\), поэтому уравнение равно \(y=3x+c\).
Теперь, когда \(x=1\), мы должны иметь \(y=2\), так как точка \((1,2)\) лежит на прямой. (Помните, что уравнение сообщает нам правило, которому должна подчиняться каждая точка на прямой: «Координата \(y\) равна \(3\) умноженной на \(x\)-координату плюс \(c\)». .)
Таким образом, мы можем подставить \(x=1\) и \(y=2\), чтобы получить \[\начать{выравнивать*} &2=3\times1+c\\ \Длиннаястрелка\четверка& 2=3+c\\ \Длиннаястрелка\четверка& c=-1\ . \конец{выравнивание*}\]
Итак, уравнение \(y=3x-1\).
На самом деле, этот метод будет работать всегда, какие бы координаты и какой градиент нам ни давали!
Мы собираемся рассмотреть некоторые другие методы, которые можно использовать вместо этого и которые часто кажутся более удобными, но этот надежный и надежный.
Второй подход: размышления о градиентах
В этом интерактивном режиме одна точка зафиксирована на \((1,2)\).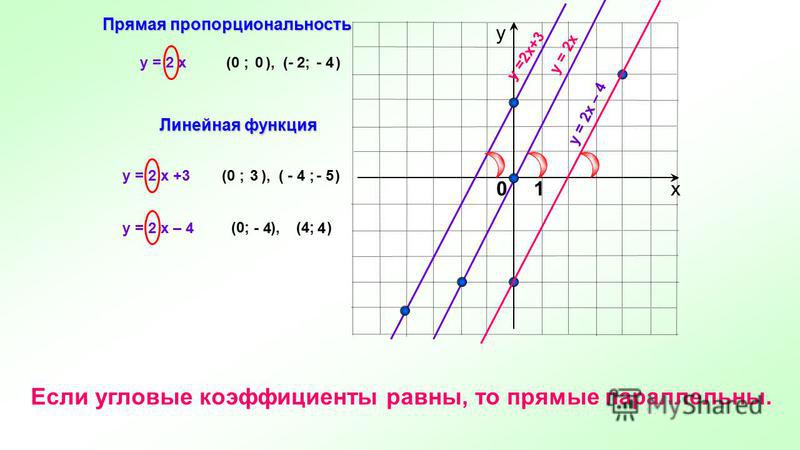 Переместите вторую точку \((x,y)\) так, чтобы она лежала на линии с градиентом \(3\), проходящей через \((1,2)\). При этом подумайте о том, как вы узнаете , что ваша точка \((x,y)\) лежит на этой прямой.
Переместите вторую точку \((x,y)\) так, чтобы она лежала на линии с градиентом \(3\), проходящей через \((1,2)\). При этом подумайте о том, как вы узнаете , что ваша точка \((x,y)\) лежит на этой прямой.
Скачать файл GeoGebra
Предположительно, вы обеспечили, чтобы градиент между \((x,y)\) и \((1,2)\) оставался равным \(3\). Напомним формулу для градиента: это изменение \(y\)-координаты (\(y-2\)) деленное на изменение \(x\)-координаты (\(x-1\)), поэтому если мы запишем это алгебраически, то обнаружим, что точка \((x,y)\) должна удовлетворять условию
\[\начало{уравнение} \frac{y-2}{x-1}=3.\label{eq:1} \конец{уравнение}\]
И это дает нам еще один способ записи нашей прямой линии!
Чтобы преобразовать его в более привычную форму, мы можем умножить обе части на \(x-1\), чтобы получить: \[\начало{уравнение} у-2 = 3 (х-1), \ метка {уравнение: 2} \конец{уравнение}\]
затем раскроем скобки, чтобы получить \[y-2=3x-3. \]. Добавление \(2\) к обеим сторонам наконец возвращает нас к \(y=3x-1\).
\]. Добавление \(2\) к обеим сторонам наконец возвращает нас к \(y=3x-1\).
На самом деле есть причина, по которой мы предпочитаем форму \(\eqref{eq:2}\) исходной \(\eqref{eq:1}\). Подумайте о самой точке \((1,2)\), лежащей на прямой. Если мы попытаемся подставить эти значения в \(\eqref{eq:1}\), мы получим \(\frac{0}{0}=3\), что не имеет математического смысла, поскольку нам не разрешено разделить на ноль.
С другой стороны, если мы подставим \(x=1\) и \(y=2\) в \(\eqref{eq:2}\), мы получим \(0=0\), т.е. совершенно правильно.
Мы можем применить этот метод в целом. Если у нас есть линия с градиентом \(m\) и проходящая через точку \((x_1, y_1)\), то наша общая точка \((x,y)\) должна удовлетворять уравнению \[\frac{ y-y_1}{x-x_1}=m\] (это просто \(\eqref{eq:1}\) переписано с заменой цифр буквами). Затем умножение на \(x-x_1\), как и раньше (и с учетом того, что при этом нам нужны скобки!) дает
\[y-y_1=m(x-x_1).\]
Это очень полезная форма, так как она позволяет нам сразу же записать уравнение для линии, когда мы знаем ее градиент и точку на линия. Затем мы можем умножить и переставить, чтобы получить уравнение в форме \(y=mx+c\), если мы хотим это сделать.
Затем мы можем умножить и переставить, чтобы получить уравнение в форме \(y=mx+c\), если мы хотим это сделать.
Как найти уравнение по двум точкам на прямой?
Мы знаем, как найти градиент линии между двумя точками. Получив это, мы можем использовать один из методов, которые мы только что обсуждали, чтобы найти уравнение прямой.
Например, найдем уравнение прямой, соединяющей \((1,3)\) и \((7,1)\).
Градиент равен \[\frac{\text{изменение $y$}}{\text{изменение $x$}} = \frac{1-3}{7-1} = \frac{-2}{6} = -\frac{1}{3}\]
Итак, уравнение линии с градиентом \(-\frac{ 1}{3}\), проходящий через \((1,3)\), равен \[y-3=-\frac{1}{3}(x-1),\], который мы можем переставить, чтобы получить \( y=-\frac{1}{3}x+\frac{10}{3}\).
В общем, если у нас есть две точки \((x_1,y_1)\) и \(((x_2,y_2)\), то градиент соединяющей их линии равен \(\dfrac{y_2-y_1}{ х_2-х_1}\). Если мы воспользуемся уравнением формы \(\eqref{eq:1}\), которое было у нас выше, мы получим очень симметричную форму для линии: \[\frac{y-y_1}{x-x_1}=\frac {y_2-y_1}{x_2-x_1}. \] Если мы теперь преобразуем это в форму, не используя дроби, умножив обе части на \((x-x_1)(x_2-x_1)\), мы получим \[( x_2-x_1)(y-y_1)=(y_2-y_1)(x-x_1),\], который снова имеет приятную симметрию.
\] Если мы теперь преобразуем это в форму, не используя дроби, умножив обе части на \((x-x_1)(x_2-x_1)\), мы получим \[( x_2-x_1)(y-y_1)=(y_2-y_1)(x-x_1),\], который снова имеет приятную симметрию.
Наконец, если мы раскроем скобки и переставим местами, мы сможем записать это еще иначе: \[(y_2-y_1)x-(x_2-x_1)y=x_1y_2-x_2y_1.\]
Не стоит и пытаться запомнить любую из этих общих формул; работайте над ними, как вам нужно!
Метод замены
Альтернативный метод состоит в том, чтобы подставить координаты двух точек в уравнение \(y=mx+c\). На примере точек \((1,3)\) и \((7,1)\) мы получаем совместные уравнения \[\начать{выравнивать*} 3&=м+с\\ 1&=7м+с \конец{выравнивание*}\]
Вычитание этих уравнений дает \(2=-6m\), поэтому \(m=-\frac{1}{3}\). Подставив это обратно в одно из уравнений, мы можем найти, что \(c=\frac{10}{3}\), как и раньше.
Другой способ записи уравнения: \(ax+by+c=0\)
Иногда числа, которые появляются в уравнении прямой, записанном как \(y=mx+c\), могут быть несколько неудобными и использовать дроби, например, наш ответ \(y=-\frac{1}{3}x+\frac{10}{3}\) в последнем разделе. Одна вещь, которая может сделать уравнение более красивым в этом случае, состоит в том, чтобы умножить на целое число, чтобы сделать все числа целыми числами. В этом случае мы можем умножить на \(3\), чтобы получить \(3y=-x+10\), в котором теперь нет дробей.
Одна вещь, которая может сделать уравнение более красивым в этом случае, состоит в том, чтобы умножить на целое число, чтобы сделать все числа целыми числами. В этом случае мы можем умножить на \(3\), чтобы получить \(3y=-x+10\), в котором теперь нет дробей.
Однако после того, как мы перестроим уравнения таким образом, может показаться, что сравнить два уравнения, чтобы решить, представляют ли они одну и ту же прямую, параллельные прямые и т. д., может оказаться труднее. Например, мы могли бы изменить это, чтобы получить \(x=10-3y\) или умножить на \(6\) вместо того, чтобы получить \(6y=-2x+20\), которые оба представляют одну и ту же линию, но выглядят несколько иначе.
Один из способов быть немного более последовательным состоит в том, чтобы изменить уравнение так, чтобы всегда помещать все в левую часть, получая \[x+3y-10=0.\]
Одним из преимуществ этого способа записи прямых линий является то, что он включает вертикальные линии, такие как \(x=4\), которые можно записать как \(x-4=0\) (или \(x+0y-4 =0\), чтобы явно указать на отсутствие \(y\)). Но у него есть недостаток, заключающийся в том, что одну и ту же строку можно записать более чем одним способом (например, в данном случае \(2x+6y-20=0\)).
Но у него есть недостаток, заключающийся в том, что одну и ту же строку можно записать более чем одним способом (например, в данном случае \(2x+6y-20=0\)).
Так что часто проще работать с формой \(y=mx+c\), особенно если вы пытаетесь решить, параллельны ли линии или перпендикулярны.
Задача: Имея две линии \(a_1x+b_1y+c_1=0\) и \(a_2x+b_2y+c_2=0\), как определить, параллельны они или перпендикулярны, без преобразования их обратно в форму \(у=мх+с\)?
Альтернативные точки зрения: Размышление о переводах
Мы знаем, что прямая, проходящая через начало координат с градиентом \(m\), имеет уравнение \(y=mx\). Если теперь мы хотим посмотреть на прямую линию, проходящую через \((x_1,y_1)\) с тем же градиентом, мы можем добиться этого, либо переместив нашу линию через начало координат, либо переместив нашу систему координат.
Мы начнем с рассмотрения того, что произойдет, если мы переместим нашу систему координат, и вернемся к размышлениям о перемещении самой линии позже.
На следующем интерактивном графике исходные оси показаны черным цветом, а новый набор осей — синим. Красная точка показана с ее координатами в соответствии с исходными черными осями (которые мы назвали \((x,y)\)) и новыми синими осями (названными \((X,Y)\)).
Можете ли вы найти связь между \((X,Y)\) и \((x,y)\)? Исследуйте, перемещая красную точку, а также синие оси (что вы можете сделать, перетащив начало синих осей; вам также может потребоваться переместить начало координат, чтобы увидеть метки синих осей из-за ошибки в GeoGebra).
Загрузить файл GeoGebra
Мы можем пойти дальше, нарисовав прямую линию на графике.
На следующем графике показана красная точка на красной линии градиента \(m\), проходящей через точку \((x_1,y_1)\).
Вы можете управлять градиентом линии с помощью ползунка, вы можете перемещать точку \((x_1,y_1)\) и вы можете перемещать точку на красной линии.
Какому условию удовлетворяют координаты красной точки в синих осях (координаты \((X,Y)\))?
Помня, как координаты синего \((X,Y)\) связаны с координатами черного \((x,y)\), сможешь ли ты понять условие, которому удовлетворяют координаты красной точки в черном оси (координаты \((x,y)\))?
Загрузить файл GeoGebra
Эта идея преобразования системы координат была развита Эйнштейном гораздо дальше, когда он разработал свою специальную теорию относительности.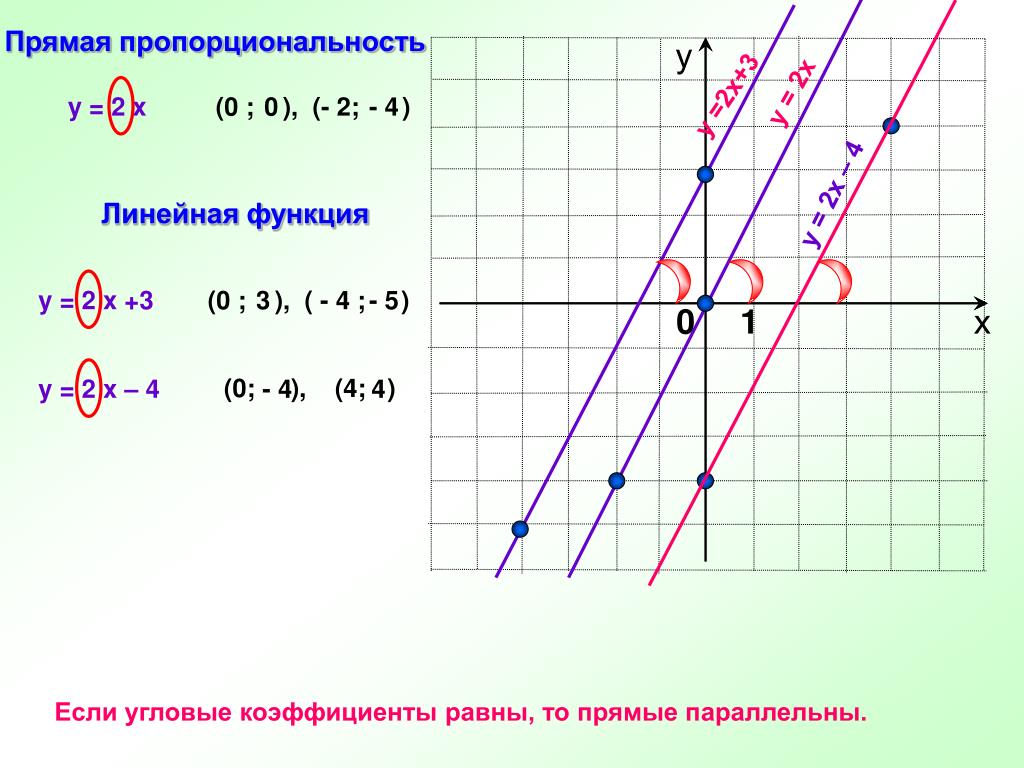 Но это история для другого дня!
Но это история для другого дня!
Эта форма уравнения также полезна, потому что она говорит нам, что \(y-y_1\) прямо пропорционально \(x-x_1\). Прямая пропорциональность сама по себе настолько хороша, что иногда бывает полезно записать уравнение прямой в таком виде.
Наконец, мы можем подумать о переносе линии вместо переноса системы координат. Когда мы перемещаем объект по вектору \(\dbinom{x_1}{y_1}\), координаты всех его точек добавляются \(x_1\) к \(x\)-координате и \(y_1\) добавляется к \(y\)-координате.
Если мы рассмотрим линию с градиентом \(m\), проходящую через начало координат, она имеет уравнение \(y=mx\). Чтобы сохранить тот же вид обозначений, который мы использовали ранее, мы выберем точку \((X,Y)\) на этой линии, так что \(Y=mX\).
Если теперь мы переместим эту линию на \(\dbinom{x_1}{y_1}\), так что начало координат переместится в \((x_1,y_1)\), точка \((X,Y)\) будет перейдите к \((X+x_1,Y+y_1)\), как показано в следующем диалоговом окне.