Прямоугольник вписанный в треугольник: Задача про прямоугольник, вписанный в равнобедренный треугольник

Содержание

Геометрические задачи на максимум / math5school.ru

Прямоугольник

Сравним между собой несколько различных прямоугольников, имеющих одинаковый периметр, равный, скажем, 12 см. Продолговатые низкие прямоугольники, ширина которых близка к 6 см, имеют незначительную площадь, тем меньшую, чем меньше их высота; точно так же площадь узких высоких прямоугольников тем меньше, чем эти прямоугольники уже. Сравнительно большую площадь имеют прямоугольники с некоторыми промежуточными пропорциями.

Встает вопрос:

какой же именно из всех прямоугольников с периметром 12 см имеет наибольшую площадь?

Такова типичная схема задачи на максимум. Приведенная задача, вероятно, самая простая и самая древняя из всех задач подобного рода. Именно поэтому на ней лучше, чем на какой-либо другой, можно разъяснить сущность задач на максимум, что мы и сделаем, прежде чем перейти к разбору того вопроса, которому, собственно, посвящена настоящая тема.

В VI книге Евклида эта задача решается следующим приемом, принцип которого мы сохраним полностью, видоизменив несколько лишь форму изложения. Возьмем произвольный прямоугольник ABCD с заданным периметром U и построим, как это показано следующем рисунке, квадрат BEFG со стороной ^U/₄ и, следовательно, с тем же самым периметром U; мы утверждаем, что

этот квадрат как раз и представляет собой решение нашей задачи,

т.е. что его площадь больше площади прямоугольника.

При том расположении квадрата и прямоугольника, которое мы видим на рисунке, у них есть общий (окрашенный в более темный цвет) прямоугольник S. Квадрат состоит из этого заштрихованного прямоугольника S и части Р; данный прямоугольник ABCD состоит из заштрихованного прямоугольника S и части Q. Но так как полупериметр квадрата

GB + ВЕ

равен полупериметру прямоугольника

АВ + BC,

то

AG + GB + BC = GB + BC + СЕ,

откуда

AG = CE,

т. е. высота прямоугольника P равна ширине прямоугольника Q. Что же касается другого измерения прямоугольника P, то им служит сторона квадрата, между тем как второе измерение Q есть лишь часть стороны квадрата и, следовательно, короче ее. Но из двух прямоугольников, имеющих по одной равной стороне, тот больше, у которого больше вторая сторона.

Таким образом, площадь Р больше площади Q и, следовательно,

P + S > Q + S,

т. е. у квадрата площадь больше, чем у прямоугольника. Сторона прямоугольника Q будет тогда равна стороне квадрата, когда за основной прямоугольник взят квадрат; в этом и только в этом случае мы имеем равенство рассматриваемых площадей. Таким образом,

квадрат действительно по площади больше всех других прямоугольников равного с ним периметра.

Если х и у – длины сторон прямоугольника в сантиметрах, то полученный результат показывает, что ху – число, измеряющее в квадратных сантиметрах площадь прямоугольника, – меньше площади квадрата с периметром

х + у + х + у = 2 · (х + у).

Сторона такого квадрата равна четвертой части этой величины, т.е.

а площадь его получится, если эту дробь возвести в квадрат. Переходя с излюбленной греками геометрической формы изложения на язык формул, получаем, что:

два любых положительных числа всегда удовлетворяют соотношению

или

т.е. среднее геометрическое двух чисел меньше или равно их среднему арифметическому;

равенство возможно лишь в том случае, когда равны сами эти числа (х = у).

Подобно этому, теорему о среднем геометрическом и среднем арифметическом трех величин:

³√xyz ≤	x + y + z	,
	3

можно сформулировать как утверждение о том, что

из всех прямоугольных параллелепипедов с данной суммой длин ребер наибольший объем имеет куб.

Треугольник

Теперь ясно, что такое задача на максимум и что мы понимаем под решением ее. Решить такую задачу – это значит указать ее ответ и доказать, что этот ответ при сравнении со всеми другими возможными превосходит их в отношении исследуемого свойства (в данном случае – величины площади).

Обратимся к основной теме этой статьи, а именно к задаче об отыскании среди всех вписанных в данный круг треугольников такого, который имеет наибольшую площадь. Одно место в «Меноне» Платона позволяет предполагать, что эта задача была, по-видимому, поставлена, если и не разрешена, еще во времена Платона, т.е. за сто лет до появления «Начал» Евклида. Впрочем, нижеследующее доказательство, которое, если судить по его стилю, вполне могло бы быть известно древним, не встречается ни у Евклида, ни в современной ему литературе.

Наряду с каким-либо вписанным в наш круг треугольником ABC рассмотрим равносторонний треугольник А₀В₀С₀, вписанный в тот же самый или в равный ему круг.

Площадь этого треугольника – вполне определенная величина и не зависит от его положения внутри круга. Мы утверждаем, что

равносторонний треугольник имеет большую площадь, чем всякий другой треугольник, вписанный в такой же круг,

т.е. что этот треугольник представляет собой решение нашей задачи.

Для доказательства будем исходить из того, что вершины равностороннего треугольника делят окружность на три равные дуги; для всякого же другого треугольника получаем три какие-либо, вообще говоря, неравные дуги, также дающие в сумме полную окружность. Заметим, что, по крайней мере, одна из этих трех дуг должна быть меньше трети полной окружности и хотя бы одна – больше этой трети. Ибо если бы не оказалось ни одной дуги, меньшей трети окружности, то все эти три дуги вместе дали бы сумму, большую целой окружности, за исключением случая, когда каждая из них была бы в точности равна трети окружности, т.е. случая равностороннего треугольника, который мы предполагаем здесь исключенным. Точно так же мы заключаем, что одна из трех дуг должна превышать треть окружности.

Вопрос о том, больше или меньше трети окружности третья дуга, остается при этом открытым; ничего определенного по этому поводу высказать нельзя, да в этом и нет необходимости.

Пусть вершины заданного нам произвольного треугольника обозначены таким образом, что дуга АВ составляет меньше трети, а дуга ВС – больше трети полной окружности.

Отложим на дуге CB, начиная от точки C, дугу CB», равную АВ, так что треугольник CAB» будет зеркальным отображением треугольника АСВ относительно диаметра круга, перпендикулярного АС. Кроме того, от точки A по направлению к B отложим дугу АВ’, равную трети окружности. Точка B’ будет лежать от A во всяком случае дальше, чем B, так как по условию дуга АВ меньше трети окружности. С другой стороны, точка B’ должна лежать перед B», т.е. между точками B и B». В самом деле, если бы она лежала за В», то дуга АВ была бы больше дуги АВ»; но последняя равна своему зеркальному отображению CB, а поскольку, по предположению, CB больше трети полной окружности, то дуга АВ», а следовательно и дуга АВ’, должна была быть больше трети окружности, между тем как дуга АВ’ по построению как раз равна трети окружности. Так как точка B’ лежит между B и B», то вершина треугольника АСВ’ расположена выше вершины треугольника АСВ, имеющего то же самое основание АС.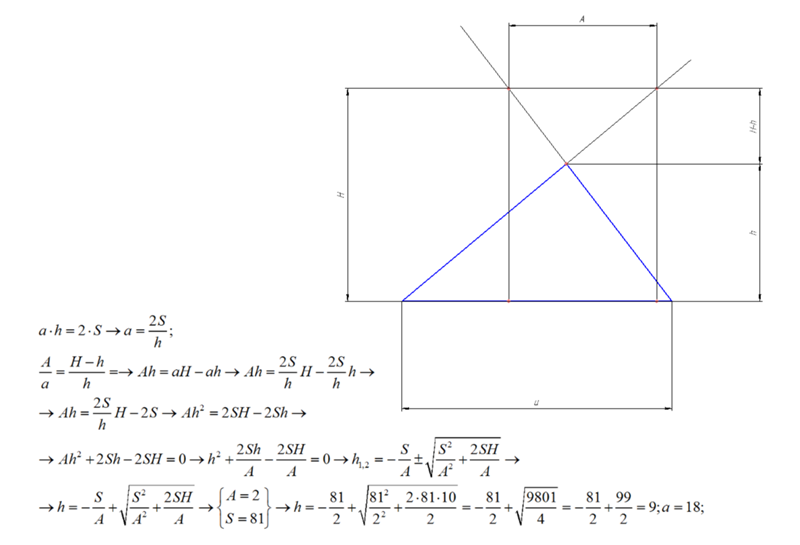

В силу известной теоремы о площади треугольника, равной половине произведения основания на высоту, площадь треугольника АСВ’ будет больше площади треугольника АСВ.

Таким образом, мы нашли новый треугольник АСВ’, вписанный в тот же самый круг и имеющий площадь большую, чем первоначально данный нам треугольник; одна сторона этого нового треугольника, именно АВ’, равна стороне вписанного в тот же круг равностороннего треугольника.

Возможно, что построенный нами треугольник АСВ’ окажется уже равносторонним. Это произойдет в том случае, если дуга АС, стягиваемая одноименной стороной данного треугольника, в точности равна трети окружности. В этом случае наше доказательство того, что равносторонний треугольник по площади больше данного неравностороннего треугольника, было бы уже закончено.

В противном случае примем за основание всей нашей фигуры вместо АС, выступавшего в этой роли до сих пор, сторону АВ’. Для этого нужно только повернуть всю фигуру против часовой стрелки, пока АВ’ не примет горизонтального положения, как на следующем рисунке и применим по отношению к треугольнику АВ’С с основанием АВ’ те же самые рассуждения, какие мы применили только что по отношению к треугольнику АСВ с основанием АС.

Для этого от точки B’ по направлению к С отложим по окружности дугу В’С’, равную трети полной окружности, так что точка С’ вместе с А и В’ образует равносторонний вписанный в круг треугольник, равный треугольнику А₀В₀С₀. По аналогии с предыдущим мы убеждаемся в том, что этот равносторонний треугольник имеет площадь еще большую, чем треугольник АВ’С, а следовательно, и большую, чем первоначально данный треугольник, если только последний сам не равносторонний.

Итак, мы приходим к выводу, что

равносторонний треугольник действительно имеет большую площадь, чем всякий другой треугольник, вписанный в тот же самый круг.

Многоугольник

С помощью подобных же рассуждений можно показать, что

из всех n-угольников, вписанных в один и тот же круг, правильный n-угольник имеет наибольшую площадь.

В дальнейшем нам понадобится следующее чрезвычайно простое предварительное замечание:

если дан какой-либо вписанный в круг n-угольник, то в тот же самый круг можно вписать новый n-угольник, стороны которого равны по величине сторонам первого n-угольника, но расположены в иной, произвольно выбранной последовательности.

Для этого стоит только разбить круг радиусами, проходящими через вершины данного

n-угольника, на n секторов, представить себе, что эти секторы вырезаны, положим, из картонного диска, и тогда легко будет непосредственно убедиться в том, что из этих секторов при расположении их в каком-либо ином, новом порядке можно опять составить тот же самый круговой диск. При этом получается и новый n-угольник. Очевидно, что площадь его от такой перестановки секторов не меняется.

Приняв во внимание это замечание, мы можем приступить к доказательству нашего утверждения. Как и в случае треугольника, начнем с утверждения, что одна какая-либо сторона вписанного в круг неправильного n-угольника должна стягивать дугу, меньшую ¹/_n доли полной окружности, а какая-нибудь другая – большую. Однако здесь уже нельзя утверждать, что обе эти стороны расположены рядом. В треугольнике это неизбежно, так как каждая из трех его сторон примыкает к обеим другим, но n-угольник с более чем тремя сторонами этим свойством уже не обладает. Тем не менее, на основании сделанного замечания, если рассматриваемые две стороны не смежные, в тот же самый круг можно вписать новый n-угольник той же самой площади, в котором эти стороны окажутся соседними.

Обозначим меньшую из этих сторон через АВ, большую – через ВС. Тогда от точки A по направлению к В можно отложить дугу АВ’, равную в точности ¹/_n доле целой окружности, и, так же как и прежде, убедиться в том, что точка В’ должна расположиться между В и ее зеркальным отображением В». Если поэтому вершину В в данном нам n-угольнике заменить через В’, сохранив все другие вершины без изменения, то площадь n-угольника при этом увеличится, а одна сторона станет равной стороне правильного вписанного n-угольника. Точно так же мы поступим последовательно и со всеми остальными n – 1 сторонами нашего n-угольника, пользуясь в случае надобности нашим предварительным замечанием. В результате мы убедимся, что данный n-угольник меньше по площади того правильного n-угольника, к которому мы должны будем прийти с помощью наших построений, при которых все стороны данного n-угольника, одна за другой, делаются последовательно равными сторонам правильного n-угольника.

Точно таким же способом можно показать, что

из всех n-угольникoв, описанных около данного круга, правильный имеет наименьшую площадь.

Источник: Ганс Радемахер, Отто Тепліц. Числа і фігури (Тернопіль, «Навчальна книга – Богдан», 2010).

<<< Назад

Смотрите так же:

И вновь о седних…

Когда произведение наибольшее?

Решения

Областная олимпиада по математике, 2015 год, 10 класс

Прямоугольник вписан в треугольник, если все его вершины лежат на сторонах треугольника. Докажите, что геометрическим местом центров (точек пересечения диагоналей) всех вписанных в данный остроугольный треугольник прямоугольников являются три пересекающихся в одной точке незамкнутых отрезка.

посмотреть в олимпиаде

Комментарий/решение:

Это предпросмотр

Комментарии от администратора Комментарии от администратора №1. Решение. Пусть $ABC$ — рассматриваемый треугольник. Обозначим через $C_1$ — середину стороны $AB$, $C_2$ — основание высоты из вершины $C$ и $C_3$ — середину отрезка $CC_2$. Аналогично определим точки $A_1,A_2,A_3,B_1,B_2,B_3$.

Из четырёх вершин прямоугольника какие-то две лежат на одной стороне. Пусть это прямоугольник $PQRS$, где точки $P$ и $S$ лежат на отрезке $AB$ (см. рис. выше). Так как $APQ$ и $AC_2C$ — прямоугольные подобные треугольники, то отрезок $AC_3$ делит отрезок $PQ$ пополам. Аналогично, $BC_3$ делит $RS$ пополам. Пусть $M$ и $N$ — середины отрезков $PQ$ и $RS$. Так как расстояния от точек $R$ и $Q$ до $AB$ равны, то расстояния от точек $M$ и $N$ до $AB$ также равны, то есть $MN \parallel AB$. Следовательно, $C_1C_3$ делит $MN$ пополам. А это значит, центр $PQRS$ лежит на отрезке $C_1C_3$. Нетрудно доказать, что для любой точки отрезка $C_1C_3$ существует вписанный прямоугольник, центр которого совпадает с данной точкой.

Чтобы построить такой прямоугольник, нужно опустить перпендикуляр из этой точки на $AB$, основание этого перпендикуляра отобразить относительно этой же точки, и через эту точки провести отрезок, параллельный к $AB$, концы которого лежат на сторонах $AC$ и $BC$, и от этих концов опустить перпендикуляры на $AB$. Так как эта точка будет располагаться ближе к $AB$ чем точка $C_3$, то такой искомый прямоугольник существует. Для завершения решения задачи осталось показать, что все отрезки $C_1C_3$, $A_1A_3$ и $B_1B_3$ пересекаются в одной точке. Это легко следует из теоремы Чевы, так как: \[\dfrac{{{A_1}{C_3}}}{{{C_3}{B_1}}} \cdot \dfrac{{{B_1}{A_3}}}{{{A_3}{C_1}}} \cdot \dfrac{{{C_1}{B_3}}}{{{B_3}{A_1}}} = \dfrac{{B{C_2}}}{{{C_2}A}} \cdot \dfrac{{A{B_2}}}{{{B_2}C}} \cdot \dfrac{{C{A_2}}}{{{A_2}B}} = 1\]

Прямоугольник — Геометрия 8 класс

Введем определение прямоугольника.

Определение. Прямоугольником называют параллелограмм, у которого все углы прямые (см. Рис. 1).

Рис. 1. Прямоугольник

Замечание. Очевидным эквивалентным определением прямоугольника (иногда его именуют признаком прямоугольника) можно назвать следующее. Прямоугольник – это параллелограмм с одним углом . Это утверждение практически очевидно, и мы оставим его без доказательства, пользуясь далее как определением.

Т.к. прямоугольник, как это видно из определения, является частным случаем параллелограмма, то ему присущи все ранее описанные свойства параллелограмма, однако у него имеются и свои специфические свойства, которые мы сейчас рассмотрим.

Теорема 1. Свойство прямоугольника. Диагонали прямоугольника равны.

Доказательство. Изобразим на Рис. 2 прямоугольник (как и у параллелограмма, противоположные стороны равны и параллельны). Все углы прямые. Необходимо доказать, что диагонали .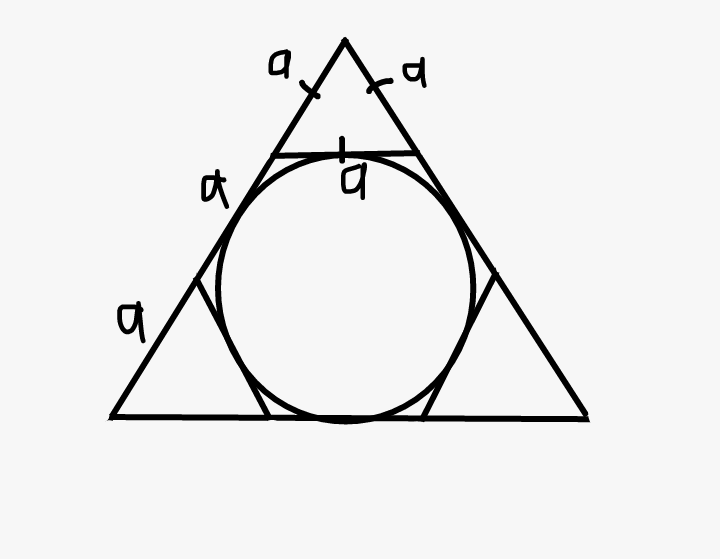

Рис. 2

Рассмотрим для доказательства прямоугольные треугольники, в которых присутствуют указанные диагонали и :

прямоугольные треугольники по двум катетам. Следовательно, равны и гипотенузы треугольников , что и требовалось доказать.

Доказано.

Обратим внимание, что это свойство специфическое и относится только к прямоугольнику, ко всем остальным параллелограммам оно не относится.

Теорема 2. Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Доказательство. Изобразим Рис. 3. Нам необходимо доказать, что изображенный параллелограмм с двумя равными диагоналями – прямоугольник, т.е. имеет прямой угол.

Рис. 3

Поскольку – параллелограмм, то можем воспользоваться его свойством: . Кроме этого, – по трем сторонам (), следовательно, . Тогда имеем:

прямоугольник, что и требовалось доказать.

Доказано.

Рассмотрим примеры.

Пример 1. В прямоугольнике диагонали пересекаются в точке . Найдите периметр треугольника , если .

Решение. Изобразим Рис. 4.

Рис. 4

Сначала будем искать стороны указанного треугольника: ( по свойству диагоналей в любом параллелограмме). Но в прямоугольнике диагонали равны .

Т.к. угол .

Рассмотрим треугольник : (аналогично углу ), равносторонний. Следовательно, его периметр .

Ответ: 18 см.

Пример 2. Найдите периметр прямоугольника , если биссектриса угла делит сторону на отрезки 2 см и 3 см.

Рис. 5 (а), рис. 5 (б)

Решение. Сразу же стоит заметить, что это пример задачи на два варианта решения, наличие которых еще надо заметить. «Изюминка» условия задачи заключается в том, что не указано, в каком именно порядке расположены отрезки, на которые биссектриса прямоугольника разбивает его сторону.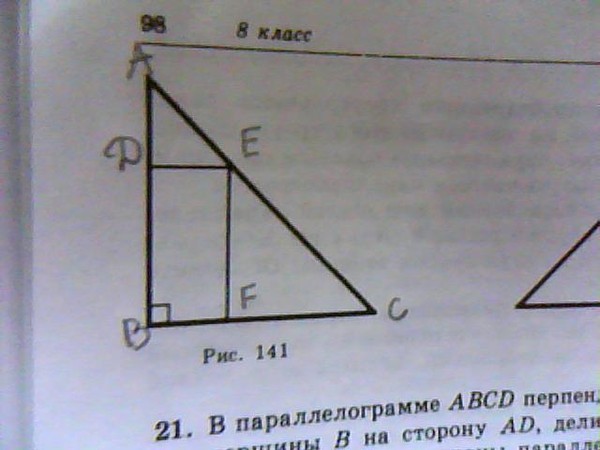 В результате имеем два варианта рисунков 5 (а, б).

Т.к. – биссектриса, то , кроме того, – как накрест лежащие углы при параллельных прямых, следовательно, равнобедренный, а из этого следует, что .

Далее разобьем решение на две части, в каждой из которых рассмотрим отдельный случай.

А. Рис. 5 (а). . Сторона прямоугольника (для обоих случаев). Периметр прямоугольника .

Б. Рис. 5 (б). . Периметр прямоугольника .

Ответ: .

Пример 3. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Доказательство. Изобразим Рис. 6.

Рис. 6

Необходимо доказать, что . Между прочим, это свойство медианы в прямоугольном треугольнике уже использовалось нами ранее, сейчас мы докажем его, используя свойства прямоугольника.

Продлим медиану на ее длину, расстояние до точки : . Мы получили четырехугольник . В нем и диагонали, и для него мы можем указать следующие факты:

параллелограмм по третьему признаку. Кроме того, известно, что в нем прямоугольник (по указанному вначале урока определению – признаку прямоугольника).

По свойству прямоугольника можно указать, что у него равны диагонали, а следовательно, равны и их половинки, т.е. получаем , что и требовалось доказать.

Доказано.

Пример 4. (обратная задача). В треугольнике медиана . Докажите, что .

Доказательство. Изобразим Рис. 7 и обозначим на нем углы .

Рис. 7

Рассмотрим , он равнобедренный ( по условию) ⇒ .

Рассмотрим , он также равнобедренный ( по условию) ⇒ .

Запишем сумму углов треугольника : . Но угол что и требовалось доказать.

Доказано.

Пример 5. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол.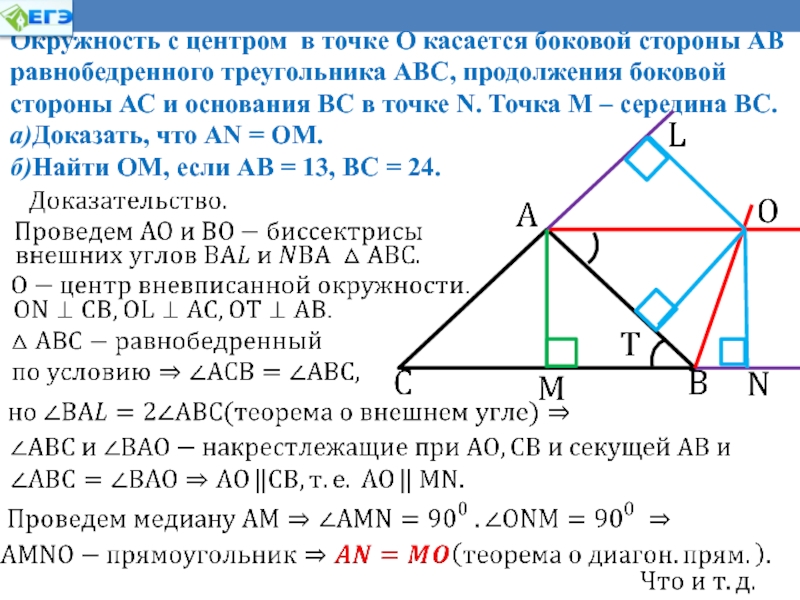 Найдите периметр прямоугольника.

Решение. Изобразим Рис. 8. Ясно, что можно построить множество различных прямоугольников, вписанных в прямоугольный треугольник, но выясняется, что их периметры будут одинаковы, покажем это и найдем искомый периметр.

Рис. 8

По условию равнобедренный .

Искомый периметр прямоугольника: .

Рассмотрим прямоугольный : .

Тогда периметр прямоугольника : .

Ответ: 12 см.

Пример 6. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны и периметр прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см?

Решение. Изобразим Рис. 9 и укажем на нем все элементы, которые мы введем в процессе решения задачи.

Рис. 9

По условию равнобедренный и прямоугольный .

Указано, что вписанный прямоугольник имеет заданные пропорции, поэтому его стороны можно ввести, как определенное количество неизвестных нам частей : .

Рассмотрим треугольники и – они прямоугольные и имеют по одному углу , следовательно, второй угол у них тоже по (см. решение предыдущей задачи), т.е. они равнобедренные, и .

Теперь можем выписать длину гипотенузы как сумму длин отрезков, на которые она разбита вписанным прямоугольником (через те части , которые мы ввели): .

Теперь можем посчитать длины сторон прямоугольника и его периметр: .

Ответ: стороны равны .

Сегодня мы рассмотрели прямоугольник, его свойства, признаки и задачи на прямоугольник. На следующем уроке мы познакомимся с такими частными случаями параллелограмма, как ромб и квадрат.

http://interneturok. ru/geometry/8-klass/chyotyrehugolniki/pryamougolnik

Практическое задание по теме «Прямоугольник»

а). Работа с математическим текстом (на каждой парте лежит текст о прямоугольнике)

Прямоугольник – это четырехугольник, у которого все углы прямые.

Прямоугольник имеет четыре вершины, которые обозначаются большими латинскими буквами:

А, В, С, Д. Сам прямоугольник можно назвать четырьмя способами: АВСД, ВСДА, СДАВ, ДАВС.

У прямоугольника четыре стороны. Важным свойством прямоугольника является равенство противоположных сторон: АВ=ДС, АД=ВС.

Периметр прямоугольника находится по формуле: Р = 2·(а+в).

Площадь прямоугольника находится по формуле: S = а·в, где а и в – стороны прямоугольника.

В любом прямоугольнике имеется две диагонали. Диагональ – это отрезок, соединяющий две несоседние вершины. Диагональ делит прямоугольник на два равных треугольника.

Задание: Прочитайте внимательно данный материал, отметьте карандашом по тексту то, что вам уже известно и новое понятие (диагональ) и выпишите в тетрадь основные понятия .

б). Расскажите о прямоугольнике все, что вы знаете. В этом вам помогут вопросы и задания на странице 57.

— почему прямоугольник получил такое название?

— как зовут этот прямоугольник? Сколькими способами можно назвать этот прямоугольник?

— что обозначено буквами а и в?

— что такое периметр прямоугольника; как его найти?

— как найти площадь прямоугольника?

— что такое диагональ прямоугольника?

— сколько диагоналей у прямоугольника?

— на какие фигуры разбивает диагональ прямоугольник?

— какие измерения надо произвести, чтобы найти периметр и площадь прямоугольника?

4. Закрепление нового материала.

1.Практическая работа

Задание1: (Используются прямоугольники из раздаточного материала).

Сделав необходимые измерения, найти периметр и площадь прямоугольника.

( Результаты измерений записываются на обратной стороне шаблона. Шаблоны подписываются и сдаются учителю на проверку ).

Задание 2:

Начертите у себя прямоугольник со сторонами 7 см и 3 см. Обозначьте его. Найдите его площадь и периметр. Назовите ответ.

2. Задача. Найти площадь и периметр фигуры, изображенной на доске. Найдите разные способы.

5. Физкультминутка.

Закройте глаза, расслабьте тело,

Представьте — вы птица, вы вдруг полетели!

Теперь в океане дельфином плывете,

Теперь в саду яблоки спелые рвете.

Налево, направо, вокруг посмотрели,

Открыли глаза, и снова за дело!

6. Самостоятельная работа ( двух уровней на выбор) с последующей проверкой по готовым решениям.

Запись домашнего задания. Стр.57, № 194(а), № 203(г).

Учитель: Проверим, как вы поняли новый материал.

Какие утверждения верные, какие неверные, а какие неточные?

• Прямоугольник – это четырёхугольник, в котором есть прямой угол.

• Смежные стороны прямоугольника – это длина и ширина.

• Периметр – это произведение сторон прямоугольника.

• Диагональ – это отрезок, соединяющий две вершины прямоугольника.

• Площадь прямоугольника равна произведению всех его сторон.

8. Итоги урока. Учитель:

— О какой геометрической фигуре шел разговор на уроке?

— Что нового вы узнали на уроке?

-Что нужно знать, чтобы найти периметр и площадь прямоугольника?

-Пригодятся ли вам в жизни полученные знания? Где?

-Что на уроке было самым сложным, простым?

— Что было на уроке самым интересным?

9.Оценивание. Выставление оценок.

Учитель:

Окончен урок, и выполнен план.

Спасибо, ребята, огромное вам.

За то, что упорно и дружно трудились,

И знания точно уж вам пригодились.

Вписанные и описанные окружности. Описанные и вписанные в треугольник, четырехугольник, ромб, прямоугольник, квадрат, трапецию и правильный многоугольник окружности.

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Вписанные и описанные окружности. Описанные и вписанные в треугольник, четырехугольник, ромб, прямоугольник, квадрат, трапецию и правильный многоугольник окружности.

Вписанные и описанные окружности.

Описанные и вписанные в треугольник, четырехугольник, ромб, прямоугольник, квадрат, трапецию и правильный многоугольник окружности.

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления.

Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2),

8 класс.

Геометрия. Четырехугольники. Прямоугольник, ромб и квадрат. — Прямоугольник.

Комментарии преподавателя

Прямоугольник

Введем определение прямоугольника.

Определение. Прямоугольником называют параллелограмм, у которого все углы прямые (см. Рис. 1).

Рис. 1. Прямоугольник

Теорема 1. Свойство прямоугольника. Диагонали прямоугольника равны.

Рис. 2

Рассмотрим для доказательства прямоугольные треугольники, в которых присутствуют указанные диагонали и :

Доказано.

Рис. 3

прямоугольник, что и требовалось доказать.

Доказано.

Рассмотрим примеры.

Пример 1. В прямоугольнике диагонали пересекаются в точке . Найдите периметр треугольника , если .

Решение. Изобразим Рис. 4.

Рис. 4

Т.к. угол .

Рассмотрим треугольник : (аналогично углу ), равносторонний. Следовательно, его периметр .

Ответ: 18 см.

Пример 2. Найдите периметр прямоугольника , если биссектриса угла делит сторону на отрезки 2 см и 3 см.

Рис. 5 (а), рис. 5 (б)

Далее разобьем решение на две части, в каждой из которых рассмотрим отдельный случай.

А. Рис. 5 (а). . Сторона прямоугольника (для обоих случаев). Периметр прямоугольника .

Б. Рис. 5 (б). . Периметр прямоугольника .

Ответ: .

Доказательство. Изобразим Рис. 6.

Рис. 6

Доказано.

Пример 4. (обратная задача). В треугольнике медиана . Докажите, что .

Доказательство. Изобразим Рис. 7 и обозначим на нем углы .

Рис. 7

Рассмотрим , он равнобедренный ( по условию) ⇒ .

Рассмотрим , он также равнобедренный ( по условию) ⇒ .

Запишем сумму углов треугольника : . Но угол что и требовалось доказать.

Доказано.

Рис. 8

По условию равнобедренный .

Искомый периметр прямоугольника: .

Рассмотрим прямоугольный : .

Тогда периметр прямоугольника : .

Ответ: 12 см.

Решение. Изобразим Рис. 9 и укажем на нем все элементы, которые мы введем в процессе решения задачи.

Рис. 9

По условию равнобедренный и прямоугольный .

Теперь можем посчитать длины сторон прямоугольника и его периметр: .

Ответ: стороны равны .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/pryamougolnik

http://www.youtube.com/watch?v=RoLxsWnSL6k

http://www.youtube.com/watch?v=IR_41PVrolM

http://nsportal.ru/sites/default/files/2014/08/25/pryamougolnik_0.zip

http://www.mathematics-repetition.com/category/8-klass-geometriya

http://player.myshared.ru/1246878/data/images/img3. jpg

http://ege-study.ru/wp-content/uploads/2013/03/%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B8.png

http://gdz7.ru/files/cub/66/ddf77a4487ef15adf56e3f1b79c34c21.jpg

http://gdz7.ru/files/cub/80/d527b10c05e422830980745055460047.jpg

вписанная в многоугольник или угол

Определения

Окружность $S$ вписана в угол $\alpha$, если $S$ касается сторон угла $\alpha$.

Окружность $S$ вписана в многоугольник $P$, если $S$ касается всех сторон $P$.

В этом случае многоугольник $P$ называется описанным около окружности.

Теорема

Центр вписанной в угол окружности лежит на его биссектрисе.

Доказательство

Пусть $O$ – центр некоторой окружности, вписанной в угол $BAC$. Пусть $B’$ – точка касания окружности и $AB$, а $C’$ – точка касания окружности и $AC$, тогда $OB’$ и $OC’$ – радиусы, проведённые в точки касания, следовательно, $OC’\perp AC$, $OB’\perp AB$, $OC’ = OB’$.

Значит, треугольники $AC’O$ и $AB’O$ – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда $\angle CAO = \angle BAO$, что и требовалось доказать.

Теорема

В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.

Доказательство

Проведем биссектрисы углов $\angle A$ и $\angle B$. Пусть они пересеклись в точке $O$.

Т.к. $O$ лежит на биссектрисе $\angle A$, то расстояния от точки $O$ до сторон угла равны: $ON=OP$.

Т.к. $O$ также лежит на биссектрисе $\angle B$, то $ON=OK$. Таким образом, $OP=OK$, следовательно, точка $O$ равноудалена от сторон угла $\angle C$, следовательно, лежит на его биссектрисе, т.е. $CO$ – биссектриса $\angle C$.

Таким образом, точки $N, K, P$ равноудалены от точки $O$, то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.

Данная окружность единственна, т.к. если предположить, что существует другая вписанная в $\triangle ABC$ окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.

Таким образом, попутно была доказана следующая теорема:

Следствие

Биссектрисы треугольника пересекаются в одной точке.

Теорема о площади описанного треугольника

Если $a,b,c$ – стороны треугольника, а $r$ – радиус вписанной в него окружности, то площадь треугольника \[S_{\triangle}=p\cdot r\] где $p=\dfrac{a+b+c}2$ – полупериметр треугольника.

Доказательство

$S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle BOC}=\frac12OP\cdot AC+\frac12 ON\cdot AB+\frac12 OK\cdot BC$.

Но $ON=OK=OP=r$ – радиусы вписанной окружности, следовательно,

\[S_{\triangle ABC}=\frac12 r (AC+AB+BC)=p\cdot r\]

Следствие

Если в многоугольник вписана окружность и $r$ – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на $r$: \[S_{\text{опис.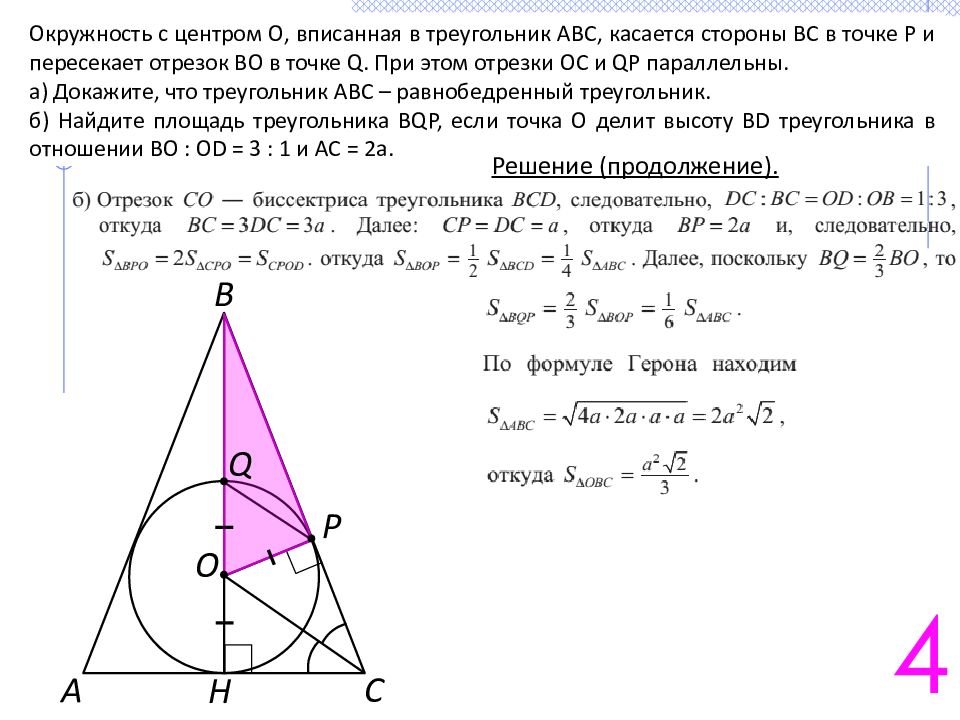 мног-к}}=p\cdot r\]

Теорема

В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Доказательство

Необходимость. Докажем, что если в $ABCD$ вписана окружность, то $AB+CD=BC+AD$.

Пусть $M,N,K,P$ – точки касания окружности и сторон четырехугольника. Тогда $AM, AP$ – отрезки касательных к окружности, проведенные из одной точки, следовательно, $AM=AP=a$. Аналогично, $BM=BN=b, \ CN=CK=c, \ DK=DP=d$.

Тогда: $AB+CD=a+b+c+d=BC+AD$.

Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

Проведем биссектрисы углов $\angle A$ и $\angle B$, пусть они пересекутся в точке $O$. Тогда точка $O$ равноудалена от сторон этих углов, то есть от $AB, BC, AD$. Впишем окружность в $\angle A$ и $\angle B$ с центром в точке $O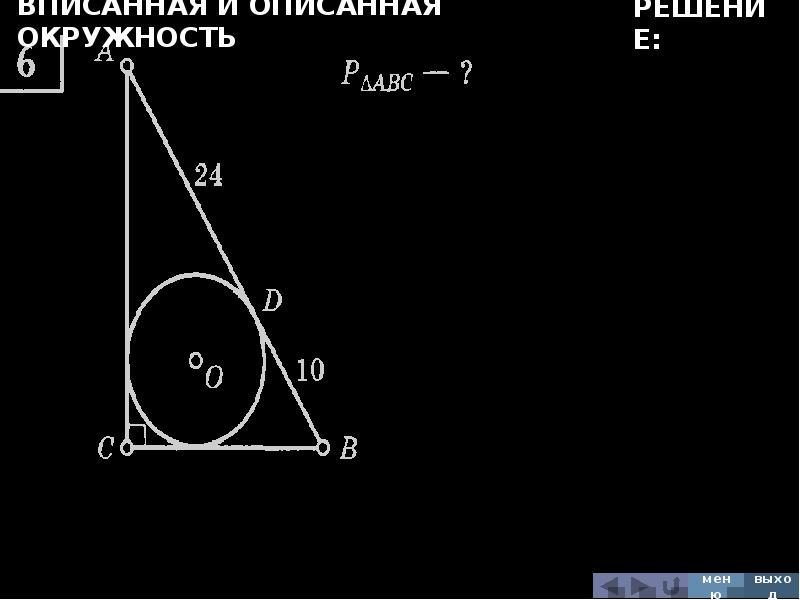$. Докажем, что эта окружность будет касаться и стороны $CD$.

Предположим, что это не так. Тогда $CD$ либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).

Проведем касательную прямую $C’D’ \parallel CD$ (как показано на рисунке). Тогда $ABC’D’$ – описанный четырехугольник, следовательно, $AB+C’D’=BC’+AD’$.

Т.к. $BC’=BC-CC’, \ AD’=AD-DD’$, то:

\[AB+C’D’=BC-CC’+AD-DD’ \Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD\]

Получили, что в четырехугольнике $C’CDD’$ сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, $CD$ касается окружности.

Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.

Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то $a+x>d$ и $b+c>x$. Складывая данные неравенства, получим: $a+x+b+c>d+x \Rightarrow a+b+c>d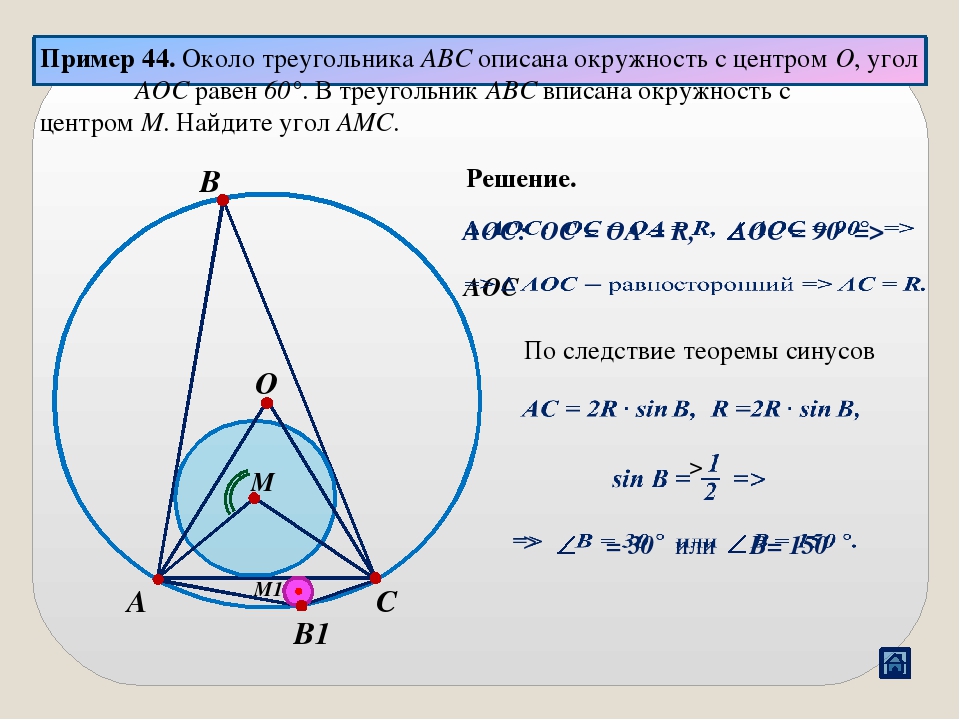$. Следовательно, сумма любых трех сторон всегда больше четвертой стороны.

Теоремы

1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).

2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).

Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.

Доказательство

1) Рассмотрим параллелограмм $ABCD$, в который вписана окружность. Тогда $AB+CD=BC+AD$. Но в параллелограмме противоположные стороны равны, т.е. $AB=CD, \ BC=AD$. Следовательно, $2AB=2BC$, а значит, $AB=BC=CD=AD$, т.е. это ромб.

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.

2) Рассмотрим прямоугольник $QWER$. Т.к. прямоугольник является параллелограммом, то согласно первому пункту $QW=WE=ER=RQ$, т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.

Решение | Прямоугольники в треугольниках | Представляем Calculus

Какова наибольшая площадь прямоугольника, вписанного в данный прямоугольный треугольник?

Рассмотрим ситуацию, когда C — вершина как прямоугольника, так и треугольника.

Эту проблему можно решить разными способами, некоторые из которых более эффективны, чем другие.

Мы могли бы рассмотреть алгебраический подход.

Шаг 1

Рассмотрим конкретный случай.

Допустим, для простоты я решил рассмотреть прямоугольный треугольник \ (3 \), \ (4 \), \ (5 \).Если я установлю ширину прямоугольника равной \ (1 \), как я могу рассчитать площадь получившегося прямоугольника?

Что ж, если \ (DE = 1 \), то длина \ (AF = 2 \), и если я заметил, что треугольник \ (AEF \) похож на треугольник \ (ABC \), то я могу вычислить линейный масштабный коэффициент увеличения. .

Коэффициент линейного масштабирования рассчитывается как отношение соответствующих длин в двух одинаковых треугольниках. В этом случае я хочу рассмотреть возможность перехода от большего треугольника \ (ABC \) к меньшему треугольнику \ (AEF \), поэтому у меня

\ [\ text {Коэффициент линейного масштабирования} = \ frac {AF} {AC} = \ frac {2} {3}.\]

Теперь я могу рассчитать длину \ (EF \) как \ [\ frac {2} {3} \ times 4 = \ frac {8} {3}. \]

Таким образом, площадь этого конкретного прямоугольника равна \ [1 \ times \ frac {8} {3} = \ frac {8} {3}. \]

Я успешно вычислил площадь одного конкретного прямоугольника, вписанного в мой прямоугольный треугольник \ (3 \), \ (4 \), \ (5 \). Однако мне все еще нужно ответить на более важный вопрос: какова наибольшая площадь прямоугольника, вписанного в прямоугольный треугольник?

Для этого мне нужно перейти к более общему случаю.

Шаг 2

Переходим к более общему случаю.

Применение метода, используемого в моем конкретном случае, к обычному прямоугольнику горизонтальной длины \ (x \), вписанному в прямоугольный треугольник \ (3 \), \ (4 \), \ (5 \), коэффициент линейного масштабирования будет задано как \ (\ dfrac {3-x} {3} \).

Площадь прямоугольника \ (CDEF \) теперь будет равна

. \ [\ begin {уравнение} 4x \ left (\ frac {3-x} {3} \ right) = \ frac {4} {3} x (3-x) \ label {eq: 1} \ конец {уравнение} \]

Теперь я вижу, что имею дело с квадратичным выражением.В данном случае это будет выглядеть как парабола с максимальной точкой. Если я смогу набросать параболу, тогда я смогу найти \ (x \) — координату максимума, которая соответствует горизонтальной длине прямоугольника с максимальной площадью.

Я вижу, что максимальная площадь будет достигнута, когда \ (x = \ dfrac {3} {2} \) (я использую свойство вертикальной симметрии параболы), и теперь я могу заменить это на \ (\ eqref {eq : 1} \), чтобы определить максимальную площадь как \ [\ frac {4} {3} x (3-x) = \ frac {12} {6} \ left (\ frac {3} {2} \ right) = 3.\]

Обратите внимание, что это ровно половина площади исходного треугольника \ (3 \), \ (4 \), \ (5 \)!

Интересно, верно ли это вообще для любого прямоугольного треугольника?

Шаг 3

Общий шкаф

Применяя тот же метод, что и раньше, но для прямоугольного треугольника с длинами сторон \ (a \), \ (b \), \ (c \), я вижу, что коэффициент линейного масштабирования равен \ [\ frac {bx} {b}. \]

Используя это, я могу теперь определить длину вертикальной стороны прямоугольника как \ [a \ left (\ frac {bx} {b} \ right) \], и поэтому площадь задается как \ [ax \ left (\ frac {bx} {b} \ right) = \ frac {a} {b} x (b — x).\]

Рисуя график этого выражения, как и раньше, я вижу, что прямоугольник максимальной площади возникает, когда \ (x = \ dfrac {b} {2} \). Подставляя это в общую формулу для площади, я нахожу, что \ [\ textrm {Максимальная площадь} = \ frac {a} {b} \ left (\ frac {b} {2} \ right) \ left (b — \ frac {b} {2} \ right) = \ frac {a} {2} \ left (\ frac {b} {2} \ right) = \ frac {ab} {4}. \]

Площадь исходного треугольника \ (ABC \) задается как \ (\ dfrac {ab} {2} \).

Следовательно, если прямоугольник вписан в прямоугольный треугольник таким образом, его наибольшая площадь будет ровно вдвое меньше площади треугольника.

Одна из первых вещей, которую мы должны сделать при использовании алгебраического подхода, — это решить, какую длину на диаграмме рассматривать как нашу переменную. Предложение на главной странице проблемы предлагало выбрать длину прямоугольника по горизонтали \ (x \). Однако мы могли легко выбрать длину прямоугольника по вертикали. Возможно, мы даже выбрали для работы одну из других длин на диаграмме.

Итак, как мы узнаем, какая переменная будет лучшим выбором? Мы можем предположить, что это не повлияет на конечный результат, но имеет ли это значение для путешествия? Будет ли «легче» работать с одним вариантом выбора переменной, чем с другим?

Дополнительное мышление

В этом конкретном сценарии, поскольку каждая из сторон прямоугольника параллельна стороне исходного треугольника, выбор длины или ширины прямоугольника в качестве нашей переменной фактически приведет к симметричной цепочке рассуждений, эквивалентному объему работы. требуется для достижения решения.

Если, однако, мы решим изменять длину гипотенузы, скажем, от точки B до верхней правой вершины прямоугольника, то мы можем ожидать некоторого дополнительного «времени в пути», чтобы определить длину и ширину прямоугольника. а значит и площадь.

Иногда трудно предсказать, какой вариант переменной будет «наилучшим». Часто, оглядываясь назад и осознавая проблему, мы можем увидеть альтернативный, потенциально более эффективный подход.

В качестве альтернативы мы могли бы рассмотреть возможный геометрический подход.

Шаг 1

Предположим, \ (x

<\ frac {b} {2} \).

Складываем по линии \ (EF \) получаем:

Показав, что треугольники \ (GDE \) и \ (BDE \) совпадают, мы можем увидеть, что площадь за пределами красного прямоугольника больше (на треугольник \ (A’CG \)), чем площадь внутри него. Следовательно, площадь красного прямоугольника меньше половины площади треугольника \ (ABC \).

Шаг 2

Предположим, \ (x = \ frac {b} {2} \).

Складываем по линии \ (EF \) получаем:

Показав, что это разбивает исходный треугольник \ (ABC \) на четыре меньших, конгруэнтных треугольника, мы можем видеть, что площадь за пределами красного прямоугольника равна площади внутри него. Следовательно, когда \ (x \) увеличивается до \ (\ dfrac {b} {2} \), площадь красного прямоугольника увеличивается до половины площади треугольника \ (ABC \).

Шаг 3

Предположим, \ (x> \ frac {b} {2} \).

Складываем по линии \ (DE \) получаем:

Показав, что треугольники \ (AEF \) и \ (HEF \) совпадают, мы можем увидеть, что площадь за пределами красного прямоугольника больше (на треугольник \ (B’CH \)), чем площадь внутри него. Следовательно, площадь красного прямоугольника, опять же, меньше половины площади треугольника \ (ABC \).

Заключение

Рассматривая каждый из этих трех случаев, мы показали, что красный прямоугольник будет иметь максимальную площадь, равную половине площади исходного треугольника \ (ABC \). Это произойдет при горизонтальной длине прямоугольника \ (x = \ frac {b} {2} \).

Вы можете пересмотреть свой подход к этой проблеме после изучения некоторых идей в Calculus of Powers.

Максимальный прямоугольник, вписанный в треугольник

Максимальный прямоугольник, вписанный в треугольник Лори Пирман
EMT 725

Проблема: Найдите максимальный прямоугольник, вписанный в треугольник.

Учитывая треугольник, как можно построить вписанный прямоугольник с максимальным область?
Я начал это расследование с того, что наугад нарисовал треугольник в GSP, отметив прямоугольник и анимацию точки таким образом, чтобы показать все возможные вписанные прямоугольники. Затем я вычислил площадь прямоугольника в следующем порядке: посмотреть (как был анимирован прямоугольник) на максимальную площадь. Для треугольников что я пробовал, максимальный прямоугольник получился, когда средние точки двух из стороны соединились, чтобы получилась сторона прямоугольника.кликните сюда чтобы увидеть пример.
Если моя догадка верна, то для построения вписанного прямоугольника максимума площадь для данного треугольника, нужно сделать следующее: найти середины двух сторон треугольника и соедините эти середины, чтобы получилась одна сторона прямоугольника. Падение перпендикуляров из средних точек определит длины других сторон прямоугольника. (Пересечение перпендикулярами, а третья сторона будет двумя другими вершинами, кроме вершины середины. ) Нажмите здесь , чтобы увидеть сценарий, который построит этот прямоугольник с учетом вершин A, B, C некоторого треугольника.

На рисунке выше показан пример треугольника, вписанный прямоугольник которого максимальной площади. Обратите внимание, что площадь прямоугольника составляет половину площади всего треугольника. Так будет с любым вписанным прямоугольник максимальной площади.

Картинка выше поможет продемонстрировать, почему вписанный прямоугольник максимальной площади (розовый прямоугольник на этом рисунке) имеет площадь, которая вдвое меньше большого треугольника.Чтобы сделать этот рисунок, я повернул треугольник Устройство автоматической подачи документов на 180 градусов вокруг точки D для создания треугольника IDB. Аналогично треугольник BHE был создан вращением треугольника EGC вокруг точки E. Если бы мы удалили треугольники ADF и EGC, то у нас осталось бы два прямоугольника DIHE и FDEG, которые имеют одинаковую площадь. Таким образом, прямоугольник FDEG равен 1/2 большого прямоугольника.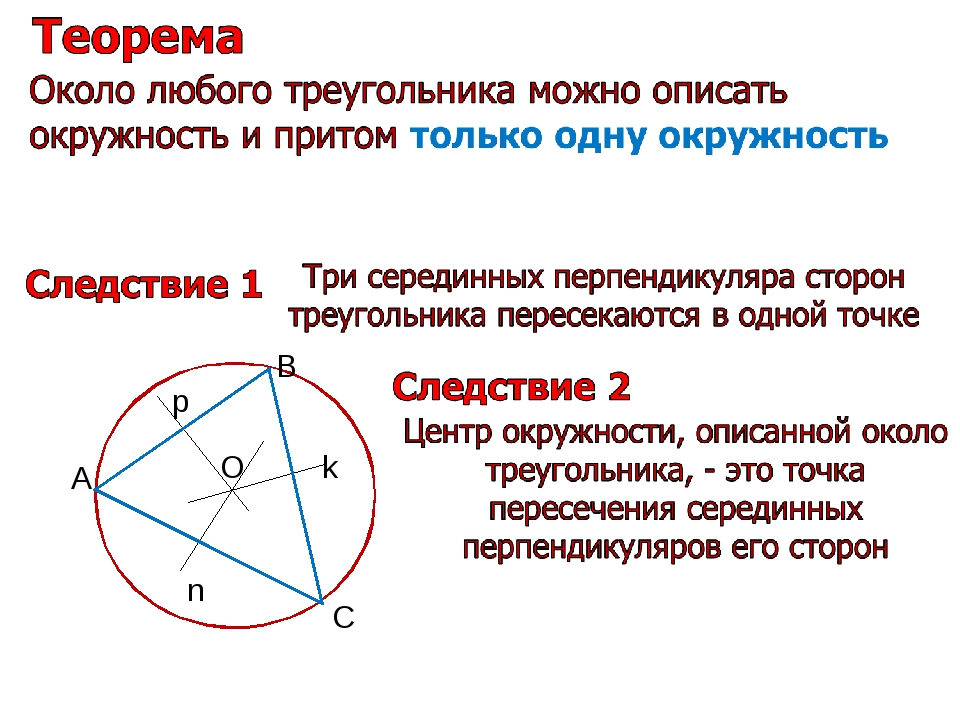 FIHG. Поскольку большой прямоугольник равен по площади большому треугольнику, мы начали с (потому что мы просто повернули две его части, чтобы прямоугольник), прямоугольник FDEG = (треугольник ABC) / 2.

Как узнать, что прямоугольники DIHE и DFGE имеют одинаковую площадь без использования ВСП для измерения своих площадей? Посмотрим на ту сторону, где был треугольник ADF. повернут, чтобы сделать DIB. (Аналогичный аргумент можно привести и для другой стороны с треугольником BHE.) DIHE и DFGE имеют одинаковую ширину. ID = DF, поскольку DF был повернут, чтобы сделать ID. Оба этих прямоугольника имеют длину, равную в DE. Также угол AFD был прямым, поэтому угол DIB правильный. AD = DB, поскольку D — середина AB.Когда треугольник ADF вращается, AD «подходит» именно по БД.

optimisation — Максимально возможная площадь прямоугольника, вписанного в данный прямоугольный треугольник

Вашему учителю не понравится метод в этом ответе, поэтому не используйте его. по домашнему заданию. Для задачи 6 нарисуйте прямоугольный треугольник $ \ треугольник ACB $ $ 6,8,10 $, как показано ниже:

Выбор любой точки $ P $ вдоль гипотенузы $ AB $ и сброс перпендикуляры от $ P $ к $ Q $ на $ AC $ и $ R $ на $ BC $, вы вписали прямоугольник $ PQCR $ в $ \ треугольник ACB $ в желаемой позиции.Теперь отразите треугольник $ \ треугольник PQA $ через линию $ PQ $. чтобы получить треугольник $ \ треугольник PQS $, и отразим треугольник $ \ треугольник PRB $ через линию $ PR $ чтобы получить треугольник $ \ треугольник PRT $. Замечает, что если вы поместите $ P $ ближе к $ B $, чем к $ A $, как показано на рисунке, то вершина $ S $ лежит вне исходной треугольник $ \ треугольник ACB $; треугольники $ \ треугольник PQS $ и $ \ треугольник PRT $ полностью покрывают прямоугольник $ PQCR $ плюс треугольник $ \ треугольник SCT $, и поэтому $$ Площадь (\ треугольник PQS) + Площадь (\ треугольник PRT)> Площадь (PQCR), $$ но с тех пор $$ Площадь (\ треугольник PQS) + Площадь (\ треугольник PRT) + Площадь (PQCR) = Площадь (\ треугольник ACB), $$ это означает, что $$ Area (PQCR) <\ frac12 Area (\ треугольник ACB).

Если вы поместите $ P $ ближе к $ A $, чем к $ B $, то по тем же причинам вы снова обнаружите, что $ Area (PQCR) <\ frac12 Area (\ треугольник ACB). $ Но если вы поместите $ P $ в середину гипотенузы $ AB $, повторение упражнения с отражающими треугольниками быстро покажет что $ Area (PQCR) = \ frac12 Area (\ треугольник ACB). $ Это максимум возможного.

Для задачи 7 нарисуйте прямоугольный треугольник $ 6,8,10 $ $ \ треугольник ACB $, как показано ниже:

То есть опустите перпендикуляр от прямого угла $ C $ к гипотенузе $ AB $, пересекая гипотенузу в точке $ H $.Теперь, если мы нарисуем прямоугольник, как показано на рисунке для задачи 7 с одной стороной, лежащей вдоль гипотенузы, часть прямоугольника будет лежать внутри треугольника $ \ треугольник AHC $ и остальное будет лежать в треугольнике $ \ треугольник BHC $. Если прямоугольник имеет вершины в серединах катетов $ AC $ и $ BC $, тогда каждая часть прямоугольника составляет половину площади треугольника внутри который лежит, и поэтому $$ Площадь (\ text {прямоугольник}) = \ frac12 Площадь (\ треугольник ACB). $$ Но если любая из этих вершин лежит в любой другой точке одного из ножек, другая вершина также будет лежать в некоторой точке, которая не является средней точкой ноги; в каждой части прямоугольника будет меньше половины площадь треугольника, в котором он лежит (как показано в решении части 6) и, следовательно, $$ Площадь (\ text {прямоугольник}) <\ frac12 Площадь (\ треугольник ACB).$$ Итак, еще раз максимальная площадь прямоугольника Площадь $ \ frac12 (\ треугольник ACB). $

Не использует ни один из стандартных инструментов для задач мин / макс, просто простая геометрия, поэтому она не поможет вам научиться решать мин / макс проблемы в более общем плане. Но это может убедить вас, что размеры прямоугольника для проблема 6 $ 3 \ times 4 $ а для задачи 7 — 2,5 $ \ times 4,8 $ (это то, что вы получаете, когда помещаете вершины в середину применимых сторон треугольника), поэтому, когда вы получите эти ответы так, как должны, вы им поверите, и если вы получите разные ответы, тогда вы узнаете вы неправильно использовали методы min / max.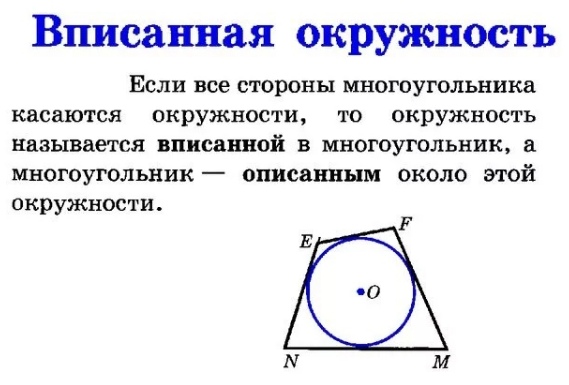

Учебное пособие

Как найти максимальную площадь прямоугольника, вписанного в равносторонний треугольник

Пожалуйста, нажмите ссылку на Учебное пособие «Как найти максимальную площадь прямоугольника, вписанного в равносторонний треугольник», которое находится ниже. Надежда может быть полезной.

Опубликовано: 04-09-2012
Продолжительность: 13:36
Определение: hd
Вид: 68603
Нравится: 651
Не нравится: 19
Любимый: 0
Комментарий: 129

Опубликован: 21-03-2016
Продолжительность: 12:37
Определение: hd
Просмотр: 2860
Нравится: 20
Не нравится: 3
Любимое : 0
Комментарий: 1

Опубликован: 07-11-2016
Продолжительность: 10:14
Определение: hd
Просмотр: 754
Нравится: 6
Не нравится: 2
Избранное: 0
Комментарий: 0

Опубликован: 23-11-2015
Продолжительность: 4:54
Определение: hd
Просмотр: 27498
Нравится: 158
Нелюбовь: 9
Любимый: 0
Комментарий: 15

Опубликован: 08-11-2017
Продолжительность: 14: 3
Определение: hd
Просмотр : 252
Нравится: 1
Не нравится: 0
Избранное: 0
Комментарий: 0

Опубликован: 07-04-2015
Продолжительность: 3:50
Определение: hd
Просмотр: 519
Нравится: 2
Не нравится: 0
Избранное: 0
Комментарий: 1

Опубликован: 17-04-2016
Продолжительность: 13: 7
Определение: hd
Просмотр: 7154
Нравится: 40
Не нравится: 4
Избранное: 0
Комментарий: 12

Опубликовано: 04-04-2018
Продолжительность: 11:13
Определение: hd
Вид: 13
Нравится: 0
Не нравится: 0
Любимый: 0
Комментарий: 0

Опубликовано: 01-04-2016
Продолжительность: 19: 5
Определение: hd
Вид: 26210
Нравится: 237
Не нравится: 6
Любимый: 0
Комментарий: 33

Опубликовано: 03-05-2014
Продолжительность: 14:36
Определение: hd
Вид: 17607
Нравится: 61
Не нравится: 5
Любимый: 0
Комментарий: 23

Опубликован: 14-10-2012
Продолжительность: 2:47
Определение: hd
Просмотр: 21203
Нравится: 67
Не нравится: 4
Избранное: 0
Комментарий: 15

Опубликован: 29-05-2013
Продолжительность: 9:25
Определение: hd
Просмотр: 1390
Нравится: 10
Нелюбовь: 0
Избранное: 0
Комментарий: 0

Опубликован: 20-02-2017
Продолжительность: 7:24
Определение: hd
Просмотр: 3118
Нравится: 41
Не нравится: 0
Избранное: 0
Комментарий: 7

Опубликовано: 02-12-2017
Продолжительность: 6:22
Определение: hd
Просмотр: 247
Нравится: 8
Не нравится: 0
Избранное: 0
Комментарий: 6

Опубликован: 17-05-2016
Продолжительность: 4:17
Определение: hd
Просмотр: 4483
Нравится: 48
Не нравится: 0
Любимый: 0
Комментарий: 6

Опубликован: 20-02-2018
Продолжительность: 7: 4
Определение: hd
Просмотр: 140
Нравится: 3
Не нравится: 1
Избранное: 0
Комментарий: 0

Опубликовано: 25-08- 2012
Продолжительность: 16: 6
Определение: hd
Вид: 78009
Нравится: 848
Не нравится: 29
Любимый: 0
Комментарий: 148

Опубликовано: 11-12-2017
Продолжительность: 5:33
Определение: hd
Вид: 996
Нравится:
Не нравится:
Любимый: 0
C omment: 8

Опубликовано: 14-11-2012
Продолжительность: 11:49
Определение: hd
Просмотр: 1938
Нравится: 13
Не нравится: 0
Любимое : 0
Комментарий: 0

Опубликован: 07-04-2016
Продолжительность: 7:37
Определение: hd
Просмотр: 6782
Нравится: 30
Не нравится: 1
Избранное: 0
Комментарий: 7

Вписанный треугольник в прямоугольнике — помните о своих решениях

В квадрате ABCD , какова площадь треугольника BEF ?

Проблема также может быть обобщена.В прямоугольнике ABCD , какова площадь треугольника BEF в терминах площадей x , y и z ?

Посмотрите видео о решении.

Вписанный треугольник в прямоугольнике

Или продолжайте читать.
.
.

«Все будет хорошо, если ты будешь использовать свой разум для принятия решений, и думать только о своих решениях». С 2007 года я посвятил свою жизнь разделению радости теории игр и математики.MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.

.
.

.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на вписанный треугольник в прямоугольник

(Практически все сообщения быстро расшифровываются после того, как я снимаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки / ошибки, и я исправлю их, спасибо).

Решим общий случай прямоугольника.

Предположим, AB = a и AF = c . Поскольку площадь треугольника ABF равна y , имеем:

ac /2 = y
c = 2 y / a

Предположим, BC = b . Тогда AD = b и FD = b -2 y / a .

Предположим, CE = d . Поскольку площадь треугольника BCE составляет x , имеем:

bd /2 = x
d = 2 x / b

Поскольку AB = a 906 = CD , имеем ED = a -2 x / b .

Площадь треугольника DEF составляет z , поэтому мы имеем:

0.5 ( a -2 x / b ) ( b -2 y / a ) = z
ab -2 x -2 y + 4 xy / ( ab ) = 2 z
ab — 2 x — 2 y — 2 z + 4 xy / ( ab ) = 0
ab — 2 ( x + y + z ) + 4 xy / ( ab ) = 0

Теперь умножьте обе части на ab , чтобы получить квадратное уравнение в переменной ab .

( ab ) ² — ( ab ) 2 ( x + y + z ) + 4 xy = 0

Мы можем решить это, используя квадратичную формулу, чтобы получить:

ab = (2 ( x + y + z ) & pm; √ [4 ( x + y + z ) ² — 4 (4 xy ) ]) / 2
ab = (2 ( x + y + z ) & pm; 2 √ (( x + y + z ) ² — 4 xy )) / 2
ab = ( x + y + z ) & pm; √ (( x + y + z ) ² — 4 xy )

Теперь вспомните, что ab — это площадь всего прямоугольника, поэтому он должен быть больше x + y + z .Следовательно, мы отвергаем отрицательный радикал и оставляем положительный радикал. Таким образом, имеем:

ab = ( x + y + z ) + √ (( x + y + z ) ² — 4 xy )

Кроме того, ab — это сумма площадей 4 треугольников — трех известных областей плюс неизвестная область w .

ab = ( x + y + z ) + w

Если мы приравняем две формулы, равные ab , мы можем заключить:

w = √ (( x + y + z ) ² — 4 xy )

У нас есть простая формула для любой такой задачи! В квадрате нам известны площади 3, 4 и 5, поэтому мы можем решить для w следующим образом:

w = √ ((3 = 4 + 5) ² — 4 (3) ( 4))
w = √ (96)
w = 4√ (6) & прибл. 9.80

Но удивительно, что у нас есть общая формула для любого прямоугольника!

w = √ (( x + y + z ) ² — 4 xy )

Источники

Квадратная задача адаптирована из твита Национального музея математики
https: / /twitter.com/MoMath2/status/1191411003021504512

Обобщение на прямоугольник из твита Мустафы Кемаля Инса
https://twitter.com/galois1724/status/1191433144945135619

Мустафа Кемаль Инсе https: www канал
// www.youtube.com/channel/UCiO8tcTfGzq5w3950Kke6-A

МОИ КНИГИ

Если вы совершите покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

(ссылки для США и других стран)
https://mindyourdecisions.com/blog/my-books
Mind Your Decisions — это сборник из 5 книг:
(1) The Joy of Game Theory: An Introduction to Strategic Мышление
(2) 40 парадоксов в теории логики, вероятностей и игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость
(4) Лучшие уловки в области умственной математики
(5) Умножать числа, рисуя линии
Радость теории игр показывает, как можно использовать математику, чтобы перехитрить своих конкурентов.(рейтинг 4,2 / 5 звезд в 200 обзорах)

40 парадоксов в логике, вероятностях и теории игр содержит наводящие на размышления и противоречащие интуиции результаты. (рейтинг 4,1 / 5 звезд в 30 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость — это руководство, которое объясняет, как мы предвзято относимся к принятию решений, и предлагает методы для принятия разумных решений. (оценка 4/5 звезд в 17 обзорах)

Лучшие уловки в области ментальной математики учит, как можно выглядеть гением математики, решая задачи в уме (оценка 4.2/5 звезд в 57 обзорах)

Умножение чисел на рисование линий Эта книга представляет собой справочное руководство для моего видео, которое набрало более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,1 / 5 звезд в 23 обзорах)

Mind Your Puzzles — это сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность и т. д. логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач счета, геометрии, вероятности и теории игр.Том 1 получил оценку 4,4 / 5 звезд в 75 отзывах.
Math Puzzles Volume 2 — это продолжение книги с более серьезными задачами. (рейтинг 4.3 / 5 звезд в 21 обзоре)
Math Puzzles Volume 3 — третья в серии. (рейтинг 4.3 / 5 звезд по 17 отзывам)
KINDLE UNLIMITED
Учителя и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.
В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте свой местный веб-сайт Amazon, чтобы узнать о доступности и условиях программы.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, результаты книги (CA)
Германия, список моих книг (DE)
Франция, список моих книг (FR)
Индия , список моих книг (IN)
Австралия, результаты книги (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга results (BR)
Мексика, книга results (MX)
MERCHANDISE
Купите кружку, футболку и многое другое на официальном сайте для товаров: Mind Your Decisions at Teespring .
Площадь прямоугольника, вписанного в круг
Беннет, у нас есть для вас два ответа.
Привет, Беннет.
Я нарисовал произвольный прямоугольник, вписанный в круг, радиус которого равен R ниже:
Как видите, радиус круга равен длине гипотенузы прямоугольного треугольника, который 8 раз дублируется в прямоугольнике:
Это означает, что площадь прямоугольника в 8 раз больше площади одного из прямоугольных треугольников.И, конечно же, площадь каждого прямоугольного треугольника — это просто ½bh , где этими переменными являются основание и высота.

Пропорциональные величины треугольника, конечно, зависят от формы прямоугольника, с предельными размерами от бесконечно короткого до бесконечно тонкого, при этом середина диапазона является квадратом. Вот набросок нескольких из них, наложенных на круг:
Итак, наименьшая область прямоугольника, несомненно, является бесконечно тонкой или короткой, поскольку ее другое измерение в основном равно R.Это означает, что наименьшая возможная площадь — 8 (½) (0) (R) , которая равна нулю. Настоящий вопрос в том, какова максимально возможная площадь.

Интуиция должна сказать вам, что квадрат — это самая большая площадь, и ваша интуиция будет правильной, но это не удовлетворительный ответ на вопрос математики. Давайте еще раз посмотрим на эти треугольники:

Вот несколько возможных форм. Гипотенуза, конечно, всегда составляет R единиц, так что это означает, что мы можем использовать тригонометрию, чтобы найти площадь треугольника.Назовем угол в углу треугольника, который находится в центре окружности, A . Это нижний левый угол в этих треугольниках.

Это означает, что длина основания составляет RcosA единиц, а высота — RsinA единиц. Таким образом, площадь треугольника ½R ² cosA sinA . Таким образом, площадь всего прямоугольника в восемь раз больше: 4R ² cosA sinA .Какое значение A дает нам наибольшую общую площадь?
Для этого мы можем использовать несколько методов, но самый простой — это расчет. Критические точки этой функции могут сказать нам, какой угол A должен быть максимальным.
Производная 4R ² cosA sinA — это 4R ² (cos ² A — sin ² A) ; Я использовал правило продукта, чтобы получить это. Когда он равен нулю, у нас есть критическая точка, которая является значением A, для которого мы получаем максимальную площадь.
Таким образом, cos ² A = sin ² A и, следовательно, cosA = sinA . Поскольку косинус — это основание над гипотенузой R , а синус — это высота над гипотенузой R , это означает, что основание = высота . Это означает равнобедренный прямоугольный треугольник, поэтому прямоугольник и есть квадрат. Мы давно доказали то, что подсказывала нам интуиция.
Таким образом, площадь прямоугольника ограничена от 0 до площади квадрата с длиной диагонали 2R .
Надеюсь, это поможет,
Стивен Ла Рок.
Беннет,
На самом деле — каждый прямоугольник можно вписать в (уникальный круг), поэтому ключевым моментом является то, что радиус круга равен R (я думаю).
Одно из свойств прямоугольника состоит в том, что диагонали делят пополам в «центре» прямоугольника, который также будет центром описывающего круга. Теперь «максимум» и «минимум» лучше всего представить (и отобразить) с помощью такой программы, как Sketchpad от Geometer, где вы можете поиграть с опциями.
Вместо того, чтобы давать ответ, позвольте мне пройти пару примеров из программы, чтобы стимулировать ваше воображение:
Вы можете видеть, что область становится больше, а затем уменьшается по мере того, как угол перемещается по четверти круга.
Думаю, отсюда можно определить наименьшую площадь. Самая большая область — это сложнее, но, опять же, я думаю, вы можете ее «увидеть». Если вы не уверены, можете подумать о максимальной площади треугольника ABC (все диагонали имеют одинаковую длину — 2R).
Целый прямоугольник — это всего лишь два из этих треугольников. Опять же, если вы не совсем уверены, визуально будет немного легче, если вы «наклоните голову» и сделаете диагональ AC горизонтально, и подумайте о том, чтобы сделать «высоту» треугольника как можно большей над этим основанием!
Уолтер
Прямоугольник, вписанный в треугольник, имеет основание, совпадающее с классом 10 по математике CBSE
Подсказка: Как мы видим, прямоугольник DEFG вписан в треугольник ABC согласно заданному вопросу, а AN представляет высоту от вершины A треугольника, равную \ [h \] единицам (дано), и основание треугольника длиной b единиц.Мы видим, что высота прямоугольника уже задана в \ [x \] единицах. Мы используем концепцию подобия треугольников, чтобы найти окончательный ответ.

Полный пошаговый ответ:
Как мы видим, прямоугольник DEFG вписан в треугольник ABC согласно заданному вопросу, а AN представляет высоту от вершины A треугольника, равную \ [h \] единиц ( дано) и основание треугольника длиной b единиц. Мы видим, что высота прямоугольника уже задана в \ [x \] единицах.
В математике мы говорим, что два объекта похожи, если они имеют одинаковую форму, но не обязательно одинакового размера. Это означает, что мы можем получить одну фигуру из другой посредством процесса расширения или сжатия, возможно, сопровождаемого перемещением, вращением или отражением; эти процессы известны как трансформации. Если объекты также имеют одинаковый размер, они совпадают.
Поскольку высота AN делит треугольник ABC на два неравных треугольника ABN и ANC, мы можем применить подобие треугольников к обоим этим треугольникам.Сначала возьмем треугольник ABN, где треугольники BDE и ABN подобны треугольнику по аксиомам угол-угол (аксиома AA подобия треугольников),
Взяв треугольники ABN и BDE, пусть \ [BN = k \] единиц и \ [BE = p \] единиц,
Теперь используя подобие треугольника,
\ [\ dfrac {AN} {BN} = \ dfrac {DE} {BE} \]
\ [\ dfrac {h} {k} = \ dfrac {x} {{ {p} _ {1}}} \]
\ [{{p} _ {1}} = \ dfrac {kx} {h} \]
Во-вторых, возьмем треугольник ABN, где треугольники GFC и ANC подобны треугольнику по углу — угловые аксиомы (аксиома подобия треугольников AA),
Взяв треугольники GFC и ANC, и используя подобие треугольников, получим
\ [\ dfrac {AN} {NC} = \ dfrac {GF} {FC} \]
\ [\ dfrac {h} {bk} = \ dfrac {x} {{{p} _ {2}}} \]
\ [{{p} _ {2}} = \ dfrac {(bk) x} { h} \]
Как мы знаем, BE + EF + FS равно BC (= b единиц), нахождение значения EF путем перестановки,
\ [EF = BC-BE-FC \]
\ [EF = BC- ( {{p} _ {1}} + {{p} _ {2}}) \]
\ [EF = b- \ left (\ dfrac {kx} {h} + \ dfrac {(bk) x} { h} \ right) \]
\ [EF = b \ left (1- \ dfrac {x} {h} \ right) \]
Теперь, когда alt Размер прямоугольника x равен половине размера его основания, получаем:
\ [DE = \ dfrac {EF} {2} \]
\ [X = \ dfrac {b} {2} \ left ( 1- \ dfrac {x} {h} \ right) \]
\ [2hx = bh-bx \]
\ [x (b + 2h) = bh \]
\ [x = \ dfrac {bh} {b + 2h} \]
Наконец, мы получаем значение x, равное \ [x = \ dfrac {bh} {b + 2h} \],
Итак, правильный ответ — «Вариант C».
No related posts.

Прямоугольник вписанный в треугольник: Задача про прямоугольник, вписанный в равнобедренный треугольник | Видеоурок

Геометрические задачи на максимум / math5school.ru

Прямоугольник

Треугольник

Многоугольник

Смотрите так же:

Решения

Областная олимпиада по математике, 2015 год, 10 класс

Прямоугольник — Геометрия 8 класс

Вписанные и описанные окружности.

Страница не найдена — ПриМат

8 класс.

вписанная в многоугольник или угол

Решение | Прямоугольники в треугольниках | Представляем Calculus

Рассмотрим конкретный случай.

Переходим к более общему случаю.

Общий шкаф

Предположим, \ (x

Предположим, \ (x = \ frac {b} {2} \).

Предположим, \ (x> \ frac {b} {2} \).

Заключение

Максимальный прямоугольник, вписанный в треугольник

optimisation — Максимально возможная площадь прямоугольника, вписанного в данный прямоугольный треугольник

Как найти максимальную площадь прямоугольника, вписанного в равносторонний треугольник

Вписанный треугольник в прямоугольнике — помните о своих решениях

МОИ КНИГИ

KINDLE UNLIMITED

MERCHANDISE

Площадь прямоугольника, вписанного в круг

Прямоугольник, вписанный в треугольник, имеет основание, совпадающее с классом 10 по математике CBSE

Добавить комментарий Отменить ответ