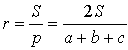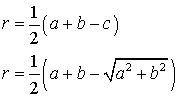Пример 5. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.
Решение. Изобразим Рис. 8. Ясно, что можно построить множество различных прямоугольников, вписанных в прямоугольный треугольник, но выясняется, что их периметры будут одинаковы, покажем это и найдем искомый периметр.
Рис. 8
По условию равнобедренный .
Искомый периметр прямоугольника: .
Рассмотрим прямоугольный : .
Тогда периметр прямоугольника : .
Ответ: 12 см.
Пример 6. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны и периметр прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см?
Решение. Изобразим Рис. 9 и укажем на нем все элементы, которые мы введем в процессе решения задачи.
Рис. 9
По условию равнобедренный и прямоугольный .
Указано, что вписанный прямоугольник имеет заданные пропорции, поэтому его стороны можно ввести, как определенное количество неизвестных нам частей : .
Рассмотрим треугольники и – они прямоугольные и имеют по одному углу , следовательно, второй угол у них тоже по (см. решение предыдущей задачи), т.е. они равнобедренные, и .
Теперь можем выписать длину гипотенузы как сумму длин отрезков, на которые она разбита вписанным прямоугольником (через те части , которые мы ввели): .
Теперь можем посчитать длины сторон прямоугольника и его периметр: .
Ответ: стороны равны .
Сегодня мы рассмотрели прямоугольник, его свойства, признаки и задачи на прямоугольник. На следующем уроке мы познакомимся с такими частными случаями параллелограмма, как ромб и квадрат.
Домашнее задание
1. В прямоугольнике диагональ образует со стороной угол, равный . Определить угол между диагоналями, обращенный к меньшей стороне.
2. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр этого прямоугольника равен 56 см. Определить его стороны.
3. Построить прямоугольник по основанию, равному 2,4 см, и диагонали, равной 3,1 см.
Урок 11: Ромб и квадрат.
На этом уроке пришло время познакомиться с ещё двумя видами параллелограмма: ромбом и квадратом. С этими фигурами каждый из нас знаком с самого детства, однако мало кто ассоциирует их с параллелограммом. А их свойства многие из нас применяли на практике, не зная даже, на чём они основаны. Мы рассмотрим определения и свойства параллелограмма и квадрата, а также решим несколько задач с использованием указанных свойств.
Ромб и его свойства
Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма. Однако есть и специфические свойства, о которых пойдёт речь. Но для начала сформулируем одно из определений ромба.
Ромб –это параллелограмм, у которого все стороны равны.
Сформулируем и докажем теорему о свойствах ромба.
Теорема
Диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов) (см. Рис. 1).
Дано:
– ромб
Доказать:
.
Доказательство:
Рис. 1
Рассмотрим : – середина (так как ромб является параллелограммом, то его диагонали в точке пересечения делятся пополам). Кроме того, из определения ромба следует, что . Значит, треугольник – равнобедренный; является медианой этого треугольника, проведённой к основанию, а, значит, и биссектрисой, и высотой. Из этого следует, что:
, то есть диагонали ромба перпендикулярны;
, то есть диагонали ромба являются биссектрисами его углов (равенство остальных углов можно доказать аналогично).
Доказано.
Ещё один частный случай параллелограмма – квадрат.
Квадрат и его свойства
Квадрат –это прямоугольник, у которого все стороны равны.
Квадрат обладает всеми свойствами прямоугольника и ромба. А именно:
· все углы квадрата прямые;
· диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делят углы квадрата пополам.
Задачи на ромб и квадрат
Теперь рассмотрим несколько задач, в которых встречаются ромб и квадрат.
Задача 1.
В ромбе одна из диагоналей равна стороне (см. Рис. 2). Найти:
а) углы ромба;
б) углы между диагоналями и сторонами.
Дано: – ромб; .
Найти: а) ; б) .
Решение:
Рис. 2
а) (так как у ромба все стороны равны). Значит, треугольник – равносторонний. Отсюда следует, что угол . Так как в любом параллелограмме сумма соседних углов равна , то .
Ответ: .
б) По доказанной выше теореме: . Аналогично получаем, что .
Ответ: .
Задача 2.
Найти периметр ромба , в котором , а меньшая диагональ равна . Найти периметр ромба.
Дано: – ромб; .
Найти:
Решение:
Рис. 3
Рассмотрим треугольник , в нём: . Значит, данный треугольник равнобедренный, угол при вершине у него равен , два других угла при основании равны, поэтому данный треугольник – равносторонний. Значит: . Так как в ромбе все стороны равны, то периметр ромба равен: .
Ответ: .
Задача 3.
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .
Дано: – ромб, .
Найти:
Решение:
Рис. 4
Вспомним, что в любом параллелограмме противоположные углы, а сумма углов, прилежащих к одной стороне, равна . Из этого следует, что: . Теперь воспользуемся доказанной вначале теоремой: .
Ответ:
Задача 4.
Докажите, что параллелограмм является ромбом, если:
а) его диагонали взаимно перпендикулярны;
б) его диагонали являются биссектрисами углов.
а) Дано: – параллелограмм, .
Доказать: – ромб.
Доказательство:
Рис. 5
Рассмотрим треугольник : в нем является одновременно и высотой (так как диагонали перпендикулярны), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть – ромб.
Доказано.
б) Дано: – параллелограмм, – биссектрисы углов параллелограмма.
Доказать: – ромб.
Доказательство:
Рис. 6
Рассмотрим треугольник : в нем является одновременно и биссектрисой (так как диагонали являются биссектрисами углов), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть, – ромб.
Доказано.
Задача 5.
Докажите, что ромб, у которого один из углов прямой, является квадратом.
Дано: – ромб,
Доказать: – квадрат.
Доказательство:
Рис. 7
Вспомним, что квадрат – это одновременно прямоугольник и ромб. Если говорить о сформулированном строгом определении, то квадрат – это прямоугольник, у которого все стороны равны. Равенство сторон следует из того, что данный четырёхугольник – ромб. Осталось доказать, что он является ещё и прямоугольником. По условию: (у любого параллелограмма противоположные углы равны). Кроме того, сумма соседних углов параллелограмма равна . Значит: . Отсюда мы получаем, что – прямоугольник, а значит, и квадрат.
Доказано.
На этом уроке мы изучили ромб и квадрат, а также рассмотрели их свойства и решили различные задачи, в которых встречаются ромб и квадрат.
На следующем уроке мы обобщим полученные знания о параллелограммах.
Домашнее задание
1. Найти углы ромба, если его сторона образует с диагоналями углы, разность которых равна .
2. Найти углы ромба, если его сторона образует с диагоналями углы, которые относятся как .
3. Доказать, что прямоугольник, у которого диагонали перпендикулярны, – квадрат.
Урок 12: Повторение теории и решение задач
На этом уроке мы повторим и обобщим все полученные знания при изучении главы «Четырехугольники. Параллелограммы». Вспомним определения, свойства и признаки таких фигур, как параллелограмм, прямоугольник, ромб, квадрат. Решим несколько примеров, которые демонстрируют применение всех изученных фактов к указанным фигурам.
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана
в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
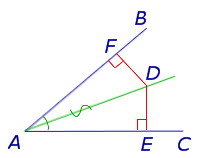
Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).
Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).
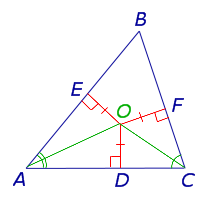
Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.
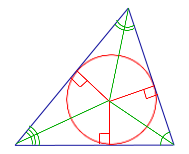
Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник |  |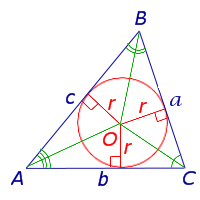
Посмотреть вывод формулы | a, b, c – стороны треугольника,
|
Посмотреть вывод формулы | |||
| Равнобедренный треугольник |  |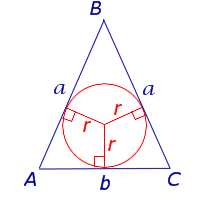
Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, |
| Равносторонний треугольник |  |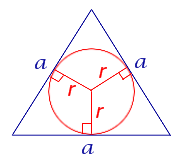
Посмотреть вывод формулы | a – сторона равностороннего треугольника, |
| Прямоугольный треугольник |  |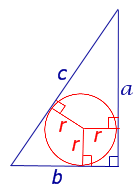
Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
|
где Посмотреть вывод формулы |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
|
где Посмотреть вывод формулы |
| Равносторонний треугольник | |
|
где Посмотреть вывод формулы |
| Прямоугольный треугольник | |
|
где Посмотреть вывод формул |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Равнобедренный треугольник |
где Посмотреть вывод формулы |
| Равносторонний треугольник |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
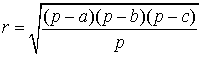
где a, b, c – стороны треугольника, r – радиус вписанной окружности,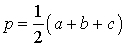
– полупериметр (рис. 6).
Рис. 6
Доказательство. Из формулы
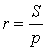
с помощью формулы Герона получаем:
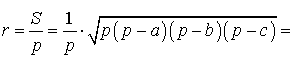
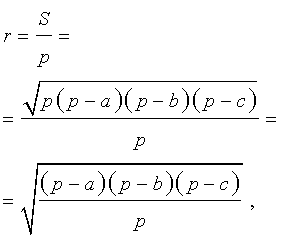
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
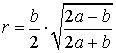
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
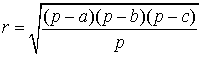
где
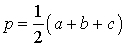
то, в случае равнобедренного треугольника, когда
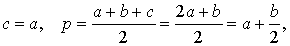
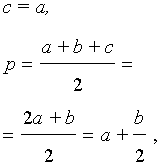
получаем
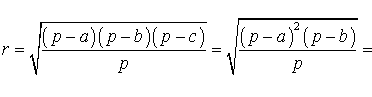
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
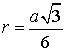
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
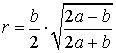
то, в случае равностороннего треугольника, когда
b = a,
получаем
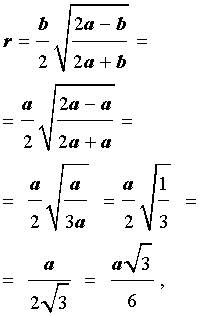
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
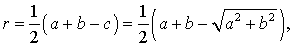
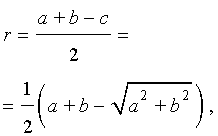
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.
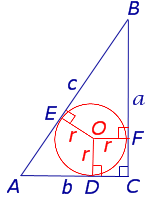
Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства
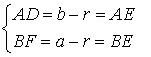
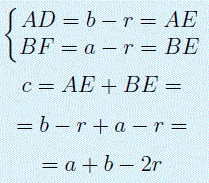
Следовательно, принимая также во внимание теорему Пифагора, получаем
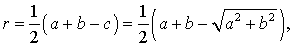
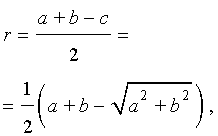
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Описанные и вписанные окружности
Наглядная геометрия 9 класс. Опорный конспект 2 Описанные и вписанные окружности
Около любого треугольника можно описать окружность. Она проходит через все вершины треугольника. Вы уже знаете, что точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Она и является центром описанной окружности.
В любой треугольник можно вписать окружность. Она касается всех сторон треугольника. Вы также знаете, что точка пересечения биссектрис треугольника равноудалена от сторон треугольника. Она и является центром вписанной окружности.
А можно ли описать окружность около любого параллелограмма? Если попробовать это сделать, то окажется, что около параллелограмма можно описать окружность, только если он — прямоугольник. Мы узнаем, каким свойством обладают вписанные и описанные четырехугольники и какие признаки позволяют судить о том, можно ли около данного четырехугольника описать и можно ли в него вписать окружность.
И вдобавок мы познакомимся с одной важной формулой площади треугольника S = рr.
ТАБЛИЦА «Описанные и вписанные окружности»
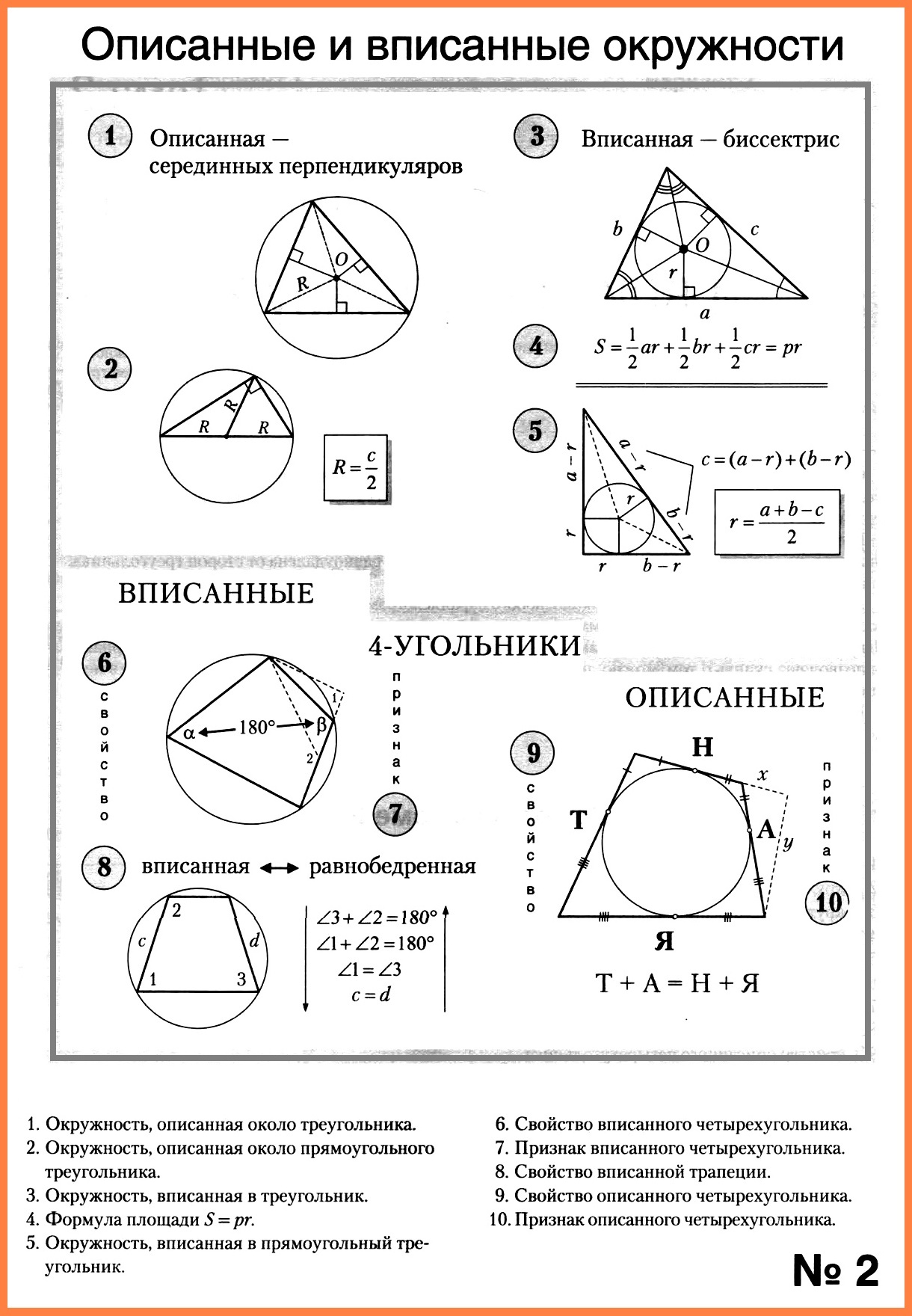
1. Окружность, описанная около треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема. Вокруг любого треугольника можно описать окружность, и только одну. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Доказательство. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин (доказано нами в 7 классе). Поэтому она является центром описанной окружности, расстояние от этой точки до любой из вершин равно радиусу.
Если существует еще одна описанная окружность, то ее центр равноудален от всех трех вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
2. Окружность, описанная около прямоугольного треугольника.
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус окружности равен половине гипотенузы.
Доказательство. Мы знаем, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы (доказано нами в 7 классе). Поэтому середина гипотенузы является центром описанной окружности, а ее радиус равен половине гипотенузы, т. е. R = c/2.
3. Окружность, вписанная в треугольник.
Окружность называется вписанной в треугольник, ест она касается всех сторон треугольника.
Теорема. В любой треугольник можно вписать окружность, и только одну. Ее центр лежит на пересечении биссектрис треугольника.
Доказательство. Точка пересечения биссектрис треугольника равноудалена от сторон треугольника (доказано нами в 7 классе). Если из этой точки опустить перпендикуляры на стороны и провести окружность радиусом, равным перпендикуляру, то стороны треугольника будут касаться окружности по признаку касательной.
Если существует еще одна вписанная окружность, то ее центр равноудален от всех трех сторон и поэтому совпадает с точкой пересечения биссектрис, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
4. Формула площади S = рr.
Теорема. Площадь треугольника S = рr, где р — полупериметр треугольника, r — радиус вписанной окружности.
Доказательство. Соединим центр вписанной окружности с вершинами треугольника, стороны которого равны а, b и с. Получим три треугольника, для которых радиусы вписанной окружности, проведенные в точки касания, являются высотами. Площадь данного треугольника равна сумме площадей этих треугольников:
где p — полупериметр треугольника.
Данная формула справедлива для любого многоугольника, в который можно вписать окружность, т. е. для любого описанного многоугольника. Доказательство аналогично.
5. Окружность, вписанная в прямоугольный треугольник.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (а + b – c)/2.
Доказательство. Проведем радиусы в точки касания. Получим квадрат со стороной r (четырехугольник, у которого все углы прямые и две соседние стороны равны по r) и отрезки катетов, равные r и а – r для катета а, r и b – r для катета b. Так как отрезки касательных, проведенных из одной точки, к окружности равны, то гипотенуза равна сумме отрезков (a – r) и (b – r). Так как с = (а – r) + (b – r), то r = (а + b – c)/2.
6. Свойство вписанного четырехугольника.
Теорема (свойство вписанного четырехугольника). Если четырехугольник вписан в окружность, то суммы его противоположных углов равны по 180°.
Доказательство. Противоположные углы α и β являются вписанными. Они опираются на дуги, которые дополняют друг друга до окружности. Окружность содержит 360°. Так как вписанный угол равен половине дуги, на которую он опирается, то сумма углов α и β равна 180°.
7. Признак вписанного четырехугольника.
Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 180°, то вокруг него можно описать окружность.
Доказательство. Через три вершины четырехугольника всегда можно провести окружность (это вершины некоторого треугольника). Если четвертая вершина будет лежать внутри окружности или вне ее, то угол при этой вершине будет больше или меньше угла β, по свойству внешнего угла треугольника, т. е. 1 < β < 2. Тогда сумма противоположных углов этого четырехугольника не будет равна 180°. Поэтому четвертая вершина такого четырехугольника обязана лежать на окружности.
8. Свойство вписанной трапеции.
Теорема. Вписанная трапеция является равнобедренной.
Доказательство. 1-й способ. ∠1 + ∠2 = 180° как внутренние односторонние при параллельных прямых и секущей, ∠3 + ∠2 = 180° по свойству вписанного четырехугольника. Тогда ∠1 = ∠3 и трапеция равнобедренная по признаку равнобедренной трапеции.
2-й способ. Параллельные прямые отсекают равные дуги. Равные дуги стягиваются равными хордами. Поэтому боковые стороны трапеции равны.
9. Свойство описанного четырехугольника.
Теорема (свойство описанного четырехугольника). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
Доказательство. Отрезки касательных, проведенных из одной точки к окружности, равны. Обозначим равные отрезки соответственно одной черточкой, двумя, тремя и четырьмя. Убеждаемся, что суммы противоположных сторон равны: Т + А = Н + Я.
10. Признак описанного четырехугольника.
Теорема (признак описанного четырехугольника). Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность.
Доказательство. Пусть окружность касается только трех сторон. Повернув четвертую сторону вокруг вершины так, чтобы она касалась окружности, получим описанный четырехугольник.
Т + А = Н + Я — по свойству описанного четырехугольника,
Т + y = (Н + х) + Я — по условию.
Тогда y = А + х. А это противоречит неравенству треугольника у < А + х. Значит, окружность касается всех четырех сторон заданного четырехугольника.
ЭТО НУЖНО ЗНАТЬ !
Это опорный конспект № 2 по геометрии для 9 класса «Описанные и вписанные окружности». Выберите дальнейшие действия:
2, а гипотенуза треугольника равн
Источник: 
Решебник
по
геометрии
за 8 класс (А.В. Погорелов, 2001 год),
задача №32
к главе «§ 6. Четырехугольники».
Все задачи >
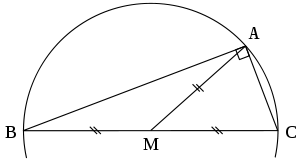
№ 32. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие — на катетах. Чему равны стороны прямоугольника, если известно, что они относятся как 5: 2, а гипотенуза треугольника равна 45 см?
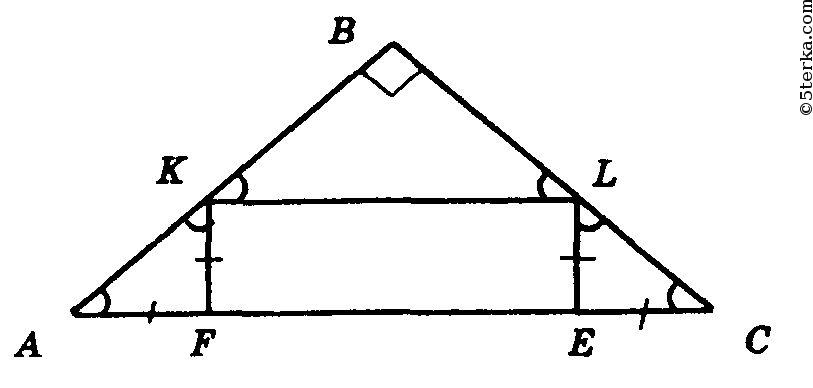
— равнобедренный, отсюда
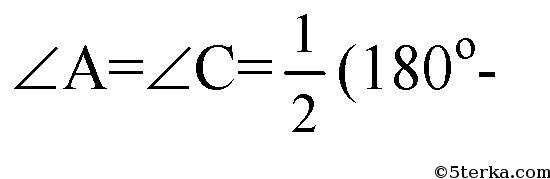
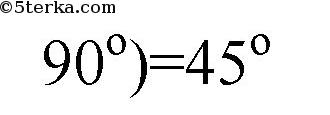
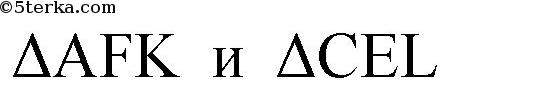— равнобедренные, так как
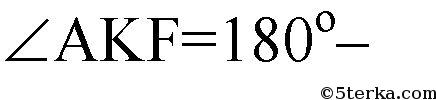
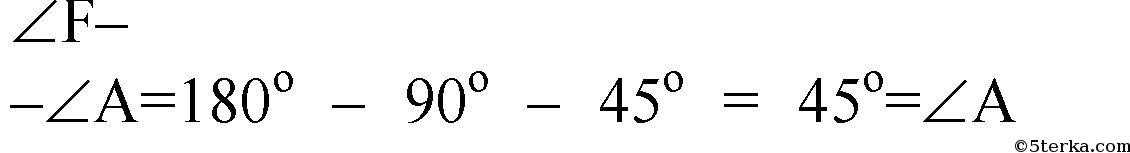
и аналогично
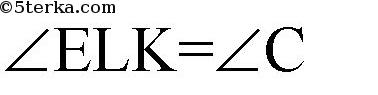
Поэтому
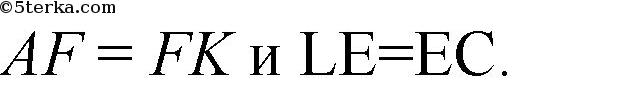
К тому же
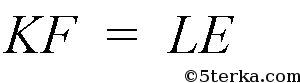
(стороны прямоугольника), так что
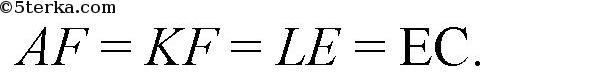
Пусть
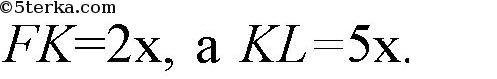
Тогда
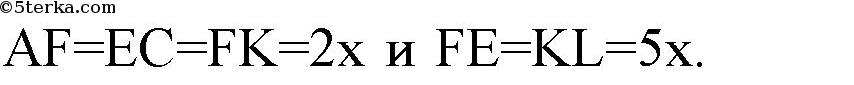
Получим
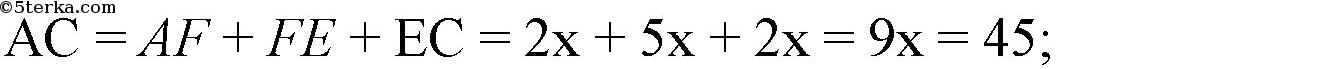
откуда
Далее,
Ответ:
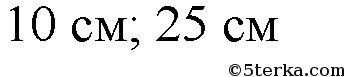← № 31. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.№ 33. Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. →- Вконтакте
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
Задача 1.
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.
Дано: ∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
BM=4 см, AM=6 см.
Найти:
Решение:
1) По свойству отрезков касательных, проведенных из одной точки,
AK=AM=6 см,
BF=BM=4 см,
CK=CF=x см.
2) AB=AM+BM=6+4=10 см,
AC=AK+CK=(6+x) см,
BC=BF+CF=(4+x) см.
3) По теореме Пифагора:
По теореме Виета,
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
4)
Ответ: 24 см, 24 см², 2 см.
Задача 2.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.
Дано:∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
AB=26 см, r=4 см.
Найти:
Решение:
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
AM=AK=x см,
BF=BM=(26-x) см,
CF=CK=r=4 см.
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
По теореме Пифагора,
Если AM=20 см, то AC=24 см, BC=10 см.
Если AM=6 см, то AC=10 см, BC=24 см.
Ответ: 120 см².
Прямоугольный треугольник — Википедия
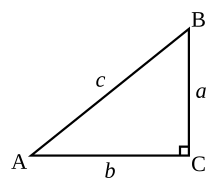Прямоугольный треугольникПрямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Связанные определения
- Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
- Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.
Типы прямоугольных треугольников
- Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.
Признаки равенства прямоугольных треугольников
- По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.
- По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны
- Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.
- По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны. Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.
- По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны. Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.
Свойства
Далее предполагаем, что a {\displaystyle a} и b {\displaystyle b} длины катетов, а c {\displaystyle c} длина гипотенузы
- Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
- S = 1 2 a b . {\displaystyle S={\tfrac {1}{2}}ab.}
- Для медиан
m
a
{\displaystyle m_{a}}
,
m
b
{\displaystyle m_{b}}
и
m
c
{\displaystyle m_{c}}
выполняется следующее соотношение:
- m a 2 + m b 2 = 5 m c 2 = 5 4 c 2 . {\displaystyle m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.}
- В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.
Высота
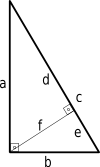Высота прямоугольного треугольника.Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:[1]
- f 2 = d e , {\displaystyle \displaystyle f^{2}=de,} (иногда это называют теоремой высоты прямоугольного треугольника)
- b 2 = c e , {\displaystyle \displaystyle b^{2}=ce,}
- a 2 = c d {\displaystyle \displaystyle a^{2}=cd}
- В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть
- d : e = a 2 : b 2 , {\displaystyle \displaystyle d:e=a^{2}:b^{2},}
Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:[2][3]
- 1 a 2 + 1 b 2 = 1 f 2 . {\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{2}}}.}
и
- f = a b c . {\displaystyle f={\frac {ab}{c}}.}
Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:
- f = r δ S = r ( 1 + 2 ) {\displaystyle f=r\delta _{S}\ =r(1+{\sqrt {2}})} , где r {\displaystyle r} — это радиус вписанной окружности, а δ S {\displaystyle \delta _{S}} — серебряное сечение.
Характеристики
Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно любое из следующих соотношений:[4]
Тригонометрические соотношения
Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:
- sin α = a c , cos α = b c , tg α = a b , ctg α = b a , sec α = c b , csc α = c a . {\displaystyle \sin \alpha ={\frac {a}{c}},\,\cos \alpha ={\frac {b}{c}},\,\operatorname {tg} \alpha ={\frac {a}{b}},\,\operatorname {ctg} \alpha ={\frac {b}{a}},\sec \alpha ={\frac {c}{b}},\,\,\csc \alpha ={\frac {c}{a}}.}
И таким образом:
- Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла
- a = c ⋅ sin α , b = c ⋅ sin β . {\displaystyle a=c\cdot \sin \alpha ,\,b=c\cdot \sin \beta .}
- Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла
- a = c ⋅ cos β , b = c ⋅ cos α . {\displaystyle a=c\cdot \cos \beta ,\,b=c\cdot \cos \alpha .}
- Катет, противолежащий углу, равен произведению второго катета на тангенс угла
- a = b ⋅ tg α , b = a ⋅ tg β . {\displaystyle a=b\cdot \operatorname {tg} \alpha ,\,b=a\cdot \operatorname {tg} \beta .}
- Катет, прилежащий углу, равен произведению второго катета на котангенс угла
- a = b ⋅ ctg β , b = a ⋅ ctg α . {\displaystyle a=b\cdot \operatorname {ctg} \beta ,\,b=a\cdot \operatorname {ctg} \alpha .}
- Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)
- c = a sin α = b sin β = a cos β = b cos α . {\displaystyle c={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {a}{\cos \beta }}={\frac {b}{\cos \alpha }}.}
Специальные прямоугольные треугольники
Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4. В частности,
- Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.
Теорема Фалеса
Медиана прямого угла треугольникаТеорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.
Другие свойства
Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:
- r = a + b − c 2 = a b a + b + c . {\displaystyle r={\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}.}
Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:[5]:pp. 216-217
- p 2 + q 2 = 5 ( c 3 ) 2 . {\displaystyle p^{2}+q^{2}=5\left({\frac {c}{3}}\right)^{2}.}
Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.[6]
Пусть h и s (h>s) сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:
- 1 c 2 + 1 h 2 = 1 s 2 . {\displaystyle {\frac {1}{c^{2}}}+{\frac {1}{h^{2}}}={\frac {1}{s^{2}}}.}
Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырех описанных окружностей:
P = 2 r + 4 R {\displaystyle P=2r+4R}
Если заданы S и r, то стороны треугольника находятся по формулам:
- a = 1 2 ( r + S r − r 2 − 6 S + S 2 r 2 ) {\displaystyle a={\frac {1}{2}}\left(r+{\frac {S}{r}}-{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}
- b = 1 2 ( r + S r + r 2 − 6 S + S 2 r 2 ) {\displaystyle b={\frac {1}{2}}\left(r+{\frac {S}{r}}+{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}
- c = S r − r {\displaystyle c={\frac {S}{r}}-r}
Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.
Примечания
- ↑ Wentworth p. 156
- ↑ Voles, Roger, «Integer solutions of a − 2 + b − 2 = d − 2 {\displaystyle a^{-2}+b^{-2}=d^{-2}} ,» Mathematical Gazette 83, July 1999, 269—271.
- ↑ Richinick, Jennifer, «The upside-down Pythagorean Theorem, » Mathematical Gazette 92, July 2008, 313—317.
- ↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
- ↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
- ↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.