«Могут ли современные математики объяснить прохожему с улицы, что такое иррациональное число?» — Яндекс Кью
Математика и математики
Популярное
Сообщества
ОбществоОбразование+3
Анонимный вопрос
·
10,6 K
ОтветитьУточнитьДостоверно
Andrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 13 янв 2022
Если прохожий освоил программу пятого класса, то, скорее всего, он и сам знает, чем рациональные вещественные числа отличаются от рациональных.
Рациональные числа — это дроби — сверху стоит целое число, снизу натуральное: 5/4, -7/2, 151/13.
В десятичном представлении дробные числа всегда превращаются либо в конечную последовательность, либо в периодические дроби: 5/4=1.25, -7/2=-3.5, 151/13=11,(615384).
Кроме дробных чисел в геометрии у нас легко возникают числа типа sqrt(2) (корень из двух) или число π (пи). Корень из двух, например — это отношение диагонали квадрата к его стороне, а пи — отношение длины окружности к радиусу круга. Эти числа в виде дроби или в виде периодической десятичной дроби записать нельзя. Любое такое вещественное число, которое не является рациональным, логично, называется нерациональным (иррациональным).
3 эксперта согласны
Сергей Чабовский
подтверждает
23 августа 2022
Совпало
Комментировать ответ…Комментировать…
Владимир Марченко
Математика
359
Православный христианин. Преподаватель математики.
«Современные математики» — слишком размытая характеристика, чтобы можно было дать ответ на вопрос. Современный математик может быть хорошим педагогом, а может, увы, и не быть им. Среди математиков я встречал и тех, и других. По существу, положительное рациональное число — это число, которое может быть получено из единицы путём операций сложения и деления на любое… Читать далее
1 эксперт согласен
Леонид Коганов
9 августа 2022
Господь Бог (и Пеано чуть-чуть с Божьей помощью прибавил) дал нам по Кронекеру натуральные, а всё остальное -… Читать дальше
Комментировать ответ…Комментировать…
Maxim Vyalkov
Математика
1,4 K
Интересующие темы: история математики, история христианства, библеистика. · 14 мар 2022
Запросто.
Для начала, объясню подробно, что такое рациональное число.
1. Это такое, которое можно задать отношением p/q , где p — произвольное целое, а q — натуральное, если мы не включаем 0 во множество натуральных чисел (по ISO ноль включается во множество натуральных).
2. Это такая пара целых, для которых определено отношение эквивалентности
(a, b) ~ (c, d)… Читать далее
Комментировать ответ…Комментировать…
Сергей Чабовский
Математика
596
Инженер-радиофизик, преподаватель физической культуры и спорта · 23 авг 2022
Да любой математик, если он математик скажет, что оно не может быть представлено в виде дроби, в том числе ограниченной и/или бесконечной периодической десятичной дроби.
Комментировать ответ…Комментировать…Максим Лапиков
Математика
2,1 K
математик-системный программист, асу тп для аэс. · 15 янв 2022
А в чём трудность?
Иррациональные это все действительные, кроме рациональных.
Представьте себе действительную ось. Пришёл вредный профессор стукнул по ней палкой и все дроби вида p/q с неё осыпались, то что осталось — это иррациональные числа.
1 эксперт не согласен
Сергей Чабовский
возражает
23 августа 2022
Сначала надо объяснить действительные, а потом уже можно на них ссылаться, а действительные — это рациональные и ир… Читать дальше
Комментировать ответ…Комментировать…
Математика
71
Кандидат физико-математических наук, выпускник ШАД · 13 янв 2022
Разве что прохожим с улиц типа Лебедева или Академика Хохлова, что на территории МГУ расположены.
1 эксперт не согласен
Сергей Чабовский
возражает
23 августа 2022
Приходится дублировать обоснование. В народе это выражается: «Ты ему про Ерёму, а он тебе про Фому»; «В огороде… Читать дальше
Комментировать ответ…Комментировать…
Топ-20
Леонид Коганов
190
Член ММО — Московского математического Общества.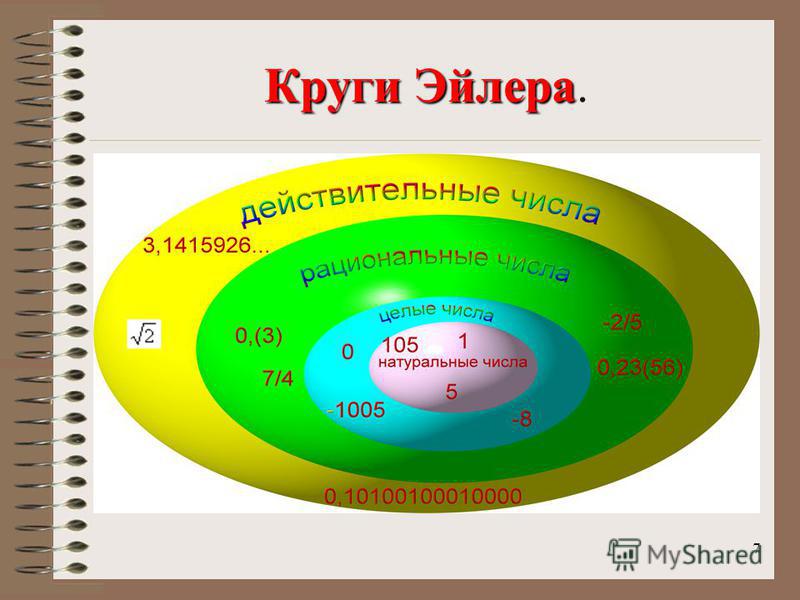
Кстати, старейшего в мире.
Л.М. Коганов. · 3 авг 2022
Да, могут и успешно. Рациональное (действительное) число есть отношение двух целых, из которых второе не нуль (делить на нуль нельзя!). Все числа (по-прежнему, изображаемые точками действительной оси), которые не суть снабжённые знаком (в зависимосим от места точки справа или, соотв., слева от нуля) рациональные дроби и отличны от нуля, эти числа иррациональные по… Читать далее
1 эксперт согласен
Andronick Arutyunov
подтверждает
3 августа 2022
Единственное, у прохожего должен быть функционирующий мозг.
Комментировать ответ…Комментировать…
Топ-20
Алексей Сивохин
572
Физика, компьютеры, электроника, велосипед, политика, диванный философ, диванный… · 1 окт 2022
Я знаю один способ.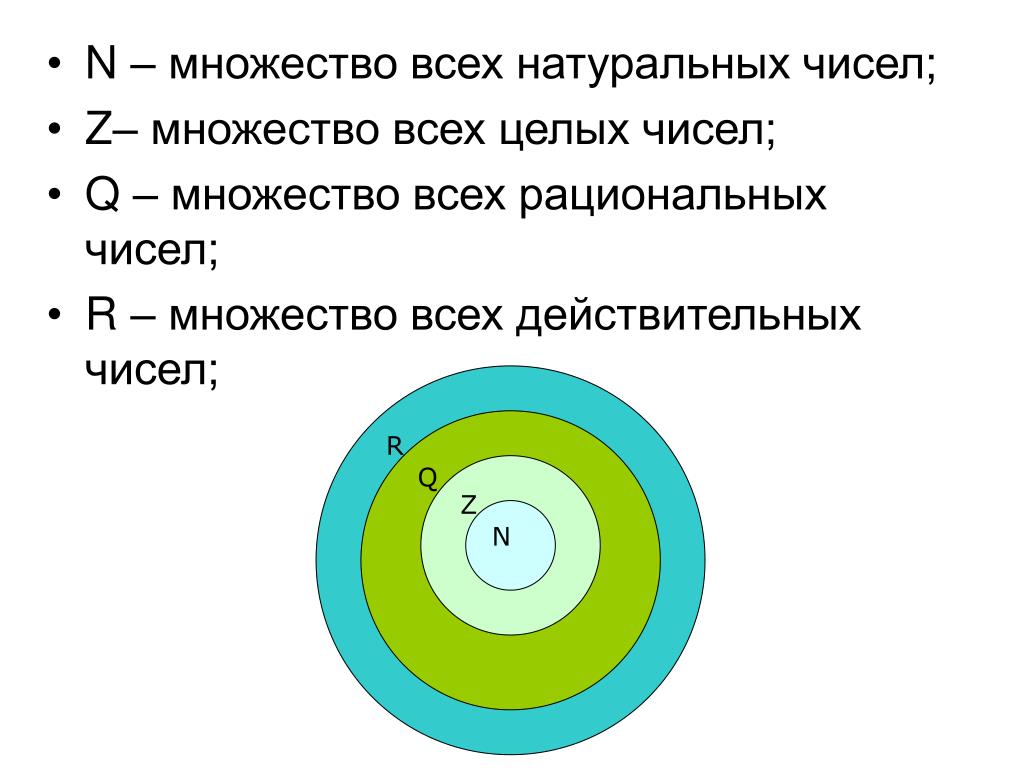
Сначала показать, что рациональных чисел достаточно, чтобы выразить любое количество чего угодно в мире с любой малой погрешностью, как бы мала она ни была. Это просто. Допустим, что у нас есть куча соли, весом от 0 до 1 кГ. если нам нужна точность, скажем, 1 миллиграмм, мы разделим килограмм на миллион равных частей и посмотрим, сколько нужно их… Читать далее
Умка Дедовский
9 октября 2022
Комментировать ответ…Комментировать…
Первый
Сергей Воробьёв
Я пенсионер. … Имя Сергей Константинович. … Увлечений много. … Морж. … · 1 окт 2022
… Современные математики вполне способны объяснить те объекты, которыми они оперируют. … Но, … не все на это способны КАК ПРЕПОДАВАТЕЛИ. …
Я думаю, … для того, чтобы объяснить «условному прохожему» что означает например иррациональное число, … ННУЖНО начать с истории возникновения этого понятия. … Как появилась необходимость ввода такого понятия как «иррациональное.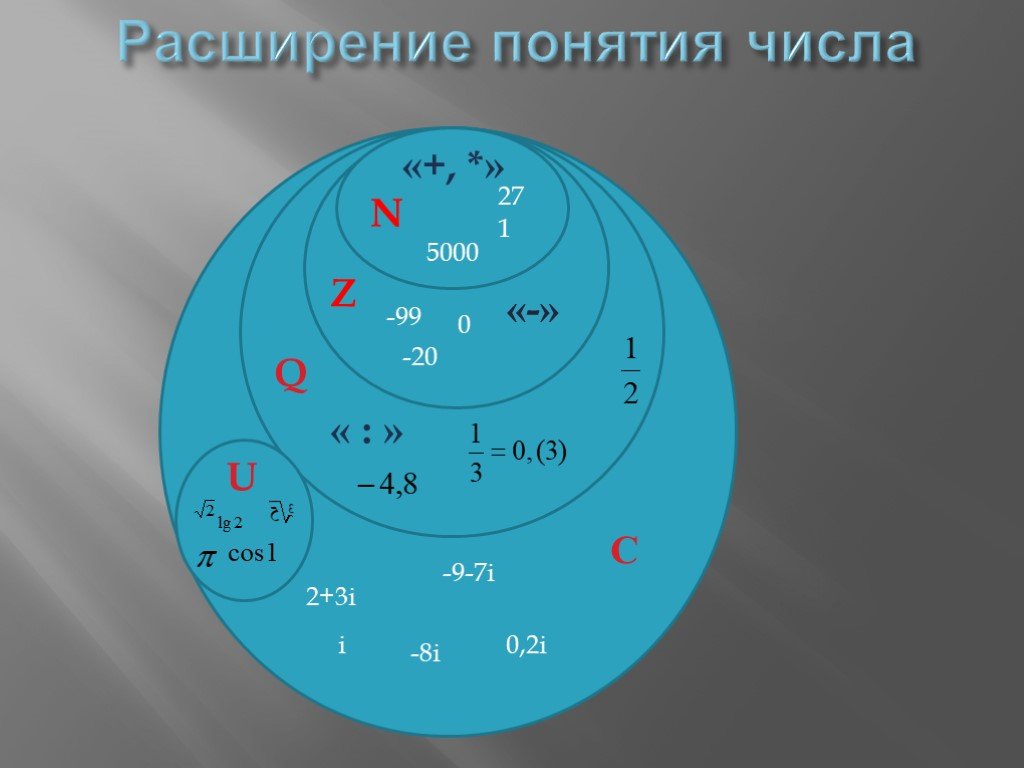
Комментировать ответ…Комментировать…
владимир уманский
34
Инженер -пенсионер · 6 авг 2022
Могут: 1.если прохожий тоже математик, 2.если читатель найдет ответ в «Книге книг», «почему Вс-шний отдыхал только на седьмой день», 3.если узнает что математики уже много веков не могут поделить Землю, чтобы хватило всем людям 4. если создано «каждой твари по паре»то никто не сможет их никак сосчитать. 5.если каждый прохожий считает себя умнее современного математика… Читать далее
Леонид Коганов
8 августа 2022
Особенно «восхитителен» пункт 6, наверное, потому,что 6 — совершенное число в смысле (исключения лишь его самого… Читать дальше
Разница между действительным числом и рациональным числом — Разница Между
Видео: Натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числаКлючевая разница: Вещественное число — это число, которое может принимать любое значение в числовой строке.
Это могут быть любые рациональные и иррациональные числа. Рациональное число — это число, которое может быть выражено в виде дроби, но с ненулевым знаменателем. Рациональные числа являются подмножеством действительных чисел.
Вещественные числа состоят из всех рациональных, а также иррациональных чисел. Система действительных чисел может быть далее разделена на множество подмножеств, таких как натуральные числа, целые числа и целые числа.
Натуральные числа (1, 2, 3,….)
Целые числа (0, 1, 2, 3, 4, 5,…)
Целые числа (… .., -3, -2, -1, 0, 1, 2, 3,… ..)
Действительное число относится к любому числу, которое можно найти в числовой строке. Числовая линия может быть выражена как фактическая геометрическая линия, где точка выбрана в качестве начала координат. Точки, попадающие в правую сторону от начала координат, считаются положительными числами, а числа, лежащие в левой части от начала координат, считаются отрицательными. Следовательно, они состоят из целых (0, 1, 3, 9, 26), рациональных (6/9, 78,98) и иррациональных чисел (квадратный корень из 3, пи).
Бесконечность не попадает в разряд вещественных чисел. Квадратный корень из -1 также не является действительным числом, и поэтому его называют мнимым числом.
Рациональное число — это число, которое определяется отношением, определенным как (p / q), где p обозначает некоторое целое число, а q обозначает некоторое ненулевое натуральное число. Эти числа образуют подмножество действительных чисел. С другой стороны, действительные числа, которые не могут быть выражены как отношение двух целых чисел, называются иррациональными числами. Рациональные числа являются результатом теоретического расчета или определения.
Сравнение между действительным числом и рациональным числом:
Настоящий номер | Рациональное число | |
Определение | Вещественное число — это число, которое может принимать любое значение в числовой строке. Это может быть любое из рациональных и иррациональных чисел. | Рациональное число — это число, которое может быть выражено в виде дроби, но с ненулевым знаменателем. |
Номерная строка | Может быть нанесен на номерной линии. | Может быть нанесен на номерной линии |
Включает в себя | Это включает (но не ограничивается) положительные и отрицательные числа, целые и рациональные числа, квадратные корни, кубические корни, π (pi) и т. Д. | 8, а 8 можно выразить в виде (8/1) 3/4, как это в виде дроби 0/3, как это в виде дроби Квадратный корень из 16, как это было бы 4, и это можно выразить как (4/1) .7777777, все повторяющиеся десятичные дроби рациональны. .12, как это можно выразить как 12/10 |
Важные моменты для запоминания |
|
|
Например, 0,1111111… = 1/9 и .245245245…. = 245/999.
| |||||||||||||||||||||||
Ключевое слово SearchAdvanced Search Поисковые книги для: Советы по поиску
966967. Show all books public access books [?] | |||||||||||||||||||||||
700677777777776 гг. 20052004200320022001200019991998199719961995199419931992199119\(q\)-Числа — Алгебры
НаверхПереключить боковую панель оглавления
Примечание
Это квантовые групповые \(q\)-аналоги, а не обычные \(q\)-аналоги
обычно используется в комбинаторике (см.
sage.combinat.q_analogues ).
- мудрец.алгебры.квантовые_группы.q_numbers.q_binomial( n , k , q = нет )
Вернуть \(q\)-биномиальный коэффициент.
Пусть \([n]_q!\) обозначает \(q\)-факториал \(n\), заданный выражением
sage.алгебры.квантовые_группы.q_numbers.q_factorial(). \(q\)-биномиальный коэффициент определяется как\[\begin{split}\begin{bmatrix} n \\ k \end{bmatrix}_q = \frac{[n]_q!}{[n-k]_q! \cdot [k]_q!}.\end{split}\]
ВВОД:
n, k– неотрицательные целые числа \(n\) и \(k\), определенные выше 9{-1}]\)) параметр \(q\) (должен быть обратимым)
Если
qне указано, то оно принимается за генератор \(q\) для кольцо многочленов Лорана над целыми числами.Примечание
Это не «обычный» \(q\)-бином, а вариант полезно для квантовых групп. Для версии, используемой в комбинаторика, см.
sage..
combinat.q_analogues Предупреждение
Этот метод использует деление на \(q\)-факториалы. Если \([k]_q!\) или \([n-k]_q!\) являются делителями нуля, или деление не осуществляется в кольце, содержащем \(q\), тогда это не сработает. 93
- sage.алгебры.quantum_groups.q_numbers.q_factorial( n , q=Нет )
Вернуть \(q\)-аналог факториала \(n!\).
\(q\)-факториал определяется:
\[[n]_q! = [n]_q \cdot [n-1]_q \cdots [2]_q \cdot [1]_q,\]
, где \([n]_q\) обозначает \(q\)-целое число, определенное в
sage.алгебры.квантовые_группы.q_numbers.q_int().ВВОД:
Если
qне указан, то по умолчанию используется генератор \(q\) для кольца полиномов Лорана над целыми числами. 93\(q\)-аналог \(n!\) определен только для \(n\) неотрицательного целое число (путевой билет № 11411):
мудрец: q_factorial(-2) Traceback (последний последний вызов): .
