Тест по теме «Законы постоянного тока»
Инструкция к тесту по физике «Законы постоянного тока»
Тест предназначен для контроля знаний по физике учащимися 10 класса (1 курса ССУЗа) по теме «Законы постоянного тока». На выполнение теста отводится 25 – 30 минут. Работа включает в себя 18 заданий и представлена в двух вариантах.
Задания 1-2 теста направлены на определение соответствия между физическими величинами и единицами их измерения, приборами, буквенными обозначениями. Ответы на данные задания следует записать по образцу: А3, Б2, В4, Г1, Д5.
Задания 3-18 представляют собой задания с выбором ответа. На каждое из таких заданий может быть предложен только один правильный вариант ответа.
Ответы теста следует внести в следующую таблицу:
вопрос | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
ответ | А… Б… В… Г… Д… | А… Б… В… Г… Д… |
Законы постоянного тока | Вариант 1. |
1. Найдите соответствие между физическими величинами и единицами их измерения:
А) сила тока | 1) ватт |
Б) напряжение | 2) ампер |
В) сопротивление | 3) вольт |
Г) мощность | 4) ом |
Д) работа тока | 5) джоуль |
2. Найдите соответствие между физическими величинами и приборами для их измерения:
А) сила тока | 1) ваттметр |
Б) напряжение | 2) омметр |
В) сопротивление | 3) вольтметр |
Г) мощность | 4) амперметр |
3.
Упорядоченным движением каких частиц создается электрических ток в металлах?
А) положительных ионов Б) отрицательных ионов
В) положительных и отрицательных ионов Г) электронов
4. Какой формулой выражается закон Ома для участка цепи?
А) A=IUt Б) P=IU В) I=U/R Г) Q=I2Rt
5. По какой формуле вычисляется мощность электрического тока?
А) A=IUt Б) P=IU В) I=U/R Г) Q=I2Rt
6. По какой формуле вычисляется электрическое сопротивление?
А) Q=I2Rt Б) P=IU В) I=U/R Г) R=ρl/S
7. Сила тока, проходящая через нить лампы, 0,3 А. Напряжение на лампе 6 В. Каково электрическое сопротивление нити лампы?
А) 2 Ом Б) 1,8 Ом В) 0,5 Ом Г) 20 Ом
8. Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В. Ответ выразите в миллиамперах.
А) 0,1 мА Б) 10 мА В) 100 мА Г) 1000 мА
9. Под каким напряжением находится одна из секций телевизора сопротивлением 24 кОм, если сила тока в ней 50 мА?
А) 1,2 В Б) 0,12 В В) 12 В Г) 1200 В
10. Какое количество теплоты выделяется в проводнике сопротивлением 100 Ом за 20 с при силе тока в цепи 20 мА?
А) 0,8 Дж Б) 40 Дж В) 800 кДж Г) 4 кДж
11. Какова мощность электрического тока в лампе при напряжении 100 В и силе тока 0,5 А?
А) 0,5 кВт Б) 0,05 кВт В) 5 мВт Г) 5 кВт
12. Рассчитайте сопротивление медного провода, используемого для питания трамвайного двигателя, если длина его провода 5 км, площадь сечения 0,75 мм2. Удельное сопротивление меди равно .
А) 11,3 Ом Б) 113,3 Ом В) 1,13 кОм Г) 0,113 МОм
13. Определите силу тока, проходящего по медному проводу длиной 100 м и площадью сечения 0,5 мм2 при напряжении 6,8 В.
Удельное сопротивление меди равно .
А) 0,2 А Б) 2 А В) 20 мА Г) 200 мА
14. Определите напряжение на концах стального проводника длиной 140 см и площадью поперечного сечения 0,2 мм2, в котором сила тока 250 мА. Удельное сопротивление стали равно .
А) 0,2625 В Б) 2,625 В В) 26,25 В Г) 262,5 В
15. К источнику тока с ЭДС 16 В и внутренним сопротивлением 2 Ом подключили сопротивление 6 Ом. Определите напряжение на зажимах источника.
А) 12 В Б) 24 В В) 36 В Г) 48 В Д) 52 В
16. При замыкании батареи сопротивлением 5 Ом ток в цепи равен 5 А, а при замыкании сопротивлением 2 Ом ток в цепи 8 А. Определите ЭДС батареи.
А) 10 В Б) 20 В В) 30 В Г) 40 В Д) 50 В
17. К источнику с ЭДС 2,5 В и внутренним сопротивлением 0,8 Ом присоединена спираль из нихромовой проволоки длиной 2,1 м с площадью поперечного сечения 0,55 мм2. Определите силу тока в цепи.
Удельное сопротивление нихрома равно
А) 0,05 А Б) 0,5 А В) 5 А Г) 50 А
18. Какой длины нужно взять кусок стальной проволоки сечением 0,2 мм2, чтобы в изготовленной из него спирали после подсоединения к источнику с ЭДС 6 В и внутренним сопротивлением 1,25 Ом сила тока была равна 3 А? Удельное сопротивление стали равно .
А) 1 м Б) 0,75 м В) 3 м Г) 10 м Д) 0,11 м
Законы постоянного тока | Вариант 2. |
1. Найдите соответствие между физическими величинами и единицами их измерения:
А) сила тока | 1) ватт |
Б) количество теплоты | 2) ампер |
В) сопротивление | 3) ом на метр |
Г) удельное сопротивление | 4) ом |
Д) работа тока | 5) джоуль |
2.
Найдите соответствие между физическими величинами и их обозначениями:
А) сила тока | 1) Р |
Б) напряжение | 2) R |
В) сопротивление | 3) U |
Г) мощность | 4) I |
Д) электрический заряд | 5) q |
3. Электрический ток в металлах представляет собой …
А) упорядоченное движение свободных протонов
Б) упорядоченное движение свободных электронов
В) хаотичное (беспорядочное) движение свободных протонов
Г) хаотичное (беспорядочное) движение свободных электронов
4. Какой формулой выражается закон Джоуля-Ленца?
А) A=IUt Б) P=IU В) I=U/R Г) Q=I2Rt
5.
По какой формуле вычисляется работа электрического тока?
А) A=I2Rt Б) P=IU В) I=U/R Г) Q=UIt
6. По какой формуле вычисляется мощность электрического тока?
А) Q=I2Rt Б) P=IU В) I=U/R Г) R=ρl/S
7. Сила тока, проходящая через нить лампы, 0,5 А. Напряжение на лампе 6 В. Каково электрическое сопротивление нити лампы?
А) 3 Ом Б) 1,2 Ом В) 0,083 Ом Г) 12 Ом
8. Найдите силу тока в участке цепи, если его сопротивление 50 Ом, а напряжение на его концах 5 В. Ответ выразите в миллиамперах.
А) 0,1 мА Б) 10 мА В) 100 мА Г) 1000 мА
9. Под каким напряжением находится одна из секций телевизора сопротивлением 12 кОм, если сила тока в ней 100 мА?
А) 1,2 В Б) 0,12 В В) 12 В Г) 1200 В
10. Какое количество теплоты выделяется в проводнике сопротивлением 150 Ом за 20 с при силе тока в цепи 30 мА?
А) 270 Дж Б) 2,7 Дж В) 2700 кДж Г) 2,7 кДж
11.
Какова мощность электрического тока в лампе при напряжении 220 В и силе тока 0,1 А?
А) 2,2 кВт Б) 0,22 кВт В) 2200 кВт Г) 22 Вт
12. Рассчитайте сопротивление медного провода, используемого для питания трамвайного двигателя, если длина его провода 2 км, площадь сечения 0,3 мм2. Удельное сопротивление меди равно .
А) 11,3 Ом Б) 113,3 Ом В) 1,13 кОм Г) 0,113 МОм
13. Определите силу тока, проходящего по медному проводу длиной 300 м и площадью сечения 0,5 мм2 при напряжении 20,4 В. Удельное сопротивление меди равно .
А) 0,2 А Б) 2 А В) 20 мА Г) 200 мА
14. Определите напряжение на концах стального проводника длиной 70 см и площадью поперечного сечения 0,1 мм2, в котором сила тока 250 мА. Удельное сопротивление стали равно .
А) 0,2625 В Б) 2,625 В В) 26,25 В Г) 262,5 В
15. К источнику тока с ЭДС 32 В и внутренним сопротивлением 2 Ом подключили сопротивление 6 Ом.
Определите напряжение на зажимах источника.
А) 24 В Б) 48 В В) 72 В Г) 96 В Д) 104 В
16. К кислотному аккумулятору, имеющему ЭДС 200 В и внутреннее сопротивление 0,2 Ом, подключен потребитель сопротивлением 3,8 Ом. Определите силу тока в цепи.
А) 10 А Б) 20 А В) 30 А Г) 40 А Д) 50 А
17. К источнику с ЭДС 2 В и внутренним сопротивлением 0,8 Ом присоединена спираль из нихромовой проволоки длиной 2,1 м с площадью поперечного сечения 0,55 мм2. Определите силу тока в цепи. Удельное сопротивление нихрома равно
А) 0,04 А Б) 0,4 А В) 4 А Г) 40 А
18. Какой длины нужно взять кусок стальной проволоки сечением 0,2 мм2, чтобы в изготовленной из него спирали после подсоединения к источнику с ЭДС 6 В и внутренним сопротивлением 1,2 Ом сила тока была равна 2 А? Удельное сопротивление стали равно .
А) 3 м Б) 1,2 м В) 2,4 м Г) 1,8 м Д) 0,36 м
Ответы
вопрос | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Вариант 1 | А2 Б3 В4 Г1 Д5 | А4 Б3 В2 Г1 | Г | В | Б | Г | Г | В | Г | А | Б | Б | Б | А | А | Г | Б | А |
Вариант 2 | А2 Б5 В4 Г3 Д5 | А4 Б3 В2 Г1 Д5 | Б | Г | А | Б | Г | В | Г | Б | Г | Б | Б | А | А | Д | Б | В |
Тест по физике Законы электрического тока 8 класс
Тест по физике Законы электрического тока для учащихся 8 класса с ответами.
Тест состоит из 4 вариантов в каждом по 20 заданий.
1 вариант
1. В каких единицах измеряют силу тока?
1) В кулонах (Кл)
2) В амперах (А)
3) В омах (Ом)
4) В вольтах (В)
2. Известно, что через поперечное сечение проводника, включенного в цепь на 2 мин, прошел заряд, равный 36 Кл. Какова была сила тока в этом проводнике?
1) 0,3 А
2) 18 А
3) 36 А
4) 72 А
3. По какой формуле определяют электрическое напряжение?
1) v = s/t
2) I = q/t
3) P = A/t
4) U = A/q
4. Нужно измерить напряжение на электролампе. Какой из представленных здесь схем можно воспользоваться для этого?
1) №1
2) №2
3) №3
5. Какая физическая величина характеризует электропроводность цепи?
1) Сила тока
2) Работа тока
3) Сопротивление
4) Напряжение
6. На рисунке показаны три графика зависимости силы тока от напряжения.
Какой из них построен для цепи, обладающей наименьшим сопротивлением?
1) №1
2) №2
3) №3
7. Напряжение на реостате сопротивлением 20 Ом равно 75 В. Какова сила тока в нем?
1) 1,5 А
2) 7,5 А
3) 37,5 А
4) 3,75 А
8. Сила тока в проводнике 0,25 А, напряжение на его концах 150 В. Каким сопротивлением обладает этот проводник?
1) 60 Ом
2) 600 Ом
3) 37,5 Ом
4) 375 Ом
9. Как сопротивление проводника зависит от его длины?
1) Изменение длины проводника не влияет на его сопротивление
2) С увеличением длины проводника его сопротивление увеличивается
3) С увеличением длины проводника сопротивление уменьшается
10. По какой формуле рассчитывают сопротивление проводника, если известны его размеры?
1) R = U/I
2) F = gρV
3) R = ρl/S
4) F = gρжVт
11. Определите сопротивление никелинового провода длиной 20 м и площадью поперечного сечения 0,4 мм2.
1) 16 Ом
2) 40 Ом
3) 10 Ом
4) 20 Ом
12. Как надо изменить положение ползунка, чтобы сопротивление реостата уменьшилось?
1) Сдвинуть его в право
2) Передвинуть влево
3) Сместить в любую сторону
13. К источнику тока подключены последовательно соединенные лампа, резистор и реостат (см. схему). Под каким номером обозначен реостат? Какова в нем сила тока, если в лампе она равна 0,3 А?
1) №3; 0,1 А
2) №2; 0,1 A
3) №3; 0,3 А
4) №2; 0,3 А
14. Две одинаковые параллельно соединенные лампы подключены к источнику тока, напряжение на полюсах которого 12 В. При этом сила тока в лампе №1 равна 1 А. Каковы напряжения на лампе №1 и №2? Какой силы ток течет в общей цепи этих ламп?
1) На той и другой лампе 12 В; 2 А
2) На той и другой лампе 12 В; 0,5 А
3) На каждой лампе по 6 В; 2 А
4) На каждой лампе по 6 В; 0,5 А
15. По каким двум формулам рассчитывают работу электрического тока?
1) A = Uq и U = IR
2) q = It и A = Ult
3) A = Uq и A = Ult
16.
Какая физическая величина характеризует быстроту выполнения работы электрическим током? В каких единицах ее измеряют?
1) Заряд, прошедший через поперечное сечение проводника; в кулонах
2) Мощность электрического тока; в ваттах
3) Напряжение; в вольтах
4) Выделяемое количество теплоты; в джоулях
17. Сила тока в лампе 0,8 А, напряжение на ней 150 В. Какова мощность электрического тока в лампе? Какую работу он совершит за 2 мин ее горения?
1) 120 Вт; 22,5 кДж
2) 187,5 Вт; 14,4 кДж
3) 1875 Вт; 14,4 кДж
4) 120 Вт; 14,4 кДж
18. От каких величин зависит количество теплоты, выделяемой проводником при прохождении по нему электрического тока?
1) Силы тока и длины проводника
2) Силы тока и площади его поперечного сечения
3) Силы тока, времени и сопротивления проводника
4) Силы тока, напряжения и материала, из которого изготовлен проводник
19. Силу тока в цепи увеличили в 2 раза, а ее сопротивление уменьшили в 2 раза.
Изменилось ли в цепи и как выделение теплоты?
1) Увеличилось в 2 раза
2) Не изменилось
3) Уменьшилось в 2 раза
4) Увеличилось в 4 раза
20. Лампа, сопротивление нити накала которой 10 Ом, включена на 10 мин в цепь, где сила тока равна 0,1 А. Сколько энергии в ней выделилось?
1) 1 Дж
2) 6 Дж
3) 60 Дж
4) 600 Дж
2 вариант
1. По какой формуле можно вычислить силу тока в цепи?
1) P = A/t
2) I = q/t
3) m = Q/λ
4) U = A/q
2. К источнику тока подключены последовательно соединенные лампа и реостат. Где следует включить в этой цепи амперметр, чтобы измерить силу тока в реостате?
1) Между лампой и реостатом
2) Между источником тока и реостатом
3) Между реостатом и ключом
4) В любом месте цепи
3. В каких единицах измеряется электрическое напряжение?
1) В джоулях (Дж)
2) В амперах (А)
3) В омах (Ом)
4) В вольтах (В)
4.
На каком из участков электрической цепи ток совершит наименьшую работу, если на первом из них напряжение равно 20 В, на втором — 10 В и на третьем — 60 В?
1) На первом
2) На втором
3) На третьем
5.
1) №1 — 4 А; №2 — 1 А
2) №1 — 1 А; №2 — 4 А
3) В обеих цепях 4 А
4) В обеих цепях 1 А
6. Как изменится сопротивление проводника, если сила тока в нем возрастет в 2 раза?
1) Увеличится в 4 раза
2) Уменьшится в 2 раза
3) Не изменится
4) Увеличится в 2 раза
7. Какова сила тока в проводнике, сопротивление которого 10 Ом, при напряжении 220 В?
1) 2,2 А
2) 22 А
3) 2,2 кА
4) 22 кА
8. При напряжении 70 В сила тока в проводнике 1,4 А. Определите его сопротивление.
1) 5 Ом
2) 50 Ом
3) 98 Ом
4) 9,8 Ом
9.
Как сопротивление проводника зависит от его поперечного сечения?
1) При увеличении сечения сопротивление уменьшается
2) С увеличением его площади сопротивление увеличивается
3) Изменение площади сечения не влияет на сопротивление
10. Серебро имеет малое удельное сопротивление. Оно — хороший или плохой проводник электричества?
1) Ответить нельзя — нет нужных данных
2) Плохой
3) Хороший
11. Спираль изготовлена из нихромового провода длиной 50 м и поперечным сечением 0,2 мм2. Каково его сопротивление?
1) 11 Ом
2) 27,5 Ом
3) 110 Ом
4) 275 Ом
12. Куда следует передвинуть ползунок, чтобы сопротивление увеличить?
1) Влево
2) Вправо
3) Поставить на середину
13. Цепь, схема которой показана на рисунке, состоит из источника тока, амперметра и двух одинаковых параллельно соединенных электроламп. Амперметр показывает силу тока, равную 0,6 А.
1) В обеих лампах 0,6 А
2) В №1 — 0,6 А; №2 — 0,3 А
3) №1 — 0,3 А; №2 — 0,6 А
4) В обеих лампах 0,3 А
14. К источнику тока подключены две одинаковые последовательно соединенные лампы сопротивлением 6 Ом каждая. Сила тока в лампе №1 равна 1,5 А. Определите напряжение на полюсах источника тока и силу тока в соединительных проводах.
1) 9 В; 1,5 А
2) 18 В; 1,5 А
3) 18 В; 3 А
4) 9 В; 3 А
15. Какими тремя приборами надо располагать, чтобы измерить величины, необходимые для расчета работы электрического тока?
1) Амперметром, аккумулятором, вольтметром
2) Амперметром, вольтметром, реостатом
3) Амперметром, вольтметром, часами
16. По какой формуле рассчитывают мощность электрического тока?
1) q = It
2) А = Uq
3) Р = UI
4) U = IR
17. Сопротивление участка цепи 75 Ом, напряжение на его концах 150 В.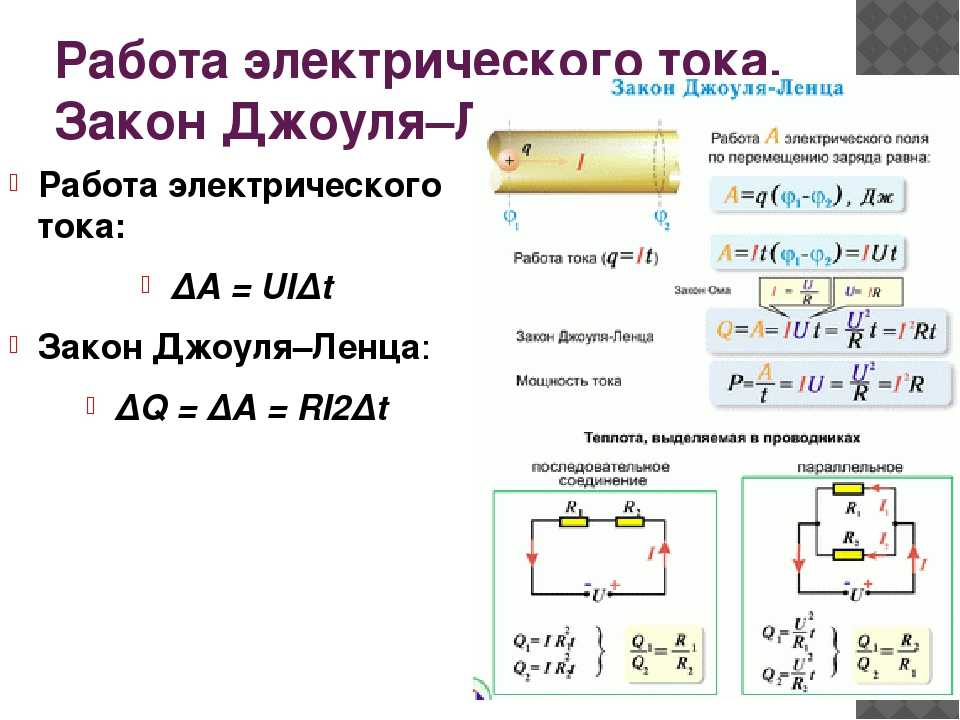
1) 300 Вт; 9 кДж
2) 300 Вт; 0,6 кДж
3) 300 Вт; 90 кДж
4) 300 Вт; 900 кДж
8. Как зависит теплота, выделяющаяся в проводнике, от силы тока?
1) Чем больше сила тока, тем больше выделяется теплоты
2) Чем больше сила тока, тем меньше выделяется теплоты
3) Количество теплоты прямо пропорционально силе тока
4) Количество теплоты прямо пропорционально квадрату силы тока
19. Как изменится выделение теплоты в цепи, если силу тока в ней уменьшить в 3 раза, а сопротивление увеличить в 3 раза?
1) Уменьшится в 9 раз
2) Уменьшится в 3 раза
3) Увеличится в 3 раза
4) Не изменится
20. Проводник сопротивлением 250 Ом при силе тока, равной 200 мА, нагревался 3 мин. Сколько энергии электрического тока перешло при этом в его внутреннюю энергию? (Потери энергии не учитывать.)
1) 180 Дж
2) 1800 Дж
3) 18 кДж
4) 30 кДж
3 вариант
1.
Выразите в амперах силу тока, равную 4250 мА и 0,8 кА.
1) 42,5 А и 80 А
2) 42,5 А и 800 А
3) 4,25 А и 800 А
4) 4,25 А и 80 А
2. В какой электролампе измеряет силу тока амперметр, включенный так, как показано на схеме?
1) №1
2) №2
3) В любой из них
3. Какую работу совершит электрический ток в реостате, напряжение на котором 35 В, если по нему пройдет заряд, равный 10 Кл?
1) 35 Дж
2) 350 Дж
3) 70 Дж
4) 700 Дж
4. Как включается в цепь вольтметр?
1) Параллельно тому участку цепи, на котором должно быть измерено напряжение
2) Последовательно с тем участком цепи, где измеряется напряжение
3) Однозначного ответа нет: в разных цепях по-разному
5. В каких единицах измеряют сопротивление проводников?
1) В вольтах (В)
2) В кулонах (Кл)
3) В омах (Ом)
4) В амперах (А)
6. Какая из приведенных здесь формул выражает закон Ома?
1) U = A/q
2) I = q/t
3) P = A/t
4) I = U/R
7.
Сила тока в электролампе 0,44 А, сопротивление ее раскаленной нити 500 Ом. При каком напряжении она горит?
1) 220 В
2) 22 В
3) 8,8 В
4) 88 В
8. Сопротивление проводника 450 Ом, напряжение на его концах 90 В. Найдите силу тока в этом проводнике.
1) 0,5 А
2) 5 А
3) 20 А
4) 0,2 А
9. Какая физическая величина характеризует зависимость сопротивления проводника от вещества, из которого он состоит?
1) Сила тока
2) Напряжение
3) Удельное сопротивление
4) Количество электричества
10. У сплава манганин довольно большое удельное сопротивление, а у серебра малое. Какое из этих веществ лучше проводит электрический ток?
1) Манганин
2) Серебро
3) Сравнения удельных сопротивлений веществ недостаточно для ответа на вопрос
11. Рассчитайте сопротивление реостата, на изготовление которого пошло 100 м константановой проволоки с площадью поперечного сечения 0,5 мм2.
1) 10 Ом
2) 25 Ом
3) 100 Ом
4) 250 Ом
12. Как изменится сила тока в цепи, если ползунок включенного в нее реостата сдвинуть вправо?
1) Уменьшится
2) Увеличится
3) Не изменится
13. В цепи, схема которой представлена на рисунке, сопротивление лампы 25 Ом, резистора 45 Ом, звонка 10 Ом. Найдите сопротивление этой цепи и силу тока в лампе, если сила тока в резисторе 0,6 А.
1) 80 Ом; 0,2 А
2) 55 Ом; 0,6 А
3) 35 Ом; 0,2 А
4) 80 Ом; 0,6 А
14. Лампа и резистор, сопротивления которых одинаковы, включены в цепь согласно показанной схеме. Сила тока в лампе 2 А, напряжение на полюсах источника тока 10 В. Каково сопротивление резистора и сила тока в нем?
1) 5 Ом; 2 А
2) 20 Ом; 2 А
3) 20 Ом; 1 А
4) 5 Ом; 1 А
15. В каких единицах измеряют работу электрического тока?
1) В омах (Ом)
2) В амперах (А)
3) В джоулях (Дж)
4) В вольтах (В)
16.
Какие нужно иметь приборы, чтобы можно было измерить величины, позволяющие определить мощность электрического тока?
1) Амперметр и реостат
2) Амперметр и вольтметр
3) Вольтметр и часы
4) Вольтметр и реостат
17. В проводнике сопротивлением 15 Ом сила тока равна 0,4 А. Какова мощность электрического тока в нем? Чему равна работа тока в этом проводнике, совершенная за 10 мин?
1) 2,4 Вт; 1,44 кДж
2) 6 Вт; 3,6 кДж
3) 6 Вт; 60 Дж
4) 2,4 Вт; 24 Дж
18. По какой формуле рассчитывают количество теплоты, выделяющейся в проводнике при прохождении по нему электрического тока?
1) Q = cm(t2 — t1)
2) Q = I2Rt
3) А = IUt
19. Во сколько раз надо увеличить сопротивление цепи, чтобы при уменьшении силы тока в 4 раза выделяющееся в ней количество теплоты осталось неизменным?
1) В 4 раза
2) В 8 раз
3) В 16 раз
20. Сила тока в проводнике сопротивлением 125 Ом равна 0,1 А.
Какое количество теплоты выделяется в нем за 1 мин?
1) 750 Дж
2) 75 Дж
3) 1,25 Дж
4) 12,5 Дж
4 вариант
1. Переведите в амперы силу тока, равную 700 мА и 0,25 кА.
1) 7 А и 250 А
2) 0,7 А и 25 А
3) 7 А и 25 А
4) 0,7 А и 250 А
2. Какой амперметр измерит силу тока в верхней (на схеме) лампе?
1) №1
2) №2
3) Любой из них
4) Ни один из этих приборов
3. При прохождении по участку цепи заряда 100 Кл электрический ток произвел работу, равную 12 кДж. Каково напряжение на этом участке цепи?
1) 120 В
2) 12 В
3) 1,2 В
4) 0,12 В
4. На каком приборе измеряет напряжение вольтметр, включенный так, как показано на схеме?
1) На звонке
2) На лампе
3) На реостате
5. В чем главная причина того, что проводники оказывают сопротивление электрическому току?
1) Постоянное хаотическое движение электронов
2) Столкновение упорядоченно движущихся электронов с ионами кристаллической решетки
3) Взаимодействие электронов с ионами решетки
6.
Пользуясь законом Ома, получите формулу для расчета сопротивления проводника.
1) R = U/I
2) I = q/t
3) P = A/t
7. При какой силе тока напряжение на концах проводника сопротивлением 125 Ом будет равно 1,5 кВ?
1) 1,2 А
2) 12 А
3) ≈ 83 А
4) ≈ 8,3 А
8. Сила тока в реостате 0,8 А, его сопротивление 100 Ом. Определите напряжение на его клеммах.
1) 125 В
2) 12,5 В
3) 80 В
4) 800 В
9. От каких физических величин зависит сопротивление проводника?
1) От его длины (l)
2) От площади его поперечного сечения (S)
4) От всех этих трех величин
10. Какое вещество — с малым или большим удельным сопротивлением — может служить хорошим проводником электричества?
1) С малым
2) С большим
3) Однозначного ответа нет
11. Железный провод длиной 6 м и площадью поперечного сечения 0,3 мм2 включен в цепь.
Какое сопротивление он оказывает электрическому току?
1) 36 Ом
2) 18 Ом
3) 2 Ом
4) 20 Ом
12. У реостата, показанного на рисунке, когда он был включен в цепь, передвинули ползунок вправо. Как изменилась при этом сила тока?
1) Уменьшилась
2) Увеличилась
3) Не изменилась
13. Сила тока в лампе №1 равна 5 А. Какова сила тока в такой же лампе №2 и какую силу тока покажет амперметр?
1) 2,5 А; 5 А
2) 5 А ; 10 A
3) 2,5 А; 7,5 А
4) 5 А; 7,5 А
14. В цепи с последовательным соединением потребителей тока (двух ламп и резистора, обладающих одинаковыми сопротивлениями) сила тока равна 0,4 А, напряжение на резисторе 20 В. Определите общее сопротивление цепи и напряжение на полюсах источника тока.
1) 150 Ом; 40 В
2) 50 Ом; 60 В
3) 150 Ом; 20 В
4) 150 Ом; 60 В
15. В каких единицах должны быть выражены величины при расчете работы электрического тока по формуле А = IUt?
1) В амперах, вольтах и секундах
2) В амперах, вольтах, минутах
3) В вольтах, омах, часах
4) В кулонах, вольтах, секундах
16.
Если известна мощность электрического тока, то как найти силу тока в цепи?
1) I = U/R
2) I = P/U
4) I = A/(Ut)
17. Электролампа, сопротивление нити накала которой 20 Ом, включена в сеть с напряжением 220 В. Какова мощность тока? Какую работу он произведет за 5 мин свечения лампы?
1) 4,4 кВт; 1320 кДж
2) 4,4 кВт; 22 кДж
3) 2,42 кВт; 22 кДж
4) 2,42 кВт; 726 кДж
18. Какая из формул выражает закон Джоуля — Ленца?
1) Q = cm(t2 — t1)
2) F = k(l2 — l1)
3) Q = I2Rt
19. Как и во сколько раз надо изменить силу тока в цепи, чтобы при уменьшении ее сопротивления в 4 раза выделение теплоты в ней осталось прежним?
1) Уменьшить в 2 раза
2) Увеличить в 4 раза
3) Уменьшить в 4 раза
4) Увеличить в 2 раза
20. Проводник обладает сопротивлением 80 Ом. Какое количество теплоты выделится в нем за 10 с при силе тока 0,3 А?
1) 7,2 Дж
2) 72 Дж
3) 720 Дж
Ответы на тест по физике Законы электрического тока
1 вариант
1-2
2-1
3-4
4-2
5-3
6-1
7-4
8-2
9-2
10-3
11-4
12-2
13-3
14-1
15-3
16-2
17-4
18-3
19-1
20-3
2 вариант
1-2
2-4
3-4
4-2
5-1
6-3
7-2
8-2
9-1
10-3
11-4
12-1
13-4
14-2
15-3
16-3
17-1
18-4
19-2
20-2
3 вариант
1-3
2-3
3-2
4-1
5-3
6-4
7-1
8-4
9-3
10-2
11-3
12-1
13-4
14-1
15-3
16-2
17-1
18-2
19-3
20-2
4 вариант
1-4
2-4
3-1
4-2
5-3
6-1
7-2
8-3
9-4
10-1
11-3
12-2
13-2
14-4
15-1
16-2
17-4
18-3
19-4
20-2
PDF-версия
Тест Законы электрического тока
(221 Кб, pdf)
Расчет потерь мощности с использованием формулы Джоуля | Блог Advanced PCB Design
Ключевые выводы
Джоулев нагрев — это физический эффект, который увеличивает внутреннюю энергию и столкновение электронов в цепи с током, что приводит к генерированию тепловой энергии.
Формула нагрева Джоуля определяется как Q=I2Rt.
Согласно формуле Джоуля для нагревания, вырабатываемая тепловая энергия пропорциональна времени, в течение которого электрический ток и электрическое сопротивление остаются постоянными.
Потери мощности из-за нагрева – главный недостаток, препятствующий использованию ламп накаливания
Системы светодиодного освещения. В рамках этого перехода от ламп накаливания отказываются. Потери мощности из-за нагрева являются основным недостатком ламп накаливания, снижающим их КПД. Сопротивление, оказываемое нитью накала потоку электрического тока, производит тепловую энергию, которую можно рассчитать, используя формулу нагревания Джоуля. Именно тепловые потери или явление джоулевого нагрева ограничивают применение ламп накаливания при попытке сэкономить электроэнергию.
В этой статье рассматривается Джоулев нагрев в электрических цепях и способы расчета энергии, теряемой в виде тепла.
Джоуль Нагрев
Мы уже знаем, что поток электронов в замкнутой цепи представляет собой электрический ток. Когда ток протекает через цепь или проводящий материал, сопротивление, связанное с цепью или материалом, вызывает столкновение электронов. Электроны, сталкиваясь друг с другом, рассеивают энергию в виде тепла и генерируют потери мощности. Часть входной электрической мощности теряется в виде тепловой энергии. Выходная мощность всегда будет меньше входной мощности при наличии тепловых потерь. Эффективность контура снижена до менее 100% из-за тепловых потерь.
В целом джоулев нагрев можно описать как физический эффект, который увеличивает внутреннюю энергию и столкновение электронов в цепи с током, что приводит к генерированию тепловой энергии. В процессе джоулевого нагрева, в зависимости от условий цепи, некоторая часть электрической энергии превращается в тепло при протекании электрического тока по цепи конечной проводимости.
Джоулев нагрев также известен как омический нагрев или резистивный нагрев. Сопротивление является важным свойством, определяющим ток, протекающий по цепи. Скорость, с которой сопротивление преобразует электрическую энергию в тепловую, можно рассчитать, используя формулу нагревания Джоуля.
Формула нагрева Джоуля
Формула нагрева Джоуля — это математическое уравнение, определяющее скорость, с которой электрическая энергия преобразуется в тепловую благодаря сопротивлению цепи. Закон назван в честь английского физика Джеймса Прескотта Джоуля, который обнаружил, что количество тепловой энергии, выделяемой в секунду в проводнике или цепи с током, пропорционально квадрату цепи и электрическому сопротивлению цепи.
Формула нагревания в Джоулях определяется следующим образом:
Q = I 2 RtQ – количество выделяемого тепла, выраженное в джоулях.
I — электрический ток в амперах.
R — сопротивление цепи протеканию электрического тока в Омах.
t — время, в течение которого ток может течь в цепи, выраженное в секундах.
Рассмотрим пример джоулевого нагрева, когда ток 5 А протекает через электрический провод сопротивлением 20 Ом в течение 10 с. Тепловая энергия, вырабатываемая в джоулях, может быть рассчитана по формуле нагревания Джоуля:
Q = 5 2 x 20 x 10 = 5 кДж
Когда полезен Джоулев нагрев?
Джоулев нагрев не всегда вреден, но может привести к потерям в электрической системе. Существуют определенные приложения, в которых полезно преднамеренное создание потерь тепла. Большинство бытовых приборов преобразуют электрическую энергию в тепловую. Некоторыми примерами, в которых используется джоулев нагрев, являются электрический нагреватель, гейзер и лампы накаливания.
Увидеть лампы накаливания в качестве применения может быть неожиданно, так как во вводном разделе мы обсуждали потери мощности из-за нагрева в этих лампах.
Однако именно из-за явления джоулевого нагрева лампы накаливания излучают не только тепловую энергию, но и свет. Вольфрамовый материал обычно имеет высокую температуру плавления и используется в качестве нити накала в лампах накаливания. Тонкая нить с высоким сопротивлением, заключенная в стеклянную оболочку, заполненную азотом и аргоном, производит большое количество тепловой энергии. Огромная теплота, выделяемая из-за протекания электрического тока в нити накала, делает ее раскаленной добела. Нить накала излучает свет и тепло одновременно, первое полезно, а второе создает проблемы из-за эффекта нагрева Джоуля.
Согласно формуле нагревания Джоуля, вырабатываемая тепловая энергия пропорциональна времени, в течение которого электрический ток и электрическое сопротивление остаются постоянными. Когда любая комбинация двух из трех параметров в формуле нагрева Джоуля (ток, сопротивление и время) постоянна, выделяемое тепло пропорционально третьему параметру, который изменяется.
С помощью программного обеспечения Cadence вы можете разрабатывать приложения, которые преднамеренно используют джоулев нагрев, а также снижают потери мощности из-за нагрева в электрических системах.
Ведущие поставщики электроники полагаются на продукты Cadence для оптимизации потребностей в мощности, пространстве и энергии для широкого спектра рыночных приложений. Если вы хотите узнать больше о наших инновационных решениях, поговорите с нашей командой экспертов или подпишитесь на наш канал YouTube.
Запросить оценку
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетите вебсайт Больше контента от Cadence PCB Solutions
УЗНАТЬ БОЛЬШЕ Калькулятор нагреваДжоулей
Автор: Доминик Черня, доктор философии
Отзыв от Bogna Szyk и Adena Benn0008
Этот калькулятор джоулевого нагрева позволяет найти тепло, выделяемое током, протекающим через резистор.
Вы когда-нибудь задумывались, зачем вам нужно охлаждать компьютер? Вы знаете, как работают обычные обогреватели? Прочтите текст ниже, чтобы найти ответы и узнать о формуле Джоуля нагрева.
Резистивный нагрев
Электроны, мельчайшие заряженные частицы, переносят электрическую энергию, которая течет по кабелю, создавая электрический ток. Вы наверняка знаете, что вся материя вокруг нас состоит из атомов. Теперь вы можете представить, что если движущийся электрон столкнется с атомом, электрон потеряет часть своей энергии. Затем эта энергия преобразуется в тепло, и поэтому температура кабеля повышается. Мы можем сказать, сколько энергии теряется таким образом, зная падение напряжения на проводе. Если вы хотите узнать об этом больше, воспользуйтесь нашим калькулятором падения напряжения.
Формула нагрева в Дж
Вы можете оценить тепло, выделяемое в токонесущем кабеле, с помощью приведенного ниже уравнения, называемого первым законом Джоуля:
Q = I² × R × t
текущий,
R сопротивление, t текущее время течения, Q это тепло.
Это уравнение можно использовать для любой электрической сети, в которой протекающий ток является постоянным (постоянным). В частности, вы можете рассчитать количество тепла, выделяемого резисторами, включенными последовательно или параллельно. Просто рассчитайте соответствующее сопротивление R с помощью нашего калькулятора.
Знаете ли вы?
Джоулев нагрев часто является нежелательным эффектом, поскольку генерируемое тепло означает потерю энергии. В электронных устройствах явление Джоуля приводит к утечке тепла внутри устройства и требует уменьшения тепла для правильной работы. Вот почему электронные устройства, такие как компьютеры, нуждаются в охлаждении.
С другой стороны, мы можем использовать джоулев нагрев для целенаправленного повышения температуры. В настоящее время большинство обычных нагревателей, встречающихся, например, в электрических чайниках или стиральных машинах, состоят из свернутого в спираль кабеля с током.
