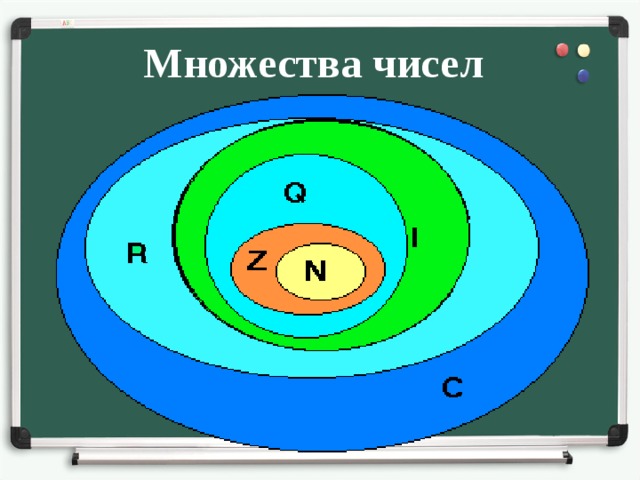
R это числа: Какие числа называются действительными?

Содержание

1. Множество действительных чисел. Основные структуры множества r.

Действительные числа — это числа, сплошь заполняющие числовую прямую (непрерывность), выполняет все операции (+-\*) и является плотным, т.к. содержит в себе Q, изображаются точками на прямой.

структура:

Неплотным называется множество, если оно содержит элементы, между которыми нет ни одного другого элемента данного множества.

1. натуральные числа N. возникли в процессе счета предметов (+*) (-/ не всегда)неплотно, не является непрерывным.

2.целые числа Z. исторически появилось в связи с понятием дома, объединение целых отрицательных, натуральных и нуля привело к появлению целых чисел. (+-*) (\ не всегда), неплотное и не непрерывное.

3.рациональные числа Q. –множество несократимых дробей, дроби могут являться различным изображением одного рационального числа.

(+-*\) (\ на 0 нельзя), плотно (между двумя числами находится еще число (доказывается полу суммой)), не является непрерывным т.к. меж рациональными числами есть иррациональные ()

Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.

R—множество действительных чисел. Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 1/2= 0,5 (= 0,500…), 1/3=0,333… — рациональные числа.(Выполняются действия + : — ×) . Оно является плотным т.к. содержит в себе плотное множество.Множ. непрерывно;геометрич.это знач.-что действительные числасплош заполняют числовую прямую,на ней нет промежутков не заполненных действ. Числ.

Основные виды структур -Множество – конечная совокупность элементов.

2) для каждого элемента, кроме первого и последнего, имеются предыдущий и последующий элементы).

3)Матрица – структура, у которой множество R состоит из двух отношений линейного порядка.

4) Дерево – множество R состоит из одного отношения иерархического порядка.

5)Граф – множество R состоит из одного отношения бинарного порядка.

6)Гиперграф – множество R состоит из двух и более отношений различного порядка.

С геометрической точки зрения свойство непрерывности означает, что R сплошь заполняют числовую прямую.

Аксиома Архимеда: (геометрически)- если на прямой даны 2 отрезка ОА и АВ, то отрезок ОА можно повторить столько раз, чтобы сумма была больше ОВ. (алгебраически)- если А положительное число, В — любое число, то всегда найдется такое натуральное число n, что n·A>B

Теорема Кантора:

1.(аксиома Кантора)-последовательность отрезков называется

стягивающейся последовательностью вложенных отрезков, если каждый последующий содержится в своем предыдущем и длины отрезков стремятся к нулю при n стремящейся к бесконечности. Всякая стягивающая последовательность вложенных отрезков имеет общую всем точку.

2.(теорема)-фактически стягивание означает что во множестве R определена новая операция, предельный переход. Следовательно, не может быть 2 разных точек принадлежащих всем сегментам последовательности.

N={1; 2; 3; . n .}- множество натуральных чисел;

Zo={0; 1; 2; .. n…}- множество целых неотрицательных чисел;

Z={0; ±1; ±2; .. ±n..}- множество целых чисел;

Q={m/n…..}-множество рациональных чисел.

R—множество действительных чисел.

.Множ. непрерывно;геометрич.это знач.-что действительные числа сплош заполняют числовую прямую,на ней нет промежутков не заполненных действ. Числ.

Аксиома Архимеда:Если имеется две величины a и b, то взяв a слагаемым достаточное количество раз, можно превзойти b:Геометрич: если даны два отрезка, то отложив достаточное количество раз меньший из них, можно покрыть больший.Теор.Кантора:послндовательность отрезков(a;b )(f;t)…наз. Стягивающейся последовательностью вложенных отрезков если каждый последующий содержит в своём пред.

И длины отрезков стремятся к 0 при n стремящемся к ∞

an-bn→0 при n→∞

Аксиома— всякая стягив.последов. вложенных отрезков имеет хотябы одну общую всем точку.

Теор.-всякая стягив. последов. Вложенных отрезков имеет единственную общую всем им точку. Док-во по аксиоме от противного.

Вещественные числа | это… Что такое Вещественные числа?

Веще́ственные, или действи́тельные^[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.

Множество вещественных чисел обозначается (Unicode: ℝ) и часто называется вещественной прямой.

Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.

Содержание

1 Примеры
2 Определения
- 2. 1 Аксиоматическое определение
  - 2.1.1 Примечания
- 2.2 Пополнение рациональных чисел
- 2.3 Дедекиндовы сечения
- 2.4 Бесконечные десятичные дроби
3 Счетность множества
4 Примечания
5 Ссылки
6 См. также

Примеры

Рациональные числа — 32, 36/29.
Иррациональные числа — π, .

Определения

Существует несколько стандартных путей определения вещественных чисел:

Аксиоматическое определение

См. основную статью Аксиоматика вещественных чисел.

Множество вещественных чисел можно определить как топологически полное, упорядоченное поле, то есть поле с отношением , которое удовлетворяет следующим аксиомам:

Отношение является отношением линейного порядка:
- Для любых или ;
- Если и , то a = b для любых ;
- Если и , то для любых ;
Порядок согласован со структурой поля:
- Если , то для любых ;
- Если и , то .
Порядок на удовлетворяет условию полноты:
- Пусть — непустые подмножества, такие что для любых и , тогда существует такое, что для любых и .

Примечания

Из свойства 3 следует, что у любого непустого ограниченного сверху множества (то есть такого, что для всех x из A все для некоторого ) существует точная верхняя грань (минимальная из всех), то есть число такое, что

Для всех x из A все
Если свойству (1) удовлетворяет также число , то .

Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля .

Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.

)

Пополнение рациональных чисел

Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике .

Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {r_i}. На таких последовательностях можно естественным образом ввести арифметические операции: {r_i} + {q_i} = {r_i + q_i} и .

Две такие последовательности и считаются эквивалентными , если при .

Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.

Дедекиндовы сечения

См. основную статью Дедекиндово сечение.

Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества A и B такие, что:

для любых и ;
B не имеет минимального элемента.

Множество вещественных чисел определяется как множество дедекиндовых сечений.

На них возможно продолжить операции сложения и умножения.

Например, вещественному числу соответствует дедекиндово сечение, определяемое или и и x² > 2}. Интуитивно, можно представить себе, что для того чтобы определить мы рассекли множество на две части: все числа, что левее и все числа, что правее ; соотвеетственно, равно точной нижней грани множества B.

Бесконечные десятичные дроби

Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.

Бесконечной десятичной дробью (со знаком) называется последовательность вида , где d_i являются десятичными цифрами, то есть .

Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где , либо если это «нулевые» последовательности (все

d_i равны 0), отличающиеся только знаком.

Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.

Значение десятичной дроби формально задаётся суммой ряда .

Счетность множества

TODO:

Примечания

↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.

Ссылки

Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.

См. также

Комплексные числа

Числа

натуральные | целые | рациональные |

R Номера

❮ Предыдущий Далее ❯

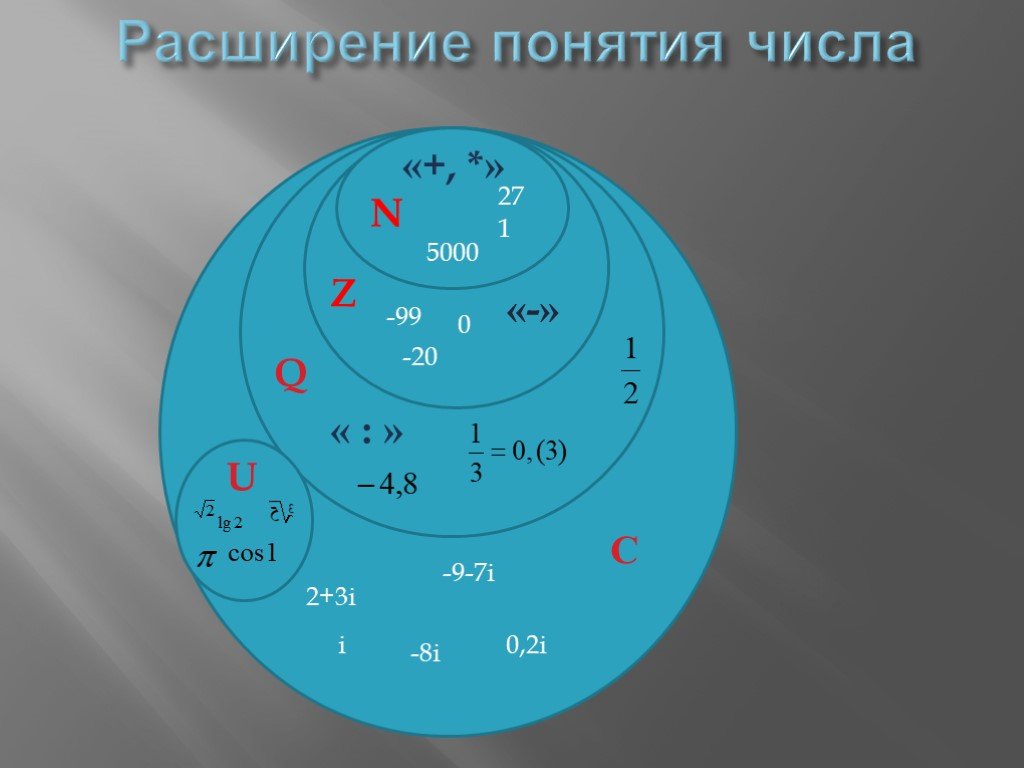
Числа

В R есть три типа чисел:

числовой
целое число
комплекс

Переменные числовых типов создаются при присвоении им значения:

Пример

x <- 10. 5   # числовое
y <- 10L    # целое число
z <- 1i     # комплексное

числовое

A числовой тип данных является наиболее распространенным типом данных. в R и содержит любое число с десятичным знаком или без него, например: 10,5, 55, 787:

Пример

x <- 10.5
y <- 55

# Вывести значения x и y
x
y

# Выведите имя класса x и y
class(x)
class(y)

Попробуйте сами »

Integer

Целые числа представляют собой числовые данные без десятичных знаков. Это используется, когда вы уверены что вы никогда не создадите переменную, которая должна содержать десятичные дроби. Чтобы создать целое число переменная, вы должны использовать букву L после целочисленного значения:

Пример

x <- 1000L
y <- 55L

# Вывести значения x и y
x
y

# Вывести имя класса x и y
class(x)
class(y)

Попробуйте сами »

Комплекс

Комплекс число записывается с « i » в качестве мнимой части:

Пример

х <- 3+5i
y <- 5i

# Вывести значения x и y
x
y

# Вывести имя класса x и y
class(x)
class(y)

Попробуйте сами »

Вы можете преобразовать один тип в другой с помощью следующих функций:

as. numeric()
as.integer()
as.complex()

Пример

x <- 1L # целое число
y <- 2 # числовое значение

# преобразовать целое число в numeric:
a <- as.numeric(x)

# преобразовать числовое значение в целое:
b <- as.integer(y)

# вывести значения x и y
x
y

# вывести имя класса a и b
class(a)
class(b)

Попробуйте сами »

❮ Предыдущий Следующий ❯

ВЫБОР ЦВЕТА

Лучшие учебники

Учебное пособие по HTML
Учебное пособие по CSS
Учебное пособие по JavaScript
How To Tutorial
SQL Tutorial
Python Tutorial
W3.CSS Tutorial
Bootstrap Tutorial
PHP Tutorial
Java Tutorial
C++ Tutorial
jQuery Tutorial

Top References

HTML Reference
CSS Reference
JavaScript Reference
SQL Reference
Python Reference
W3.

CSS Reference
Bootstrap Reference
PHP Reference
HTML Colors
Java Reference
Angular Reference
jQuery Reference

Лучшие примеры

Примеры HTML
Примеры CSS
Примеры JavaScript
Примеры инструкций
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery

| О

W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения. Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования, куки-файлы и политика конфиденциальности.

Числа R

В этом уроке вы подробно узнаете о типах чисел в R с помощью примеров.

Числа в R можно разделить на 3 разные категории:

Числовые : Представляет как целые числа, так и числа с плавающей запятой. Например, 123, 32,43 и т. д.
Целое число: Представляет только целые числа и обозначается цифрой 9.0011 л . Например, 23л, 39л и т.д.
Комплекс : Представляет комплексные числа с мнимыми частями. Мнимые части обозначаются и . Например, 2+3i, 5i и т. д.

Числовой тип данных

Числовой тип данных является наиболее часто используемым типом данных в R. Это тип данных по умолчанию при объявлении переменной с числами.

Вы можете хранить числа любого типа (с десятичными знаками или без них) в переменной с числовой тип данных . Например,

 # десятичная переменная
  my_decimal <- 123,45 
печать (класс (my_decimal))
# переменная без десятичной точки
  мой_номер <- 34 
печать (класс (мой_номер))

Вывод

  [1] "числовой"
[1] "numeric"

Здесь обе переменные my_decimal и my_number имеют тип numeric .

Целочисленный тип данных

Целые числа — это тип числовых данных, которые могут принимать значения без десятичных знаков. Это в основном используется, когда вы уверены, что переменная не может иметь никаких десятичных значений в будущем.

Чтобы создать целочисленную переменную , необходимо использовать суффикс L в конце значения. Например,

  my_integer <- 123L 
# вывести значение my_integer
печать (мое_целое число)
# вывести тип данных my_integer
печать (класс (my_integer))

Вывод

  [1] 123
[1] "integer"

Здесь переменная my_integer содержит значение 123L . Суффикс L в конце значения указывает, что my_integer имеет тип integer .

Сложный тип данных

В R переменные со сложными типами данных содержат значения с мнимой частью. Это можно указать, используя i в качестве суффикса. Например,

 # переменная только с мнимой частью
  z1 <- 5i 
печать (z1)
печать (класс (z1))
# переменная с реальной и мнимой частями
  z2 <- 3 + 3i 
печать (z2)
печать (класс (z2))

Выход

  [1] 0+5i
[1] «сложный»
[1] 3+3i
[1] "complex"

Здесь переменные z1 и z2 объявлены как комплексные типы данных с мнимой частью, обозначенной суффиксом i .

Часто задаваемые вопросы

В R мы используем функцию as.numeric() для преобразования любого числа в числовое значение . Например,

 # целочисленная переменная
а <- 4л
печать (класс (а))
# комплексная переменная
б <- 1 + 2i
печать (класс (б))
  # преобразовать целое число в числовое
x <- as.numeric(a) 
печать (класс (х))
  # преобразовать из комплексного в числовой
у <- as.numeric(b) 
print(класс(y))

Вывод

  [1] "целое число"
[1] «сложный»
[1] "числовой"
[1] "числовой"
Предупреждающее сообщение:
мнимые части отбрасываются при приведении

Здесь вы можете видеть, что при преобразовании сложного числа в числовое значение мнимые части отбрасываются.

1. Множество действительных чисел. Основные структуры множества r.

Вещественные числа | это… Что такое Вещественные числа?

Содержание

Примеры

Определения

Аксиоматическое определение

Примечания

Пополнение рациональных чисел

Дедекиндовы сечения

Бесконечные десятичные дроби

Счетность множества

Примечания

Ссылки

См. также

R Номера

Числа

Пример

числовое

Пример

Integer

Пример

Комплекс

Пример

Пример

ВЫБОР ЦВЕТА

Лучшие учебники

Top References

Лучшие примеры

| О

Числа R

Числовой тип данных

Целочисленный тип данных

Сложный тип данных

Часто задаваемые вопросы

Добавить комментарий Отменить ответ