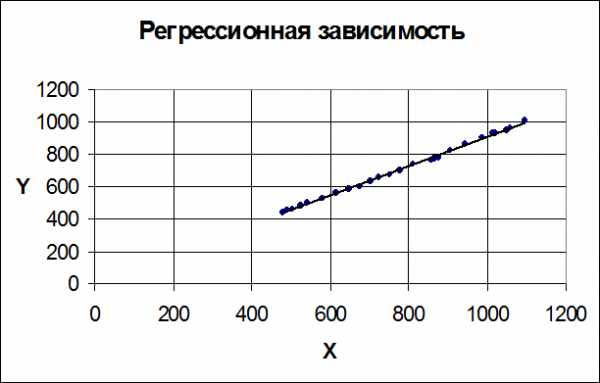
Классический метод наименьших квадратов
Данный курсовой проект включает в себя информацию о методе наименьших квадратов и его разновидностях. В работе приведена информация по классическому методу наименьших квадратов, подробно описан взвешенный МНК, дана краткая информация о двухшаговом и трёхшаговым методах наименьших квадратов.
При анализе различных источников информации (смотри список литературы) предпочтение отдано работам, описывающим не просто математический и статистический базисы исследуемых методов. В работе сделан акцент на возможность практического использования различных статистико-математических методик главным образом в области экономических и финансовых исследований.
Парная линейная регрессия. Метод наименьших квадратов
Рис.1
На рисунке изображены три ситуации:
• на графике (а) взаимосвязь х и у близка к линейной; прямая линия (1) здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий;
• на графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией (2), и какую бы мы ни провели прямую линию (например, 1), отклонения точек наблюдений от нее будут существенными и неслучайными;
• на графике (с) явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, прямые линии 1 и 2, проведенные через «центр» «облака» точек наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Если имеется некоторое «облако» точек наблюдений, через него всегда можно попытаться провести такую прямую линию, которая является наилучшей в определенном смысле среди всех прямых линий, то есть «ближайшей» к точкам наблюдений по их совокупности. Для этого мы вначале должны определить понятие близости прямой к некоторому множеству точек на плоскости; меры такой близости могут быть различными. Однако любая разумная мера должна быть, очевидно, связана с расстояниями от точек наблюдений до рассматриваемой прямой линии (задаваемой уравнением у= а + bх).
Обычно в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной у и теоретических, рассчитанных по уравнению регрессии значений (а + bхi):
Q = Sei2 =S (yi-(a+bxi))2® min (1)
считается, что у и х — известные данные наблюдений, а и b — неизвестные параметры линии регрессии. Поскольку функция Q непрерывна, выпукла и ограничена снизу нулем, она имеет минимум. Для соответствующих точке этого минимума значений а и b могут быть найдены простые и удобные формулы (они будут приведены ниже). Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, называется Методом наименьших квадратов (МНК), или Least Squares Method (LS).
«Наилучшая» по МНК прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y=f(х) является, например, квадратичной (как на рисунке 1(b)), то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется «наилучшая». Если величины х и у вообще не связаны (рис. 1 (с)), мы также всегда сможем найти «наилучшую» линейную функцию у = а+bх для данной совокупности наблюдений, но в этом случае конкретные значения а и Ь определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности. Возможно, на рис. 1(с) прямая 1 является наилучшей среди всех прямых линий (в смысле минимального значения функции Q), но любая другая прямая, проходящая через центральную точку «облака» (например, линия 2), ненамного в этом смысле хуже, чем прямая 1, и может стать наилучшей в результате небольшого изменения выборки.
Рассмотрим теперь задачу оценки коэффициентов парной линейной регрессии более формально. Предположим, что связь между х и .у линейна: у = a+bх. Здесь имеется в виду связь между всеми в
mirznanii.com
Метод наименьших квадратов.
Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития). Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей):
(9.1)
где — квадратичное отклонение между наблюдаемой фактической величиной
и соответствующей ей расчетной величиной тренда,
— фактическое (наблюдаемое) значение изучаемого явления,
— расчетное значение модели тренда,
— число наблюдений за изучаемым явлением.
МНК самостоятельно применяется довольно редко. Как правило, чаще всего его используют лишь в качестве необходимого технического приема при корреляционных исследованиях. Следует помнить, что информационной основой МНК может быть только достоверный статистический ряд, причем число наблюдений не должно быть меньше 4-х, иначе, сглаживающие процедуры МНК могут потерять здравый смысл.
Инструментарий МНК сводится к следующим процедурам:
Первая процедура. Выясняется, существует ли вообще какая-либо тенденция изменения результативного признака при изменении выбранного фактора-аргумента, или другими словами, есть ли связь между « у» и «х».
Вторая процедура. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать эту тенденцию.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Пример. Допустим, мы имеем информацию о средней урожайности подсолнечника по исследуемому хозяйству (табл. 9.1).
Таблица 9.1
Номер наблюдения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Годы | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
Урожайность, ц/га | 14,2 | 15,6 | 17,5 | 14,5 | 15,3 | 17,0 | 16,6 | 17,5 | 15,0 | 17,7 |
Поскольку уровень технологии при производстве подсолнечника в нашей стране за последние 10 лет практически не изменился, значит, по всей видимости, колебания урожайности в анализируемый период очень сильно зависели от колебания погодно-климатических условий. Действительно ли это так?
Первая процедура МНК. Проверяется гипотеза о существовании тенденции изменения урожайности подсолнечника в зависимости от изменения погодно-климатических условий за анализируемые 10 лет.
В данном примере за «y» целесообразно принять урожайность подсолнечника, а за «x» – номер наблюдаемого года в анализируемом периоде. Проверку гипотезы о существовании какой-либо взаимосвязи между «x» и «y» можно выполнить двумя способами: вручную и при помощи компьютерных программ. Конечно, при наличии компьютерной техники данная проблема решается сама собой. Но, чтобы лучше понять инструментарий МНК целесообразно выполнить проверку гипотезы о существовании связи между «x» и «y» вручную, когда под рукой находятся только ручка и обыкновенный калькулятор. В таких случаях гипотезу о существовании тенденции лучше всего проверить визуальным способом по расположению графического изображения анализируемого ряда динамики — корреляционного поля:
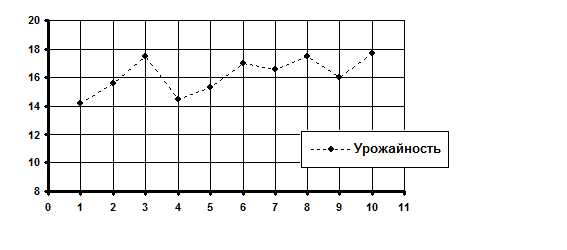
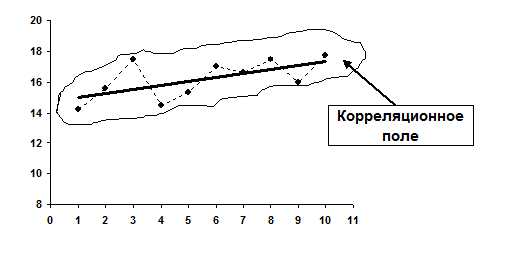
Корреляционное поле в нашем примере расположено вокруг медленно возрастающей линии. Это уже само по себе говорит о существовании определенной тенденции в изменении урожайности подсолнечника. Нельзя говорить о наличии какой-либо тенденции лишь тогда, когда корреляционное поле похоже на круг, окружность, строго вертикальное или строго горизонтальное облако, или же состоит из хаотично разбросанных точек. Во всех остальных случаях следует подтвердить гипотезу о существовании взаимосвязи между «x» и «y», и продолжить исследования.
Вторая процедура МНК. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать тенденцию изменения урожайности подсолнечника за анализируемый период.
При наличии компьютерной техники подбор оптимального тренда происходит автоматически. При «ручной» обработке выбор оптимальной функции осуществляется, как правило, визуальным способом – по расположению корреляционного поля. То есть, по виду графика подбирается уравнение линии, которая лучше всего подходит к эмпирическому тренду (к фактической траектории).
Как известно, в природе существует огромное разнообразие функциональных зависимостей, поэтому визуальным способом проанализировать даже незначительную их часть — крайне затруднительно. К счастью, в реальной экономической практике большинство взаимосвязей достаточно точно могут быть описаны или параболой, или гиперболой, или же прямой линией. В связи с этим, при «ручном» варианте подбора лучшей функции, можно ограничиться только этими тремя моделями.
Прямая: |
| Гипербола: |
|
Парабола второго порядка: :
Нетрудно заметить, что в нашем примере лучше всего тенденцию изменения урожайности подсолнечника за анализируемые 10 лет характеризует прямая линия, поэтому уравнением регрессии будет уравнение прямой.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Нахождение значений параметров уравнения регрессии, в нашем случае параметров и , является сердцевиной МНК. Данный процесс сводится к решению системы нормальных уравнений.
(9.2)
Эта система уравнений довольно легко решается методом Гаусса. Напомним, что в результате решения, в нашем примере, находятся значения параметров и . Таким образом, найденное уравнение регрессии будет иметь следующий вид:
В линейном уравнении параметр – коэффициент регрессии указывает, на сколько единиц в среднем изменится с изменением на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи – величина положительная, а при обратном – отрицательная. Параметр – свободный член уравнения регрессии, то есть это значениепри . Если не получает нулевых значений, этот параметр имеет лишь расчетное назначение.
Приведем также системы нормальных уравнений для отыскивания параметров нелинейных уравнений.
Таблица 9.2
Форма связи | Уравнение связи | Система нормальных уравнений |
параболическая | ||
гиперболическая |
Следует помнить, что при изменении хотя бы одного значения входных данных (пары значенийили одного из них) все коэффициенты изменят в общем случае свои значения, потому что они полностью определяются входными данными. Поэтому при повторной аппроксимации с несколькими измененными данными будет получена другая аппроксимирующая функция с другими коэффициентами.
www.ekonomstat.ru
Метод наименьших квадратов — Википедия
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés)[1]. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения[2]. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Работы А. А. Маркова в начале XX века позволили включить метод наименьших квадратов в теорию оценивания математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф.Дэвида, А. Эйткена, С. Рао было получено множество немаловажных результатов в этой области[3].
Видео по теме
Сущность метода наименьших квадратов
Пусть x{\displaystyle x} — набор n{\displaystyle n} неизвестных переменных (параметров), fi(x){\displaystyle f_{i}(x)}, i=1,…,m{\displaystyle i=1,\ldots ,m}, m>n{\displaystyle m>n} — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x{\displaystyle x}, чтобы значения этих функций были максимально близки к некоторым значениям yi{\displaystyle y_{i}}. По существу речь идет о «решении» переопределенной системы уравнений fi(x)=yi{\displaystyle f_{i}(x)=y_{i}}, i=1,…,m{\displaystyle i=1,\ldots ,m} в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей |fi(x)−yi|{\displaystyle |f_{i}(x)-y_{i}|}. Таким образом, сущность МНК может быть выражена следующим образом:
- ∑iei2=∑i(yi−fi(x))2→minx{\displaystyle \sum _{i}e_{i}^{2}=\sum _{i}(y_{i}-f_{i}(x))^{2}\rightarrow \min _{x}}.
В случае, если система уравнений имеет решение, то наименьшее значение суммы квадратов будет равно нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор x{\displaystyle x} в смысле максимальной близости векторов y{\displaystyle y} и f(x){\displaystyle f(x)} или максимальной близости вектора отклонений e{\displaystyle e} к нулю (близость понимается в смысле евклидова расстояния).
Пример — система линейных уравнений
В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений
- Ax=b{\displaystyle Ax=b},
где A{\displaystyle A} прямоугольная матрица размера m×n,m>n{\displaystyle m\times n,m>n} (т.е. число строк матрицы A больше количества искомых переменных).
Такая система уравнений в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора x{\displaystyle x}, чтобы минимизировать «расстояние» между векторами Ax{\displaystyle Ax} и b{\displaystyle b}. Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть (Ax−b)T(Ax−b)→minx{\displaystyle (Ax-b)^{T}(Ax-b)\rightarrow \min _{x}}. Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
- ATAx=ATb⇒x=(ATA)−1ATb{\displaystyle A^{T}Ax=A^{T}b\Rightarrow x=(A^{T}A)^{-1}A^{T}b}.
Используя оператор псевдоинверсии, решение можно переписать так:
- x=A+b{\displaystyle x=A^{+}b},
где A+{\displaystyle A^{+}} — псевдообратная матрица для A{\displaystyle A}.
Данную задачу также можно «решить» используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
МНК в регрессионном анализе (аппроксимация данных)
Пусть имеется n{\displaystyle n} значений некоторой переменной y{\displaystyle y} (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных x{\displaystyle x}. Задача заключается в том, чтобы взаимосвязь между y{\displaystyle y} и x{\displaystyle x} аппроксимировать некоторой функцией f(x,b){\displaystyle f(x,b)}, известной с точностью до некоторых неизвестных параметров b{\displaystyle b}, то есть фактически найти наилучшие значения параметров b{\displaystyle b}, максимально приближающие значения f(x,b){\displaystyle f(x,b)} к фактическим значениям y{\displaystyle y}. Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно b{\displaystyle b}:
f(xt,b)=yt,t=1,…,n{\displaystyle f(x_{t},b)=y_{t},t=1,\ldots ,n}.
В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными
yt=f(xt,b)+εt{\displaystyle y_{t}=f(x_{t},b)+\varepsilon _{t}},
где εt{\displaystyle \varepsilon _{t}} — так называемые случайные ошибки модели.
Соответственно, отклонения наблюдаемых значений y{\displaystyle y} от модельных f(x,b){\displaystyle f(x,b)} предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b{\displaystyle b}, при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) et{\displaystyle e_{t}} будет минимальной:
- b^OLS=argminbRSS(b){\displaystyle {\hat {b}}_{OLS}=\arg \min _{b}RSS(b)},
где RSS{\displaystyle RSS} — англ. Residual Sum of Squares[4] определяется как:
- RSS(b)=eTe=∑t=1net2=∑t=1n(yt−f(xt,b))2{\displaystyle RSS(b)=e^{T}e=\sum _{t=1}^{n}e_{t}^{2}=\sum _{t=1}^{n}(y_{t}-f(x_{t},b))^{2}}.
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции RSS(b){\displaystyle RSS(b)}, продифференцировав её по неизвестным параметрам b{\displaystyle b}, приравняв производные к нулю и решив полученную систему уравнений:
- ∑t=1n(yt−f(xt,b))∂f(xt,b)∂b=0{\displaystyle \sum _{t=1}^{n}(y_{t}-f(x_{t},b)){\frac {\partial f(x_{t},b)}{\partial b}}=0}.
МНК в случае линейной регрессии
Пусть регрессионная зависимость является линейной:
- yt=∑j=1kbjxtj+ε=xtTb+εt{\displaystyle y_{t}=\sum _{j=1}^{k}b_{j}x_{tj}+\varepsilon =x_{t}^{T}b+\varepsilon _{t}}.
Пусть y — вектор-столбец наблюдений объясняемой переменной, а X{\displaystyle X} — это (n×k){\displaystyle ({n\times k})}-матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
- y=Xb+ε{\displaystyle y=Xb+\varepsilon }.
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
- y^=Xb,e=y−y^=y−Xb{\displaystyle {\hat {y}}=Xb,\quad e=y-{\hat {y}}=y-Xb}.
соответственно сумма квадратов остатков регрессии будет равна
- RSS=eTe=(y−Xb)T(y−Xb){\displaystyle RSS=e^{T}e=(y-Xb)^{T}(y-Xb)}.
Дифференцируя эту функцию по вектору параметров b{\displaystyle b} и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- (XTX)b=XTy{\displaystyle (X^{T}X)b=X^{T}y}.
В расшифрованной матричной форме эта система уравнений выглядит следующим образом:
(∑xt12∑xt1xt2∑xt1xt3…∑xt1xtk∑xt2xt1∑xt22∑xt2xt3…∑xt2xtk∑xt3xt1∑xt3xt2∑xt32…∑xt3xtk⋮⋮⋮⋱⋮∑xtkxt1∑xtkxt2∑xtkxt3…∑xtk2)(b1b2b3⋮bk)=(∑xt1yt∑xt2yt∑xt3yt⋮∑xtkyt),{\displaystyle {\begin{pmatrix}\sum x_{t1}^{2}&\sum x_{t1}x_{t2}&\sum x_{t1}x_{t3}&\ldots &\sum x_{t1}x_{tk}\\\sum x_{t2}x_{t1}&\sum x_{t2}^{2}&\sum x_{t2}x_{t3}&\ldots &\sum x_{t2}x_{tk}\\\sum x_{t3}x_{t1}&\sum x_{t3}x_{t2}&\sum x_{t3}^{2}&\ldots &\sum x_{t3}x_{tk}\\\vdots &\vdots &\vdots &\ddots &\vdots \\\sum x_{tk}x_{t1}&\sum x_{tk}x_{t2}&\sum x_{tk}x_{t3}&\ldots &\sum x_{tk}^{2}\\\end{pmatrix}}{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\\\vdots \\b_{k}\\\end{pmatrix}}={\begin{pmatrix}\sum x_{t1}y_{t}\\\sum x_{t2}y_{t}\\\sum x_{t3}y_{t}\\\vdots \\\sum x_{tk}y_{t}\\\end{pmatrix}},} где все суммы берутся по всем допустимым значениям t{\displaystyle t}.
Если в модель включена константа (как обычно), то xt1=1{\displaystyle x_{t1}=1} при всех t{\displaystyle t}, поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений n{\displaystyle n}, а в остальных элементах первой строки и первого столбца — просто суммы значений переменных: ∑xtj{\displaystyle \sum x_{tj}} и первый элемент правой части системы — ∑yt{\displaystyle \sum y_{t}}.
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
- b^OLS=(XTX)−1XTy=(1nXTX)−11nXTy=Vx−1Cxy{\displaystyle {\hat {b}}_{OLS}=(X^{T}X)^{-1}X^{T}y=\left({\frac {1}{n}}X^{T}X\right)^{-1}{\frac {1}{n}}X^{T}y=V_{x}^{-1}C_{xy}}.
Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
- y¯=b1^+∑j=2kb^jx¯j{\displaystyle {\bar {y}}={\hat {b_{1}}}+\sum _{j=2}^{k}{\hat {b}}_{j}{\bar {x}}_{j}}.
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Простейшие частные случаи
В случае парной линейной регрессии yt=a+bxt+εt{\displaystyle y_{t}=a+bx_{t}+\varepsilon _{t}}, когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:
- (1x¯x¯x2¯)(ab)=(y¯xy¯){\displaystyle {\begin{pmatrix}1&{\bar {x}}\\{\bar {x}}&{\bar {x^{2}}}\\\end{pmatrix}}{\begin{pmatrix}a\\b\\\end{pmatrix}}={\begin{pmatrix}{\bar {y}}\\{\overline {xy}}\\\end{pmatrix}}}.
Отсюда несложно найти оценки коэффициентов:
- {b^=Cov(x,y)Var(x)=xy¯−x¯y¯x2¯−x¯2,a^=y¯−bx¯.{\displaystyle {\begin{cases}{\hat {b}}={\frac {\mathop {\textrm {Cov}} (x,y)}{\mathop {\textrm {Var}} (x)}}={\frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\overline {x}}^{2}}},\\{\hat {a}}={\bar {y}}-b{\bar {x}}.\end{cases}}}
Несмотря на то что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа a{\displaystyle a} должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид U=I⋅R{\displaystyle U=I\cdot R}; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели y=bx{\displaystyle y=bx}. В этом случае вместо системы уравнений имеем единственное уравнение
(∑xt2)b=∑xtyt{\displaystyle \left(\sum x_{t}^{2}\right)b=\sum x_{t}y_{t}}.
Следовательно, формула оценки единственного коэффициента имеет вид
b^=∑t=1nxtyt∑t=1nxt2=xy¯x2¯{\displaystyle {\hat {b}}={\frac {\sum _{t=1}^{n}x_{t}y_{t}}{\sum _{t=1}^{n}x_{t}^{2}}}={\frac {\overline {xy}}{\overline {x^{2}}}}}.
Случай полиномиальной модели
Если данные аппроксимируются полиномиальной функцией регрессии одной переменной f(x)=b0+∑i=1kbixi{\displaystyle f(x)=b_{0}+\sum \limits _{i=1}^{k}b_{i}x^{i}}, то, воспринимая степени xi{\displaystyle x^{i}} как независимые факторы для каждого i{\displaystyle i} можно оценить параметры модели исходя из общей формулы оценки параметров линейной модели. Для этого в общую формулу достаточно учесть, что при такой интерпретации xtixtj=xtixtj=xti+j{\displaystyle x_{ti}x_{tj}=x_{t}^{i}x_{t}^{j}=x_{t}^{i+j}} и xtjyt=xtjyt{\displaystyle x_{tj}y_{t}=x_{t}^{j}y_{t}}. Следовательно, матричные уравнения в данном случае примут вид:
(n∑nxt…∑nxtk∑nxt∑nxt2…∑nxtk+1⋮⋮⋱⋮∑nxtk∑nxtk+1…∑nxt2k)[b0b1⋮bk]=[∑nyt∑nxtyt⋮∑nxtkyt].{\displaystyle {\begin{pmatrix}n&\sum \limits _{n}x_{t}&\ldots &\sum \limits _{n}x_{t}^{k}\\\sum \limits _{n}x_{t}&\sum \limits _{n}x_{t}^{2}&\ldots &\sum \limits _{n}x_{t}^{k+1}\\\vdots &\vdots &\ddots &\vdots \\\sum \limits _{n}x_{t}^{k}&\sum \limits _{n}x_{t}^{k+1}&\ldots &\sum \limits _{n}x_{t}^{2k}\end{pmatrix}}{\begin{bmatrix}b_{0}\\b_{1}\\\vdots \\b_{k}\end{bmatrix}}={\begin{bmatrix}\sum \limits _{n}y_{t}\\\sum \limits _{n}x_{t}y_{t}\\\vdots \\\sum \limits _{n}x_{t}^{k}y_{t}\end{bmatrix}}.}
Статистические свойства МНК-оценок
В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
- математическое ожидание случайных ошибок равно нулю, и
- факторы и случайные ошибки — независимые случайные величины.
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы Vx{\displaystyle V_{x}} к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
- Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности): V(εt)=σ2=const{\displaystyle V(\varepsilon _{t})=\sigma ^{2}=const}.
- Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой cov(εi,εj)=0∀1≤i<j≤n{\displaystyle cov(\varepsilon _{i},\varepsilon _{j})=0\quad \forall 1\leq i<j\leq n}.
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок V(ε)=σ2I{\displaystyle V(\varepsilon )=\sigma ^{2}I}.
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbiased Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
V(b^OLS)=σ2(XTX)−1{\displaystyle V({\hat {b}}_{OLS})=\sigma ^{2}(X^{T}X)^{-1}}.
Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
s2=RSS/(n−k){\displaystyle s^{2}=RSS/(n-k)}.
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.
Обобщенный МНК
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков eTWe{\displaystyle e^{T}We}, где W{\displaystyle W} — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно, для симметрических матриц (или операторов) существует разложение W=PTP{\displaystyle W=P^{T}P}. Следовательно, указанный функционал можно представить следующим образом eTPTPe=(Pe)TPe=e∗Te∗{\displaystyle e^{T}P^{T}Pe=(Pe)^{T}Pe=e_{*}^{T}e_{*}}, то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагает
wiki2.red
|
Допустим, что имеется четыре наблюдения, для x и y, представленные на рис. 1, и поставлена задача, – определить значения a и b в управлении (1). В качестве грубой аппроксимации можно сделать это, отложив четыре точки P и построив прямую, в наибольшей степени соответствующую этим точкам. Это сделано на рис. 2. Отрезок, отсекаемый на прямой по оси y, представляет собой оценку a и обозначен а, а угловой коэффициент прямой представляет собой оценку b и обозначен b. Построение линии регрессии на глаз является достаточно субъективным. Более того, это просто невозможно, если переменная y зависит не от одной, а от двух или более независимых переменных. Возникает вопрос о существовании способа достаточно точной оценки a и b алгебраическим путем. Первым шагом является определение остатка для каждого наблюдения. За исключением случаев чистого совпадения, построенная линия регрессии не пройдет точно ни через одну точку наблюдения. Например, на рис. 3 при x=x1 соответствующей ему точкой на линии регрессии будет R1 со значением y, которое обозначено вместо фактически наблюдаемого значения y1. Величина описывается как расчетное значение y, соответствующее x1. Разность между фактическим и расчетным значениями (y1— ), определяемая отрезком P1R1,описывается как остаток в первом наблюдении. Обозначим его e1. Соответственно, для других наблюдений остатки будут обозначены как e2, e3 и e4.
Рис. 2. Прямая, построенная по точкам
Рис. 3. Построенная по точкам линия регрессии, показывающая остатки. Очевидно, что требуется построить линию регрессии таким образом, чтобы эти остатки были минимальными. Очевидно также, что линия, строго соответствующая одним наблюдениям, не будет соответствовать другим, и наоборот. Необходимо выбрать какой-то критерий подбора, который будет одновременно учитывать величину всех остатков. Один из способов решения поставленной проблемы состоит в минимизации суммы квадратов остатков S. Для рис. 3 верно такое соотношение: S=e12+e22+e32+e42 (2) Величина S будет зависеть от выбора a и b, так как они определяют положение линии регрессии. В соответствие с этим критерием, чем меньше S, тем строже соответствие. Если S=0, то получено абсолютно точное соответствие, так как это означает, что все остатки равны нулю. В этом случае линия регрессии будет проходить через все точки, однако, вообще говоря, это не возможно из-за наличия случайного члена. При выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки a и b. Детальное рассмотрение остатков. После построения линии регрессии рассмотрим более детально общее выражение для остатка в каждом наблюдении.
Рис. 4. На рис. 4 линия регрессии =a+bx (3) построена по выборке наблюдений. Для того чтобы не загромождать график, показано только одно такое наблюдение: наблюдение i, представленное точкой P с координатами (xi, yi). Когда x=xi линия регрессии предсказывает значение y= , что соответствует точке R на графике, где =a+bxi (4) Используя условные обозначения, принятые на рис. 4, это уравнение можно переписать следующим образом: RT=ST+RS, (5) так как отрезок ST равен a,а отрезок RS равен bxi. Остаток PR – это разность между PT и RT: PR= PT- RT= PT- ST — RS (6) Используя обычную математическую запись, представим формулу (6) в следующем виде: ei=yi— = yi-a-bxi(7) Если в примере, показанном на графике, выбрать несколько большее значение a или несколько большее значение b, то прямая прошла бы ближе к P, и остаток ei был бы меньше. Однако это повлияло бы на остатки всех других наблюдений, и это необходимо учитывать. Минимизируя сумму квадратов остатков, необходимо найти некоторое равновесие между ними. Регрессия по методу наименьших квадратов с одной Независимой переменой. Рассмотрим случай, когда имеется n наблюдений двух переменных x и y. Предположим, что y зависит от x, и надо подобрать уравнение =a+bx (8) расчетное значение зависимой переменной и остаток ei для наблюдения i заданы уравнениями (4) и (7). Требуется выбрать a и b,чтобы минимизировать величину S: S=Sei2=e12+…+en2(9) Заметим, что величина S минимальна, когда (10) и (11) Варианты выражения для b Так как (12) и (13) можно получить следующие значения для b: (14) . (15) Далее будет использоваться первоначальное определение . Вывод выражений для a и b Осуществим вывод выражений для a и b в соответствии с той же процедурой, которая использовалась ранее, и сравним общий вариант с примерами на каждом этапе. Выразим квадрат i-го остатка через a и b и наблюдения значений через x и y: ei2=(yi— )2=(yi-a-bxi)2=yi2+a2+b2xi2-2ayi+2abxi-2bxiyi. (16) Суммируя по всем n наблюдениям, запишем S в виде: S=Syi2+na2+b2Sxi2-2aSyi+2abSxi-2bSxiyi. (17) Заметим, что данное выражение для S является квадратичной формой по a и b, и ее коэффициенты определяются выборочными значениями x и y. Можно влиять на величину S, только задавая значения a и b. Значения x и y, которые определяют положение точек на диаграмме расстояния, уже не могут быть изменены после того, как взята определенная выборка. Условия первого порядка для минимума, то есть и , принимают вид: . (18) . (19) Эти уравнения известны как нормальные уравнения для коэффициентов регрессии. Уравнение (18) позволяет выразить a через и пока неизвестное b. Подставим вместо Sxi, получим: . (20) Следовательно, . (21) Подставив выражение для a в уравнение (2.33) и помня, что Sxi равно , имеем: (22) После деления на 2n и перегруппировки получим: (23) С учетом формул (12) и (13) это выражение можно переписать в следующем виде: (24) и, таким, мы получим уравнение (10). Найдя из этого выражения b, выразим затем a из уравнения (11). Качество оценки: коэффициент R2 Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y. В любой данной выборке y оказывается сравнительно низким в одних наблюдениях и сравнительно высоким в других. Разброс значений y в любой выборке можно суммарно описать с помощью выборочной дисперсии Var(y). После построения уравнения регрессии можно разбить значение yi в каждом наблюдении на две составляющих ‑ и ei: (25) Величина ‑ расчетное значение y в наблюдении i. Остаток ei есть расхождение между фактическим и спрогнозированным значениями величины y. Используя (25), разложим дисперсию y: (26) Так как должна быть равна нулю, получим: (27) Согласно (27), коэффициент детерминации , (28) что равносильно . (29) Максимальное значение коэффициента R2 равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что для всех i и все остатки равны нулю. Тогда , Var(e)=0 и R2=1. Если в выборке отсутствует видимая связь между y и x, то коэффициент R2 будет близок к нулю. При прочих равных условиях желательно, чтобы коэффициент R2 был как можно больше. Альтернативное представление коэффициента R2 Очевидно, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений y, и наоборот. Покажем, что R2 фактически равен квадрату такого коэффициента корреляции между y и , который обозначается : (30) Экспериментальная часть В качестве примера рассмотрим данные из расчетной работы № 1. Рассчитаем коэффициенты регрессии с одной независимой переменной по методу наименьших квадратов. Результаты расчета приведены в таблице1. Таблица 1.
Суммируя по всем n наблюдениям, запишем S в виде: S = 13307716,16 + 25a2 + b2 ×380281200,64 — 2a×17694,2 +2ab×19500,8 — 2b×14664884,21 Условия первого порядка для минимума принимают вид: = 50×a — 35388,4 + 39001,6×b = 0; = 760562401,28×b+39001,6×a-29329768,42 = 0 Решив полученную систему нормальных уравнений для коэффициентов регрессии, найдем: а = 0,19378; b = 0,907109. Оценим коэффициенты регрессии с использованием формул для расчета ковариации двух случайных величин и выборочной дисперсии. Результаты расчета приведены в таблице 2. Таблица 2
Так как Cov (х, y) = 34513,68 и Var(x) = 38047,99, то
Расмотрим интерпретацию уравнения регрессии. Истинная модель описывается выражением y =a+bx+u. Оценена регрессия = 0,19378+0,907109×x. Полученный результат можно истолковать следующим образом. Коэффициент при x показывает, что если x увеличивается на 1 единицу, то y возрастает на 0,907109 единиц. Предположив, что x и y измеряются в тысячах долларов, коэффициент наклона показывает, что если личный располагаемый доход увеличивается на 1 тыс. долл., то совокупные личные расходы возрастают на 0,907109 тыс. долл. Постоянная в уравнении показывает прогнозируемый уровень y, когда x=0. Т.о. в случае, когда личный располагаемый доход равен нулю, совокупные личные расходы равны 0,19378 тыс. долл. Однако подобная буквальная интерпретация может привести к неверным результатам, т.к. x=0 находится достаточно далеко от выборочных значений x. Экстраполяция влево может нарушить точность линии регрессии. Для полученной регрессионной зависимости проверим качество оценки с использованием коэффициента детерминации R2. Результаты расчетов приведены в табл.3.
Следовательно = = 0,99791454 = 0,998956726 Прокомментируем полученный результат. Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y. Для определения качества такой оценки служит коэффициент детерминации R2. Максимальное значение коэффициента R2 равно единице. Мы заинтересованы в таком выборе коэффициентов a и b, чтобы максимизировать R2. В нашем случае R2= 0,99791454, что близко максимальному значению, следовательно можно говорить о том, что в выборке присутствует видимая связь между y и x. Коэффициент корреляции ry,y=0,998956726, что также говорит о достаточно хорошем качестве выбранной модели. Задание на расчетную работу 1. Провести регрессию по методу наименьших квадратов: Ø Рассчитать и оценить коэффициенты регрессии (используя МНК и Cov(x,y) и Var(x)). Ø Построить регрессионную зависимость и дать экономическую интерпретацию. 2. Проверить качество оценки с использованием коэффициента детерминации, используя формулы Прокомментировать полученный результат При выполнении данной расчетной работы рекомендуется использовать пакет прикладных программ Microsoft Excel. Содержание отчета Отчет должен содержать: — титульный лист; — задание; — постановку задачи; — результаты выполнения задания; — выводы с экономической трактовкой. 5. Контрольные вопросы 1. Запишите простейшую модель (уравнение) регрессии. 2. В чем состоит регрессия по методу наименьших квадратов? 3. Объясните пример регрессии по методу наименьших квадратов с двумя наблюдениями. 4. Запишите нормальные уравнения для коэффициентов регрессии. 5. Назовите два этапа интерпретации уравнения регрессии и опишите их. 6. В чём состоит цель регрессионного анализа? 7. В каком случае значение коэффициента R2 равно единице?
Практическая работа №3 ОЦЕНКА КОЭФФИЦИЕНТОВ РЕГРЕССИИ МЕТОДОМ МОНТЕ-КАРЛО Цель практической работы Цель: освоение методики проверки метода наименьших квадратов методом Монте-Карло; оценивание точности прогнозируемых коэффициентов регрессии; вычисление для них доверительных интервалов. Рекомендуемые страницы: |
lektsia.com
Сущность метода наименьших квадратов — КиберПедия
ВВЕДЕНИЕ
Метод наименьших квадратов
Требование «наилучшего» согласования кривой и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от расчетных обращалась в минимум.
Метод наименьших квадратов был описан Лагранжем в 1806 г. в его труде Nouvelles methodes pour la determination des orbites des cometes.Этот математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Сущность метода наименьших квадратов
Пусть x — набор n неизвестных переменных (параметров),
f i ( x ), i = 1 , … , m, m > n — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x , чтобы значения этих функций были максимально близки к некоторым значениям yi. По существу речь идет о «решении» переопределенной системы уравнений
f i ( x ) = y i , i = 1 , … , m в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей
| f i ( x ) − y i | . Таким образом, сущность МНК может быть выражена на
рисунке 1.1.
Рисунок 1.1 – Сущность МНК
В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор x в смысле максимальной близости векторов y и f ( x ) или максимальной близости вектора отклонений e к нулю (близость понимается в смысле евклидова расстояния).
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Простейшие частные случаи
В случае парной линейной регрессии y t = a + b x t + ε t {\displaystyle y_{t}=a+bx_{t}+\varepsilon _{t}} , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:
( 1 x ¯ x ¯ x 2 ¯ ) ( a b ) = ( y ¯ x y ¯ ) {\displaystyle {\begin{pmatrix}1&{\bar {x}}\\{\bar {x}}&{\bar {x^{2}}}\\\end{pmatrix}}{\begin{pmatrix}a\\b\\\end{pmatrix}}={\begin{pmatrix}{\bar {y}}\\{\overline {xy}}\\\end{pmatrix}}}
Рисунок 2.1 – парная регрессия
Отсюда несложно найти оценки коэффициентов:
{ b ^ = Cov ( x , y ) Var ( x ) = x y ¯ − x ¯ y ¯ x 2 ¯ − x ¯ 2 , a ^ = y ¯ − b x ¯ . {\displaystyle {\begin{cases}{\hat {b}}={\frac {{\mathop {\textrm {Cov}}}(x,y)}{{\mathop {\textrm {Var}}}(x)}}={\frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\overline {x}}^{2}}},\\{\hat {a}}={\bar {y}}-b{\bar {x}}.\end{cases}}}
Рисунок 2.2 — оценки коэффициентовРР
Несмотря на то, что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа a {\displaystyle a} а должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид U = I ⋅ R {\displaystyle U=I\cdot R} U = I * R; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели y = b x {\displaystyle y=bx} y = bx. В этом случае вместо системы уравнений имеем единственное уравнение
( ∑ x t 2 ) b = ∑ x t y t {\displaystyle \left(\sum x_{t}^{2}\right)b=\sum x_{t}y_{t}}
Рисунок 2.3 – уравнение y = bx
Следовательно, формула оценки единственного коэффициента имеет вид
b ^ = ∑ t = 1 n x t y t ∑ t = 1 n x t 2 = x y ¯ x 2 ¯ {\displaystyle {\hat {b}}={\frac {\sum _{t=1}^{n}x_{t}y_{t}}{\sum _{t=1}^{n}x_{t}^{2}}}={\frac {\overline {xy}}{\overline {x^{2}}}}}
Рисунок 2.4 – формула для оценки 1 коэффициента
Основные сведения
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.
Среднеквадратическое отклонение:
s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n ( x i − x ¯ ) 2 ; {\displaystyle s={\sqrt {{\frac {n}{n-1}}\sigma ^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};}
· Примечание: Очень часто встречаются разночтения в названиях СКО (Среднеквадратического отклонения) и СТО (Стандартного отклонения) с их формулами. Например, в модуле numPy языка программирования Python функция std() описывается как «standart deviation», в то время как формула отражает СКО (деление на корень из выборки). В Excel же функция СТАНДОТКЛОН() другая (деление на корень из n-1).
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии) s {\displaystyle s} S:
σ = 1 n ∑ i = 1 n ( x i − x ¯ ) 2 . {\displaystyle \sigma ={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}
где σ 2 {\displaystyle \sigma ^{2}} — дисперсия; x i {\displaystyle x_{i}} — i-й элемент выборки; n {\displaystyle n} — объём выборки; x ¯ {\displaystyle {\bar {x}}} — среднее арифметическое выборки:
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + … + x n ) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
В соответствии с ГОСТ Р 8.736-2011 среднеквадратическое отклонение считается по второй формуле данного раздела. Пожалуйста, сверьте результаты.
ВВЕДЕНИЕ
Метод наименьших квадратов
Требование «наилучшего» согласования кривой и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от расчетных обращалась в минимум.
Метод наименьших квадратов был описан Лагранжем в 1806 г. в его труде Nouvelles methodes pour la determination des orbites des cometes.Этот математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Сущность метода наименьших квадратов
Пусть x — набор n неизвестных переменных (параметров),
f i ( x ), i = 1 , … , m, m > n — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x , чтобы значения этих функций были максимально близки к некоторым значениям yi. По существу речь идет о «решении» переопределенной системы уравнений
f i ( x ) = y i , i = 1 , … , m в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей
| f i ( x ) − y i | . Таким образом, сущность МНК может быть выражена на
рисунке 1.1.
Рисунок 1.1 – Сущность МНК
В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор x в смысле максимальной близости векторов y и f ( x ) или максимальной близости вектора отклонений e к нулю (близость понимается в смысле евклидова расстояния).
cyberpedia.su
Метод наименьших квадратов — это… Что такое Метод наименьших квадратов?
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.
Сущность МНК
Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x
где — вектор неизвестных параметров модели
- — случайная ошибка модели.
Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть — номер наблюдения (). Тогда — значения переменных в -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:
Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):
Величина остатков зависит от значений параметров b.
Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков (англ. Residual Sum of Squares) будет минимальной:
где:
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).
МНК в случае линейной модели
Пусть регрессионная зависимость является линейной:
Пусть y — вектор-столбец наблюдений объясняемой переменной, а — матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
соответственно сумма квадратов остатков регрессии будет равна
Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- .
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
Для аналитических целей оказывается полезным последнее представление этой формулы. Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Пример: простейшая (парная) регрессия
В случае парной линейной регрессии формулы расчета упрощаются (можно обойтись без матричной алгебры):
Свойства МНК-оценок
В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
- математическое ожидание случайных ошибок равно нулю, и
- факторы и случайные ошибки — независимые случайные величины.
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
- Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.
Обобщенный МНК
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков , где — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
Ковариационная матрица этих оценок соответственно будет равна
Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный МНК
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
Некоторые частные случаи применения МНК на практике
Аппроксимация линейной зависимости
Рассмотрим случай, когда в результате изучения зависимости некоторой скалярной величины от некоторой скалярной величины (Это может быть, например, зависимость напряжения от силы тока : , где — постоянная величина, сопротивление проводника) было проведено измерений этих величин, в результате которых были получены значения и соответствующие им значения . Данные измерений должны быть записаны в таблице.
Таблица. Результаты измерений.
Вопрос звучит так: какое значение коэффициента можно подобрать, чтобы наилучшим образом описать зависимость ? Согласно МНК это значение должно быть таким, чтобы сумма квадратов отклонений величин от величин
была минимальной
Сумма квадратов отклонений имеет один экстремум — минимум, что позволяет нам использовать эту формулу. Найдём из этой формулы значение коэффициента . Для этого преобразуем её левую часть следующим образом:
Далее идёт ряд математических преобразований:
Последняя формула позволяет нам найти значение коэффициента , что и требовалось в задаче.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés)[2]. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения[3]. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Альтернативное использование МНК
Идея метода наименьших квадратов может быть использована также в других случаях, не связанных напрямую с регрессионным анализом. Дело в том, что сумма квадратов является одной из наиболее распространенных мер близости для векторов (евклидова метрика в конечномерных пространствах).
Одно из применений — «решение» систем линейных уравнений, в которых число уравнений больше числа переменных
,
где матрица не квадратная, а прямоугольная размера .
Такая система уравнений, в общем случае не имеет решения (если ранг на самом деле больше числа переменных). Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
Используя оператор псевдоинверсии, решение можно переписать так:
- ,
где — псевдообратная матрица для .
Данную задачу также можно «решить» используя взвешенный МНК, когда разные уравнения системы получают разный вес из теоретических соображений.
Естественно, данный подход может быть использован и в случае нелинейных систем уравнений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
См. также
Примечания
Литература
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
- Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6
- Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
- Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003-2004. — 311 с. — ISBN 8-86225-458-7
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0
- Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3
- Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4
Ссылки
dic.academic.ru
Метод наименьших квадратов примеры решения задач: мнк
Программа МНК
Введите данные
Данные и аппроксимация y = a + b·x
i – номер экспериментальной точки;
xi – значение фиксированного параметра в точке i;
yi – значение измеряемого параметра в точке i;
ωi – вес измерения в точке i;
yi, расч. – разница между измеренным и вычисленным по регрессии значением y в точке i;
Sxi(xi) – оценка погрешности xi при измерении y в точке i.
Данные и аппроксимация y = k·x
| i | xi | yi | ωi | yi, расч. | Δyi | Sxi(xi) |
|---|
Кликните по графику,
чтобы добавить значения в таблицу
Инструкция пользователя онлайн-программы МНК.
В поле данных введите на каждой отдельной строке значения `x` и `y` в одной экспериментальной точке. Значения должны отделяться пробельным символом (пробелом или знаком табуляции).
Третьим значением может быть вес точки `w`. Если вес точки не указан, то он приравнивается единице. В подавляющем большинстве случаев веса экспериментальных точек неизвестны или не вычисляются, т.е. все экспериментальные данные считаются равнозначными. Иногда веса в исследуемом интервале значений совершенно точно не равнозначны и даже могут быть вычислены теоретически. Например, в спектрофотометрии веса можно вычислить по простым формулам, правда в основном этим все пренебрегают для уменьшения трудозатрат.
Данные можно вставить через буфер обмена из электронной таблицы офисных пакетов, например Excel из Майкрософт Офиса или Calc из Оупен Офиса. Для этого в электронной таблице выделите диапазон копируемых данных, скопируйте в буфер обмена и вставьте данные в поле данных на этой странице.
Для расчета по методу наименьших квадратов необходимо не менее двух точек для определения двух коэффициентов `b` – тангенса угла наклона прямой и `a` – значения, отсекаемого прямой на оси `y`.
Для оценки погрешности расчитываемых коэффициентов регресии нужно задать количество экспериментальных точек больше двух.
Метод наименьших квадратов (МНК).
Чем больше количество экспериментальных точек, тем более точна статистическая оценка коэффицинетов (за счет снижения коэффицинета Стьюдента) и тем более близка оценка к оценке генеральной выборки.
Получение значений в каждой экспериментальной точке часто сопряжено со значительными трудозатратами, поэтому часто проводят компромиссное число экспериментов, которые дает удобоваримую оценку и не привеодит к чрезмерным трудо затратам. Как правило число экспериментах точек для линейной МНК зависимости с двумя коэффицинетами выбирает в районе 5-7 точек.
Краткая теория метода наименьших квадратов для линейной зависимости
Допустим у нас имеется набор экспериментальных данных в виде пар значений [`y_i`, `x_i`], где `i` – номер одного эксперементального измерения от 1 до `n`; `y_i` – значение измеренной величины в точке `i`; `x_i` – значение задаваемого нами параметра в точке `i`.
В качестве примера можно рассмотреть действие закона Ома. Изменяя напряжение (разность потенциалов) между участками электрической цепи, мы замеряем величину тока, проходящего по этому участку. Физика нам дает зависимость, найденную экспериментально:
`I = U / R`,
где `I` – сила тока; `R` – сопротивление; `U` – напряжение.
В этом случае `y_i` у нас имеряемая величина тока, а `x_i` – значение напряжения.
В качестве другого примера рассмотрим поглощение света раствором вещества в растворе. Химия дает нам формулу:
`A = ε l C`,
где `A` – оптическая плотность раствора; `ε` – коэффициент пропускания растворенного вещества; `l` – длина пути при прохождении света через кювету с раствором; `C` – концентрация растворенного вещества.
В этом случае `y_i` у нас имеряемая величина отптической плотности `A`, а `x_i` – значение концентрации вещества, которое мы задаем.
Мы будем рассматривать случай, когда относительная погрешность в задании `x_i` значительно меньше, относительной погрешности измерения `y_i`. Так же мы будем предполагать, что все измеренные величины `y_i` случайные и нормально распределенные, т.е. подчиняются нормальному закону распределения.
В случае линейной зависимости `y` от `x`, мы можем написать теоретическую зависимость:
`y = a + b x`.
С геометрической точки зрения, коэффициент `b` обозначает тангенс угла наклона линии к оси `x`, а коэффициент `a` – значение `y` в точке пересечения линии с осью `y` (при `x = 0`).
Нахождение параметров линии регресии.
В эксперименте измеренные значения `y_i` не могут точно лечь на теоеретическую прямую из-за ошибок измерения, всегда присущих реальной жизни. Поэтому линейное уравнение, нужно представить системой уравнений:
`y_i = a + b x_i + ε_i` (1),
где `ε_i` – неизвестная ошибка измерения `y` в `i`-ом эксперименте.
Зависимость (1) так же называют регрессией, т.е. зависимостью двух величин друг от друга со статистической значимостью.
Задачей восстановления зависимости является нахождение коэффициентов `a` и `b` по экспериментальным точкам [`y_i`, `x_i`].
Для нахождения коэффициентов `a` и `b` обычно используется метод наименьших квадратов (МНК). Он является частным случаем принципа максимального правдоподобия.
Перепишем (1) в виде `ε_i = y_i — a — b x_i`.
Тогда сумма квадратов ошибок будет
`Φ = sum_(i=1)^(n) ε_i^2 = sum_(i=1)^(n) (y_i — a — b x_i)^2`. (2)
Принципом МНК (метода наименьших квадратов) является минимизация суммы (2) относительно параметров `a` и `b`.
Минимум достигается, когда частные производные от суммы (2) по коэффициентам `a` и `b` равны нулю:
`frac(partial Φ)(partial a) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial a) = 0`
`frac(partial Φ)(partial b) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial b) = 0`
Раскрывая производные, получаем систему из двух уравнений с двумя неизвестными:
`sum_(i=1)^(n) (2a + 2bx_i — 2y_i) = sum_(i=1)^(n) (a + bx_i — y_i) = 0`
`sum_(i=1)^(n) (2bx_i^2 + 2ax_i — 2x_iy_i) = sum_(i=1)^(n) (bx_i^2 + ax_i — x_iy_i) = 0`
Раскрываем скобки и переносим независящие от искомых коэффициентов суммы в другую половину, получим систему линейных уравнений:
`sum_(i=1)^(n) y_i = a n + b sum_(i=1)^(n) bx_i`
`sum_(i=1)^(n) x_iy_i = a sum_(i=1)^(n) x_i + b sum_(i=1)^(n) x_i^2`
Решая, полученную систему, находим формулы для коэффициентов `a` и `b`:
`a = frac(sum_(i=1)^(n) y_i sum_(i=1)^(n) x_i^2 — sum_(i=1)^(n) x_i sum_(i=1)^(n) x_iy_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.1)
`b = frac(n sum_(i=1)^(n) x_iy_i — sum_(i=1)^(n) x_i sum_(i=1)^(n) y_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.2)
Эти формулы имеют решения, когда `n > 1` (линию можно построить не менее чем по 2-м точкам) и когда детерминант `D = n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2 != 0`, т.е. когда точки `x_i` в эксперименте различаются (т.е. когда линия не вертикальна).
Оценка погрешностей коэффициентов линии регресии
Для более точной оценки погрешности вычисления коэффициентов `a` и `b` желательно большое количество экспериментальных точек. При `n = 2`, оценить погрешность коэффициентов невозможно, т.к. аппроксимирующая линия будет однозначно проходить через две точки.
Погрешность случайной величины `V` определяется законом накопления ошибок
`S_V^2 = sum_(i=1)^p (frac(partial f)(partial z_i))^2 S_(z_i)^2`,
где `p` – число параметров `z_i` с погрешностью `S_(z_i)`, которые влияют на погрешность `S_V`;
`f` – функция зависимости `V` от `z_i`.
Распишем закон накопления ошибок для погрешности коэффициентов `a` и `b`
`S_a^2 = sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial a)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 `,
`S_b^2 = sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial b)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 `,
т.к. `S_(x_i)^2 = 0` (мы ранее сделали оговорку, что погрешность `x` пренебрежительно мала).
`S_y^2 = S_(y_i)^2` – погрешность (дисперсия, квадрат стандартного отклонения) в измерении `y` в предположении, что погрешность однородна для всех значений `y`.
Подставляя в полученные выражения формулы для расчета `a` и `b` получим
`S_a^2 = S_y^2 frac(sum_(i=1)^(n) ( sum_(i=1)^(n) x_i^2 — x_i sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2) sum_(i=1)^(n) x_i^2 ) (D^2) = S_y^2 frac(sum_(i=1)^(n) x_i^2) (D)` (4.1)
`S_b^2 = S_y^2 frac(sum_(i=1)^(n) ( n x_i — sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(n ( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 frac(n) (D)` (4.2)
В большинстве реальных экспериментов значение `Sy` не измеряется. Для этого нужно проводить несколько паралельных измерений (опытов) в одной или нескольких точках плана, что увеличивает время (и возможно стоимость) эксперимента. Поэтому обычно полагают, что отклонение `y` от линии регрессии можно считать случайным. Оценку дисперсии `y` в этом случае, считают по формуле.
`S_y^2 = S_(y, ост)^2 = frac(sum_(i=1)^n (y_i — a — b x_i )^2) (n-2)`.
Делитель `n-2` появляется потому, что у нас снизилось число степеней свободы из-за расчета двух коэффициентов по этой же выборке экспериментальных данных.
Такую оценку еще называют остаточной дисперсией относительно линии регрессии `S_(y, ост)^2`.
Оценка значимости коэффициентов проводится по критерию Стьюдента
`t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)`
Если рассчитанные критерии `t_a`, `t_b` меньше табличных критериев `t(P, n-2)`, то считается, что соответсвующий коэффициент не значимо отличается от нуля с заданной вероятностью `P`.
Если `t_a
Если `t_b
Для оценки качества описания линейной зависимости, можно сравнить `S_(y, ост)^2` и `S_(bar y)` относительно среднего с использованием критерия Фишера.
`S_(bar y) = frac(sum_(i=1)^n (y_i — bar y)^2) (n-1) = frac(sum_(i=1)^n (y_i — (sum_(i=1)^n y_i) /n )^2) (n-1)` – выборочная оценка дисперсии `y` относительно среднего.
Для оценки эффективности уравнения регресии для описания зависимости расчитывают коэффициент Фишера
`F = S_(bar y) / S_(y, ост)^2`,
который сравнивают с табличным коэффициентом Фишера `F(p, n-1, n-2)`.
Если `F > F(P, n-1, n-2)`, считается статистически значимым с вероятностью `P` различие между описанием зависимости `y = f(x)` с помощью уравенения регресии и описанием с помощью среднего. Т.е. регрессия лучше описывает зависимость, чем разброс `y` относительно среднего.
Кликните по графику,
чтобы добавить значения в таблицу
laservirta.ru