Рациональное число и иррациональное число: Иррациональное число — Википедия – Рациональные и иррациональные числа

Иррациональное число — Википедия

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби ±mn{\displaystyle \pm {\frac {m}{n}}}, где m,n{\displaystyle m,n} — натуральные числа. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

Другими словами, множество иррациональных чисел есть разность I=R∖Q{\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } множеств вещественных и рациональных чисел.

О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа 2{\displaystyle {\sqrt {2}}}^[1].

К числу иррациональных чисел относятся отношение π окружности круга к его диаметру, число Эйлера e, золотое сечение φ и квадратный корень из двух^[2]

^[3][4]; на самом деле все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.

Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа неисчислимы, а рациональные счетны, отсюда следует, что почти все действительные числа иррациональны^[5].

• Сумма двух положительных иррациональных чисел может быть рациональным числом.
• Иррациональные числа определяют дедекиндовы сечения во множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
• Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя различными числами имеется иррациональное число.

Алгебраические и трансцендентные числа[править | править код]

Каждое иррациональное число является либо алгебраическим, либо трансцендентным. Множество алгебраических чисел является счётным множеством. Так как множество вещественных чисел несчётно, то множество иррациональных чисел также несчётно.

Множество иррациональных чисел является множеством второй категории^[6].

Каждое вещественное трансцендентное число является иррациональным.

Иррациональные числа и непрерывные дроби[править | править код]

Иррациональное число представляются бесконечной непрерывной дробью. Пример, число e:

e=[2;1,2,1,1,4,1,1,6,1,…,1,2n,1,…].{\displaystyle e=[2;1,2,1,1,4,1,1,6,1,\ldots ,1,2n,1,\ldots ].}

Квадратичным иррациональностям соответствуют периодические непрерывные дроби.

ϕ=1+52=[1;1,1,1,1,…].{\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}=[1;1,1,1,1,\dots ].}

Иррациональными являются:

Примеры доказательства иррациональности[править | править код]

Корень из 2[править | править код]

Допустим противное: 2{\displaystyle {\sqrt {2}}} рационален, то есть представляется в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} — целое число, а n{\displaystyle n} — натуральное число.

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

В каноническое разложение левой части равенства число 2{\displaystyle 2} входит в чётной степени, а в разложение 2n2{\displaystyle 2n^{2}} — в нечётной. Поэтому равенство m2=2n2{\displaystyle m^{2}=2n^{2}} невозможно. Значит, исходное предположение было неверным, и 2{\displaystyle {\sqrt {2}}} — иррациональное число.

Двоичный логарифм числа 3[править | править код]

Допустим противное: log2⁡3{\displaystyle \log _{2}3} рационален, то есть представляется в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} и n{\displaystyle n} — целые числа. Поскольку log2⁡3>0{\displaystyle \log _{2}3>0}, m{\displaystyle m} и n{\displaystyle n} могут быть выбраны положительными. Тогда

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

e[править | править код]

См. раздел «Доказательство иррациональности» в статье «e».

Античность[править | править код]

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (приблизительно 750—690 года до нашей эры) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены^{[источник не указан 1605 дней]}.

Первое доказательство существования иррациональных чисел, а точнее существование несоизмеримых отрезков, обычно приписывается пифагорейцу Гиппасу из Метапонта (приблизительно 470 год до нашей эры)^[7]. Нет точных данных о том, иррациональность какого числа было доказано Гиппасом. Согласно легенде он нашёл его, изучая длины сторон пентаграммы^[8][9]. Поэтому разумно предположить, что это было золотое сечение, так как это и есть отношение диагонали к стороне в правильном пятиугольнике.

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал^[10] иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному^[11] предположению Жана Итара^[fr], оно было основано на теореме о том, что нечётное квадратное число делится на восемь с остатком один^[12].

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5^[13]. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами^[14]. Десятая книга «Начал» Евклида посвящена классификации иррациональных величин.

Средние века[править | править код]

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 «Начал» Евклида, персидский математик аль-Махани (ок. 800 года н. э.) исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например^[15]:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких, как 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин^[15]:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени^[16]. В X веке иракский математик Аль-Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами^[17]. Аль-Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины^[18]:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от неё, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой

[19]. Та же нотация появилась затем в работах Фибоначчи в XIII веке^[20]. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π{\displaystyle \pi }, а также показали иррациональность некоторых значений тригонометрических функций. Джестадева привёл эти результаты в книге «Йуктибхаза».

Новое время[править | править код]

В XVII—XVIII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 году были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с работами Гейне, именно 1872 год принято считать годом рождения теории. Метод Вейерштрасса был полностью изложен Сальваторе Пинкерле в 1880 году

[21], а Дедекинд получил дополнительную известность благодаря более поздней работе автора (1888) и одобрению Поля Таннери (1894). Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемыми) дедекиндовыми сечениями множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей. В 1761 году Ламберт с помощю цепных дробей показал, что π{\displaystyle \pi } не является рациональным числом, а также что ex{\displaystyle e^{x}} и tg⁡x{\displaystyle \operatorname {tg} x} иррациональны при любом ненулевом рациональном x{\displaystyle x}

[22]. Хотя доказательство Ламберта можно назвать незавершённым, принято считать его достаточно строгим, особенно учитывая время его написания. Лежандр в 1794 году, после введения функции Бесселя — Клиффорда, показал, что π2{\displaystyle \pi ^{2}} иррационально, откуда иррациональность π{\displaystyle \pi } следует тривиально (рациональное число в квадрате дало бы рациональное).

Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π{\displaystyle \pi }. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом^[23].

1. ↑ История, 1970, Том 1, с. 73.
2. ↑ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 October 2007.
3. ↑ Irrational Numbers // mathsisfun.com; URL retrieved 24 October 2007.
4. ↑ Weisstein, Eric W. Irrational Number (англ.) на сайте Wolfram MathWorld. URL retrieved 26 October 2007.
5. ↑ Cantor, Georg. Contributions to the Founding of the Theory of Transfinite Numbers (англ.) / Philip Jourdain (англ.)русск.. — New York: Dover, 1955. — ISBN 978-0-486-60045-1.
6. ↑ Ильин, Садовничий, Сендов, 2006, с. 64.
7. ↑ Kurt Von Fritz, 1945.
8. ↑ James R. Choike. The Pentagram and the Discovery of an Irrational Number (англ.) // The Two-Year College Mathematics Journal (англ.)русск. : magazine. — 1980.
9. ↑ Kurt Von Fritz, 1945, p. 242—264.
10. ↑ История, 1970, Т 1. С древнейших времен до начала Нового времени, с. 74.
11. ↑ А. И. Щетников. Как древнегреческие математики доказывали иррациональность.
12. ↑ Jean Itard. Les livres arithmétiques d’Euclide. — Paris: Hermann, 1961.
13. ↑ Kline 1990, p.48.
14. ↑ Kline 1990, p.49.
15. ↑ ^{1 2} Matvievskaya, 1987, p. 253–277 [259].
16. ↑ Jacques Sesiano, «Islamic mathematics», p. 148, in Selin, Helaine; D’Ambrosio, Ubiratan. Mathematics Across Cultures: The History of Non-western Mathematics (англ.). — Springer, 2000. — ISBN 1-4020-0260-2..
17. ↑ Matvievskaya, 1987, p. 253–277 [260].
18. ↑ Matvievskaya, 1987, p. 253–277 [261].
19. ↑ Cajori, Florian (1928), A History of Mathematical Notations (Vol.1), La Salle, Illinois: The Open Court Publishing Company  pg. 269.
20. ↑ (Cajori 1928, pg.89)
21. ↑ Salvatore Pincherle. Saggio di una introduzione alla teoria delle funzioni analitiche secondo i principii del prof. C. Weierstrass (итал.) // Giornale di Matematiche : diario. — 1880. — P. 178—254,317—320.
22. ↑ J. H. Lambert. Mémoire sur quelques propriétés remarquables des quantités transcendentes, circulaires et logarithmiques (фр.) // Mémoires de l’Académie royale des sciences de Berlin : magazine. — 1761. — P. 265—322. Архивировано 28 апреля 2016 года.
23. ↑ Gordan, Paul. Transcendenz von e und π (неопр.) // Mathematische Annalen. — Teubner, 1893. — Т. 43. — С. 222—224. — doi:10.1007/bf01443647.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Рациональные и иррациональные числа. Понятие о вещественных числах

      Целые числа и рациональные дроби (простые дроби и смешанные числа) составляют множество рациональных чисел, которое принято обозначать буквой   Q .

      Каждое из рациональных чисел можно представить в виде

,

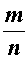где   m   – целое число, а   n   – натуральное число.

      При обращении рациональных дробей в десятичные дроби получаются конечные и бесконечные периодические десятичные дроби.

      Числа

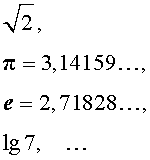
и т.п. являются примерами иррациональных чисел.

      Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.

      При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.

      Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.

      Множество вещественных чисел обозначают буквой   R .  

Иррациональность числа

      Проведем доказательство иррациональности числа 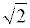методом «от противного». С этой целью предположим, что число 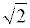является рациональным числом. Тогда существует дробь вида

,

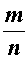удовлетворяющая равенству

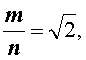
и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.

      Используя данное равенство, получаем:

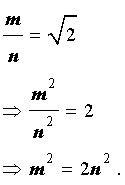
      Отсюда вытекает, что число   m² является четным числом, а, значит, и число   m   является четным числом. Действительно, если мы предположим противное, т.е. предположим, что число   m   является нечетным числом, то найдется такое целое число   k ,   которое удовлетворяет соотношению

m = 2k + 1 .

Следовательно,

m² = (2k + 1)² =
= 4m² + 4k +1 ,

т.е.   m   является нечетным числом. Полученное противоречие доказывает, что число   m   является четным числом. Значит, найдется такое целое число   k ,  которое удовлетворяет соотношению

m = 2k .

      Поэтому,

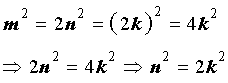
      Отсюда вытекает, что число   n² является четным, а, значит, и число   n   является четным числом.

      Итак, число   m   является четным, и число   n   является четным, значит, число   2   является общим делителем числителя и знаменателя дроби

.

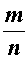      Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению

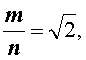
не существует. Следовательно, число 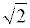 является иррациональным числом, что и требовалось доказать.

Десятичные приближения иррациональных чисел
с недостатком и с избытком

      Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число

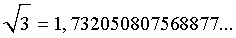
      Это число, как и любое другое иррациональное число, изображается бесконечной непериодической  десятичной дробью.

      Последовательностью десятичных приближений числа 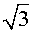с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа 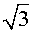отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.

      Если последний десятичный знак каждого десятичного приближения числа с недостатком увеличить на   1 ,   то получится десятичное приближение числа с избытком.

      Само число 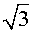располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.

      Для числа 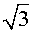возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:

и т.д.

      Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Рациональное и иррациональное число: описание и чем они отличаются?

Откуда же произошли следующие термины такие, как:

• Рациональное число.
• Иррациональное число.

А свои корни они извлекли из латинского слова «ratio», что означает «разум». Исходя из дословного перевода:

• Рациональное число — это «разумное число».
• Иррациональное число, соответственно, «неразумное число».

Общее понятие рационального числа

Рациональным числом считается то число, которое можно записать в виде:

1. Обыкновенной положительной дроби.
2. Отрицательной обыкновенной дроби.
3. В виде числа нуль (0).

Иными словами, к рациональному число подойдет следующие определения:

• Любое натуральное число является по своей сути рациональным, так как любое натуральное число можно представить в виде обыкновенной дроби.
• Любое целое число, включительно число нуль, так как любое целое число можно записать как ввиде положительной обыкновенной дроби, в виде отрицательной обыкновенной дроби, так и ввиде числа нуль.
• Любая обыкновенная дробь, и здесь не имеет значение положительная она или отрицательная, тоже напрямую подходит к определению рационального числа.
• Так же в определение можно отнести и смешанное число, конечную десятичную дробь либо бесконечную периодическую дробь.

Примеры рационального числа

Рассмотрим примеры рациональных чисел:

• Натуральные числа — «4», «202», «200».
• Целые числа — «-36», «0», «42».
• Обыкновенные дроби.

Из вышеперечисленных примеров совершенно очевидно, что рациональные числа могут быть как положительными так и отрицательными. Естественно, число 0 (нуль), которое тоже в свою очередь является рациональным числом, в тоже время не относится к категории положительного или отрицательного числа.

Отсюда, хотелось бы напомнить общеобразовательную программу с помощью следующего определения: «Рациональными числами» — называются те числа, которые можно записать в виде дроби х/у, где х (числитель) — целое число, а у (знаменатель) — натуральное число.

Общее понятие и определение иррационального числа

Помимо «рациональных чисел» нам известны и так называемые «иррациональные числа». Вкратце попробуем дать определение данным числам.

Еще древние математики, желая вычислить диагональ квадрата по его сторонам, узнали о существовании иррационального числа.
Исходя из определения о рациональных числах, можно выстроить логическую цепь и дать определение иррациональному числу.
Итак, по сути, те действительные числа, которые не являются рациональными, элементарно и есть иррациональными числами.
Десятичные дроби же, выражающие иррациональные числа, не периодичны и бесконечны.

Примеры иррационального числа

Рассмотрим для наглядности небольшой пример иррационально числа. Как мы уже поняли, бесконечные десятичные непериодические дроби называются иррациональными, к примеру:

• Число «-5,020020002… (прекрасно видно, что двойки разделены последовательностью из одного, двух, трех и т.д. нулей)
• Число «7,040044000444… (здесь ясно, что число четверок и количество нулей каждый раз цепочкой увеличивается на единицу).
• Всем известное число Пи (3,1415…). Да, да — оно тоже является иррациональным.

Вообще все действительные числа являются как рациональными так и иррациональными. Говоря простыми словами, иррациональное число нельзя представить ввиде обыкновенной дроби х/у.

Общее заключение и краткое сравнение между числами

Мы рассмотрели каждое число по отдельности, осталось отличие между рациональным числом и иррациональным:

1. Иррациональное число встречается при извлечении квадратного корня, при делении окружности на диаметр и т.д.
2. Рациональное число представляет обыкновенную дробь.

Заключим нашу статью несколькими определениями:

• Арифметическая операция, произведенная над рациональным числом, кроме деления на 0 (нуль), в конечном результате приведет тоже к рациональному числу.
• Конечный результат же, при совершении арифметической операции над иррациональным числом, может привести как к рациональному так и к иррациональному значению.
• Если же в арифметической операции принимают участие и те и другие числа (кроме деления или умножения на нуль), то результат нам выдаст иррациональное число.

Иррациональные числа — урок. Алгебра, 8 класс.

Термины рациональное число, иррациональное число происходят от латинского слова ratio — разум
(буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).

Иррациональным числом называют бесконечную десятичную непериодическую дробь.

Если натуральное число \(n\) не является точным квадратом, т. е. n≠k2, где k∈ℚ, то  n — иррациональное число.

Пример:

5=2,23606798…11=3,31662479…

Иррациональные числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чём вы не раз убедитесь в старших классах.

Если длину любой окружности разделить на её диаметр, то в частном получится иррациональное число \(3,141592…\) Для этого числа в математике введено специальное обозначение π (буква греческого алфавита «пи»; версия происхождения этого понятия такова: с буквы π начинается греческое слово периферия — окружность). Иррациональность числа π была доказана в \(1766\) г. немецким математиком И. Ламбертом.

Итак,

1. любая арифметическая операция над рациональными числами (кроме деления на \(0\)) приводит в результате к рациональному числу.

2. Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу.

3. Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на \(0\)).

4. Поскольку операция извлечения квадратного и кубического корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного и кубического корня из переменной, называть иррациональным выражением.

Рациональные числа: определения, примеры

Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет. 

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой. 

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа — числа, которые можно представить в виде положительной обыкновенной дроби ab, отрицательной обыкновенной дроби -ab или числа ноль. 

Таким образом, можно оставить ряд свойств рациональных чисел:

1. Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1n.
2. Любое целое число, включая число 0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15=151, -352=-3521.
3. Любая положительная или отрицательная обыкновенная дробь ab является рациональным числом. Это следует напрямую из данного выше определения.
4. Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
5. Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом. 
6. Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа 5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа -2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 35, 87, -358 также являются примерами рациональных чисел.  

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа — это такие числа, которые можно представить в виде дроби ±zn, где z — целое число, 

Действительные числа, рациональные числа и иррациональные числа

В ходе изучения математики мы сталкивались с различными числами.

Натуральные числа

Числа, используемые при счете называются натуральными числами. Например, $1,2,3$ и т.д. Натуральные числа образуют множество натуральных чисел, которое обозначают $N$ .Данное обозначение исходит от латинского слова naturalis- естественный.

Противоположные числа

Определение 1

Если два числа отличаются только знаками, их называют в математике противоположными числами.

Например, числа $5$ и $-5$ противоположные числа, т.к. отличаются только знаками.

Замечание 1

Для любого числа есть противоположное число, и притом только одно.

Замечание 2

Число нуль противоположно самому себе.

Целые числа

Определение 2

Целыми числами называют натуральные, противоположные им числа и нуль.

Множество целых чисел включает в себя множество натуральных и противоположных им.

Обозначают целые числа $Z.$

Дробные числа

Числа вида $\frac{m}{n}$ называют дробями или дробными числами. Так же дробные числа можно записывать десятичной форме записи, т.е. в виде десятичных дробей.

Например:$\ \frac{3}{5}$ , $0,08$ и Т.Д.

Так же, как и целые, дробные числа могут быть как положительными, так и отрицательными.

Рациональные числа

Определение 3

Рациональными числами называется множество чисел, содержащее в себе множество целых и дробных чисел.

Любое рациональное число, как целое, так и дробное можно представить в виде дроби $\frac{a}{b}$, где $a$- целое число, а $b$- натуральное.

Таким образом, одно и то же рациональное число можно записать разными способами.

Например,

Отсюда видно, что любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби.

Множество рациональных чисел обозначается $Q$.

В результате выполнения любого арифметического действия над рациональными числами полученный ответ будет рациональным числом. Это легко доказуемо, в силу того, что при сложении, вычитании, умножении и делении обыкновенных дробей получится обыкновенная дробь

Иррациональные числа

В ходе изучения курса математики часто приходится сталкиваться в решении с числами, которые не являются рациональными.

Например, чтобы убедиться в существовании множества чисел, отличных от рациональных решим уравнение $x^2=6$.Корнями этого уравнения будут числа $\surd 6$ и -$\surd 6$. Данные числа не будут являться рациональными.

Так же при нахождении диагонали квадрата со стороной $3$ мы применив теорему Пифагора получим, что диагональ будет равна $\surd 18$. Это число также не является рациональным.

Такие числа называются иррациональными.

Итак, иррациональным числом называют бесконечную десятичную непериодическую дробь.

Одно из часто встречающихся иррациональных чисел- это число $\pi $

При выполнении арифметических действий с иррациональными числами получаемый результат может оказаться и рациональным, так и иррациональным числом.

Докажем это на примере нахождения произведения иррациональным чисел. Найдем:

1. $\ \sqrt{6}\cdot \sqrt{6}$

2. $\ \sqrt{2}\cdot \sqrt{3}$

Решениею

1. $\ \sqrt{6}\cdot \sqrt{6} = 6$

2. $\sqrt{2}\cdot \sqrt{3}=\sqrt{6}$

На этом примере видно, что результат может оказаться как рациональным, так и иррациональным числом.

Если в арифметических действиях участвуют рациональное и иррациональные числа одновременно, то в результате получится иррациональное число ( кроме, конечно, умножения на $0$).

Действительные числа

Множеством действительных чисел называется множество содержащее множество рациональных и иррациональных чисел.

Обозначается множество действительных чисел $R$. Символически множество действительных чисел можно обозначить $(-?;+?).$

Мы говорили ранее о том, что иррациональным числом называют бесконечную десятичную непериодическую дробь, а любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби, поэтому действительным числом будет являться любая конечная и бесконечная десятичная дробь.

При выполнении алгебраических действий будут выполняться следующие правила

1. при умножении и делении положительных чисел полученное число будет положительным
2. при умножении и делении отрицательных чисел полученное число будет положительным
3. при умножении и делении отрицательного и положительного чисел полученное число будет отрицательным

Также действительные числа можно сравнивать друг с другом.

Иррациональное число — это… Что такое Иррациональное число?

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби , где  — целые числа, . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

Множество иррациональных чисел обычно обозначается заглавной латинской буквой в полужирном начертании без заливки. Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .

Свойства

• Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
• Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
• Каждое вещественное трансцендентное число является иррациональным.
• Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
• Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
• Порядок на множестве иррациональных чисел изоморфен порядку на множестве вещественных трансцендентных чисел.
• Множество иррациональных чисел несчётно, является множеством второй категории.^[1]

Примеры

Иррациональными являются:

Примеры доказательства иррациональности

Корень из 2

Допустим противное: рационален, то есть представляется в виде несократимой дроби , где и  — целые числа. Возведём предполагаемое равенство в квадрат:

.

Отсюда следует, что чётно, значит, чётно и . Пускай , где целое. Тогда

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и  — иррациональное число.

Двоичный логарифм числа 3

Допустим противное: рационален, то есть представляется в виде дроби , где и  — целые числа. Поскольку , и могут быть выбраны положительными. Тогда

Но чётно, а нечётно. Получаем противоречие.

e

См. раздел «Доказательство иррациональности» в статье «e».

История

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.

Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:

• Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
• По теореме Пифагора: a² = 2b².
• Так как a² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
• Поскольку a:b несократима, b обязано быть нечетным.
• Так как a четное, обозначим a = 2y.
• Тогда a² = 4y² = 2b².
• b² = 2y², следовательно b² четное, тогда и b четно.
• Однако было доказано, что b нечетное. Противоречие.

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.

Средние века

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.

Наше время

В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.

В 1761 году Ламберт показал, что π не может быть рационально, а также что иррационально при любом ненулевом рациональном n. Хотя доказательство Ламберта можно назвать незавершённым, принято считать его достаточно строгим, особенно учитывая время его написания. Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал, что π² иррационально, откуда иррациональность π следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.

См. также

Примечания

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.