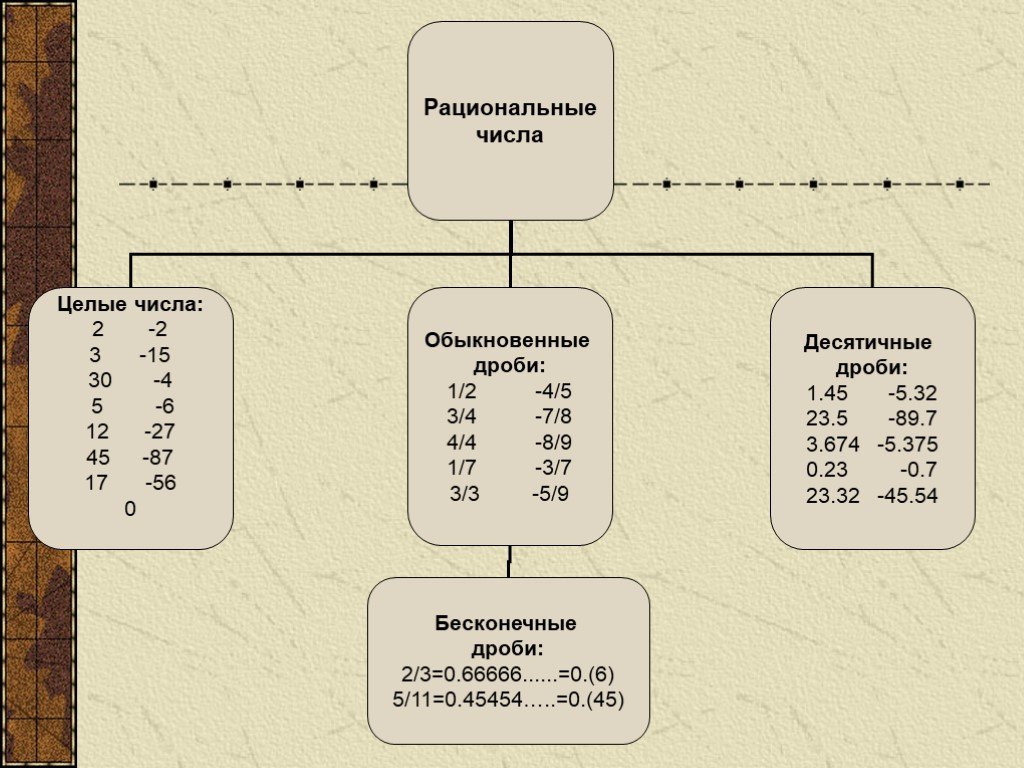
Раціональні числа приклади: Цілі та раціональні числа — урок. Математика, 6 клас.

Раціональні числа: властивості, приклади та операції — Наука

Відеоролик: Целые и рациональные числа. 6 класс.

Зміст

• Властивості раціональних чисел
• Приклади раціональних чисел
• Десяткове подання раціонального числа
• Перетвори десятковий знак на дріб
• Операції з раціональними числами
• — Додавання і віднімання
• Дроби з однаковим знаменником
• Приклад
• Дроби з різними знаменниками
• Приклад
• — Множення і ділення
• Приклад 1
• Відповідь на
• Відповідь b
• Приклад 2
• Рішення
• Список літератури

раціональні числа — це всі числа, які можна отримати як ділення двох цілих чисел. Прикладами раціональних чисел є: 3/4, 8/5, -16/3 та ті, що наведені на наступному малюнку. У раціональному числі вказано фактор, який можна зробити пізніше, якщо потрібно.

На малюнку зображений будь-який предмет, круглий для більшого комфорту. Якщо ми хочемо розділити його на 2 рівні частини, як праворуч, у нас залишилося дві половинки, і кожна коштує 1/2.

Поділивши його на 4 рівні частини, ми отримаємо 4 штуки, і кожна коштує 1/4, як на зображенні в центрі. І якщо вам доведеться розділити його на 6 рівних частин, кожна частина буде коштувати 1/6, що ми бачимо на зображенні зліва.

Звичайно, ми могли б також розділити його на дві нерівні частини, наприклад, ми могли б зберегти 3/4 частини та заощадити 1/4 частини. Можливі й інші поділи, наприклад, 4/6 частин та 2/6 частин. Важливо те, що сума всіх частин дорівнює 1.

Таким чином, очевидно, що за допомогою раціональних чисел такі речі, як їжа, гроші, земля та всі види предметів, можна розділити, порахувати та розподілити частками. І тому кількість операцій, які можна робити з числами, розширюється.

Раціональні числа також можуть бути виражені в десятковій формі, як це видно з наступних прикладів:

1/2 = 0,5

1/3 = 0,3333…..

3/4 = 0,75

1/7 = 0,142857142857142857………

Пізніше ми вкажемо, як переходити від однієї форми до іншої, на прикладах.

Властивості раціональних чисел

Раціональні числа, набір яких ми позначимо буквою Q, мають такі властивості:

-Q включає натуральні числа N і цілі числа Z.

Беручи до уваги, що будь-яке число до Це можна виразити як частку між собою та 1, неважко помітити, що серед раціональних чисел є також натуральні числа та цілі числа.

Таким чином, натуральне число 3 можна записати у вигляді дробу, а також -5:

3 = 3/1

-5= -5/1 = 5/-1 = -(5/1)

Таким чином, Q є числовим набором, що включає більшу кількість чисел, що є дуже необхідним, оскільки «круглих» чисел недостатньо для опису всіх можливих операцій.

-Раціональні числа можна додавати, віднімати, множити і ділити, результатом операції є раціональне число: 1/2 + 1/5 = 7/10; 1/2 — 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Поміж кожною парою раціональних чисел завжди можна знайти інше раціональне число. Насправді між двома раціональними числами є нескінченні раціональні числа.

Наприклад, між обґрунтуваннями 1/4 та 1/2 є обгрунтування 3/10, 7/20, 2/5 (та багато інших), які можна перевірити, виражаючи їх як десяткові крапки.

-Будь-яке раціональне число може бути виражене як: i) ціле число або ii) обмежений (строгий) або періодичний десятковий знак: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,16666666 ……

-Це саме число може бути представлено нескінченними еквівалентними частками, і всі вони належать Q. Подивимось на цю групу:

Всі вони представляють десяткову 0,428571 …

-З усіх еквівалентних дробів, що представляють одне і те ж число, незведеною часткою, найпростішою з усіх, є канонічний представник цього числа. Канонічним представником наведеного вище прикладу є 3/7.

Приклади раціональних чисел

-Правильні дроби, ті, у яких чисельник менше знаменника:

-Неправильні дроби, чисельник яких більший за знаменник:

-Натуральні числа і цілі числа:

-Еквівалентні фракції:

Десяткове подання раціонального числа

Коли чисельник поділяється на знаменник, знайдеться десяткова форма раціонального числа. Наприклад:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111…

6/11 = 0.545454…

У перших двох прикладах кількість десяткових знаків обмежена. Це означає, що після ділення остаточно отримується залишок 0.

З іншого боку, у наступні два числа десяткових знаків нескінченні, і тому розміщуються еліпсиси. В останньому випадку існує десяткова цифра. У випадку з часткою 1/9 цифра 1 повторюється нескінченно, тоді як у 6/11 вона дорівнює 54.

Коли це трапляється, десятковий код називається періодичним і позначається такою каретою:

Перетвори десятковий знак на дріб

Якщо це обмежений десятковий знак, просто видаліть кому, і знаменник стане одиницею, за якою слідує стільки нулів, скільки в десятковій цифрі. Наприклад, щоб перетворити десятковий 1.26 у дріб, запишіть його так:

1.26 = 126/100

Тоді отримана дріб максимально спрощується:

126/100 = 63/50

Якщо десятковий знак необмежений, спочатку визначається період. Потім виконуються ці дії, щоб знайти отриману частку:

-Чисельник — це віднімання між числом (без коми та каретки) та частиною, яка не несе циркумфлексний акцент.

-Знаменник — це ціле число із стільки 9, скільки є цифр під циркумфлексом, і стільки 0, скільки є цифр десяткова частина є такі, що не знаходяться під циркумфлексом.

Давайте виконуватимемо цю процедуру, щоб перетворити десяткове число 0,428428428… у дріб.

-По-перше, визначається період, який є послідовністю, що повторюється: 428.

-Тоді виконується операція віднімання числа без коми або наголосу: 0428 з тієї частини, яка не має циркумфлексу, що дорівнює 0. Залишається таким 428 — 0 = 428.

-Знаменник побудований, знаючи, що під циркумфлексом є 3 фігури і всі знаходяться під циркумфлексом.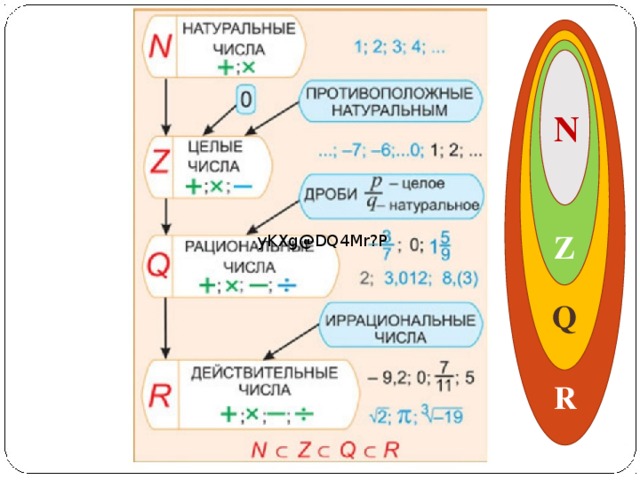 Тому знаменник 999.

-Нарешті дріб формується і спрощується, якщо це можливо:

0.428= 428/999

Спростити більше неможливо.

Операції з раціональними числами

— Додавання і віднімання

Дроби з однаковим знаменником

Коли дроби мають однаковий знаменник, додавати та / або віднімати їх дуже просто, оскільки чисельники просто додаються алгебраїчно, залишаючи те саме, що додається, як знаменник результату. Нарешті, якщо це можливо, це спрощується.

Приклад

Виконайте наступне алгебраїчне додавання та спростіть результат:

Отримана частка вже не піддається зниженню.

Дроби з різними знаменниками

У цьому випадку додавання замінюються еквівалентними дробами з однаковим знаменником, а потім виконується вже описана процедура.

Приклад

Додайте алгебраїчно такі раціональні числа, спрощуючи результат:

Етапи:

-Визначити найменший загальний кратний (LCM) знаменників 5, 8 і 3:

lcm (5,8,3) = 120

Це буде знаменником отриманого дробу без спрощення.

-Для кожного дробу: розділіть LCM на знаменник і помножте на чисельник. Результат цієї операції розміщується з відповідним знаком у чисельнику дробу. Таким чином отримується дріб, еквівалентний оригіналу, але із знаменником LCM.

Наприклад, для першого дробу чисельник будується так: (120/5) x 4 = 96 і отримуємо:

Подібні дії виконайте так само для решти дробів:

Нарешті, еквівалентні дроби замінюються, не забуваючи про свій знак, і проводиться алгебраїчна сума чисельників:

(4/5) + (14/8) – (11/3) + 2 = (96/120) + (210/120) – (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

— Множення і ділення

Множення та ділення виконуються за правилами, наведеними нижче:

У будь-якому випадку важливо пам’ятати, що множення є комутативним, що означає, що порядок факторів не змінює добуток. З поділом цього не відбувається, тому слід дотримуватись дотримання порядку між дивідендами та дільниками.

Приклад 1

Виконайте такі операції та спростіть результат:

а) (5/3) x (8/15)

б) (-4/5) ÷ (2/9)

Відповідь на

(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15/120 = 1/8

Відповідь b

(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5

Приклад 2

У Луїзи було 45 доларів. Десяту частину він витратив на покупку книги та 2/5 того, що залишилось на футболці. Скільки грошей залишилось у Луїзи? Виразіть результат у вигляді незнижуваної частки.

Рішення

Вартість книги (1/10) х 45 доларів = 0,1 х 45 доларів = 4,5 доларів

Тому Луїза залишилася з:

45 – 4.5 $ = 40.5 $

На ці гроші Луїза пішла до магазину одягу і придбала сорочку, ціна якої:

(2/5) x 40,5 $ = 16,2 $

Зараз у своєму портфоліо Луїза:

40.5 – 16.2 $ = 24.3$

Щоб виразити це як дріб, це пишеться так:

24.3 = 243 / 10

Що незводимо.

Список літератури

1. Бальдор, А. 1986. Арифметика. Видання та розповсюджувальний кодекс.
2. Карена, М. 2019. Посібник з математики. Національний університет Літораль.
3. Фігера, Дж. 2000. Математика 8. Ediciones Co-Bo.
4. Хіменес, Р. 2008. Алгебра. Прентіс Холл.
5. Раціональні числа. Отримано з: Cimanet.uoc.edu.
6. Раціональні числа. Відновлено з: webdelprofesor. ula.ve.

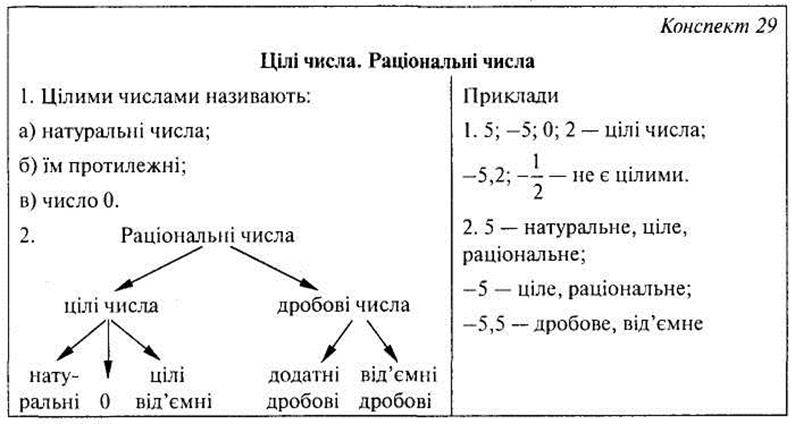
Раціональні числа

Додатні та від’ємні числа

Координатна пряма

Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається координатною ­прямою.
Число, що показує положення точки на координатній прямій, називається координатою точки.
Приклад
Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це означає, що координата точки А — число . Позначається: А (2,5).

Точка B на рисунку розташована ліворуч від 0 на відстані 4 одинакових відрізків. Позначається: B .
Отже, числа зі знаком «+» називають ­додатними. При записі додатних чисел знак «+», як правило, опускають.
Числа зі знаком «–» називають від’єм­ними.
Число 0 не є ні додатним, ні від’ємним. Два числа, що відрізняються одне від одного лише знаком, називаються протилежними ­числами.
Число, протилежне числу а, позначають . Таким чином, якщо , то ; якщо , то , тобто . Число 0 протилежне саме собі: . Якщо дане число додатне, то протилежне йому — від’ємне і навпаки.
Зверніть увагу, що за записом не можна сказати, яке це число — додатне чи від’ємне.
Якщо х — додатне, то — від’ємне; якщо х — від’ємне, то — додатне; якщо , то .
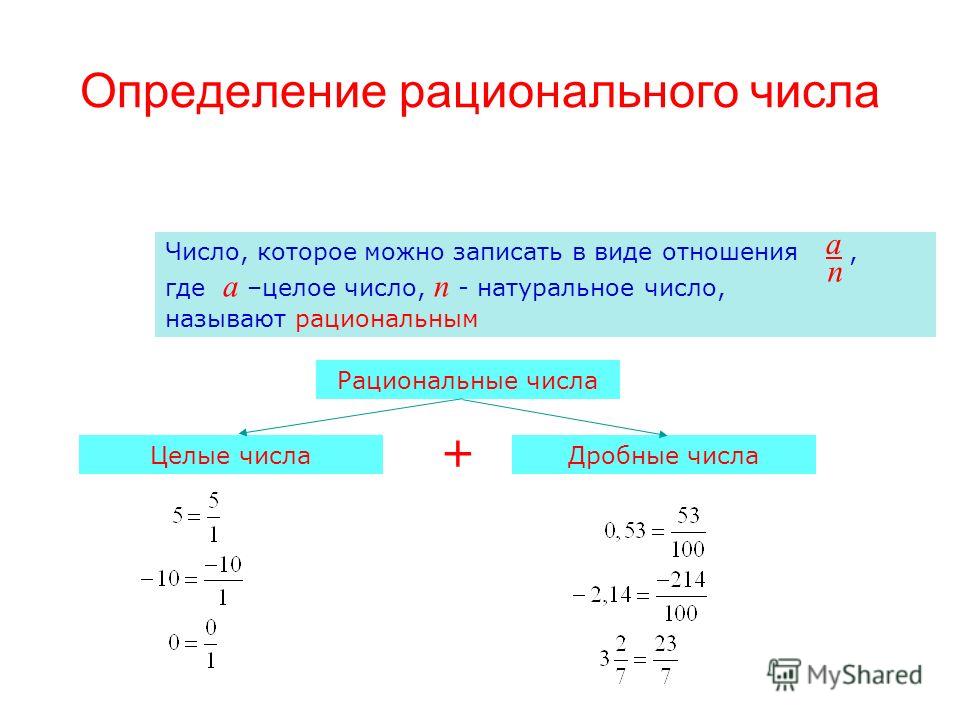
Натуральні числа, протилежні їм числа і число 0 називаються цілими числами. Числа, які можна записати у вигляді дробу , де m — ціле число, а n — натуральне число, називають раціональними числами.
Кожне раціональне число можна записати у вигляді скінченного або нескінченного періодичного десяткового дробу.

Модуль числа

Відстань від початку відліку до точки, що зображає число на координатній прямій, називається модулем даного числа. Позначення: — модуль а. Очевидно, що для додатних чисел і 0 , для від’ємних .

для будь-якого числа а.
Модулі протилежних чисел рівні: .
Приклади
1) ; ; .
2) Розв’яжіть рівняння.
а) ; або .
б) ; .
в) ; рівняння не має коренів, тому що модуль числа не може бути від’ємним.

Порівняння чисел

Із двох чисел меншим є те, зображення якого на горизонтальній координатній прямій розташовано ліворуч, більшим — те, зображення якого розташовано праворуч.
Будь-яке додатне число більше від нуля.
Будь-яке від’ємне число менше від нуля.
Будь-яке додатне число більше від будь-якого від’ємного.
Із двох від’ємних чисел меншим є те, модуль якого більший.
Приклади
; ; ; ; .

Додавання раціональних чисел

Щоб додати два від’ємних числа, треба додати їхні модулі й поставити перед одержаним числом знак «–»:
.
Щоб додати два числа з різними знаками, треба від більшого модуля відняти менший і поставити перед одержаним числом знак того доданка, модуль якого більший:
;
.
Сума двох протилежних чисел дорівнює нулю.
.

Властивості додавання

1. Переставна: .
2. Сполучна: .
3. .
4. .
Властивості додавання дають змогу виконувати дії у зручному порядку. Іноді зручно додати окремо всі від’ємні числа, окремо — всі додатні, а потім додати суми.
Приклади
1)
;
2)

.

Віднімання

Щоб від одного числа відняти друге, досить до зменшуваного додати число, протилежне від’ємнику: .
Приклади
1) ;
2) ;
3) ;
4) .
Оскільки віднімання можна замінити додаванням протилежного числа, то будь-який вираз, який містить дії додавання і віднімання, можна сприймати як суму. Наприклад:

Розкриття дужок

Щоб розкрити дужки, перед якими стоїть знак «+», треба опустити дужки і знак «+», що стоїть перед ними, і записати всі доданки зі своїми знаками.
Щоб розкрити дужки, перед якими стоїть знак «–», треба опустити дужки і знак «–», що стоїть перед ними, і записати всі доданки з протилежними знаками.
Приклади
1)

2) .

Множення

Щоб знайти добуток двох чисел із різними знаками, треба перемножити їхні модулі й поставити перед одержаним числом знак «–».
Щоб перемножити два від’ємних числа, треба перемножити їхні модулі (тобто добуток двох від’ємних чисел є додатне число).
При зміні знака одного з множників змінюється знак усього добутку.
Якщо добуток містить парне число від’ємних множників, він є додатним числом, а якщо непарне — від’ємним.
Приклади
1) ;
2) ;
3) ;
4) .
Квадрат будь-якого числа є число невід’ємне. Наприклад:
; .
Тобто для будь-яких значень а.
Знак куба числа збігається зі знаком самого числа. Наприклад:
;
; .
Тобто, якщо , то і ; якщо , то і .
Зверніть увагу: ; .
Для множення раціональних чисел справджуються властивості:
переставна — ;
сполучна — ;
розподільна — ;
.
Для будь-якого раціонального а пра­­вильно:
; ;
.
Приклади
1)
.
Добуток є додатним, тому що містить два від’ємних множники.
2) .
3) .
4) Винести за дужки спільний множник.
а) ;
б) ;
число 2 є НСД (4; 10).
Якщо буквений вираз можна записати як добуток числа й однієї чи кількох букв, то це число називають числовим коефіцієнтом виразу. Наприклад:
, коефіцієнт 2,5;
, коефіцієнт ;
а, коефіцієнт 1;
, коефіцієнт .
Доданки, які мають однакову буквену частину, називаються подібними.
Щоб звести (тобто додати) подібні доданки, треба додати їхні коефіцієнти й результат помножити на спільну буквену частину.
Приклади
1)
;
2) .

Ділення раціональних чисел

Часткою двох від’ємних чисел є число додатне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника.
Часткою двох чисел із різними знаками є число від’ємне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника.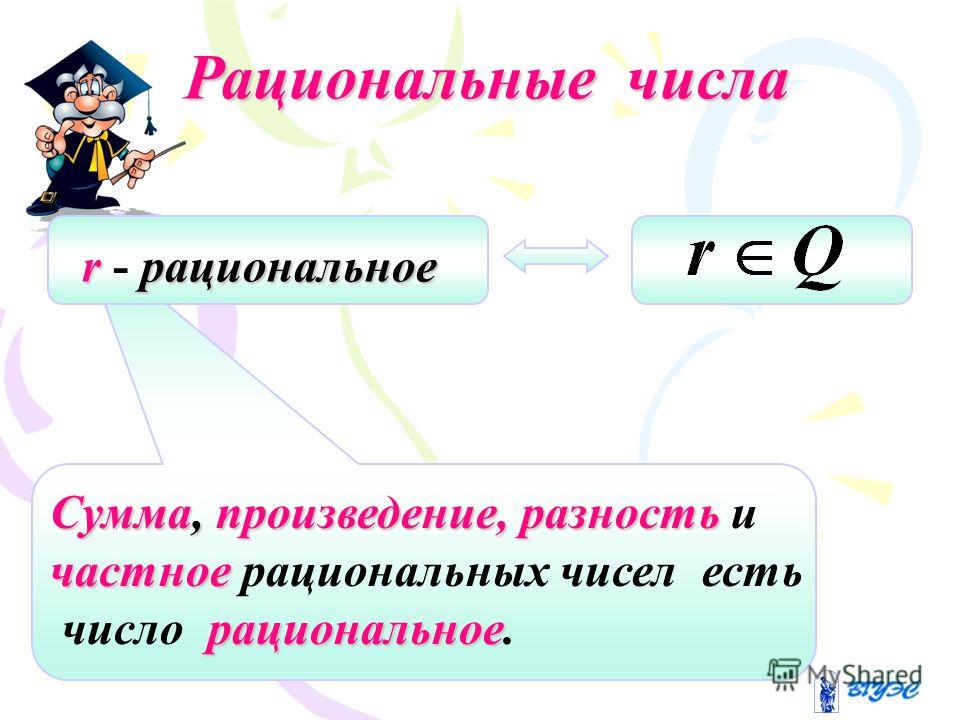
Для будь-якого числа а:
; ;
Для : ; ; . Ділити на 0 не можна.
Приклади
1) ;
2) ;
3) ;
4) ;
5) .

Розв’язування рівнянь

Властивості рівнянь

Корені рівнянь не змінюються, якщо до обох частин додати будь-який доданок.
Отже, при розв’язуванні рівнянь доданки можна переносити з однієї частини в другу, змінюючи при цьому їхні знаки на проти­лежні.
Корені рівнянь не змінюються, якщо обидві його частини помножити або поділити на одне й те ж число, що не дорівнює 0.

Приклади
1) ,
,
,
,
, .
2) .
Помножимо обидві частини наведеного рівняння на НСК (4; 6; 3), тобто на 12:

,
,
,
,
.
Отже, при розв’язуванні рівнянь доцільно спростити обидві частини, потім усі доданки, які містять невідоме, зібрати в одній частині, а ті, що не містять невідомого, — у другій, звести подібні доданки й отримати рівняння виду:
, де a і b — деякі числа.

Координатна площина

Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку — точці О. Ці прямі називаються осями координат. Горизон­тальну пряму називають віссю абсцис і позначають Ox, вертикальну — віссю ординат і позначають Oy. Точку О називають початком координат. Ці координатні прямі утворюють декартову прямо­кутну систему координат. Пло­щи­на, на якій задана прямокутна система координат, називається

координатною площиною. Через будь-яку точку А координатної площини можна провести прямі, перпендикулярні до осей Ox і Oy.
Нехай ці прямі перетнуть відповідно вісь абсцис — у точці з координатою а, а вісь ординат — у точці з координатою b.
Пара чисел (а, b) визначає положення точки А на координатній площині й називається її координатами. Позначають А(а, b). Число а називається абсцисою точки А, число b — її ординатою. Зверніть увагу: має значення, в якому порядку записані числа а і b. Точка В(b; а) не збігається з А(а; b).
Якщо точка лежить на осі абсцис, то її ордината дорівнює 0; якщо точка лежить на осі ординат, то її абсциса дорівнює нулю. Початок координат — О(0; 0).
Осі координат розбивають площину на 4 частини, які називаються координатними чвертями. Нумерація чвертей, знаки координат у кожній чверті, а також приклади точок з їх координатами показані на рисунку.

Таким чином, щоб побудувати, наприклад, точку М(k; р), треба поставити олівець в О(0; 0), потім пересунутися по осі абсцис на одиничних відрізків праворуч (якщо ) або ліворуч (якщо ). Від отриманої точки на осі абсцис треба рухатись угору на одиничних відрізків (якщо ) або униз (якщо ).

 

• Правила: Цілі числа. Раціональні числа

Использование рациональных чисел

Как складывать, вычитать, умножать и делить рациональные числа

Рациональное число — это число, которое можно записать в виде простой дроби (т. е. в виде отношения ).

Примеры:

Номер	Как дробь
5	5/1
1,75	7/4
.001	1/1000
0,111…	1/9

В целом…

Итак, рациональное число выглядит так:

р к

Но q не может быть нулем, так как это деление на ноль.

Как складывать, вычитать, умножать и делить

Когда рациональное число представляет собой что-то простое, например 3 или 0,001 , тогда просто используйте арифметику в уме или калькулятор!

Но как насчет формы p q ?

½

Ну, рациональное число — это дробь, поэтому мы можем использовать: Сложение дробей, Вычитание дробей, Умножение дробей и Деление дробей

Здесь мы увидим эти операции в более общем стиле алгебры.

Вы также можете прочитать Дроби в алгебре.

Начнем с умножения, так как это проще всего.

Умножение

Чтобы умножить два рациональных числа , умножьте отдельно верхние и нижние части , например:

Вот пример:

Подразделение

Чтобы разделить два рациональных числа, сначала переверните второе число (сделайте его обратным), а затем выполните умножение, как указано выше:

Вот пример:

Сложение и вычитание

Мы рассмотрим сложение и вычитание за один раз, так как это один и тот же метод.

Прежде чем мы сложим или вычтем, рациональные числа должны иметь одно и то же нижнее число (называемое общим знаменателем).

Проще всего это сделать на

Умножить обе части одного числа на нижнюю часть другого

Вот так (обратите внимание, что точка · означает умножение):

Вот пример добавления:

И пример вычитания (средний шаг пропущен для ускорения):

Простейшая форма

Иногда у нас есть такое рациональное число:

10 15

Но это не так просто!

Мы можем разделить верх и низ на 5, чтобы получить:

÷ 5

10 15   =   2 3

÷ 5

Теперь он в «самой простой форме», как и хочет большинство людей!

Будьте осторожны со «смешанными дробями»

У нас может возникнуть соблазн записать неправильную дробь (дробь, которая является «тяжелой сверху», т.

е. где верхнее число больше нижнего числа) как смешанную дробь:

Например, ⁷ / ₄ = 1 ³ / ₄ , показано здесь:

Неправильная дробь		Смешанная фракция
7 / 4		1 3 / 4
	=

Но для математики «Неправильная» форма (например, ⁷ / ₄ ) на самом деле лучше .

Потому что смешанные дроби (такие как 1 ³ / ₄ ) могут сбивать с толку, когда мы записываем их в формулу, так как это может выглядеть как умножение :

Смешанная фракция:		Что такое:	1 + 2 1 4 ?
		Это:	1 + 2 + 1 4 = 3 1 4 ?
		Или это:	1 + 2 × 1 4 = 1 1 2 ?
Неправильная дробь:		Что такое:	1 + 9 4 ?
		Это:	4 4 + 9 4 = 13 4

Попробуйте использовать Неправильную дробь при выполнении математических операций.

 

 

7 класс. Операции с рациональными числами

---

7 класс. Операции с рациональными числами

Рейтинг:

https://www.georgiastandards.org/Georgia-Standards/Frameworks/7th-Math-Unit-1.pdf

Common Core Standards

7.NS.1 — Применить и расширить предыдущие понимание сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.

7.NS.1a — Опишите ситуации, в которых противоположные величины объединяются в 0.

7.NS.1b — Понимание  p  +  q  как число, расположенное на расстоянии | q | от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.

7.NS.1c — Понимать вычитание рациональных чисел как сложение обратной добавки, p  —  q  =  p  + (- q ). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.

7.NS.1d — Применение свойств операций в качестве стратегий сложения и вычитания рациональных чисел.

7.NS.2 — Применять и расширять прежнее понимание умножения и деления и дробей для умножения и деления рациональных чисел.

7.NS.2a — Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1)(-1) = 1 и правила умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.

7.NS.2b — Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то -( p / q ) = (- p )/ q  = p /(-90 9 02). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.

7.NS.2c — Применение свойств операций в качестве стратегий умножения и деления рациональных чисел.

7.NS.2d — Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на Os или со временем повторяется.

7.NS.3 — Решение реальных и математических задач, связанных с четырьмя операциями с рациональными числами.

Стандарты математической практики

MP.1 Разбираться в проблемах и настойчиво решать их.

MP.2 Рассуждайте абстрактно и количественно.

Модель MP.3 с математикой.

Описание модуля

Модуль «Операции с рациональными числами» Министерства энергетики Джорджии посвящен пониманию операций с рациональными числами. Учащиеся расширяют предыдущее понимание операций с дробями на сложение, вычитание, умножение и деление рациональных чисел. Блок рассчитан на 20-25 дней и состоит из 8 заданий на выполнение. Каждое задание представлено в реальном контексте и позволяет учащимся разрабатывать свои собственные стратегии. Учащиеся моделируют операции с рациональными числами несколькими способами и ищут закономерности для создания алгоритмов.

Предупреждения

Учителя штата Коннектикут должны знать, что рабочие задания не определяют, какие стандарты (содержание или практика) учитываются. В состав блока не входят следующие компоненты:

• конструкции для реализации и выполнения исполнительских задач. Инструктивных заметок нет (ключи ответов, рубрики, образцы работ учащихся).
• дифференциация или поддержка для учащихся, работающих выше/ниже уровня своего класса, изучающих английский язык или учащихся с ограниченными возможностями.
• суммативное задание или другой тип итоговой оценки.

  No related posts.