Рациональные действительные натуральные целые числа: Числа: натуральные, целые, рациональные, иррациональные, действительные

числа (неокончено) / Хабр

Без лишних слов

pre scriptum: Любые замечания, уточнени, требования изъсниться более чётко, конструктивное участие в обсуждении приветствуются всеми конечностями (конечностями, я сказал, для тех, кто на подумал не только о конечностях: ), хотя, если прекрасная… ну, да ладно).

Числа бывают разные, но в физике используются действительные и комплексные. Для строгой последовательности построения которых требуются числа натуральные, целые, рациональные.

Натуральные числа задаются аксиомами. Чаще всего, аксиомами Пеано

1. 0 существует и это натуральное число.
2. для каждого натурального числа n определено следующее натуральное число — s(n)
3. нет такого натурального числа m, для которого s(m) = 0
4. если a != b, тo s(a) != s(b)
5. если для 0 верно свойство С, и если из того, что свойство C верно для n так же следует то, что оно верно для s(n), тогда свойство C верно для всех натуральных чисел.

Заметьте, что обозначения пунктов аксиом — это не натуральные числа. Это просто значки, чтобы их различать. Никакая конечная система не может являться натуральными числами, для какого-то элемента x в ней не будет определён s(x), который так же лежит внутри этой системы.

Пока натуральные числа выглядят так 0, s(0), s(s(0)), s(s(s(0))),… И предлагают такой взгляд на природу.

Существует 0 (впрочем, это просто обозначение). Просто существует нечто. Ну, нечто существует, в крайнем случае, существует ничто. Возьмом это нечто. Далее, сказано, но раз нечто взято, то существует и другое нечто. Можно это тоже взять, обозначить следующим к ранее взятому, нечто, но и этим наш мир не исчерпывается. Раз взяты первые несколько нечто, существует и отличное от всех них нечто’, которое можно взять и обозначить следующим к последнему из нештрихованных нечто.

В нас пытаются вселить веру в возможность бесконечно брать и брать отличные от предыдущих элементы. Является ли это интуитивной конструкцией? Так ли это в окружающем нас мире? Можно подумать, что да.

Ведь, для каждого шага необходимо взять один элемент. Но… Тонкость в том, что этот элемент должен быть отличным от всех тех, что были взяты ранее. При достаточном количестве шагов, для определения этого понадобиться гигантское хранилище информации. А как его построить? И насколько оно будет разбухать при добавлении очередного элемента? Такая простая медитация над простыми аксиомами вполне может (?) привести к гипотезе постоянно расширяющейся вселенной.

Казалось бы, можно не прибегать к динамической интерпретации этих аксиом. Например, можно сказать. Это множество N — просто существует. Натуральные числа есть, как Дао, и существуют. Но что с того, что они просто существуют? По меркам современной физики этого не достаточно. Нужно, например, чтобы электроны ‘умели’ считать интегралы Фейнмана и выделывать прочие трюки. А оперировать этим множеством ничуть не легче. Если нечто решиться найти следующий элемент для некоторого натурального числа n, то этому нечто придётся опять же проделывать громоздкую процедуру по поиску, сначала всех предыдущих элементов, а затем по поиску следующего, такого, который отличен от всех предыдущих.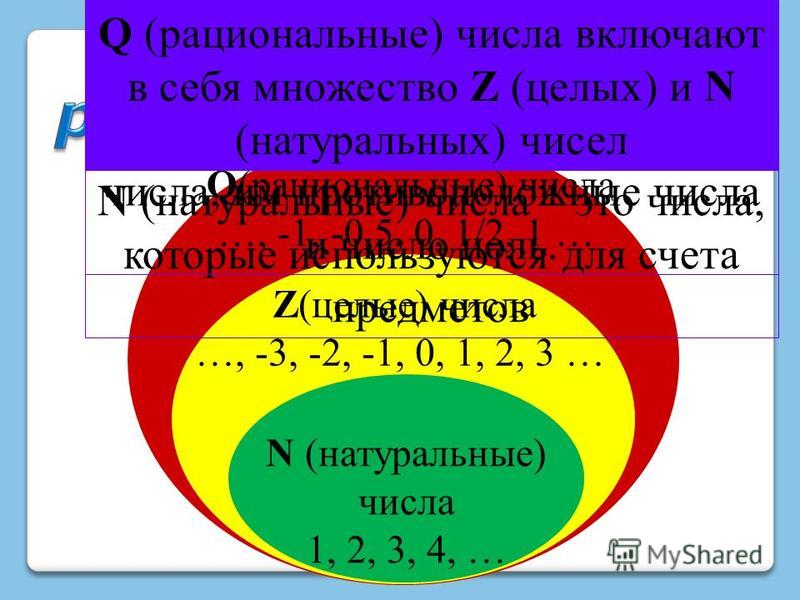

n + 1 при достаточно большом n. Чем вороны хуже людей, а компьютеры проще протонов?

Это всё странно, но из этой перепутанности сознания, возможно, есть выход. Ведь, аксиомоприменительная практика заключается в том, что нужно найти некоторую систему, в которой можно ткнуть пальцы на некоторые составляющие и состояния, увидеть, что они удовлетворяют нужной аксиоматике и торжественно объявить эту систему системой натуральных чисел, например. Но опять же не ясно, что в физике удовлетворяет этим свойствам? И вообще где бы то ни было. Уж очень требования к бесконечному продолжению жёсткие.

Сами по себе натуральные числа никому не нужны. Естественно. Хочется их умножать и складывать. Что же, это можно сделать строго, определив операции так:

1. n + 0 = n
2. n + 1 = s(n)
3. n + s(m) = s(n + m)

4. n * 0 = 0
5. n * 1 = n
6. n * s(m) = n * m + n

Номера по-прежнему — просто числа. Без доказательств (которые не трудно раздобыть) сразу скажу — из этого всего получается привычное нам умножение и сложение в столбик, и даже деление, и умение записывать числа в системах счисления. Вот теперь 1, 2, 3,… стали натуральными числами. При этом, очень интересна концепция, которая записана вторым правилом: оказывается, что понятие следующего можно заменить концепцией того, что все натуральные числа состоят из 1. То есть, можно теперь считать на палочках, а весь мир состоит из элементарных элементов.

То есть, нам показывают однородный мир. Электроны знают о том, что мир однородный? Странно. Кроме того, по прежнему сохраняется ситуация со всё возрастающей информационной сложностью. Можно взять n — натуральное число, которое, для того, чтобы отличаться от других, записано огромной цепочкой цифр, а потом попробовать взять s(n). По идее, теперь заранее известно, что взятие такого числа — это всего лишь добавление 1. Но все помнят сложение столбиком? Операция может затянуться на долго. Изменения могут быть нелокальными, информационные зависимости чудовищно длинными. Даже если природа делает это мгновенно. Даже если эта структура со сложениями существует в каждой точке. Да, кстати, если она существует в каждой точке, то вселенная уже решила все алгоритмические задачи, занятно. 654536798234235 — 1? Вслед за Эйнштейном скажем — а ничем. Не должно быть так, чтобы структура была бесконечно сложной, и значительно усложнялась при отдалении от нуля.

Но это означает, что мы можем отцентроваться теперь в числе n, и все другие числа записать, считая, что n — пуп земли. Тогда, сложность конструкций может быть ограничена. Тогда, n — 1 станет числом -1, а n + 5 — числом +5. Нормально и достаточно согласовано, пока не делать попыток понять, а что же такое -1 для начала натуральных чисел? Хм… А вот не понятно.

Поэтому, мы делаем очередное духовное усилие, свершаем акт веры и начинаем верить в то, что, а пусть 0 действительно не отличается от n. И -1 действительно существует. Это число, стоящее перед n. А перед -1 тоже должно быть нечто, ведь всё у нас равномерно. Во всех точках должна быть одинаковая структура. И получаем мы кольцо целых чисел.

Напомню, всего лишь из трёх представлений о природе вещей.

1. Всегда нечто существует.
2. Всегда можно взять следующий элемент.

3. Всё можно построить из единицы — чего-то элементарного и общего.
4. Вокруг любого элемента должна быть одинаково сложная (на самом деле, хотелось одинаково простой, но она сложная, в каждой точке существует система целых чисел) структура.

Вот и всё. Но дальше (очередной шаг в теории относительности), поверив в то, что всё состоит из 1, мы снова заставляем себя поверить в очередной факт. И единица тоже из чего-то состоит.

Можно ли её разделить на n частей? Приходит, кажется, Фалес и говорит: естественно, ученики мои. Возьмите единичный отрезок, отложите его от точки A n раз вдоль одной прямой, получите число n (ну, да, Фалес прав, действительно, процесс откладывания отрезков на прямой — это в точности применение при помощи циркуля процедуры s(n), а раз она имеет место быть с нужными свойствами, то у нас есть натуральные числа). Теперь, из точки A нарисуй другую прямую, а она есть, сиё нам гарантирует Евклид. Теперь отложи на ней единичный отрезок, конец которого соедини с числом n на другой прямой, а теперь, параллельно этому соединению, построй n прямых, проходящих через точки 1, 2, 3,… n — 1.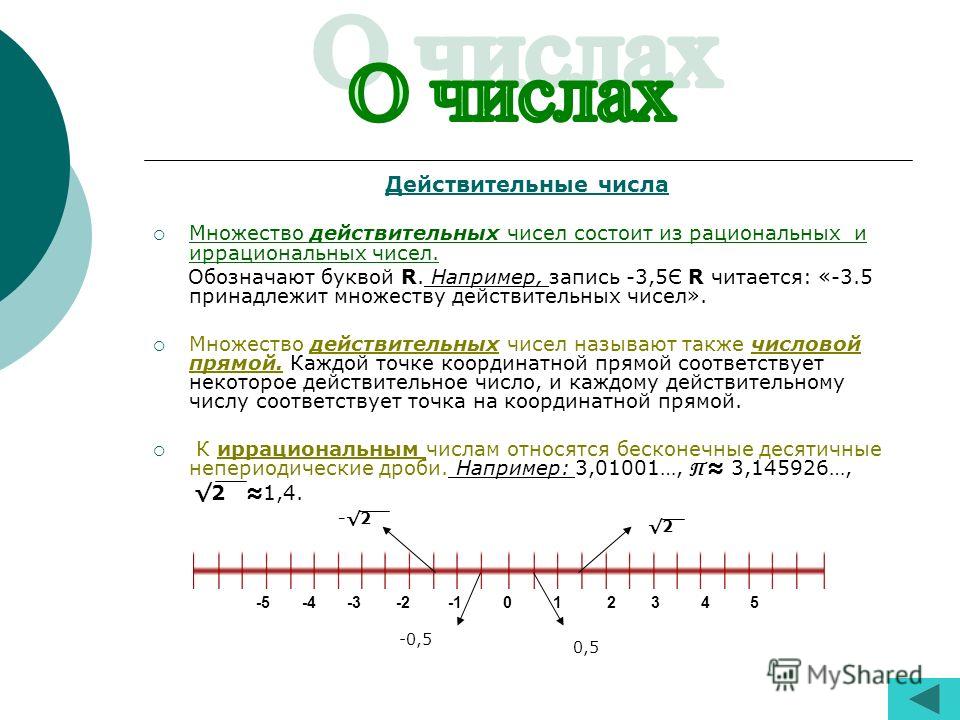

5679087 — 1, значит, как и эти числа можно разделить на соответсвующее число 1, то и 1 можно разделить на соответствующее число таких отрезков.

Но вообще говоря, в алгебре 1 имеет вполне определённые уникальные свойства. Например, для любого числа x, x * 1 = x. Имеется ли в этом противоречие с ранее написанным? Нет. Потому что ранее написанное говорит лишь о том, что сама по себе 1 никогда не ходит. В 1 нет никакого смысла. Ну а на самом деле. Скажу я вам 1. И что это будет означать? Дальше можно конечно, предположить, что я вам назвал натуральное число 1 и обсудить его свойства.

Греки не знали натуральных чисел. Зато они знали, что такое 1. 1 для них была общей мерой двух отрезков. Все помнят алгоритм Евклида по нахождению НОД? Так вот, Евклид не знал, что такое НОД, и алгоритм использовал для нахождения общей меры двух отрезков (просто вычитая (при помощи циркуля) каждый раз кратчайщий из них из более длинного, длины он определял на глазок, естественно). Но тем не менее, его интуиция не подводила, и это действительно давало общую меру отрезков.

То, что пять минут назад считалось 1, могло быть соизмерено с отрезком длиной в 1/4 (два раза поделённый поплоам при помощи циркуля и линейки отрезок), и сразу становилось ясно, что новый масштаб измерений — это 1/4 = 1′, а 1 — это теперь 4′.

Полный нигилизм и отрицание наличия чего бы то ни было основательного. Мало того, что у нас существует бесконечно сложная структура в каждом элементе вселенной, так ещё более сложная структура существует между любой парой.

Угу, а когда мы начнём задумываться над общей структурой, связывающей три элемента, куда мы попадём? Правильно, прямиком в комплексные числа. Пройдя перед этим действительные.

Можно этот процесс расписать, указать, например по ходу на то, что sqrt(2) не существует без полного построения действительных чисел, без этого построения даже теорему Пифагора строго не доказать, так что, существование действительных чисел подобно существованию 0, в аксиомах Пеано. Они просто существуют и всё. Как данность, как Дао?

И структуры там возникнут ещё более сложные.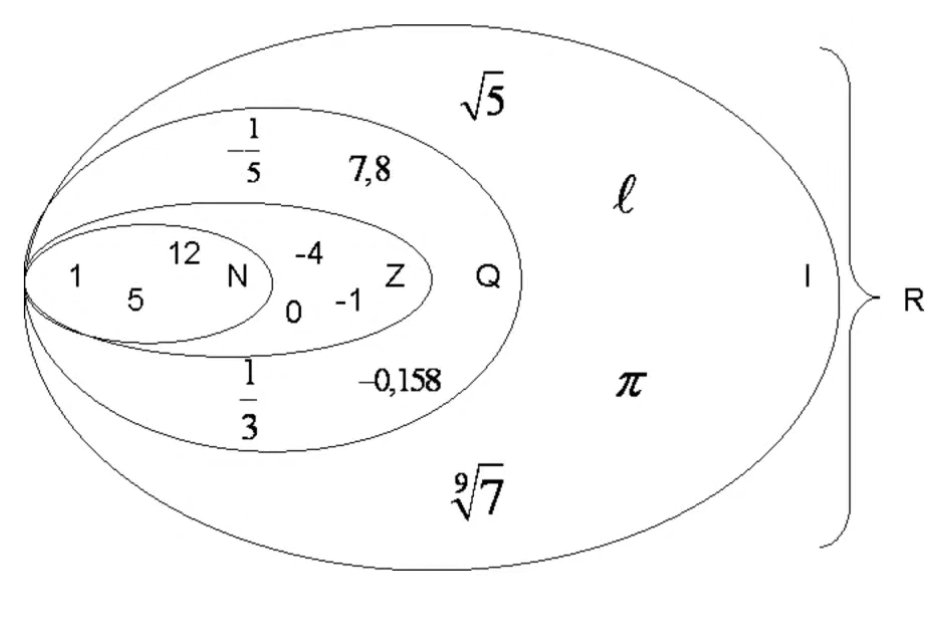 Ещё более навороченные, потому что sqrt(2) пресловутый содержит в себе бесконечно много информации, которая нужна, чтобы построить его при помощи простых движений в пространстве. Но, конечно же, его можно объявить единицей, и не беспокоиться, двигаясь по точкам sqrt(2) * N/M. Но так мы никогда не попадём в единицу.

Отношения между числами ОЧЕНЬ сложные, если смотреть на них не в терминах аксиом, а пытаясь найти житейскую трактовку всего этого множества концепций. При этом, единственный способ принять их существование — это поверить в то, что они существуют все скопом, сразу же и безгранично, здесь и сейчас, во всей своей сложности и (вобщем-то) великолепии.

Но при этом, ситуация сильно дуальная. Числа не могут сами себя складывать. Да, может существовать трёхмерное множество (x, y, z) с тем свойством, что z = x + y. Но… А зачем мы тогда вообще пыхтим и складываем числа столбиком? Где это множество? Как получить к нему доступ? Тут самое время уверовать в единое информационное пространство, в котором всё есть, и из которого индийские факиры черпают данные, когда складывают офигеннозначные числа в уме за пять секунд.

Но знаете, это fake. И вот почему. Потому что сложение, даже через доступ к этому множеству — это всё-равно операция. Действие, более того, исполнение действия. Поэтому, единственная, предлагаемая математикой трактовка: это просто существует, несоответствует действительности.

При этом, ситуация меняется, если мы начнём воспринимать математику, как язык (как и нужно её вобщем-то воспринимать). Это всего лишь способ описать (при этом даже не объекты, хотя выглядит всё именно как описание объектов) процесс. Например, аксиомы Пеано, показанные математикам сказали им о том, как они могут конструировать натуральные числа, а договорённость с определениями операций + и * позволила поднять эффективность конструирования на очень высокий уровень. Не существует натуральных чисел, существуют математики динамически интерпретирующие аксиоматику Пеано.

Так же и со всем. Аксиомы нам просто говорят: если у тебя есть нечто, в чём ты видишь такие-то и такие-то свойства, то ты можешь делать с ним то-то и то-то, и при этом свойства эти сохранятся.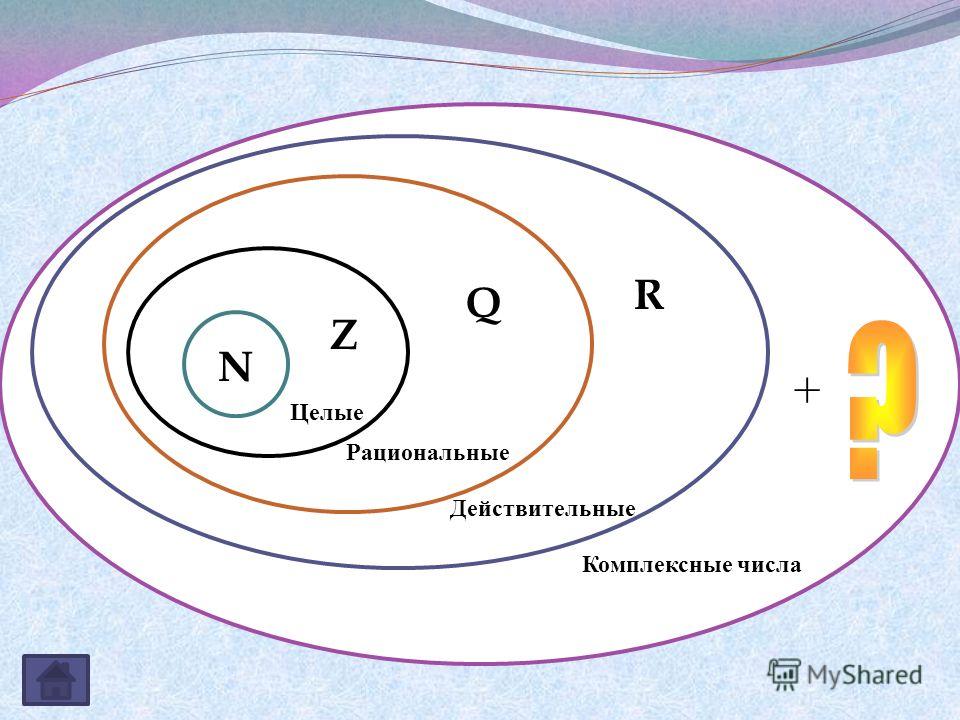 Ну, на самом деле, процессор может выполнять операции с кольцами целых остатков (ну, операции по модулю какому-нибудь). Может. Но означает ли это, что множество существует для процессора? То, что для него существует математика в каждом из его состояний? А если процессор сломать, куда денется вся эта сложная структура?

Вобщем вот. Всё это вызывает первую стадию когнитивного диссонанса при восприятии современных построений теоретической физики. Будь то теория относительности, которая движется по пути, намеченному для целых и рациональных чисел, и заявляет, что везде всё должно быть однообразным, одинаковым, и двигаться мы можем только со скоростью света, по заранее созданным траекториям. И всего этого чуда очень сложная структура.

Или будь то квантовая физика, в которой очевидно делимые и дискретные вещи пытаются описывать бесконечно сложным и бесконечно делимым, бесконечно неспособным различить сосотояния, если они не сопоставлены извне системы с другими состояниями (хотя, эта формулировка очень важна, для понимания того, что же такое физический эксперимент). Хорошо, бесконечную и величественную сложность и предрешённость пространства-времени ещё можно принять. Но то, что электрон знает обо всём том же, о чём знаем мы, ставя над ним эксперимент… Хм. Звучит странновато, пока мы не примем то, что электрон (ну, или любое наблюдаемое явление) — это не элементарный элемент вселенной, а элементарная составляющая нашего эксперимента.

Ладно. Я действительно не могу написать это точнее. Я пробовал четыре дня, и ничего не выходит, кроме такого вот потока сознания. Хотя, если без привязки к реальности, я запросто могу вам изложить основные концепции и выводы хоть теории чисел, хоть теории относительности, хоть квантовой хромодинамики (тут мне, впрочем, понадобиться подглядывать в учебник).

Но связать всё с тем, что мы видим вокруг — очень сложно. И основной причиной после всех переживаний (я подчёркиваю, переживаний, а не анализа) связанных с этими размышлениями, я могу назвать только одну: математика оперируют статичными объектами. Вот, хоть тресни. Даже машина Тьюринга лучше всего представима, как некая траектория (о чём я напишу позже) в некотором пространстве состояний.

Именно поэтому, вся математика разваливается, когда мы пишем программы, которые активно общаются со внешним миром. Внешний мир изменчив, а математика нет. Она должна работать в любой точки пространства и времени, с любой скоростью, с предельной точностью. Так бывает, если в этой точке пространства присутствует достаточно умный интерпретатор или интерпретаторы математического языка. Но что если там нет никакого интерпретатора?

И ещё вопрос: так почему физика пытается оперировать только такими вневременными конструкциями, пытаясь описать очевидно динамичную систему? Уж не поэтому ли у физиков возникают парадоксы и ‘антиинтуитивные’ конструкции в теориях?

Хотите пример? Всё тот же электрон. Для физиков было существенной перетряской представлений, когда появилось уравнение Шрёдингера, которое разрешало электрону жить только на определённых энергетических уровнях. А зачем это уравнение усердно искалось? Чтобы разрешить противоречие в классической электродинамике, которая предписывает болтающемуся вокруг протона электрону вскорости потерять всю энергию и рухнуть на этот протон, чего не происходит. А должно происходить, согласно анализу траекторий и прочих существующих вне времени математических конструкций.

Но, ведь, всё очевидно… Надо только принять то, что электрон подвижен. И это основное его свойство: ни положение в точке, ни обладание энергией, а подвижность. Соответсвенно, он просто не может упасть на протон. Он не может быть в точке — это нонсенс. Собственно, любая элементарная частица этому нонсенсу и сопротивляется. Принцип неопределённости Гейзенберга как раз об этом — фига вы задавите электрон в точку, потому что вам энергии на это не хватит, чтобы сдержать его флуктуации. Это логично. Никакого нонсенса… Но про время я попишу позже. И, надеюсь, построже, потому что там не будет ковыряния в элементарных основаниях теорий.

Классификация действительных чисел | Магазин развивающей математики

Результаты обучения

• Определение рациональных и иррациональных чисел
• Классифицировать различные типы действительных чисел

Вещественные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или –). В этом разделе мы дополнительно определим действительные числа и используем их свойства для решения линейных уравнений и неравенств.

Для начала мы рассмотрим натуральные числа, целые числа и целые числа, которые уже были рассмотрены в этом курсе. Затем мы более подробно обсудим рациональные числа и иррациональные числа.

Натуральные числа

Самые известные числа — это натуральные числа (иногда называемые счетными числами): [латекс]1, 2, 3[/латекс] и так далее. Это числа, которые мы используем для подсчета или перечисления предметов. Математический символ для множества всех натуральных чисел записывается как [латекс]\mathbb{N}[/латекс]. Мы описываем их в системе обозначений как [латекс]\{1, 2, 3, …\}[/латекс], где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно же, также называются 9.0017 подсчет чисел . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел.

Целые числа

Множество целых чисел включает все натуральные числа, а также [латекс]0[/латекс]: [латекс]\{0, 1, 2, 3,…\}[/латекс].

Целые числа

Когда набор отрицательных чисел объединяется с набором натуральных чисел (включая 0), результат определяется как набор целых чисел [latex]\mathbb{Z}[/latex]. Набор из 9 0027 целых чисел  добавляет противоположности натуральных чисел к набору целых чисел: {…−3,−2,−1,0,1,2,3,…}{…−3,−2,−1,0 ,1,2,3,…}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел. В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом состоит в том, что натуральные числа являются подмножеством целых чисел.

[латекс]\begin{array}{lll}{\text{целые отрицательные}}\hfill & {\text{ноль}}\hfill & {\text{целые положительные числа}}\\{\dots, -3 ,-2,-1,}\hfill & {0,}\hfill & {1,2,3,\dots }\end{массив}[/latex]

Рациональные числа

Какие числа вы бы получили, если бы начали со всех целых чисел, а затем включили все дроби? Числа, которые вы получили бы, образуют множество рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.

Рациональные числа

Рациональное число — это число, которое можно записать в виде [латекс]{\большой\разрыв{р} {q}}[/латекс], где [латекс]р[/латекс] и [ латекс]q[/латекс] являются целыми числами и [латекс]q\ne 0[/латекс].

Рациональное число [латекс]\mathbb{Q}[/латекс] — это число, которое можно представить в виде дроби с целым числителем и положительным целым знаменателем. Набор из рациональных чисел записывается как [латекс]\left\{\dfrac{m}{n}\normalsize |m\text{ и }{n}\text{ являются целыми числами, а }{n}\ne{ 0 }\право\}[/латекс]. Обратите внимание на определение, что рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен [latex]0[/latex]. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом со знаменателем [латекс]1[/латекс].

Все дроби, как положительные, так и отрицательные, являются рациональными числами.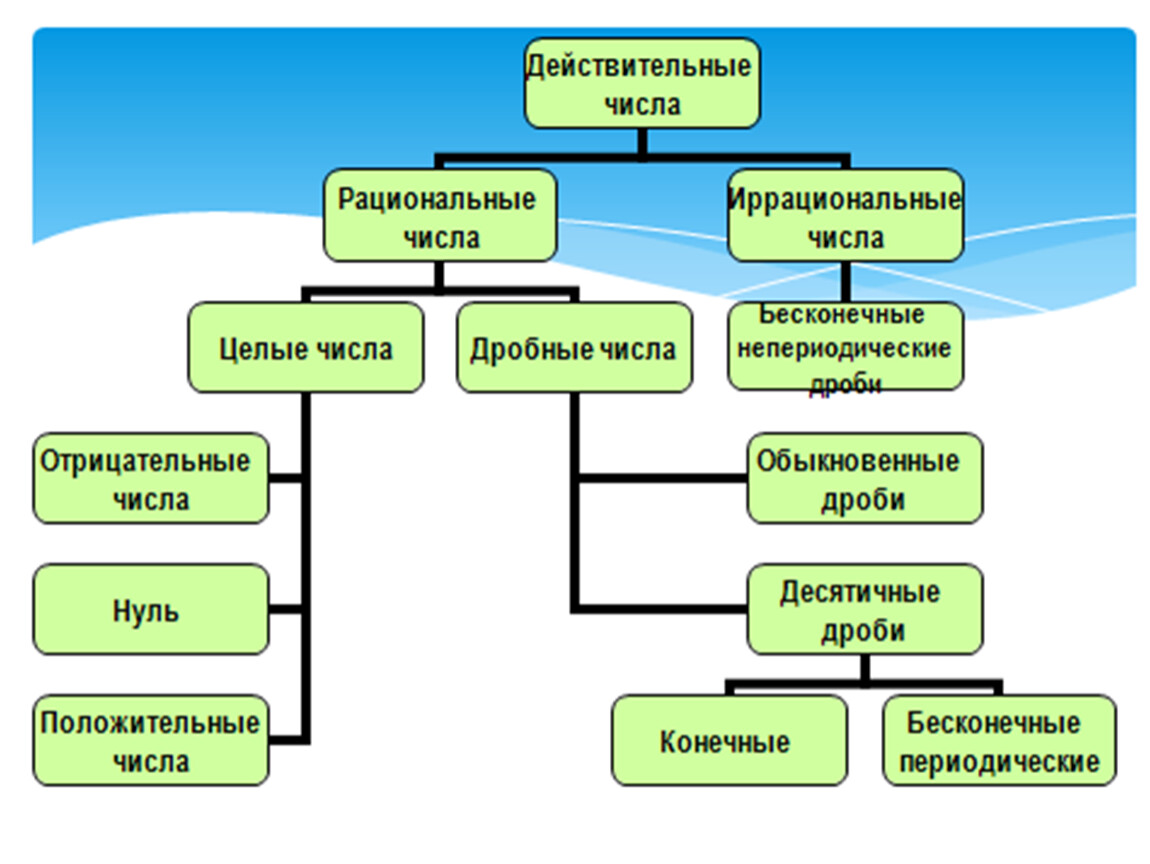 Вот несколько примеров:

[латекс]\Large\frac{4}{5}\normalsize,-\Large\frac{7}{8}\normalsize,\Large\frac{13}{4}\normalsize,\ text{and}-\Large\frac{20}{3}[/latex]

Каждый числитель и каждый знаменатель являются целыми числами.

Нам нужно просмотреть все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы рассмотрим счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.

Целые числа рациональны

Целые числа рациональны? Чтобы решить, является ли целое число рациональным, мы пытаемся записать его как отношение двух целых чисел. Самый простой способ сделать это — записать дробь со знаменателем один.

[латекс]3=\Large\frac{3}{1}\normalsize ,\space-8=\Large\frac{-8}{1}\normalsize ,\space0=\Large\frac{0}{ 1}[/latex]

Поскольку любое целое число можно представить как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.

Десятичные дроби рациональны

Что насчет десятичных дробей? Являются ли они рациональными? Давайте рассмотрим несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа являются рациональными числами. Целое число [латекс]-8[/латекс] можно записать как десятичное число [латекс]-8.0[/латекс]. Итак, ясно, что некоторые десятичные дроби рациональны.

Подумайте о десятичной дроби [латекс]7.3[/латекс]. Можем ли мы записать это как отношение двух целых чисел? Поскольку [latex]7.3[/latex] означает [latex]7\Large\frac{3}{10}[/latex], мы можем записать его в виде неправильной дроби: [latex]\Large\frac{73}{10 }[/латекс]. Итак, [латекс]7,3[/латекс] — это отношение целых чисел [латекс]73[/латекс] и [латекс]10[/латекс]. Это рациональное число.

В общем, любое десятичное число, которое заканчивается после нескольких цифр, таких как [латекс]7. 3[/латекс] или [латекс]-1.2684[/латекс], является рациональным числом. Мы можем использовать разрядное значение последней цифры в качестве знаменателя при записи десятичной дроби.

пример

Запишите каждое как отношение двух целых чисел:

1. [латекс]-15[/латекс]

2. [латекс]6.81[/латекс]

3. [латекс]-3\Large \frac{6}{7}[/latex]

Решение:

1.
	[латекс]-15[/латекс]
Запишите целое число в виде дроби со знаменателем 1.	[латекс]\большой\фрак{-15}{1}[/латекс]

2.
	[латекс]6.81[/латекс]
Запишите десятичную дробь как смешанное число.	[латекс]6\Большой\фракция{81}{100}[/латекс]
Затем преобразуйте его в неправильную дробь.	[латекс]\большой\фрак{681}{100}[/латекс]

«>

3.
	[латекс]-3\Большой\фрак{6}{7}[/латекс]
Преобразуйте смешанное число в неправильную дробь.	[латекс]-\Большой\фрак{27}{7}[/латекс]

 

попробуйте

Рациональные числа в виде десятичных дробей

Давайте посмотрим на десятичную форму чисел, которые, как мы знаем, являются рациональными. Мы видели, что каждое целое число является рациональным числом, поскольку [latex]a=\Large\frac{a}{1}[/latex] для любого целого числа [latex]a[/latex]. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.

Целое [латекс]-2,-1,0,1,2,3[/латекс]

Десятичное [латекс]-2.0,-1.0,0.0,1.0,2.0,3.0[/латекс]

Эти десятичные цифры останавливаются.

Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму дробей, которые мы только что рассмотрели.

Отношение целых чисел [латекс]\Large\frac{4}{5}\normalsize ,\Large\frac{7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\ frac{20}{3}[/latex]

Десятичные формы [латекс]0,8,-0,875,3,25,-6,666\ldots,-6. \overline{66}[/latex]

Эти десятичные дроби либо останавливаются, либо повторяются.

О чем говорят вам эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассмотрели, выраженные в виде отношения целых чисел и десятичных дробей.

Рациональные числа
	Дроби	Целые числа
Номер	[латекс]\Large\frac{4}{5}\normalsize,-\Large\frac{7}{8}\normalsize,\Large\frac{13}{4}\normalsize,\Large\frac{- 20}{3}[/латекс]	[латекс]-2,-1,0,1,2,3[/латекс]
Отношение целого числа	[латекс]\Large\frac{4}{5}\normalsize ,\Large\frac{-7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\frac{- 20}{3}[/латекс]	[латекс]\Large\frac{-2}{1}\normalsize ,\Large\frac{-1}{1}\normalsize ,\Large\frac{0}{1}\normalsize ,\Large\frac{ 1}{1}\normalsize ,\Large\frac{2}{1}\normalsize ,\Large\frac{3}{1}[/latex]
Десятичное число	[латекс]0,8,-0,875,3,25,-6. \overline{6}[/латекс]	[латекс]-2.0,-1.0,0.0,1.0,2.0,3.0[/латекс]

 

Поскольку это дроби, любое рациональное число также может быть представлено в десятичной форме. Любое рациональное число может быть представлено как:

1. завершающая десятичная дробь: [латекс]\dfrac{15}{8}\normalsize =1,875[/латекс] или
2. повторяющееся десятичное число: [латекс]\dfrac{4}{11}\normalsize =0,36363636\dots =0.\overline{36}[/latex]

Мы используем линию, проведенную над повторяющимся блоком чисел, вместо многократного написания группы.

 

Пример

Каждое из следующих чисел запишите в виде рационального числа.

1. [латекс]7[/латекс]
2. [латекс]0[/латекс]
3. [латекс]–8[/латекс]

Показать решение

Пример

Запишите каждое из следующих рациональных чисел либо как завершающее, либо как повторяющееся десятичное число.

1. [латекс]-\dfrac{5}{7}[/латекс]
2. [латекс]\dfrac{15}{5}[/латекс]
3. [латекс]\dfrac{13}{25}[/латекс]

Показать решение

Иррациональные числа

Существуют ли десятичные дроби, которые не заканчиваются и не повторяются? Да. В какой-то момент в далеком прошлом кто-то обнаружил, что не все числа являются рациональными числами. Строитель, например, мог обнаружить, что диагональ квадрата с единичными сторонами равна не [латекс]2[/латекс] и даже не [латекс]\dfrac{3}{2}[/латекс], а чему-то другому. . Или швейник мог заметить, что отношение длины окружности к диаметру рулона ткани немного больше, чем [латекс]3[/латекс], но все же это не рациональное число. Число [латекс]\пи [/латекс] (греческая буква пи, произносится как «пирог»), очень важное для описания кругов, имеет десятичную форму, которая не заканчивается и не повторяется ([латекс]\пи =\текст {3.141592654…….}[/латекс]). Такие числа называются иррациональными , потому что их нельзя записать в виде дробей. Эти числа составляют набор из иррациональных чисел . Иррациональные числа не могут быть представлены в виде дроби от двух целых чисел. Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно не рационально. Итак, мы пишем это как {h | h не является рациональным числом}.

Точно так же десятичные представления квадратных корней чисел, которые не являются полными квадратами, никогда не останавливаются и никогда не повторяются. Например,

[латекс]\sqrt{5}=\текст{2.236067978…..}[/латекс]

Десятичное число, которое не заканчивается и не повторяется, не может быть записано как отношение целых чисел. Мы называем такие числа иррациональными числами.

Иррациональное число

Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не прерывается и не повторяется.

Давайте обобщим метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа

• останавливается или повторяется, число является рациональным.
• не останавливается и не повторяется, число иррациональное.

пример

Определите каждое из следующего как рациональное или иррациональное:
1. [латекс]0,58\overline{3}[/латекс]
2. [латекс]0,475[/латекс]
3. [латекс]3,605551275\ точки [/латекс]

Показать решение

 

попробуйте

 

Давайте теперь подумаем о квадратных корнях. Квадратные корни из полных квадратов всегда являются целыми числами, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются идеальными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.

пример

Определите каждое из следующего как рациональное или иррациональное:
1. [латекс]\sqrt{36}[/латекс]
2. [латекс]\sqrt{44}[/латекс]

Показать решение

 

попробуйте

В следующем видео мы покажем больше примеров того, как определить, является ли число иррациональным или рациональным.

Пример

Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если оно рационально, определите, является ли оно завершающим или повторяющимся десятичным числом.

1. [латекс]\sqrt{25}[/латекс]
2. [латекс]\dfrac{33}{9}[/латекс]
3. [латекс]\sqrt{11}[/латекс]
4. [латекс]\dfrac{17}{34}[/латекс]
5. [латекс]0.3033033303333\точки[/латекс]

Показать решение

Действительные числа

Для любого числа n мы знаем, что n либо рационально, либо иррационально. Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор из действительных чисел .

Действительные числа

Действительные числа — это числа, которые могут быть рациональными или иррациональными.

Реальные числа включают в себя все измеренные числа. Символ для действительных чисел [латекс]\mathbb{R}[/латекс]. Действительные числа обычно представляются десятичными числами. Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или –). Ноль не считается ни положительным, ни отрицательным.

Действительные числа можно изобразить на горизонтальной числовой прямой с произвольной точкой, выбранной как [latex]0[/latex], с отрицательными числами слева от [latex]0[/latex] и положительными числами справа от [латекс]0[/латекс]. Затем используется фиксированное единичное расстояние, чтобы отметить каждое целое число (или другое базовое значение) по обе стороны от [latex]0[/latex]. Каждое действительное число соответствует уникальной позиции на числовой прямой. Верно и обратное: каждое место на числовой прямой соответствует ровно одному вещественному числу. Это известно как переписка один на один. Мы называем это строка реального числа , как показано ниже.

Действительная числовая линия.

 

Пример

Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Находится ли число слева или справа от 0 на числовой прямой?

1. [латекс]-\dfrac{10}{3}[/латекс]
2. [латекс]\sqrt{5}[/латекс]
3. [латекс]-\sqrt{289}[/латекс]
4. [латекс]-6\пи[/латекс]
5. [латекс]0.615384615384\точки[/латекс]

Показать решение

Мы видели, что все счетные числа являются целыми числами, все целые числа являются целыми числами и все целые числа являются рациональными числами. Иррациональные числа представляют собой отдельную категорию. Когда мы складываем рациональные числа и иррациональные числа, мы получаем множество действительных чисел. Начав с натуральных чисел, мы расширили каждый набор, чтобы сформировать больший набор, а это означает, что между наборами чисел, с которыми мы сталкивались до сих пор, существует отношение подмножества. Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.

На этой диаграмме показаны отношения между различными типами действительных чисел.

Вот еще одна визуализация подмножеств действительных чисел.

Наборы цифр. N : множество натуральных чисел W : множество целых чисел I : множество целых чисел Q : множество рациональных чисел Q´ : множество иррациональных чисел

A Общее примечание : Наборы цифр

Набор из натуральных чисел включает числа, используемые для счета: [латекс]\{1,2,3,\точки\}[/латекс].

Набор из целых чисел — это набор натуральных чисел и нуля: [латекс]\{0,1,2,3,\точки\}[/латекс].

Набор из целых чисел добавляет отрицательные натуральные числа к набору целых чисел: [латекс]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[ /латекс].

Набор из рациональных чисел включает дроби, записанные как [латекс]\{\dfrac{m}{n}\normalsize |m\text{ и }n\text{ являются целыми числами и }n\ne 0\}[ /латекс].

Набор из иррациональных чисел — это набор нерациональных чисел. Это неповторяющиеся и неконечные десятичные числа: [латекс]\{ч|ч\текст{ не является рациональным числом}\}[/латекс].

Вам не кажется странным термин «действительные числа»? Существуют ли числа, которые не являются «настоящими», и если да, то какими они могут быть? На протяжении веков единственными числами, о которых люди знали, были те, которые мы сейчас называем реальными числами. Затем математики открыли множество из мнимых чисел. В этом модуле вы не столкнетесь с мнимыми числами, но вы столкнетесь с ними позже при изучении алгебры.

пример

Определите, является ли каждое из чисел в следующем списке 1. целым числом, 2. целым числом, 3. рациональным числом, 4. иррациональным числом и 5. действительным числом.

[латекс]-7,\Large\frac{14}{5}\normalsize ,8,\sqrt{5},5.9,-\sqrt{64}[/latex]

Решение:
1. Целое числа [латекс]0,1,2,3\точки[/латекс] Число [латекс]8[/латекс] — единственное заданное целое число.

2. Целые числа — это целые числа, их противоположности и [латекс]0[/латекс]. Из заданных чисел [латекс]-7[/латекс] и [латекс]8[/латекс] являются целыми числами. Также обратите внимание, что [латекс]64[/латекс] является квадратом [латекса]8[/латекса], поэтому [латекс]-\sqrt{64}=-8[/латекс]. Итак, целые числа равны [латекс]-7,8,-\sqrt{64}[/латекс].

3. Поскольку все целые числа рациональны, числа [латекс]-7,8,\текст{и}-\sqrt{64}[/латекс] также рациональны. Рациональные числа также включают дроби и десятичные дроби, которые заканчиваются или повторяются, поэтому [latex]\Large\frac{14}{5}\normalsize\text{and}5. 9[/latex] рациональны.

4. Число [латекс]5[/латекс] не является полным квадратом, поэтому [латекс]\sqrt{5}[/латекс] иррационально.

5. Все указанные номера действительны.

Сведем результаты в таблицу.

Номер	Целиком	Целое число	Рационал	Иррациональный	Реальный
[латекс]-7[/латекс]		[латекс]\quad\галочка [/латекс]	[латекс]\quad\галочка [/латекс]		[латекс]\quad\галочка [/латекс]
[латекс]\большой\фрак{14}{5}[/латекс]			[латекс]\quad\галочка [/латекс]		[латекс]\quad\галочка [/латекс]
[латекс]8[/латекс]	[латекс]\quad\галочка [/латекс]	[латекс]\quad\галочка [/латекс]	[латекс]\quad\галочка [/латекс]		[латекс]\quad\галочка [/латекс]
[латекс]\sqrt{5}[/латекс]				[латекс]\quad\галочка [/латекс]	[латекс]\quad\галочка [/латекс]
[латекс]5. 9[/латекс]			[латекс]\quad\галочка [/латекс]		[латекс]\quad\галочка [/латекс]
[латекс]-\sqrt{64}[/латекс]		[латекс]\quad\галочка [/латекс]	[латекс]\quad\галочка [/латекс]		[латекс]\quad\галочка [/латекс]

Пример

Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).

1. [латекс]\sqrt{36}[/латекс]
2. [латекс]\dfrac{8}{3}[/латекс]
3. [латекс]\sqrt{73}[/латекс]
4. [латекс]-6[/латекс]
5. [латекс]3.2121121112\точки [/латекс]

Показать решение

 

попробуй

Следующий мини-урок содержит больше примеров того, как классифицировать действительные числа.

Поддержите!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Рабочие листы | TPT

от

My Nerdy Teacher от Alina V

$100.00

$19.00

! (СТОИМОСТЬ 100 долл. США) Вы ищете веселые и увлекательные занятия по программе Reading Intervention, связанные с наукой о чтении? Получите МЕГАНАБОР Ultimate Phonics Reading Intervention всего за 19 долларов США! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти упражнения помогут вашим ученикам практиковать фонетические модели, которые вы преподаете

Предметы:

Акустика, чтение, письмо

Классы:

ПреК — 1-й

Типы:

Мероприятия, Центры, Печатные формы

CCSS:

РФ. К.1, РФ.К.1а, РФ.К.1б, РФ.К.1с, РФ.К. 1d…

by

My Nerdy Teacher by Alina V

$100,00

$19,00

⭐⭐⭐ FLASH SALE ⭐⭐⭐Купите The Decodable Readers Just Mega Bundle за $9! Спешите, время истекает! Ваши ученики могут практиковаться в чтении весело и увлекательно, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 2-й

Виды:

Занятия, Центры, Печатные формы

CCSS, RFK.3d.K.3.K. .K.3c, RF.1.2c, RF.1.2d…

by

Lucky Little Learners

128,00 $

34,99 $

Это годовой набор из 576 дифференцированных вопросов по чтению 2-го класса и трем отрывкам на понимание. разные уровни. Эти отрывки для беглого чтения меняют правила игры! Цифровые отрывки и вопросы для понимания прочитанного во 2-м классе также включены! ⭐️Загрузите файл предварительного просмотра, чтобы увидеть каждый заголовок! ⭐️Хотите улучшить беглость чтения? Каждый отрывок для понимания прочитанного во 2-м классе включает подсчет слов и трекер беглости. Идеально подходит для повторного чтения и практики беглости чтения.

Предметы:

Английский язык, чтение, стратегии чтения

Классы:

Типы:

Оценка, печатные формы

CCSS:

, RL.2.1, RL.2.2 .2.5…

by

Aimee’s Edventures LLC

10,75 $

5,50 $

У меня разрывалось сердце, когда я смотрел, как мои ученики бродят по комнате, пытаясь не заплакать, когда я сказал: «Пожалуйста, найдите себе партнера». Вот я и создал эти открытки! Теперь их любят тысячи учителей, которые преследуют одну и ту же цель — включить всех учащихся в свой класс.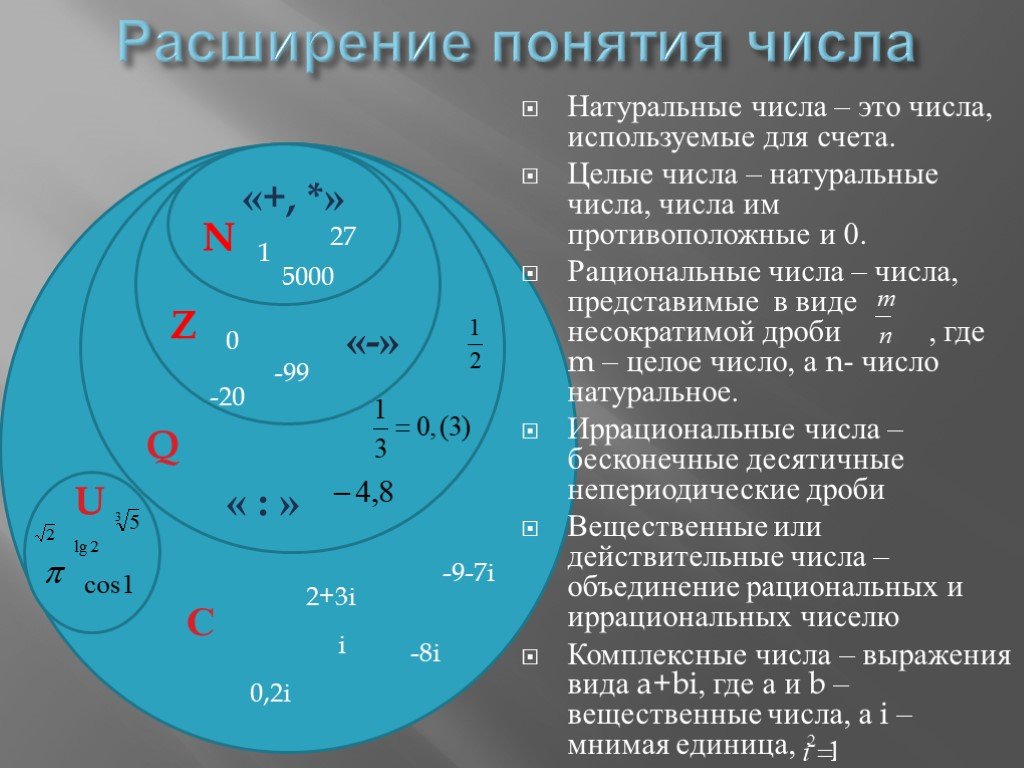 Эти партнерские карточки позволяют быстро и легко организовать дифференцированную работу в малых группах и идеально подходят для детей с любым уровнем способностей. Самое приятное то, что им не нужно угадывать, кто их партнер, это прямо на карте (whi

Темы:

Вернуться в школу, сообщество классных комнат, управление классом

Оценки:

Не Оценка. Teaching Pal

22,00 $

15,00 $

Bundle

Этот комплект содержит ОГРОМНЫЕ 263 математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D

Предметы:

Основные операции, математика, числа

Классы:

Типы:

Печатные формы, рабочие тетради, рабочие листы

by

My Teaching Pal .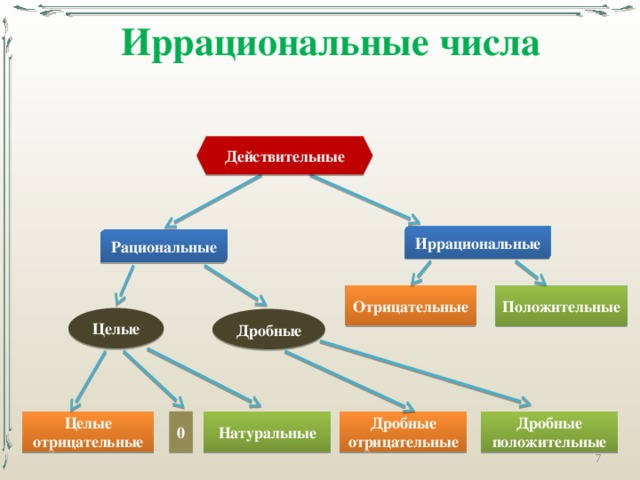 Он включает рабочие листы для орграфов ch, sh, th, ph и wh. Бонусное включение диграфов ph и wh идеально подходит для того, чтобы бросить вызов вашим ученикам с более высокими способностями. Пакет включает в себя 42 увлекательных рабочих листа, которые позволяют учащимся практиковаться в написании диграфов, чтении диграфов, определении звуков диграфов и многому другому! Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и

Предметы:

Английский языковой искусство, Фоника, чтение

Оценки:

K — 2 -й

Типы:

Центры, печатные изготовления, рабочие листы

по

Обучение с горой

$ 22.

Обучение с горой

$ 22.

11111111111111111111110.

Bundle

Этот НАБОР из трех ресурсов со скидкой включает 90 печатных (и ЦИФРОВЫХ!) страниц для обучения, повторения и применения навыков чтения и письма! В комплект включены следующие ресурсы: Использование иллюстраций для обучения навыкам чтения 40 страниц, обучающих 8 основным навыкам чтения. Каждому навыку чтения посвящено пять страниц! Использование иллюстраций для обзора смешанных навыков чтения20 страниц, посвященных основным навыкам чтения. На каждой странице рассматриваются различные навыки чтения. Использование иллюстраций для обучения изобразительному языку15, стр.

Subjects:

English Language Arts, Reading, Reading Strategies

Grades:

3rd — 5th

Types:

Centers, Printables

by

Melissa Mazur

$15.00

$12.00

These third grade отрывки по беглости чтения и пониманию содержат 30 готовых к печати отрывков (15 художественных и 15 научно-популярных). Каждый уровневый отрывок находится в диапазоне 520L и 830L и содержит от 196 до 222 слов. Используйте вопросы на понимание, чтобы оценить понимание после того, как учащиеся прочитают текст! *ОБНОВЛЕНИЕ* Теперь вы можете поделиться этим со своими учениками в цифровом виде! Этот ресурс был создан с помощью Google Forms.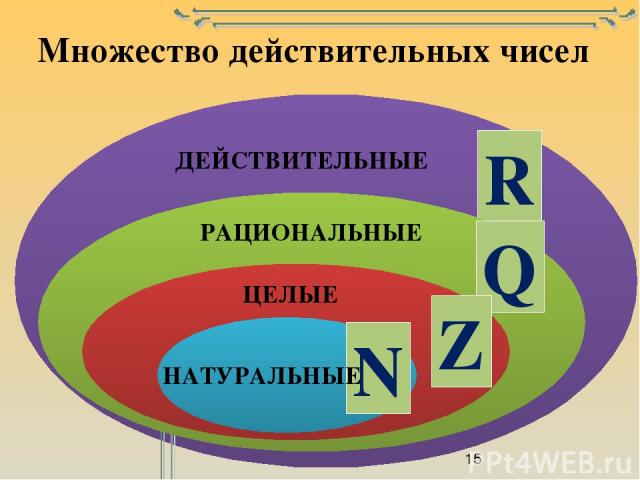 Для использования у вас должна быть электронная почта Google. Каждому проходу можно присвоить в Google Classr

Предметы:

Чтение

Классы:

Типы:

Деятельность, оценка

CCSS:

RF.3.4, RF.3.4a, RF.0111c Также включены 9 в: RF.0111c 9 НАБОР отрывков для чтения и беглости чтения – скидка 30%

на

Teaching Trove

242,00 $

20,00 $

Этот массивный набор из 123 первоклассных и второстепенных центров обучения грамоте обеспечивает идеальный способ обеспечить увлекательное, в течение года. Все центры имеют аналогичный формат, что делает их идеальными для самостоятельной практики, оставляя вам больше времени для обучения с меньшим количеством перерывов! Отлично подходит для центров или быстрых финишеров, с этим пакетом вы сможете легко дифференцировать потребности всем вашим ученикам с огромным выбором игр на выбор.Каждое общее ядро ​​соответствует

Предметы:

Английский язык, акустика, правописание

Классы:

1–2

CCSS:

RF. 1.1a, RF.1.2, RF.1.2a, RF.1.2b, RF.1.2b, RF.1.2b c…

by

My Teaching Pal

13,75 $

10,00 $

Bundle

Этот комплект содержит очень много забавных математических листов для учащихся детского сада. Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и повторения. Рабочие листы охватывают сложение и вычитание до 10, разрядное значение, 2D и 3D-фигуры и числа до 20. Включено в общей сложности 126 рабочих листов, которые отлично подходят для использования круглый год. Этот комплект состоит из следующих пакетов: Рабочие листы для детского сада на сложение и вычитание. Детский сад Числа до 20. Работа 9.0011

Объекты:

Основные операции, математика, номера

Оценки:

Prek — 1st

Типы:

Центры, печатные изделия, рабочие листы

по

Обучение с горой

$ 27.54

$

. Bundle

Читайте и понимайте художественную литературу и информационные тексты с помощью идеального комплекта для чтения и повторения. Это лучший набор для проверки навыков чтения на ВЕСЬ ГОД. «Быстрое чтение и повторение» — идеальный способ вовлечь учащихся в актуальную и тщательную проверку навыков чтения! Этот набор обзоров — идеальный способ поддерживать навыки чтения у ваших учеников ИЛИ помочь вам обучить их навыкам. Его можно использовать в центрах, небольших группах, всем классом или в качестве домашнего задания для повторения основного информационного текста com

Темах:

закрытие чтения, английский язык, стратегии чтения

Оценки:

4th — 5th

Типы:

Мероприятия, центры

CCS:

RL.4.1, RL.4.2, RL.4.3 , RL.4.4, RL.4.5…

by

Kaitlynn Albani

Внутри вы найдете 60 отрывков для понимания детского сада! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете.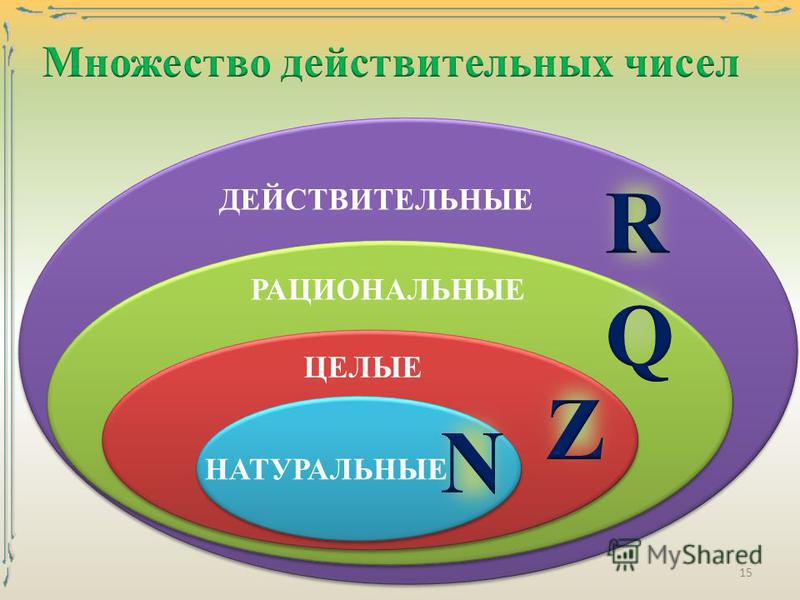 В комплекте много разнообразия. Пожалуйста, проверьте изображения и просмотрите, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый

Subjects:

English Language Arts, Reading, Reading Strategies

Grades:

K — 1st

Types:

Centers, Printables, Worksheets

by

My Teaching Pal

$12.50

$8.00

Bundle

Предложите своим ученикам попрактиковаться во всем, что связано с алфавитом, с помощью этого ОГРОМНОГО комплекта рабочих листов по алфавиту. Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Всего включено 104 рабочих листа.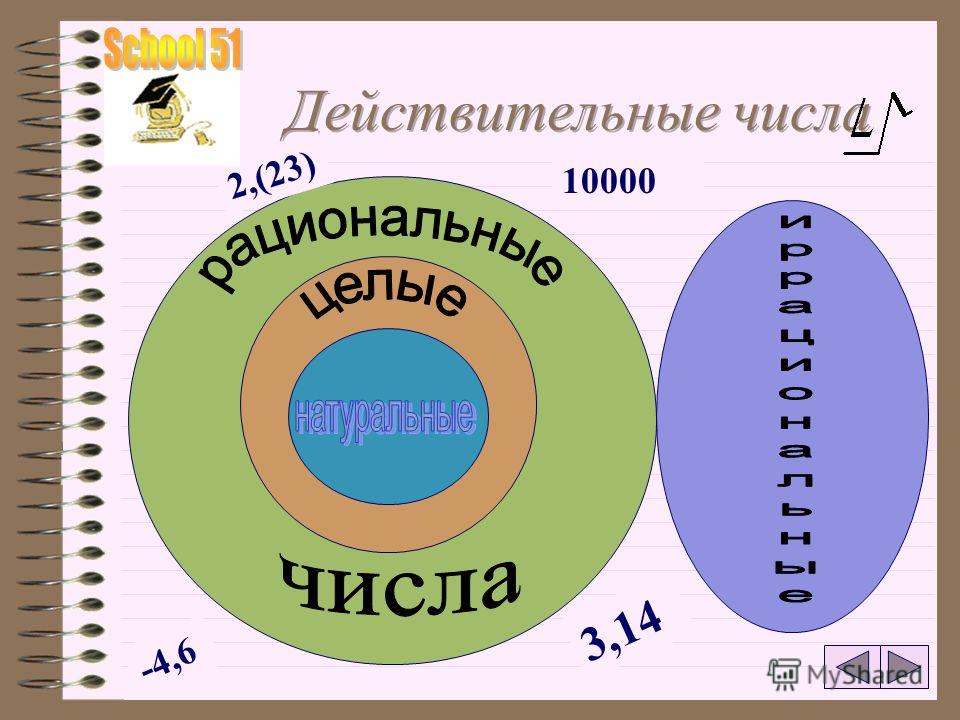 Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M

Тема:

Английский язык искусства, фонетика, написание

Оценки:

Prek — K

Типы:

Мероприятия, печатные изготовления, рабочие листы

на

, что Kindermama

$ 10.0011111110 Это четыре недели. блок, чтобы помочь писателям детского сада / первого класса стать уверенными в своих навыках рисования и раскрашивания. Учащиеся начальных классов научатся рисовать фигуры и людей с разными выражениями лица, прическами и оттенками кожи. Это иллюстративное исследование настраивает учащихся детского сада на успех до конца года во время писательского семинара. Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили

Предметы:

Искусство и музыка, снова в школу, письмо

Классы:

PreK — 1st

Типы:

Уроки, печатные формы

Также включены в: LEGROWND Writing Units | Writers Workshop

by

Тара Уэст

$14. 00

FirstieMath® Intervention: 30-недельный комплексный и систематический учебный курс по математике. Что такое вмешательство FirstieMath™? FirstieMath® Intervention — это очень универсальная учебная программа по математике, созданная учителем для учителей! Программа универсальна для реализации и разного уровня учащихся. Вы можете добиться успеха в использовании этой программы в своих интервенционных группах, группах RTI, математических группах с гидом, общегрупповой математике или в качестве ресурса для несертифицированных сотрудников, помогающих в 9.0011

Объекты:

Math, Mental Math, номера

Оценки:

K — 1 -й

Типы:

Урок, печатные изделия

по

. СОДЕРЖАНИЕ. В наборе есть все, что нужно для обучения учащихся названиям букв, звукам букв, развитию мелкой моторики, почерка и многому другому! Этот пакет предназначен для дошкольников, pre-k, переходного детского сада и учащихся детского сада. Дети любят делать поделки с алфавитом, якорные диаграммы, лабиринты, мазки, рисование алфавита, вырезание и вставку, рабочие листы и игры.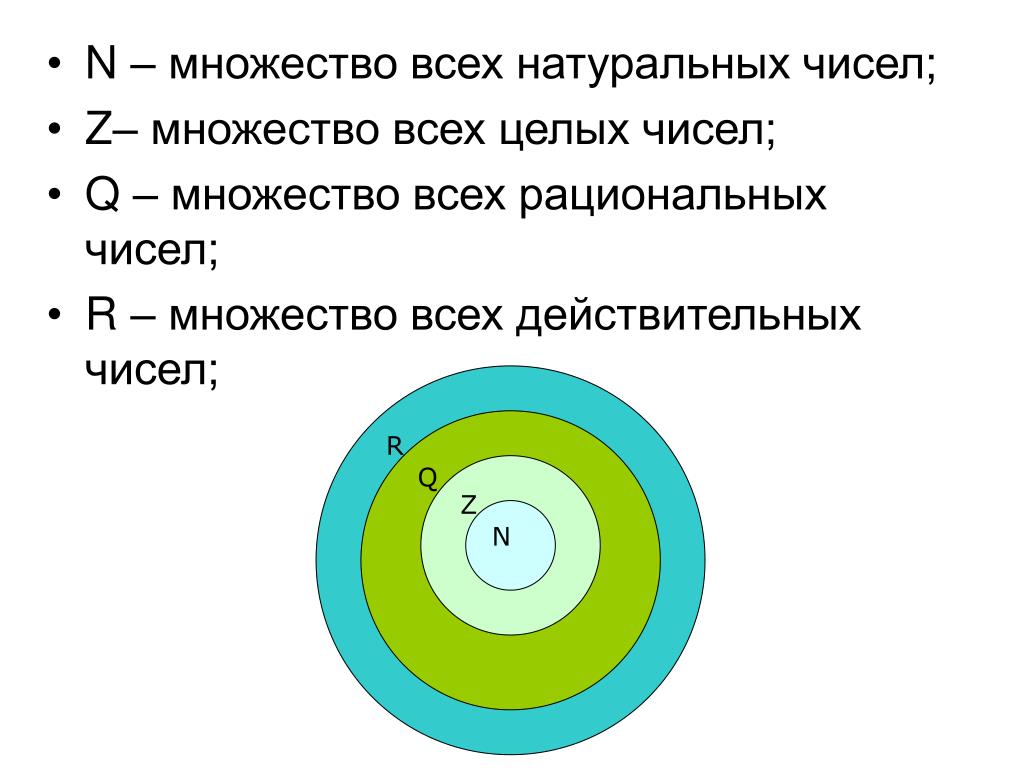 получается

Предметы:

Снова в школу, Акустика, Чтение

Классы:

PreK — 1-й

Типы:

Занятия, Плакаты, Рабочие листы

CCSS:

11 9.Ka, RF.Ka, RF.Ka, RF.Ka, RF.Ka, RF.K.011

11

, RF.K.1b, RF.K.1c, RF.K.1d…

Также включено в: Полная учебная программа для детского сада — Математические разделы — Чтение — Акустика — Письмо

by

Кейтлин Олбани

6 забавных и уникальных шрифтов в ZIP-файле! Большинство символов ударения включено во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты

Предметы:

Для всех предметов, Товары для продавцов ТРТ, Специальность

Классы:

PreK — 12th, Высшее образование, Обучение взрослых, Персонал

Типы:

По ТРТ Продавцы для ТРТ 1 Арт 902 by

Polka Dots Please

14,00 $

10,00 $

Bundle

Вы понимаете важность практики словесного зрения! Эти карточки со словами для зрения помогают детям читать часто встречающиеся слова по отдельности и в расшифровываемых предложениях! Каждая карточка помогает читателям улучшить свои навыки распознавания слов, беглости и декодирования! Они идеально подходят для чтения с гидом, уроков чтения и выполнения домашних заданий. Нажмите на предварительный просмотр, чтобы увидеть, что делает эти карточки такими особенными! Исследование чтения поддерживает изучение новых слов в предложении. Что включено? 400 карточек со словами с расшифровкой

Объекты:

Фоника, чтение, стратегии чтения

Оценки:

Prek — 3 -й

Типы:

Flash Card Шаблоны информационных бюллетеней идеально подходят для использования в течение всего года и облегчают общение с родителями! Держите родителей в курсе того, что происходит в вашем классе в течение года. Независимо от того, отправляете ли вы информационный бюллетень домой еженедельно или ежемесячно, эти шаблоны облегчат вам задачу, а редактировать их очень просто! В эту загрузку включены: 24 различных ЦВЕТНЫХ шаблона информационного бюллетеня (цветной и черно-белый) 24 различных ЧЕРНО-БЕЛЫХ шаблона информационного бюллетеня шаблоны информационных бюллетеней

Предметы:

Снова в школу, По всем предметам, По всем предметам

Классы:

PreK — 5-е

Типы:

Классные формы, Для родителей

Классные формы, Для родителей

1 по

My

36,00 $

19,00 $

Bundle

⭐⭐⭐ ФЛЭШ-РАСПРОДАЖА ⭐⭐⭐ПОЛУЧИТЕ НАБОР «НАУКА ЧТЕНИЯ» ВСЕГО ЗА 19! (СТОИМОСТЬ 140 долл.  США) Получите комплект The Ultimate Science of Reading всего за 19 долларов США! Спешите, время истекает! Ваши ученики могут практиковаться в декодировании (чтении) и кодировании (орфографии) слов. Требуется низкая подготовка. Просто распечатайте и идите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Идеально подходит для детского сада, 1-го класса и RTI для второго класса. ЧТО ВКЛЮЧЕНО В ЭТОТ НАБОР: 500+ карточек для смешивания и сегментации — стоимостью 25180 долларов США + Blendi

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 2-й

Виды:

Занятия, Центры, Печатные формы

CCSS, RFb.1.K.1

. .K.2, RF.K.2b, RF.K.2c…

by

Учительница с обсыпанным верхом

$18,00

Рукописный ввод должен быть интересным и для старших школьников! Это набор ежедневных листов для практики почерка, которые ученики действительно будут просить! Этот набор для рукописного ввода отлично подходит для учащихся, которые уже знают, как составлять буквы, но просто не могут замедлить темп и писать аккуратно! Практика письма для всех возрастов! ВКЛЮЧЕННЫЕ ЗАНЯТИЯ: 26 страниц глупых предложений с алфавитом, 20 страниц положительных утверждений, 20 страниц потрясающих фактов о животных, 20 страниц общих фактов, 20 страниц удивительных математических фактов, 20 страниц Space 9.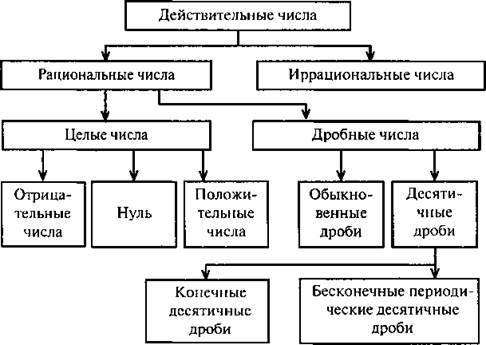 0011

Предметы:

Английский язык, правописание, письмо

Классы:

1–6

Типы:

Упражнения, оценка

Также включено в: Рабочие листы для рукописного ввода | CURSIVE PRINT D’NEALIAN BUNDLE для старших школьников

by

The Little Ladybug Shop

10,95 $

6,95 $

Расширьте круг своих читателей с помощью этого замечательного набора отрывков и вопросов для понимания прочитанного (теперь доступны цифровые варианты отрывков и вопросов для 3–5 классов) ! Пакет «Отрывки для чтения» включает в себя 20 недель еженедельной практики, идеально подходящей для: разминки, работы с колокольчиками, домашних заданий или быстрой оценки. Учащиеся могут использовать эти наборы самостоятельно, в группах по обучению грамоте, в группах по чтению с гидом для выполнения домашних заданий или в качестве замены. Эти занятия проверяют навыки учащихся без утомительной болтовни, а также позволяют научить их

Темах:

закрытие чтения, ELA Test Prep, стратегии чтения

Оценки:

3 -е место — 5 -е

Типы:

Действия, печатные изготовления

CCS:

RL. 3.1, RL.3.2, RL.3.4 , RL.4.1, RL.4.2…

Также включено в: Документальная поэзия Отрывки и вопросы на понимание чтения 3–4 классы

by

Pocket of Preschool

Community Helpers Центры математики и грамотности полны веселья и практических занятий тематические мероприятия, которые помогут вашим ученикам построить математические концепции и грамотность! Теперь включает в себя два занятия по мелкой моторике, один центр письма, шесть заданий по обучению грамоте и восемь заданий по математике. Охватываемые навыки грамотности включают определение букв, начальные звуки, почерк, написание дружественных писем, группы рифм/слов, слоги, построение словарного запаса слов, зрительные слова, и письмо / ведение журнала. Охватываемые математические навыки от одного до

Предметы:

Английский язык, математика

Классы:

PreK — K

Типы:

Мероприятия, центры

Также включены в: Тематические центры математики и грамотности, TK-K, BUNDLE for Preschool & Детский сад

by

Мой друг-преподаватель

40,00 $

30,00 $

Bundle

Decodable Phonics ReadersЭта ОГРОМНАЯ НАБОР декодируемых ридеров предназначена для того, чтобы помочь вашим учащимся научиться декодировать слова во время чтения! Каждый ридер основан на различных сочетаниях букв и звуков, благодаря чему эти ридеры органично впишутся в ваши программы чтения и фонетики.