Рациональные и действительные числа: Какие числа называются действительными?

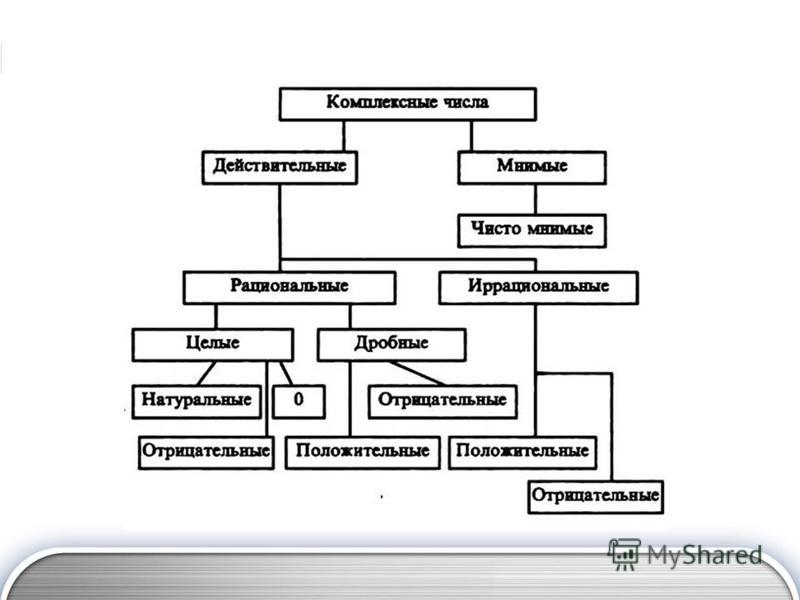
«Определение целых и рациональных действительных чисел?» — Яндекс Кью

1. Целые числа — это такие числа, которые задаются кортежем натуральных чисел с отношением эквивалентности (a, b) ~ (c,d) , где a, b, c, d ∈ N таким, что

a + d = b + c или a \ b = c \ d

По наивному определению, целые числа — это такие, которыми можно обозначить мощности множеств целых объектов, выраженные модулем этого числа, и их направление на числовой оси, выраженное знаком перед числом: положительные числа — доход, прибыль, кредит, отрицательные — расход, убыток, дебит, ноль — баланс, ниль.

Целые числа обозначаются буквой Z (от zahlen — «числа») и являются упорядоченным кольцом ( гуглится), и абелевой группой (гуглится) относительно сложения.

Множество целых чисел счетно (гуглится).

2. Рациональные числа — это такие числа, которые задаются кортежем целых чисел с отношением эквивалентности

(a,b) = (c,d) , где a, b, c, d ∈ Z

таким, что:

a * d = b * c или a / b = c / d

По наивному определению целые числа — это такие, которые можно задать отношением p / q , где p ∈ Z, q ∈ N, при условии, что мы не включаем ноль во множество натуральных чисел.

Рациональные числа обозначаются буквой Q (Quoziente , Quotient — «частное») и являются полем (гуглится) с определенными операциями сложения, умножения, взятием обратных элементов для сложения и умножения и нейтральными элементами относительно сложения (0) и относительно умножения (1).

Множество Q является счётным, множества Q и Z — равномощны.

3. Самое сложное — это конструктивное определение действительных чисел. Здесь я Вас отсылаю к описанию конструкции через Дедекиндовы Сечения у Эдмунда Ландау и Уолтера Рудина и к аксиоматмческому способу определения у Бориса Трушина, а также к конструированию действительных чисел через сюрреальные у Джона Конвея и Дональда Кнута. Альтернативные методы конструирования действительных чисел см. у Кнопфмахера старшего, Кнопфмахера младшего и де Брюйна.

По наивному определению, действительные числа получают как объединение множеств рациональных и иррациональных. Рациональные, как мы уже ранее разобрали, это такие, которые можно задать в виде отношения целого и натурального p/q , а иррациональные — это такие, которые в виде такого отношения задать нельзя. Это, например, sqrt (2), π, φ, Φ, τ, e, cbrt (5), log (7), exp (2) и др. Например, sqrt (2) и π нельзя представить в виде отношения целого и натурального числа, но можно только приблизить таким отношением (например 22/7 — приближение числа π).

По другому наивному определению, десятичные иррациональные — это такие, которые записываются в виде непериодической десятичной дроби (пример — π = 3,1415…), тогда как рациональные — в виде периодической бесконечной ( 1/3 = 0,(3), 2/1 = 2,(0) и т. д.) .

Действительные числа обозначаются буквой R (Real Numbers). Когда хотят обозначить только множество иррациональных чисел, то пишут так: R \ Q ( множество действительных без множества рациональных) .

Множество действительных чисел является полем.

Мощность множества R — континуум, множество R не является счётным.

Это если вкратце. Если же Вы хотите менее сложно и в минимально достаточном объеме, читайте учебник (вот берите и читайте) — там вам все подано в сжатой форме.

Целые и рациональные числа. Действительные числа

ТЕМА 1.1
ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ
ЧИСЛА.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.

2. Содержание:

1.
2.
3.
4.
5.
Натуральные числа.
Целые числа.
Рациональные числа
Действительные числа
Преобразование выражений с
действительными числами.

3. Знакомьтесь:

Натуральные
числа
Целые
числа
Рациональные
числа
Действительные
числа
N
Z
Q
R
Для счета предметов используются числа , которые
называются натуральными. Для обозначения
множества натуральных чисел употребляется
буква N -первая буква латинского слова Naturalis,
«естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z — первой буквой
немецкого слова Zahl — «число».
Натуральные числа
1, 2, 3, 4, 5, 6…
n — натуральное
n∈ N
Сумма и произведение натуральных
чисел есть число натуральное.

6. Целые числа

Целыми числами называют множество
натуральных чисел, им
противоположных и число нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны
суммы, произведения и разности.
Целые числа
…-3;-2;-1;0,1, 2, 3,…
m — целое
m Z
Сумма, произведение и разность
целых чисел есть число целое.
Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)его работа была обнаружена в 1848
году.
Числа,
им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые
m
Множество чисел, которое можно представить в виде
,
n Q
называется множеством рациональных чисел и обозначаетсяпервой буквой французского слова Quotient
— «отношение».

11. Рациональные числа

Целые и дробные числа составляют
множество рациональных чисел.
Q=(целые числа, дробные числа)
Рациональные числа замкнуты
относительно суммы, разности,
произведения и частного (
исключая деления на нуль)
Рациональное число (лат. ratio —
отношение, деление, дробь) — число,
представляемое обыкновенной дробью ,
где числитель m — целое число, а
знаменатель n — натуральное число.
Такую дробь следует понимать как
результат деления m на n, даже если
нацело разделить не удаётся. В реальной
жизни рациональные числа используются
для счёта частей некоторых целых, но
делимых объектов, например, тортов или
других продуктов, разрезаемых на
несколько частей
Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные
Выполнить действия
.
Вычислите:
Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.
Дробные числа
1
1
23 1
;
;
.
;
8 123
2
67
3
1
1
;
;
;
16 16 4
34 5
; ;
1 1
1
21
;
;
5
100
1
;
3600
Сумма, произведение и частное
дробных чисел есть число дробное.
Десятичные дроби в XV веке
ввел самаркандский ученый
ал — Каши.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
Множество рациональных чисел
Множество рациональных чисел обозначается
и может быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби
такие как, например, 3/4 и 9/12 , входят в
это множество как одно число.
Поскольку делением числителя и знаменателя
дроби на их наибольший общий делитель
можно получить единственное несократимое
представление рационального числа, то можно
говорить об их множестве как о множестве
несократимых дробей со взаимно простыми
целым числителем и натуральным
знаменателем:
Рациональные числа
r — рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.
Замените данные рациональные числа
десятичными дробями.
1
2
1
5
1
8
1
3
1
4
2
5
3
8
2
3
3
4
3
5
5
8
1
6
Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
1 цифра
9
0,(81)=
81
2 цифры
99
9
11
Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного
цифрами, стоящими после запятой до начала второго
периода, и числа, образованного из цифр, стоящих после
запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько
цифр в периоде, и со столькими нулями, сколько цифр
между запятой и началом периода.
0,4(6)=
46
1 цифра
1 цифра
90
42 7
90 15

24. Рациональные числа как бесконечные десятичные дроби

Для всех рациональных чисел можно
использовать один и тот же способ
записи. Рассмотрим
1. Целое число 5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)

25. Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.

Положим, что х=1,(23), т.е.
1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
122
99
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё на 100
1000х=1523,2323…
10х= 5,232323…
990х=1508
х=
Итак: 1,5(23)=
1508
999
1508
999

27. Иррациональные числа

Бесконечная
непериодическая дробь
называется иррациональным
числом.
Например:
Множество иррациональных чисел
обоначается J.

28. Действительные числа

R=(рациональные числа,
иррациональные числа)
Действительные числа не обладают
свойством замкнутости — не всякое
уравнение имеет корни.

29. Задания для самопроверки

• Какие дроби называются
десятичными
• Действия с обыкновенными и
десятичными дробями
• Какие числа называются
действительными?
• Действия с действительными
числами.

Разница между действительным числом и рациональным числом

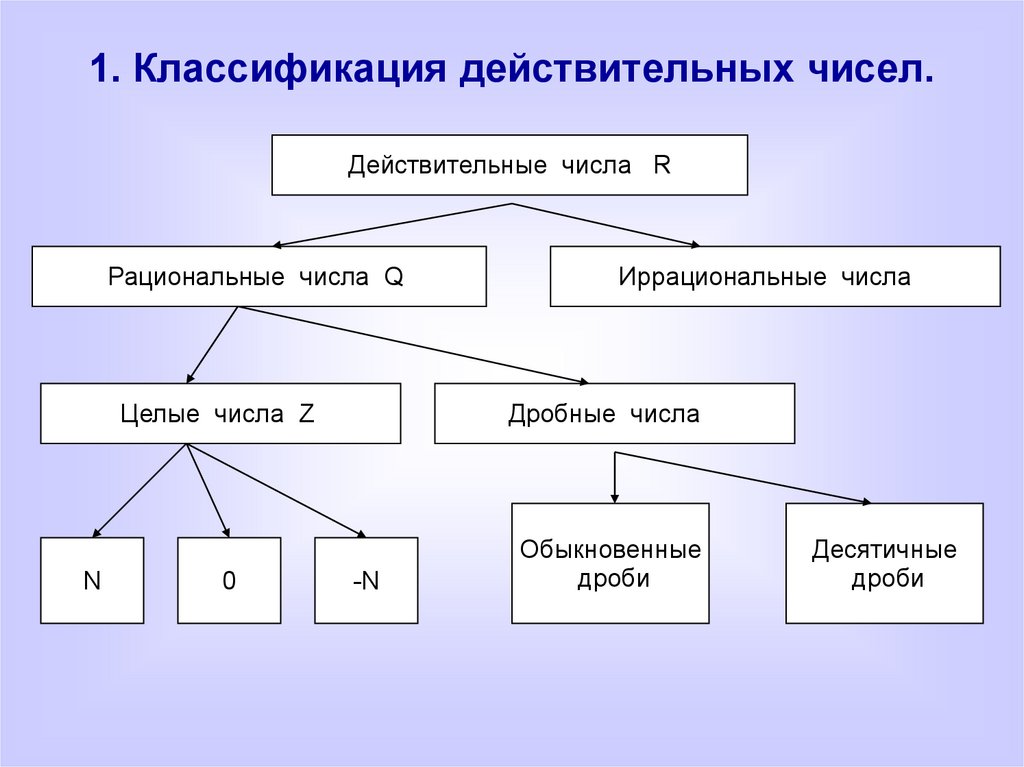
Ключевая разница: Вещественное число — это число, которое может принимать любое значение на числовой прямой. Это могут быть любые рациональные и иррациональные числа. Рациональное число — это число, которое можно представить в виде дроби, но с ненулевым знаменателем. Рациональные числа являются подмножеством действительных чисел.

Действительные числа состоят из всех рациональных и иррациональных чисел. Систему действительных чисел можно дополнительно разделить на множество подмножеств, таких как натуральные числа, целые числа и целые числа.

Натуральные числа (1, 2, 3,….)

Целые числа (0, 1, 2, 3, 4, 5,…)

Целые числа (…..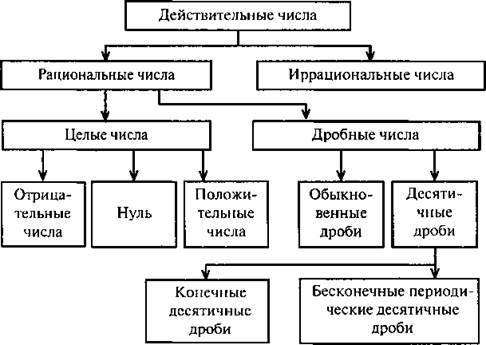 , -3, -2, -1, 0, 1, 2, 3,…..)

Вещественным числом называется любое число, которое можно найти на числовой прямой. Числовая линия может быть выражена как фактическая геометрическая линия, где точка выбрана в качестве начала координат. Точки, находящиеся справа от начала координат, считаются положительными числами, тогда как числа, лежащие слева от начала координат, считаются отрицательными. Следовательно, они состоят из целых (0, 1, 3, 9, 26), рациональные (6/9, 78,98) и иррациональные числа (квадратный корень из 3, пи). Бесконечность не попадает в категорию действительных чисел. Квадратный корень из -1 также не является действительным числом, поэтому его называют мнимым числом.

Рациональное число — это число, определяемое отношением, определяемым как (p/q), где p обозначает некоторое целое число, а q обозначает некоторое ненулевое натуральное число. Эти числа образуют подмножество действительных чисел. С другой стороны, действительные числа, которые не могут быть выражены как отношение двух целых чисел, известны как иррациональные числа. Рациональные числа получаются в результате теоретических расчетов или определений.

Сравнение реального и рационального чисел:

	Реальный номер	Рациональный номер
Определение	Вещественное число — это число, которое может принимать любое значение на числовой прямой. Это могут быть любые рациональные и иррациональные числа.	Рациональное число — это число, которое можно представить в виде дроби, но с ненулевым знаменателем.
Номер строки	Можно нанести на числовую прямую.	Можно нанести на числовую прямую
Включает	Сюда входят (но не ограничиваются) положительные и отрицательные числа, целые и рациональные числа, квадратные корни, кубические корни, π (пи) и т. д.	8, так как 8 можно представить в виде (8/1) 3/4 , так как это дробная форма 0/3, так как в виде дроби Квадратный корень из 16, так как это было бы 4, и это можно выразить как (4/1) .7777777, все повторяющиеся десятичные дроби рациональны. .12, так как это можно выразить как 12/10
Важные моменты, которые следует помнить	Объединение множеств рациональных и иррациональных чисел. Действительные числа включают ноль.	Набор рациональных чисел включает все десятичные числа, которые либо имеют конечное число знаков после запятой, либо повторяются в одной и той же последовательности цифр. Например, 0,1111111… = 1/9и .245245245…. = 245/999. Множество натуральных чисел является подмножеством множества целых чисел, которое содержится в множестве целых чисел, которое находится внутри множества рациональных чисел.

Чем действительные числа отличаются от рациональных?

Ответить

Проверено

183,6 тыс.+ просмотров

Подсказка: Сначала мы определим термины действительные числа и рациональные числа один за другим с помощью нескольких примеров. Теперь мы проверим, являются ли все рациональные числа действительными или нет, и аналогично, могут ли все действительные числа быть включены в множество рациональных чисел или нет.

Полный пошаговый ответ:
Здесь нас спросили о различиях между действительными числами и рациональными числами, но сначала нам нужно узнать об этих терминах. Давайте проверим их определения одно за другим, чтобы обнаружить различия.
(1) Рациональные числа: число вида $\dfrac{p}{q}$, где p и q — целые числа, а q не равно 0, называется рациональным числом. Например: $\dfrac{1}{2},\dfrac{5}{11},\dfrac{9}{18}$ и т.  д. Все целые числа также являются рациональными числами, поскольку их можно записать в виде $ \dfrac{p}{q}$, где q будет принято за 1. Например: мы можем записать 5 как $\dfrac{5}{1}$.

(2) Действительные числа: Действительные числа — это наборы всех рациональных чисел, а также иррациональных чисел. Мы видели определение рациональных чисел выше, поэтому давайте теперь узнаем об иррациональных числах. Иррациональные числа — это числа, которые не повторяются и не заканчиваются. Оно отличается от рациональных чисел, которые обычно заканчиваются или не заканчиваются, но повторяются. Например: $\sqrt{2},\sqrt{3},\sqrt{5}$ и т. д. — иррациональные числа. Мы не можем записать эти числа в виде $\dfrac{p}{q}$.
Из приведенных выше определений мы можем сказать, что действительные числа включают как рациональные, так и иррациональные числа, что означает, что мы можем сказать, что все рациональные числа являются действительными числами, а все действительные числа не являются рациональными.