Как узнать радиус шара зная его объем. Как найти объем шара
Определение.
Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара :
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.
Шар и сфера
Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.
Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.
Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.
Объем шара
Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.
Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров.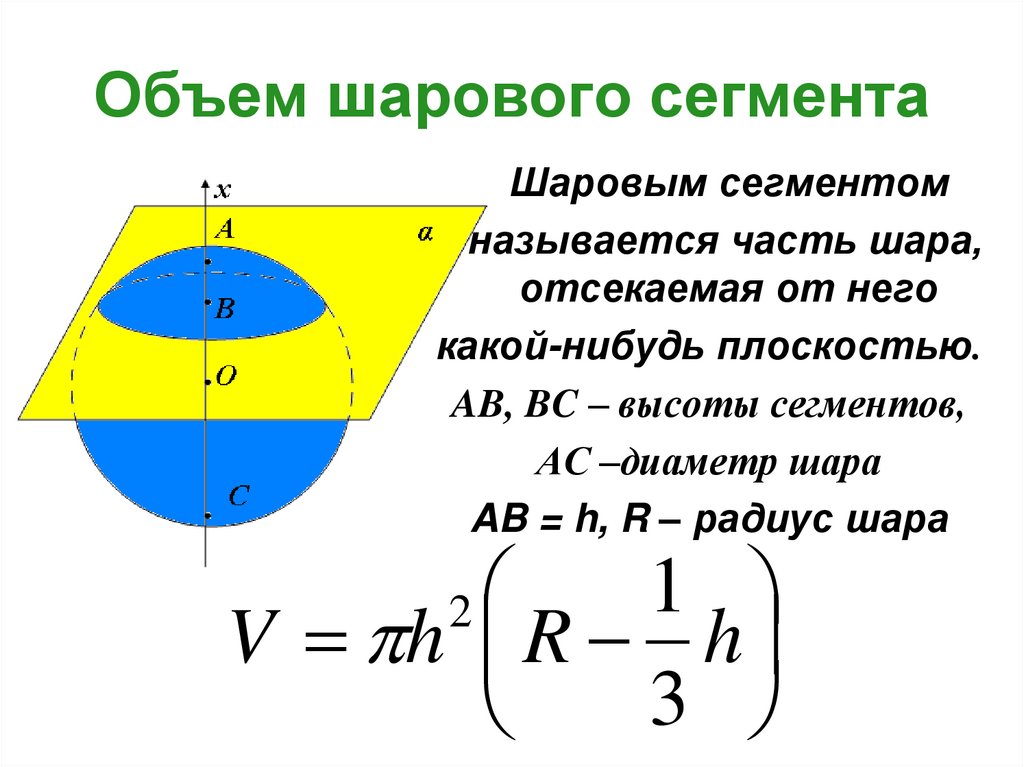 Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:
Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:
0,5 Vsh = Vc − Vk
Объем конуса вычисляется по простой формуле:
Vk = 1/3 × So × h,
но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:
Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3
Объем цилиндра вычисляется по формуле:
Vc = pi × R 2 × h,
но считая, что высота цилиндра равна его радиусу, мы получаем:
Vc = pi × R 3 .
Используя эти формулы, Архимед получил:
0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3
Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же
Vsh = 4/3 pi × R 3
Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Примеры из жизни
Пушечные ядра
Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде
Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.
Воздушные шары
Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.
Заключение
Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.
Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.
Сферические фигуры окружают нас практически везде, однако, мы настолько к ним привыкли, что не придаем этому внимания. Тем временем, случается так, что нам необходимо узнать объем какой-нибудь из них. Но все ли знают, как найти объем шара ? Углубляться в школьные воспоминания, чтобы восстановить в голове курс геометрии? Не затрудняйте себе задачу. Давайте лучше включим логику, и разберемся с этим вопросом.
Инструкция:
- Начнем с примера, когда формула объема шара нам не понадобится — представим, что у нас есть возможность произвести вычисления практическим путем . Один из наиболее простых способов это сделать — последовать по стопам Архимеда, определив объем не самого шара непосредственно, а вытесненной им воды . Для этого нужно положить его в емкость, подходящую по размерам, предварительно отметив уровень воды.
 Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры. - Если вы уверены в том, из какого именно материала сделана сфера, постарайтесь определить ее плотность — эта информация наверняка найдется на просторах всемирной сети. В этой ситуации от вас потребуется лишь взвесить данную фигуру, после чего воспользоваться простой формулой объема шара, разделив вес предмета на его плотность: V=m/p .
- Может случиться, что предыдущие варианты вам недоступны. Не отчаивайтесь — если есть возможность узнать радиус шара, к нам на помощь придет нужная формула, более сложная, чем предыдущая, но доступная.
 Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³. - Бывает и так, что гораздо легче найти
Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема.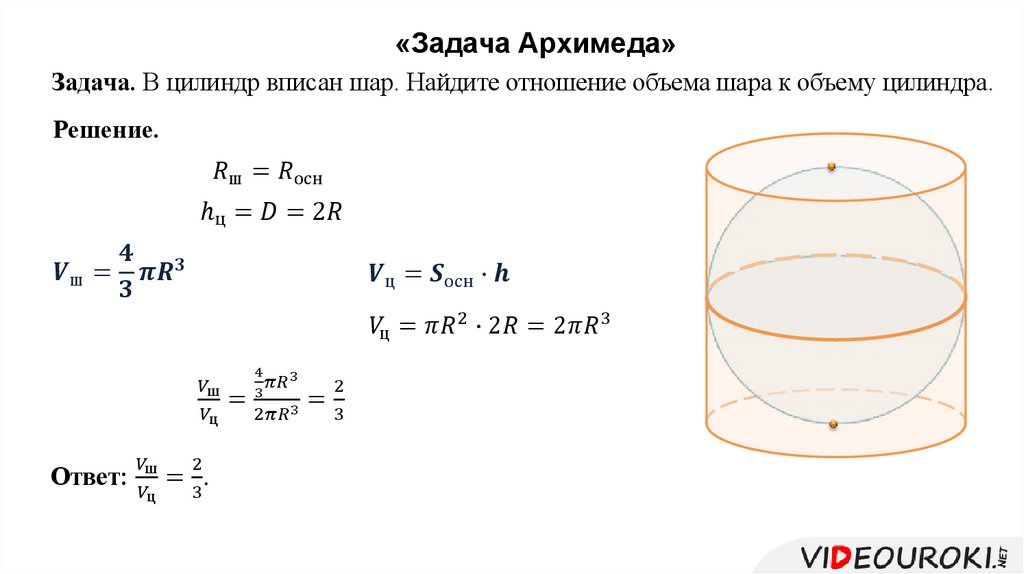 Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.
Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.
Шаги
Формулы для вычисления радиуса
Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2 . Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.
- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см . Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).
Вычислите радиус по длине окружности. Используйте формулу: r = C/2π . Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.
- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см .
- Такая же формула используется при вычислении радиуса и длины окружности круга.

- Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
- ((V/π)(3/4)) 1/3 = r
- ((100/π)(3/4)) 1/3 = r
- ((31,83)(3/4)) 1/3 = r
- (23,87) 1/3 = r
- 2,88 см = r
Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)) . Площадь поверхности шара вычисляется по формуле А = 4πr 2 . Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π.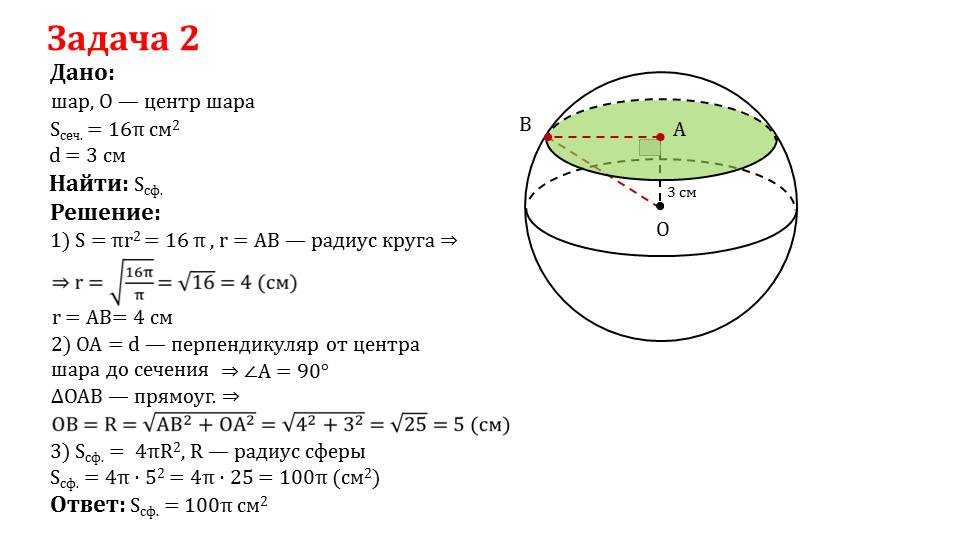 Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.
Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.
- Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r
Определение основных величин
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин.
 Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
Нахождение радиуса по расстоянию между двумя точками
Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12) . Воспользуйтесь этими координатами, чтобы найти радиус шара.
Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара.
 Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0) . Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
Вычислите радиус по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2), где d – расстояние между точками, (x 1 ,y 1 ,z 1) – координаты центра шара, (x 2 ,y 2 ,z 2) – координаты точки, лежащей на поверхности шара.
- В рассматриваемом примере вместо (x 1 ,y 1 ,z 1) подставьте (4,-1,12), а вместо (x 2 ,y 2 ,z 2) подставьте (3,3,0):
- d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2)
- d = √((3 — 4) 2 + (3 — -1) 2 + (0 — 12) 2)
- d = √((-1) 2 + (4) 2 + (-12) 2)
- d = √(1 + 16 + 144)
- d = √(161)
- d = 12,69 .
 Это искомый радиус шара.
Это искомый радиус шара.
- В рассматриваемом примере вместо (x 1 ,y 1 ,z 1) подставьте (4,-1,12), а вместо (x 2 ,y 2 ,z 2) подставьте (3,3,0):
Имейте в виду, что в общих случаях r = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками «d» заменить на «r», получится формула для вычисления радиуса шара по известным координатам (x 1 ,y 1 ,z 1) центра шара и координатам (x 2 ,y 2 ,z 2) любой точки, лежащей на поверхности шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r 2 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2 . Отметьте, что это уравнение соответствует уравнению сферы r 2 = x 2 + y 2 + z 2 с центром с координатами (0,0,0).
- Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
- В этой статье рассказывается о вычислении радиуса шара.
 Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса. - π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.
Многие тела, которые мы встречаем в жизни или о которых слышали, имеют шарообразную форму, например футбольный мяч, падающая капля воды во время дождя или наша планета. В связи с этим является актуальным рассмотрение вопроса, как находить объем шара.
Фигура шар в геометрии
Перед тем как ответить на вопрос, шара, рассмотрим подробнее это тело. Некоторые люди путают его со сферой. Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.
Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.
С точки зрения геометрии шар можно представить совокупностью точек, причем те из них, которые лежат на его поверхности (они образуют сферу), находятся на одинаковом расстоянии от центра фигуры. Это расстояние называют радиусом. По сути, радиус — это единственный параметр, с помощью которого можно описать любые свойства шара, такие как площадь его поверхности или объем.
На рисунке ниже приведен пример шара.
Если внимательно посмотреть на этот идеальный круглый объект, то можно догадаться, как его получить из обычного круга. Для этого достаточно вращать эту плоскую фигуру вокруг оси, совпадающей с его диаметром.
Одним из известных древних литературных источников, в котором достаточно подробно рассматриваются свойства этой объемной фигуры, является труд греческого философа Евклида — «Элементы».
Площадь поверхности и объем
Рассматривая вопрос, как находить объем шара, помимо этой величины, следует привести формулу для его площади, поскольку оба выражения можно связать друг с другом, как будет показано ниже.
Итак, чтобы вычислить объем шара, следует применить одну из следующих двух формул:
- V = 4/3 *pi * R3;
- V = 67/16 * R3.
Здесь R — радиус фигуры. Первая из приведенных формул является точной, однако, чтобы воспользоваться этим преимуществом, необходимо использовать соответствующее число знаков после запятой для числа pi. Второе выражение дает вполне хороший результат, отличаясь от первого всего на 0,03 %. Для ряда практических задач этой точности более чем достаточно.
Равна этой величине для сферы, то есть выражается формулой S = 4 * pi * R2. Если отсюда выразить радиус, а затем подставить его в первую формулу для объема, тогда получим: R = √ (S / (4 * pi)) = > V = S / 3 * √ (S / (4 * pi)).
Таким образом, мы рассмотрели вопросы, как найти объем шара через радиус и через площадь его поверхности. Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.
Задача с каплей дождя
Вода, когда находится в невесомости, приобретает форму шарообразной капли. Связано это с наличием сил поверхностного натяжения, которые стремятся минимизировать площадь поверхности. Шар, в свою очередь, обладает наименьшим ее значением среди всех геометрических фигур с одинаковой массой.
Связано это с наличием сил поверхностного натяжения, которые стремятся минимизировать площадь поверхности. Шар, в свою очередь, обладает наименьшим ее значением среди всех геометрических фигур с одинаковой массой.
Во время дождя падающая капля воды находится в невесомости, поэтому ее формой является шар (здесь пренебрегаем силой сопротивления воздуха). Необходимо определить объем, площадь поверхности и радиус этой капли, если известно, что ее масса составляет 0,05 грамма.
Объем определить просто, для этого следует поделить известную массу на плотность H 2 O (ρ = 1 г/см 3). Тогда V = 0,05 / 1 = 0,05 см 3 .
Зная, как найти объем шара, следует выразить из формулы радиус и подставить полученное значение, имеем: R = ∛ (3 * V / (4 * pi)) = ∛ (3 * 0,05 / (4 * 3,1416)) = 0,2285 см.
Теперь значение радиуса подставляем в выражение для площади поверхности фигуры, получаем: S = 4 * 3,1416 * 0,22852 = 0,6561 см 2 .
Таким образом, зная, как находить объем шара, мы получили ответы на все вопросы задачи: R = 2,285 мм, S = 0,6561 см 2 и V = 0,05 см 3 .
основные формулы и пример их использования
Сферические фигуры окружают нас практически везде, однако, мы настолько к ним привыкли, что не придаем этому внимания. Тем временем, случается так, что нам необходимо узнать объем какой-нибудь из них. Но все ли знают, как найти объем шара ? Углубляться в школьные воспоминания, чтобы восстановить в голове курс геометрии? Не затрудняйте себе задачу. Давайте лучше включим логику, и разберемся с этим вопросом.
Инструкция:
- Начнем с примера, когда формула объема шара нам не понадобится — представим, что у нас есть возможность произвести вычисления практическим путем . Один из наиболее простых способов это сделать — последовать по стопам Архимеда, определив объем не самого шара непосредственно, а вытесненной им воды . Для этого нужно положить его в емкость, подходящую по размерам, предварительно отметив уровень воды. Погрузив сферу целиком в жидкость, сделайте повторные измерения.
 Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры. - Если вы уверены в том, из какого именно материала сделана сфера, постарайтесь определить ее плотность — эта информация наверняка найдется на просторах всемирной сети. В этой ситуации от вас потребуется лишь взвесить данную фигуру, после чего воспользоваться простой формулой объема шара, разделив вес предмета на его плотность: V=m/p .
- Может случиться, что предыдущие варианты вам недоступны. Не отчаивайтесь — если есть возможность узнать радиус шара, к нам на помощь придет нужная формула, более сложная, чем предыдущая, но доступная. Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе.
 В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³. - Бывает и так, что гораздо легче найти диаметр фигуры , нежели его радиус. Этот вариант даже лучше — можно не производить таких сложных вычислений, формула становится значительно проще. Нам нужно будет лишь умножить диаметр в кубе на число Пи, после чего разделить получившееся число на шесть: V=π*d³/6 . К примеру, вы узнали, что диаметр вашей сферы составляет 25 см., тогда ее объем будет равняться: 3,14*25³/6 = 8177,08333см³ ≈ 0,818м³.
Многие тела, которые мы встречаем в жизни или о которых слышали, имеют шарообразную форму, например футбольный мяч, падающая капля воды во время дождя или наша планета. В связи с этим является актуальным рассмотрение вопроса, как находить объем шара.
Фигура шар в геометрии
Перед тем как ответить на вопрос, шара, рассмотрим подробнее это тело.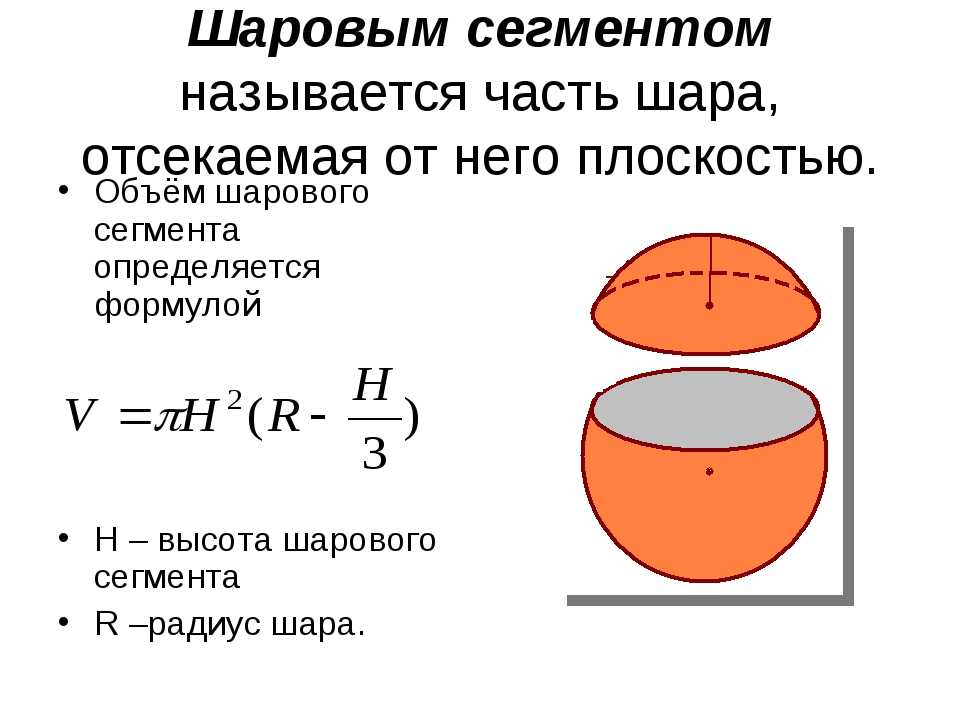 Некоторые люди путают его со сферой. Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.
Некоторые люди путают его со сферой. Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.
С точки зрения геометрии шар можно представить совокупностью точек, причем те из них, которые лежат на его поверхности (они образуют сферу), находятся на одинаковом расстоянии от центра фигуры. Это расстояние называют радиусом. По сути, радиус — это единственный параметр, с помощью которого можно описать любые свойства шара, такие как площадь его поверхности или объем.
На рисунке ниже приведен пример шара.
Если внимательно посмотреть на этот идеальный круглый объект, то можно догадаться, как его получить из обычного круга. Для этого достаточно вращать эту плоскую фигуру вокруг оси, совпадающей с его диаметром.
Одним из известных древних литературных источников, в котором достаточно подробно рассматриваются свойства этой объемной фигуры, является труд греческого философа Евклида — «Элементы».
Площадь поверхности и объем
Рассматривая вопрос, как находить объем шара, помимо этой величины, следует привести формулу для его площади, поскольку оба выражения можно связать друг с другом, как будет показано ниже.
Итак, чтобы вычислить объем шара, следует применить одну из следующих двух формул:
- V = 4/3 *pi * R3;
- V = 67/16 * R3.
Здесь R — радиус фигуры. Первая из приведенных формул является точной, однако, чтобы воспользоваться этим преимуществом, необходимо использовать соответствующее число знаков после запятой для числа pi. Второе выражение дает вполне хороший результат, отличаясь от первого всего на 0,03 %. Для ряда практических задач этой точности более чем достаточно.
Равна этой величине для сферы, то есть выражается формулой S = 4 * pi * R2. Если отсюда выразить радиус, а затем подставить его в первую формулу для объема, тогда получим: R = √ (S / (4 * pi)) = > V = S / 3 * √ (S / (4 * pi)).
Таким образом, мы рассмотрели вопросы, как найти объем шара через радиус и через площадь его поверхности.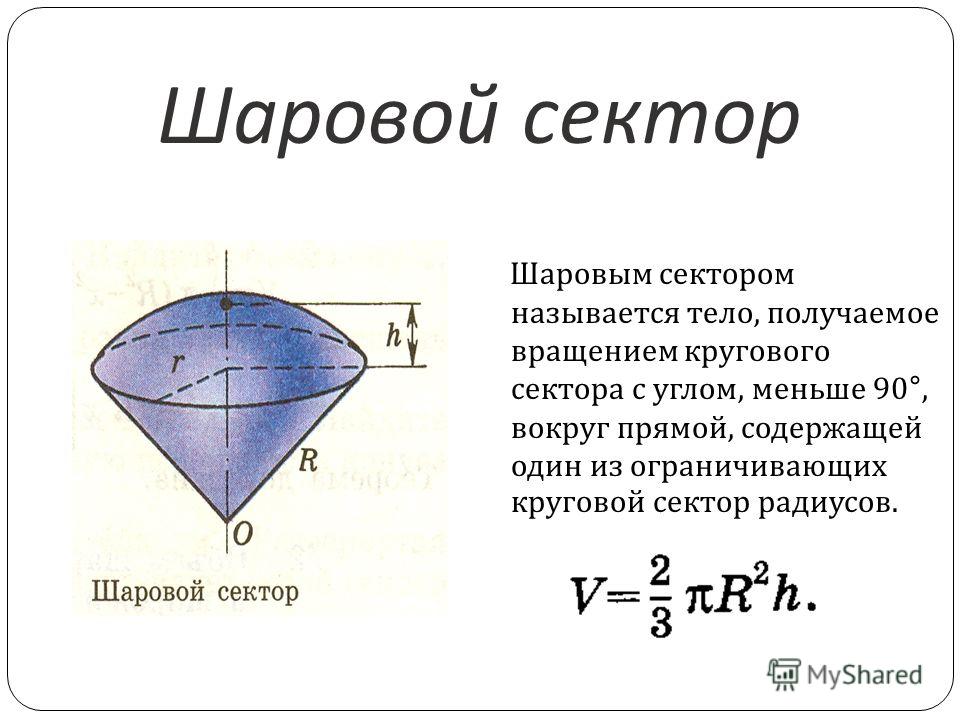 Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.
Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.
Задача с каплей дождя
Вода, когда находится в невесомости, приобретает форму шарообразной капли. Связано это с наличием сил поверхностного натяжения, которые стремятся минимизировать площадь поверхности. Шар, в свою очередь, обладает наименьшим ее значением среди всех геометрических фигур с одинаковой массой.
Во время дождя падающая капля воды находится в невесомости, поэтому ее формой является шар (здесь пренебрегаем силой сопротивления воздуха). Необходимо определить объем, площадь поверхности и радиус этой капли, если известно, что ее масса составляет 0,05 грамма.
Объем определить просто, для этого следует поделить известную массу на плотность H 2 O (ρ = 1 г/см 3). Тогда V = 0,05 / 1 = 0,05 см 3 .
Зная, как найти объем шара, следует выразить из формулы радиус и подставить полученное значение, имеем: R = ∛ (3 * V / (4 * pi)) = ∛ (3 * 0,05 / (4 * 3,1416)) = 0,2285 см. 1/3 — извлечение кубического корня.
1/3 — извлечение кубического корня.
Источники:
- диаметр это
Окружностью называется геометрическая фигура на плоскости, которая состоит из всех точек этой плоскости находящихся на одинаковом расстоянии от заданной точки. Заданная точка при этом называется центром окружности , а расстояние, на котором точки окружности находятся от её центра – радиусом окружности . Область плоскости ограниченная окружностью называется кругом.Существует несколько методов расчёта диаметра окружности , выбор конкретного зависти от имеющихся первоначальных данных.
Инструкция
Видео по теме
При проведении построений различных геометрических фигур иногда требуется определить их характеристики: длину, ширину, высоту и так далее. Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой отрезок прямой, который соединяет две наиболее удаленных друг от друга точки, расположенные на окружности.
Вам понадобится
- — измерительная линейка;
- — циркуль;
- — калькулятор.
Инструкция
В самом простом случае определите диаметр по формуле D = 2R, где R – радиус окружности с центром в точке О. Такая удобна, если вы вычерчиваете круг с заранее оговоренным . Например, если при построении фигуры вы установите раствор ножек циркуля равным 50 мм, то диаметр круга, полученного в результате, будет равен удвоенному радиусу, то есть 100 мм.
Если вам известна длина окружности, составляющей внешнюю границу круга, то используйте для определения диаметра формулу:
D = L / p, где
L – длина окружности;
p – число «пи», равное приблизительно 3,14.
Например, если длина 180 мм, то диаметр будет равняться приблизительно: D = 180 / 3,14 = 57,3 мм.
Если вы имеете предварительно вычерченный круг с радиусом, диаметром и длиной окружности, то для приблизительного диаметра используйте и измерительную линейку . Сложность заключается в том, чтобы найти на
Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.
Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.
Шар и сфера
Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.
Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.
Объем шара
Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.
Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:
0,5 Vsh = Vc − Vk
Объем конуса вычисляется по простой формуле:
Vk = 1/3 × So × h,
но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:
Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3
Объем цилиндра вычисляется по формуле:
Vc = pi × R 2 × h,
но считая, что высота цилиндра равна его радиусу, мы получаем:
Vc = pi × R 3 .
Используя эти формулы, Архимед получил:
0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3
Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же
Vsh = 4/3 pi × R 3
Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.
Примеры из жизни
Пушечные ядра
Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде
Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.
Воздушные шары
Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.
Заключение
Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.
Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.
Шар
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.
Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.
Объем шара
Формула для вычисления объема шара имеет вид:
где R — радиус шара.
Если нужно найти объем шарового сегмента — воспользуйтесь формулой:
V сег =πh 2 (R-h/3), h — высота шарового сегмента.
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
где R — радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»
Формула объема шара
- Главная
- Справочник
- Геометрия
- Формулы объема
- Формула объема шара
- Что такое шар?
- Объем шара
- Калькулятор объёма шара
- Объем шарового сегмента
- Калькулятор объема шарового сегмента
Шар (сфера) — геометрическое место точек пространства, равноудаленных от одной точки — центра шара.
Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра. 3 $$
3 $$
Уровень5 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема куба
Объем куба равен кубу его ребра
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объёма параллелепипеда
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Закон Дальтона
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.

Законы Уравнение Формулы Физика Химия Закон Термодинамика
Калькулятор для ЕГЭ. Как отличить непрограммируемый калькулятор от программируемого?
ЕГЭ Экзамены
Большая таблица Римских цифр от 1 до 1000
Таблицы Таблицы
Калькулятор идеального веса
Калькуляторы веса и калорий Калькулятор Расчёт
Сколько грамм в чайной ложечке, столовой ложке и стакане?
1 чайная ложка, 5 мл жидкости это приблизительно 5 грамм
Масса и вес Масса Физика Теория Единицы измерения
Закон Гука
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Законы Формулы Физика Теория Закон
Сколько весит ребенок?
Согласно нормам Всемирной Организацией Здравоохранения (ВОЗ)
Масса и вес Масса Теория Единицы измерения
Таблица перевода сухопутных миль в километры (mi в км)
1 сухопутная миля (США и Британия) = 1,60934 км
Размеры и расстояния Теория Расстояния
Радиус отверстия Тора с учетом объема и малого радиуса Калькулятор
✖Объем — это количество пространства, которое занимает вещество или объект или которое заключено в контейнере. | Акр-футАкр-фут (служба США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертной (Великобритания)Десертной (США)драхмаКапляОбъем ЗемлиFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Quart (Великобритания)Quart (США)StereСтоловую (метрическая система)Столовую (Великобритания)Столовую (США)Таза (испанский)Чайную (метрическая система)Чайную (Великобритания)Чайную (США)тералитрTon РегистрацияТун | +10% -10% | |
✖Малый радиус — это измерение наименьшего радиуса любой формы или объекта. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Радиус отверстия — это радиус отверстия формы или объекта. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Радиус отверстия Тора с учетом объема и малого радиуса Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. 2))-(rMinor)
2))-(rMinor)
Что такое Тор?
В геометрии тор (множественное число торов) — это поверхность вращения, созданная вращением круга в трехмерном пространстве вокруг оси, которая копланарна окружности. Если ось вращения не касается круга, поверхность имеет форму кольца и называется тором вращения.
Share
Copied!
Во сколько раз увеличится объем шара если его радиус увеличить в 2 раза
Обновлено: 02.10.2022
Во сколько раз увеличится объем шара, если его радиус увеличить в десять раз?
Поэтому при увеличении радиуса в 10 раз, объем шара увеличится в 1000 раз.
Во сколько раз увеличится объем шара, если его радиус увеличить в четыре раза?
Это задание ещё не решено, приводим решение прототипа.
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
При увеличении радиуса втрое, объем шара увеличится в 27 раз.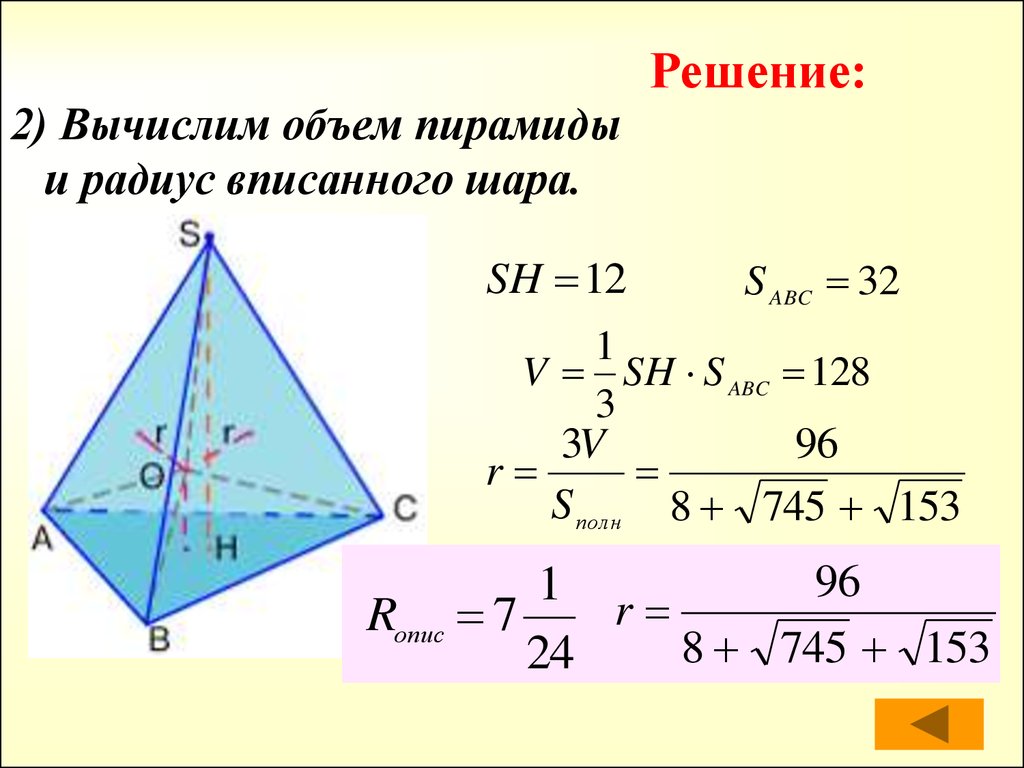
Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
Это задание ещё не решено, приводим решение прототипа.
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
При увеличении радиуса втрое, объем шара увеличится в 27 раз.
Во сколько раз увеличится объем шара, если его радиус увеличить в пятнадцать раз?
Это задание ещё не решено, приводим решение прототипа.
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
При увеличении радиуса втрое, объем шара увеличится в 27 раз.
Во сколько раз увеличится объем шара, если его радиус увеличить в одиннадцать раз?
Это задание ещё не решено, приводим решение прототипа.
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 4 раза?
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 4 раза?
Liudkin2002 8 окт. 2018 г., 09:04:31 | 10 — 11 классы
2018 г., 09:04:31 | 10 — 11 классы
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 7 раз?
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 7 раз?
Как изменится объем шара его ее диаметр увеличить в 2 раза?
Как изменится объем шара его ее диаметр увеличить в 2 раза?
Если радиус круга увеличить в 3 раза, то площадь круга увеличится?
Если радиус круга увеличить в 3 раза, то площадь круга увеличится?
Если длину окружности уменьшить в 8 раз, то диаметр окружности уменьшится?
Если площадь круга уменьшить в 4 раза, то радиус круга уменьшится?
Если длину окружности уменьшить в 6 раз, то площадь соответствующего круга уменьшится.
Если площадь круга увеличить в 9 раз, то радиус круга увеличится ?
Если площадь круга увеличить в 144 раза, то длина соответствующей окружности увеличится?
Madalina1 18 мая 2018 г. , 23:29:17 | 10 — 11 классы
, 23:29:17 | 10 — 11 классы
Во сколько раз увеличиться объем куба, если его ребро увеличить в 2 раза?
Во сколько раз увеличиться объем куба, если его ребро увеличить в 2 раза?
Как изменится объем шара если площадь его большого круга увеличится в 4 раза?
Как изменится объем шара если площадь его большого круга увеличится в 4 раза?
Вы открыли страницу вопроса Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Если треугольник равнобедренный, то вторая боковая сторона тоже 15 см 48 — (15 + 15) = 18 (см) — основания Ответ : 18 см.
трапеция ⊥ ? трапеция ⊥ ( по условию) Учитывая, что диагонали трапецииперпендикулярны, проведём дополнительные построения : Через вершину N меньшего основания MN проведём прямую, параллельную диагонали MK, т. Е. MK║ NF параллелограмм, так как..
Ответ ответ ответ ответ ответ.
Угол АВС = 2 * 50 = 100 АС = 2АD = 8.
По теореме медиана проведенная к гипотенузе равна половине гипотенузы, т. Е BM = AM = CM⇒ медиана СM делит ABC на два равнобедренных треугольника. По правилу в равнобедренных треугольниках углы при основании равны, т. Е. MCA = MAC и MBC = MCB MAC ..
АС = 18 : 2 = 9 так как угол В равен 30 градусов Ответ : 9.
Ответ 9, так как катет, лежащий против угла в 30 * равен половине гипотенузы.
Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?
Чтобы найти экстремумы, для начала нам нужно найти производную, а потом приравнять её к нулю, решив уравнение:
y’ = (x⁴ — 2x²)’ = (x⁴)’ — (2x²)’ = 4 · x⁴⁻¹ — 2 · 2 · x²⁻¹ = 4x³ — 4x
4x · (x² — 1) = 0 в том случае, когда:
Проведём числовую прямую и по методу интервалов определим, на каких промежутках значение функции положительно, а где отрицательно:
Чтобы определить знак функции на определённом промежутке, нужно подставить какое-то значение из этого промежутка в производную.
Точки экстремума — это точки максимума и минимума. Точка максимума — это точка, до которой график функции возрастал, а после этой точки убывал. Точка минимум — наоборот. На нашей числовой прямой таких экстремумов 3:
Во сколько раз надо увеличить высоту цилиндра, не меняя его основания, чтобы объем увеличился в n раз?
Во сколько раз надо увеличить высоту цилиндра, не меняя его основания, чтобы объем увеличился в n раз?
Во сколько раз надо увеличить радиус основание цилиндра, не меняя высоту, чтобы объем увеличился в n раз?
Во сколько раз увеличится объем куба если его ребро увеличить в m раз?
Во сколько раз увеличится объем куба если его ребро увеличить в m раз.
Во сколько раз увеличится площадь шара, если его радиус увеличить в три раза?
Во сколько раз увеличится площадь шара, если его радиус увеличить в три раза?
Во сколько раз увеличится объем куба, если все его ребра увеличились в 2 раза?
Во сколько раз увеличится объем куба, если все его ребра увеличились в 2 раза?
Sergeymargarita 12 февр. =27*R_$, то есть объем шара при увеличении его радиуса в 3 раза возрастет в 27 раз.
=27*R_$, то есть объем шара при увеличении его радиуса в 3 раза возрастет в 27 раз.
Alena124rus 18 мар. 2018 г., 12:28:34 | 10 — 11 классы
Во сколько раз увеличится обьем шара если его радиус увеличить в 10 раз?
Во сколько раз увеличится обьем шара если его радиус увеличить в 10 раз.
Во сколько раз увеличится объем конуса, если радиус его основания увеличить в 3 раза, а высоту оставить прежней?
Во сколько раз увеличится объем конуса, если радиус его основания увеличить в 3 раза, а высоту оставить прежней?
Вы находитесь на странице вопроса Во сколько раз увеличится объем шара если его радиус увеличить в три раза? из категории Алгебра. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Во сколько увеличится объем шара, если его радиус увеличить в два раза?
Во сколько увеличится объем шара, если его радиус увеличить в два раза?
Ребро куба увеличили в 2 раза ?
Ребро куба увеличили в 2 раза .
На сколько процентов увеличился объем куба?
(Пожалуйста с решением подробным)!
Во сколько раз увеличиться площадь круга, если его радиус увеличить 3 раза?
Во сколько раз увеличиться площадь круга, если его радиус увеличить 3 раза?
Amina030359 10 июл. 2020 г., 15:40:55 | 10 — 11 классы
Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?
Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?
Приувелечении радиуса шара в 2 раза объем изменится в 2 раза.
Во сколько раз увеличиваешь радиус во столько раз увеличиться и объем.
Дан ШАР S увеличили в 4 раза, во сколько раз увеличился V — ?
Дан ШАР S увеличили в 4 раза, во сколько раз увеличился V — ?
Длины ребер прямоугольного параллелепипеда увеличили соответственно в 2, 3 и 4 раза?
Длины ребер прямоугольного параллелепипеда увеличили соответственно в 2, 3 и 4 раза.
Во сколько раз увеличился его объем?
Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?
Во сколько раз увеличится объем шара, если его радиус увеличить в два раза?
Увеличив радиус окружности, длину окружности увеличили на 20%?
Увеличив радиус окружности, длину окружности увеличили на 20%.
На сколько процентов увеличили её радиус?
Во сколько раз увеличится объем кругового конуса, если высоту увеличить в 3 раза?
Во сколько раз увеличится объем кругового конуса, если высоту увеличить в 3 раза.
Лапуля03 28 нояб. 2018 г., 18:36:52 | 10 — 11 классы
Читайте также:
- Игра плохой майнкрафт как у жеки
- Как изменить проходимость у машины в спин тирес
- Baldur s gate 3 как изменить сложность
- Ты должен идти туда где властвует мрак такая судьба твоя ведьмак
- Monster bass колонка как подключить
Презентация по теме «Объем шара»
ОБЪЕМ ШАРА
Теорема. Объем шара радиуса R выражается формулой
Объем шара радиуса R выражается формулой
ОБЪЕМ ШАРОВОГО СЕГМЕНТА
Шаровым сегментом называется меньшая часть шара, отсекаемая от него какой-нибудь плоскостью, не проходящей через центр шара. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть радиуса шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента.
Теорема. Объем шарового сегмента высоты h , отсекаемого от шара радиуса R , выражается формулой
ОБЪЕМ ШАРОВОГО СЕКТОРА
Шаровым сектором называется часть шара, составленная из шарового сегмента и конуса, основанием которого является основание шарового сегмента, а вершиной — центр шара.
Теорема. Объем шарового сектора радиуса R и углом при вершине выражается формулой
В режиме слайдов ответы и решения появляются после кликанья мышкой
ОБЪЕМ ПАРАБОЛИЧЕСКОГО СЕГМЕНТА
ОБЪЕМ ТОРА
Упражнение 1
Найдите объем шара, диаметр которого равен 4 см.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: см 3 .
Упражнение 2
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите объем шара.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: см 3 .
Упражнение 3
Во сколько раз увеличится объем шара, если его радиус увеличить: а) в 3 раза; б) в 4 раза?
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: а) В 27 раз; б) в 64 раза.
Упражнение 4
Медный куб, ребро которого равно 10 см, переплавлен в шар. Найдите радиус шара. (Потерями металла при переплавке можно пренебречь.)
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: см.
Упражнение 5
Радиусы трех шаров равны 3 см, 4 см и 5 см. Найд ите радиус шара, объем которого равен сумме их объемов.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 6 см 3 .
Упражнение 6
Сколько нужно взять шаров радиуса 2 см, чтобы сумма их объемов равнялась объему шара радиуса 6 см?
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 27.
Упражнение 7
Найдите объем шара, впи санного в куб с ребром, равным единице.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 8
Найдите объем шара, описанного около куба с ребром, равным единице.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 9
Найдите объем шара, вписанного в правильную треугольную призму, сторона основания которой равна 1.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 10
Найдите объем шара, описанного около правильной треугольной призмы, ребра которой равны 1.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 11
Найдите объем шара, описанного около правильного тетраэдра с ребром 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 12
Найдите объем шара, в писанного в правильн ый тетраэдр с ребром 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 13
Найдите объем шара, о писанного около октаэдр а с ребром 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 14
Найдите объем шара, вписанного в октаэдр с ребром 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 15
В конус, радиус основания которого равен 1, а образующая равна 2, вписан шар. Найдите его объем.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 16
В усеченный конус, радиусы оснований которого равны 2 и 1, вписан шар. Найдите его объем.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 1 7
Шар радиуса 10 см пересечен плоскостью, проходящей на расстоянии 4 см от центра шара. Найдите объем отсеченного шарового сегмента.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: см 3 .
Упражнение 1 8
Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара?
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Упражнение 19
Чему равен объем шарового сектора, если радиус окружности его сегмента равен 60 см, а радиус шара 75 см?
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: см 3 .
Упражнение 2 0
Найдите объем шарового пояса, если радиусы его оснований равны 3 см и 4 см, а радиус шара — 5 см. (Рассмотрите два случая.)
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: Если центр шара лежит между основаниями пояса, то
см 3 . В противном случае см 3 .
Упражнение 2 1
Шар касается всех двенадцати ребер единичного куба. Найдите объем части шара, заключенной внутри этого куба.
Решение: Часть шара, заключенная внутри куба, получается отсечением от шара радиуса шести шаровых сегментов высоты Объем каждого такого сегмента равен
Объем части шара, содержащейся в кубе, равен
В режиме слайдов ответ появляется после кликанья мышкой
Ответ:
Калькулятор радиуса сферы
Автор Dominik Czernia, кандидат наук
Отзыв от Bogna Szyk
Последнее обновление: 10 мая 2022 г.
Содержание:- Что такое радиус формулы сферы?
- Как найти радиус сферы?
- Часто задаваемые вопросы
Наш калькулятор радиуса сферы — это идеальный инструмент, который может оценить каждый параметр сферы, исходя из одной другой величины. Тем не менее, он в основном предназначен для поддержки вычисление радиуса сферы . Попробуйте этот калькулятор прямо сейчас, введя один из выбранных параметров в соответствующее поле, или читайте дальше и узнайте, как найти радиус сферы. В следующем тексте мы также представили четыре различных формулы радиуса сферы .
Тем не менее, он в основном предназначен для поддержки вычисление радиуса сферы . Попробуйте этот калькулятор прямо сейчас, введя один из выбранных параметров в соответствующее поле, или читайте дальше и узнайте, как найти радиус сферы. В следующем тексте мы также представили четыре различных формулы радиуса сферы .
Сфера — идеально круглый геометрический объект в трехмерном пространстве. Точки на его поверхности равноудалены от центра сферы. Это аналог круга в двумерном пространстве. Калькулятор радиуса сферы использует пять переменных, которые могут полностью описать любую сферу:
- rrr — радиус сферы,
- ddd — диаметр сферы,
- ВВВ — объем шара,
- AAA — площадь сфера,
- A/VA / VA/V — отношение поверхности к объему сферы.
Сфера является особым объектом, поскольку имеет наименьшее отношение поверхности к объему среди всех других замкнутых поверхностей с заданным объемом. Также здесь мы можем найти аналогию с кругом, который охватывает наибольшую площадь с заданным периметром. Этот калькулятор радиуса сферы, как следует из названия, содержит информацию, посвященную в основном радиусу сферы. Для получения более общей информации о сферах ознакомьтесь с нашим калькулятором сфер!
Также здесь мы можем найти аналогию с кругом, который охватывает наибольшую площадь с заданным периметром. Этот калькулятор радиуса сферы, как следует из названия, содержит информацию, посвященную в основном радиусу сферы. Для получения более общей информации о сферах ознакомьтесь с нашим калькулятором сфер!
Существует объект под названием полушарие , который вы можете построить из любой сферы, какой захотите. Вам просто нужно разделить сферу на две равные части. Описание полусферы несколько сложнее, чем полной сферы, но возможно. Если вы хотите узнать больше о таких объектах, посмотрите калькуляторы площади и объема полушария!
Какова формула радиуса сферы?
Как найти радиус сферы? На самом деле, есть много разных ответов на этот вопрос, потому что это зависит от того, что мы знаем о конкретной сфере. Ниже мы привели исчерпывающий набор формул радиуса сферы:
- Дан диаметр : r=d/2r = d / 2r=d/2,
- Учитывая площадь : r=A/(4×π)r = \sqrt{A/(4×π)}r=A/(4×π),
- Учитывая объемов : r=3×V/(4×π)3r = \sqrt[3]{3 \times V / (4 \times π)}r=33×V/(4×π),
- Учитывая отношение поверхности к объему : r=3/(A/V)r = 3/(A/V)r=3/(A/V).

Наш калькулятор радиуса сферы использует все приведенные выше уравнения одновременно, поэтому вам нужно ввести только одну выбранную величину. Более того, вы можете свободно менять единицы измерения (СИ и имперские единицы). Посмотрите наше преобразование длины, чтобы узнать, как переключаться между различными единицами длины! 93V=4/3×π×r3,
Как найти радиус сферы?
Сначала этот вопрос кажется очень простым. Вам нужно только найти центр сферы и измерить расстояние до любой точки на ее поверхности. Но как найти этот центр в реальной, физической сфере , особенно когда он закрыт? Давайте рассмотрим два наших предложения:
- Найдите диаметр . Вы можете использовать две параллельные плоскости и поместить сферу между ними. Расстояние между этими пластинами равно диаметру сферы.
- Найти том .
 Подготовьте градуированную цилиндрическую емкость, наполненную водой. Поместите шар в этот цилиндр, затем достаньте шар и измерьте объем вытесненной воды (для этого вы можете использовать наш калькулятор объема цилиндра). Если вы хотите увидеть, как объекты ведут себя в жидкости, воспользуйтесь нашим калькулятором плавучести прямо сейчас!
Подготовьте градуированную цилиндрическую емкость, наполненную водой. Поместите шар в этот цилиндр, затем достаньте шар и измерьте объем вытесненной воды (для этого вы можете использовать наш калькулятор объема цилиндра). Если вы хотите увидеть, как объекты ведут себя в жидкости, воспользуйтесь нашим калькулятором плавучести прямо сейчас!
Мы не писали сначала о нахождении площади поверхности сферы, потому что это намного сложнее (по сравнению с нахождением радиуса).
Стоит отметить, что сферы часто могут упростить различные задачи в физике. Вот почему они широко используются в этой области, т.е. для моделирования сферических конденсаторов или атомов газа.
Часто задаваемые вопросы
Как рассчитать радиус сферы по объему?
Чтобы вычислить радиус сферы по объему:
- Умножить объем на три.
- Разделите результат на четыре числа «пи».
- Найдите кубический корень из результата шага 2.
- Результат — радиус вашей сферы!
Каков радиус сферы с площадью
50 см² ? 1,99 см . Чтобы вычислить радиус
Чтобы вычислить радиус r сферы с учетом площади поверхности ( A ), измените формулу:
A = 4 * π * r²
Чтобы выделить радиус:
r = √[A / (4 * π)]
Обратите внимание, что площадь сферы ровно в четыре раза больше площади круга того же радиуса!
Как рассчитать радиус Земли по ее объему?
Если вы аппроксимируете Землю идеальной сферой (это, по сути, геоид) и знаете объем, то можете вычислить ее радиус. Но цифры будут большие!
Объем V Земли равен:
1 083 206 916 846 км³
Применим обратную формулу для объема сферы, чтобы найти радиус:
r = ³√[3 * V / (4 * π)] = 6371 км .
Это неплохое приближение, так как на самом деле радиус Земли колеблется в пределах 6357-6378 км!
Как измерить радиус сферы?
Измерить радиус сферы не так просто. Вы можете обмотать его веревкой и надеяться, что у вас получился большой круг, или вы можете проявить немного изобретательности:
- Наполните открытый контейнер (площадь поверхности которого вам известна) водой.

- Отметить уровень воды.
- Погрузите шарик (рукой) и измерьте новый уровень воды.
- Опустите только руку на ту же глубину, что и раньше, и снова измерьте уровень воды.
- Вычислите объем воды, вытесненной мячом, вычтя перемещение только вашей руки из перемещения обоих объектов.
- Примените формулу
r = ³√[3 * V / (4 * π)], чтобы найти радиусr.
Доминик Черня, кандидат наук
Диаметр
Окружность
Площадь поверхности
Том
Радиус
Радиус
Проверьте 20 аналогичных калькуляторов 3D геометрии 📦
Область гемисферекубюбе.
Можно вычислить
масса
любого объекта путем умножения
плотность
материала по объему объекта.
Объем объекта – это трехмерное пространство,
заняты объектом, и нас учат
формулы для вычисления объема некоторых простых трехмерных
предметы в средней школе. На этом слайде мы перечисляем некоторые уравнения для
вычисление объема объектов, которые часто встречаются в
аэрокосмический. Есть аналогичные уравнения
для вычисления
область
объектов.
Величина
аэродинамические силы
зависит от площади поверхности объекта, а
сила гравитации
и определенные
термодинамические эффекты
зависит от объема предмета.
Уравнения для вычисления площади и объема используются каждый день
инженеры-конструкторы.
Есть аналогичные уравнения
для вычисления
область
объектов.
Величина
аэродинамические силы
зависит от площади поверхности объекта, а
сила гравитации
и определенные
термодинамические эффекты
зависит от объема предмета.
Уравнения для вычисления площади и объема используются каждый день
инженеры-конструкторы.
Простая проверка любой формулы площади или объема проверка размеров . Площадь — это двумерное пространство, которое занимает объект. Площадь измеряется вдоль поверхности объекта и имеет размеры длина в квадрате; например, квадратные футы материала или квадратные сантиметры. Объем — это трехмерное пространство, которое занимает объект. Объем имеет размеры длина в кубе; например, кубические футы материала или кубические сантиметры (см). 92*ч/4
Для прямоугольной призмы с размерами a , b , а ч объем есть произведение трех длин;
V = а * б * ч
Куб — это частный случай прямоугольной призмы, у которого все стороны
равны a . 3
3
Вот некоторые специальные уравнения объема, которые используются для носовых обтекателей ракет:
Для конуса расстояние от вершины до основания называется высота . Основание представляет собой круг диаметром d . Объем V конуса равен пи (3,14159), умноженному на диаметр d квадрат умножить на высоту ч разделить на двенадцать; 92*ч/12
Параболический конус имеет гладкую криволинейную поверхность и острый заостренный носик. На стандартном конусе есть край между носом и цилиндром, который образует тело ракета. Но на параболическом конусе поверхность входит в основание с наклоном, равным нулю. Есть отсутствие ребра между параболическим носовым обтекателем и цилиндрическим корпусом ракеты. Уравнение для объем в два раза pi 92*ч/6
Усеченный конус образуется, если вершина срезана параллельно основанию. Формы усеченного конуса часто встречаются на моделях ракет в виде обтекателей между цилиндрическими
участки тела.
Уравнение для
объем пи умножить на высоту ч разделить на двенадцать раз
количество: диаметр основания b в квадрате плюс диаметр основания, умноженный на диаметр разреза d плюс диаметр реза в квадрате:
92)
Формы усеченного конуса часто встречаются на моделях ракет в виде обтекателей между цилиндрическими
участки тела.
Уравнение для
объем пи умножить на высоту ч разделить на двенадцать раз
количество: диаметр основания b в квадрате плюс диаметр основания, умноженный на диаметр разреза d плюс диаметр реза в квадрате:
92)
Примечание. Для всех фигур с изогнутыми (круглыми) поверхностями мы используем диаметр
круг при выводе объема. Мы не используем радиус, который часто используется в математике.
текстовые книги. Причина такого выбора в том, что
большинство стандартных инженерных измерений основаны на диаметре, а не на радиусе. Легче точно измерить
диаметр круглого объекта, чем для измерения радиуса. Чтобы использовать радиус, вам нужно определить, где
лежит центр окружности. Для трубы в центре круга нет материала. Для сферы,
до центра нельзя добраться, так как он находится внутри тела. Вы можете преобразовать диаметр в радиус
(радиус = диаметр / 2). 2_0\\ &=& \left(\frac{32}{3}\pi-8\pi\right)-\left( 0-0\right)\\ &=& \frac{8\pi}{3},\quad{\small\textrm{как найдено ранее.}} \end{eqnarray*} Это называется 9d 2\pi y[F(y)-G(y)]\, dy.\]
2_0\\ &=& \left(\frac{32}{3}\pi-8\pi\right)-\left( 0-0\right)\\ &=& \frac{8\pi}{3},\quad{\small\textrm{как найдено ранее.}} \end{eqnarray*} Это называется 9d 2\pi y[F(y)-G(y)]\, dy.\]
Примечания
- В методах с дисками и шайбами вы интегрируете по та же переменная , что и ось, вокруг которой вы вращали область, край.
- В методе цилиндрических оболочек вы интегрируете относительно к другой переменной .
Вычисление объемов с использованием этих методов требует некоторой практики. С
опыт, вы сможете лучше визуализировать твердые тела и
определить, какой метод применить.
9d_c 2\pi y[F(y)-G(y)]\, dy. \\
\end{выравнивание*}
[Я готов пройти тест.]
[Мне нужно просмотреть больше.]
OpenStax College Physics Solution, глава 34, задача 30 (задачи и упражнения)
Глава 34 вопрос:
1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE22PE23PE24PE26PE27PE28PE29PE30PE31PE
Изменить главу 93$ считал необходимым остановить расширение Вселенной. 3$ 9{3}\textrm{ ly}$
3$ 9{3}\textrm{ ly}$Видеорешение
Зарегистрируйтесь для просмотра этого видеорешения!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
Голоса еще не отправлены.
Скриншоты калькулятора
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Чтобы получить представление о том, насколько пусто глубокое пространство, мы найдем, какой объем занимало бы наше Солнце, если бы оно имело плотность, равную критической плотности, которая, как считается, необходима для остановки расширения Вселенной. Таким образом, плотность — это масса, деленная на объем, и мы можем преобразовать это число, чтобы получить объем, умножив его на 9.0347 V над ρ с обеих сторон, поэтому объем равен массе, деленной на плотность. Таким образом, это 1,99 умножить на 10 в 30 килограммах — массу Солнца — разделить на критическую плотность 10 в минус 26 килограммах на кубический метр, и это 2 умножить на 10 в 56 кубических метрах. Часть (b) просит нас найти радиус сферы, имеющей этот объем, и выразить его в единицах световых лет. Таким образом, объем сферы равен четырем третям, умноженным на π , умноженным на радиус в кубе, и мы можем найти радиус в кубе, умножив обе стороны на 3 на 4 9.0347 № . Таким образом, радиус в кубе равен объему, умноженному на 3, деленному на 4 π , а затем мы возводим обе стороны в показатель степени, равный одной трети, чтобы найти радиус r . Таким образом, радиус в 3 раза больше объема 4 π , все в степени одной трети. Таким образом, 3 умножить на 1,99 умножить на 10 для 56 кубических метров — наш ответ из части (а) — разделить на 4 π до одной трети, что равно 3,6218 умножить на 10 для 18 метров. А затем мы переведем это в световые годы и сначала нам нужно узнать, сколько метров в световом году. Итак, световой год — это расстояние, которое нечто, движущееся со скоростью света, пройдет за один год. Так это 2,998 умножить на 10 до 8 метров в секунду — скорость света умножить на год — умножить на 365,25 дня в году умножить на 24 часа в день умножить на 3600 секунд в час, и это 9,461 умножить на 10 на 15 метров.
Часть (b) просит нас найти радиус сферы, имеющей этот объем, и выразить его в единицах световых лет. Таким образом, объем сферы равен четырем третям, умноженным на π , умноженным на радиус в кубе, и мы можем найти радиус в кубе, умножив обе стороны на 3 на 4 9.0347 № . Таким образом, радиус в кубе равен объему, умноженному на 3, деленному на 4 π , а затем мы возводим обе стороны в показатель степени, равный одной трети, чтобы найти радиус r . Таким образом, радиус в 3 раза больше объема 4 π , все в степени одной трети. Таким образом, 3 умножить на 1,99 умножить на 10 для 56 кубических метров — наш ответ из части (а) — разделить на 4 π до одной трети, что равно 3,6218 умножить на 10 для 18 метров. А затем мы переведем это в световые годы и сначала нам нужно узнать, сколько метров в световом году. Итак, световой год — это расстояние, которое нечто, движущееся со скоростью света, пройдет за один год. Так это 2,998 умножить на 10 до 8 метров в секунду — скорость света умножить на год — умножить на 365,25 дня в году умножить на 24 часа в день умножить на 3600 секунд в час, и это 9,461 умножить на 10 на 15 метров. Таким образом, этот радиус равен 3,6218 умножить на 10 на 18 метров и умножить на 1 световой год на каждые 9,461 умножить на 10 на 15 метров, а это около 400 световых лет. Часть (c) спрашивает, каким был бы радиус, если бы плотность была равна плотности светящегося вещества, что составляет примерно 5 процентов от критической плотности? Таким образом, мы могли бы снова выполнить все эти вычисления, сначала найдя объем, а затем подставив его в нашу формулу для радиуса, но вместо этого мы собираемся немного сократить и посмотреть, на какой коэффициент мы должны умножить наш ответ от части ( б) для того, чтобы получить наш ответ на часть (в). Итак, этот новый объем, который мы хотим рассчитать — V 2 — это масса, деленная на эту новую плотность, и нам говорят, что эта плотность составляет 5 процентов от старой критической плотности, то есть в 0,05 раза больше плотности, которую мы использовали раньше. Итак, у нас есть масса, деленная на старую плотность, которую мы можем заменить старым объемом, так что новый объем тогда — V 2 — это старый объем, деленный на 0,05.
Таким образом, этот радиус равен 3,6218 умножить на 10 на 18 метров и умножить на 1 световой год на каждые 9,461 умножить на 10 на 15 метров, а это около 400 световых лет. Часть (c) спрашивает, каким был бы радиус, если бы плотность была равна плотности светящегося вещества, что составляет примерно 5 процентов от критической плотности? Таким образом, мы могли бы снова выполнить все эти вычисления, сначала найдя объем, а затем подставив его в нашу формулу для радиуса, но вместо этого мы собираемся немного сократить и посмотреть, на какой коэффициент мы должны умножить наш ответ от части ( б) для того, чтобы получить наш ответ на часть (в). Итак, этот новый объем, который мы хотим рассчитать — V 2 — это масса, деленная на эту новую плотность, и нам говорят, что эта плотность составляет 5 процентов от старой критической плотности, то есть в 0,05 раза больше плотности, которую мы использовали раньше. Итак, у нас есть масса, деленная на старую плотность, которую мы можем заменить старым объемом, так что новый объем тогда — V 2 — это старый объем, деленный на 0,05.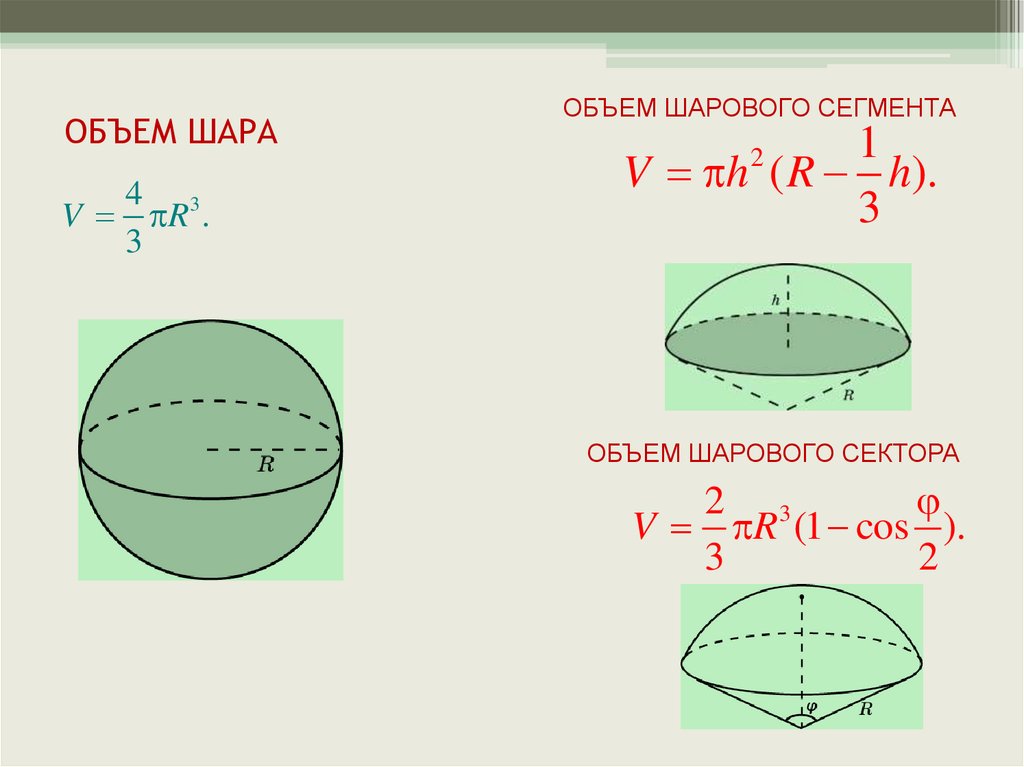 И тогда наш второй радиус будет в 3 раза больше этого нового объема — 90 347 V 2 90 348 — более 4 90 347 π 90 348, все в степени одной трети, но мы можем заменить это V 2 теперь с V более 0,05, поэтому мы делаем это здесь, и мы видим, что у нас есть в 3 раза больше старого объема более 4 π в степени одной трети, умноженной на 1 более 0,05, умноженной на одну треть и это коэффициент, на который мы хотим умножить наш старый радиус, чтобы получить ответ для этого нового радиуса, чтобы он был заменен старым радиусом. Итак, у нас есть 382,81 светового года — это выражение нашего ответа для части (b) с большей точностью, чтобы избежать промежуточной ошибки округления, и мы умножаем это на 1 на 0,05 до одной трети, что составляет около 1000 световых лет. И в части (d) говорится, что сравните радиус, который мы нашли в части (c), со средним расстоянием между звездами в рукавах Млечного Пути в 4 световых года. Так 1039световых лет, разделенных на 4 световых года, составляет около 300, поэтому этот радиус будет больше среднего расстояния между звездами в Млечном Пути примерно в 300 раз.
И тогда наш второй радиус будет в 3 раза больше этого нового объема — 90 347 V 2 90 348 — более 4 90 347 π 90 348, все в степени одной трети, но мы можем заменить это V 2 теперь с V более 0,05, поэтому мы делаем это здесь, и мы видим, что у нас есть в 3 раза больше старого объема более 4 π в степени одной трети, умноженной на 1 более 0,05, умноженной на одну треть и это коэффициент, на который мы хотим умножить наш старый радиус, чтобы получить ответ для этого нового радиуса, чтобы он был заменен старым радиусом. Итак, у нас есть 382,81 светового года — это выражение нашего ответа для части (b) с большей точностью, чтобы избежать промежуточной ошибки округления, и мы умножаем это на 1 на 0,05 до одной трети, что составляет около 1000 световых лет. И в части (d) говорится, что сравните радиус, который мы нашли в части (c), со средним расстоянием между звездами в рукавах Млечного Пути в 4 световых года. Так 1039световых лет, разделенных на 4 световых года, составляет около 300, поэтому этот радиус будет больше среднего расстояния между звездами в Млечном Пути примерно в 300 раз.
Решения проблем, описанных в главе 34
Твердые тела — объемы и поверхности
Куб
Объем
V = a 3 ) 0526
, где
V = объем (M 3 , FT 3 )
A = сторона (M, FT)
.
2 (1b)where
A 0 = surface area (m 2 , ft 2 )
Diagonal
d = a 3 1/2 ( 1в)
where
d = inside diagonal (m, ft)
Diagonal of Cube Face
d s = a 2 1/2 (1d)
Cuboid — Square Prism
Том
V = A B C (2)
, где
V = объем твердого вещества (M 3 , FT 3 ))0003
a = длина прямоугольной призмы (м, фут)
b = ширина прямоугольной призмы (м, фут)
c = высота прямоугольной призмы (м, фут) 3
9 9
d = (a 2 + b 2 + c 2 ) 1/2 (2b)
Surface Area
A 0 = 2 (a b + a c + b c) (2c)
where
A 0 = surface area of solid (m 2 , ft 2 )
length
Ширина
Высота
MDMCMMMINFT
Том:
Поверхность:
Parallelepeped
VOLUCT
7373737373737373737373737373737373737373737373737373737737373737377373737377373737373737373737373737373737н.0002 V = A 1 h (3a)
where
A 1 = side area (m 2 , ft 2 )
Related Sketchup Components from The Engineering ToolBox
- Геометрические фигуры — цилиндры, коробки, конусы, плоскости, сферы, линии, кривые и т. д.
— бесплатный плагин Engineering ToolBox для использования с потрясающим приложением Sketchup для трехмерного рисования/моделирования.
Cylinder
Volume
V = π r 2 h = ( π / 4) d 2 h (4a)
where
d = диаметр цилиндра (м, фут)
r = радиус цилиндра (м, фут)
h = высота цилиндра (м, фут)
Поверхность
0 A = 5523730 9 2 π р ч + 2 π р 2 (4b)
radius
height
mdmcmmminft
Volume:
Surface:
Hollow Cylinder
Volume
V = π/4 H (D 2 — D 2 ) (5)
Пирамида
Том
V = 1/3 H A
V = 1/3 H A0548 1 (6)
, где
A 1 = площадь основания (M 2 , FT 2 )
333 H = Pirpid Irminder).
Surface
A = ∑ Сумма областей треугольников, образующих стороны + A B (6B)
, где
.
Frustum of Pyramid
Том
V = H/3 (A 1 + A 2 + (A 1 A 2 + (A 1 A 2 ) (A 1 .
Конус
Том
33V = 1/3 π R 2 H (8A)
, где
.0002 h = height of cone (m, ft)
Surface
A = π r l + π r 2 (8b)
where
l = (r 2 + h 2 ) 1/2 = длина со стороны конуса (M, FT)
RADIUS
Высота
MDMCMMINMINFT
VOUSTMDMCMMINMINFT
.Side
m = (h 2 + r 2 ) 1/2 (8c)
A 2 / A 1 = x 2 / h 2 (8d)
Frustum of Cone
Volume
V = π/12 h (D 2 + D d + d 2 ) (9a)
m = ( ( (Д — д) / 2 ) 2 + H 2 ) 1/2 (9C)
Сфера
Том
V = 4/3 ° R 3
9 V = 4/3 ° R 39 V = 4/3 ° R 39 V = 4/3 № 39 В. π D 3 (10A), где
R = радиус сферы (M, FT)
Surface
9Surface
92
.
 0525
0525 = π d 2 (10b)
radius
mdmcmmminft
Volume:
Surface:
Spheres with Fractional Diameters — Surface Area and Volume
| Дробный диаметр — d – (дюйм) | Десятичный диаметр — d – (6 дюймов) | Decimal Radius – r – (inch) | Surface Area — A – (in 2 ) | Volume — V — (in 3 ) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/64 | 0.015625 | 0.007813 | 0.0007670 | 0.0000020 | ||||||||||||||
| 1/32 | 0.031250 | 0.015625 | 0.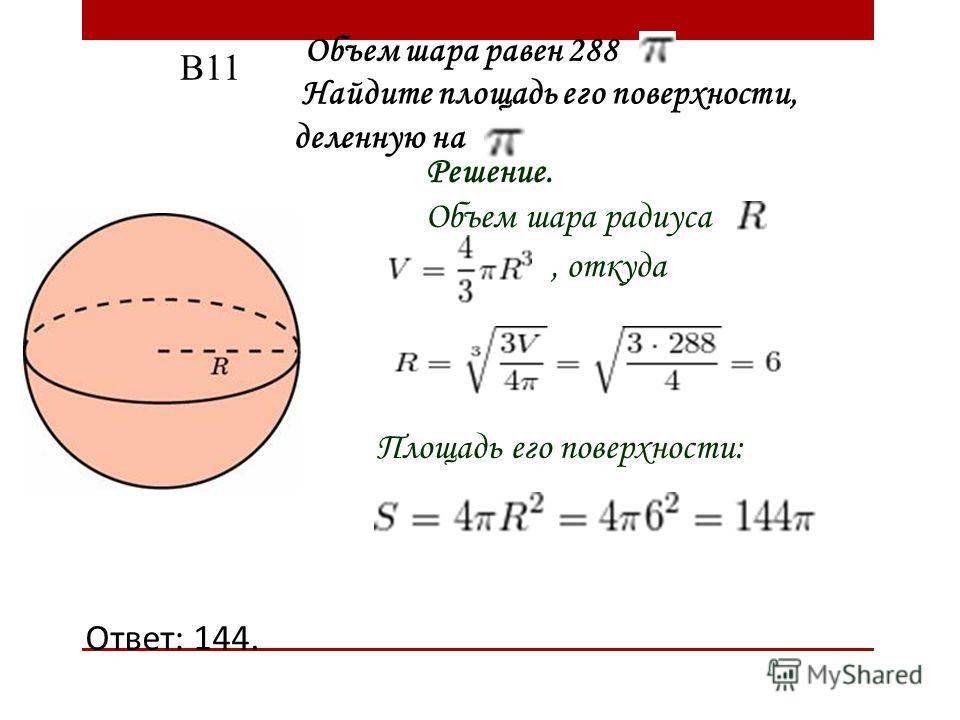 0030680 0030680 | 0.0000160 | ||||||||||||||
| 3/64 | 0.046875 | 0.023438 | 0.0069029 | 0.0000539 | ||||||||||||||
| 1/64 | 0.062500 | 0.031250 | 0.0122718 | 0.0001278 | ||||||||||||||
| 5/ 64 | 0.078125 | 0.039063 | 0.01 | |||||||||||||||
| 0.0002497 | ||||||||||||||||||
| 3/32 | 0.093750 | 0.046875 | 0.0276117 | 0.0004314 | ||||||||||||||
| 7/64 | 0.109375 | 0.054688 | 0.0375825 | 0.0006851 | ||||||||||||||
| 1/8 | 0.125000 | 0.062500 | 0.04 | 0.0010227 | ||||||||||||||
| 9/ 64 | 0,140625 | 0,070313 | 0,0621262 | 0,0014561 | ||||||||||||||
| 5/32 | 0,156250 | 0,0715125 | 0,156250 | 07125. | 0,156250 | .01125 | . 1126 1126 | 0.0766990 | 0.0019974 | |||||||||
| 11/64 | 0.171875 | 0.085938 | 0.0928058 | 0.0026585 | ||||||||||||||
| 3/16 | 0.187500 | 0.093750 | 0.1104466 | 0.0034515 | ||||||||||||||
| 13/ 64 | 0,203125 | 0,101563 | 0,1296214 | 0,0043882 | ||||||||||||||
| 7/32 | 0,218750 | 0,1099999999999926 | 0,2118750 | 0,10999999999999999999999999999999999999,375 | 0.1503301 | 0.0054808 | ||||||||||||
| 15/64 | 0.234375 | 0.117188 | 0.1725728 | 0.0067411 | ||||||||||||||
| 1/4 | 0.250000 | 0.125000 | 0.1963495 | 0.0081812 | ||||||||||||||
| 17 /64 | 0,265625 | 0,132813 | 0,2216602 | 0,0098131 | ||||||||||||||
| 9/32 | 0,281250 | 9/32 | 0,281250 | 50.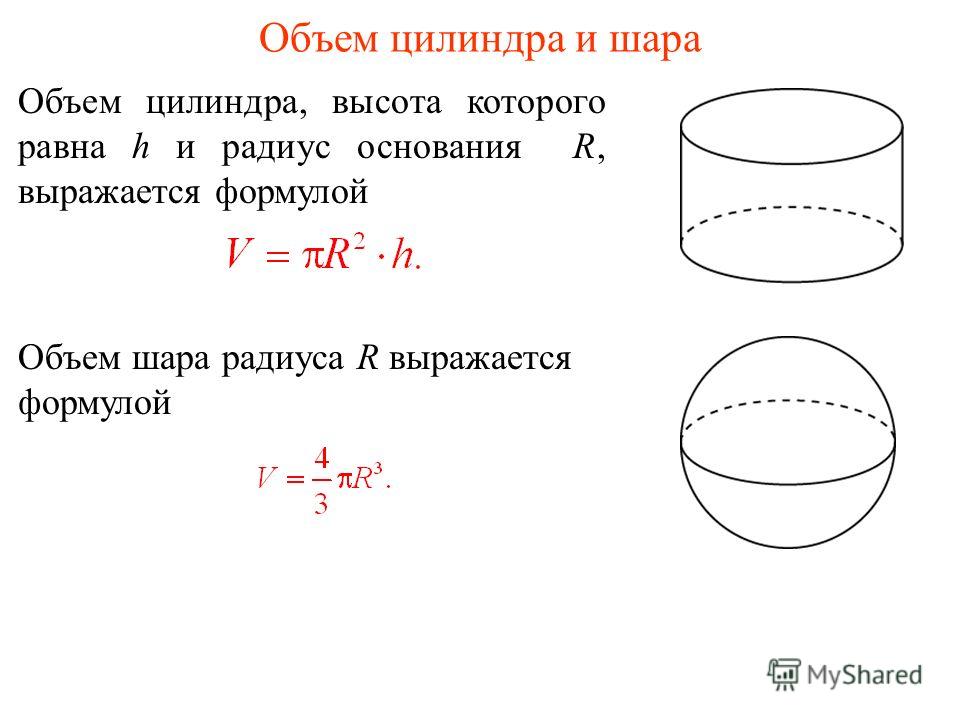 114065065.1125 114065065.1125 | 0,281250 | 50.114065.1125 | 0,281250 | 032 | .1126 | 0.2485049 | 0.0116487 | |||||||
| 19/64 | 0.296875 | 0.148438 | 0.2768835 | 0.0137000 | ||||||||||||||
| 5/16 | 0.312500 | 0.156250 | 0.3067962 | 0.0159790 | ||||||||||||||
| 21/ 64 | 0.328125 | 0.164063 | 0.3382428 | 0.0184977 | ||||||||||||||
| 11/32 | 0.343750 | 0.171875 | 0.3712234 | 0.0212680 | ||||||||||||||
| 23/64 | 0.359375 | 0.179688 | 0.4057379 | 0.0243020 | ||||||||||||||
| 3/8 | 0.375000 | 0.187500 | 0.4417865 | 0.0276117 | ||||||||||||||
| 25/ 64 | 0,3 | 0,195313 | 0,4793690 | 0,0312089 | ||||||||||||||
| 13/32 | 0,406250 | 031125 | 0,406250 | 0,201125 | 0,406250 | 0,201125 | .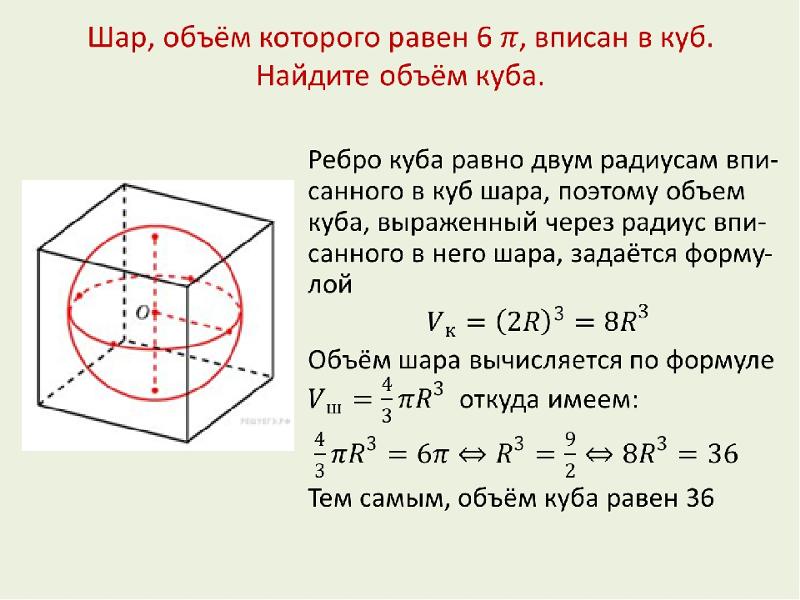 1126 1126 | 0.5184855 | 0.0351058 | |||||||||
| 27/64 | 0.421875 | 0.210938 | 0.55 | 0.0393142 | ||||||||||||||
| 7/16 | 0.437500 | 0.218750 | 0.6013205 | 0.0438463 | ||||||||||||||
| 29/ 64 | 0,453125 | 0,226563 | 0,6450389 | 0,0487139 | ||||||||||||||
| 15/32 | 0,468750 | .112334126 | 0,468750 | 0.23412341269126 | 0,468750 | .11234.234126 | .1126 | 0.64 | 0.0539290 | |||||||||
| 31/64 | 0.484375 | 0.242188 | 0.7370778 | 0.0595037 | ||||||||||||||
| 1/2 | 0.500000 | 0.250000 | 0.7853982 | 0.0654498 | ||||||||||||||
| 33/ 64 | 0,515625 | 0,257813 | 0,8352525 | 0,0717795 | ||||||||||||||
| 17/32 | 0,531250 | . 11256665656565665656656656565665656665665665656656665665665665656656.1125925 11256665656565665656656656565665656665665665656656665665665665656656.1125925 | .1126 | 0.8866409 | 0.0785047 | |||||||||||||
| 35/64 | 0.546875 | 0.273438 | 0.9395632 | 0.0856373 | ||||||||||||||
| 9/16 | 0.562500 | 0.281250 | 0.9940196 | 0.0931893 | ||||||||||||||
| 37/ 64 | 0.578125 | 0.289063 | 1.0500098 | 0.1011728 | ||||||||||||||
| 19/32 | 0.593750 | 0.296875 | 1.1075341 | 0.1095997 | ||||||||||||||
| 39/64 | 0.609375 | 0.304688 | 1.1665924 | 0.1184820 | ||||||||||||||
| 5/8 | 0.625000 | 0.312500 | 1.2271846 | 0.1278317 | ||||||||||||||
| 41 /64 | 0,640625 | 0,320313 | 1,2893109 | 0,1376608 | ||||||||||||||
20 6 91/32 6| 0. | 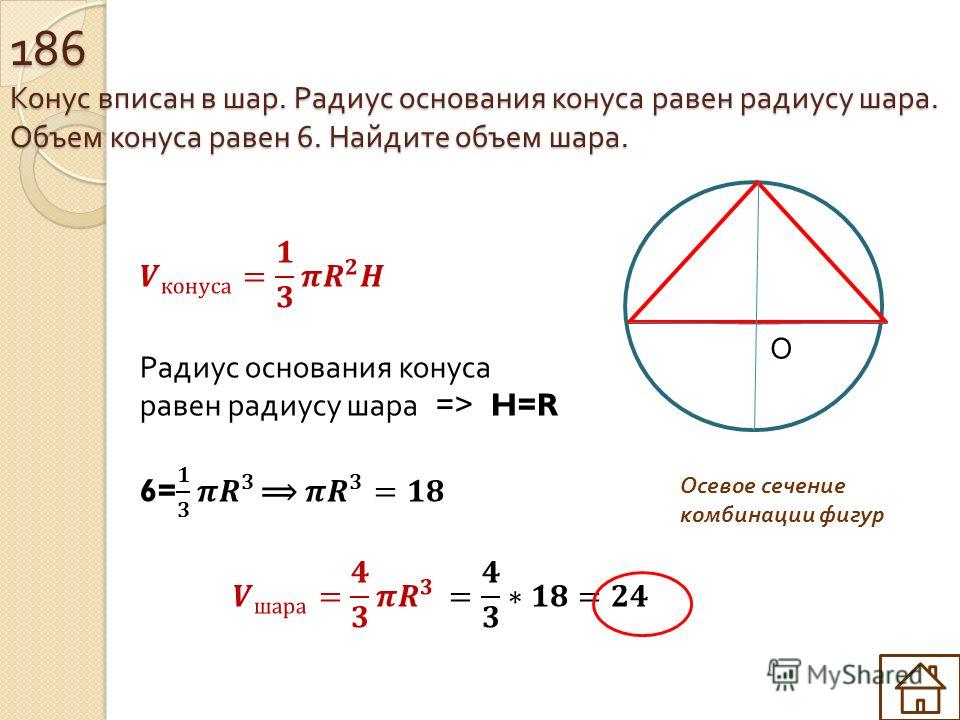 328125 328125 1.3529711 | 0.1479812 | | |||||||||||||||
| 43/64 | 0.671875 | 0.335938 | 1.4181652 | 0.1588050 | ||||||||||||||
| 11/16 | 0.687500 | 0.343750 | 1.4848934 | 0.1701440 | ||||||||||||||
| 45/64 | 0,703125 | 0,351563 | 1,5531555 | 0,1820104 | ||||||||||||||
| 6,5 9198 23/321126 | 0.359375 | 1.6229517 | 0.1944161 | |||||||||||||||
| 47/64 | 0.734375 | 0.367188 | 1.6942818 | 0.2073730 | ||||||||||||||
| 3/4 | 0.750000 | 0.375000 | 1.7671459 | 0.2208932 | ||||||||||||||
| 49/64 | 0,765625 | 0,382813 | 1,8415439 | 0,2349887 | ||||||||||||||
| 25/32 | 0,781250 | |||||||||||||||||
| 25/32 | 0,781250 | |||||||||||||||||
| 25/32 | 0,781250 | |||||||||||||||||
| 25/32 | 0,781250 | |||||||||||||||||
| 25/32 | 0,71250 | |||||||||||||||||
| 25/32 | 0,71250 | |||||||||||||||||
| 1126 | 0. 3 3 | 1. | 0.2496714 | |||||||||||||||
| 51/64 | 0.796875 | 0.398438 | 1.9949420 | 0.2649532 | ||||||||||||||
| 13/16 | 0.812500 | 0.406250 | 2.0739420 | 0.2808463 | ||||||||||||||
| 53/64 | 0,828125 | 0,414063 | 2,1544760 | 0,2973626 | ||||||||||||||
| 27/32 | 0,843750 | |||||||||||||||||
| 27/32 | 0,843750 | |||||||||||||||||
| 27/32 | 0,83750 | |||||||||||||||||
| 27/32 | 0,843750 | |||||||||||||||||
| 27/32 | 0,843750 | |||||||||||||||||
| 27/32 | 0,83750 | |||||||||||||||||
| 0.421875 | 2.2365440 | 0.3145140 | ||||||||||||||||
| 55/64 | 0.859375 | 0.429688 | 2.3201459 | 0.3323126 | ||||||||||||||
| 7/8 | 0.875000 | 0.437500 | 2.4052819 | 0.3507703 | ||||||||||||||
| 0.453125 | 2.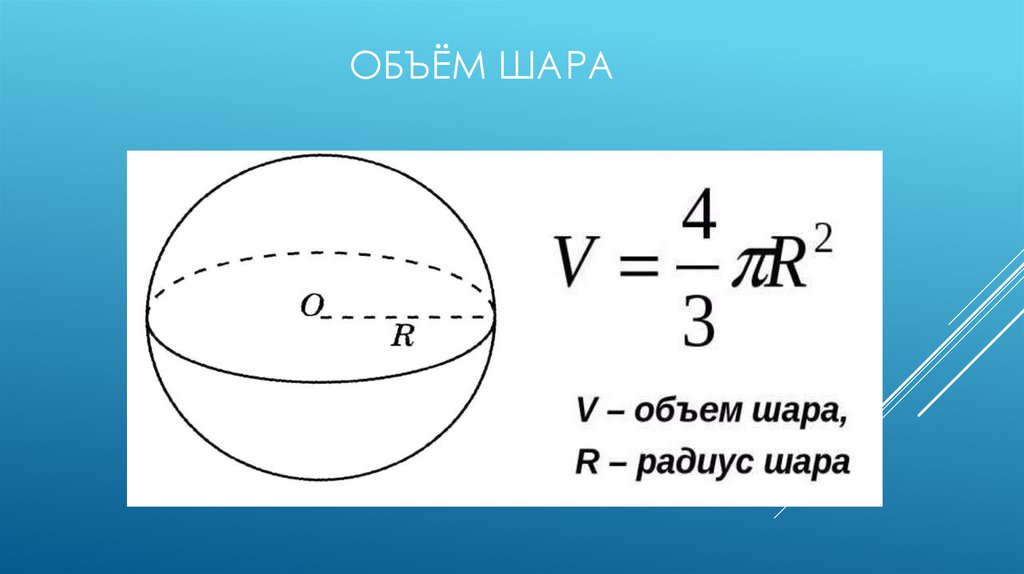 5801557 5801557 | 0.3897110 | ||||||||||||||||
| 59/64 | 0.5 | 0.460938 | 2.6698936 | 0.4102180 | ||||||||||||||
| 15/16 | 0.937500 | 0.468750 | 2.7611654 | 0.4314321 | ||||||||||||||
| 61/64 | 0,953125 | 0,476563 | 2,8539713 | 0,4533652 | 1132/1125 0.968750| 0.484375 | 2.9483111 | 0.4760294 | 63/64 | 0.984375 | 0.4 | 3.0441849 | 0.4994366 | 1 | 1.000000 | 0.500000 | 3.1415927 | 0.5235988 | |
Зона сферы
V = π/6 ч (3a 2 + 3b 2 + h) 0526
A m = 2 π r h (11b)
A 0 = π (2 r h + a 2 + b 2 ) (11c)
Сегмент сферы
V = π/6 H (3/4 S 2 + H 2 )
= π H 4 2 = π H 2 = π H 2 = π H 2 = π H 2 = π H 2 = π H 2 = π H 2 = . A M = 2 π r H = π/4 (S 2 + 4 H 2 ) + 4 H 2 )  (12а)
(12а)
V = 2/3 π R 2 H (13A)
A 0 = π/2 R (4 H + S) (13B)
π/2 R (4 H + S) (13B) π/2 R (4 H + S) (13B).0113 V = π/6 h 3 (14a)
A 0 = 4 π ((R + r) 3 (R — r)) 1/ 2
= 2 π H (R + R) (14B)
H = 2 (R 2 — R 2 2 ) 2 ) 2 ) 2 ).
Сфера с коническим отверстием
V = 2/3 π R 2 h (15a)
A 0 = 2 π R (h + (R 2 — h 2 /4 ) 1/2 ) (15b)
h = 2 (R 2 — r 2 ) 1/2 (15c)
Torus
V = π 2 /4 Д д 2 (16a)
A 0 = π 2 D d (16b)
Sliced Cylinder
V = π/4 d 2 h
= π R 2 ((H 1 + H 2 ) / 2) (17A)
A M
A M A M
A M
A M
A M
A0526
= 2 π r (H 1 + H 2 ) / 2) (17B)
333366 (17B)
33333333366 (17B)
3333333333333333333366 9666666666666666666666666666696666666666666969н.
V = π/6 h 3 (14a)
A 0 = 4 π ((R + r) 3 (R — r)) 1/ 2
= 2 π H (R + R) (14B)
H = 2 (R 2 — R 2 2 ) 2 ) 2 ) 2 ).
Сфера с коническим отверстием
V = 2/3 π R 2 h (15a)
A 0 = 2 π R (h + (R 2 — h 2 /4 ) 1/2 ) (15b)
h = 2 (R 2 — r 2 ) 1/2 (15c)
Torus
V = π 2 /4 Д д 2 (16a)
A 0 = π 2 D d (16b)
Sliced Cylinder
V = π/4 d 2 h
= π R 2 ((H 1 + H 2 ) / 2) (17A)
A M
A MA M
A M
A M
A M
A0526
= 2 π r (H 1 + H 2 ) / 2) (17B)
33333333366 (17B)
3333333333333333333366 9666666666666666666666666666696666666666666969н.

A 0 = π r (h 1 + h 2 + r + (r 2 + (h 1 — h 2 ) 2 /4) 1/2 ) (17C)
, где
A 0 = площадь поверхности
UNGULA
V = 2/3 R 2 593 V = 2/3 R 2 593 V = 2/3 R 2 5. M A 0 = A M + π/2 R 2 + + π/2 R 2 +
Баррель
В ≈ π/12 ч (2 D 2 + D 2 ) 2 ). , и уравнение сферы — Krista King Math
, и уравнение сферы — Krista King Math
Формула уравнения сферы
Мы можем рассчитать уравнение сферы по формуле
92}???где ???D??? длина радиуса, ???(x_1,y_1,z_1)??? является одной точкой на поверхности сферы и ???(x_2,y_2,z_2)??? является центром сферы.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Как использовать две точки на сфере, чтобы найти уравнение сферы
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Давайте попробуем пример, где нам даны точка на поверхности и центр сферы.
Пример
Найти уравнение сферы с центром ???(1,1,2)??? которая проходит через точку ???(2,4,6)???.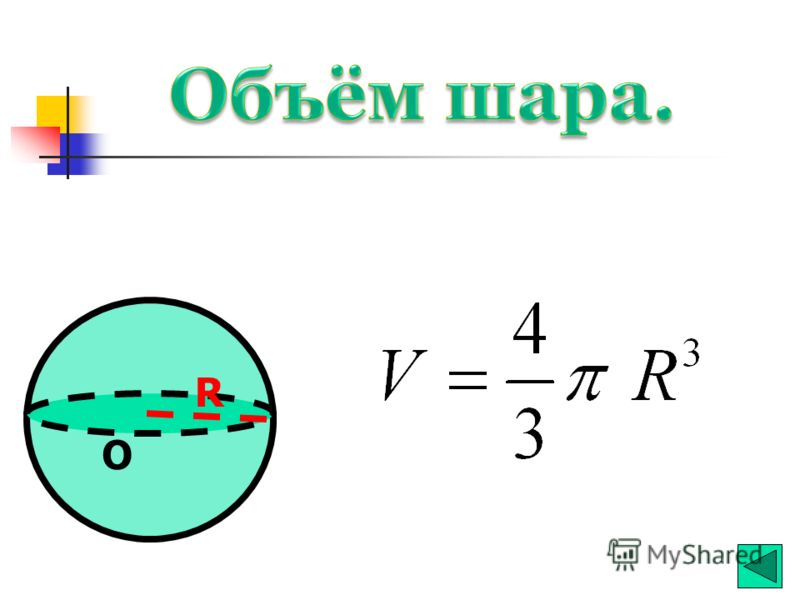
Поскольку в вопросе нам дан центр сферы, мы можем сразу же подставить его в уравнение сферы. 92??? в уравнение, или
решить для ???r???, заменить ???r??? в уравнение, затем возведите его в квадрат, чтобы упростить.
Подойдет любой способ, поэтому выполняйте шаги в любом порядке.
Давайте попробуем другой пример, когда нам дана развернутая форма уравнения и нам нужно найти центр и радиус.
Как найти центр и радиус из уравнения сферы
Пример
Найти центр и радиус сферы. 92???
Для этого нам нужно заполнить квадрат по каждой переменной. Помните, что процесс заполнения квадрата требует от нас использования коэффициента при члене первой степени. За ???х??? это ???2x??? поэтому коэффициент равен ???2???; для тебя??? это ???-2г??? так что коэффициент ???-2???; для ???z??? это ???-6z??? так что коэффициент ???-6???. Завершение квадрата говорит нам, что мы разделим каждый из этих коэффициентов на ???2???, а затем возьмем полученный результат и возведем его в квадрат.

 Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры. Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³. 
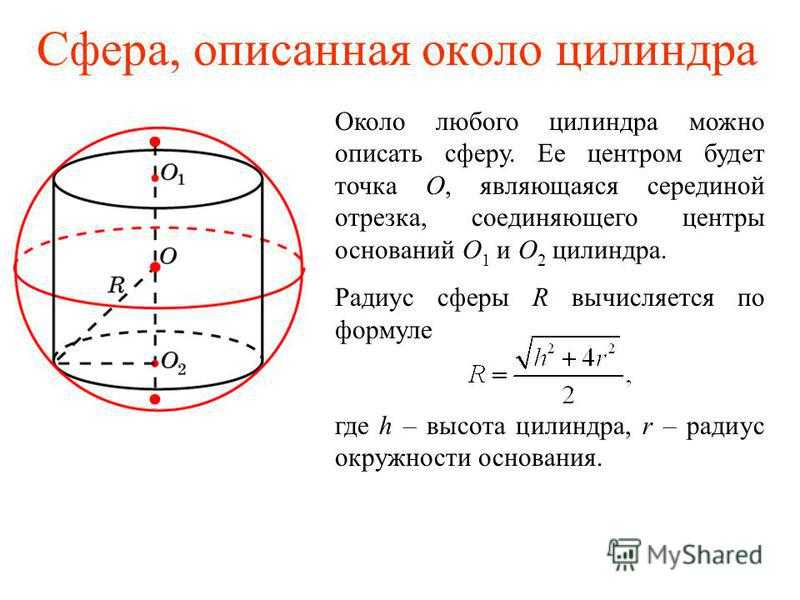 Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.  Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку. Это искомый радиус шара.
Это искомый радиус шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.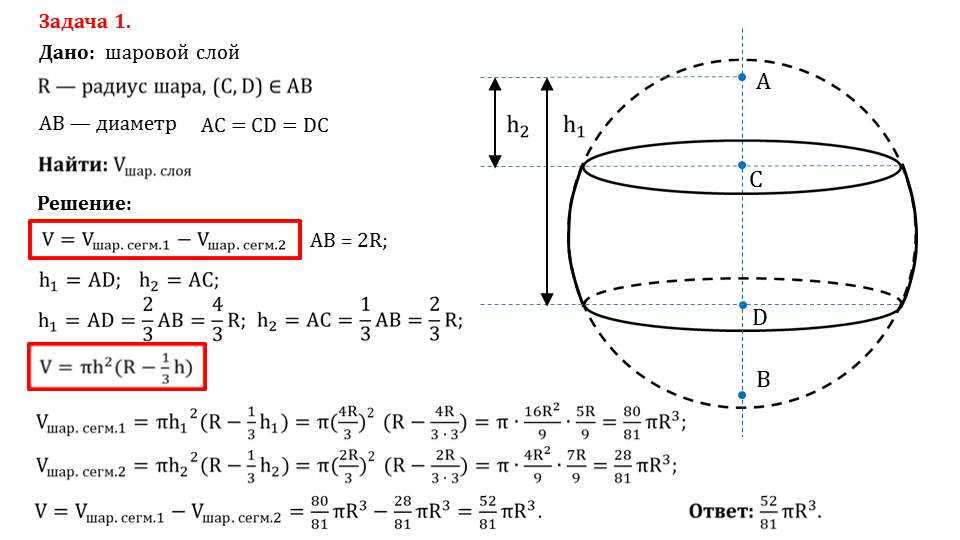 Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³. 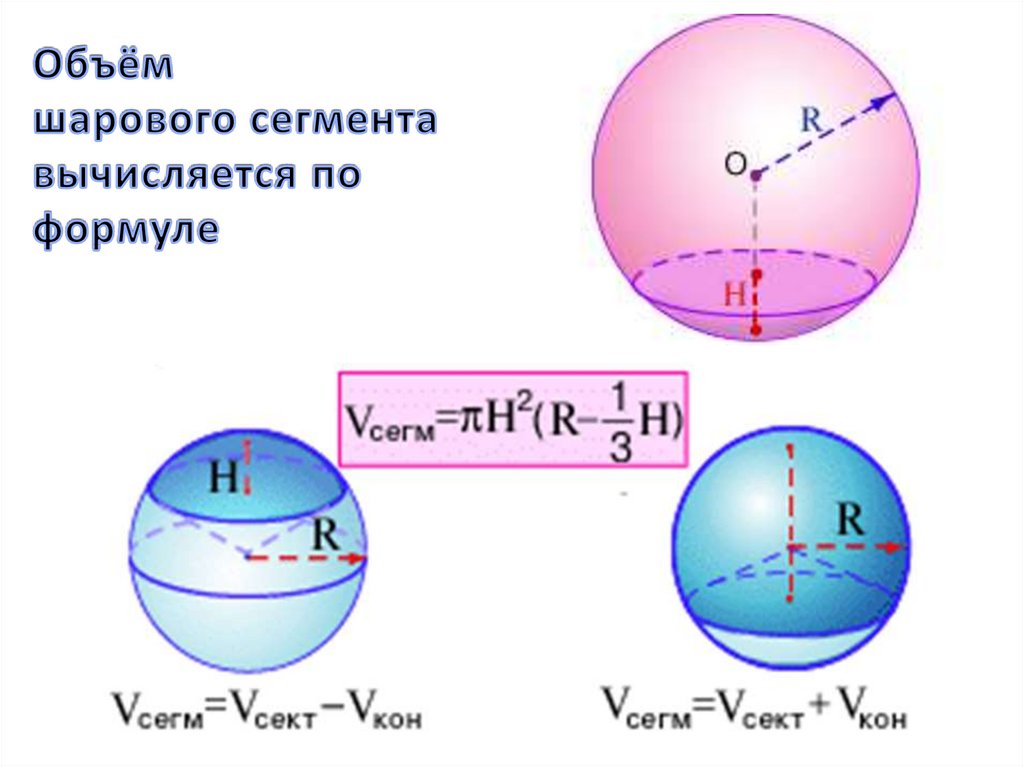
 ⓘ Объем [VT]
ⓘ Объем [VT] ⓘ Малый радиус [rMinor]
ⓘ Малый радиус [rMinor]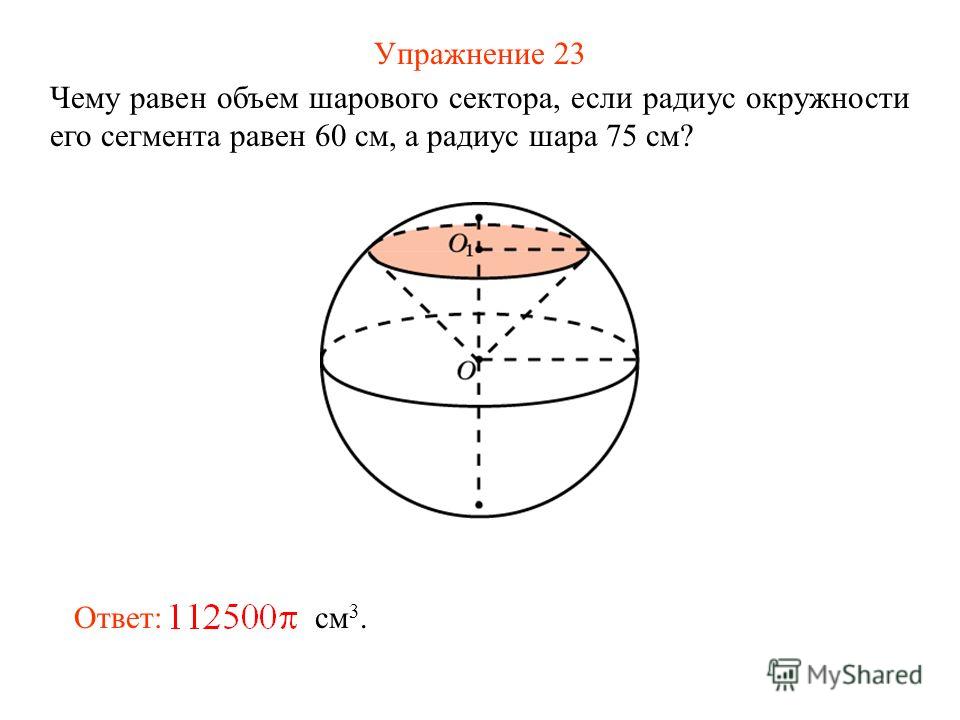 ⓘ Радиус отверстия Тора с учетом объема и малого радиуса [rHole]
ⓘ Радиус отверстия Тора с учетом объема и малого радиуса [rHole]

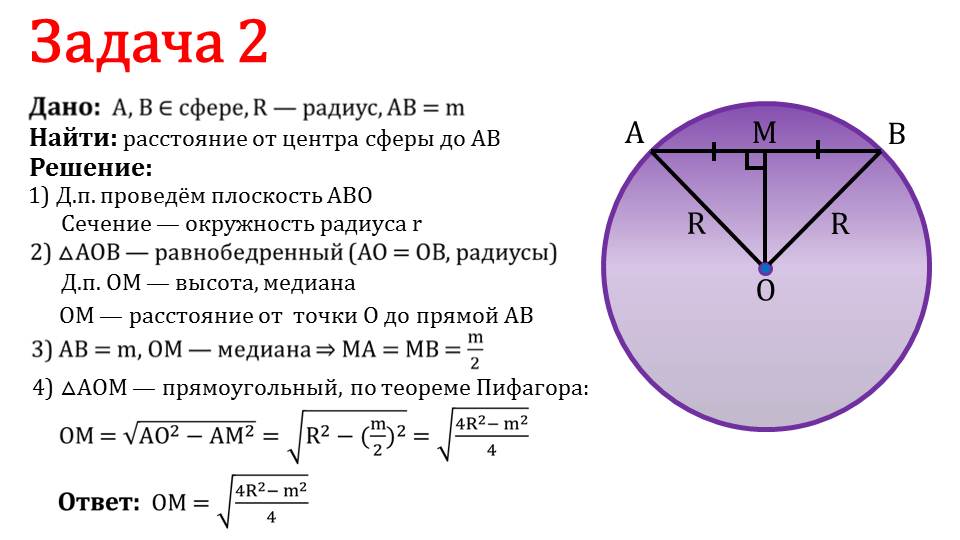 Подготовьте градуированную цилиндрическую емкость, наполненную водой. Поместите шар в этот цилиндр, затем достаньте шар и измерьте объем вытесненной воды (для этого вы можете использовать наш калькулятор объема цилиндра). Если вы хотите увидеть, как объекты ведут себя в жидкости, воспользуйтесь нашим калькулятором плавучести прямо сейчас!
Подготовьте градуированную цилиндрическую емкость, наполненную водой. Поместите шар в этот цилиндр, затем достаньте шар и измерьте объем вытесненной воды (для этого вы можете использовать наш калькулятор объема цилиндра). Если вы хотите увидеть, как объекты ведут себя в жидкости, воспользуйтесь нашим калькулятором плавучести прямо сейчас!
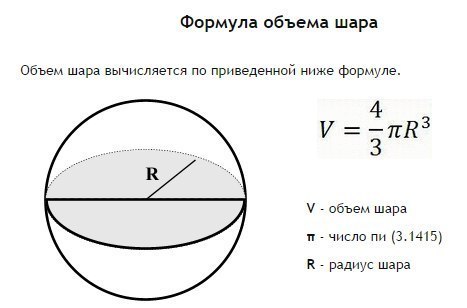 0002 V = A 1 h (3a)
0002 V = A 1 h (3a) 
