Радиус диаметр хорда: Определение окружности ,центра радиуса, хорды и диаметра

Содержание

Взаимное расположение прямой и окружности 8 класс онлайн-подготовка на Ростелеком Лицей

Основные определения

Напомним важное определение – определение окружности]

Определение:

Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R.

Обратим внимание на то, что окружностью называют именно множество всех точек, удовлетворяющих описанному условию. Рассмотрим пример:

Точки A, B, C, D квадрата равноудалены от точки Е, но они не являются окружностью (рис. 1).

Рис. 1. Иллюстрация к примеру

В данном случае фигура является окружностью, так как это все множество точек, равноудаленных от центра.

Если соединить любые две точки окружности – получаем хорду. Хорда, проходящая через центр, называется диаметром.

MB – хорда; АВ – диаметр; MnB – дуга, она стягивается хордой МВ;

Угол называется центральным.

Точка О – центр окружности.

Рис. 2. Иллюстрация к примеру

Таким образом, мы вспомнили, что такое окружность и основные ее элементы. Теперь перейдем к рассмотрению взаимного расположения окружности и прямой.

Задана окружность с центром О и радиусом r. Прямая Р, расстояние от центра до прямой, то есть перпендикуляр ОМ, равна d.

Считаем, что точка О не лежит на прямой Р.

Взаимное расположение прямой и окружности, случай с двумя общими точками

По заданным окружности и прямой нам необходимо найти число общих точек.

Случай 1 – расстояние от центра окружности до прямой меньше радиуса окружности:

В первом случае, когда расстояние d меньше радиуса окружности r, точка М лежит внутри окружности. От этой точки мы отложим два отрезка – МА и МВ, длинна которых будет . Значения r и d нам известны, d меньше r, значит, выражение существует и точки А и В существуют. Эти две точки лежат на прямой по построению. Проверим, лежат ли они на окружности. Вычислим по теореме Пифагора расстояние ОА и ОВ:

Рис. 3. Иллюстрация к случаю 1

Расстояние от центра до двух точек равно радиусу окружности, таким образом, мы доказали, что точки А и В принадлежат окружности.

Итак, точки А и В принадлежат прямой по построению, принадлежат окружности по доказанному – окружность и прямая имеют две общих точки. Докажем, что других точек нет (рис. 4).

Рис. 4. Иллюстрация к доказательству

Для этого возьмем на прямой произвольную точку С и предположим, что она лежит на окружности – расстояние ОС=r. В таком случае треугольник равнобедренный и его медиана ON, которая не совпадает с отрезком ОМ, является высотой. Мы получили противоречие: из точки О опущено два перпендикуляра на прямую.

Таким образом, на прямой Р нет других общих точек с окружностью. Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки.

Взаимное расположение прямой и окружности, случай с одной общей точкой

Случай второй – расстояние от центра окружности до прямой равно радиусу окружности (рис. 5):

Рис. 5. Иллюстрация к случаю 2

Напомним, что расстояние от точки до прямой – это длина перпендикуляра, в данном случае ОН – перпендикуляр. Так как, по условию, длина ОН равна радиусу окружности, то точка Н принадлежит окружности, таким образом, точка Н общая для прямой и окружности.

Докажем что других общих точек нет. От противного: предположим, что точка С на прямой принадлежит окружности. В таком случае, расстояние ОС равно r, и тогда ОС равно ОН. Но в прямоугольном треугольнике гипотенуза ОС больше катета ОН. Получили противоречие. Таким образом, предположение неверно и нет никакой точки кроме Н, общей для прямой и окружности. Мы доказали, что в данном случае общая точка единственная.

Взаимное расположение прямой и окружности, случай, когда нет общих точек

Случай 3 – расстояние от центра окружности до прямой больше радиуса окружности:

Расстояние от точки до прямой – длина перпендикуляра. Проводим из точки О перпендикуляр к прямой Р, получаем точку Н, которая не лежит на окружности, так как ОН по условию больше радиуса окружности. Докажем, что любая другая точка прямой не лежит на окружности. Это хорошо видно из прямоугольного треугольника , гипотенуза ОМ которого больше катета ОН, а значит, больше радиуса окружности, таким образом, точка М не принадлежит окружности, как и любая другая точка на прямой. Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 6).

Рис. 6. Иллюстрация к случаю 3

Теоремы о диаметре и хорде

Рассмотрим теорему. Предположим, что прямая АВ имеет две общих точки с окружностью (рис. 7).

Рис. 7. Иллюстрация к теореме

Имеем хорду АВ. Точка Н, по условию, – середина хорды АВ и лежит на диаметре СD.

Требуется доказать, что в таком случае диметр перпендикулярен хорде.

Доказательство:

Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как .

Точка Н, по условию, – середина хорды, значит середина медианы АВ равнобедренного треугольника. Мы знаем, что медиана равнобедренного треугольника перпендикулярна его основанию, значит, является высотой: , отсюда , таким образом, доказано, что диаметр, проходящий через середину хорды, перпендикулярен ей.

Справедлива и обратная теорема: если диаметр перпендикулярен хорде, то он проходит через ее середину.

Задана окружность с центром О, ее диаметр СD и хорда АВ. Известно, что диаметр перпендикулярен хорде, нужно доказать, что он проходит через ее середину (рис. 8).

Рис. 8. Иллюстрация к теореме

Доказательство:

Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как . ОН, по условию, – высота треугольника, так как диаметр перпендикулярен хорде. Высота в равнобедренном треугольнике одновременно является медианой, таким образом, АН=НВ, значит, точка Н является серединой хорды АВ, значит, доказано, что диаметр, перпендикулярный хорде, проходит через ее середину.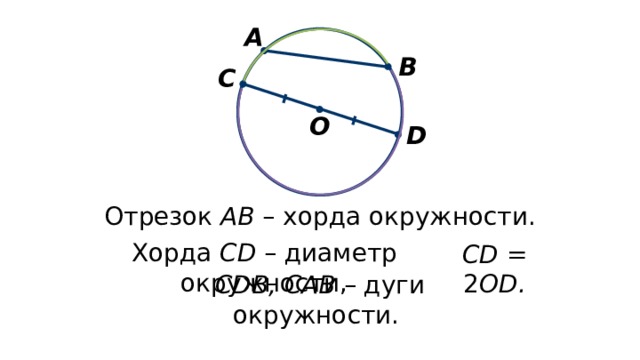

Прямую и обратную теорему можно обобщить следующим образом.

Теорема:

Диаметр перпендикулярен хорде тогда и только тогда, когда он проходит через ее середину.

Выводы по уроку

Итак, мы рассмотрели все случаи взаимного расположения прямой и окружности. На следующем уроке мы рассмотрим касательную к окружности.

Список литературы

Александров А.Д. и др. Геометрия 8 класс. – М.: Просвещение, 2006.
Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия 8. – М.: Просвещение, 2011.
Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Edu.glavsprav.ru (Источник).
Webmath.exponenta.ru (Источник).
Fmclass.ru (Источник).

Домашнее задание

Задание 1. Найти длины двух отрезков хорды, на которые разделяет ее диаметр окружности, если длина хорды – 16 см, а диаметр ей перпендикулярен.

Задание 2. Указать количество общих точек прямой и окружности, если:

а) расстояние от прямой до центра окружности – 6 см, а радиус окружности – 6,05 см;

б) расстояние от прямой до центра окружности – 6,05 см, а радиус окружности – 6 см;

в) расстояние от прямой до центра окружности – 8 см, а радиус окружности – 16 см.

Задание 3. Найти длину хорды, если диаметр ей перпендикулярен, а один из отрезков, отсекаемых диаметром от нее, равен 2 см.

Геометрия 7-9 класс. Окружность — math200.ru

Геометрия 7-9 класс. Окружностьadmin2022-12-14T21:48:52+03:00

Скачать файл в формате pdf.

Геометрия 7-9 класс. Окружность

Задача 1. Из точки окружности проведены радиус и равная ему хорда. Найдите угол между этим радиусом и хордой. Ответ дайте в градусах. Ответ ОТВЕТ: 60.
Задача 2. Из точки окружности проведены две хорды, каждая из которых равна радиусу. Найдите угол между этими хордами. Ответ дайте в градусах. Ответ ОТВЕТ: 120.
Задача 3. Из точки окружности проведены диаметр и хорда, равная половине диаметра. Найдите угол между диаметром и хордой. Ответ дайте в градусах. Ответ ОТВЕТ: 60.
Задача 4. В окружности проведен диаметр AB. Из точки C, лежащей на окружности, опущен перпендикуляр CH на диаметр. Найдите \(\angle \,ABC,\) если AC = 2 CH. Ответ дайте в градусах. Ответ ОТВЕТ: 60.
Задача 5. Треугольник ABC вписан в окружность так, что AC – диаметр, вершина B лежит на окружности. \circ }.\) Найдите расстояние от точки C до прямой AB, если радиус окружности равен 10,4. Ответ ОТВЕТ: 10,4.
Задача 7. Из конца диаметра AB проведены равные хорды AC и AD по разные стороны от диаметра. Докажите, что CB = DB.
Задача 8. Из концов диаметра AB проведены равные хорды AC и BD по одну стороны от диаметра. Докажите, что AD = BC.
Задача 9. Дана окружность с центром в точке O. Из конца диаметра AB проведена хорда BC. Докажите, что \(\angle \,AOC\) в два раза больше \(\angle \,ABC.\)
Задача 10. Дана окружность с центром в точке O, AB – хорда окружности, AC – касательная к окружности. Докажите, что \(\angle \,AOB\) в два раза больше \(\angle \,BAC. \)
Задача 11. Известно, что BK = BC, AM = AC, AB – диаметр окружности, описанной около треугольника ABC. Найдите \(\angle \,MCK.\) Ответ дайте в градусах. Ответ ОТВЕТ: 135.

Поддержать нас

Q3 Нарисуйте любой круг и отметьте a его центр b радиус c диаметр d a сектор e сегмент f точку в…

Перейти к

Упражнение 4.1
Упражнение 4.2
Упражнение 4.3

Упражнение 4. 4
Упражнение 4.5
Упражнение 4.6

Зная наши цифры
Целые числа
Игра с числами

Основные геометрические идеи
Понимание элементарных форм
Целые числа
Фракции
Десятичные
Обработка данных

Измерение
Алгебра
Соотношение и пропорция
Симметрия
Практическая геометрия

Главная > Решения НЦЭРТ Класс 6 Математика > Глава 4.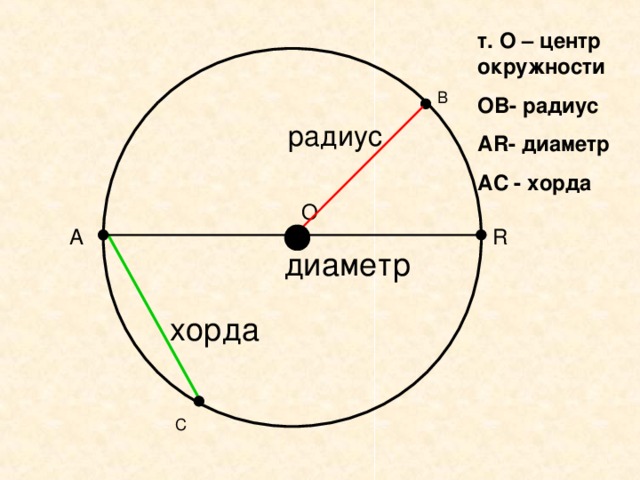

Основные геометрические идеи > Упражнение 4.6 > Вопрос 6

Вопрос 6 Упражнение 4.6

Q3) Нарисуйте любой круг и отметьте

(а) его центр (б) радиус

(в) диаметр (г) сектор

(д) отрезок (f ) точка внутри

(g) точка на его внешней стороне (h) дуга

Ответ:

Решение 3:

Расшифровка видео

Нарисуйте любой круг и метку и не обращайте внимания на засовы. Прежде всего, возьмите свой циркуль и нарисуйте круг. Итак, это ваша схема. Пожалуйста, нарисуйте его с помощью маршрутизатора, только не запускайте. Все в порядке. Итак, после этого давайте проверим, что все, что у нас есть на рынке, это в первую очередь вы должны отметить Так что возьмите свой карандаш, а затем вы должны найти радиус диаметра. Так вот радиус окружности можно сделать радиусом любой предыдущей сторонней надо сделать диаметр.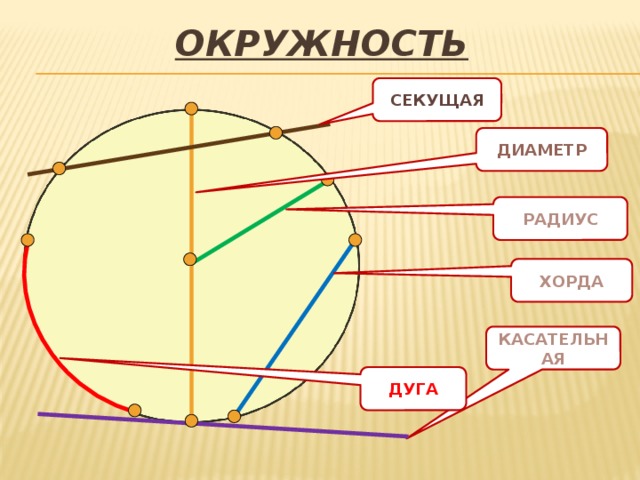

Таким образом, диаметр — это любой извиняемый диаметр — это ядро, которое проходит. Таким образом, сектор представляет собой сердце, сделанное радиусом Солнца, и сделайте точку в любом месте и назовите это как хотите. Я получу так эту часть оттуда отсюда вы с вашими друзьями, которые не понимают эту концепцию. Большое спасибо

Связанные вопросы

По рисунку определите: (а) центр окружности (б) три радиуса (в) диаметр (г) хорду (д) две точки…

Q1) По рисунку определите: (a) центр окружности (b) три радиуса (c) диаметр (d) хорду (e)…

Q2) (a) Является ли каждый диаметр окружности также хордой? (b) Является ли каждая хорда окружности также диаметром?

а) Является ли каждый диаметр окружности также хордой? (б) Является ли каждая хорда окружности также диаметром?

Начертите любой круг и отметьте (а) его центр (б) радиус (в) диаметр (г) сектор (д) сегмент (е) точку. ..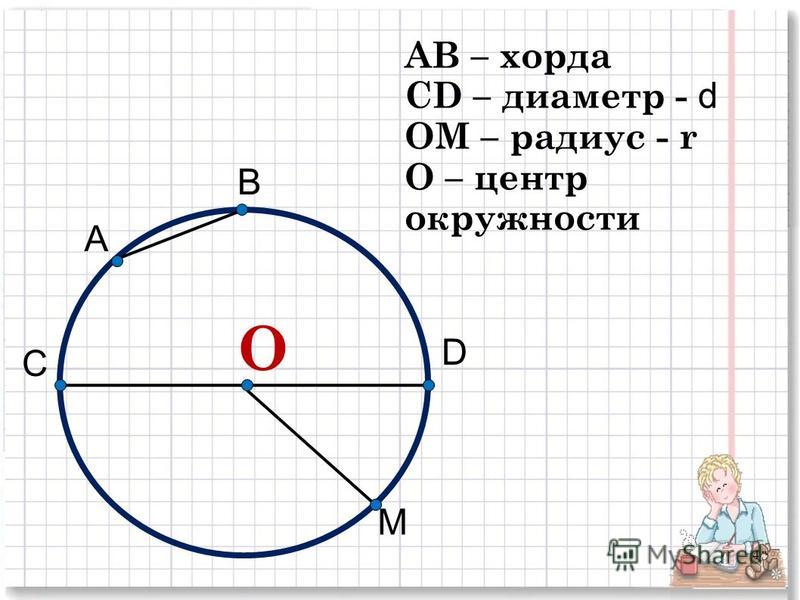

Q4) Верно или неверно: (а) Два диаметра круга обязательно пересекаются. (б) Центр …

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Задание

Задание 4.1

Задание 4.2

Задание 4.3

Задание 4.4

Задание 4.5

Задание 4.6

Главы

Знание наших чисел

Целые числа

играют с номерами

Основные геометрические идеи

Понимание элементарных форм

Интеллект

Фракции

DECIMAL

Симметрия

Практическая геометрия

Курсы

Быстрые ссылки

Условия и политика

Circles | GMAT Free

Окружность — это набор всех точек, находящихся на равном расстоянии от центральной точки. Расстояние между любой из точек и центром равно радиусу r . Радиус, другими словами, не является свойством круга — это определяющее свойство круга.

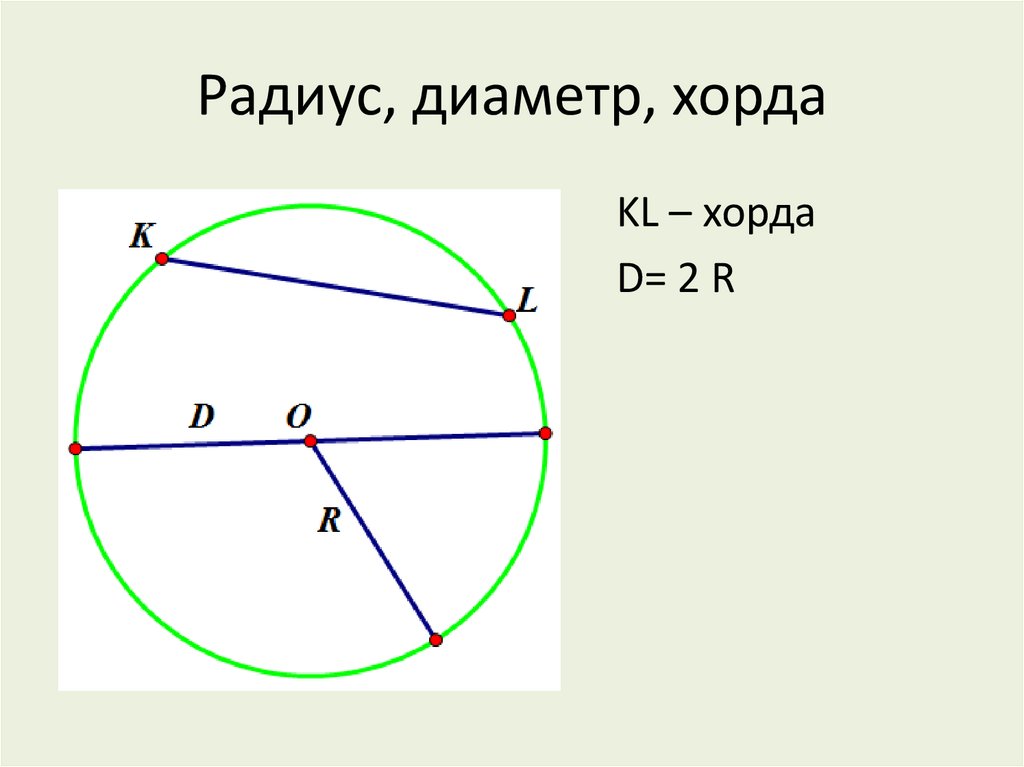
Радиус, хорды и касательные

Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через центр. Его длина всегда равна двум радиусам.

На рисунке выше показана окружность с показанными диаметром и радиусом (бесконечно много возможных диаметров и радиусов). На рисунке также показаны хорда, секущая (очень похожая на хорду) и касательная. Для GMAT единственными ключевыми фактами об этих других линиях являются:

Любая хорда, которая не является диаметром круга, будет короче диаметра круга.
Любая линия, касательная к окружности, перпендикулярна радиусу или диаметру в этой точке, как показано на рисунке выше.

Площадь и окружность

Площадь круга определяется уравнением:

где r — радиус круга.

Здесь пи — постоянное число, представленное греческой буквой пи, равное примерно 3,14.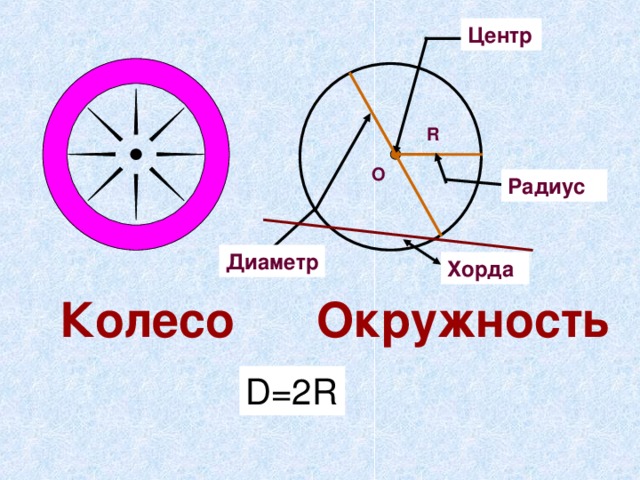 Число пи, как и любое иррациональное число, состоит из бесконечного числа неповторяющихся цифр. (Однажды ради развлечения я выучил первые 1000 цифр числа пи. Готов поспорить, что вы тоже сможете это сделать, если у вас будет месяц или пара месяцев!) Для GMAT вам нужно только запомнить, что

или, по-другому,

Никакой дополнительной точности от вас никогда не потребуется. Кроме того, варианты ответов довольно часто будут выражаться в виде пи, и в этом случае вам никогда не нужно будет выражать пи в цифрах, а можно будет работать с ним как с символом. Например, если радиус круга равен 4, то его площадь равна

Окружность круга — это его периметр, хотя термин «периметр» обычно не используется с кругами. Длина окружности равна

Информация, необходимая для вычисления площади и длины окружности, одинакова: нам нужен радиус и все. Это означает, что если мы знаем длину окружности, мы сможем вычислить ее площадь, и наоборот. Кроме того, поскольку диаметр просто в два раза больше радиуса, знание диаметра также позволит нам вычислить длину окружности и ее площадь.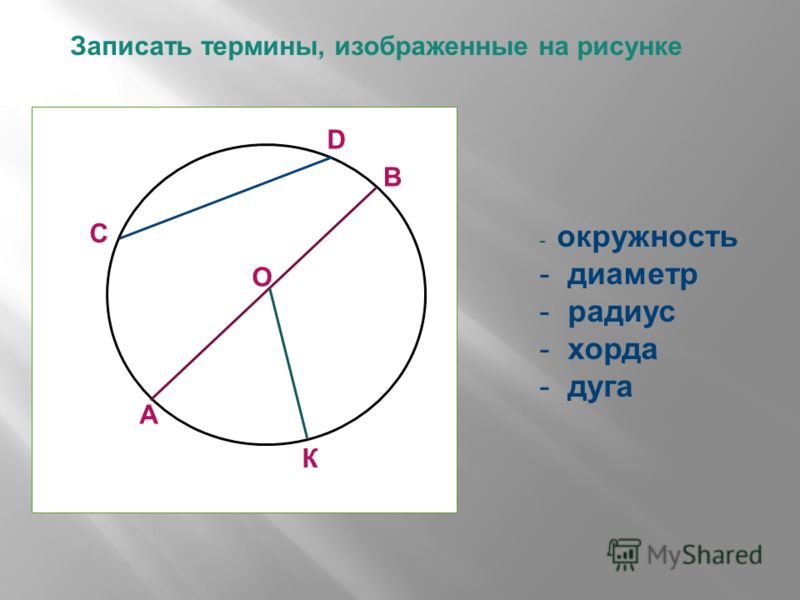 Таким образом, уравнение окружности, например, эквивалентно

, где d это диаметр.

Это последнее уравнение дает нам классический способ представить число пи: если мы переставим его, мы получим

Другими словами, пи — это отношение длины окружности к диаметру любого круга. Если вас беспокоит число пи, которое кажется вам слишком загадочным, этот факт может помочь уменьшить загадочность (хотя число пи, безусловно, загадочно и всплывает в других странных местах математики, хотя их нет на GMAT).

Градусы, дуги и сечения

На рисунке ниже показана частично заштрихованная окружность радиусом r . Заштрихованная область ограничена двумя радиусами с углом θ (это греческая буква тета) между ними. На таком рисунке θ — центральный угол, а L — дуга, охватывающая этот угол.

Поскольку общий размах вокруг центральной точки составляет 360 градусов, мы можем сравнить θ с 360 градусами, чтобы количественно определить длину любой дуги L и заштрихованную область, очерченную дугой.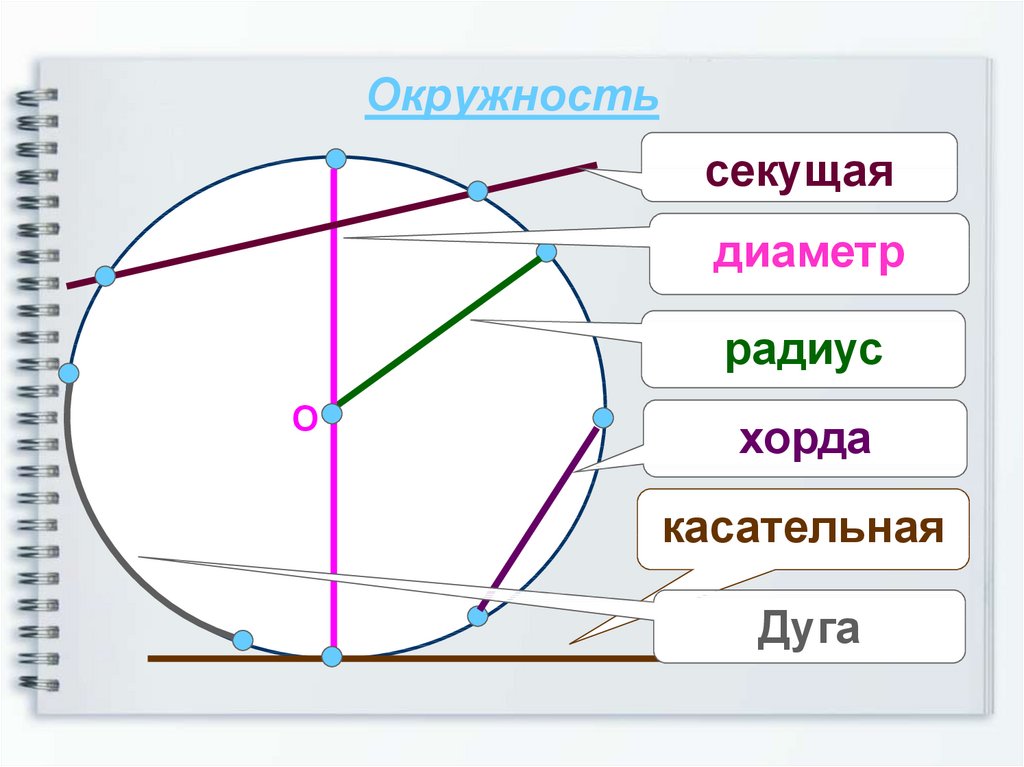 Например, если θ составляет 120 градусов, то это будет одна треть от 360 градусов. В этом случае длина L будет равна одной трети длины окружности, а площадь сектора будет равна одной трети площади окружности. В общем,

, а площадь сектора равна

Вписанные фигуры

«Вписанная» фигура — это фигура, которая «плотно прилегает» к другой фигуре, а это означает, что фигуры имеют общие точки на своих краях. Окружности могут быть вписаны в другие многоугольники, а другие многоугольники могут быть вписаны в окружности:

Некоторые цифры с надписями

Официальные языки GMAT не дают вам многого для изучения или запоминания цифр с надписями. Скорее, от вас требуется просто понять термин, чтобы GMAT мог дать вам вопросы, в которых одна цифра вписана в другую, и ожидать, что вы правильно поймете вопрос.

С практической точки зрения, вписанные фигуры обычно важны тем, что вы можете сделать вывод, что они имеют одно или несколько общих измерений.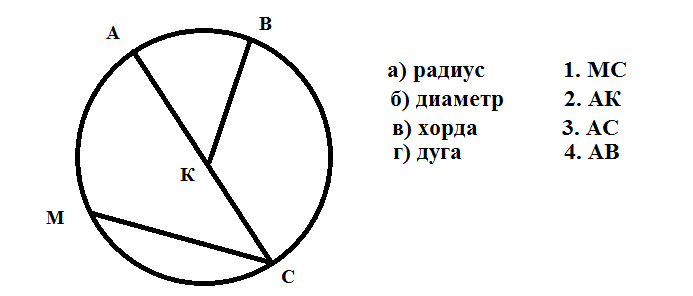 Например, рассмотрим верхний правый пример на рисунке выше, круг, вписанный в квадрат. Если бы мы знали, что площадь квадрата равна 9, например, мы могли бы определить, скажем, длину окружности. Если площадь квадрата равна 9, и мы называем сторону квадрата с, , то

и, следовательно, с = 3. Так как фигуры вписаны, то с равно диаметру круга. Следовательно, длина окружности равна

Чтобы сделать этот вывод, мы должны приравнять s и d , а для этого использовать тот факт, что окружность вписана в квадрат.

Прямоугольный треугольник, вписанный в окружность

Есть еще один факт, который часто упускают из виду, о вписанных фигурах, который вы должны знать для GMAT. Если треугольник вписан в окружность так, что одна сторона треугольника равна диаметру окружности, то этот треугольник является прямоугольным. Этот факт называется теоремой Фалеса.

Верно и обратное: если прямоугольный треугольник вписан в окружность, то одна из его сторон проходит через центр окружности и является диаметром.

Теорема резюмируется следующей диаграммой:

Другими словами, если нам дан приведенный выше рисунок и сказано, что O является центром круга и что AC проходит через O , то мы могли бы сделать вывод, что ABC является прямоугольным треугольником даже без обозначения прямого угла на диаграмме.

Вам не нужно знать, почему теорема Фалеса верна для GMAT. Однако вас может раздражать то, что вы не знаете, почему это правда. Суть в том, что на рисунке выше OB — радиус окружности. Поскольку OA и OC также являются радиусами окружности, это означает, что AOB и COB являются равнобедренными треугольниками. Отсюда, написав уравнения для углов этих двух треугольников, можно доказать, что угол ABC = 90. Опять же, вам не нужно запоминать доказательство для GMAT. Однако тип рассуждений, используемых в доказательстве, типичен для ответов на вопросы геометрии GMAT: вы находите новые способы использования и связи между различными геометрическими фактами, которыми в данном случае являются определение радиуса и диаметр, тот факт, что углы треугольников в сумме составляют 180 градусов, и тот факт, что равные стороны в треугольниках обращены к равным углам.