Радиус равен: Чему равен радиус окружности ,если диаметр равен 12см,6м,44дм,18см?

Как найти радиус описанной около треугольника abc окружности

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

• Формулы вычисления радиуса описанной окружности
  • Произвольный треугольник
  • Прямоугольный треугольник
  • Равносторонний треугольник
• Примеры задач

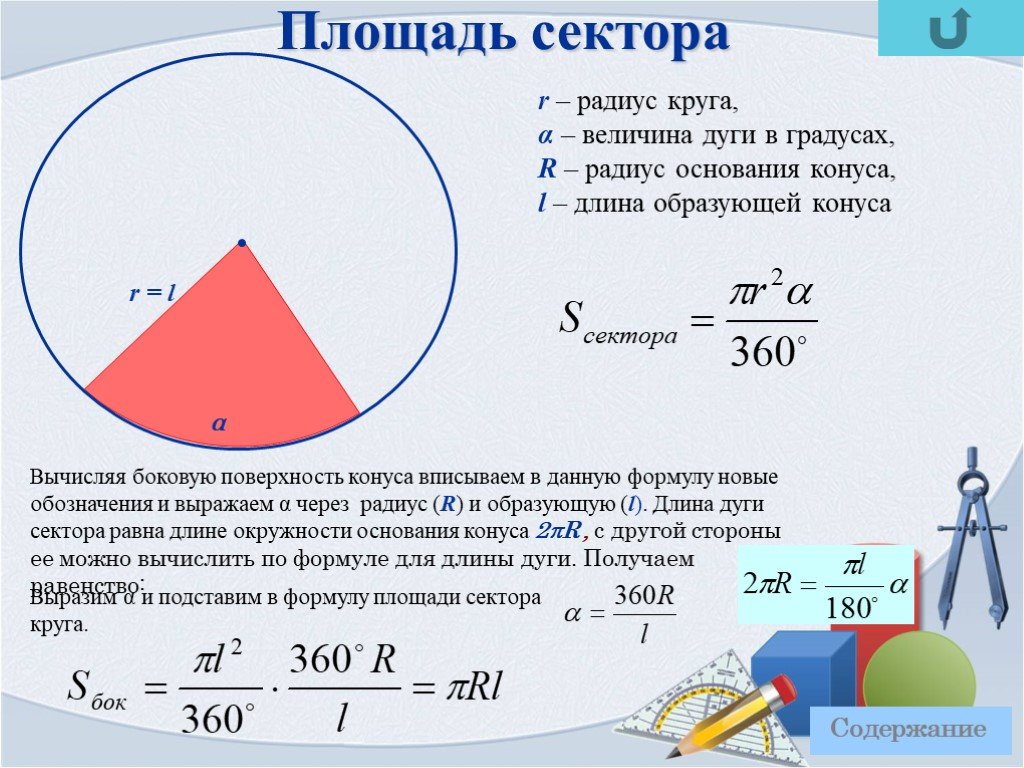
Формулы вычисления радиуса описанной окружности

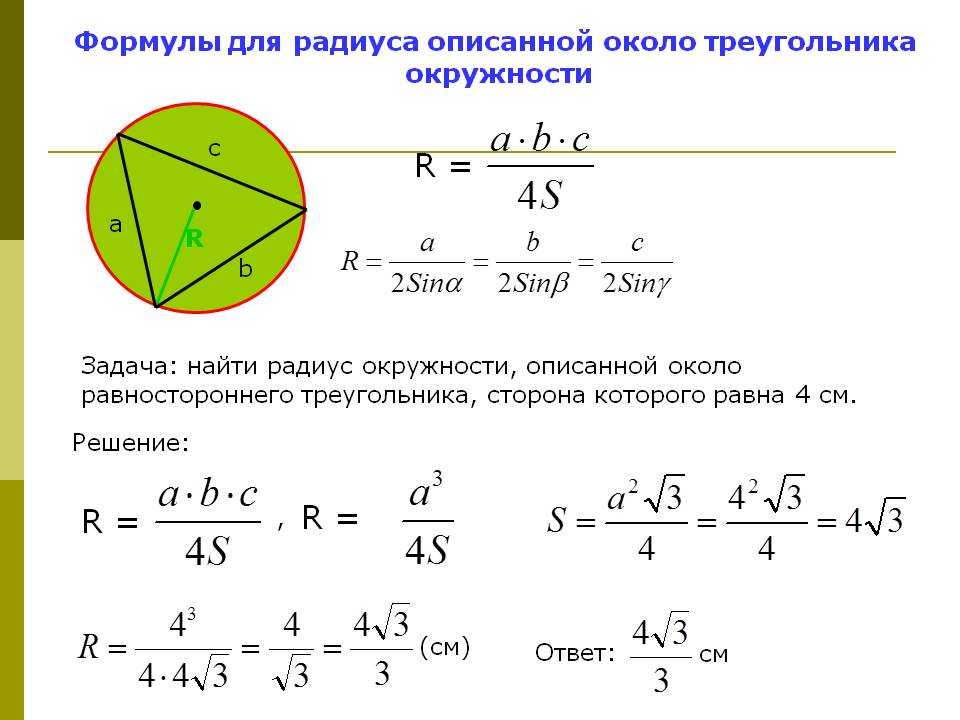
Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

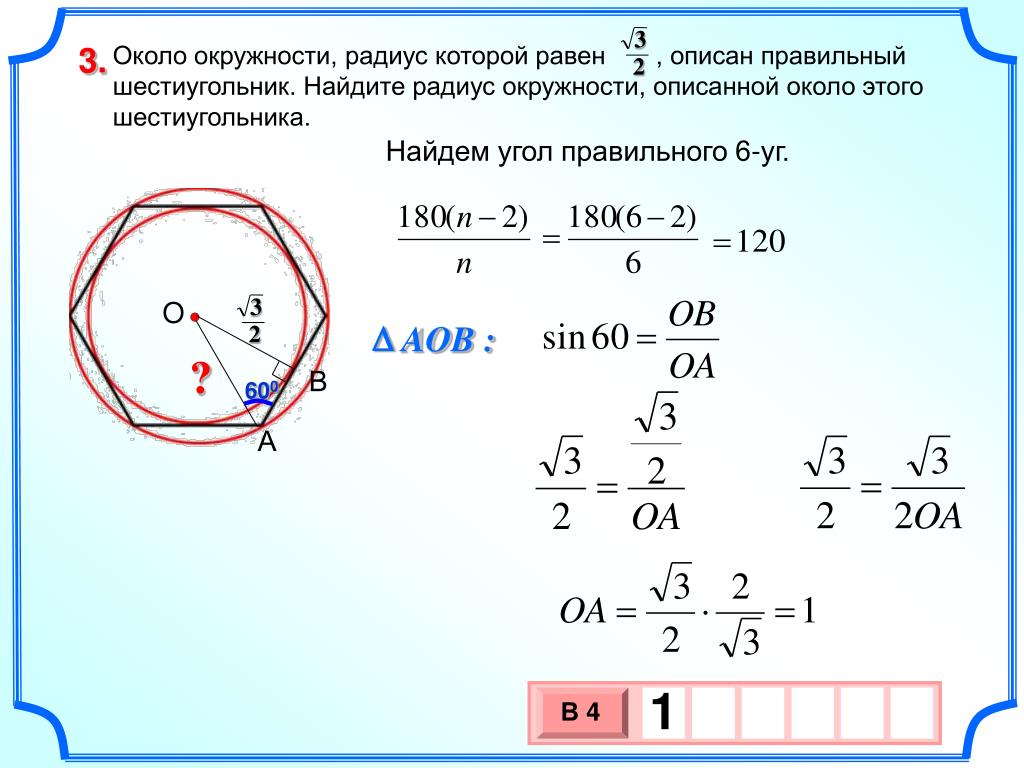
Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

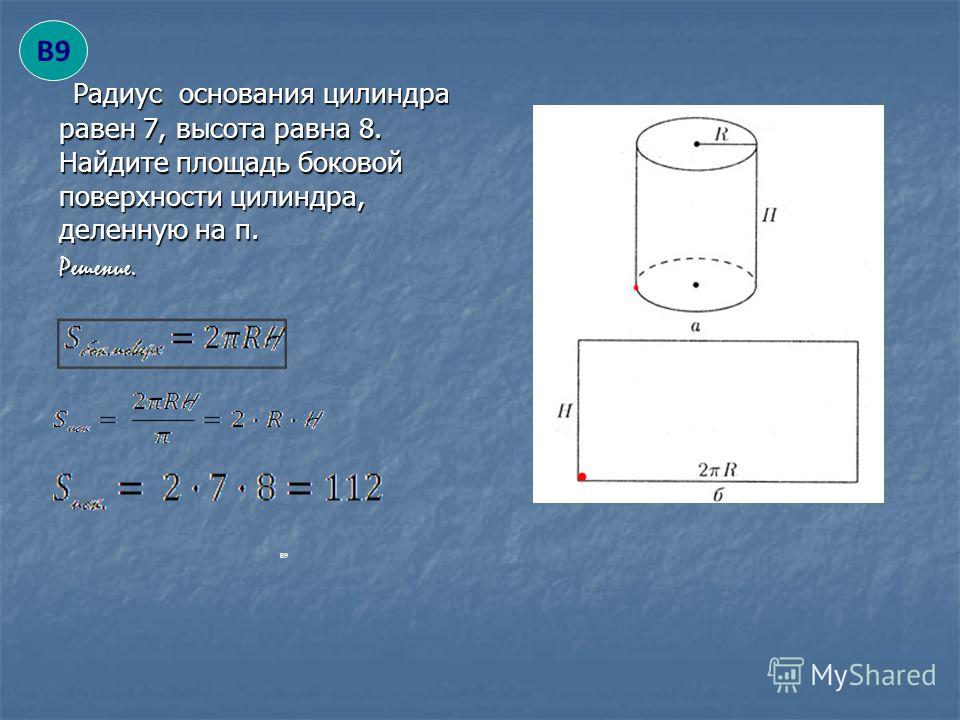
Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно:

R = 10 : 2 = 5.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Радиус окружности

Узнаем как найти радиус окружности: в помощь школьникам

Как найти радиус окружности? Формулы расчета зависят от того, является ли эта фигура вписанной в многоугольник или же она описана вокруг него, а также от входных данных задачи.

В статье рассмотрим несколько примеров.

Что это — окружность как геометрическая фигура: основные свойства и характеристики

Чтобы иметь четкое представление о том, что такое окружность, нужно обязательно знать о ее основных характеристиках, свойствах и взаимосвязях с другими геометрическими фигурами. Подробнее обо всем этом читайте в статье далее.

Для начала дадим определение радиуса. В переводе с латинского radius – это «луч, спица колеса». Радиус окружности – это отрезок прямой, соединяющий центр окружности с точкой, которая находится на ней. Длина данного отрезка – это значение радиуса. В математических расчётах для обозначения данной величины используют латинскую букву R.

Советы по нахождению радиуса:

1. Диаметр окружности является отрезком прямой, проходящей через ее центр и соединяющей точки, лежащие на окружности, которые максимально удалены друг от друга. Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр.
2. Длина закрытой кривой, которая образуется на плоскости – это длина окружности. Если вы знаете ее длину, то для нахождения радиуса окружности вы можете применить универсальную в своем роде формулу: R = L/(2*π), где L является длиной окружности, а π – константой, равной 3,14. Константа π представляет собой отношение длины окружности к длине ее диаметра, она одинакова для всех окружностей.
3. Круг представляет собой геометрическую фигуру, являющуюся частью плоскости, ограниченной кривой – окружностью. В том случае, если вы знаете площадь какого либо круга, то радиус окружности может быть найден по специальной формуле R = √(S/π), где S является площадью круга.
4. Радиус вписаной окружности (в квадрат) находится следующим образом: r = a/2, где а является стороной квадрата.
5. Радиус описанной окружности (вокруг прямоугольника) вычисляют по формуле: R = √ (a2 + b 2)/2, где а и b являются сторонами прямоугольника.
6. В том случае, если вы не знаете длину окружности, но знаете высоту и длину какого-либо ее сегмента, то вид формулы будет таков:

R = ( h3 + L2)/8*h, где h является высотой сегмента, а L является его длиной.

Находим радиус окружности, вписанной в треугольник (прямоугольный). В треугольник, какой бы вид он не имел, может быть вписана лишь одна-единственная окружность, центр которой будет одновременно той точкой, где пересекаются биссектрисы его углов. Прямоугольный треугольник имеет множество свойств, которые должны быть учтены, когда вычисляется радиус вписанной окружности. В задаче могут быть приведены различные данные, следовательно, требуется выполнить дополнительные вычисления, необходимые для ее решения.

Советы по нахождению радиуса вписанной окружности:

1. Сначала нужно построить треугольник с теми размерами, которые уже были заданы в вашей задаче. Это необходимо делать, зная размеры всех трёх сторон или двух сторон и угла между ними. Так как размер одного угла вам уже известен, то в условии должны быть два катета. Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r.
2. Для применения стандартной формулы определения радиуса вписанной окружности требуется найти все три стороны прямоугольного треугольника. Зная размеры всех сторон, вы сможете найти полупериметр треугольника из формулы: p = (a + b+ c)/2.
3. Если вы знаете один угол и катет, то вам следует определить, прилежащий он или противолежащий. Если он прилежащий, то гипотенузу можно вычислить, используя теорему косинусов: c = a/cosCBA. Если он противолежащий, то тогда требуется воспользоваться теоремой синусов: c=a/sinCAB.
4. Если у вас есть полупериметр, то вы можете определить радиус вписанной окружности. Вид формулы для радиуса будет таким: r=√(p-b)(p-a)(p-c)/p.
5. Следует отметить, что найти радиус можно по формуле: r = S/p. Так что если вам известны два катета, то процедура вычисления будет более лёгкой. Гипотенуза, требуемая для полупериметра, может быть найдена по сумме квадратов его катетов. Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.

Круг. Круг — геометрическая фигура

Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца, а центр круга был …

далее

Узнаем как рассчитать длину окружности, если не указан диаметр и …

Бывают задачи в геометрии, когда необходимо рассчитать длину окружности, при этом в условии, кроме рисунка, ничего не дано. В статье мы расскажем, какими формулами необходимо воспользоваться, чтобы решить такую задачу.

далее

Что это — окружность и круг, в чем их отличия и примеры данных фигур …

Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни.

Одним из таких является вопрос о …

далее

Узнаем как рассчитывается длина окружности

Эта статья для тех, кому необходимо узнать, чему равна длина окружности. Здесь вы найдете формулы и небольшое объяснение по теме.

далее

• Главная
• Образование
• / Среднее образование и школы

Узнаем как вычислить диаметр окружности?

Чем отличается круг от окружности? По каким параметрам определяется размер окружности? Как вычислить диаметр окружности? Ответы на все эти вопросы даны в следующей статье. Также представлены самые известные формулы для вычисления диаметра окружности.

далее

Тупоугольный треугольник: длина сторон, сумма углов. Описанный тупоугольный треугольник

Тупоугольный треугольник ничем не отличается от других фигур с тремя сторонами и углами. Правда, один угол у него больше 90 градусов. На этом и основаны все особенности тупоугольных треугольников.

далее

Радиус — Анатомические изображения и информация

• Скелет
• Мускулистый
• Сердечно-сосудистые заболевания
• Пищеварительный
• Нервный
• Респираторные органы
• Мочевой
• Покровный
• Руководство по питанию

• Лучший онлайн-доктор
• Лучшая онлайн-терапия
• Лучший онлайн-психиатр
• Часто задаваемые вопросы по онлайн-терапии
• Получение максимальной отдачи от онлайн-терапии
• BetterHelp против Talkspace
• Обзоры BetterHelp
• Роман Отзывы
• Химс Отзывы
• Ее отзывы
• Церебральные обзоры

• Лучший домашний тест на ЗППП
• Лучший тест на пищевую чувствительность
• Лучший тест ДНК на здоровье
• Лучшее тестирование микробиома
• Лучшее тестирование тяжелых металлов
• Лучший домашний тест щитовидной железы
• Everlywell Отзывы
• myLAB Box Отзывы
• Давайте проверим Отзывы
• STDcheck отзывы
• Виоме Отзывы
• Отзывы Thryve
• Отзывы о самодекодировании
• Мира Отзывы
• Обзоры InsideTracker

• Крепости против Химса
• Сохраняет отзывы
• Отзывы о слуховых аппаратах MD
• Химс ED Обзор
• Ритуальные витамины Отзывы
• Откровенные отзывы
• Отзывы о BlueChew
• Тру Ниаген Отзывы
• ScalpMED Отзывы
• Hair Club Отзывы
• Лучшие невидимые брекеты
• Лучшие средства от выпадения волос для мужчин
• Лучшее масло CBD
• Лучший спрей задержки
• Бесплатная пробная версия BlueChew

• 10 лучших и худших штатов для телездравоохранения
• города с самыми высокими показателями ЗППП
• Наиболее уязвимые государства в условиях пандемии COVID-19
• Анализ пакета стимулов для коронавируса по штатам
• Статистика STD по штатам

Критерий поиска

Автор: Tim Taylor

Последнее обновление: 10 октября 2017 г.

Лучевая кость является более латеральной и немного короче из двух костей предплечья. Он находится на предплечье со стороны большого пальца и вращается, позволяя руке поворачиваться на запястье. Несколько мышц руки и предплечья имеют начало и прикрепление на лучевой кости, чтобы обеспечить движение верхней конечности. Эти движения необходимы для многих повседневных задач, таких как письмо, рисование и бросание мяча.

Лучевая кость расположена на латеральной стороне предплечья между локтевым и лучезапястным суставами. Он образует локтевой сустав на своем проксимальном конце с плечевой костью плеча и локтевой костью предплечья. Продолжите прокрутку, чтобы прочитать больше ниже…

Отображается на другой странице

Нажмите, чтобы просмотреть увеличенное изображение

Продолжение сверху… Хотя лучевая кость начинается как меньшая из двух костей предплечья в локтевом суставе, она значительно расширяется по мере прохождения вдоль предплечья и становится намного шире локтевой кости на запястье.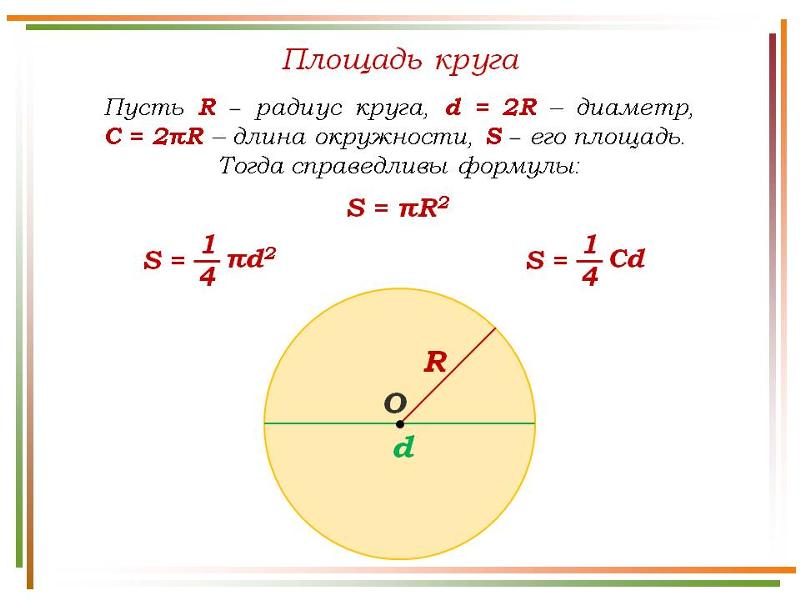 Короткий цилиндр из гладкой кости образует головку лучевой кости в месте соединения с головкой плечевой кости и лучевой вырезкой локтевой кости в локтевом суставе. Головка лучевой кости позволяет предплечью сгибаться и поворачиваться в локтевом суставе. Дистальнее головки лучевая кость значительно сужается, образуя шейку лучевой кости, а затем расширяется медиально, образуя лучевой бугорок, костный отросток, служащий местом прикрепления двуглавой мышцы плеча.

Дистальнее локтя тело лучевой кости продолжается по прямой линии вдоль латеральной стороны предплечья, а затем резко расширяется непосредственно над лучезапястным суставом. На широком дистальном конце лучевая кость заканчивается тремя гладкими вогнутыми поверхностями, образующими лучезапястный сустав с локтевой костью и запястными костями кисти. Две из этих впадин встречаются с ладьевидной и полулунной костями запястья, образуя лучезапястную часть лучезапястного сустава. На медиальной стороне локтевая вырезка лучевой кости образует дистальный лучелоктевой сустав с локтевой костью, позволяя лучевой кости вращаться вокруг локтевой кости для супинации и пронации кисти и запястья.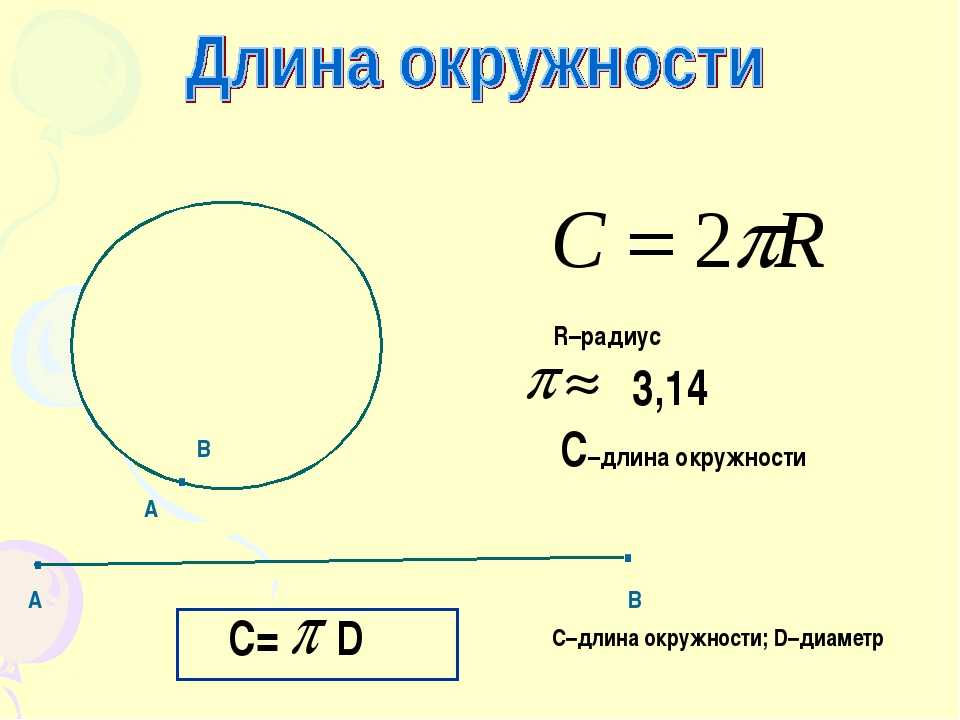 Шиловидный отросток — небольшой заостренный отросток кости — выступает из латерального края лучевой кости, чтобы закрепить лучевую коллатеральную связку запястья.

Одной из важнейших функций лучевой кости является фиксация мышц плеча и предплечья. Двуглавая мышца плеча образует место прикрепления на лучевой бугристости, чтобы сгибать и супинировать предплечье в локтевом суставе. Мышцы супинатора, круглого пронатора и квадратного пронатора предплечья также образуют вставки на лучевой кости для супинации и пронации кисти и запястья за счет вращения дистального конца лучевой кости вокруг локтевой кости. Несколько мышц, приводящих в движение кисть и пальцы, в том числе длинный сгибатель большого пальца и поверхностный сгибатель пальцев, также берут начало на лучевой кости.

Лучевая кость структурно классифицируется как длинная кость, поскольку ее длина намного превышает ширину. Как и все длинные кости, лучевая кость состоит из компактной кости с полым центром и губчатыми костями, заполняющими концы. Компактная кость является самой твердой и тяжелой частью лучевой кости и составляет большую часть ее структуры. Множество слоев минералов и коллагеновых волокон придают компактной кости прочность и гибкость.

Глубоко под компактной костью находится полая полость, которая проходит по всей длине кости и заполнена желтым костным мозгом, богатым жировыми отложениями. Желтый костный мозг хранит энергию для клеток организма в виде триглицеридов.

На проксимальном и дистальном концах лучевой кости компактная кость укреплена тонкими колоннами губчатой ​​кости, которые придают лучевой кости дополнительную прочность без значительного увеличения ее массы. Небольшие полые пространства в губчатой ​​кости содержат красную ткань костного мозга, которая производит все клетки крови организма.

Наружная поверхность лучевой кости покрыта тонким слоем волокнистой соединительной ткани, известной как надкостница, а ее проксимальный и дистальный концы покрыты гиалиновым хрящом. Надкостница содержит множество коллагеновых волокон, которые образуют прочные связи между лучевой костью и сухожилиями и связками, соединяющими ее с костями и мышцами руки. Гиалиновый хрящ придает концам лучевой кости гладкую поверхность для уменьшения трения при движениях предплечья. Он также действует как гибкий амортизатор для снижения ударной нагрузки на локтевой и лучезапястный суставы.

При рождении лучевая кость начинается как костный стержень, известный как диафиз, с крышками из гиалинового хряща на обоих концах. Гиалиновый хрящ обеспечивает дополнительную гибкость локтевого и лучезапястного суставов и обеспечивает среду для роста кости. Примерно в возрасте двух лет дистальный гиалиновый хрящ возле лучезапястного сустава начинает превращаться в отдельную кость, называемую дистальным эпифизом. Тонкий слой хряща, называемый эпифизарной пластинкой (или пластинкой роста), разделяет диафиз и эпифиз. Хрящ в зоне роста растет в длину, чтобы разделить диафиз и эпифиз и увеличить общую длину лучевой кости.

В возрасте около пяти лет хрящ на проксимальном конце лучевой кости около локтевого сустава окостеневает, образуя проксимальный эпифиз.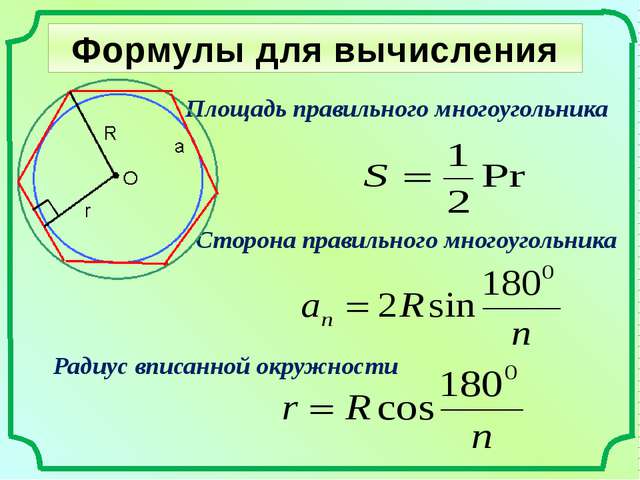 Как и дистальный эпифиз, эпифизарная пластинка отделяет проксимальный эпифиз от диафиза, чтобы дать лучевой кости возможность расти. Эпифизы соединяются с диафизом к концу полового созревания, образуя единую лучевую кость, после чего она перестает расти в длину. Область срастания диафиза и эпифиза называется метафизом.

Лучевая кость — проксимальная — дистальная — диафиз

• 1 Проксимальная область лучевой кости
• 2 Диафрагма лучевой кости
• 3 Дистальная область лучевой кости
• CC-BY-SA-2.1-jp], через Wikimedia Commons

  Рис. 1.0 – Анатомическое положение лучевой кости.

  Лучевая кость — длинная кость предплечья. Она лежит латерально и параллельно локтевой кости, второй из костей предплечья. Лучевая кость поворачивается вокруг локтевой кости, образуя движение в проксимальном и дистальном лучелоктевых суставах.

  Лучевая кость сочленяется в четырех местах:

  • Локтевой сустав – Частично образован сочленением между головкой лучевой кости и головкой плечевой кости.
  • Проксимальный лучелоктевой сустав – Сочленение между головкой лучевой кости и лучевой вырезкой локтевой кости.
  • Лучезапястный сустав – Сочленение между дистальным концом лучевой кости и костями запястья.
  • Дистальный лучелоктевой сустав – Сочленение между локтевой вырезкой и головкой локтевой кости.

  В этой статье мы рассмотрим костные ориентиры и остеологические особенности лучевой кости.

  Проксимальный отдел лучевой кости

  Проксимальный конец лучевой кости сочленяется как в локтевом, так и в проксимальном лучелоктевом суставах.

  Важные костные ориентиры включают головку , шейку и бугристость лучевой кости :

  • Головка лучевой кости — Дискообразная структура с вогнутой сочленяющейся поверхностью. Он толще медиально, где принимает участие в проксимальном лучелоктевом суставе.
  • Шейка  – Узкая область кости, расположенная между головкой лучевой кости и бугристостью лучевой кости.
  • Лучевой бугорок  – костный выступ, служащий местом прикрепления двуглавой мышцы плеча.

  TeachMeSeries Ltd (2023)

  Рис. 1.1. Костные ориентиры проксимального отдела лучевой кости.

  Стержень лучевой кости

  Диафрагма лучевой кости расширяется в диаметре по мере продвижения в дистальном направлении. Как и локтевая кость, она имеет треугольную форму с тремя краями и тремя поверхностями.

  Посередине латеральной поверхности имеется небольшая шероховатость для прикрепления круглого пронатора .

  Дистальная часть лучевой кости

  В дистальной области диафиз лучевой кости расширяется, образуя прямоугольный конец. Боковая сторона выступает дистально как шиловидный отросток . На медиальной поверхности имеется вогнутость, называемая локтевой вырезкой , которая сочленяется с головкой локтевой кости, образуя дистальный лучелоктевой сустав .

  Дистальная поверхность лучевой кости имеет две фасетки для сочленения с ладьевидной и полулунной костями запястья. Это составляет лучезапястный сустав .

  TeachMeSeries Ltd (2023)

  Рис. 1.0 – Суставные поверхности лучезапястного сустава.

  Клиническая значимость: распространенные переломы лучевой кости

  Предплечье является частым местом переломов костей. Здесь мы рассмотрим распространенные типы переломов лучевой кости:

  • Перелом Коллеса  – Наиболее распространенный тип перелома лучевой кости. Падение на вытянутую руку с переломом дистального отдела лучевой кости. Структуры, дистальные к перелому (запястье и кисть), смещаются кзади. Это вызывает то, что известно как «деформация обеденной вилки».
  • Переломы головки лучевой кости – Характерно падение на вытянутую руку. Головка лучевой кости вдавливается в головку плечевой кости, вызывая ее перелом.

    No related posts.