Радиус в окружности: Радиус круга | Онлайн калькулятор

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

Радиус описанной окружности около треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной около треугольника окружности. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

1. Радиус окружности описанной около треугольника, если известны три стороны треугольника
2. Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A
3. Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A
4. Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

1.

Радиус окружности описанной около треугольника, если известны три стороны треугольника

Пусть известны три стороны a, b, c треугольника. Найдем радиус описанной окружности около треугольника.

Площадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:

\( \small S=\frac{\large abc}{\large 4R}, \)

откуда

\( \small R=\frac{\large abc}{\large 4S}. \)

(1)

Площадь треугольника по трем сторонам имеет вид:

\( \small S= \sqrt{p(p-a)(p-b)(p-c),}\)

(2)

где

\( \small p= \frac{\large a+b+c}{\large 2}. \)

(3)

Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:

\( \small R=\frac{\large abc}{\large 4\ \cdot \ \sqrt{p(p-a)(p-b)(p-c)}}. \)

(4)

где p вычисляется из формулы (3).

Пример 1. Известны три стороны треугольника: \( \small a=6, \ b=5, \ c=4.5 \). Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где \( \small р \) вычисляется из формулы (3).

Найдем p из (2):

Подставим значения a, b, c, p в (1):

Ответ:

2. Радиус окружности описанной около треугольника, если известны сторона

a и противолежащий угол A

Пусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:

Откуда:

Пример 2. Сторона треугольника равна: а противолежащий угол \( \small \angle A=35°.\) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5). Подставим значения и \( \small \angle A=35° \) в (5):

Ответ:

3. Радиус окружности описанной около треугольника, если известны стороны

b и c треугольника и угол между ними A

Пусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.

Из теоремы косинусов, имеем:

или

Подставляя (6) в (5), получим требуемую формулу:

Пример 3. Известны две стороны треугольника: и угол между ними: \( \small \angle A=30°. \) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения и \( \small \angle A=30° \) в (7):

Ответ:

4. Радиус окружности описанной около треугольника, если известны сторона треугольника

a и прилежащие углы B и C

Пусть известны сторона a треугольника и прилежащие к ней углы B и C.

Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: \( \small \angle A=180°- (\angle B+ n\angle C). \) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):

Получили следующую формулу:

Пример 4. Известны сторона треугольника: и прилежащие к ней углы: \( \small \angle B=21°, \;\angle C=34°. \) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения и \( \small \angle B=21°, \;\angle C=34° \) в (8):

Ответ:

Смотрите также:

• Радиус описанной окружности около равнобедренного треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около прямоугольного треугольника онлайн

Калькулятор радиуса окружности

Инструкции: Используйте этот калькулятор, чтобы вычислить радиус круга из его окружности или площади, показывая все шаги. Пожалуйста, введите значение и укажите, является ли это его периметр или его площадь, в форме ниже.

Подробнее об этом калькуляторе радиуса

Этот калькулятор позволит вам найти радиус окружности при условии, что вы укажете правильную длину окружности или области. Поэтому вам нужно ввести значение и использовать раскрывающееся меню, чтобы указать, является ли это периметром. или область, которую вы предоставляете. Калькулятор покажет все этапы процесса.

Вам необходимо ввести допустимое числовое выражение, например 3 или 2π. Подойдет любое допустимое выражение, если оно неотрицательно. .

После того, как вы ввели правильное выражение и указали, является ли оно окружностью или площадью, все, что вам нужно сделать, это щелкнуть на кнопку «Рассчитать», и вам будут показаны все шаги.

По умолчанию в раскрывающемся меню будет установлено значение «Окружность», но вы можете изменить его, если указываете область.

Как вычислить радиус круга?

Радиус круга имеет очень специфическую связь с окружностью и площадью. Существует формула для площадь круга, и есть формула для длины окружности с учетом радиуса. Итак, все, что нам нужно сделать, это найти радиус r, в зависимости от того, с какой формулой мы имеем дело.

— Во-первых, предположим, что вы знаете длину окружности: формула, связывающая длину окружности C и радиус r, равна 9.2 \]

Тогда, найдя r, находим, что

\[r = \displaystyle \sqrt{\frac{A}{\pi}} \]

Каковы шаги для вычисления радиуса?

• Шаг 1: Определите, знаете ли вы длину окружности или площадь. В любом случае должно быть неотрицательное значение
.
• Шаг 2: Если известна длина окружности C: Найдите r по формуле \(r = \displaystyle \frac{C}{2 \pi} \)
• Шаг 3: Если известна площадь A: Найдите r по формуле \(r = \displaystyle \sqrt{\frac{A}{\pi}}\)

Таким образом, процедура будет зависеть от того, указали ли вы длину окружности или площадь.

Не забудьте изменить для него раскрывающийся список, если это необходимо.

Значит, существует более одной формулы для радиуса круга?

Да. Радиус, по-видимому, участвует во многих аспектах вычислений, связанных с кругом, поэтому радиус можно получить во многих различных формах.

Самые распространенные способы, которыми мы и занимались, это нахождение радиуса по окружности или по площади, но они не единственные варианты.

Обратите внимание, что в данном случае не имеет значения, измеряются ли углы в радианах или градусах. Все, что нам нужно, чтобы получить радиус, это значение окружности или площадь.

Зачем нужен радиус окружности?

Радиус является ключевой метрикой, полностью определяющей окружность (сохраните перевод). Поэтому естественно иметь интерес к его вычислению. Радиус, площадь и окружность — фундаментальные понятия, которые полностью переплетаются между собой.

Обратите внимание, что центр круга не имеет значения для расчета радиуса, а также для расчета площади и периметра.

2\), поэтому решение для \(r\) приводит к:

\[r = \displaystyle\sqrt{\frac{A}{\pi}}\]

Следовательно, все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение площади \(A = 24\pi\). Получается следующее:

\[ \begin{array}{ccl}\displaystyle r & = & \displaystyle\sqrt{\frac{A}{\pi}} \\\\ \\\\ & = & \displaystyle\sqrt{\frac{ 24\pi}{\pi}} \\\\ \\\\ & = & \displaystyle 2\sqrt{6} \end{массив} \]

На этом расчет завершен. Мы обнаружили, что радиус окружности равен \(\displaystyle r = 2\sqrt{6}\).

Пример: Расчет радиуса

Теперь предположим, что у вас есть круг с площадью, равной \(-4\pi\). Можно ли найти его радиус?

Решение: В данном случае мы не можем найти радиус, потому что отрицательная площадь в этом контексте не имеет смысла.

Пример: вычисление радиуса круга

Найдите радиус круга, предполагая, что его длина окружности равна \(\frac{4\pi}{3}\).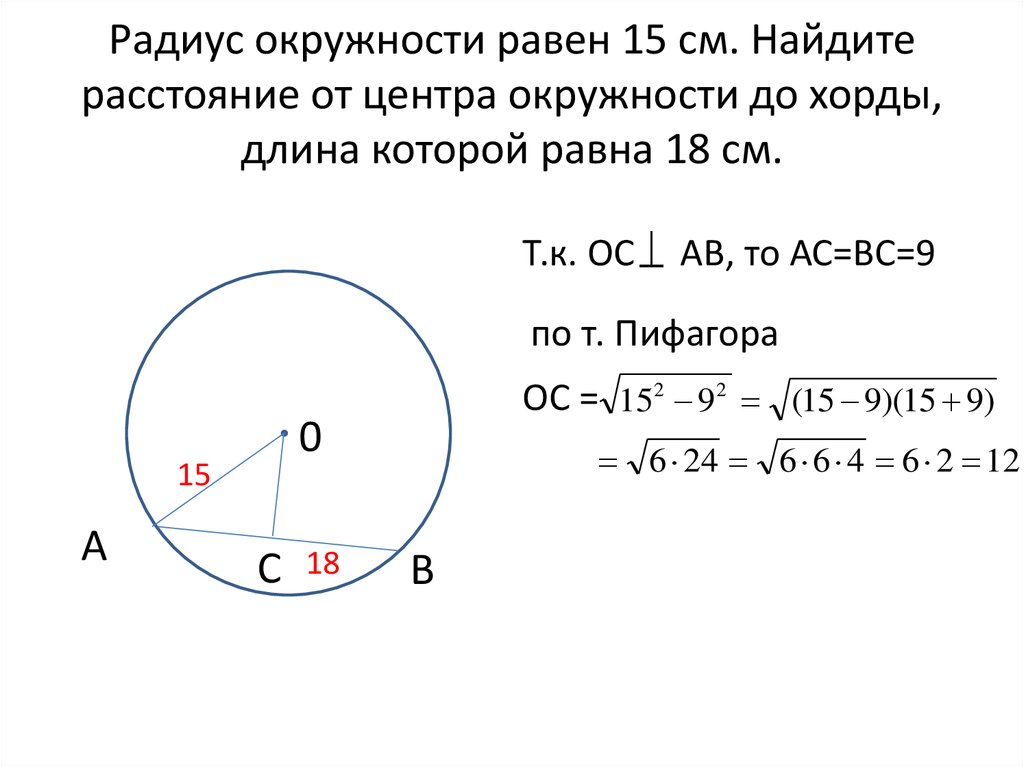

Решение: Нам нужно найти радиус \(r\) окружности, и из предоставленной информации мы знаем, что длина окружности окружности равно \(C = \frac{4\pi}{3}\).

Теперь формула для длины окружности равна \(C = 2\pi r\), поэтому решение для \(r\) приводит к:

\[r = \displaystyle\frac{C}{2\pi}\]

Следовательно, все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение длины окружности \(C = \frac{4\pi}{3}\). Получается следующее:

\[ \begin{array}{ccl}\displaystyle r & = & \displaystyle\frac{C}{2\pi} \\\\ \\\\ & = & \displaystyle\frac{\frac{4\pi {3}}{2\pi} \\\\ \\\\ & = & \displaystyle \frac{2}{3} \end{массив} \]

На этом расчет завершен. Мы обнаружили, что радиус окружности равен \(\displaystyle r = \frac{2}{3}\).

Другие калькуляторы, связанные с кругами

Круги являются одними из самых интересных объектов в математике. Понятие радиуса тесно связано с представление о вычислении площади круга и длины окружности.

Другая тесно связанная идея — это углы и их эквивалентность между различными системами.

Найдите радиус круга, длина окружности которого равна сумме длин двух окружностей…

Перейти к

• Площади, связанные с кругами — упражнение 11.1
• Площади, связанные с кругами — упражнение 11.2
• Площади, связанные с кругами — упражнение 11.3
• Площади, связанные с кругами — упражнение 11.4

• Действительные числа
• Полиномы
• Пара линейных уравнений с двумя переменными
• Квадратные уравнения
• Арифметические прогрессии
• Треугольники
• Согласованная геометрия
• Введение в тригонометрию и ее уравнения
• Круги
• Конструкции
• Области, связанные с кругами
• Площади поверхности и объемы
• Статистика и вероятность

Главная > Образцовые решения NCERT Класс 10 Математика > Глава 11 — Области, связанные с кругами > Площади, связанные с кругами — упражнение 11. 3 > Вопрос 2

Вопрос 2 Области, связанные с кругами – Упражнение 11.3

Найдите радиус круга, длина окружности которого равна сумме длин окружностей двух окружностей радиусами 15 см и 18 см.

Answer:

Radius of first circle = r ₁  = 15 cm

Radius of second circle = r ₂  = 18 cm

∴ Circumference of first circle = 2πr ₁  = 30π cm

Длина окружности второго круга = 2πr ₂  = 36π см

Пусть радиус круга = R

Согласно вопросу,

Окружность круга = окружность первого круга + окружность второго круга

2πr = 2πr ₁ + 2πr ₂

⇒ 2πr = 30π + 36π59

⇒ 66π ⇒ R = R = R = R = R = R = 30. 33

⇒ Радиус = 33 см

Следовательно, требуемый радиус окружности равен 33 см.

Связанные вопросы

Кусок проволоки длиной 20 см согнут в виде дуги окружности, образующей угол 60°. ..

**На данном рисунке квадрат с диагональю 8 см вписан в окружность. Найдите площадь тени…

**Найдите площадь сектора круга радиусом 28 см и центральным углом 45°.**

** Колесо мотоцикла имеет радиус 35 см. Сколько оборотов в минуту должно делать колесо…

**На данном рисунке АВ — диаметр окружности, АС = 6 см и ВС = 8 см. Найдите площадь этого…

** Корова привязана веревкой длиной 14 м в углу прямоугольного поля размером 20 м × …

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Области, связанные с кругами — Упражнение 11.