Коэффициент парной корреляции в Excel
Коэффициент корреляции отражает степень взаимосвязи между двумя показателями. Всегда принимает значение от -1 до 1. Если коэффициент расположился около 0, то говорят об отсутствии связи между переменными.
Если значение близко к единице (от 0,9, например), то между наблюдаемыми объектами существует сильная прямая взаимосвязь. Если коэффициент близок к другой крайней точке диапазона (-1), то между переменными имеется сильная обратная взаимосвязь. Когда значение находится где-то посередине от 0 до 1 или от 0 до -1, то речь идет о слабой связи (прямой или обратной). Такую взаимосвязь обычно не учитывают: считается, что ее нет.
Расчет коэффициента корреляции в Excel
Рассмотрим на примере способы расчета коэффициента корреляции, особенности прямой и обратной взаимосвязи между переменными.
Значения показателей x и y:
Y – независимая переменная, x – зависимая. Необходимо найти силу (сильная / слабая) и направление (прямая / обратная) связи между ними. Формула коэффициента корреляции выглядит так:
Формула коэффициента корреляции выглядит так:
Чтобы упростить ее понимание, разобьем на несколько несложных элементов.
- Найдем средние значения переменных, используя функцию СРЗНАЧ:
- Посчитаем разницу каждого y и yсредн., каждого х и хсредн. Используем математический оператор «-».
- Теперь перемножим найденные разности:
- Найдем сумму значений в данной колонке. Это и будет числитель.
- Для расчета знаменателя разницы y и y-средн., х и х-средн. Нужно возвести в квадрат.
- Находим суммы значений в полученных колонках (с помощью функции АВТОСУММА). Перемножаем их. Результат возводим в квадрат (функция КОРЕНЬ).
- Осталось посчитать частное (числитель и знаменатель уже известны).
Между переменными определяется сильная прямая связь.
Встроенная функция КОРРЕЛ позволяет избежать сложных расчетов. Рассчитаем коэффициент парной корреляции в Excel с ее помощью. Вызываем мастер функций. Находим нужную. Аргументы функции – массив значений y и массив значений х:
Покажем значения переменных на графике:
Видна сильная связь между y и х, т. к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
Матрица парных коэффициентов корреляции в Excel
Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.
Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
- На вкладке «Данные» в группе «Анализ» открываем пакет «Анализ данных» (для версии 2007). Если кнопка недоступна, нужно ее добавить («Параметры Excel» — «Надстройки»). В списке инструментов анализа выбираем «Корреляция».
- Нажимаем ОК. Задаем параметры для анализа данных. Входной интервал – диапазон ячеек со значениями. Группирование – по столбцам (анализируемые данные сгруппированы в столбцы). Выходной интервал – ссылка на ячейку, с которой начнется построение матрицы.
 Размер диапазона определится автоматически.
Размер диапазона определится автоматически. - После нажатия ОК в выходном диапазоне появляется корреляционная матрица. На пересечении строк и столбцов – коэффициенты корреляции. Если координаты совпадают, то выводится значение 1.
Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.
Изобразим наглядно корреляционные отношения с помощью графиков.
- Сильная прямая связь между y и х1.
- Сильная обратная связь между y и х2. Изменения значений происходят параллельно друг другу. Но если y растет, х падает. Значения y увеличиваются – значения х уменьшаются.
- Отсутствие взаимосвязи между значениями y и х3. Изменения х3 происходят хаотично и никак не соотносятся с изменениями y.
Скачать вычисление коэффициента парной корреляции в Excel
Для чего нужен такой коэффициент? Для определения взаимосвязи между наблюдаемыми явлениями и составления прогнозов.
Как рассчитать коэффициент корреляции в Excel
Microsoft Excel — утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Excel, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!
Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.
Теперь, разобравшись с теорией, перейдём к практике.
Определение коэффициента через «Мастер функций»
Чтобы найти взаимосвязь между переменными х и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого выполните следующие действия:
Для этого выполните следующие действия:
- Выделите ячейку, куда будет выведен результат подсчёта, и нажмите на кнопку мастера функций (она расположена рядом с полем для формул).
- В открывшемся окне выберите из списка функций «КОРРЕЛ» и нажмите «Ок».
- После этого в окне аргументов функции задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х.
В нашем примере в строке «Массив1» вносим координаты диапазона ячеек значения, зависимость которого нужно определить (у нас это доходы от продаж). Чтобы добавить в поле адрес массива, выделяем ячейки в столбце. В строку «Массив2» следует ввести координаты другого столбца (в нашем случае это будет предусмотренный рекламный бюджет). Ниже в пункте «Значение» можно сразу же увидеть результат подсчёта. Добавив данные в поля «Массив1» и «Массив2», жмите «Ок».
- В итоге вы получите рассчитанный программой коэффициент корреляции в ранее выбранной ячейке.

В нашем случае показатель средний, зависимость доходности от рекламы не впечатляет, хотя и однозначно присутствует.
Расчёт корреляции с помощью средств пакета анализа
Корреляционную зависимость можно вычислить также с применением специального инструмента, предварительно его активировав. Для выполнения задачи потребуется совершить следующие манипуляции:
- Перейдите из меню «Файл» в раздел «Параметры».
- В меню слева перейдите в раздел «Надстройки».
- Внизу окна в блоке «Управление» нужно выставить «Надстройки Excel» (если выставлено иное, меняем) и перейти к надстройкам.
- В открывшемся окошке надстроек отмечаем «Пакет анализа» и кликаем «Ок», что позволяет активировать инструментарий.
- Теперь перейдите на вкладку «Данные» — на ленте будет доступен ещё один блок инструментов «Анализ». Здесь нажмите «Анализ данных».
- Среди предлагаемых вариантов выделите «Корреляция» и кликните «Ок», после чего будут доступны необходимые настройки.

- В открывшемся окошке в строчке «Входной интервал» следует ввести интервал сразу всех столбцов, задействованных в процессе вычислений зависимости.
- Напротив «Группирование» оставьте «по столбцам», поскольку в нашем примере данные разделены на столбцы, а не построчно.
- В параметрах вывода результатов можно оставить по умолчанию «Новый рабочий лист» (данные выведутся на новом листе) или выбрать «Выходной интервал» и в строчке указать координаты ячеек, чтобы коэффициент появился в указанном месте на странице. Вывести итог вычислений можно также в новой рабочей книге, переместив маркер в соответствующий пункт.
- Установив необходимые настройки, кликаем «Ок» и получаем итоги выполненной работы. Он не будет отличаться от того, что был получен при использовании первого метода вычисления, поскольку, хотя действия и отличаются, программа выполняет те же вычисления.
Коэффициент корреляции рассчитывается программой
Расчёт корреляционной зависимости по формуле
Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y, после чего на основании полученных данных можно подсчитать взаимосвязь:
Прежде всего, нужно знать средние значения переменных x и y, после чего на основании полученных данных можно подсчитать взаимосвязь:
- Выделите значения переменной и воспользуйтесь функцией «СРЗНАЧ».
- Далее необходимо вычислить разницу между каждым x и xср,и yср. В выбранных ячейках напишите формулы x-x, y-. Не забудьте закрепить ячейки со средними значениями. Затем растяните формулу вниз, чтобы она применилась и к остальным числам.
- Теперь, когда есть все необходимые данные, можно посчитать корреляцию. Перемножьте полученные разности таким образом: (x-xср) * (y-yср). После того как вы получите результат для каждой из переменных, просуммируйте полученные числа при помощи функции автосуммы. Таким образом рассчитывается числитель.
- Теперь перейдём к знаменателю. Посчитанные разности нужно возвести в квадрат. Для этого в отдельной колонке введите формулы: (x-xср)2и (y-yср)2.
 Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y).
Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y). - Осталось перемножить найденные суммы и извлечь из них квадратный корень.
- Последний шаг — поделите числитель на знаменатель. Полученный результат и будет искомым коэффициентом корреляции.
Как видите, умея правильно работать с функциями Microsoft Excel, можно существенно упростить себе задачу расчёта непростых математических выражений. Благодаря средствам, реализованным в программе, вы без труда сделаете корреляционный анализ в Excel всего за пару минут, сэкономив время и силы. Пишите в комментариях, помогла ли вам статья разобраться в вопросе, спрашивайте обо всём, что заинтересовало вас по рассмотренной теме.
Калькулятор коэффициента корреляции — Онлайн-калькулятор коэффициента корреляции
Калькулятор коэффициента корреляции помогает вычислить значение коэффициента корреляции, который используется для установления связи между двумя заданными наборами данных. Коэффициент корреляции всегда будет находиться в диапазоне от -1 до 1.
Что такое калькулятор коэффициента корреляции?
Калькулятор коэффициента корреляции — это онлайн-инструмент, который помогает рассчитать значение коэффициента корреляции для двух заданных наборов данных. Сила связи между двумя переменными или наборами данных определяется коэффициентом корреляции. Чтобы использовать Калькулятор коэффициента корреляции , введите значения в поля ввода.
Калькулятор коэффициента корреляции
ПРИМЕЧАНИЕ. Длина набора данных значений x и y должна быть одинаковой.
Как пользоваться калькулятором коэффициента корреляции?
Чтобы найти коэффициент корреляции с помощью калькулятора коэффициента корреляции, выполните следующие действия:
- Шаг 1: Перейдите к онлайн-калькулятору коэффициента корреляции Cuemath.

- Шаг 2: Введите числа в скобках, разделенные запятыми, в указанных полях ввода.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти значение коэффициента корреляции для заданных наборов данных.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор коэффициента корреляции?
Коэффициент корреляции дает нам возможность установить взаимосвязь между фактическими и прогнозируемыми значениями, полученными в конце статистического эксперимента. Это помогает нам оценить точность между фактическими и прогнозируемыми значениями. С помощью этого коэффициента мы можем анализировать зависимость одной переменной от другой.
- Если коэффициент корреляции отрицательный, это означает, что две переменные имеют обратную зависимость.
- Если коэффициент корреляции положительный, это показывает, что две переменные имеют прямую связь.
 {2}]}}\)
{2}]}}\)n = объем выборки.
Σx = сумма всех значений в наборе данных x.
Σy = Сумма всех значений в наборе данных y.
Σxy = сумма произведений соответствующих значений в наборах данных x и y.
Σx 2 = сумма квадратов значений в наборе данных x.
Σy 2 = сумма квадратов значений в наборе данных y.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами. 9{2}]}}\)
n = 4.
Σx = 4 + 8 + 12 +16 = 40Σy = 7 + 14 + 21 + 28 = 70
Σx + 2 = 11 + 144 + 256 = 480
σy 2 = 49 + 196 + 441 + 784 = 1470
σxy = 28 + 112 + 252 + 448 = 840
Заменить эти значения в данном уравнении. = 1.
Положительное значение коэффициента корреляции указывает на то, что переменные имеют прямую связь.
 9{2}]}}\)
9{2}]}}\)n = 5.
Σx = 43 + 44 + 45 + 46 = 178
Σy = 2,5 + 2,4 + 2,3 + 2,2 = 9,4
Σx + 2025 + 2116 = 7926
σy 2 = 6,25 + 5,76 + 5,29 + 4,84 = 22,14
σxy = 107,5 + 105,6 + 103,5 + 101,2 = 417,8
. = -1
Значение коэффициента корреляции отрицательное, что указывает на обратную зависимость между переменными.
Точно так же вы можете попробовать калькулятор коэффициента корреляции, чтобы найти значение коэффициента корреляции для следующих наборов данных:
- x = {5, 8, 11, 15} и y = {10,5, 9,5, 8,5, 7,5 }
- х = {12,8, 13,1, 15,4, 17,9} и у = {-2, -3, -4, -5}
☛ Математические калькуляторы:
Калькулятор скалярного произведения — примеры, онлайн-калькулятор скалярного произведения
Калькулятор скалярного произведения вычисляет скалярное произведение двух заданных векторов. Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром.
 Скалярный продукт может быть положительным или отрицательным действительным числом.
Скалярный продукт может быть положительным или отрицательным действительным числом.Что такое калькулятор скалярного произведения?
Калькулятор скалярного произведения – это онлайн-инструмент, который помогает определить скалярную величину, являющуюся результатом скалярного произведения заданных двух векторов. Величина, полученная после скалярного произведения, будет находиться в той же плоскости, что и два заданных вектора. Чтобы использовать калькулятор скалярного произведения, введите значения в соответствующие поля ввода.
Калькулятор скалярного произведения
Как использовать калькулятор скалярного произведения?
Выполните следующие шаги, чтобы вычислить скалярное произведение двух заданных векторов с помощью калькулятора скалярного произведения
- Шаг 1: Перейдите к онлайн-калькулятору скалярного произведения Cuemath.
- Шаг 2: Введите коэффициенты двух векторов в заданные поля ввода.

- Шаг 3: Нажмите кнопку «Умножить» , чтобы вычислить скалярный продукт.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как найти калькулятор скалярного произведения?
Скалярное произведение определяется как произведение величины двух векторов и косинуса угла между двумя заданными векторами. Если \(\overrightarrow{a}\) и \(\overrightarrow{b}\) являются двумя векторами, то скалярное произведение дается следующим образом:
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = |\(\overrightarrow{a}\)|.|\(\overrightarrow{b}\)|cosθ.
Предположим, нам даны два вектора, которые выражены в виде их единичных векторов i, j, k вдоль осей x, y и z. Затем шаги, которые необходимо выполнить, чтобы найти скалярное произведение между двумя векторами, приведены ниже:
\(\overrightarrow{a}\) = \(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)
\(\ overrightarrow{b}\) = \(b_{1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\)
Чтобы найти скалярное произведение
\ (\overrightarrow{а}\).
 \(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))
\(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))= \((a_{1}b_{1})(\шляпа{ i}.\шляпа{i}) + (a_{1}b_{2})(\шляпа{i}.\шляпа{j}) + (a_{1}b_{3})(\шляпа{i} .\шляпа{k})\) + \((a_{2}b_{1})(\шляпа{j}.\шляпа{i}) + (a_{2}b_{2})(\шляпа{ j}.\шляпа{j}) + (a_{2}b_{3})(\шляпа{j}.\шляпа{k})\) + \((a_{3}b_{1})(\ шляпа{k}.\шляпа{i}) + (a_{3}b_{2})(\шляпа{k}.\шляпа{j}) + (a_{3}b_{3})(\шляпа{ к}.\шляпа{к})\)
\(\шляпа{i}.\шляпа{j}\) = \(\шляпа{i}.\шляпа{k}\) = \(\шляпа{k}.\шляпа{j}\) = cos 90 = 0. Это потому, что эти векторы ортогональны.
\(\шляпа{i}.\шляпа{i}\) = \(\шляпа{k}.\шляпа{k}\) = \(\шляпа{j}.\шляпа{j}\) = cos 0 = 1. Потому что эти векторы сонаправлены.
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.
 С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.Запись на бесплатный пробный урок
Решенные примеры на калькуляторе скалярного произведения
Пример 1:Найдите скалярное произведение двух векторов \(\overrightarrow{a}\) = \(4\hat{i} + 2\шляпа{j} — 5\шляпа{k}\) и \(\overrightarrow{b}\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\). Проверьте результат с помощью калькулятора скалярного произведения.
Решение:
Учитывая \(\overrightarrow{a}\) = \(4\hat{i} + 2\hat{j} — 5\hat{k}\) и \(\overrightarrow{b }\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\)
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
\(\overrightarrow{a}\ ). \(\overrightarrow{b}\) = (4 . 3) + (2 . (-2)) + ((-5) . 1)
= 12 — 4 — 5
= 3
Следовательно, скалярное произведение двух векторов равно 3.
Пример 2:
Найдите скалярное произведение двух векторов \(\overrightarrow{a}\) = \(2.


 Размер диапазона определится автоматически.
Размер диапазона определится автоматически.

 Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y).
Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y).
 {2}]}}\)
{2}]}}\)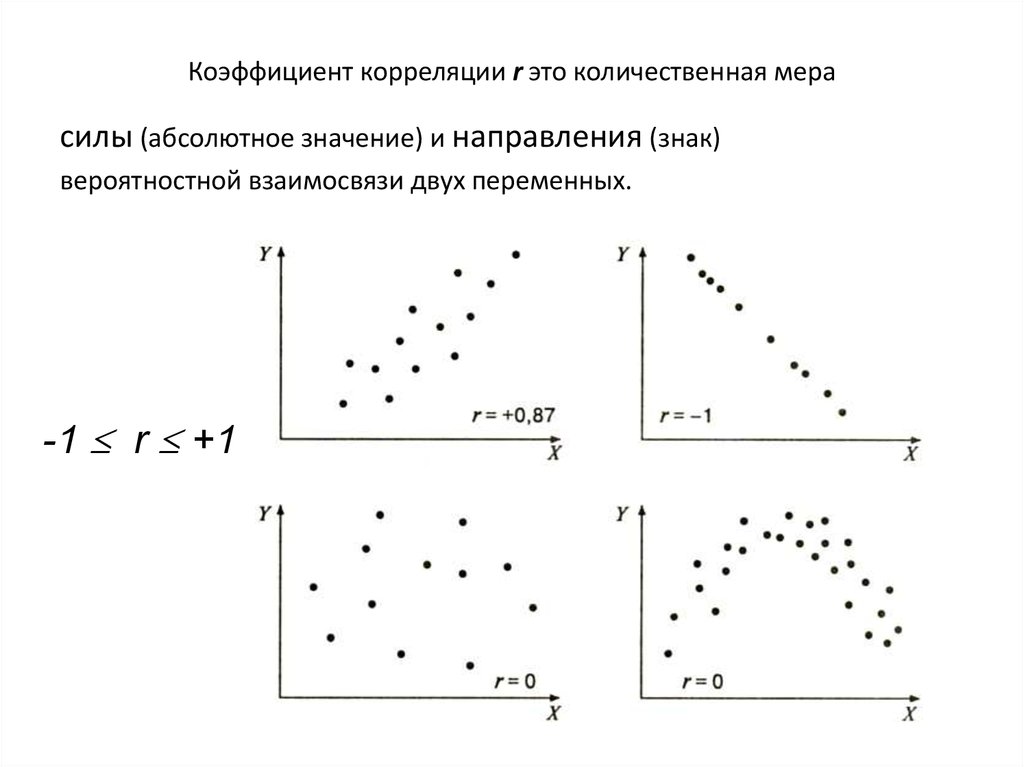 9{2}]}}\)
9{2}]}}\) Скалярный продукт может быть положительным или отрицательным действительным числом.
Скалярный продукт может быть положительным или отрицательным действительным числом.
 \(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))
\(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\)) С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.