Расчёт электрических цепей методом структурных чисел для детей и взрослых / Хабр
В нулевые годы, когда, скорее в качестве отдушины, я подрабатывал в Альма-матер, ведя лабораторные работы по радиотехнике, мне попалась на глаза эта книжечка:
С.Беллерт, Г. Возняцки
«Анализ и синтез электрических цепей методом структурных чисел».
Перевод с польского
Под редакцией проф. П.А. Ионкина
ИЗДАТЕЛЬСТВО «МИР»
Москва 1972
После беглого просмотра я испытал странное ощущение, которое, наверное, правильно было бы назвать когнитивным диссонансом. В этой книге предлагался эффективный и очень простой в применении (но не с точки зрения теории) метод расчета электрических цепей, но при этом я никогда даже не слышал об этом подходе. Не могу назвать себя профессионалом, радиотехника была скорее хобби, но я неплохо знал всё, что преподавалось у нас в институте и всё же.
Чем больше я вникал в теорию, тем больше очаровывался. Получив эстетическое удовлетворение, я благополучно забыл об этом небольшом открытии, к тому же через некоторое время я переехал в Европу, и моя преподавательская деятельность, да и вообще любая деятельность, связанная с радиотехникой, закончилась.
Получив эстетическое удовлетворение, я благополучно забыл об этом небольшом открытии, к тому же через некоторое время я переехал в Европу, и моя преподавательская деятельность, да и вообще любая деятельность, связанная с радиотехникой, закончилась.
Но вот, недавно, приехав погостить в Россию, разбирая старые книжки, я опять наткнулся на этот забытый мною (и возможно миром) труд. Покопавшись в интернете, я обнаружил некоторые статьи на эту тему, но, по-прежнему, всё выглядит так, что этот метод мало кому знаком.
И я подумал, что может быть это будет интересно читателям Хабра.
О простоте
Кажется, что этому алгоритму можно научить даже ребенка, что я и попытался проверить.
Думаю, эксперимент удался. За 10 минут я сумел научить рассчитывать электрические цепи моего сына. На картинке вы видите его расчет передаточной функции по напряжению для двухкаскадного делителя. Поверьте моему опыту преподавателя радиотехники — не каждый студент с этим справится.
Ах, да. Сыну 7 лет!
Сыну 7 лет!
Черными чернилами я составил «карту», которая должна помочь сыну в расчетах.
Синие чернила — это его расчёт.
Внизу вы видите правильный ответ — коэффициент усиления по напряжению.
Умея получать правильный результат, он, конечно же, абсолютно ничего не понимает — для него это просто картинка. Но, если я нарисую ему другую схему того же уровня сложности, он найдет правильный ответ.
Пояснения к записям:
Я нарисовал граф, соответствующий данной цепи. Ребра графа пронумерованы так же, как и импедансы.
Далее, мне пришлось немного рассказать сыну о графах — я показал, что такое вершины и что такое ребра графа. Потом объяснил ему, что такое элементарные контуры (пустые «кружочки») и обратил внимание на грани, из которых они состоят.
Предварительная стадия на этом была закончена, и мы перешли к расчетам.
Комментарий Далее в статье мы будем называть это структурным числом графа, и это будет главным объектом, вокруг которого всё и крутится.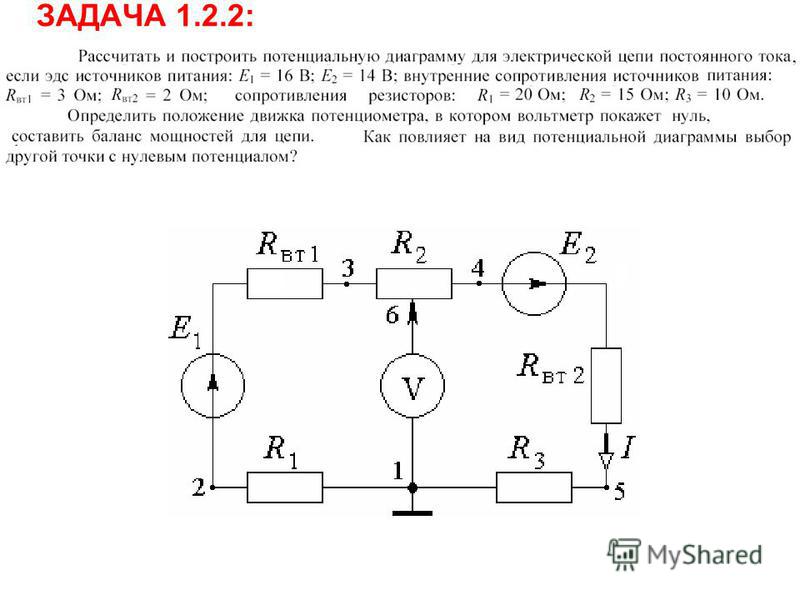 Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
В общем случае нужно удалять не только столбцы, в которых есть одинаковые элементы, но и попарно убирать столбцы с одинаковым набором элементов (порядок следование элементов в столбцах и порядок следования самих столбцов неважны).
Затем (это написано мною на листке) я попросил найти все столбцы с единичкой («входное» ребро) и удалить единичку из этих столбцов. Понятно, что столбцы с единичкой это
Отбросив единичку, получаем , что и написано в виде
То же самое нужно сделать для двойки («выходное» ребро):
В теории структурных чисел эта функция называется алгебраической производной по элементу.
КомментарийЭта функция от двух структурных чисел и называется конъюнкцией. Мы будем обозначать её как . В данном случае имеем
В принципе на этом все вычисления закончены.
 Осталось только написать ответ.
Осталось только написать ответ.Я провел черту (деление), и попросил сына над чертой написать (независимо от наших расчетов, выходное сопротивление присутствует всегда в формуле передаточной функции по напряжению) и с индексом, который он получил в предыдущем пункте (конъюнкция) — вы видите мою чёрную стрелочку на картинке, указывающую на этот индекс.
Под чертой интересней. Для каждого столбца структурного числа нужно взять числа в этом столбце и использовать их как индексы для в произведении и сложить все полученные таким образом «столбцевые» произведения. Это тот случай, когда легче показать, чем объяснить. Так, в нашем случае для столбцов, которые мы получили
это будет .
Это отношение и есть искомый коэффициент передачи.
Функция в знаменателе — это детерминант структурного числа по и записывается как . Точное определение будет дано ниже в статье.
Комментарий 2В общем виде для данного вида графов (входное и выходное ребра имеют общую вершину и сонаправлены) коэффициент передачи напряжения может быть выражен следующей формулой
Более общая формула, которая подходит для всех пассивных четырёхполюсников
Функция совпадения будет объяснена позже в этой статье
Теперь давайте по-взрослому.
Основные понятия теории структурных чисел
Мы ограничимся достаточно узкой прикладной областью данной математики — для нашей статьи нам будет интересен только расчет пассивных электрических цепей с одним источником (пассивный четырёхполюсник).
Нас будет интересовать лишь прикладной аспект. Мы не будем ничего доказывать. Также некоторые понятия будут представлены упрощенно, главная цель — научиться получать результат. Нас будет интересовать только вопрос «как», и мы даже не будем пытаться ответить на вопрос «почему». Тем, кому станет интересен математический аспект — обращайтесь к первоисточнику.
Структурное число
Структурное число это неупорядоченный набор столбцов элементов со следующими свойствами:
в общем случае, столбцы могут содержать разное количество элементов, но в рамках нашей задачи структурное число всегда будет иметь вид прямоугольной матрицы, то есть все столбцы в структурном числе будут иметь равную длину
каждый столбец представляет собой неупорядоченный (порядок не важен) набор натуральных чисел
в столбце нет повторяющихся элементов.
 Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.в структурном числе нет повторяющихся столбцов. Если в процессе алгебраических операций появляются такие столбцы, то они попарно удаляются. Это значит, что четное количество одинаковых столбцов аннигилируют, а при нечетном количестве один столбец остаётся.
Дополнительное структурное число
Найдем множество всех элементов в структурном числе. Возьмем произвольный столбец этого числа и составим столбец из элементов, которых не хватает в этом столбце до множества всех элементов. Структурное число, составленное из таких столбцов называется дополнительным.
ПримерРассмотрим структурное число
Множество всех элементов:
Тогда дополнительное число:
Сумма структурных чисел
Комментарий:
Мы нигде не будем использовать сумму структурных чисел в данной статье.
Суммой двух структурных чисел A и B называется структурное число, содержащее все столбцы чисел A и B, за исключением идентичных столбцов.
Произведение структурных чисел
Комментарий:
В данной статье мы будем иметь дело только с произведением структурных чисел состоящих из строк (все столбцы имеют лишь один элемент), например,
Произведением двух структурных чисел A и B называется структурное число, столбцы которого представляют собой суммы (согласно понятиям теории множеств) всех возможных комбинаций столбцов A и B, за исключением наибольшего четного числа идентичных столбцов и таких столбцов, в которых какой-либо элемент повторяется.
ПримерСтолбцы 2,3,4,6,7,9 удаляются потому что содержат повторяющиеся элементы.
Столбцы 1 и 5 удаляются в паре потому, что содержат идентичный набор элементов (важно помнить, что если бы одинаковых столбцов было бы нечетное количество, то один столбец остался бы).
Поэтому остается только столбец 8.
Алгебраическая производная
Алгебраическая производная структурного числа по элементу называется структурное число , состоящее только из столбцов , содержащих элементы с исключением этих элементов.
Возьмём структурное число
Алгебраическая обратная производная
Обратная производная структурного числа по элементу называется структурное число состоящее только из столбцов , не содержащих элементы .
ПримерКонъюнкция
Конъюнкцией двух структурных чисел и называется структурное число , состоящее из совпадающих столбцов и . Мы будет обозначать ее как .
ПримерДетерминантная фунция
Давайте возьмем -й столбец структурного числа . Возьмем все индексы в этом столбце и найдем произведение импедансов с этими индексами. Далее, если сложить такие произведения для всех столбцов, то это и будет детерминант. Детерминант от пустого (нет столбцов) структурного числа равен 1.
ПримерСтруктурные числа и электрические схемы
Мы подбираемся к сути, которая заключается в том, что каждому пассивному четырёхполюснику может быть поставлено в соответствие структурное число, и с помощью нововведенной алгебры может быть произведен ее расчет.
Сначала построим граф, соответствующий электрической цепи.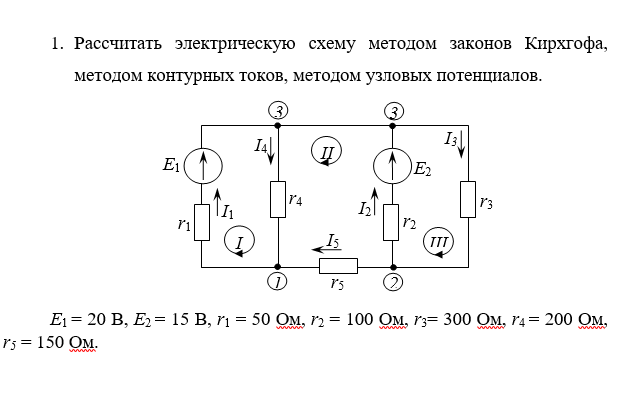
Построение графа
Проще всего это понять на примерах. Начнем с элементарных схем.
Схемы делителя:
Первая схема — элементарный делитель. При этом мы считаем источник напряжения идеальным (сопротивление = 0), и вольтметр (или следующий каскад) имеет входное сопротивление равное бесконечности.
Вторая схема относится к случаю, когда вы подаете напряжение E, на сопротивление , но источник напряжения не идеальный (сопротивление Z1), и вольтметр (или следующий каскад) имеет входное сопротивление Z2.
Третья схема — уже знакомая нам схема двухкаскадного делителя.
То есть, чтобы получить граф, мы просто перерисовываем схему с импедансами со следующими изменениями:
мы «опускаем» идеальный источник напряжения, что выглядит разумно, т.к. его выходное сопротивления равно 0 (его сопротивление мы вынесли в )
мы заменяем импедансы на их индексы
у нас только 2 направленных ребра: входное (мы всегда будем обозначать его индексом 1) и выходное (индекс 2).
 Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное)
Попробуем применить этот подход для более сложного случая.
Мост Уитстона:
Нахождение структурного числа графа
Теперь давайте построим структурные числа для каждого случая.
Есть два подхода: через произведение структурных чисел, соответствующих вершинам графа, и через произведение структурных чисел, соответствующих элементарным контурам.
Рассмотрим первый метод — через произведение «вершинных» структурных чисел
Метод перемножения «вершинных» структурных чисел
Предположим, что в нашем графе вершин. «Отбрасываем» любую вершину и берем оставшиеся вершины.
Для каждой вершины найдем «вершинное» структурное число. Для этого выписываем все ребра графа, опирающиеся на эту вершину. Предположим, что для i-ой вершины мы имеем ребер. Тогда такое «вершинное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра.
 То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).Перемножаем эти вершинных структурных числа. Получаем некое структурное число .
Находим дополнительное к структурное число . Это и будет наше искомое структурное число.
Для первой схемы (простой делитель) получим:
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .
У нас всего одно число, поэтому произведением является то же самое число.
У нас всего два элемента: , поэтому дополнительным элементом опять-таки является тоже самое число.
Итак, для первой схемы нашим структурным числом будет .
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .

У нас всего одно число, поэтому произведением является то же самое число.
У нас есть три элемента: , поэтому дополнительным структурным числом будет
В графе три вершины, значит, для нашего расчета мы будем использовать две.
Возьмем верхнюю и нижнюю вершины. Структурные числа для них: и .
Произведение этих двух структурных чисел даёт:
У нас есть 4 элемента: , поэтому дополнительным структурным числом будет
Это совпадает с результатом, который получил мой сын. Там мы использовали метод перемножения «контурных» структурных чисел, который рассматривается ниже.
Пример 4. Мост УитстонаМы видим 4 вершины. Отбросим нижнюю вершину.
Тогда для оставшихся трех вершин мы получим следующие «вершинные» структурные числа:
Перемножим эти 3 числа
Всевозможная комбинация столбцов будет выглядеть следующим образом:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы.
 Получаем
Получаем
Теперь мы можем выписать структурное число, соответствующее данной схеме — это будет число , являющееся дополнением к
Метод перемножения «контурных» структурных чисел
Найдем наименьшее количество замкнутых контуров, покрывающее все ребра графа.
Для каждого такого контура составим «контурное» структурное число. Предположим, что для -го контура мы имеем рёбер. Тогда такое «контурное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра. То есть, не строго говоря, это строка, состоящая из ребер (для данного контура).
Выполним произведение всех таких контурных чисел — получим искомое структурное число.
Опять-таки проще это понять на примерах.
Очевидно, что у нас только один контур.
Контурное структурное число для него: .

Т.к. это единственное структурное число, то оно и будет ответом, что, как и ожидалось, совпадает с результатом первого метода.
Таких контуров 2.
У нас есть возможность разных комбинаций, но возьмем следующие: , .
Найдем произведение этих двух чисел, что и будет искомым структурным числом:
И опять, конечно же, структурные числа полученные двумя разными методами совпадают.
Пример 3. Двухкаскадный делитель.Структурное число, соответсвующее двухкаскадному делителю, мы нашли в самом начале статьи. Оно равно
Пример 4. Мост УитстонаТаких контуров 3.
Возьмем, например, следующие:
.
Найдем искомое структурное число A через произведение этих трех чисел.
Берем все возможные комбинации столбцов:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы. Получаем искомое структурное число:
Получаем искомое структурное число:
С учетом того, что порядки следования столбцов и элементов в самих столбцах неважны, легко видеть, что в обоих методах мы получили одинаковые результаты.
Расчет пассивной трёхточки (трёхполюсника)
Комментарий:
Не уверен, что термины «трёхточка» или «трёхполюсник» является общепринятыми, но дальнейшее поясняет, что я имею ввиду.
У нас всё готово для расчета пассивной трёхточки, которую можно представить в виде пассивного четырёхполюсника с общей землей на входе и выходе.
Например, схемы делителей, которые мы рассматривали выше — это трёхточки (в том смысле, в котором мы определили трёхточку).
Передаточные функции напряжения и тока в этой схеме это
а первичный, входной и выходной импедансы:
А теперь самое главное — все эти величины мы легко можем найти, если знаем структурное число A, соответствующее схеме.
Расчет схем трёхточек
Давайте начнем с простейших схем. Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Схема 1. Простой делитель
Вспомним наше структурное число:
Тогда, помня, что детерминант от пустого (нет столбцов) структурного числа равен 1, легко получить:
Схема 2. Напряжение на сопротивлении.
Что соответствует действительности (расчетам другими известными методами).
Схема 3. Двукаскадный делитель (который мы рассчитывали с сыном)
Рассматриваемые нами трёхточки покрывают довольно большой процент случаев, поэтому уже здесь можно было бы поставить точку.
Но всё же не всегда вход и выход схемы имеют общий контакт (например, мост Уитстона). Метод структурных чисел позволяет найти решение и для общего случая пассивного четырёхполюсника.
Расчет четырехполюсника
Трехполюсник рассмотренный выше является частным случаем четырехполюсника.
Разница лишь в том, что вход и выход в данном случае необязательно имеют общий контакт.
Формулы расчета для четырехполюсника
Как можно видеть, формулы для четырехполюсника такие же, как и для трехполюсника, за исключением коэффициентов передачи по напряжению и току. Здесь в числителе вместо
мы имеем
Это новая функция, которую проще объяснить на примере, и это будет рассмотрено ниже на примере моста Уитстона.
Понятно, что в случае трёхточки, которую мы рассматривали (с правильным выбором направления выходного ребра) мы имеем
Мост Уитстона
Структурное число
Давайте найдем некоторые важные для нашего анализа функции этого структурного числа.
Это рассмотрение позволит нам также ввести последнюю важную функцию — функция совпадения.
Детерминант
Легко видеть что детерминант этого числа это
Алгебраическая производная
Для обратных алгебраических производных соответственно имеем
Конъюнкция
Функция совпадения
Комментарий:
Это и есть та дополнительная функция, которой нам не хватало для расчет четырехполюсника.
Найдем функцию совпадения чисел и . Эта функция вычисляется через конъюнкцию, найденную выше:
где , равны или .
То есть эта функция похожа на детерминант конъюнкции, но со знаками «+» или «-» у каждого слагаемого (в детерминанте все слагаемые имеют знак «+»). Как найти эти коэффициенты? Чтобы найти знак у каждого слагаемого мы должны исключить из графа рёбра, определенные в этом слагаемом. При этом получится цикл, в котором «входное» и «выходное» ребра ориентированы согласно или встречно. В первом случае (согласно) — это даст нам «+», а во втором — «-«. Так, например, в нашем случае для мы должны исключить ребра 5 и 6 из нашего графа, а в случае — ребра 3 и 4. Таким образом получим
В первом случае направления ребер 1 и 2 согласованы, а во втором случае противоположны. Таким образом имеем
Расчет моста Уитстона
Для моста Уитстона, логика и уровень простоты в точности тот же. Но расчет требует внимательности и аккуратности.
В принципе у нас уже все готово.
О блеске и нищете
Этот метод создавался в эпоху зарождения компьютеров и предназначался для компьютерного расчёта и синтеза электрических цепей. Поэтому наряду с эффективностью и, не побоюсь этого слова, поразительной простотой в применении этот подход обладает еще и органичной программируемостью. Вы легко можете автоматизировать процесс, описанный выше, и больше не переживать по поводу внимательности и большого количества бумаги.
И, несмотря на все явные достоинства, я не сумел найти этот метод в списке методов расчета электрических цепей в википедии, также я не встречал ни одного учебника или институтского курса, где бы давался этот метод. Думаю профессионалы (коим я никогда не был) знают об этом подходе, но ему не обучают в ВУЗах и, похоже, мало кто им пользуется.
Причина, думаю, понятна. Несмотря на весь блеск, эта тема просто не вписывается в учебную программу. То, что мы можем позволить себе в рамках статьи недопустимо в рамках учебного процесса — невозможно обойтись без теории, представив только манипулятивный подход. А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
И получается, что оригинальность, во многом определяющая изящество и красоту данного подхода, обернулась для него своего рода проклятием.
1.2. Методы расчета электрических схем
20
Федеральное агентство по образованию
Рыбинская государственная авиационная технологическая академия им. П. А. Соловьева
Кафедра «Вычислительные системы»
В. М. Комаров
Расчет линейных электрических цепей
постоянного тока
Лабораторная работа по дисциплине
«Основы электротехники и электроники»
Рыбинск 2008
Введение
Линейные электрические цепи постоянного
тока составляют значительную часть
многих электротехнических и радиоэлектронных
устройств, проектирование которых тесно
связано с анализом этих цепей, опирающимся
на их свойства и различные методы
расчета.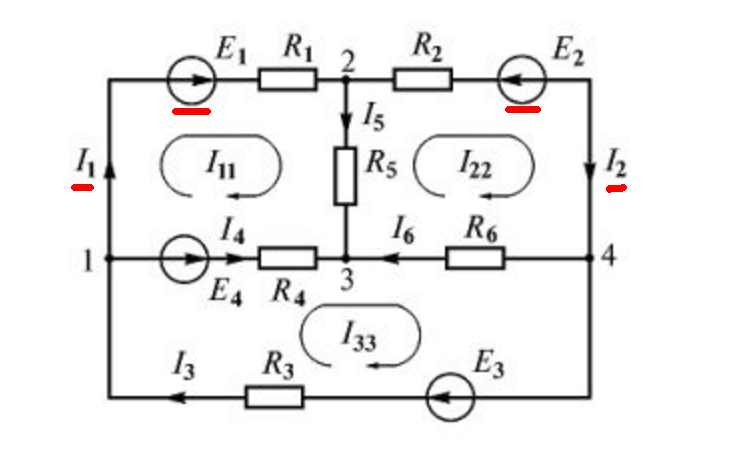
Цель работы
Целью настоящей работы является изучение свойств и основных методов расчета электрических цепей постоянного тока:
– метода расчета на основании законов Кирхгофа;
– метода узловых потенциалов;
– метода контурных токов;
– линейных соотношений в электрических цепях.
1. Краткие теоретические сведения
1.1. Электрическая цепь, ее схема и граф
Электрическая цепь характеризуется совокупностью элементов, которые она содержит, и способом их соединения. Линейная электрическая цепь состоит из линейных элементов, свойства которых не зависят от величины и направления воздействующих на них токов и напряжений, температуры и т. п. Напряжение и ток в любом линейном элементе связаны линейным алгебраическим или дифференциальным уравнением первого порядка. Основными линейными элементами электрических цепей являются источник э.д.с., источник тока, сопротивление, индуктивность и емкость.
Для упрощения расчетов реальные элементы
электрических цепей заменяются их
идеализированными моделями, которым
приписываются свойства, позволяющие с
достаточной степенью точности представлять
процесс, происходящий в реальном
элементе.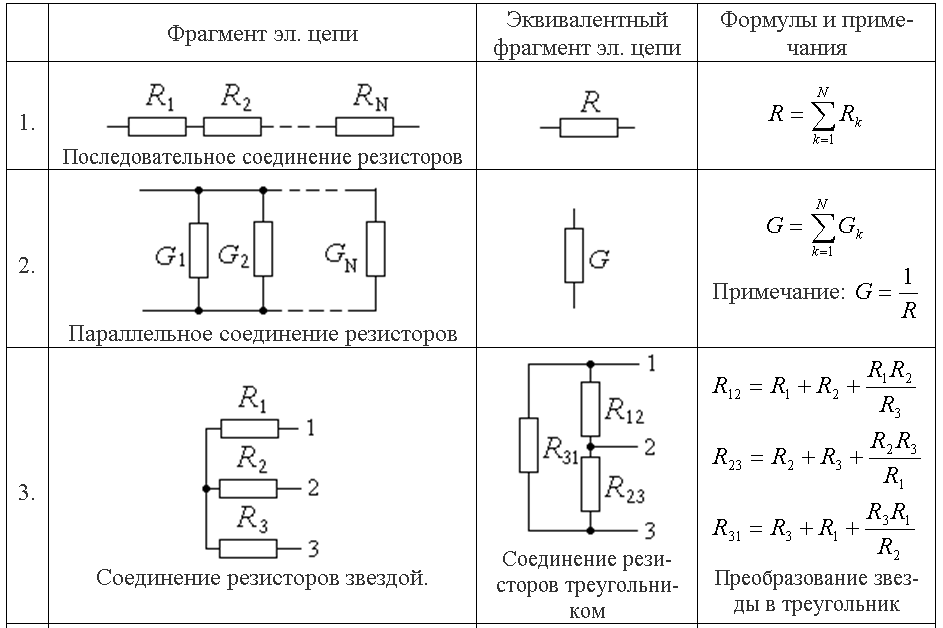
Графическое изображение электрической цепи с помощью условных графических обозначений ее элементов называется электрической схемой этой цепи. Электрические цепи постоянного тока, как правило, состоят из идеальных источников э.д.с. и сопротивлений. На рис. 2, в качестве примера, приведены электрические схемы некоторых цепей.
а) б) в) г) д)
Р ис. 1. Основные элементы линейных электрических цепей а) идеальный источник э.д.с.; б) идеальный источник тока; в) сопротивление; г) индуктивность; д) емкость
Участок схемы, характеризующийся одним
и тем же током в его начале и конце в
любой момент времени, называется ветвью
электрической схемы. Следовательно,
любая ветвь содержит только последовательное
соединение элементов. Например, ветвями
являются участки цепей, состоящие из
элементов e1,R1; e2,R2; R3; R4; R5; R6 (см. рис. 2,а), а также элементов e1,R1,R7; e2,R2; e3,R3; R4; R5; R6 (см. рис. 2,б).
Например, ветвями
являются участки цепей, состоящие из
элементов e1,R1; e2,R2; R3; R4; R5; R6 (см. рис. 2,а), а также элементов e1,R1,R7; e2,R2; e3,R3; R4; R5; R6 (см. рис. 2,б).
Место соединения трех или большего числа ветвей называется узлом. На электрических схемах, приведенных на рис. 2, узлы обозначены цифрами 1, 2, 3, 4.
Любой замкнутый путь, проходящий по нескольким ветвям электрической схемы, называется контуром. При расчете схемы необходимо выбирать независимые контура. Независимые контура удобно выбирать, используя понятия графа электрической схемы и его дерева.
Графом электрической схемы называется
ее условное изображение, в котором
каждая ветвь заменяется отрезком линии,
называемой ветвью графа.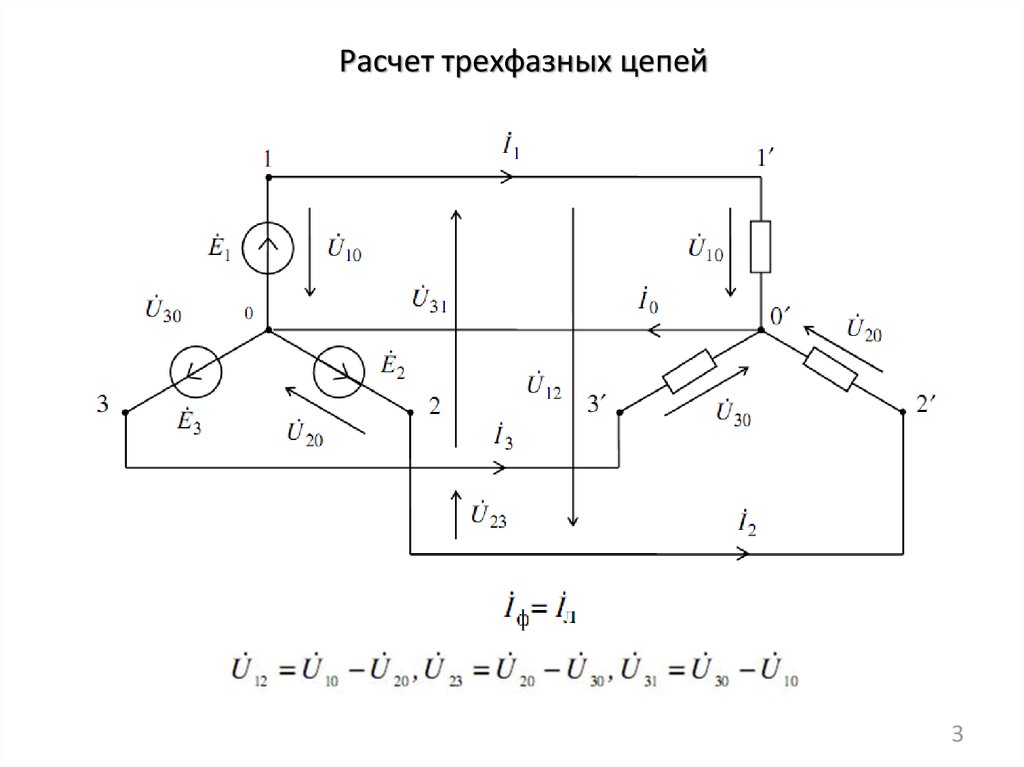 На рис. 3
приведены графы вышерассмотренных
электрических схем.
На рис. 3
приведены графы вышерассмотренных
электрических схем.
Совокупность ветвей графа, соединяющая все узлы, но не образующая ни одного контура, называется деревом графа. Каждый граф может иметь несколько деревьев. На рис. 4 в каждом из вышерассмотренных графов толстыми линиями выделено по одному (из нескольких возможных) дереву. Если граф содержит Ny узлов, то число ветвей любого дерева равно
Рис. 3. Графы электрических схем
Рис. 4. Дерево, ветви, связи и главные контура графов
Ветви графа, дополняющие его дерево до полного графа, называются ветвями связи. На рис. 4 ветви связи изображены тонкими линиями. Если граф схемы содержит Nв ветвей, то число ветвей связи всегда равно Nвс = Nв– (Ny – 1).
В качестве независимых контуров при
расчете электрической схемы выбираются
ее главные контура, состоящие из ветвей
дерева и только одной ветви связи.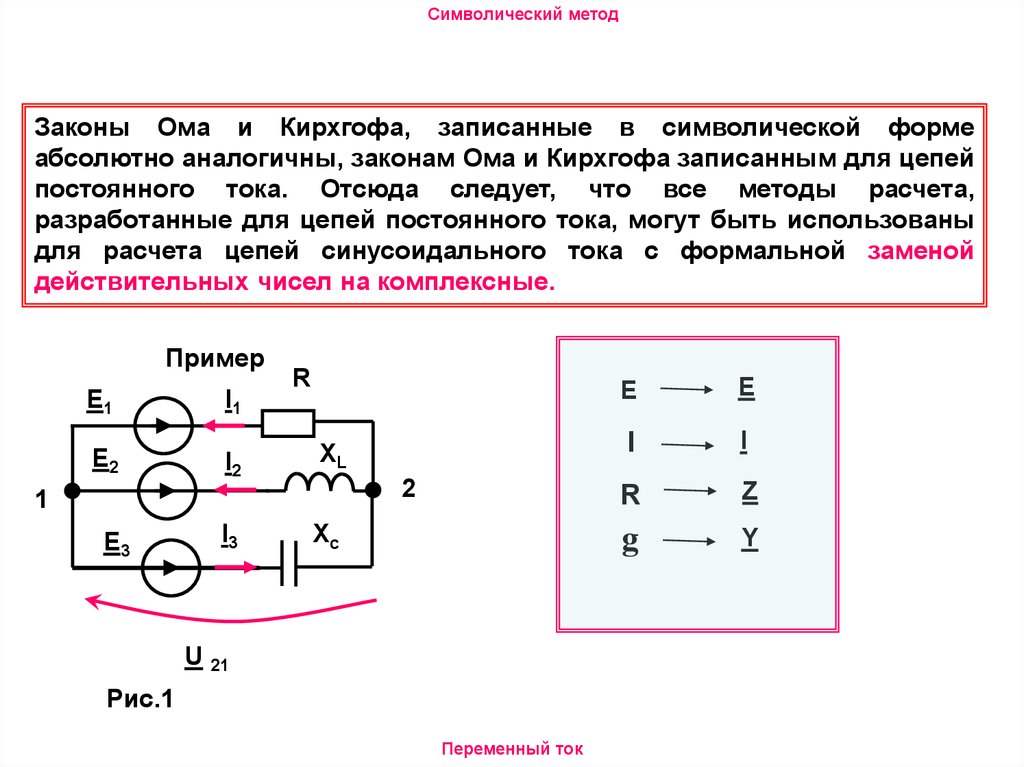 Следовательно, число главных контуров
равно числу ветвей связи. На рис. 4 главные
контура выделены цифрами I,
II, III, IV.
Следовательно, число главных контуров
равно числу ветвей связи. На рис. 4 главные
контура выделены цифрами I,
II, III, IV.
Суть расчета электрической схемы сводится к определению токов во всех ее ветвях. Все методы расчета рассмотрим на примере схемы, приведенной на рис. 5,а. Эта схема имеет 3 узла и 5 ветвей.
e3
а) б)
в) г)
Рис. 5. Расчет электрических схем а) на основании законов Кирхгофа; б) выбор независимых контуров; в) метод узловых потенциалов; г) метод контурных токов
1.2.1. Расчет схемы на основании законов Кирхгофа
Законы Кирхгофа устанавливают соотношение между токами и напряжениями в электрической цепи.
Первый закон Кирхгофа:
Алгебраическая сумма токов в любом узле равна нулю
где m – общее количество ветвей, подключенных к данному узлу.
Общее количество уравнений, которое
может быть составлено по первому закону
Кирхгофа, равно числу узлов Ny схемы.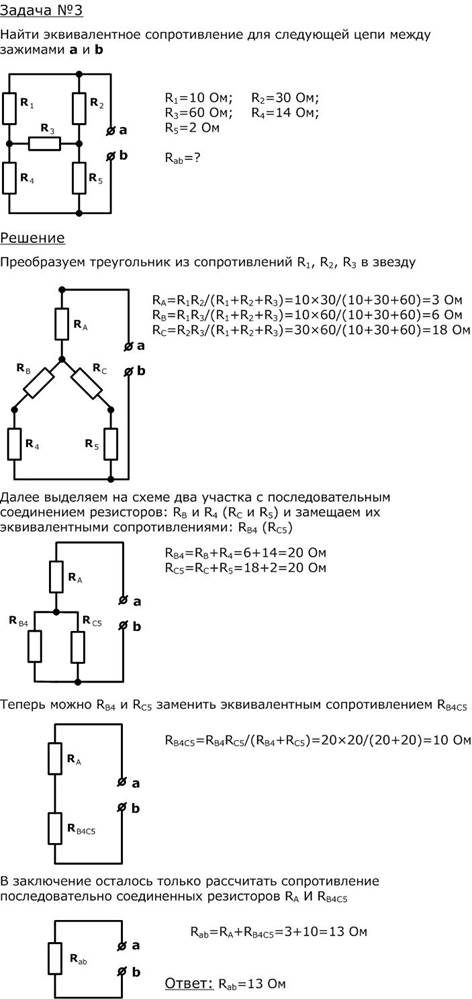 Однако из них только
Однако из них только
Для составления этих уравнений необходимо произвольным образом выбрать положительные направления токов в ветвях и обозначить их на чертеже. При этом токи, направленные к рассматриваемому узлу считаются положительными, а от узла – отрицательными.
Отсюда, для рассматриваемой схемы (см. рис. 5,а) количество уравнений, составляемое по первому закону Кирхгофа, равно N1 = 3 – 1 = 2 и они имеют вид:
(узел 1)
(узел 2)
Этих уравнений недостаточно для расчета схемы. Недостающие уравнения составляются на основании второго закона Кирхгофа.
Второй закон Кирхгофа:
Алгебраическая сумма э.
где l – общее количество источников э.д.с. в контуре;
t – общее количество сопротивлений в контуре.
Для составления уравнений по второму закону Кирхгофа необходимо с помощью дерева графа схемы выбрать главные контура и направление их обхода (рис. 5,б). При этом соблюдается следующее правило знаков для э.д.с. и падений напряжений, входящих в ( ): э.д.с. и падения напряжения, совпадающие по направлению с направлением обхода, считаются положительными, а противоположно направленные – отрицательными. Общее количество независимых уравнений, записываемое по второму закону Кирхгофа, равно количеству главных контуров и составляет N2 = Nв – (Ny – 1).
Отсюда, для рассматриваемой схемы (см. рис. 5,а,б) количество уравнений, составляемое по второму закону Кирхгофа, равно
 Учитывая, что Uk = ikRk,
их можно записать в виде:
Учитывая, что Uk = ikRk,
их можно записать в виде:(контур I)
(контур II)
(контур III).
Таким образом, по законам Кирхгофа составлены пять уравнений, полностью описывающих состояние электрической цепи. После этого расчет схемы сводится к решению системы этих уравнений и нахождению искомых токов.
Решение системы линейных уравнений можно искать методом Крамера. В этом случае
где Δ – общий определитель системы, составленной из коэффициентов при неизвестных;
Δk – частный определитель системы, полученный из общего определителя Δ путем замены столбца, содержащего коэффициенты при ik, свободными членами.
Для рассматриваемой системы уравнений
Для определенности положим R1 = 100 Ом, R2 = 500 Ом, R3 = 1 К, R4 = 50 ОМ, R5 = 300 Ом, e1 = 2 В, e2 =10 В, e3 = 20 В и, пользуясь свойствами определителей, найдем, в качестве примера, значение Δ
Аналогичным образом можно найти значения
остальных определителей Δ1 =
–2,05·106, Δ2 = –6,1·106, Δ3 = –5,2·106, Δ4 = 0,9·106, Δ5 = 1,15·106.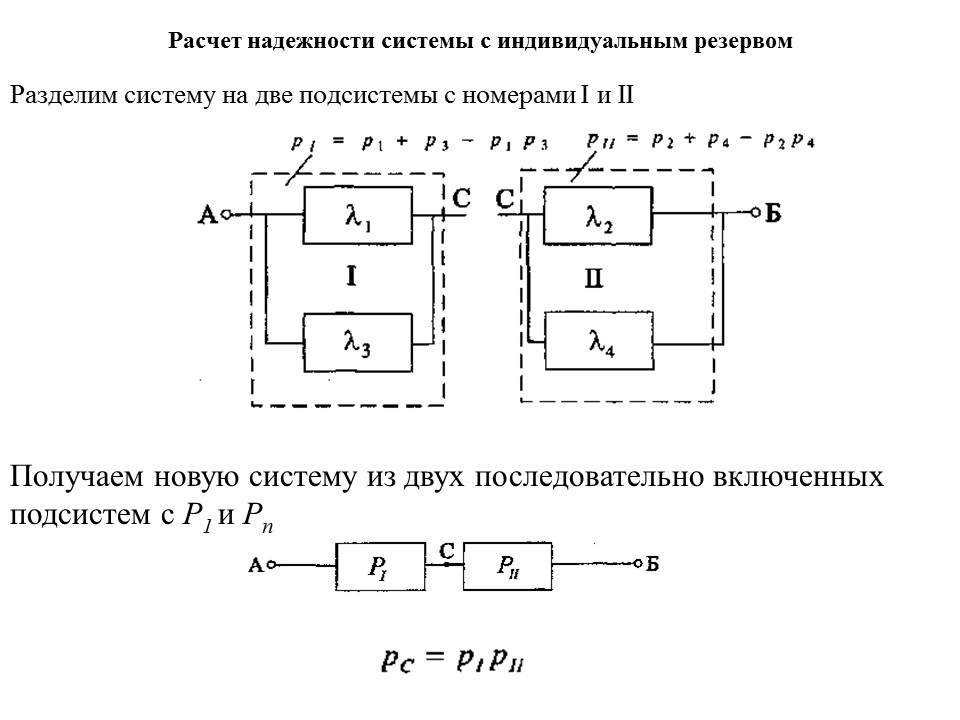
Таким образом, искомые токи имеют следующие значения
Положительные значения токов i1, i2, i3, полученные при расчете, означают, что их фактическое направление совпадает с направлением этих токов, принятом и расчете; отрицательные значения токов i4 и i5 означают, что их фактическое направление противоположно принятому при расчете направлению этих токов.
После определения токов в ветвях расчет электрической схемы можно считать практически законченным, т.к. определение потенциалов узлов, падений напряжений на сопротивлениях и рассеиваемой в них мощности в этом случае не составляет труда. Узловые потенциалы и падения напряжений на сопротивлениях могут быть определены в соответствии с законом Ома, а мощность, рассеиваемая в сопротивлениях, – по формуле .
Недостатком метода расчета электрических
схем на основании законов Кирхгофа
является необходимость совместного
решения большого количества уравнений,
т. е. громоздкость математических
расчетов.
е. громоздкость математических
расчетов.
Использование схемы в качестве калькулятора
2. Использование схемы в качестве калькулятора
Нажмите Start → All Programs → MIT Scheme → Schemeдля запуска Появится интерпретатор схемы и консоль, как на следующем рисунке.
Во-первых, давайте посчитаем «1+2». Дайте (+ 1 2) подсказке.
1 ]=> (+ 1 2) ;значение: 3 1 ]=>Интерпретатор возвращает 3 в качестве ответа.
Обратите внимание на следующие три момента:
- Пара круглых скобок указывает на один шаг расчета. В этом случае (+ 1 2) указывают на шаг 1+2.
- Имя функции следует после открывающей скобки, за которой следуют аргументы. Большинство операторов в Scheme являются функциями. В этом случае сначала идет функция ‘+’, затем следуют два аргумента 1 и 2.
- Разделителями токенов являются пробелы, табуляции и символы новой строки. Ни запятая, ни двоеточие не используются в качестве разделителя.

- Символ «+» оценивается как добавление процедуры.
Дайте только «+» с внешнего интерфейса, и интерпретатор ответит
[arity-dispatched-procedure 1]
, что указывает, что «+» является символом для «процедуры 1». - ‘1’ оценивается как 1. Обычно логические значения, числа, символы и строки оцениваются как сами по себе. С другой стороны, символ оценивается как нечто другое.
- ‘2’ оценивается как 2.
- Наконец, вычисляется (+ 1 2) и из скобок выходит 3. На схеме оцененные значения выходят из скобок и значение, исходящее из крайних круглых скобок, печатается на переднем конце.
(+) → 0 (+ 1) → 1 (+ 1 2) → 3 (+ 1 2 3) → 6
3. Четыре основных арифметических действия
Scheme (и большая часть Лиспа) может обрабатывать дробные числа. Функция точная->неточная заключается в преобразовании дробных чисел в числа с плавающей запятой.
Схема также может обрабатывать комплексные числа. Комплексные числа представлены а + б я, где a и b — действительная и мнимая части.
+, -, * и / представляют
сложение, вычитание, умножение и деление соответственно.
Эти функции принимают произвольное количество аргументов.
Функция точная->неточная заключается в преобразовании дробных чисел в числа с плавающей запятой.
Схема также может обрабатывать комплексные числа. Комплексные числа представлены а + б я, где a и b — действительная и мнимая части.
+, -, * и / представляют
сложение, вычитание, умножение и деление соответственно.
Эти функции принимают произвольное количество аргументов.Примеры:
(- 10 3) → 7 (- 10 3 5) → 2 (* 2 3) → 6 (* 2 3 4) → 24 (/ 29 3) → 29/3 (/ 29 3 7) → 29/21 (/ 9 6) → 3/2 (точно->неточно (/ 29 3 7)) → 1,380952380952381Скобки могут быть вложены следующим образом:
(* (+ 2 3) (- 5 3)) → 10 (/ (+ 9 1) (+ 2 3)) → 2Формулы, состоящие из круглых скобок, токенов и разделителей, называются S-выражениями .
Упражнение 1
Вычислите следующие с помощью интерпретатора схемы.- (1+39) * (53-45)
- (1020/39) + (45*2)
- Сумма 39, 48, 72, 23 и 91
- Среднее значение 39, 48, 72, 23 и 91 в виде числа с плавающей запятой.

4. Прочие арифметические операции
4.1. частное, остаток, модуль и квадрат
- Функция частное состоит в том, чтобы получить частное.
- Функции остаток и по модулю для получения остатка.
- Функция sqrt предназначена для получения квадратного корня аргумента.
(частное 7 3) → 2 (по модулю 7 3) → 1 (кв. 8) → 2,8284271247461903
4.2. Тригонометрические функции
Функции sin , cos , tan , asin , acos и atan доступны. atan принимает один или два аргумента. если ожидается, что значение atan будет равно 1/2 π, используйте два аргумента.(атан 1) → 0,7853981633974483 (атан 1 0) → 1,5707963267948966
4.3. Экспонента и логарифм
Экспонента и логарифм вычисляются по exp и log соответственно. Значение b в степени a можно рассчитать по формуле ( доб а б ).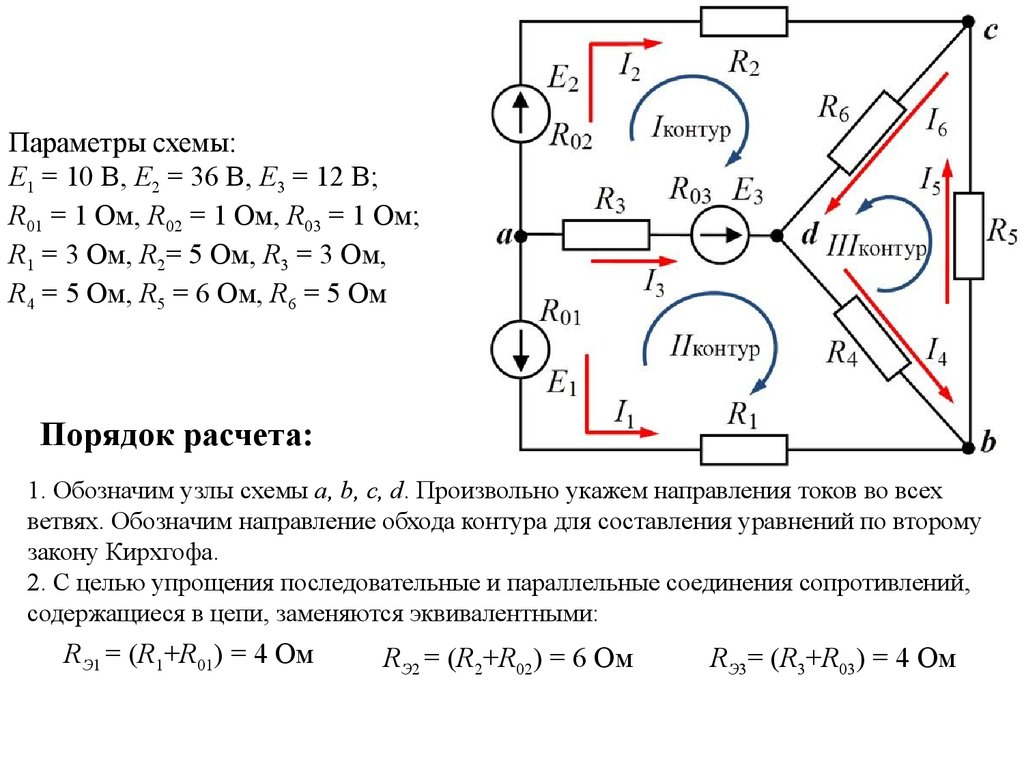
Упражнение 2
Рассчитайте следующие значения с помощью интерпретатора схемы.- отношение окружности, π
- доп. (2/3)
- 3 в степени 4
- логарифм 1000
5. Резюме
В этой главе мы использовали интерпретатор Scheme в качестве калькулятора. Это поможет вам привыкнуть к Scheme. Я объясню о типе данных «список» в схеме в следующей главе.Ответы на упражнения
Ответ 1
;1 (* (+ 1,39) (- 53,45)) ⇒ 320. ;2 (+ (/ 1020 39) (* 45 2)) ⇒ 1510/13. ;3 (+ 39 48 72 23 91) ⇒ 273. ;4 (точно->неточно (/ (+ 39 48 72 23 91) 5)) ⇒ 54,6.
Ответ 2
;1 (* 4 (атан 1,0)) ⇒ 3,141592653589793. ;2 (экспы 2/3) ⇒ 1,9477340410546757. ;3 (дополнение 3.4) ⇒ 81. ;4 (логарифм 1000) ⇒ 6,907755278982137.
Sukanya Samriddhi Yojana Calculator — SSY Calculator Online
Sukanya Samriddhi Yojana (SSY) — это схема сбережений, запущенная еще в 2015 году в рамках правительственной инициативы Beti Bachao, кампании Beti Padhao. Эта схема позволяет опекунам открывать для своих девочек сберегательный счет в уполномоченном коммерческом банке или в отделении Почты Индии.
Эта схема позволяет опекунам открывать для своих девочек сберегательный счет в уполномоченном коммерческом банке или в отделении Почты Индии.
Счета SSY предлагают процентную ставку 7,6%. Калькулятор Sukanya Samriddhi Yojana может помочь вам определить прибыль, которую вы получаете, в соответствии с инвестированной суммой и сроком владения.
Кто может использовать этот калькулятор?Первым шагом к использованию калькулятора SSY является проверка соответствия критериям приемлемости схемы. Счет SSY может быть открыт законными опекунами девочки при соблюдении следующих условий:
- Девушка должна быть резидентом Индии
- Возраст девочки не должен превышать 10 лет
- В семье с двумя девочками можно открыть до двух счетов.
Кроме того, законным опекунам также необходимо будет предоставить следующие документы, чтобы иметь возможность начать внесение депозитов в схему:
- Должным образом заполненный документ об открытии схемы, который включает основные личные данные владельца счета и девочки для которому открывается счет.

- Свидетельство о рождении девочки.
- Документы, удостоверяющие личность вкладчика, а также подтверждение действительного адреса.
- Медицинская справка в случае рождения нескольких детей по одному свидетельству о рождении.
- Дополнительные документы, запрошенные соответствующим органом.
Лица, которые соответствуют вышеупомянутым предварительным требованиям, а также имеют соответствующие подтверждающие документы, имеют право на участие в схеме и, следовательно, могут использовать онлайн-калькулятор SSY.
Чем может помочь калькулятор SSY? Часто родители девочки стремятся сделать инвестиции от имени своего ребенка, которые могут помочь покрыть расходы на образование дочери и расходы на брак. Несмотря на то, что существует множество способов инвестирования, которые могут помочь родителям достичь этого, Sukanya Samriddhi Yojana стала одной из самых популярных из-за высокой процентной ставки, а также предлагаемых налоговых льгот. В соответствии с разделом 80 C Закона о подоходном налоге, 1961, физические лица могут требовать освобождения от уплаты налогов в размере до 1,5 лакха с суммы, внесенной на счет SSY.
В соответствии с разделом 80 C Закона о подоходном налоге, 1961, физические лица могут требовать освобождения от уплаты налогов в размере до 1,5 лакха с суммы, внесенной на счет SSY.
Кроме того, процентный доход, полученный от инвестирования, также не облагается налогом. Налоговые льготы распространяются и на сумму погашения. При этом родители, которые выбрали Суканья Самриддхи в качестве предпочтительного варианта инвестиций, теперь нуждаются в инструменте для расчета общей суммы, которую они получат по истечении срока. Ручной расчет громоздок и подвержен ошибкам. Здесь пригодится калькулятор Sukanya Samriddhi Calculator. В зависимости от суммы погашения инвесторы могут вносить коррективы в регулярные взносы для достижения желаемого корпуса. Калькулятор бесплатен для использования и может генерировать безошибочный вывод для нескольких итераций.
Sukanya Samriddhi Yojana — это схема долгосрочных инвестиций, которая может обеспечить высокую рентабельность инвестиций. Вы должны вносить минимальный взнос каждый год, чтобы поддерживать активную учетную запись.
Следовательно, использование онлайн-калькулятора Sukanya Samriddhi Yojana полезно для общей оценки ваших инвестиций и доходов.
Некоторые преимущества калькуляторов SSY включают:
- Показывает год погашения вашей учетной записи SSY.
- Отображает сумму, которую вы получите по истечении срока.
- Помогает более эффективно планировать свой инвестиционный портфель.
Sukanya Samriddhi Yojana предлагает процентную ставку 7,6% годовых. Срок погашения этой суммы составляет 21 год. Важно отметить, что для отдельных лиц важно делать как минимум один взнос в год, чтобы схема оставалась в силе до тех пор, пока не будет завершено 14 лет. Физическое лицо может решить не делать взносы на счет SSY в период от года до 21 года, если оно того пожелает. Тем не менее, предыдущие инвестиции, сделанные на счете, будут продолжать приносить доход по действующей процентной ставке. Таким образом, окончательная сумма рассчитывается на основе вашего чистого вклада плюс заработанные проценты. 9нт
9нт
Где –
| А | Сложные проценты |
| П | Основная сумма |
| р | Процентная ставка |
| нет | Количество начислений процентов в год |
| т | Количество лет |
Просто введите сумму инвестиций в год, возраст вашей девочки и год начала инвестиций.
Калькулятор автоматически отобразит год погашения и сумму, которую вы получите при погашении, после того, как вы введете данные.
Преимущества использования Groww Sukanya Samriddhi Калькулятор схемИспользование онлайн-калькулятора Groww Sukanya Samriddhi Yojana дает вам следующие преимущества –
- Калькулятор Groww Sukanya Yojana можно использовать бесплатно, он может генерировать безошибочные выходные данные для нескольких итераций.

- Калькулятор выдает результат в течение нескольких секунд.
- Инструмент доступен онлайн на веб-сайте Groww и не требует загрузки утилиты.
- Вам не нужно регистрироваться или входить в систему, чтобы использовать калькулятор, он не запрашивает никакой информации о пользователе, кроме полей ввода.
- Вы можете использовать калькулятор SSY неограниченное количество раз.
- Расчеты производятся на основе преобладающих процентных ставок SSY для большей точности; физическим лицам не нужно вручную вводить процентные ставки.
- Калькулятор SSY обновлен, и любые изменения, внесенные в саму схему, которые влияют на расчет корпуса, будут автоматически отражены в работе калькулятора Sukanya Samriddhi.
- Инструмент одинаково эффективно работает на всех устройствах.
Калькулятор Sukanya Samriddhi Yojana поможет вам определить сумму, которую вы можете комфортно инвестировать каждый год. Открытие учетной записи SSY — это один из способов обезопасить будущее вашего ребенка от таких расходов, как получение высшего образования.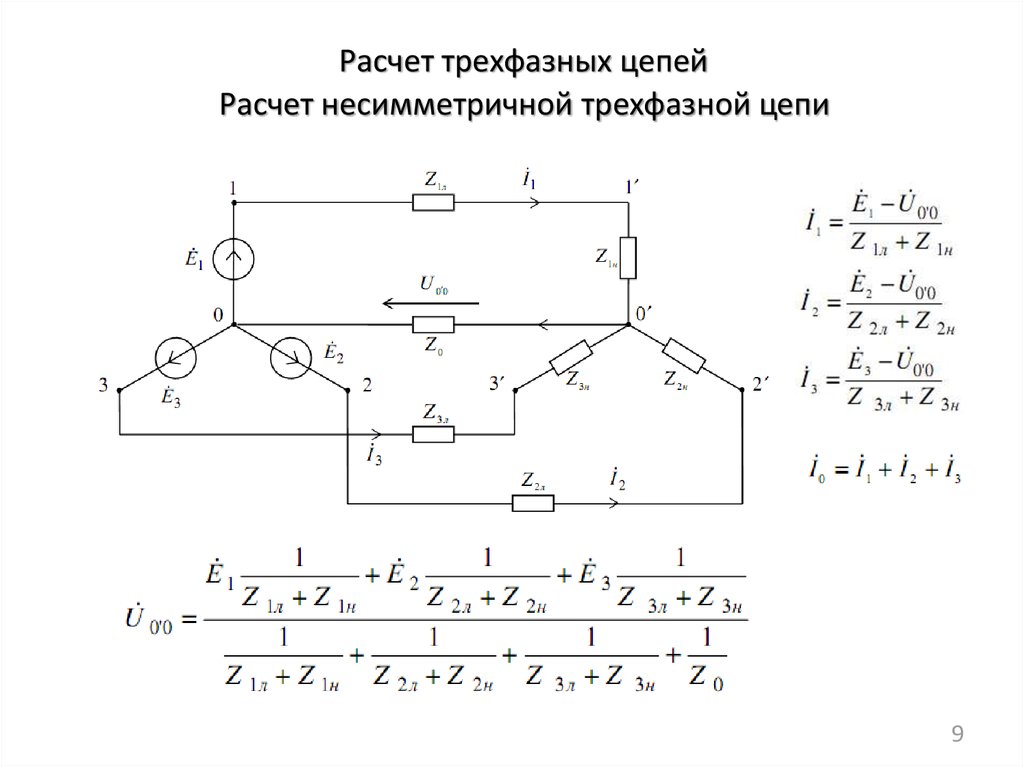

 Осталось только написать ответ.
Осталось только написать ответ. Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.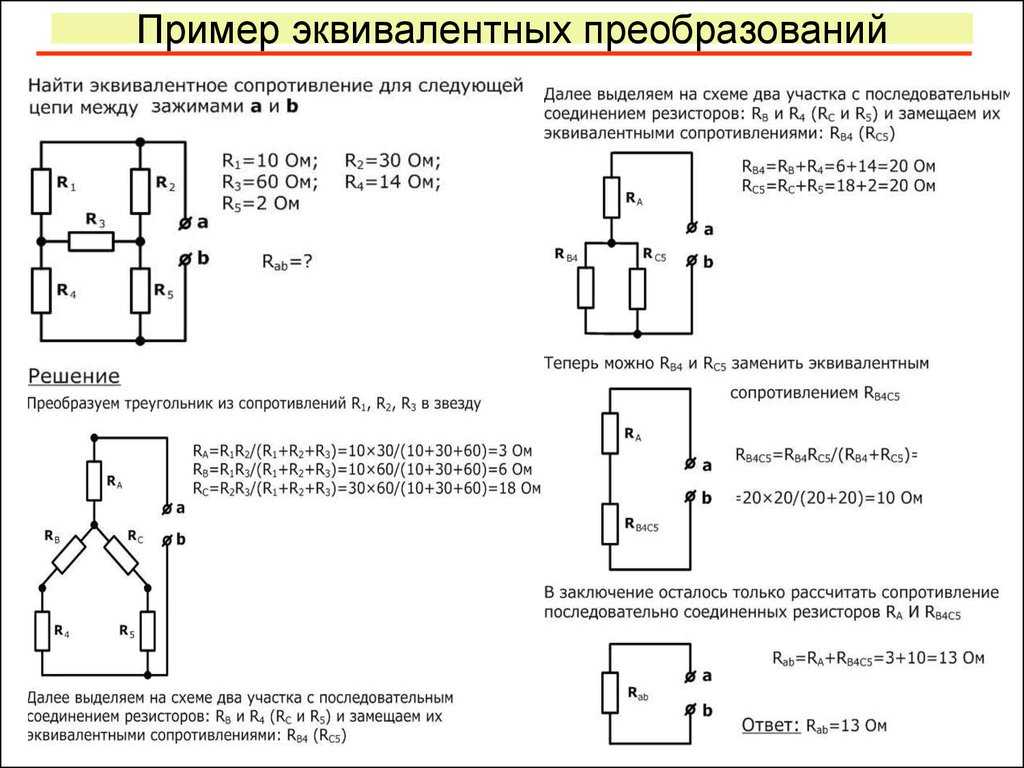 Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное) То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
 Получаем
Получаем