Два угла и сторона треугольника C
Для того чтобы рассчитать в треугольнике все возможные показатели, необходимо, как минимум, иметь данные о его сторонах. Зная два угла и сторону а, можно найти остальные две стороны и угол, построив высоту в таком треугольнике. (рис. 76.1) Высота разделит произвольный треугольник на два прямоугольных, в которых катетами будет высота и часть известной стороны x или y, а гипотенузами – неизвестные стороны a и b. Кроме того, что мы задаем известную сторону a, как сумму двух катетов x и y, тригонометрия полученных треугольников, определяет высоту с одной стороны как произведение y на тангенс β, а с другой стороны как произведение x на тангенс γ. Приравнивая эти выражения друг к другу, можно составить систему уравнений, из которых могут быть найдены части x и y, а затем неизвестные стороны первоначального треугольника a и b. {█(x+y=a@y tanβ=x tanγ )┤{█(x=a-y@y(tanβ+tanγ )=a tanγ )┤{█(x=a-y@y=(a tanγ)/(tanβ+tanγ ))┤ b=x/cosγ , c=y/cosβ h_a=y tanβ
Можно также найти сразу две другие высоты треугольника, опущенные на стороны b и c соответственно.
Чтобы найти биссектрисы треугольника, которые делят пополам его углы, также необходимо знать все три стороны треугольника. Формула биссектрисы выглядит немного сложнее, чем формула медианы, но достаточно проста в расчетах. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)
Средняя линия треугольника – это прямая, проведенная параллельно одной из его сторон. Ее особенность заключается в том, что она делит стороны на которые опирается на две равные части, и сама равна половине стороны, ей параллельной. (рис.75.7) M_a=a/2 M_b=b/2 M_c=c/2
Также в произвольном треугольнике через стороны можно найти радиус окружности, которую можно вписать в треугольник или описать около него. Радиус вписанной окружности будет начинаться в точке пересечения биссектрис треугольника и опускаться на любую из сторон под прямым углом. Радиус описанной окружности начинается в точке пересечения медиатрисс треугольника и заканчивается в любой из его вершин.
Калькуляторы
Калькулятор расчета объема видеоархива Калькулятор расчета угла обзора
Расчет объема видеоархива
Группы камер
Параметры записи
Часов в сутки:
| 1 | 6 | 12 | 18 | 24 |
Дней в неделю:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Продолжительность хранения видеоархива,
| день | неделя | месяц | год |
Результат вычислений
Рекомендуемый объем дискового пространства: ГБайт
Расчет углов обзора и области видимости
Выбор камеры
По модели
По параметрам
Формат матрицы
1/4″1/3″1/2. 8″1/2.7″1/2.5″1/2″1/1.8″
8″1/2.7″1/2.5″1/2″1/1.8″
Размер матрицы
ширина, мм
Разрешение (max)
3072×20482688х15122592х19442560х19202560х14402304х12962048х15361920х10801600х12001280х10241280х9601280х7201024х768960х528800х600720х576720х480704х576640х480640х360640х352480x256400x288352х288352х240320х288320х240320×184320х176192×144176х144176х120160х120160х112
Модель камеры B1210RB2710B4230B1210DMBD4640RCBD4640DRBD46CSV2017MSV2218M
Посмотреть товар
Разрешение (max)
Опциональное исполнение
Посмотреть товар
Выбор объектива
По модели
По параметрам
Тип объектива варифокальныйфиксированный
Фокусное расстояние, мм
2. 0
0
120.0
Модель объектива
Фокусное расстояние, мм
Посмотреть товар
Параметры наблюдателя
Расстояние до объекта, м
Результат вычислений
Область видимости
высота, м: 40
ширина, м: 2
Угол обзора
по вертикали: 60
по горизонтали: 60
Теоретически рассчитанные углы обзора могут отличаться от реальных непосредственно на объекте
Совместимые объективы
AN-1057: Использование акселерометра для определения наклона
по Кристофер Дж. Фишер Скачать PDF
Введение
Одним из распространенных методов определения наклона или наклона системы является интегрирование выходного сигнала гироскопа. Хотя этот метод прост, ошибка, связанная со стабильностью нулевого смещения, может быстро увеличиваться по мере увеличения периода интегрирования, вызывая кажущееся вращение, даже когда устройство неподвижно.
Хотя этот метод прост, ошибка, связанная со стабильностью нулевого смещения, может быстро увеличиваться по мере увеличения периода интегрирования, вызывая кажущееся вращение, даже когда устройство неподвижно.
В некоторых приложениях, где суммарное ускорение или сила, действующая на систему с течением времени, представляет собой силу тяжести, для измерения статического угла наклона или наклона можно использовать акселерометр. Такие приложения включают игры, обнаружение горизонта в цифровых камерах и определение направления устройства в промышленных и медицинских приложениях.
В основе определения наклона с помощью акселерометра лежит допущение, что единственный стимул ускорения связан с гравитацией. На практике обработка сигнала может выполняться на выходе сигнала, чтобы удалить высокочастотную составляющую из выходного сигнала, поэтому можно допустить некоторое ускорение переменного тока.
Датчик наклона использует вектор силы тяжести и его проекцию на оси акселерометра для определения угла наклона. Поскольку гравитация представляет собой ускорение постоянного тока, любые силы, приводящие к дополнительному ускорению постоянного тока, искажают выходной сигнал и приводят к неверным расчетам. Источники ускорения постоянного тока включают период времени, когда транспортное средство ускоряется с постоянной скоростью, и вращающиеся устройства, вызывающие центростремительное ускорение на акселерометре. Кроме того, вращение акселерометра под действием силы тяжести вызывает кажущееся ускорение переменного тока при изменении проекции силы тяжести на интересующие оси. Любая фильтрация сигнала ускорения перед расчетом наклона влияет на то, как быстро выходной сигнал устанавливается на новое статическое значение.
Поскольку гравитация представляет собой ускорение постоянного тока, любые силы, приводящие к дополнительному ускорению постоянного тока, искажают выходной сигнал и приводят к неверным расчетам. Источники ускорения постоянного тока включают период времени, когда транспортное средство ускоряется с постоянной скоростью, и вращающиеся устройства, вызывающие центростремительное ускорение на акселерометре. Кроме того, вращение акселерометра под действием силы тяжести вызывает кажущееся ускорение переменного тока при изменении проекции силы тяжести на интересующие оси. Любая фильтрация сигнала ускорения перед расчетом наклона влияет на то, как быстро выходной сигнал устанавливается на новое статическое значение.
В этих рекомендациях по применению обсуждаются основные принципы преобразования выходного сигнала акселерометра в угол наклона. Это обсуждение включает в себя, как рассчитать идеальный угол наклона для решения с одной, двумя или тремя осями. Кроме того, включена некоторая базовая информация о калибровке, чтобы уменьшить ошибку из-за смещения и несоответствия чувствительности.
Расчет наклона/наклона
Расчет наклона по одной оси
В приложениях, где определение наклона требуется только для ограниченного угла и с несколько грубым разрешением, можно использовать одноосное устройство (или одну ось многоосевого устройства).
Например, на рис. 1 одна ось (ось x в данном примере) вращается под действием силы тяжести. Поскольку в этом подходе используется только одна ось и требуется вектор силы тяжести, расчетный угол наклона является точным только тогда, когда устройство ориентировано так, что ось x всегда находится в плоскости силы тяжести. Любое вращение вокруг других осей уменьшает величину ускорения по оси x и приводит к ошибке в вычисленном угле наклона.
Рис. 1. Одна ось, используемая для определения наклона.
Ссылаясь на базовую тригонометрию, проекция вектора силы тяжести на ось x создает выходное ускорение, равное синусу угла между осью x акселерометра и горизонтом. Горизонт обычно принимается за плоскость, ортогональную вектору силы тяжести.
При использовании одноосного решения обратите внимание, что чувствительность — т. е. изменение выходных данных при некотором изменении входных данных — вычисления наклона уменьшается по мере увеличения угла между горизонтом и осью x и приближается к 0 по мере увеличения угла приближается к ±90°. Это видно на рис. 2, где выходное ускорение в g изображено в зависимости от угла наклона. Вблизи ±90° большое изменение угла наклона приводит к небольшому изменению выходного ускорения.
Рис. 2. Выходное ускорение в зависимости от угла наклона для измерения наклона по одной оси.
Поскольку расчет наклона выполняется в цифровом виде, выходное ускорение представляется как постоянное ускорение на младший значащий бит (LSB) или код, полученный либо из аналого-цифрового преобразователя (АЦП), либо непосредственно из части цифрового выхода. Поскольку выходное разрешение представляет собой постоянное ускорение, разрешение в градусах наклона является переменным, при этом наилучшее разрешение близко к 0°, а наихудшее разрешение равно ±9.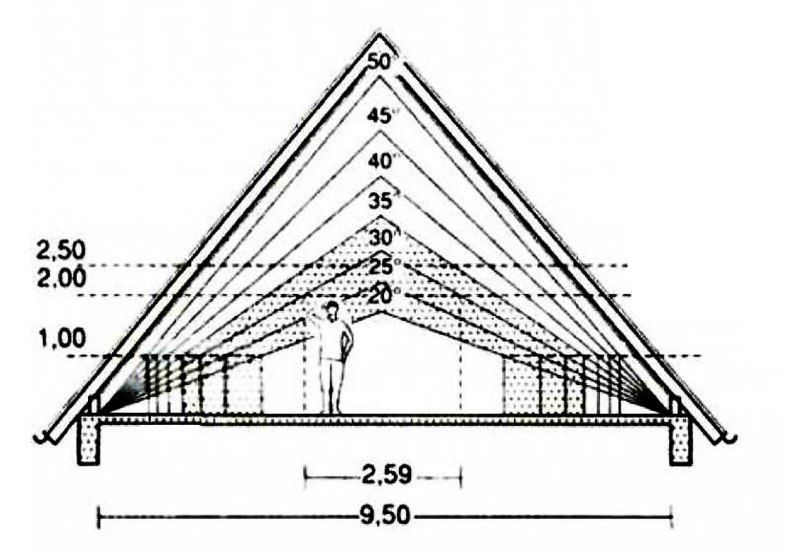
На Рисунке 3 и Рисунке 4 показана инкрементальная чувствительность для шагов угла наклона 1° и 0,25°. Инкрементальная чувствительность представляет собой изменение выходного сигнала, показанное в m g , на шаг угла наклона или
где:
N текущий угол.
P — размер шага.
Рис. 3. Инкрементальная чувствительность к наклону с шагом 1°.
Рис. 4. Инкрементальная чувствительность к наклону для шагов 0,25°.
Эти кривые можно использовать для определения минимально необходимого разрешения при измерении выходного ускорения, чтобы обеспечить требуемое разрешение по наклону для всего диапазона применения. Например, при расчете максимального размера шага в 1° разрешение не менее 8 м г /LSB необходимо для диапазона ±63°. Точно так же для достижения максимального размера шага 0,25° для диапазона ±63 требуется разрешение не менее 2 м г /LSB. Обратите внимание, что при наличии достаточного дизеринга можно использовать передискретизацию для достижения лучшего разрешения.
Поскольку выходной сигнал акселерометра подчиняется синусоидальной зависимости, поскольку он вращается под действием силы тяжести, преобразование ускорения в угол выполняется с помощью функции обратного синуса.
, где угол наклона θ выражен в радианах.
Если требуется узкий диапазон наклона, вместо функции обратного синуса можно использовать линейное приближение. Линейное приближение относится к приближению синуса для малых углов.
где угол наклона, θ , в радианах.
В линейную аппроксимацию угла наклона можно включить дополнительный коэффициент масштабирования k, что позволяет увеличить допустимый диапазон аппроксимации при увеличении допустимой ошибки.
, где угол наклона θ выражен в радианах.
Преобразование в градусы выполняется путем умножения результата уравнения 5 на (180/π). На рис. 5 показано сравнение использования функции обратного синуса и линейной аппроксимации при k, равном 1. По мере увеличения величины угла наклона линейная аппроксимация начинает давать сбои, и расчетный угол отклоняется от фактического угла.
Рис. 5. Сравнение функции обратного синуса и линейной аппроксимации для расчета угла наклона.
Поскольку расчетный угол отображается в зависимости от фактического угла наклона, кажется, что линейное приближение изгибается ближе к концам. Это связано с тем, что линейное приближение является линейным только по сравнению с выходным ускорением, и, как показано на рисунке 2, выходное ускорение ведет себя аналогично при увеличении фактического угла наклона. Однако функция обратного синуса должна давать выходной сигнал, который один к одному соответствует фактическому углу наклона, в результате чего вычисленный угол представляет собой прямую линию при построении графика относительно фактического угла наклона.
Например, если желаемое разрешение измерения наклона составляет 1°, допустима ошибка ±0,5°, поскольку она ниже ошибки округления вычисления. Если ошибка между фактическим углом наклона и расчетным углом наклона нанесена на график для k, равного 1, как показано на рисунке 6, действительный диапазон для линейного приближения составляет только ±20°. Если коэффициент масштабирования отрегулирован таким образом, чтобы ошибка была максимальной, но оставалась в пределах пределов округления вычислений, допустимый диапазон линейной аппроксимации увеличивается до значения, превышающего ±30°.
Если коэффициент масштабирования отрегулирован таким образом, чтобы ошибка была максимальной, но оставалась в пределах пределов округления вычислений, допустимый диапазон линейной аппроксимации увеличивается до значения, превышающего ±30°.
Рис. 6. Вычисленная угловая ошибка для различных коэффициентов масштабирования.
Расчет наклона по двум осям
Одним из ограничений измерения наклона по одной оси является потребность в АЦП с высоким разрешением или цифровом выходе для достижения большого диапазона действительных углов наклона, как показано на рис. 3 и рис. 4. Другое ограничение заключается в том, что измерение по одной оси не может обеспечить измерение 360°, потому что ускорение, генерируемое при наклоне N°, такое же, как ускорение, генерируемое при наклоне 180° − N°. Для некоторых приложений это допустимо, но для приложений, требующих более высокого разрешения или способности различать углы наклона в полной дуге 360°, необходима вторая ось, как показано на рис. 7, или второй датчик. Если используется второй датчик, он должен быть ориентирован так, чтобы ось восприятия второго датчика была ортогональна оси восприятия первого датчика.
7, или второй датчик. Если используется второй датчик, он должен быть ориентирован так, чтобы ось восприятия второго датчика была ортогональна оси восприятия первого датчика.
Рис. 7. Две оси, используемые для определения наклона.
Включение второй оси при определении угла наклона дает три основных преимущества. Эти преимущества описаны в следующих разделах.
Постоянная чувствительность
Первое важное преимущество использования второй оси связано с ортогональностью осей. Как и в одноосном решении, ускорение, определяемое осью x, пропорционально синусу угла наклона. Ускорение по оси Y из-за ортогональности пропорционально косинусу угла наклона (см. рис. 8). По мере снижения инкрементальной чувствительности одной оси, например, когда ускорение этой оси приближается к +1 г или -1 г увеличивается инкрементальная чувствительность другой оси.
Рис. 8. Выходное ускорение в зависимости от угла наклона для измерения наклона по двум осям.
Одним из способов преобразования измеренного ускорения в угол наклона является вычисление арксинуса оси x и арккосинуса оси y аналогично решению для одной оси. Однако более простым и эффективным подходом является использование отношения двух значений, что приводит к следующему:
, где угол наклона θ выражен в радианах.
В отличие от примера с одной осью, использование отношения двух осей для определения угла наклона очень затрудняет определение инкрементной чувствительности. Вместо этого полезнее определить минимально необходимое разрешение акселерометра при желаемом разрешении наклона. Учитывая, что инкрементальная чувствительность одной оси увеличивается по мере уменьшения другой, конечным результатом является эффективная инкрементальная чувствительность, которая примерно постоянна. Это означает, что выбор акселерометра с достаточным разрешением для достижения желаемого размера шага наклона по одному углу достаточен для всех углов.
Чтобы определить минимально необходимое разрешение акселерометра, проверяется уравнение 6, чтобы определить, где находятся ограничения разрешения. Поскольку выход каждой оси зависит от синуса или косинуса угла наклона, а угол наклона для каждой функции одинаков, минимальный разрешаемый угол соответствует минимальному разрешенному ускорению.
Поскольку выход каждой оси зависит от синуса или косинуса угла наклона, а угол наклона для каждой функции одинаков, минимальный разрешаемый угол соответствует минимальному разрешенному ускорению.
Как показано на рисунках 3 и 4, функция синуса имеет наибольшую скорость изменения вблизи 0°, и можно показать, что функция косинуса имеет наименьшую скорость изменения в этой точке. По этой причине изменение ускорения по оси x из-за изменения наклона распознается до изменения ускорения по оси y. Следовательно, разрешение системы вблизи 0° зависит в первую очередь от разрешения по оси x. Чтобы обнаружить изменение наклона P°, акселерометр должен обнаруживать изменение примерно на 9°.0006
Рисунок 9 можно использовать для определения минимально необходимого разрешения акселерометра или максимального масштабного коэффициента акселерометра для желаемого размера шага наклона. Обратите внимание, что увеличенное разрешение акселерометра соответствует уменьшению масштабного коэффициента акселерометра и способности обнаруживать меньшее изменение выходного ускорения. Следовательно, при выборе акселерометра с соответствующим разрешением масштабный коэффициент должен быть меньше предела, показанного на рисунке 9, для предполагаемого размера шага наклона.
Следовательно, при выборе акселерометра с соответствующим разрешением масштабный коэффициент должен быть меньше предела, показанного на рисунке 9, для предполагаемого размера шага наклона.
Рис. 9. Минимальное разрешение акселерометра для желаемого угла наклона. Разрешение уменьшенной зависимости от совмещения с плоскостью.
Уменьшенная зависимость от выравнивания с плоскостью гравитации
Вторым важным преимуществом использования по крайней мере двух осей является то, что в отличие от решения с одной осью, где наклон по любой оси, кроме оси x, может привести к значительной ошибке, использование второй оси позволяет измерить точное значение. даже при наличии наклона по третьей оси. Это связано с тем, что эффективная инкрементная чувствительность пропорциональна значению силы тяжести на осях интереса из суммы квадратов (RSS).
Когда гравитация полностью сосредоточена в плоскости xy, значение ускорения RSS, обнаруженное на этих осях, идеально равно 1 g . Если в плоскости xz или yz присутствует наклон, общее ускорение под действием силы тяжести уменьшается, что также снижает эффективную инкрементальную чувствительность. Это, в свою очередь, увеличивает размер шага наклона для данного разрешения акселерометра, но по-прежнему обеспечивает точное измерение. Результирующий угол из расчета наклона соответствует повороту в плоскости xy.
Если в плоскости xz или yz присутствует наклон, общее ускорение под действием силы тяжести уменьшается, что также снижает эффективную инкрементальную чувствительность. Это, в свою очередь, увеличивает размер шага наклона для данного разрешения акселерометра, но по-прежнему обеспечивает точное измерение. Результирующий угол из расчета наклона соответствует повороту в плоскости xy.
Если система достаточно наклонена, так что ускорение силы тяжести в плоскости xy очень мало, размер шага угла наклона будет слишком грубым, чтобы его можно было использовать; поэтому рекомендуется ограничивать наклон в плоскости xz или yz.
Полный датчик наклона на 360°
Третьим важным преимуществом использования второй оси является возможность различать каждый квадрант и измерять углы по всей дуге 360°. Как показано на рисунке 10, каждый квадрант имеет различную комбинацию знаков, связанных с ускорением по осям x и y.
Рис. 10. Угол наклона и знак ускорения для квадрантного обнаружения.
Функция арктангенса возвращает значение в квадранте I, если операнд A X,OUT /A Y,OUT положительный; если операнд отрицательный, функция арктангенса возвращает значение в квадранте IV. Поскольку операнд в квадранте II отрицательный, к результату вычисления следует добавить значение 180°, когда угол находится в этом квадранте. Поскольку операнд в квадранте III положительный, значение 180° следует вычесть из результата вычисления, когда угол находится в этом квадранте. Правильный квадрант вычисленного угла можно определить, изучив знак измеренного ускорения по каждой оси.
Расчет наклона по трем осям
Когда вводится третья ось, ориентация датчика может быть определена в полной сфере. Классический метод преобразования прямоугольных (x, y, z) в сферические (ρ, θ, φ) можно использовать для связи угла наклона в плоскости xy, θ, и угла наклона от вектора силы тяжести, φ , к измеренному ускорению по каждой оси следующим образом:
Учитывая допущение, что единственное измеренное ускорение связано с гравитацией, знаменатель операнда в уравнении 10 можно заменить константой, в идеале 1, потому что значение RSS по всем осям постоянно, когда единственным ускорением является сила тяжести. Углы показаны на рис. 11, где на рис. 11с показано θ только в плоскости xy, а на рис. 11d показано φ как угол между осью z и вектором силы тяжести.
Углы показаны на рис. 11, где на рис. 11с показано θ только в плоскости xy, а на рис. 11d показано φ как угол между осью z и вектором силы тяжести.
Рис. 11. Углы сферической системы координат.
Из-за схожести уравнений для метода трех осей и уравнений для методов с одной и двумя осями, анализ решения по трем осям такой же, как и для объединенных методов с одной и двумя осями. Измерение θ выигрывает от отношения двух ортогональных осей, а желаемое разрешение наклона требует минимального разрешения акселерометра, как описано уравнением 8.
Измерение φ соответствует измерению угла наклона для одноосного решения вместе с методом определения минимального разрешения акселерометра, необходимого для определенного разрешения угла наклона в желаемом диапазоне. Разница заключается в том, что использование функции арккосинуса для определения φ дает максимальную чувствительность приращения, когда φ составляет 90°, и минимальную чувствительность приращения при 0° и 180°.
График, аналогичный рисункам 3 и 4, можно получить, заменив синус на косинус в уравнении 2. Важно отметить, что, хотя θ находится в диапазоне от -180° до +180°, φ находится в диапазоне только от 0° до 180°. Отрицательный угол для φ приводит к тому, что угол θ становится отрицательным.
Альтернативный метод измерения наклона по трем осям заключается в определении угла отдельно для каждой оси акселерометра из исходного положения. За исходное положение принимается типичная ориентация устройства с осями x и y в плоскости горизонта (0 g поле) и осью z ортогонально горизонту (1 g поле). Это показано на рисунке 12, где θ — угол между горизонтом и осью x акселерометра, ψ — угол между горизонтом и осью y акселерометра и φ — угол между вектором силы тяжести и ось Z. Когда в исходном положении 0 < g по осям x и y и 1 g по оси z, все расчетные углы будут равны 0°.
Рис. 12. Углы для независимого измерения наклона.
Основы тригонометрии можно использовать, чтобы показать, что углы наклона можно рассчитать с помощью уравнения 11, уравнения 12 и уравнения 13.
Кажущаяся инверсия операнда в уравнении 13 связана с тем, что исходная позиция представляет собой поле размером 1 g . Если в качестве точки отсчета для оси Z требуется горизонт, операнд можно инвертировать. Положительный угол означает, что соответствующая положительная ось акселерометра направлена над горизонтом, тогда как отрицательный угол означает, что ось направлена ниже горизонта.
Поскольку используется функция арктангенса и отношение ускорений, применяются преимущества, упомянутые в примере с двумя осями, а именно то, что эффективная инкрементная чувствительность постоянна и что углы могут быть точно измерены для всех точек вокруг единичной сферы.
Ошибка калибровки смещения и несоответствия чувствительности
Анализ в этих указаниях по применению был выполнен в предположении, что использовался идеальный акселерометр. Это соответствует устройству без 0 g смещения и с идеальной чувствительностью (выражается как мВ/ g для аналогового датчика или LSB/g для цифрового датчика). Хотя датчики поставляются подрезанными, устройства имеют механический характер, а это означает, что любое статическое напряжение на детали после сборки системы может повлиять на смещение и чувствительность. Это, в сочетании с ограничениями заводской калибровки, может привести к ошибкам, превышающим допустимые пределы для приложения.
Хотя датчики поставляются подрезанными, устройства имеют механический характер, а это означает, что любое статическое напряжение на детали после сборки системы может повлиять на смещение и чувствительность. Это, в сочетании с ограничениями заводской калибровки, может привести к ошибкам, превышающим допустимые пределы для приложения.
Последствия ошибки смещения
Чтобы продемонстрировать, насколько велика может быть ошибка, представьте себе сначала двухосевое решение с идеальной чувствительностью, но с 50-метровым г смещение по оси x. При 0° по оси абсцисс отсчитывается 50 м г , а по оси у — 1 г . Результирующий расчетный угол будет равен 2,9°, что приведет к ошибке 2,9°. При ±180° по оси x будет указано 50 м г , тогда как по оси Y будет указано -1 г . Это приведет к расчетному углу и ошибке -2,9 °. Ошибка между вычисленным углом и фактическим углом показана на рисунке 13 для этого примера. Ошибка из-за смещения может быть не только велика по сравнению с требуемой точностью системы, но и может варьироваться, что затрудняет простую калибровку угла ошибки. Это становится более сложным, когда включено смещение для нескольких осей.
Это становится более сложным, когда включено смещение для нескольких осей.
Рис. 13. Расчетная ошибка угла из-за смещения акселерометра.
Последствия ошибки несоответствия чувствительности
Основная составляющая ошибки из-за чувствительности акселерометра в двухосевом приложении измерения наклона возникает, когда существует разница в чувствительности между интересующими осями (в отличие от одноосного решения, где любое отклонение между фактической чувствительностью и ожидаемой чувствительностью приводит к ошибке). Поскольку используется соотношение осей x и y, большая часть ошибки устраняется, если чувствительности одинаковы.
В качестве примера эффекта несоответствия чувствительности акселерометра предположим, что используется двухосевое решение с идеальной подстройкой смещения, идеальной чувствительностью по оси Y и +5% чувствительностью по оси X. Это означает, что в поле 1 г по оси Y отображается 1 г , а по оси X — 1,05 г . На рис. 14 показана ошибка вычисленного угла из-за этого несоответствия чувствительности. Подобно ошибке смещения, ошибка из-за несоответствия чувствительности акселерометра варьируется во всем диапазоне поворота, что затрудняет компенсацию ошибки после расчета угла наклона. Дальнейшее искажение несоответствия путем изменения чувствительности по оси Y приводит к еще большей ошибке.
На рис. 14 показана ошибка вычисленного угла из-за этого несоответствия чувствительности. Подобно ошибке смещения, ошибка из-за несоответствия чувствительности акселерометра варьируется во всем диапазоне поворота, что затрудняет компенсацию ошибки после расчета угла наклона. Дальнейшее искажение несоответствия путем изменения чувствительности по оси Y приводит к еще большей ошибке.
Рис. 14. Ошибка расчета угла из-за несоответствия чувствительности акселерометра.
Основные методы калибровки
Когда ошибки из-за смещения и несоответствия чувствительности объединяются, ошибка может стать довольно большой и выйти далеко за допустимые пределы в приложении для измерения наклона. Чтобы уменьшить эту ошибку, необходимо откалибровать смещение и чувствительность, а откалиброванное выходное ускорение использовать для расчета угла наклона. При включении эффектов смещения и чувствительности выходной сигнал акселерометра выглядит следующим образом:
где:
A OFF ошибка смещения, в г .
Усиление — усиление акселерометра, в идеале значение равное 1.
A АКТУАЛЬНОЕ — реальное ускорение, действующее на акселерометр, и желаемое значение в g .
Простой метод калибровки заключается в предположении, что коэффициент усиления равен 1, и измерении смещения. Затем эта калибровка ограничивает точность системы некалиброванной ошибкой чувствительности. Простой метод калибровки можно выполнить, поместив интересующую ось в 0 g поле и измеряющий вывод, который будет равен смещению. Затем это значение следует вычесть из выходного сигнала акселерометра перед обработкой сигнала. Это часто называют калибровкой без поворота или калибровкой по одной точке, потому что типичная ориентация устройства помещает оси x и y в поле 0 g . Если используется трехосное устройство, по крайней мере один поворот или вторая точка должны быть включены для оси Z.
Более точный метод калибровки заключается в использовании двух точек на каждой оси интереса (до шести точек для трехосевой модели). Когда ось помещается в +1 g и −1 g , измеренные выходные значения следующие:
Когда ось помещается в +1 g и −1 g , измеренные выходные значения следующие:
, где смещение A OFF выражено в г .
Эти две точки можно использовать для определения смещения и усиления следующим образом:
, где измерения +1 г и -1 г , А +1 г и А -1 г , выражены в г .
Этот тип калибровки также помогает свести к минимуму влияние поперечной чувствительности, поскольку ортогональные оси находятся в 0 g поле при выполнении измерений для интересующей оси. Эти значения можно использовать, сначала вычитая смещение из измерения акселерометра, а затем разделив результат на коэффициент усиления.
, где A OUT и A OFF находятся в г .
Расчеты A OFF и усиления в уравнениях с 15 по 19 предполагают, что значения ускорения A +1g и A −1g находятся в г . Если используется ускорение в m g , расчет A OFF в уравнении 17 остается неизменным, но расчет коэффициента усиления в уравнении 18 должен быть разделен на 1000, чтобы учесть изменение в единицах измерения.
Если используется ускорение в m g , расчет A OFF в уравнении 17 остается неизменным, но расчет коэффициента усиления в уравнении 18 должен быть разделен на 1000, чтобы учесть изменение в единицах измерения.
Автор
Кристофер Дж. Фишер
координат — Расчет угла обзора
Задавать вопрос
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 335 раз
При расчете угла обзора? принятый ответ содержит следующие расчеты:
Для двух точек (x, y, z) и (x’, y’, z’) в системе координат с центром на Земле вектор из первой во вторую равен (dx,dy,dz) = (x’ -х, у’-у, з’-з)
А затем приводит пример:
Координаты самолетов XYZ (x,y,z) = (1285410, -4797210, 3994830) и (x’,y’,z’) = (1202990, -4824940, 3999870) соответственно (в ITRF00 датум, в котором используется эллипсоид GRS80).
Таким образом, вектор обзора пилота равен (dx,dy,dz) = (-82404,5, -27735,3, 5034,56).
Что мне не хватает такого, что:
1202990 — 1285410 = -82404,5 (заместитель -82420)
-4824940 — -4797210 = -27735,3 (заместитель -27730)
3999870 — 3994830 = 5034,56 (заместитель 5040) ?
- координаты
- углы
Координаты ECEF, предоставленные @whuber, округлены до ближайших 10 метров. Глядя на поправки к ответу, видно, что изначально он использовал опорные точки (N39°, W75°, 4000 м) и (N39°, W76°, 12000 м) , переводя их в координаты ECEF:
( 1285408.203, -4797208.722, 3994834.304) (1202993.662, -4824944.042, 3999868.867)
Тогда векторы равны:
dX = -82414,541 дГ = -27735,320 dZ = 5034,563
Итак, все они совпадают, кроме dX, который выглядит как опечатка.
РЕДАКТИРОВАТЬ
После более тщательной проверки ответа @whuber я заметил небольшую проблему с методологией.

 Таким образом, вектор обзора пилота равен (dx,dy,dz) = (-82404,5, -27735,3, 5034,56).
Таким образом, вектор обзора пилота равен (dx,dy,dz) = (-82404,5, -27735,3, 5034,56).