Расположение координатных четвертей на графике: В каких координатных четвертях расположен график функции y=k/x если ему принадлежит точка (-5:2)?

Координатные четверти – расположение

4.6

Средняя оценка: 4.6

Всего получено оценок: 112.

4.6

Средняя оценка: 4.6

Всего получено оценок: 112.

Человечество с самого начала своего существования нуждалось в определении своего места положения. Как узнать конкретное расположение точки с точностью до миллиметра? Только с помощью системы координат, об особенностях которой и пойдет речь сегодня.

Что такое система координат?

Система координат это комплекс мер, которые позволяют определить положение точки в пространстве или на плоскости.

В физике помимо комплекса определения положения точки используется еще и прибор для определения времени. В математике достаточно определить положение точки в один момент времени.

Существует две разновидности систем координат:

• Прямоугольная система координат. Это система координат, которая была изобретена английским математиком Декартом, потому второе название системы координат: декартова. Система представляет собой два взаимно перпендикулярных луча. Началом отсчета является точка пересечения лучей, на лучах отмечают единичные отрезки.
• Полярная система координат. Эта система куда более древняя. Она использовалась еще мореплавателями в древней Греции. В качестве координат используется еще и угол. Число откладывается на луче, от точки поднимается перпендикуляр. После из начала координат проводится прямая под заданным углом. Точка пересечения проведенной прямой и перпендикуляра и есть искомое положение точки.

Полярная система в современности используется крайне редко, она сложнее декартовой системы, а потому утратила свою популярность.

Координатные четверти

Два взаимно перпендикулярных луча образуют четыре координатные четверти. Горизонтальная ось называется осью абсцисс или осью Ох, вертикальная оси называется осью ординат или осью Оу. Начало координат рассекает оси на положительную и отрицательную часть.

Каждая из координатных четвертей имеет свой номер и обозначение в виде римской цифры.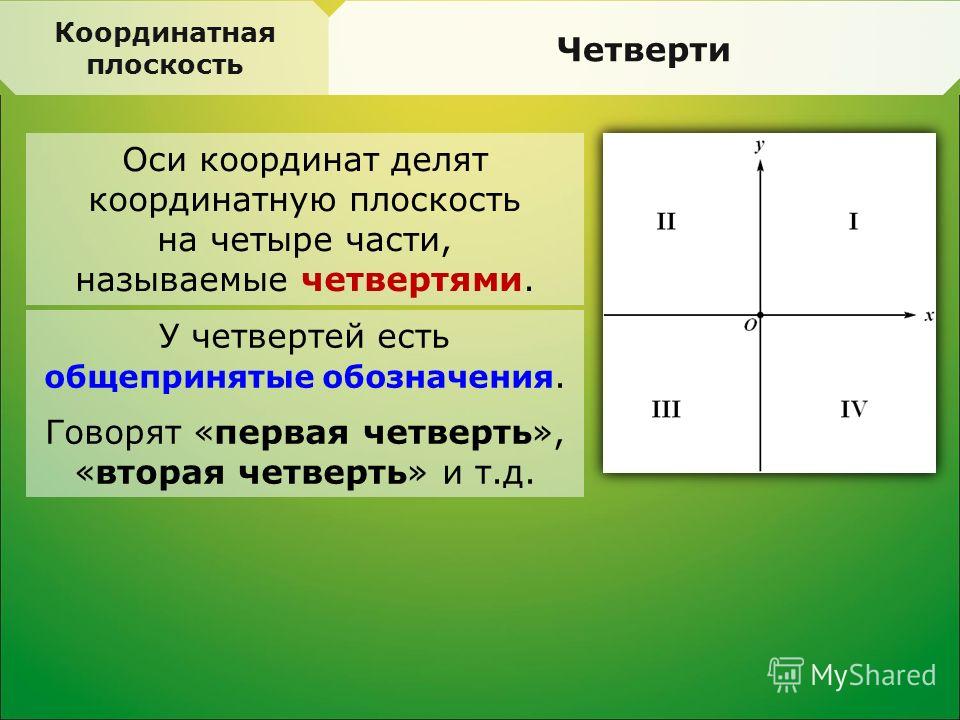

Сначала нумеруют верхние четверти, так верхняя правая четверть зовется первой, верхняя левая второй, нижняя левая третье, а нижняя правая четвертой.

Для того, чтобы узнать координаты точки в прямоугольной системе координат, следует опустить от точки перпендикуляры на оси и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты прописываются в скобочках, первой идет координата по оси Ох, второй по Оу.

Разберемся, какие координаты могут быть в осях:

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательна, а координата у положительна, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительна, а координата у отрицательна, то точка лежит в четвертой четверти.

Что мы узнали?

Мы поговорили о системах координат. Выделили две системы координат. Поговорили о координатных четвертях, а также сказали, как определить расположение точки в зависимости от ее координат.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 112.

---

А какая ваша оценка?

особенности координатной плоскости в геометрии

Математика

12.11.21

6 мин.

Прямоугольная система координат является очень удобным инструментом в математике. С ее помощью осуществляется возможность описания свойств и фигур в геометрии методом, включающим уравнения и неравенства. Такой математический способ помогает узнавать определенное место точек в пространстве.

Оглавление:

• Графики четвертей
• В трехмерном пространстве
• Прямоугольные координаты
• Точка на плоскости

Графики четвертей

Чтобы ввести четверти координатной плоскости, нужно провести 2 прямые в перпендикулярных вариациях. Для этого подбирают положительное направление и масштабирование. Точку пересечения прямых называют началом отсчета. С ее помощью задают прямоугольную систему координат, которая имеет следующие характеристики:

1. Прямые с началом в точке О, которые имеют направление и масштаб, считаются прямой или осью координат.
2. Система обозначается как Oxy. Координатными называются Ox и Oy, которые соответствуют осям абсцисс и ординат.
3. Нумерация координатных четвертей на графике имеет одинаковую единицу измерений. Обычное направление Ox идет слева направо, а Oy располагается снизу вверх. Иногда могут применяться альтернативные варианты, которые создаются с поворотом под необходимым вторым координатным углом в пространстве.

В свое время прямоугольная система получила название декартовой.

Это легко объяснить тем, что ее впервые открыл математик Рене Декарт. Иногда встречается объединенное название — математическая декартовая координатная система. Со временем она развивалась в плане дополнительного описания, математического аппарата и пришла к современному варианту.

В трехмерном пространстве

Трехмерное пространство евклидового типа задают аналогично, только применяются оси Ox, Oy и Oz. Они представляют собой 3 прямые со взаимной перпендикулярностью, где одна из них носит название аппликаторной. По направлениям оси разделяют левосторонние и правосторонние координаты пространства в трехмерном прямоугольном варианте.

Главные моменты, связанные с таким видом прямоугольной геометрической системы:

1. Оси пересекаются в определенной точке О, называемой началом или первой.
2. У каждой есть положительный вариант направления, его показывают стрелками на определенных осях координат.
3. При повороте Ox против стрелки на 90 градусов положительное направление совпадет с Oy. Такое же утверждение верно и для Oz. Это называется правой системой.

Таким же способом создается и левый вариант трехмерной разновидности координат. Но при этом нет возможности совместить между собой оба имеющихся варианта. Это происходит, поскольку соответствующие оси не смогут совпасть между собой.

Прямоугольные координаты

Сначала стоит откладывать точку на оси Ox. Всякое действительное число будет равно единственной точке, располагаемой на прямой. Началом отсчетной части координатных прямых всегда выступает ноль, то есть каждый элемент, который расположен на Ox, равен действительному числу Xm. Им будет ноль, если M располагается на пересечении Ox и Oy.

Численно длина отрезка всегда со знаком плюс, если точка удаляется в соответствующем направлении.

Любая точка M на задаваемой плоскости в прямоугольном варианте расположения имеет пару чисел, которые являются координатами. Обратное утверждение также является верным.

Точка на плоскости

Чтобы определить точку M в пространстве трех измерений, задаются проекции на определенные оси. Значения Mx, My, Mz принимают значения xM, yM, zM. Добавляют прямые перпендикуляры, которые изображают как плоскости через M.

У каждой точки имеются свои координаты для M.

В трехмерной оси есть ордината, абсцисса и аппликата. Любая распределенная тройка чисел действительного вида в координатах прямоугольного типа вводится для соответствующей точки пространства трех измерений.

Прямоугольная система считается очень важным разделом в математике и смежных науках. Именно она помогает определить местоположение точек в пространстве с наибольшей точностью. Дополнительным условием является описание геометрических фигур за счёт выражений и неравенств. Это самое наглядное объяснение координатных плоскостей как в трехмерных, так и в прямоугольных пространственных координатах.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Обучение числам квадрантов на графике

Назад к форме

Математика

Фигурный посох

01 сентября 2021 г.

6 минут чтения

Есть много способов осмыслить концепцию математики фундаментально. Один из способов состоит в том, чтобы разделить тему на то, как писать математику (часто алгебру) и как писать математику.0013 рисовать это (часто геометрия). График координатной плоскости находится в пространстве между математикой письма и рисования, поскольку график часто можно описать как письменными уравнениями, так и визуальными формами.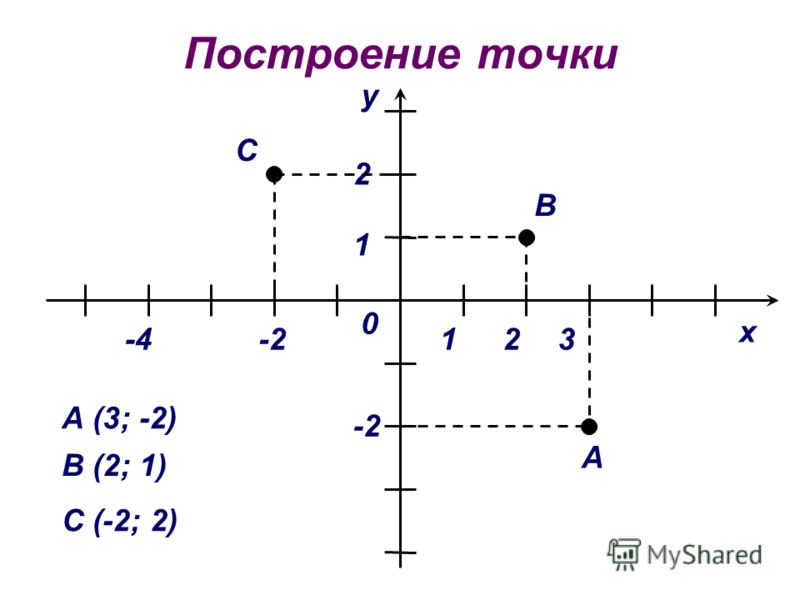

В США учащиеся 5-х классов и старше обычно сначала учатся строить графики с осями x и y на координатной плоскости. Как только они будут готовы к положительным и отрицательным целым числам , часто к 6 классу, вы можете распространить графическое представление на все четыре квадранта координатной плоскости.

• Стандарт ключа: Точки графика во всех четырех квадрантах координатной плоскости. (Common Core 6.NS.C.8, Florida BEST MA.6.GR.1.1)

Точки на сетке

Местоположение или точка на сетке может быть идентифицирована с помощью упорядоченных пара , такая как (3,2), которая называет координаты этой точки. Первое число говорит, насколько далеко вправо или влево расположена точка по горизонтали. Второе число говорит о том, насколько вверх или вниз расположена точка по вертикали. Обратите внимание, что точка (3,2) не совпадает с точкой (2,3). Числа в упорядоченной паре называются координаты .

Целые числа

Наиболее распространенные числа, с которыми мы сталкиваемся во всем, от ограничений скорости до серийных номеров, — это натуральных чисел . Это счетные числа, которые начинаются с 1, 2 и 3 и продолжаются бесконечно. Если вместо этого мы начнем считать с 0, набор чисел вместо этого будет называться целыми числами . Целые числа чисел (или просто целых чисел ) расширяют целые числа до их противоположностей: … ^– 3, ^– 2, ^– 1, 0, 1, 2, 3…. Обратите внимание, что 0 – это единственное число, противоположным которому является оно само.

Исторически сложилось так, что отрицательные числа в значительной степени возникли как способ решения уравнений, которые в противном случае не имели бы решений, таких как x + 8 = 3. Однако у людей уже давно есть некоторое представление об отрицательных числах из-за таких явлений, как измерение уровня моря или долга. Обратите внимание, как математика редко представляет только одну модель реального мира. Ничто не мешает вам представить долг в 5 долларов, представив «5 долларов» красным текстом вместо черного или добавив рядом с ним слово «должен».

Представление понятия противоположности с помощью отрицательного знака позволяет представить все целые числа на числовой прямой, проходящей как слева, так и справа от нуля. Положительные целые числа представлены справа от 0, а отрицательные числа представлены слева от 0. Обратите внимание, что такие числа, как ^— 3 и ⁺ 3, равны напротив чисел.

Координатная плоскость

Координатный график — это визуальный метод отображения отношений между числами. Отношения показаны на координатная плоскость . Координатная плоскость имеет две перпендикулярные линии или оси (произносится как AK-seez), помеченные так же, как числовые линии. С расширением системы счисления для включения отрицательных чисел каждая ось может быть расширена в двух направлениях.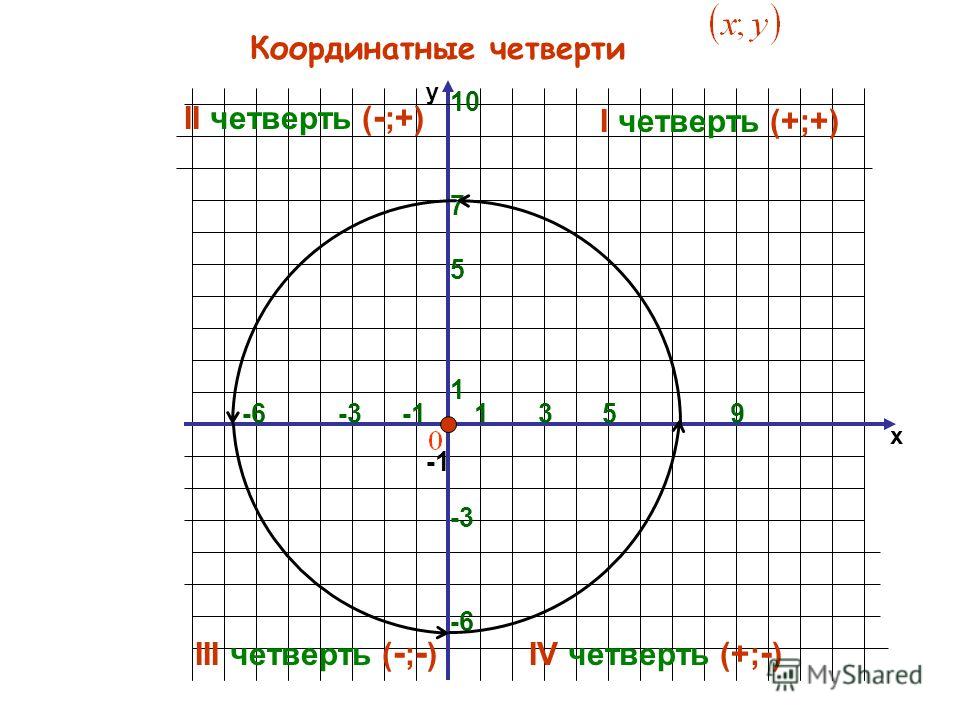 Горизонтальную ось обычно называют осью x . Вертикальную ось обычно называют осью и . Точка пересечения осей x и y называется началом координат.

Числа на координатной плоскости используются для определения местоположения точек. Каждая точка может быть идентифицирована заказанная пара номеров; то есть число на оси x называется координатой x , а число на оси y называется y -координатой . Упорядоченные пары записываются в скобках ( x -координата, y -координата). Начало находится в (0,0). Обратите внимание, что координаты часто записываются без пробела после запятой.

Расположение (3,2) показано на координатной плоскости ниже. x -координата равна 3. y -координата равна 2. Чтобы найти (3,2), переместитесь на 3 единицы вправо по оси x и на 2 единицы вверх по оси y .

Что такое квадранты на графике?

Оси координат делят плоскость на четыре области, называемые квадрантами (или иногда квадрантами сетки или декартовыми координатными квадрантами). Студенты часто спрашивают, как нумеруются квадранты? Обычная эвристика состоит в том, чтобы думать, что нумерация происходит в том же порядке, в котором мы пишем букву C. Квадранты координатной плоскости нумеруются I, II, III и IV, как показано на сетке ниже.

В 5 классе учащимся обычно не нужно знать систему нумерации, но они должны понимать, что соответствующие квадранты для упорядоченных пар можно определить по знакам чисел.

• Все точки в квадранте У меня две положительные координаты.
• Все точки в квадранте II имеют отрицательную координату x и положительную координату y .
• Все точки в квадранте III имеют две отрицательные координаты.
• Все точки в квадранте IV положительны x -координата и минус y -координата.

Существует множество возможностей для дискурса, сосредоточенного на всех квадрантах координатной плоскости. Предложите учащимся провести мозговой штурм, например, как кто-то, делающий анимацию или видеоигру, мог бы использовать это. Или покажите учащимся различные графики, взятые из разных занятий и книг, и попросите их поделиться тем, что они замечают и удивляются.

Координатная плоскость позволяет визуализировать и вычислять длину сегмента линии. Хотя учащиеся не учатся вычислять длину наклонных отрезков до тех пор, пока не изучат теорему Пифагора (обычно в 8 классе), четырехквадрантной плоскости достаточно, чтобы найти длину горизонтальных или вертикальных отрезков.

Для горизонтальных сегментов длина равна разнице между x -координатами конечных точек. Для вертикальных сегментов длина равна разнице между и -координатами конечных точек.

Функции

Примерно в 5 классе функции строятся в виде графиков из таблиц заданных значений. Все значения положительны, поэтому графики функций, изучаемые в этой главе, относятся только к квадранту I. Формальным определениям и расширенной работе с функциями обычно не учат, по крайней мере, до 8 класса.

Функция — это правило, которое связывает одно и только одно значение одной переменной с каждым значением другой переменной. Например, функция y = 2 x выражает y через x . Для каждого значения x существует одно и только одно значение y:

• Если x равно 3, то y равно 6.
• г это ^– 80.
• Если x равно 0, то y равно 0.

дать ровно одно значение y , тогда уравнение является функцией. Уравнение, которое можно записать Ax + By = C , где A , B и C — фиксированные числа, представляет собой линейное уравнение .

График линейного уравнения представляет собой прямую линию. Один из способов убедиться в этом — создать таблицу значений для x и y , а затем интерпретировать каждую строку таблицы как координаты x и y точек на координатной плоскости. Соединив точки, вы получите линию.

См., например, график y = x + 3.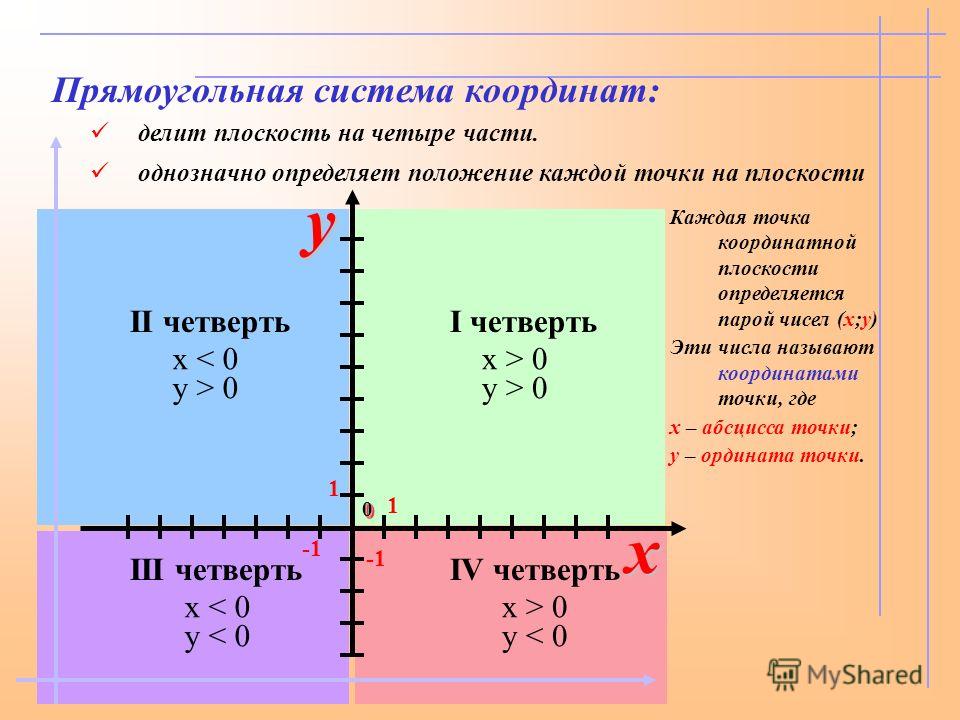 Отображение точек в приведенной таблице означает размещение точек в точках ( ^– 2,1), ( ^– 1,2), (0,3), (1,4) и (2,5). Затем соедините точки прямой линией.

***

Разблокируйте числа квадрантов на графике и многое другое для учащихся, у которых проблемы с математикой, с помощью Math 180 , нашего революционного подхода к математическому вмешательству для 5–12 классов.

Математика Мероприятия и уроки 6-8 классы

Дополнительная литература

• Алисса Фуллер
  Преподаватель по математике; Дизайнер учебного процесса, HMH

  20 октября 2022 г.

• Дженнифер Прескотт
  Фасонный Депонент

  07 октября 2022 г.

• Дженнифер Прескотт
  Форма Участник

  27 сентября 2022 г.

Математика Мероприятия и уроки 6–8 классы

Подпишитесь на нашу рассылку новостей

Будьте первыми, кто прочитает последние новости от Shaped .

Подписаться

4 квадранта графика: определение и примеры

Декартова плоскость (или плоскость x-y) представляет собой двухлинейный график, на котором вы наносите упорядоченные пары. Две пересекающиеся линии декартовой плоскости образуют четыре различных квадранта графа.

В этой статье мы обсудим, что такое квадранты графа, как манипулировать точками данных в квадрантах графа, а также рассмотрим некоторые примеры задач квадрантов графа.

  

Что такое 4 квадранта графика?

Две линии на декартовой плоскости образуют четыре квадранта графика. В этом разделе мы обсудим определение квадранта графа и определим каждую часть плоскости.

 

Определение квадранта

Квадрант — это одно из четырех сечений декартовой плоскости. Каждый квадрант содержит комбинацию положительных и отрицательных значений x и y.

 

4 квадранта графика

Декартову плоскость составляют четыре квадранта графика.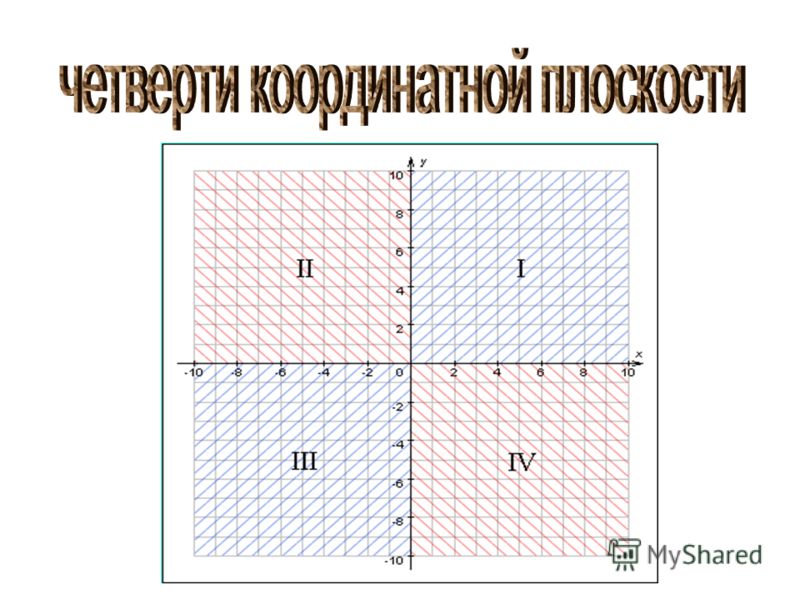 Каждый квадрант графика имеет четкую комбинацию положительных и отрицательных значений.

Вот квадранты графика и их значения:

Квадрант I: Первый квадрант находится в верхнем правом углу плоскости. И x, и y имеют положительные значения в этом квадранте.

Квадрант II: Второй квадрант находится в верхнем левом углу плоскости. X имеет отрицательные значения в этом квадранте, а y имеет положительные значения.

Квадрант III: Третий квадрант находится в нижнем левом углу. И x, и y имеют отрицательные значения в этом квадранте.

Квадрант IV: Четвертый квадрант находится в правом нижнем углу. X имеет положительные значения в этом квадранте, а y имеет отрицательные значения.

 

Диаграмма квадрантов графика

На этой диаграмме вы можете видеть четыре квадранта графика, а также то, являются ли x и y положительными или отрицательными.

 

Числа квадрантов графика, объяснение

Числа нанесены на квадранты графика так называемыми упорядоченными парами. Упорядоченная пара состоит из двух значений, x и y. В упорядоченной паре x всегда является первым значением, а y всегда вторым значением. Например, в упорядоченной паре (5, -2) 5 — это значение x, а -2 — это значение y.

При построении упорядоченной пары значение x относится к горизонтальному положению пары на графике. Значение y относится к вертикальному положению.

Посмотрите, как выглядит пара (5, -2) на графике.

 

Квадранты графа Примеры задач

Используя следующую диаграмму квадрантов, определите квадранты для следующих упорядоченных пар.

Заказная пара	Квадрант
(-9, 11)
(4, 8)
(-3, -4)

 

 

Примеры задач на квадранты графа: ответы

Найдите ответы на приведенные выше примеры задач на квадранты графа ниже.

Заказная пара	Квадрант
(-9, 11)	II
(4, 8)	я
(-3, -4)	III

 

 

Математические квадранты: основные выводы

Математический квадрант — это еще одна фраза для квадранта графика. Квадрант графа — это одно из четырех сечений на декартовой плоскости.

В каждом из четырех разделов есть определенная комбинация отрицательных и положительных значений x и y.

Вы наносите упорядоченную пару на квадранты графика. Упорядоченные пары имеют значения x и y . X — первое значение в упорядоченной паре; у второй.

 

Что дальше?

Хотите освежить в памяти другие основные математические навыки? Тогда ознакомьтесь с нашими экспертными руководствами о том, как складывать и вычитать дроби и как использовать формулу ускорения.