Умножение дробей с разными степенями: Свойства степеней, действия со степенями

Умножение дробей, формулы и примеры решений

Содержание:

• Умножение дроби на число
• Умножение дробей
• Умножение смешанных дробей

Умножение дроби на число

Умножение дроби $\frac{a}{b}$ на число $n$ равносильно сложению одинаковых слагаемых:

Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой дроби умножить на это число, а знаменатель оставить без изменения.

Пример

Задание. Найти произведение  $\frac{1}{3} \cdot 4$

Решение. Выполним умножение по описанному выше правилу

$\frac{1}{3} \cdot 4=\frac{1 \cdot 4}{3}=\frac{4}{3}=1 \frac{1}{3}$

Ответ.   $\frac{1}{3} \cdot 4=1 \frac{1}{3}$

Аналогично выполняется умножения числа на дробь.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение  3$\cdot \frac{1}{4}$

Решение. Выполним умножение по описанному выше правилу

$3 \cdot \frac{1}{4}=\frac{3 \cdot 1}{4}=\frac{3}{4}$

Ответ.   $3 \cdot \frac{1}{4}=\frac{3}{4}$

Умножение дробей

Определение

Произведением дробей называется такая дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель — произведению их знаменателей:

$\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}$

Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.

Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.

Пример

Задание. Найти произведение дробей  $\frac{1}{3}$  и  $\frac{4}{5}$ 

Решение. Выполним умножение дробей по описанному выше правилу

$\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}$

Ответ.   $\frac{1}{3} \cdot \frac{4}{5}=\frac{4}{15}$

Пример

Задание. Умножить  $\frac{13}{14}$  на  $\frac{14}{39}$ 

Решение. Необходимо найти произведение $\frac{13}{14} \cdot \frac{14}{39}$ . Как видим, числа 13 и 39 можно сократить на общее число 13. Для этого сами указанные величины зачеркиваем, а над ними пишем число, которое получается после деления. Аналогично поступает со знаменателем первой дроби и числителем второй:

Ответ.   $\frac{13}{14} \cdot \frac{14}{39}=\frac{1}{3}$

Умножение смешанных дробей

Чтобы перемножить смешанные дроби, нужно представить их в виде неправильных дробей, а затем уже выполнить умножение как обыкновенных дробей.

Пример

Задание. Найти произведение дробей 3$\frac{1}{3} \cdot 4 \frac{2}{5}$

Решение. Выполним умножение смешанных дробей по описанному выше правилу

$3 \frac{1}{3} \cdot 4 \frac{2}{5}=\frac{3 \cdot 3+1}{3} \cdot \frac{4 \cdot 5+2}{5}=\frac{10}{3} \cdot \frac{22}{5}=$

Ответ.   $3 \frac{1}{3} \cdot 4 \frac{2}{5}=14 \frac{2}{3}$

Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число, либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.

Пример

Задание. Умножить смешанную дробь 3$\frac{3}{4}$ на 2

Решение. Выполним умножение смешанной дроби на число по описанному выше правилу

Либо

$=(6+1)+\frac{1}{2}=7+\frac{1}{2}=7 \frac{1}{2}$

Ответ.   $3 \frac{3}{4} \cdot 2=7 \frac{1}{2}$

Читать следующую тему: деление дробей.

Как делить числа с разными степенями и основаниями?

Как делить числа с разными степенями и основаниями?

Как перемножить степени с разными основаниями в виде чисел?

1. Если надо умножить два числа с одинаковыми основаниями, но разными показателями степеней, то общее основание возводится в сумму степеней. …
2. Если основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.

Когда умножаются степени?

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

Как складывать числа с одинаковыми основаниями?

Как складывать числа с одинаковыми степенями Сначала возводим каждое число в степень и затем выполняем сложение. В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать.

Как умножить число на дробь в квадрате?

Чтобы возвести в квадрат дробь, нужно умножить ее на себя, то есть нужно умножить числитель на себя, а затем умножить знаменатель на себя. Например: (5/2)2 = 5/2 × 5/2 = (52/22).

Как возводить отрицательные дроби в степень?

Чтобы возвести число в отрицательную степень нужно:

1. «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
2. заменить отрицательную степень на положительную;
3. возвести число в положительную степень.

Как возвести в степень Алгебраическую?

Правило возведения алгебраической дроби в степень производится последовательно: сначала числитель , потом знаменатель. Когда в числителе и знаменателе имеется многочлен, тогда само задание сведется к возведению заданного многочлена в степень. После чего будет указана новая дробь, которая равна исходной.

Как умножить число на дробь в степени?

Умножение дробей. Возведение дробей в степень

1. Чтобы умножить дробь на дробь, надо просто перемножить их числители и знаменатели. …
2. Чтобы умножить дробь на целое число, надо целое число умножить на числитель. …
3. Чтобы возвести дробь в степень, надо возвести в эту степень и числитель, и знаменатель.

Как сократить число в степени?

Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а при делении степеней показатели вычитаем. a² и a⁷ сокращаем на a².

В каком случае нельзя сократить дробь?

Сокращать можно только множители. Слагаемые сокращать нельзя! Красным отмечены цифры, которые сокращаются в числителе и знаменателе. Как видите, в числителе стоит произведение, знаменателе — обыкновенное число.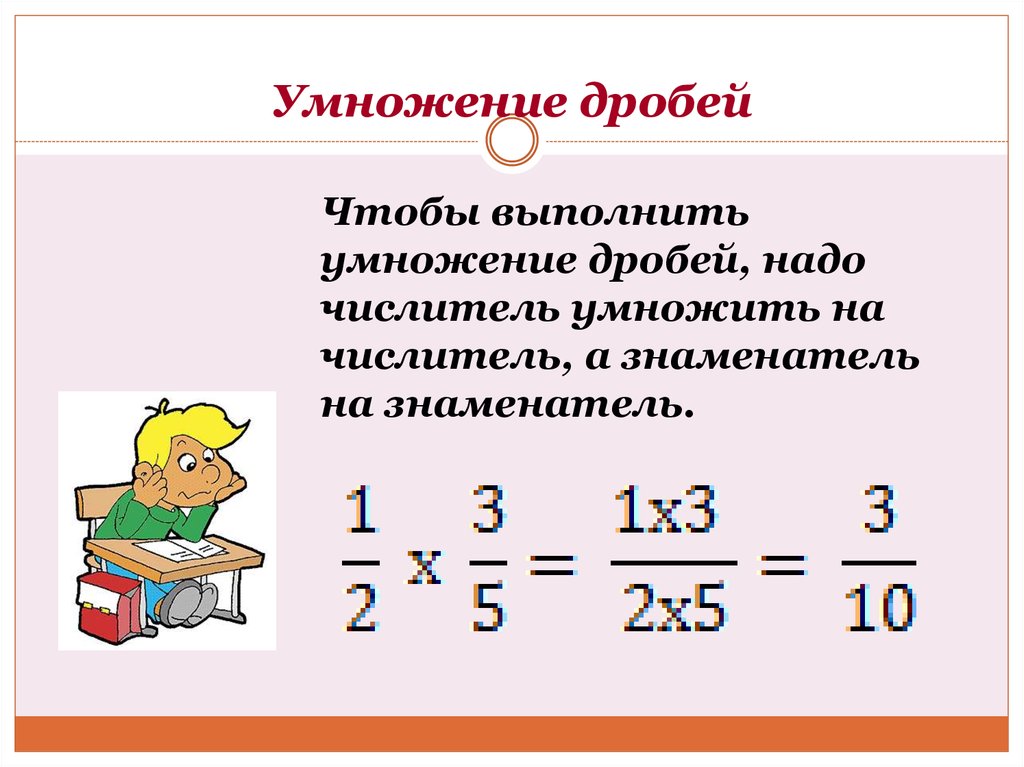

Как сократить дробь со степенями и буквами?

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель….Сокращение дробей с буквами и степенями проходит в три этапа:

1. Определите общий множитель.
2. Сократите коэффициенты.
3. Поделите все числители и все знаменатели на общий множитель.

Как упрощать дроби с буквами?

Сокращение дробей состоит в том, что числителя и знаменателя дроби делят на одно и то же число. и т. п. Итак, если в числителе и знаменателе имеются множителями различные степени одной и той же буквы, то можно сократить эту дробь на меньшую степень этой буквы.

3

Multiplying Exponents

Multiplying Negative Exponents

Multiplying Fractions with Exponents

Multiplying Terms with Fractional Exponents

Multiplying negative exponents

Simplify: 

When the bases то же самое добавьте показатели степени, помните свои правила числового знака!

Когда основания разные, нельзя объединять показатели степени. Оставьте условия! 911)

Стандарт Common Core: 8.EE.A.1

8 -й класс MATH

Page 1 Page 2 Page 3 Page 40003 .

Стр. 1 Стр. 2 Page 3 Page 4

Каковы правила для умножения экспоненты?

94 =  Вы не можете комбинировать из-за разных баз.

Умножение экспоненты, поднятые на Power

Как умножить экспоненты

Вы также можете насладиться ……

Exponents Exponents 0009000

.

9000 2.

9000 2.

9000 2.

9000

2.

9000 2.