6 реальных примеров нормального распределения
Редакция Кодкампа
читать 2 мин
Нормальное распределение является наиболее часто используемым распределением вероятностей во всей статистике.
Он имеет следующие свойства:
- колоколообразный
- Симметричный
- Унимодальный – имеет одну «вершину».
- Среднее и медиана равны; оба расположены в центре распределения
- Около 68% данных находятся в пределах одного стандартного отклонения от среднего
- Около 95% данных находятся в пределах двух стандартных отклонений от среднего
- Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.
В этом руководстве представлены 6 примеров реальных явлений, которые на самом деле следуют нормальному распределению.
Пример 1: Масса тела младенцев при рожденииХорошо задокументировано, что вес новорожденных при рождении обычно распределяется со средним значением около 7,5 фунтов.
Гистограмма массы тела при рождении новорожденных в США имеет колоколообразную форму, которая обычно имеет нормальное распределение:
Пример 2: Рост мужчинРаспределение роста мужчин в США примерно нормальное со средним значением 70 дюймов и стандартным отклонением 3 дюйма.
Гистограмма роста всех мужчин США имеет форму колокола:
Пример 3: Размеры обувиРаспределение размеров обуви для мужчин в США примерно нормальное распределение со средним размером 10 и стандартным отклонением 1.
Гистограмма размеров обуви всех мужчин США показывает форму колокола с одним пиком в размере 10:
Пример 4: баллы ACTРаспределение баллов ACT для старшеклассников в США обычно распределяется со средним значением 21 и стандартным отклонением около 5.
Гистограмма результатов ACT для всех учащихся средних школ США иллюстрирует это нормальное распределение:
Пример 5: Средний пенсионный возраст игроков НФЛРаспределение пенсионного возраста для игроков НФЛ обычно распределяется со средним значением 33 года и стандартным отклонением около 2 лет.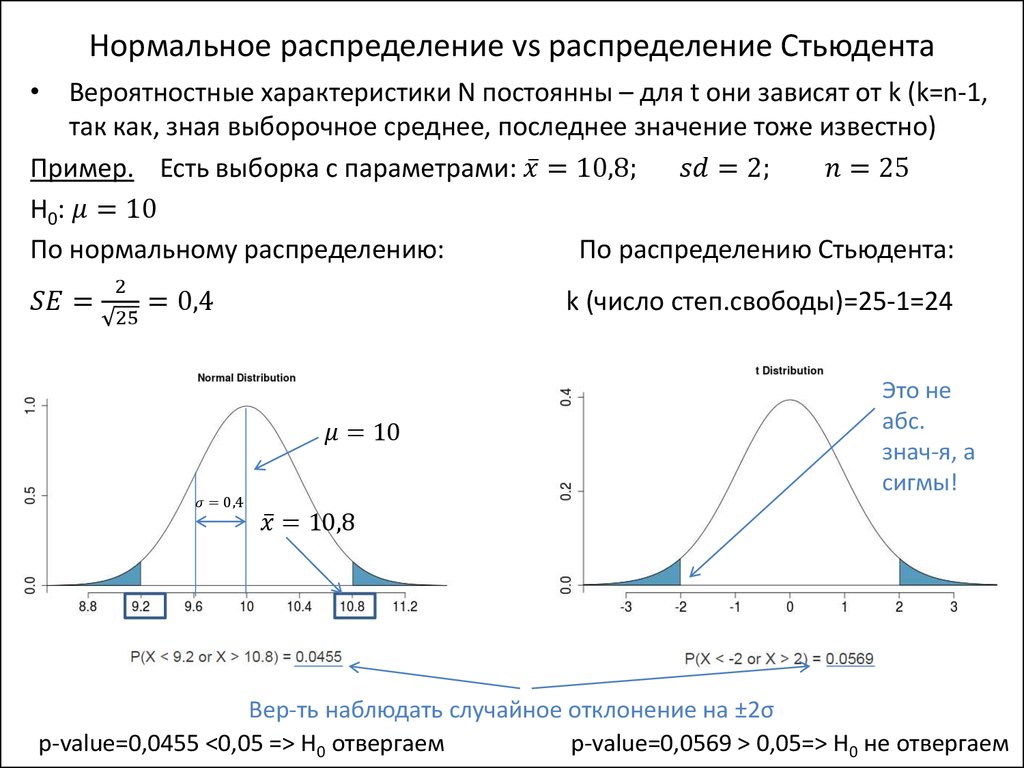
Гистограмма этого распределения имеет классический колоколообразный вид:
Пример 6: Артериальное давлениеРаспределение диастолического артериального давления у мужчин обычно распределяется со средним значением около 80 и стандартным отклонением 20.
Гистограмма распределения артериального давления для всех средних значений показывает нормальное распределение в форме колокола:
Дополнительные ресурсыВ следующих руководствах представлены примеры других распределений вероятностей в реальной жизни:
5 реальных примеров распределения Пуассона
5 реальных примеров биномиального распределения
5 реальных примеров геометрического распределения
5 реальных примеров равномерного распределения
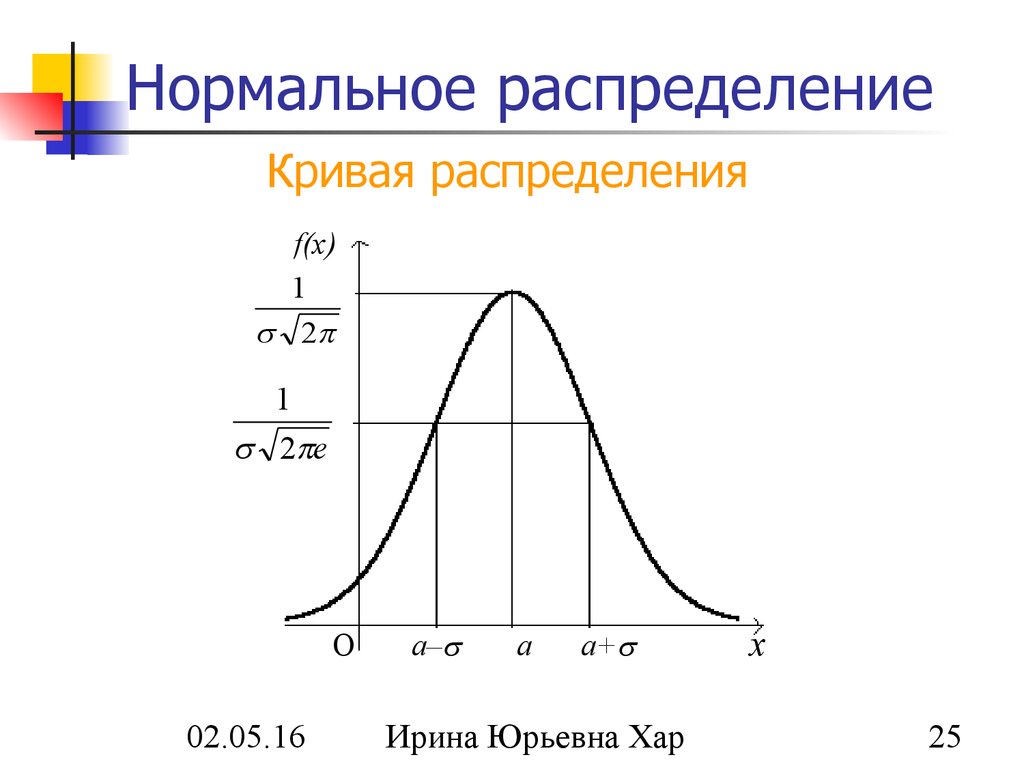
18.5.1. Нормальное распределение
Определение 2. Общим нормальным распределением вероятностей непрерывной случайной величины
Нормальное распределение задается двумя параметрами: А и σ. Согласно определениям математического ожидания и дисперсии (формулы (18.36) и (18.38)), после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы формулы
Согласно определениям математического ожидания и дисперсии (формулы (18.36) и (18.38)), после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы формулы
Определение 3. Нормальное распределение с параметрами А = 0 и σ = 1 называется Нормированным; его плотность равна
Рассмотрим функцию нормального распределения как первообразную плотности распределения вероятностей. Для случая нормированного нормального распределения (18.41) она, согласно формуле (18.34), имеет вид
Поскольку функция (18.41) является четной, то неопределенный интеграл от нее является нечетной функцией, и потому вместо функции распределения (18.42) используется функция Лапласа (см. п. 17.5)
Функции (18.41) и (18.43) табулированы (см. Приложение).
График плотности нормального распределения (18.40) для разных значений А показан на рис. 18.6.
Определение 4. Модой Мо(Х) называется возможное значение случайной величины X, при котором плотность распределения имеет максимум.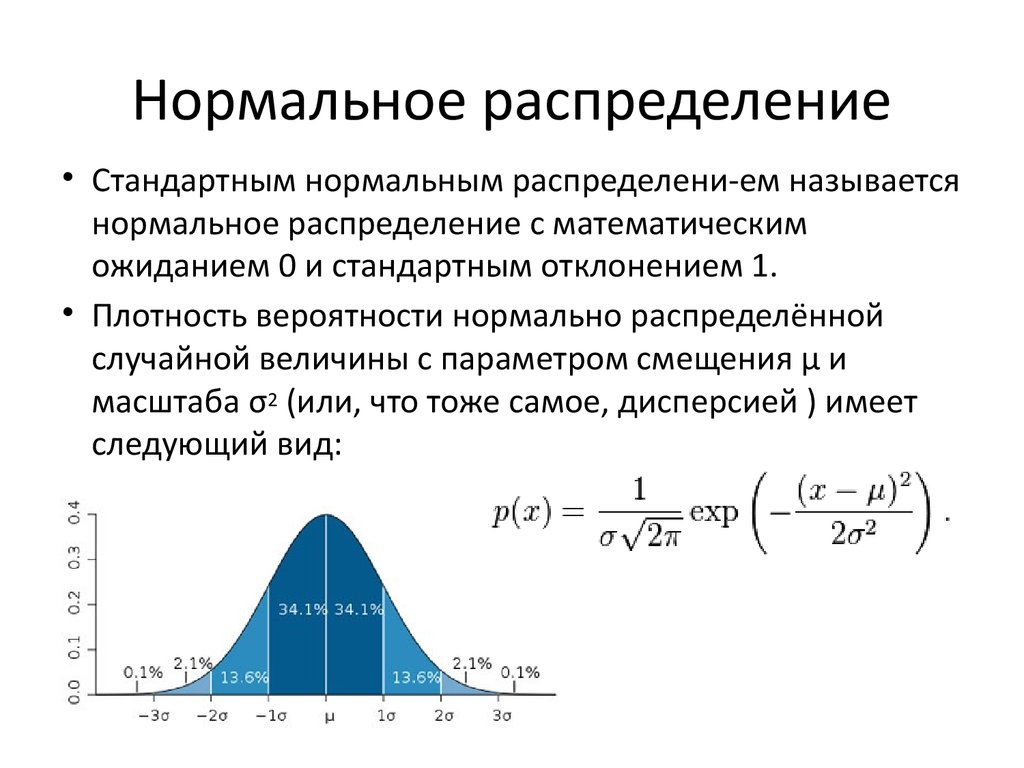
Определение 5. Медианой Ме(Х) называется такое возможное значение случайной величины X, что вертикальная прямая Х = Me(X) делит пополам площадь, ограниченную кривой плотности распределения.
Нетрудно видеть, что график плотности нормального распределения симметричен относительно прямой Х = а, и потому и мода и медиана в данном случае совпадают с математическим ожиданием:
Пусть случайная величина
Преобразование этой формулы путем введения новой переменной интегрирования Z = (х — А)/σ приводит к удобной вычислительной формуле:
Где Ф — функция Лапласа, определенная по формуле (18.43).
Пример 3. Случайная величина распределена по нормальному закону с математическим ожиданием и средним квадратическим отклонением, соответственно равными 10 и 5.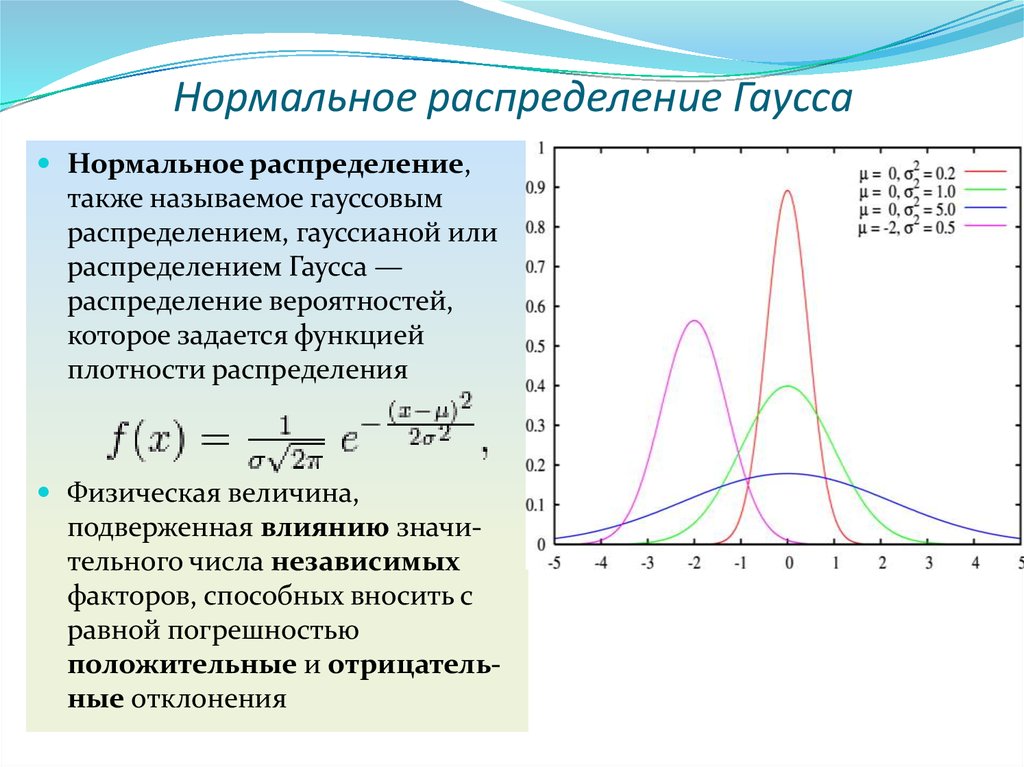 Найти вероятность того, что Х примет значение на интервале (20, 30).
Найти вероятность того, что Х примет значение на интервале (20, 30).
Решение. Воспользуемся формулой (18.44). По условию А = 10, σ = 5, α = 20 и β = 30. Следовательно,
По табл. 2 Приложения находим соответствующие значения функции Лапласа и окончательно получаем
Пример 4. Магазин производит продажу мужских костюмов. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равными 48 и 2. Определить процент спроса на 50-й размер при условии разброса значений этой величины в интервале (49, 51).
Решение. По условию задачи А = 48, σ = 2, α = 49, β = 51. Используя формулу (18.44), получаем, что вероятность спроса на 50-й размер в заданном интервале равна
Следовательно, спрос на 50-й размер костюмов составит около 24%, и магазину нужно предусмотреть это в общем объеме закупки.
| < Предыдущая | Следующая > |
|---|
9 реальных примеров нормального распределения – StudiousGuy
Нормальное распределение широко используется для понимания распределения факторов в популяции. Поскольку нормальное распределение так хорошо аппроксимирует многие природные явления, оно превратилось в эталон для многих проблем вероятности.
Поскольку нормальное распределение так хорошо аппроксимирует многие природные явления, оно превратилось в эталон для многих проблем вероятности.
Нормальное/гауссово распределение представляет собой колоколообразный график, который включает два основных термина – среднее значение и стандартное отклонение. Это симметричное расположение набора данных, в котором большинство значений группируются в среднем, а остальные симметрично сужаются к любому из крайних значений. На этот признак влияют многочисленные генетические факторы и факторы окружающей среды.
Центральная предельная теорема
Нормальное распределение следует теории центрального предела, согласно которой на конкретный признак влияют различные независимые факторы. Когда все эти независимые факторы вносят свой вклад в явление, их нормализованная сумма имеет тенденцию давать распределение Гаусса.
Нормальная кривая Среднее значение распределения определяет положение центра графика, а стандартное отклонение определяет высоту и ширину графика, а общая площадь под нормальной кривой равна 1.
Давайте разберемся с примерами нормального распределения из повседневной жизни.
1. ВысотаРост населения является примером нормального распределения. Большинство людей в конкретной популяции имеют средний рост. Количество людей выше и ниже людей среднего роста почти одинаково, и очень небольшое количество людей либо очень высокие, либо очень низкие. Однако рост не является единственной характеристикой, на рост влияют несколько генетических факторов и факторов окружающей среды. Следовательно, он следует нормальному распределению.
2. Бросание игральной кости Правильный бросок игральной кости также является хорошим примером нормального распределения. В ходе эксперимента было установлено, что при броске игральной кости 100 раз шансы выпадения «1» составляют 15-18%, а если мы бросаем кости 1000 раз, то шансы выпадения «1» опять же одинаковы. , что в среднем составляет 16,7% (1/6). Если мы бросим два кубика одновременно, то получится 36 возможных комбинаций. Вероятность выпадения «1» (с шестью возможными комбинациями) снова в среднем составляет около 16,7%, то есть (6/36). Чем больше число игральных костей, тем более сложным будет график нормального распределения.
Вероятность выпадения «1» (с шестью возможными комбинациями) снова в среднем составляет около 16,7%, то есть (6/36). Чем больше число игральных костей, тем более сложным будет график нормального распределения.
Подбрасывание монеты — один из старейших способов разрешения споров. Все мы подбрасывали монетку перед матчем или игрой. Воспринимаемая справедливость подбрасывания монеты заключается в том, что она имеет равные шансы получить любой результат. Шансы выпадения решки равны 1/2, то же самое и с решкой. Когда мы складываем оба, это равно единице. Если мы будем подбрасывать монеты несколько раз, сумма вероятностей выпадения орла и решки всегда будет равна 1,9.0003
4. IQ В этом сценарии растущей конкуренции большинство родителей, как и детей, хотят проанализировать уровень интеллекта. Что ж, IQ определенного населения — это кривая нормального распределения; где IQ большинства людей в популяции находится в пределах нормы, тогда как IQ остального населения находится в отклоненном диапазоне.
Большинство из нас слышали о росте и падении цен на акции на фондовом рынке.
наши родители или в новостях о падении и росте цен на акции. Эти изменения в логарифмических значениях курсов Forex, индексов цен и доходности цен на акции часто образуют колоколообразную кривую. Для доходности акций стандартное отклонение часто называют волатильностью. Если доходность распределяется нормально, ожидается, что более 99 процентов доходности попадут в пределы отклонений от среднего значения. Такие характеристики нормального распределения в форме колокола позволяют аналитикам и инвесторам делать статистические выводы об ожидаемой доходности и риске акций.
6. Распределение доходов в экономике Доход страны находится в руках прочной политики и правительства. От них зависит, как они распределят доход между богатыми и бедными. Все мы прекрасно понимаем тот факт, что население среднего класса немного выше, чем богатое и бедное население. Таким образом, заработная плата населения среднего класса составляет среднее значение кривой нормального распределения.
Таким образом, заработная плата населения среднего класса составляет среднее значение кривой нормального распределения.
Задумывались ли вы, что было бы, если бы стеклянная туфелька, оставленная Золушкой в доме принца, подошла другой женщине? В конце концов он женился бы на другой женщине. Это было одно из забавных предположений, с которыми мы все когда-либо сталкивались. Согласно данным, собранным в США, продажи женской обуви по размеру обычно распределяются, потому что физические данные большинства женщин почти одинаковы.
8. Вес при рожденииНормальная масса тела новорожденного при рождении колеблется от 2,5 до 3,5 кг. Большинство новорожденных имеют нормальный вес при рождении, тогда как лишь у небольшого процента новорожденных вес выше или ниже нормального. Следовательно, вес при рождении также соответствует кривой нормального распределения.
9. Средний балл учащегося
Средний балл учащегося В настоящее время школы рекламируют свои выступления в социальных сетях и на телевидении. Они представляют средний результат своей школы и уговаривают родителей отдать ребенка в эту школу. Школьные власти определяют среднюю успеваемость всех учащихся, и в большинстве случаев она соответствует кривой нормального распределения. Количество среднего умного студента выше, чем у большинства других студентов.
Нормальное распределение — определение, формула, примеры и характеристики
Нормальное распределение или распределение Гаусса относится к распределению вероятностей, при котором значения случайной величины распределены симметрично. Эти значения одинаково распределены слева и справа от центральной тенденции. Таким образом, формируется колоколообразная кривая.
Кроме того, максимальное количество значений близко к среднему; хвост состоит всего из нескольких значений. Эмпирическое правилоЭмпирическое правилоЭмпирическое правило в статистике утверждает, что почти все (95%) наблюдений в нормальном распределении лежат в пределах 3 стандартных отклонений от среднего. К таким функциям вероятности относится и многое другое. Следовательно, 68% значений лежат в пределах одного диапазона стандартных отклонений. 95% наблюдений находятся в пределах двух стандартных отклонений, а 99,7% значений находятся в пределах трех стандартных отклонений.
К таким функциям вероятности относится и многое другое. Следовательно, 68% значений лежат в пределах одного диапазона стандартных отклонений. 95% наблюдений находятся в пределах двух стандартных отклонений, а 99,7% значений находятся в пределах трех стандартных отклонений.
Содержание
- Что такое нормальное распределение в статистике?
- Нормальное распределение Объяснение
- Характеристики нормального распределения
- Normal Distribution Curve
- Normal Distribution Formula
- Examples
- Example #1
- Example #2
- Uses
- Frequently Asked Questions (FAQs)
- Recommended Articles
- A normal distribution is статистическое явление, представляющее собой симметричную колоколообразную кривую. Большинство значений расположены вблизи среднего значения; также лишь немногие появляются на левом и правом хвостах.
- Следует эмпирическому правилу или правилу 68-9правило 5-99,7.

- Здесь среднее значение, медиана и мода равны; среднее значение и стандартное отклонение функции равны 0 и 1 соответственно.
- Эта математическая функция имеет два ключевых параметра:
Среднее значение (µ) и стандартное отклонение (σ).
Нормальное распределение Объяснение
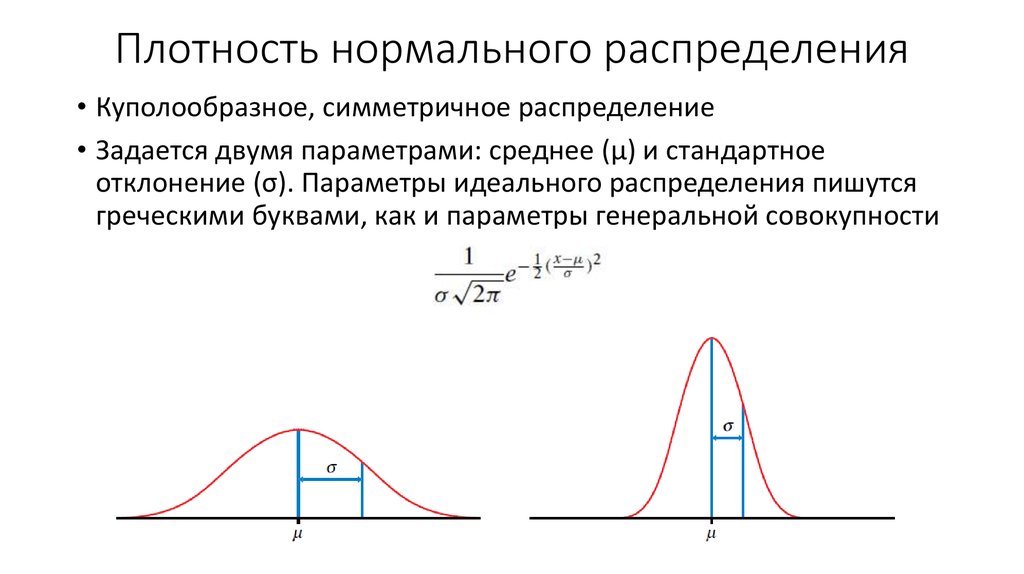
Нормальное распределение напоминает асимметричное расположение большинства значений вокруг среднего, так что построенная таким образом кривая выглядит как колокол. Он имеет два ключевых параметра: среднее значение (µ) и стандартное отклонение (σ). Этот вероятностный метод играет решающую роль в расчете доходности активов и принятии решений по стратегии управления рисками. На следующем рисунке показано, что функция статистической вероятности представляет собой колоколообразную кривую. Он получил свое название из-за формы графика, напоминающего колокол. читать далее, что следует эмпирическому правилу:
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т.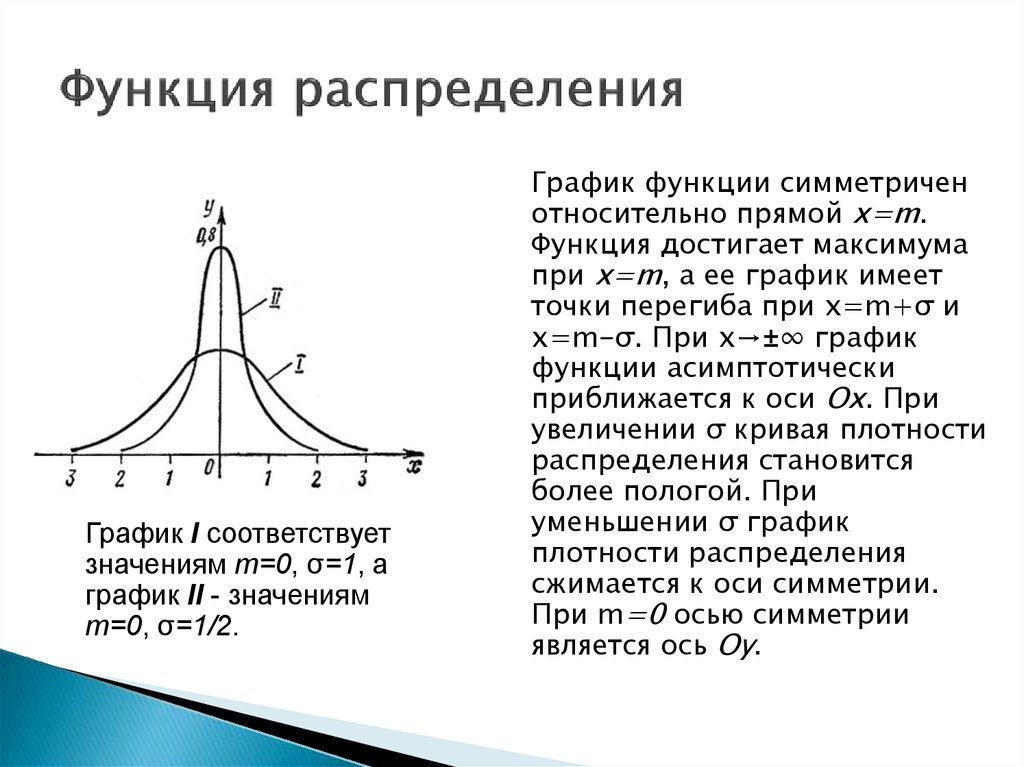 д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?
д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?
Возможные результаты функции представлены целыми действительными числами, лежащими в диапазоне от -∞ до +∞. Хвосты колоколообразной кривой простираются по обеим сторонам графика (+/-) без ограничений.
- Приблизительно 68% всех наблюдений попадают в пределы +/- одного стандартного отклонения (σ).
- Около 95% всех наблюдений находятся в пределах +/- двух стандартных отклонений (σ).
- Почти 99,7% всех наблюдений находятся в пределах +/- трех стандартных отклонений (σ).
Асимметрия относится к симметрии. Если skewnessSkewnessSkewness — это отклонение или степень асимметрии, показанная кривой нормального распределения в заданном наборе данных. Если кривая смещается вправо, это считается положительной асимметрией, а кривая, сдвинутая влево, представляет собой отрицательную асимметрию. Читать далее 0, данные идеально симметричны. Если нормальное распределение неравномерно с асимметрией больше нуля или положительной асимметрией, то его правый хвост будет более длинным, чем левый. Аналогично, для отрицательной асимметрииОтрицательная асимметрияОтрицательно асимметричное распределение — это распределение, в котором хвост распределения длиннее с левой стороны, а больше значений нанесено на правую сторону графика. Из-за отрицательного распределения данных среднее значение ниже медианы и моды. Читать далее, левый хвост будет длиннее правого. Отрицательная асимметрия означает, что асимметрия меньше нуля.
Аналогично, для отрицательной асимметрииОтрицательная асимметрияОтрицательно асимметричное распределение — это распределение, в котором хвост распределения длиннее с левой стороны, а больше значений нанесено на правую сторону графика. Из-за отрицательного распределения данных среднее значение ниже медианы и моды. Читать далее, левый хвост будет длиннее правого. Отрицательная асимметрия означает, что асимметрия меньше нуля.
KurtosisKurtosisKurtosis в статистике используется для описания распределения набора данных и показывает, в какой степени точки набора данных определенного распределения отличаются от данных нормального распределения. Он определяет, являются ли данные тяжелыми или легкими хвостами. Подробнее — это мера пиковости. Если эксцесс равен 3, данные о вероятности не являются ни слишком острыми, ни слишком тонкими на концах. Если эксцесс больше трех, то кривая данных усиливается с более толстыми хвостами. В качестве альтернативы, если эксцесс меньше трех, то представленные данные имеют тонкие хвосты с пиковой точкой ниже нормального распределения. Для нормального распределения эксцесс равен 3,9.0003
Для нормального распределения эксцесс равен 3,9.0003
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?
Характеристики нормального распределения
Нормальное распределение имеет следующие характеристики, которые отличают его от других форм представления вероятностей:
- Эмпирическое правило : В нормальном распределении 68% наблюдений ограничены -/+ одним стандартом отклонение, 95% значений находятся в пределах -/+ двух стандартных отклонений, и почти 99,7% значений находятся в пределах -/+ трех стандартных отклонений.
- Колоколообразная кривая : Большинство значений лежат в центре, а меньшее количество значений лежит на концах хвоста. В результате получается колоколообразная кривая.
- Среднее значение и стандартное отклонение : Это представление данных сформировано средним значением и стандартным отклонением.

- Равные центральные тенденции : Среднее значение, медиана и мода этих данных равны.
- Симметричный : Кривая нормального распределения центрально-симметричная. Таким образом, половина значений находится слева от центра, а остальные значения отображаются справа.
- Асимметрия и эксцесс : Асимметрия — это симметрия. Асимметрия для нормального распределения равна нулю. Куртосис изучает хвост представленных данных. Для нормального распределения эксцесс равен 3.
- Общая площадь = 1 : Общее значение стандартного отклонения, т. е. полная площадь кривой для этой функции вероятности, равна единице. Кроме того, все среднее равно нулю.
Кривая нормального распределения
Кривая принимает форму колокола из-за симметричного расположения значений, сконцентрированных по направлению к центральной тенденции. Центральная тенденция. найдите его, используя 3 различных показателя, т.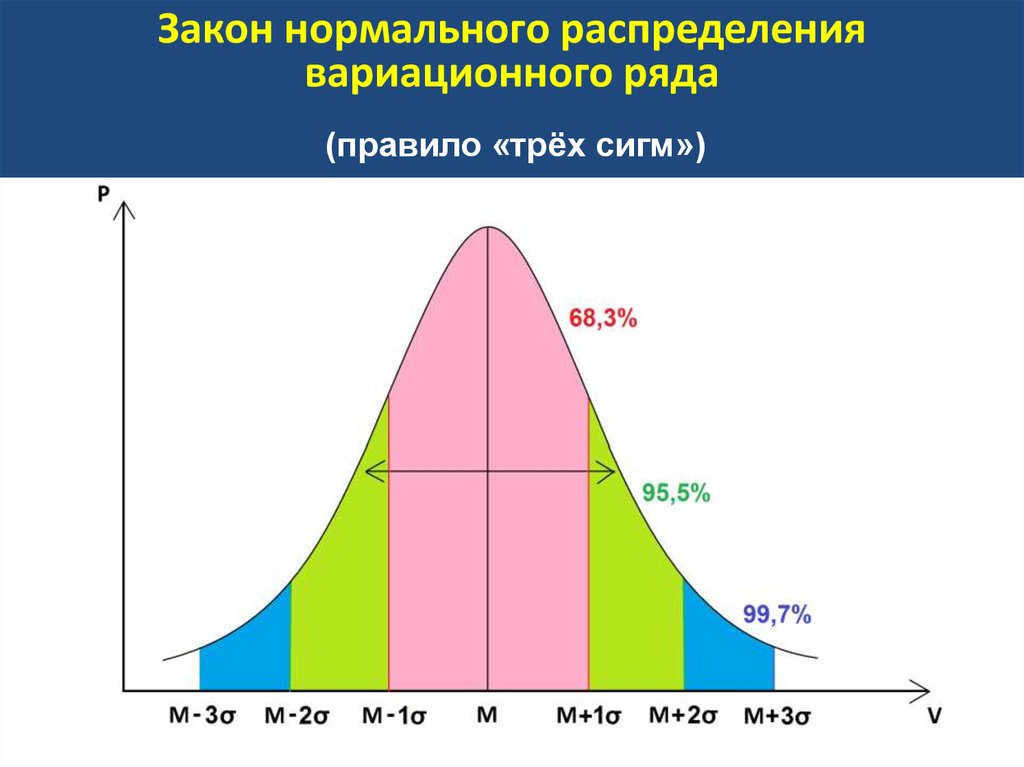 е. среднее значение, медиану и моду. Подробнее. При этом хвост состоит из незначительного количества значений.
е. среднее значение, медиану и моду. Подробнее. При этом хвост состоит из незначительного количества значений.
Посмотрите на кривую ниже, чтобы лучше понять ее форму:
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?
Формула нормального распределения
Функция плотности вероятности (PDF) случайной величины (X) определяется как:
Где;
- -∞ < х < ∞; -∞ < µ < ∞; σ > 0
- F(x) = функция нормальной вероятности
- x = Случайная переменная
- µ = среднее распределение
- σ = стандартное отклонение
- из распределения
- π = 3,14159
- E = 2,71828
- E = 2,71828
- 777777777777777777777777777.
- E = 2,71828
- 7777777777777.
- e = 2,71828
- e = 2,71828 . при сравнительном исследовании двух и более выборок возникает необходимость перевода их значений в z-показатели.
- Среднее (µ) = 60 000 долл. США
- Стандартное отклонение (σ) = 15000 долл. США
- Случайная переменная (x) = 45000 долл. США
 Это называется z-преобразованием.
Это называется z-преобразованием.Формула преобразования
Для определения z-показателя используется следующая формула:
Где X = Случайная величина.
Таблица нормального распределения
Таблица, на которую ссылаются для стандартного отклонения, представляет собой z-таблицу. Здесь мы определяем вероятность получения определенного результата, используя формулу преобразования, чтобы установить значение z-показателя, которое отображается в процентах с использованием z-таблицы.
Примеры
Пример #1
Предположим, что в компании 10000 сотрудников и несколько структур заработной платы в соответствии с конкретными должностными обязанностями. Заработная плата, как правило, распределяется со средним значением населения. Среднее значение населения. Среднее значение населения является средним или средним значением всех значений в данном населении и рассчитывается как сумма всех значений в населении, обозначаемая суммой X, деленная на количество значений в населении, которое обозначается N. Подробнее о µ = 60 000 долларов США, а стандартное отклонение населения σ = 15 000 долларов США. Какова вероятность того, что случайно выбранный сотрудник заработает менее 45000 долларов в год?
Подробнее о µ = 60 000 долларов США, а стандартное отклонение населения σ = 15 000 долларов США. Какова вероятность того, что случайно выбранный сотрудник заработает менее 45000 долларов в год?
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Обычное распространение (wallstreetmojo.com)
Решение :
Как показано на рисунке выше, нам нужно найти площадь под кривой нормали от 45 до левой хвостовой части, чтобы ответить на этот вопрос. Кроме того, нам нужно использовать значение z-таблицы, чтобы получить правильный ответ.
Во-первых, нам нужно преобразовать данное среднее значение и стандартное отклонение. ), таким образом, интерпретируя надежность данных в виде стандартного нормального распределения со средним значением (µ) = 0 и стандартным отклонением (σ) = 1 с использованием формулы преобразования.
После преобразования нам нужно просмотреть z-таблицу, чтобы узнать соответствующее значение, которое даст нам правильный ответ.
, дано,
Трансформация (Z) = (45000–60000 / 150137
(Z) = (45000–60000 / 15000)
(Z) = (45000–60000 / 15000)
(Z) = (45000–60000 / 15000)
(Z) = (45000–60000 / 15013
(Z) = (45000–60000 / 15000)
. z) = -1
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: нормальное распространение ( www.wallstreetmojo.com)
Значение, эквивалентное -1 в z-таблице, составляет 0,1587, представляющее площадь под кривой от 45 влево. Таким образом, это показало, что при случайном выборе сотрудника вероятность заработать менее 45000 долларов в год составляет 15,87%.
Таким образом, это показало, что при случайном выборе сотрудника вероятность заработать менее 45000 долларов в год составляет 15,87%.
Важно отметить, что мы преобразовали значение z-показателя 0,1587 в процентное значение, умножив его на 100, чтобы получить 15,87%.
Пример #2
Теперь для описанного выше сценария найдите вероятность того, что случайно выбранный сотрудник заработает более 85 000 долларов в год.
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Обычное распространение (wallstreetmojo.com)
Решение :
Итак, в этом вопросе нам нужно найти заштрихованную область от 85 до правого хвоста, используя ту же формулу.
Дано:
- Среднее значение (µ) = 60 000 долл. США
- Стандартное отклонение (σ) = 15 000 долл.
 США
США - Случайная величина (X) = 85 000 долларов США
Преобразование (z) = (85000 – 60000/15000)
Преобразование (z) = 1,67 %, что показывает, что вероятность случайного выбора работника с доходом менее 85 000 долларов в год составляет 95,25 %.
Но согласно вопросу нам нужно определить вероятность того, что случайные сотрудники заработают более 85 000 долларов в год, поэтому нам нужно вычесть вычисленное значение из 100.
- Случайная величина (X) = 100 % – 95,25 %
- Случайная величина (X) = 4,75 %
Таким образом, вероятность того, что сотрудники зарабатывают более 85 000 долларов в год, составляет 4,75 %.
Использование
Эта математическая функция применяется в различных областях науки, будь то наука, экономикаЭкономикаЭкономика — это область социальных наук, изучающая производство, распределение и потребление ограниченных ресурсов в обществе. наука, стоящая за выявлением, сбором, организацией и обобщением, анализом, интерпретацией и, наконец, представлением таких данных, как качественных, так и количественных, что помогает принимать более правильные и эффективные решения с уместностью.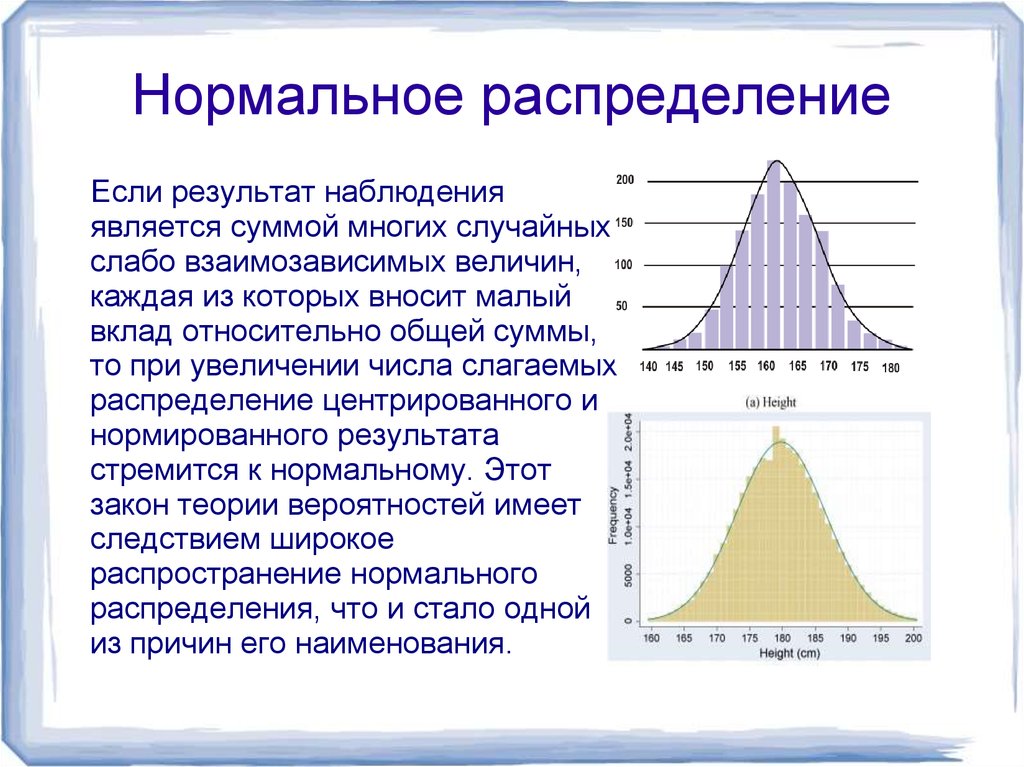 подробнее, финансы, бизнес, инвестиции, психология, здоровье, генетика , биотехнологии или ученых. Некоторые из его типичных применений обсуждаются ниже:
подробнее, финансы, бизнес, инвестиции, психология, здоровье, генетика , биотехнологии или ученых. Некоторые из его типичных применений обсуждаются ниже:
- Технический график фондового рынка часто представляет собой кривую нормального распределения, позволяющую аналитикам и инвесторам делать статистические выводы об ожидаемой доходности и риске акций.
- Он используется для определения наилучшего времени для доставки пиццы и других подобных приложений в реальной жизни.
- Он также применяется в бизнес-операциях. Деловые операции. Деловые операции относятся ко всем тем действиям, которые сотрудники ежедневно выполняют в рамках организационной структуры для производства товаров и услуг для достижения целей компании, таких как получение прибыли. Узнайте больше, чтобы определить эффективность продуктов, ресурсов, и продаж.
- Он используется для сравнения роста данной группы населения, в которой большинство людей имеют средний рост. Очень немногие люди будут иметь рост выше среднего или ниже среднего.

- Используются при определении средней успеваемости учащихся. Эта математическая функция используется при определении ранга студента.
Функция Гаусса обычно используется в науке о данных и анализе данных. Передовые технологии, такие как искусственный интеллект (ИИ) и машинное обучение, могут давать лучшие результаты при использовании вместе с функциями нормальной плотности.
Часто задаваемые вопросы (FAQ)
Почему нормальное распределение важно?
Эта функция Гаусса является одной из самых популярных функций плотности вероятности. Это связано с тем, что он эффективно обеспечивает близкие результаты или вероятность природных явлений. Таким образом, он повсеместно применяется во многих областях, таких как экономика, финансы, инвестиции, психология, наука, здравоохранение, бизнес и экономика.
Что делать, если данные не распределены нормально?
Можно проверить наличие ошибок ввода данных, ошибок измерения и выбросов в случае асимметричного или ненормального распределения.



 США
США