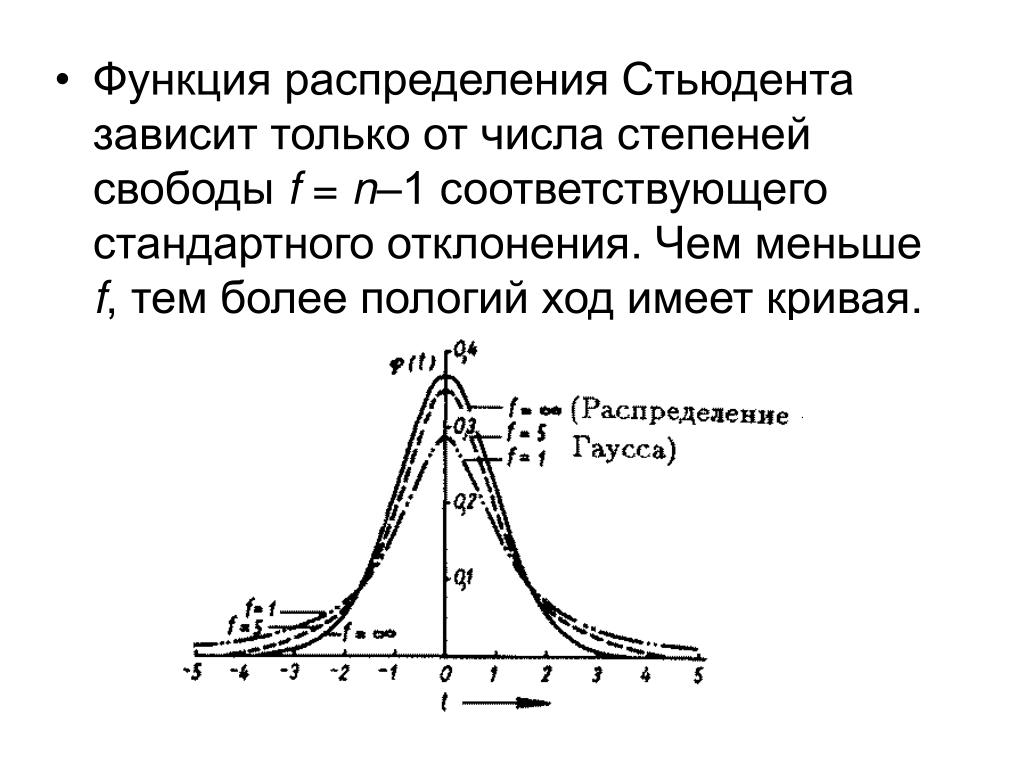
Распределение Стьюдента (t — распределение)
Распределение Стьюдента (t — распределение)Из курса А.А.Авдеева, читавшегося в Страсбургском университете в 2003-2005 годах (перевод на русский и адаптация к традиции русской терминологии еще не закончены)
|
|
||||||||||||
|
[Теоретические пояснения] [Распределение t]
Распределение Стьюдента по сути
представляет собой сумму нескольких нормально распределенных случайных величин. Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное
распределение. Таким образом, количество суммруемых величин определяет важнейший
параметр формы данного распредения — число степеней свободы (DL).
График слева показывает, как меняется форма распределения при
увеличение количества степеней свободы (DL).
Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное
распределение. Таким образом, количество суммруемых величин определяет важнейший
параметр формы данного распредения — число степеней свободы (DL).
График слева показывает, как меняется форма распределения при
увеличение количества степеней свободы (DL).
Распределение t
Первая лини таблицы содержит значение верятности получить значение вышего того, что находится в ячейке, соответствующей определенному числу степеней свободы. Критическое значение, соответствующее вероятности 0,05 распределения t с 6 степенями свободы, находится на пересечении колоники 0,05 и линии 6: t(.05,6) = 1,943180.
| df\p | 0. |
0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0005 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.324920 | 1.000000 | 3.077684 | 6.313752 | 12.70620 | 31.82052 | 63.65674 | 636.6192 |
| 2 | 0.288675 | 0.816497 | 1.885618 | 2.919986 | 4.30265 | 6.96456 | 9.92484 | 31.5991 |
| 3 | 0.276671 | 0.764892 | 1.637744 | 2.353363 | 3.18245 | 4.54070 | 5.84091 | 12.9240 |
| 4 | 0.270722 | 0.740697 | 1.533206 | 2.131847 | 2. 77645 77645 |
3.74695 | 4.60409 | 8.6103 |
| 5 | 0.267181 | 0.726687 | 1.475884 | 2.015048 | 2.57058 | 3.36493 | 4.03214 | 6.8688 |
| 6 | 0.264835 | 0.717558 | 1.439756 | 1.943180 | 2.44691 | 3.14267 | 3.70743 | 5.9588 |
| 7 | 0.263167 | 0.711142 | 1.414924 | 1.894579 | 2.36462 | 2.99795 | 3.49948 | 5.4079 |
| 8 | 0.261921 | 0.706387 | 1.396815 | 1.859548 | 2.30600 | 2.89646 | 3.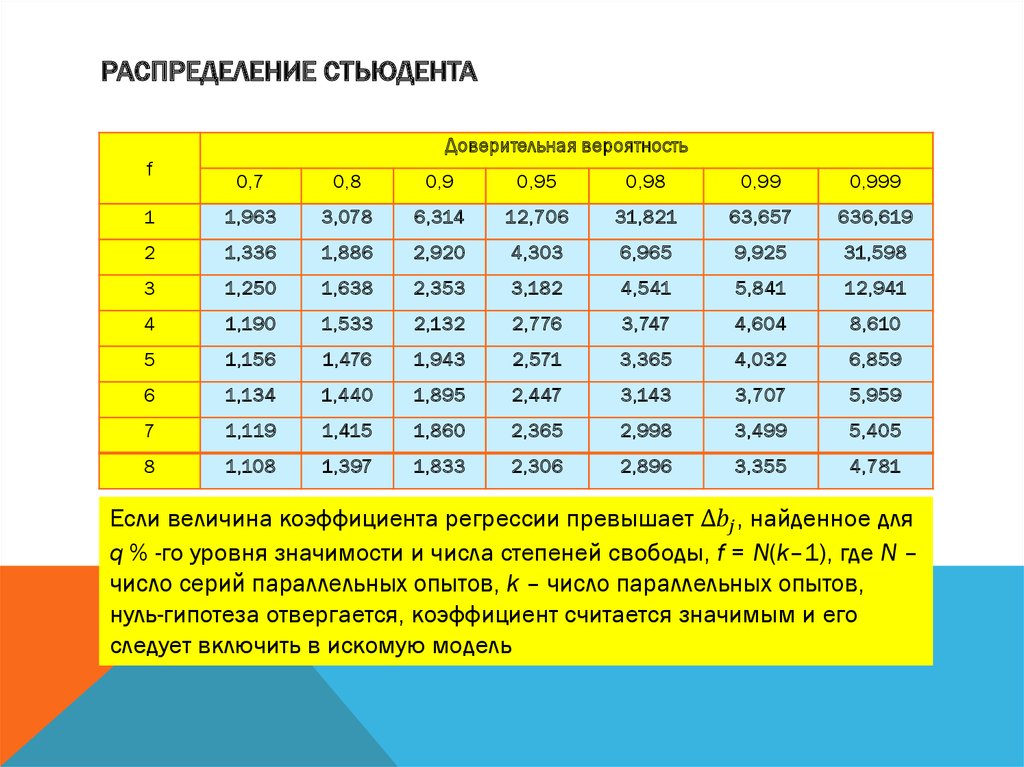 35539 35539 |
5.0413 |
| 9 | 0.260955 | 0.702722 | 1.383029 | 1.833113 | 2.26216 | 2.82144 | 3.24984 | 4.7809 |
| 10 | 0.260185 | 0.699812 | 1.372184 | 1.812461 | 2.22814 | 2.76377 | 3.16927 | 4.5869 |
| 11 | 0.259556 | 0.697445 | 1.363430 | 1.795885 | 2.20099 | 2.71808 | 3.10581 | 4.4370 |
| 12 | 0.259033 | 0.695483 | 1.356217 | 1.782288 | 2.17881 | 2.68100 | 3.05454 | 4.3178 |
| 13 | 0. 258591 258591 |
0.693829 | 1.350171 | 1.770933 | 2.16037 | 2.65031 | 3.01228 | 4.2208 |
| 14 | 0.258213 | 0.692417 | 1.345030 | 1.761310 | 2.14479 | 2.62449 | 2.97684 | 4.1405 |
| 15 | 0.257885 | 0.691197 | 1.340606 | 1.753050 | 2.13145 | 2.60248 | 2.94671 | 4.0728 |
| 16 | 0.257599 | 0.690132 | 1.336757 | 1.745884 | 2.11991 | 2.58349 | 2.92078 | 4.0150 |
| 17 | 0.257347 | 0.689195 | 1.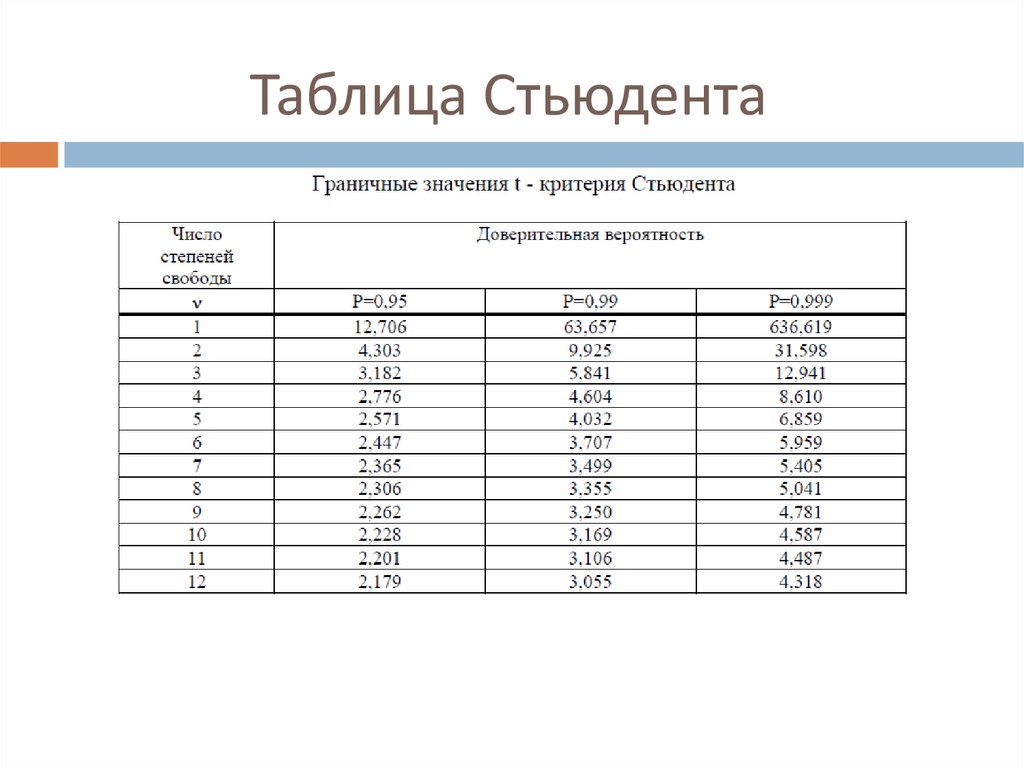 333379 333379 |
1.739607 | 2.10982 | 2.56693 | 2.89823 | 3.9651 |
| 18 | 0.257123 | 0.688364 | 1.330391 | 1.734064 | 2.10092 | 2.55238 | 2.87844 | 3.9216 |
| 19 | 0.256923 | 0.687621 | 1.327728 | 1.729133 | 2.09302 | 2.53948 | 2.86093 | 3.8834 |
| 20 | 0.256743 | 0.686954 | 1.325341 | 1.724718 | 2.08596 | 2.52798 | 2.84534 | 3.8495 |
| 21 | 0.256580 | 0.686352 | 1.323188 | 1.720743 | 2. 07961 07961 |
2.51765 | 2.83136 | 3.8193 |
| 22 | 0.256432 | 0.685805 | 1.321237 | 1.717144 | 2.07387 | 2.50832 | 2.81876 | 3.7921 |
| 23 | 0.256297 | 0.685306 | 1.319460 | 1.713872 | 2.06866 | 2.49987 | 2.80734 | 3.7676 |
| 24 | 0.256173 | 0.684850 | 1.317836 | 1.710882 | 2.06390 | 2.49216 | 2.79694 | 3.7454 |
| 25 | 0.256060 | 0.684430 | 1.316345 | 1.708141 | 2.05954 | 2.48511 | 2.78744 | 3.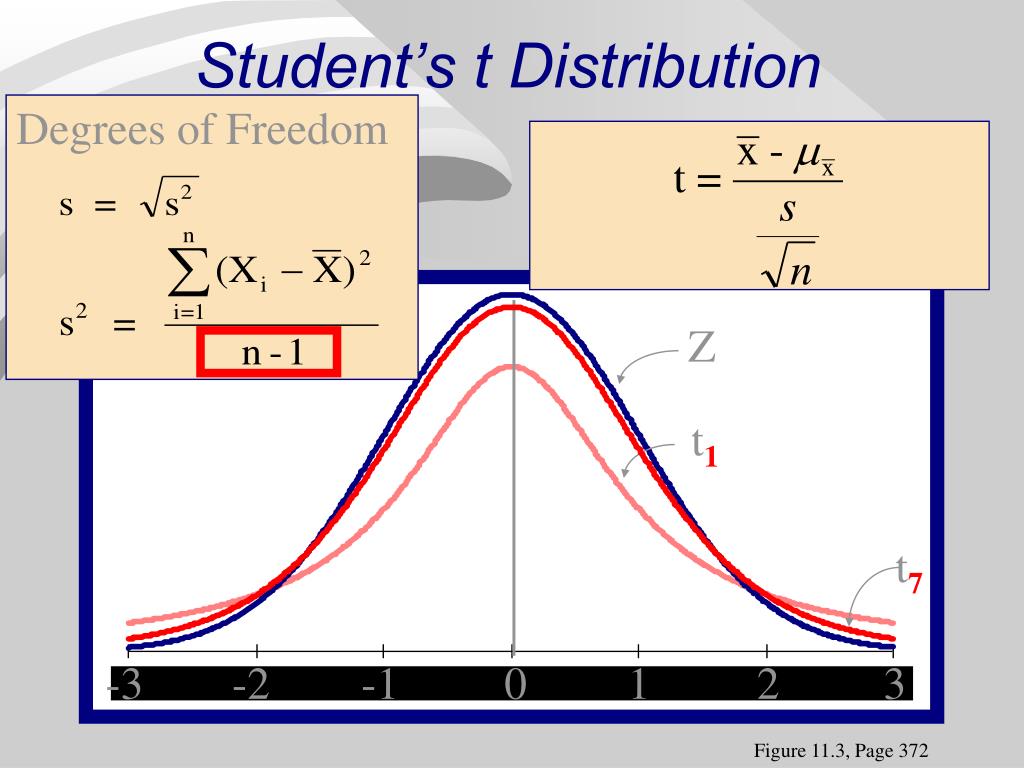 7251 7251 |
| 26 | 0.255955 | 0.684043 | 1.314972 | 1.705618 | 2.05553 | 2.47863 | 2.77871 | 3.7066 |
| 27 | 0.255858 | 0.683685 | 1.313703 | 1.703288 | 2.05183 | 2.47266 | 2.77068 | 3.6896 |
| 28 | 0.255768 | 0.683353 | 1.312527 | 1.701131 | 2.04841 | 2.46714 | 2.76326 | 3.6739 |
| 29 | 0.255684 | 0.683044 | 1.311434 | 1.699127 | 2.04523 | 2.46202 | 2.75639 | 3.6594 |
| 30 | 0. |
0.682756 | 1.310415 | 1.697261 | 2.04227 | 2.45726 | 2.75000 | 3.6460 |
| inf | 0.253347 | 0.674490 | 1.281552 | 1.644854 | 1.95996 | 2.32635 | 2.57583 | 3.2905 |
Распределение Стьюдента (t-распределение). Расчет критерия Стьюдента в Excell
Содержание
- Распределение Стьюдента и нормальное распределение в Excel
- Определение одностороннего и двустороннего t распределение Стьюдента
- Расчет показателя в Excel
- Мастер функций
- Работа со вкладкой «Формулы»
- Этапы статистического вывода (statistic inference)
- Пример использования т-критерия Стьюдента
- Для чего используется t-критерий Стьюдента?
- В каких случаях можно использовать t-критерий Стьюдента?
- Как интерпретировать значение t-критерия Стьюдента?
- Внесите исходные данные группы
- Внесите исходные данные группы
- Критические точки распределения Стьюдента
- Условия применения t-критерия Стьюдента
- Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Примечания:
- Распределение Стьюдента является одним из видов распределения случайной величины, близкое к нормальному распределению с характерным отличием – сниженная концентрацией отклонений в средней части распределения. Иное название – t-распределение.
- Квантилем считается некоторое значение, которое с определенной вероятностью (фиксированной) не будет превышено случайной величиной.
- Функция СТЮДРАСПОБР считается устаревшей начиная с версии MS Office 2010. Она оставлена для обеспечения совместимости с другими табличными редакторами и документами, созданными в более старых версиях табличного редактора. В новых версиях следует использовать усовершенствованные аналоги: СТЬЮДЕНТ.ОБР.2Х или СТЬЮДЕНТ.ОБР.
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:
Для расчета двустороннего t-значения используем функцию:
=СТЬЮДРАСПОБР(B2;B1)
Результат вычислений:
Для двустороннего t используем удвоенное значение вероятности:
=СТЬЮДРАСПОБР(2*B2;B1)
В результате получим:
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.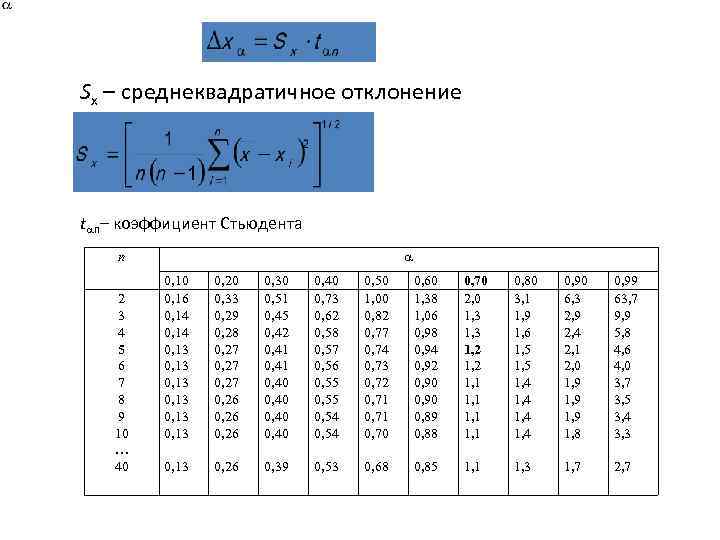
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.

- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Внесите исходные данные группы
Вы можете внести данные для расчета критерия Т-Стьюдента поочередно вручную или скопировать их из вашего Excel файла.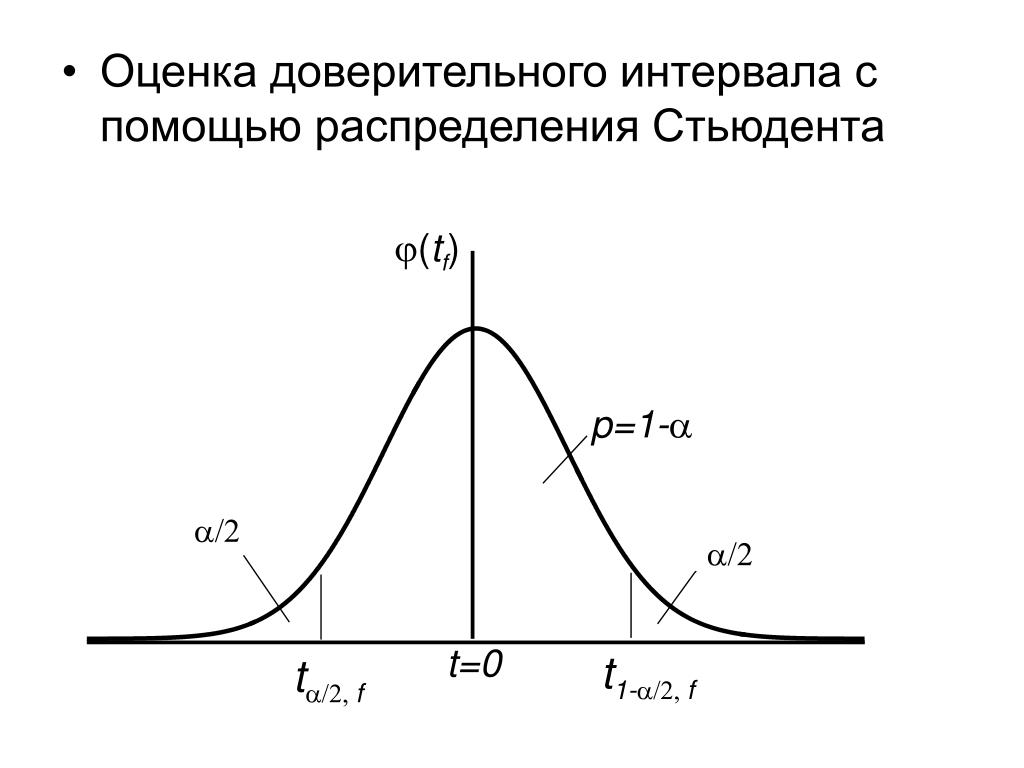
Внесите исходные данные группы
Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.
Критические точки распределения Стьюдента
| Число степеней свободы k | Уровень значимости α (двусторонняя критическая область) | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3. 14 14 | 3.71 | 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.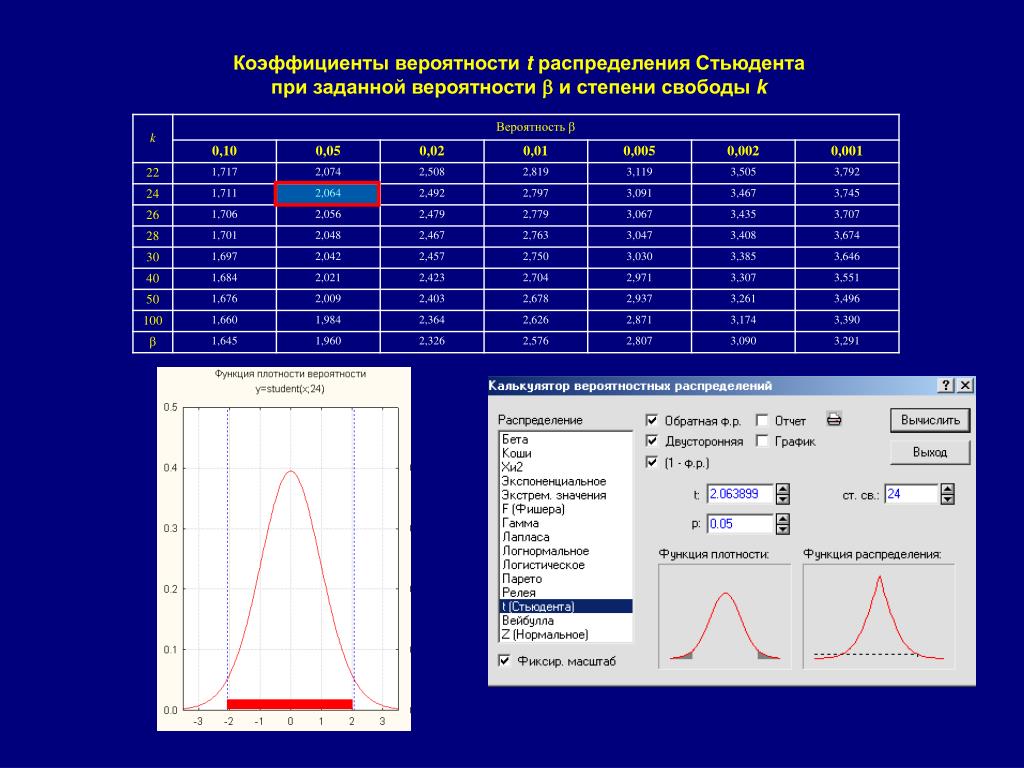 75 75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3. 45 45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ∞ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.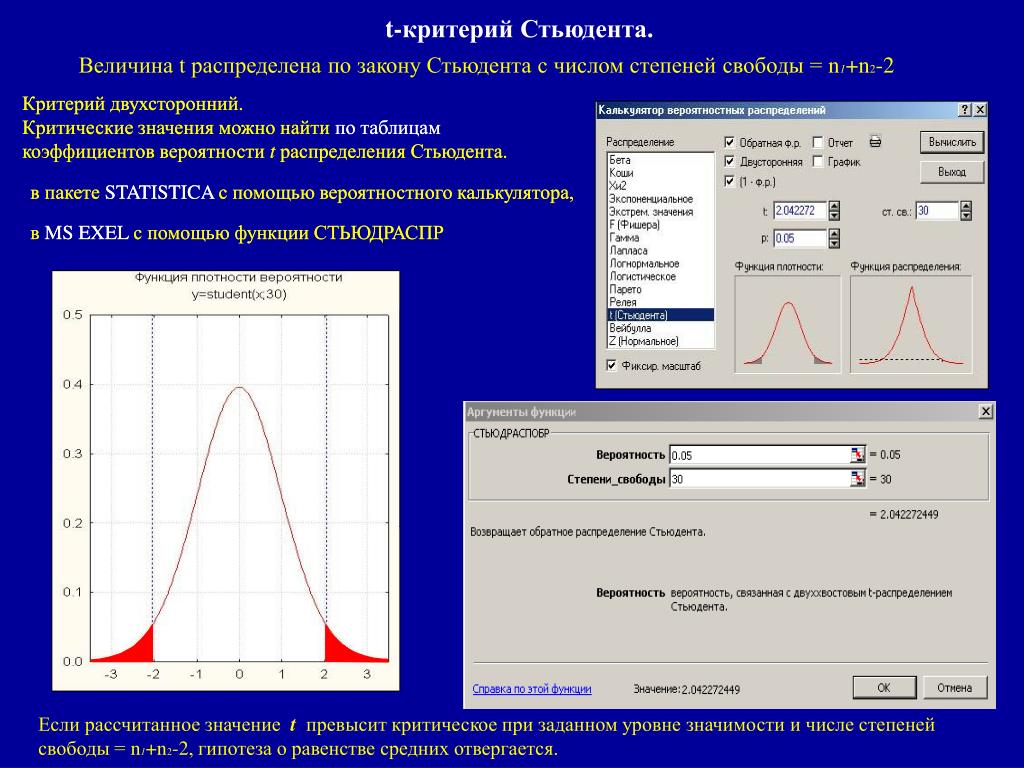 025 025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости α (односторонняя критическая область) | ||||||
Условия применения t-критерия Стьюдента
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.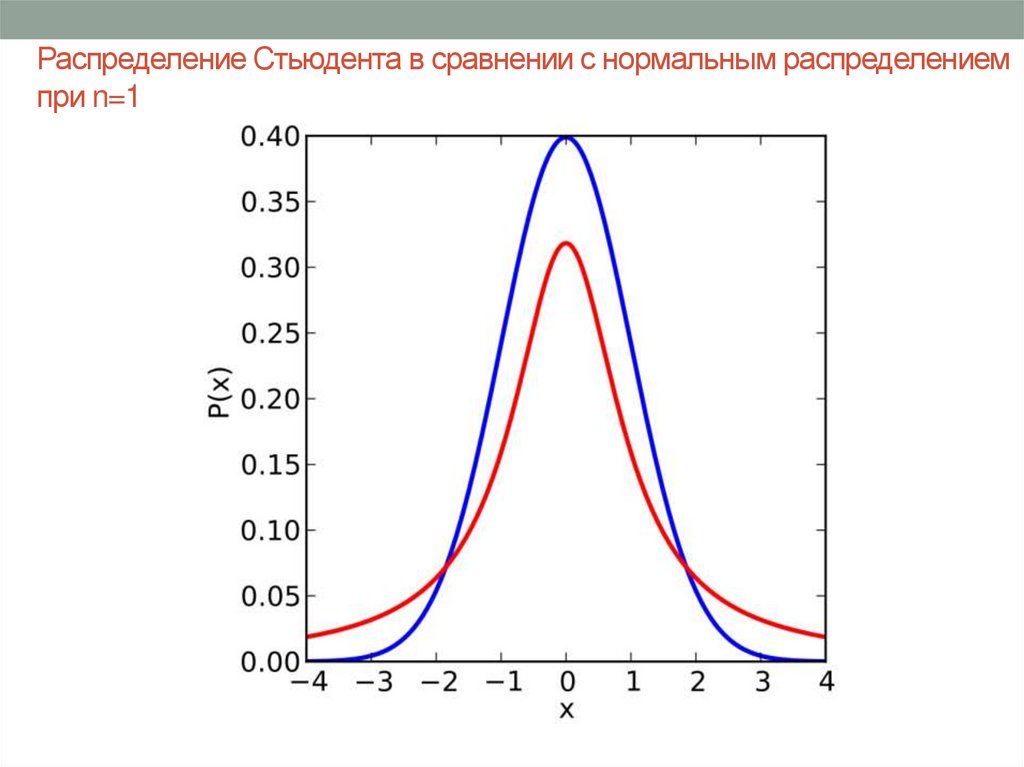 РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т. к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой.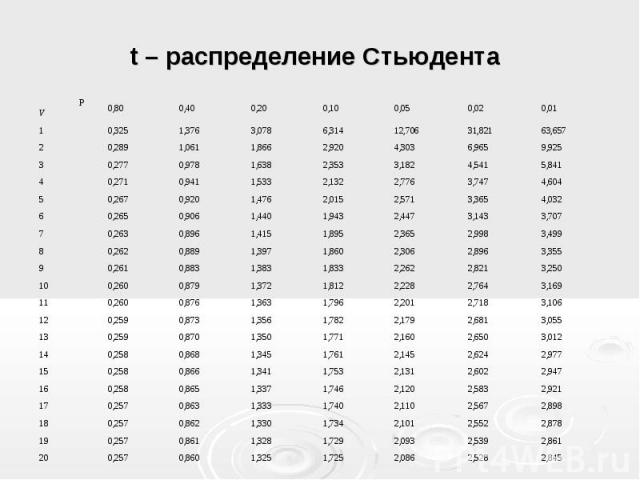 Требуется его проверка и настройка.
Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975.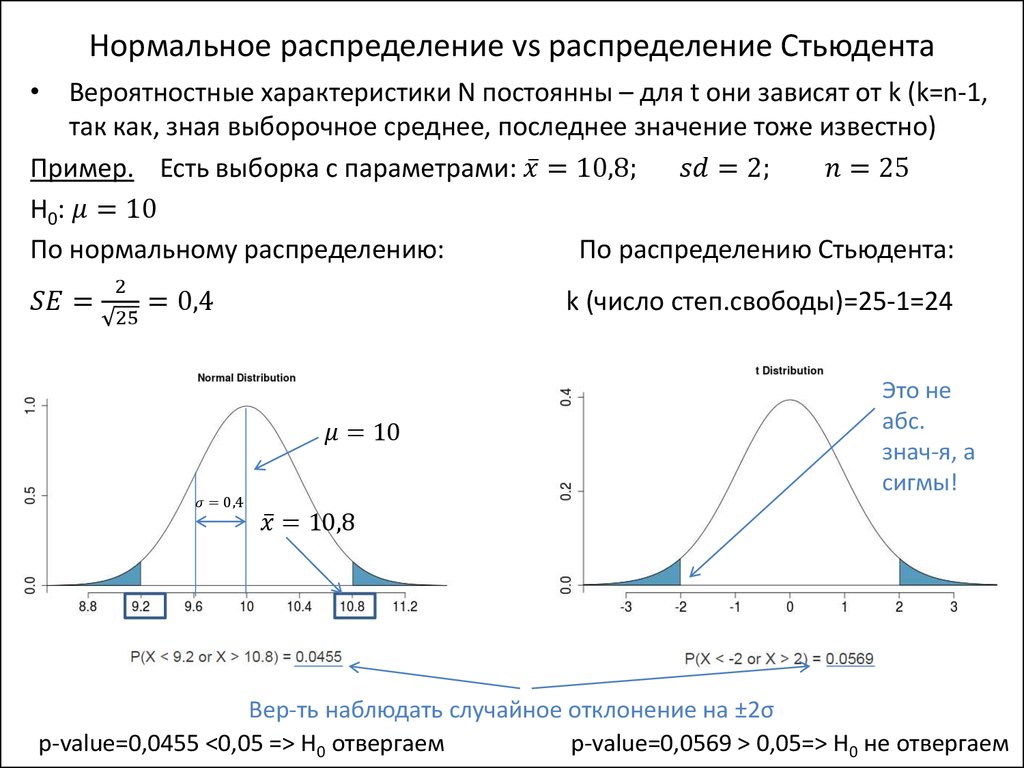 Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Источники
- https://exceltable.
 com/funkcii-excel/raspredeleniya-styudenta-styudraspobr
com/funkcii-excel/raspredeleniya-styudenta-styudraspobr - https://lumpics.ru/calculation-student-test-in-excel/
- https://lit-review.ru/biostatistika/t-kriterijj-styudenta-za-12-minut/
- https://medstatistic.ru/methods/methods.html
- https://statpsy.ru/t-student/onlajn-raschet-kriteriya-t-styudenta-dlya-nezavisimyh-vyborok/
- https://math.semestr.ru/corel/table-student.php
- https://statanaliz.info/statistica/proverka-gipotez/raspredelenie-t-kriteriya-styudenta-dlya-proverki-gipotezy-i-rascheta-doveritelnogo-intervala-v-ms-excel/
Распределение Стьюдента (t-распределение)
Примеры решенийКоэффициент СпирменаКоэффициент Фехнера Множественная регрессияНелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров трендаОшибка аппроксимации
| уровень значимости α | ||||||||
| 0,40 | 0,25 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | ||
| число степеней свободы | 1 | 0,325 | 1,000 | 3,078 | 6,314 | 12,706 | 31,821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | |
| 6 | 0,265 | 0,718 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | |
| 11 | 0,260 | 0,697 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | |
| 12 | 0,259 | 0,695 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | |
| 13 | 0,259 | 0,694 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | |
| 14 | 0,258 | 0,692 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | |
| 15 | 0,258 | 0,691 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | |
| 16 | 0,258 | 0,690 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | |
| 17 | 0,257 | 0,689 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | |
| 18 | 0,257 | 0,688 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | |
| 19 | 0,257 | 0,688 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | |
| 20 | 0,257 | 0,687 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | |
| 21 | 0,257 | 0,686 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | |
| 22 | 0,256 | 0,686 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | |
| 23 | 0,256 | 0,685 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | |
| 24 | 0,256 | 0,685 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | |
| 25 | 0,256 | 0,684 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | |
| 26 | 0,256 | 0,684 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | |
| 27 | 0,256 | 0,684 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | |
| 28 | 0,256 | 0,683 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 | |
| 29 | 0,256 | 0,683 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | |
| 30 | 0,256 | 0,683 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | |
| 40 | 0,255 | 0,681 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | |
| 50 | 0,255 | 0,680 | 1,296 | 1,676 | 2,009 | 2,403 | 2,678 | |
| 60 | 0,255 | 0,679 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | |
| 80 | 0,254 | 0,679 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 | |
| 100 | 0,254 | 0,678 | 1,290 | 1,660 | 1,984 | 2,365 | 2,626 | |
| 120 | 0,254 | 0,677 | 1,289 | 1,658 | 1,980 | 2,358 | 2,467 | |
| 200 | 0,254 | 0,676 | 1,286 | 1,653 | 1,972 | 2,345 | 2,601 | |
| Число степеней свободы
k | Уровень значимости α (двусторонняя критическая область) | |||||
|
0.  10 10
|
0.05 |
0.02 |
0.01 |
0.002 |
0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3.14 | 3. 71 71
| 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2. 65 65
| 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2. 09 09
| 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1. 71 71
| 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ∞ | 1. 64 64
| 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости α (односторонняя критическая область) | ||||||
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Определение, пошаговые статьи, видео
Содержание:
- Что такое Т-распределение?
- ТИ 83 шага.
- ТИ 89 шагов.
- Другие статьи T-Dist
Посмотрите видео для получения доступа к дистрибутиву:
T-Distribution Intro
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.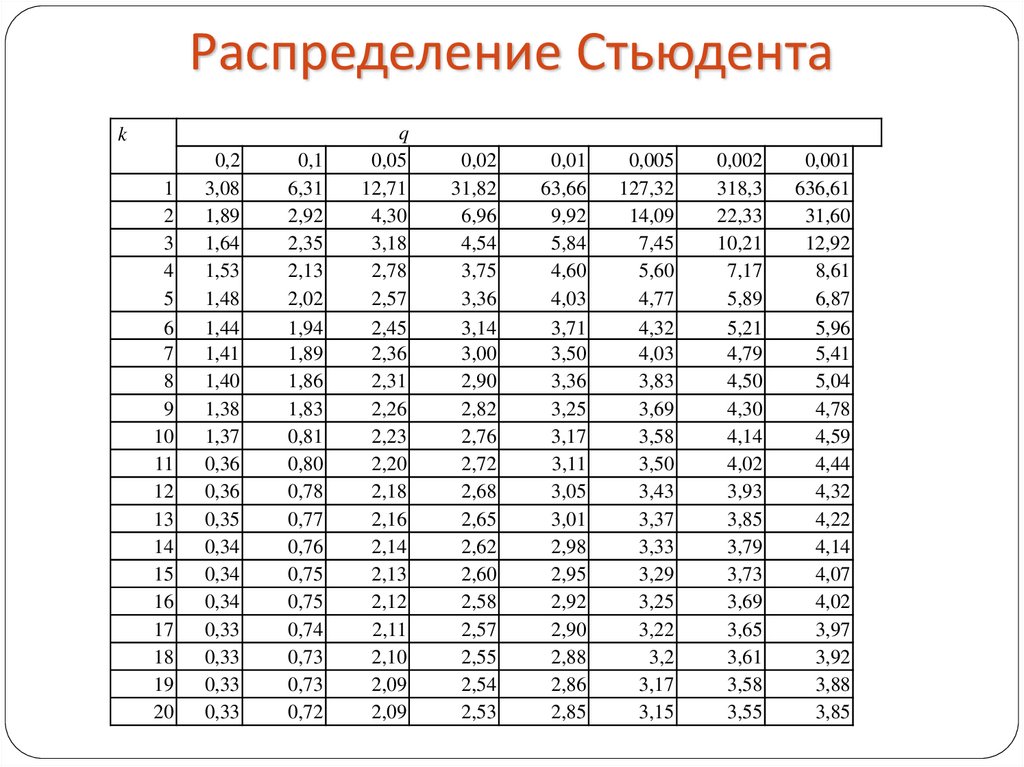
T-распределение (также называемое T-распределением Стьюдента ) — это семейство распределений, которые выглядят почти так же, как кривая нормального распределения, только немного короче и толще. Распределение t используется вместо нормального распределения, когда у вас есть небольшие выборки (подробнее об этом см.: t-показатель против z-показателя). Чем больше размер выборки, тем больше распределение t похоже на нормальное распределение. Фактически, для размеров выборки больше 20 (например, больше степеней свободы) распределение почти точно такое же, как нормальное распределение.
Как рассчитать показатель для T-распределения
Когда вы посмотрите на таблицы t-распределения, вы увидите, что вам нужно знать «df». Это означает «степени свободы» и представляет собой размер выборки минус один.
Шаг 1: Вычтите единицу из размера выборки. Это будут ваши степени свободы.
Шаг 2: Найдите df в левой части таблицы t-распределения. Найдите столбец под вашим альфа-уровнем (альфа-уровень обычно указывается в вопросе).
Найдите столбец под вашим альфа-уровнем (альфа-уровень обычно указывается в вопросе).
Более подробные шаги, включая видео , см. в формуле t-счета.
Использование
T-распределение (и связанные с ним t-показатели) используются при проверке гипотез, когда вы хотите выяснить, следует ли принять или отклонить нулевую гипотезу.
Центральная область на этом графике — это область принятия, а хвост — область или области отклонения. На этом конкретном графике двустороннего теста область отбраковки заштрихована синим цветом. Область в хвосте может быть описана с помощью z-показателей или t-показателей. Например, на изображении слева показана площадь в хвостах 5% (по 2,5% с каждой стороны). Z-оценка будет 1,96 (из таблицы z), что соответствует 1,96 стандартным отклонениям от среднего значения. Нулевая гипотеза будет отклонена, если z меньше -1,96 или больше 1,96.
Как правило, это распределение используется при небольшом размере выборки (менее 30) или при неизвестном стандартном отклонении генеральной совокупности. Для практических целей (то есть в реальном мире) это почти всегда так. Таким образом, в отличие от вашего урока элементарной статистики, вы, вероятно, будете использовать его в реальных жизненных ситуациях чаще, чем нормальное распределение. Если размер вашей выборки достаточно велик, два распределения практически одинаковы.
Для практических целей (то есть в реальном мире) это почти всегда так. Таким образом, в отличие от вашего урока элементарной статистики, вы, вероятно, будете использовать его в реальных жизненных ситуациях чаще, чем нормальное распределение. Если размер вашей выборки достаточно велик, два распределения практически одинаковы.
Посмотрите видео для примера:
T Раздача на TI 83
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Взгляните на традиционную T-таблицу из учебника, и вы на самом деле найдете множество T-таблиц, которые могут быть немного ошеломляющими. Вместо того, чтобы корпеть над таблицами, вы можете использовать графический калькулятор TI 83 , который поможет вам найти значения T.
Вас могут попросить найти площадь под T-кривой или (как Z-баллы) вам могут дать определенную область и попросить найти T-балл.
Поиск T-критического значения на TI 83
Нажмите здесь, чтобы прочитать нашу статью о поиске T-критических значений на TI 83. площадь под кривой T со степенями свободы 10 для P ( 1 ≤ X ≤ 2 ). Используйте распределение t на TI 83.
площадь под кривой T со степенями свободы 10 для P ( 1 ≤ X ≤ 2 ). Используйте распределение t на TI 83.
Шаг 1: Нажмите 2nd VARS 5, чтобы выбрать tcdf( .
Шаг 2: Введите нижнюю границу, верхнюю границу и степени свободы. Граница — это наименьшее число, а верхняя граница — это наибольшее число: 1,2,10
Теперь на экране должно быть написано tcdf(1,2,10)
Шаг 3: Нажмите ENTER. Ответ .133752549 , или примерно 13,38% .
Вот как найти T-распределение на TI 83!
Посетите мой канал на YouTube, чтобы получить больше помощи и советов по статистике.
Для большинства вопросов о Т-распределении вам обычно будет предоставлена вся информация, необходимая для того, чтобы подключиться к калькулятору и получить Т-показатель . Вас могут попросить найти площадь под T-кривой или (как Z-баллы) вам могут дать определенную область и попросить найти T-балл.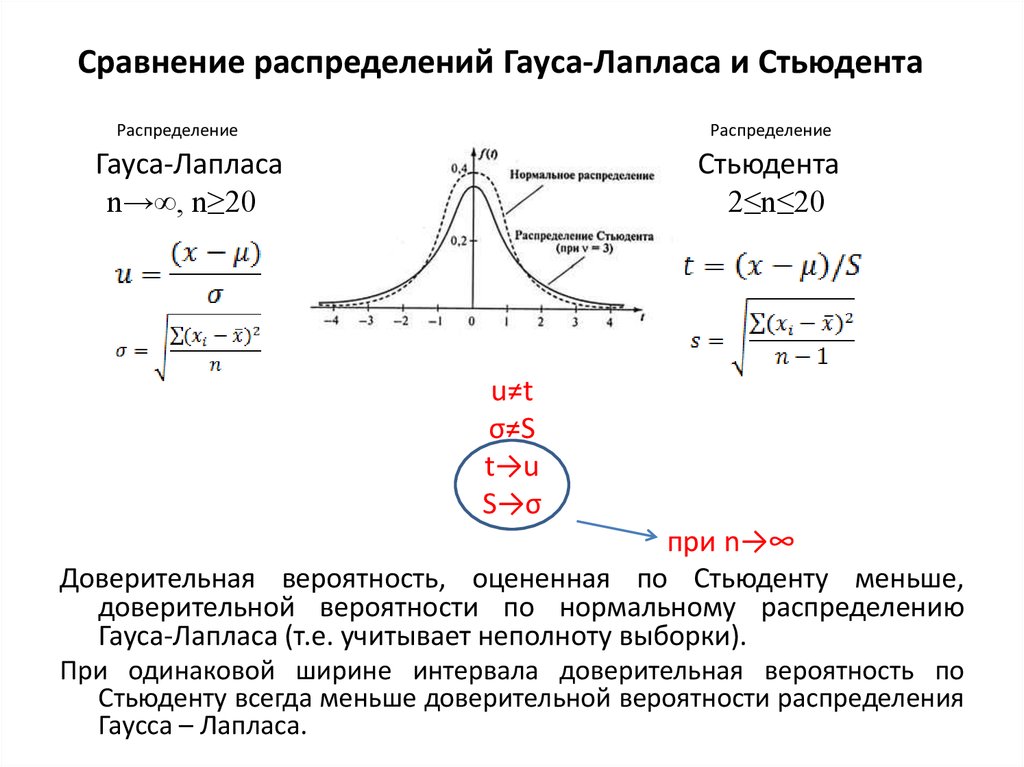
Распределение T на TI 89 Шаги
Примечание : Для выполнения этих процедур необходимо установить редактор STAT/LIST. Вы можете бесплатно загрузить копию с веб-сайта TI.
Пример задачи : найти площадь под T-кривой со степенями свободы 10 для P(1 ≤ X ≤ 2).
Шаг 1: Нажмите APPS.
Шаг 2: Дважды нажмите ENTER, чтобы войти в редактор STATS/LIST.
Шаг 3: Нажмите F5 для F5Дистр .
Шаг 4: Выберите 6 для 6:t Cdf .
Шаг 5: Введите 1 в поле Нижнее значение .
Шаг 6: Введите 2 в поле Верхнее значение .
Шаг 7: Введите 10 в поле Степень свободы, df .
Шаг 8: Нажмите ENTER. Это возвращает результат .133753 .
Пример задачи: найти показатель T со значением 0,25 влево и df 10,
Шаг 1: Нажмите APPS.
Шаг 2: Дважды нажмите ENTER для входа в редактор STAT/LIST.
Шаг 3: Нажмите F5 для F5Distr .
Шаг 4: Нажмите 2 для Инверсия .
Шаг 5: Нажмите кнопку со стрелкой вправо .
Шаг 6: Нажмите 2 для Инвертировать t и затем нажмите ENTER.
Шаг 7: Введите 0,25 в поле 999 в поле для нижнего значения.
Вот как найти T-дистрибутив на TI 89!
- Как построить доверительный интервал на основе данных с использованием t-Dist.
- Т-тест: что это такое и как его рассчитать.
- Т-тест для независимых выборок.
- Приближение Саттертуэйта.
- Формула T-показателя.
Посетите наш канал YouTube, где вы найдете сотни видеороликов со статистикой.
Ссылки
Beyer, WH CRC Standard Mathematical Tables, 31st ed. Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Фишер, Р. А. Статистические методы для научных работников, 10-е изд. Эдинбург: Оливер и Бойд, 1948.
Шпигель, М. Р. Шаум. Очерк теории и проблем вероятности и статистики. Нью-Йорк: McGraw-Hill, стр. 116-117, 1992.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «T-Distribution / T студента: определение, пошаговые статьи, видео» с StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/t-distribution/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .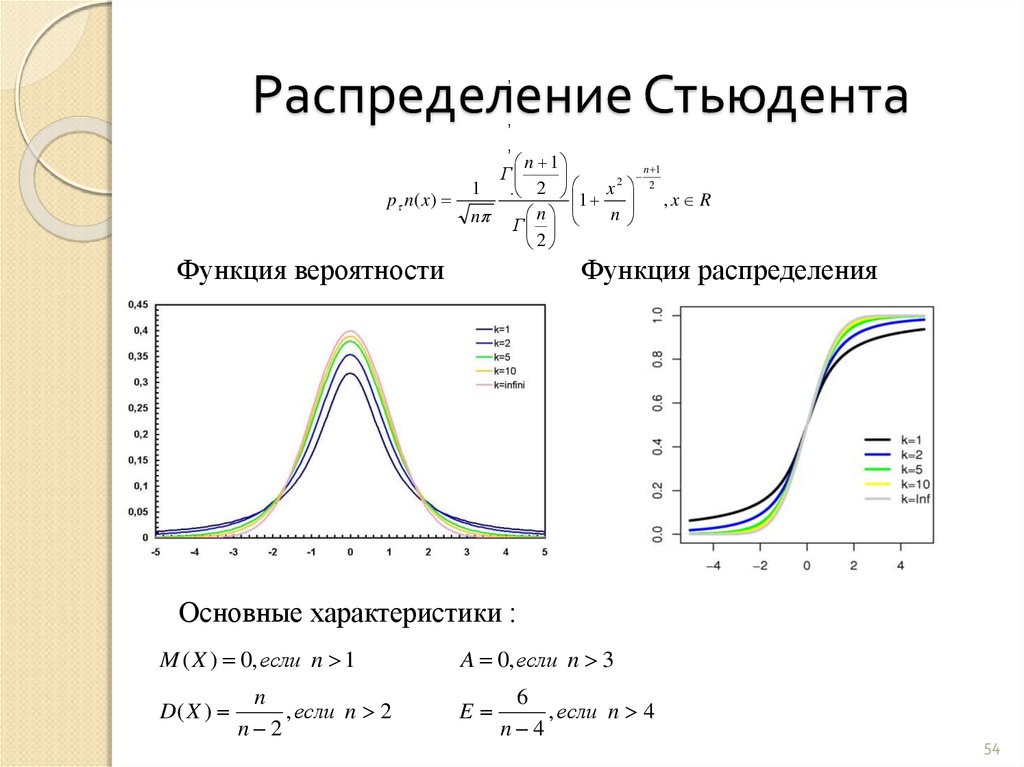
T Определение распределения
По
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 07 октября 2021 г.
Рассмотрено
Чип Стэплтон
Рассмотрено Чип Стэплтон
Полная биография
Чип Стэплтон является обладателем лицензий Серии 7 и Серии 66, сдал экзамен CFA уровня 1 и в настоящее время имеет лицензию на жизнь, несчастный случай и здоровье в Индиане. Он имеет 8-летний опыт работы в области финансов, от финансового планирования и управления активами до корпоративных финансов и планирования и анализа.
Он имеет 8-летний опыт работы в области финансов, от финансового планирования и управления активами до корпоративных финансов и планирования и анализа.
Узнайте о нашем Совет по финансовому обзору
Факт проверен
Тимоти Ли
Факт проверен Тимоти Ли
Полная биография
Тимоти Ли — консультант, бухгалтер и финансовый менеджер со степенью магистра делового администрирования Университета Южной Калифорнии и более чем 15-летним опытом работы в сфере корпоративных финансов. Тимоти помог предоставить генеральным и финансовым директорам глубокую аналитику, рассказав красивые истории о цифрах, графиках и финансовых моделях.
Узнайте о нашем редакционная политика
Что такое T-распределение?
T-распределение, также известное как t-распределение Стьюдента, представляет собой тип распределения вероятностей, который похож на нормальное распределение своей колоколообразной формой, но имеет более тяжелые хвосты. T-распределения имеют больше шансов на экстремальные значения, чем нормальные распределения, отсюда и более толстые хвосты.
T-распределения имеют больше шансов на экстремальные значения, чем нормальные распределения, отсюда и более толстые хвосты.
Ключевые выводы
- T-распределение представляет собой непрерывное распределение вероятностей z-показателя, когда в знаменателе используется оценочное стандартное отклонение, а не истинное стандартное отклонение.
- Т-распределение, как и нормальное распределение, имеет форму колокола и симметрично, но имеет более тяжелые хвосты, что означает, что оно имеет тенденцию давать значения, далекие от своего среднего значения.
- T-тесты используются в статистике для оценки значимости.
О чем говорит T-распределение?
Тяжесть хвоста определяется параметром распределения T, называемым степенями свободы, при этом меньшие значения дают более тяжелые хвосты, а более высокие значения делают распределение T похожим на стандартное нормальное распределение со средним значением 0 и стандартным отклонением 1. Т-распределение также известно как «Т-распределение Стьюдента».
Когда выборка из n наблюдений берется из нормально распределенной совокупности, имеющей среднее значение M и стандартное отклонение D, среднее значение выборки m и стандартное отклонение выборки d будут отличаться от M и D из-за случайности выборки.
Z-показатель можно рассчитать со стандартным отклонением населения как Z = (x – M)/D, и это значение имеет нормальное распределение со средним значением 0 и стандартным отклонением 1. Но при использовании расчетного стандартного отклонения t-показатель вычисляется как T = (m – M)/{d/sqrt(n)}, разница между d и D делает распределение T-распределением с (n – 1) степенями свободы, а не нормальным распределением со средним значением 0 и стандартное отклонение 1.
Пример использования T-распределения
Возьмем следующий пример того, как t-распределения используются в статистическом анализе. Во-первых, помните, что доверительный интервал для среднего значения — это диапазон значений, рассчитанный на основе данных, предназначенных для получения среднего значения «популяции». Этот интервал равен m +- t*d/sqrt(n), где t — критическое значение из распределения T.
Этот интервал равен m +- t*d/sqrt(n), где t — критическое значение из распределения T.
Например, 95-процентный доверительный интервал для средней доходности промышленного индекса Доу-Джонса за 27 торговых дней до 9/11/2001, равно -0,33%, (+/- 2,055) * 1,07 / sqrt(27), что дает (постоянную) среднюю доходность в виде некоторого числа от -0,75% до +0,09%. Число 2,055, количество стандартных ошибок для корректировки, находится из T-распределения.
Поскольку T-распределение имеет более толстые хвосты, чем нормальное распределение, его можно использовать в качестве модели финансовой доходности, которая демонстрирует избыточный эксцесс, что позволит в таких случаях более реалистично рассчитать стоимость под риском (VaR).
Разница между T-распределением и нормальным распределением
Нормальные распределения используются, когда предполагается, что распределение населения является нормальным. Распределение T похоже на нормальное распределение, только с более толстыми хвостами.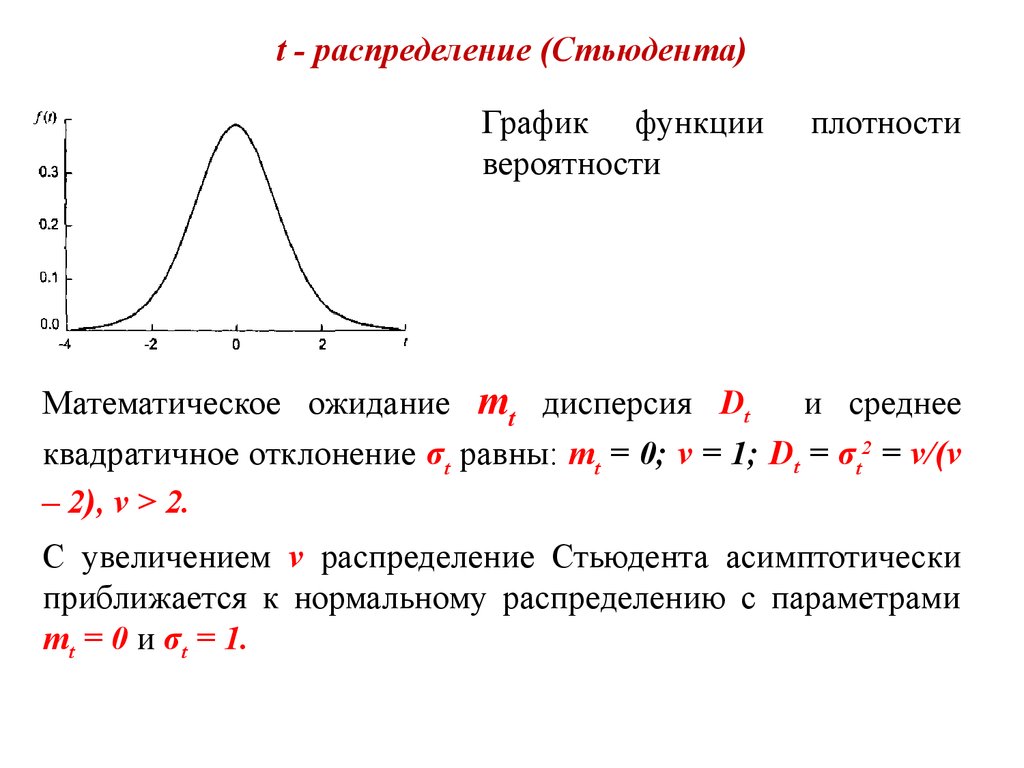 Оба предполагают нормально распределенную популяцию. Распределения T имеют более высокий эксцесс, чем нормальные распределения. Вероятность получения значений, очень далеких от среднего, больше при Т-распределении, чем при нормальном распределении.
Оба предполагают нормально распределенную популяцию. Распределения T имеют более высокий эксцесс, чем нормальные распределения. Вероятность получения значений, очень далеких от среднего, больше при Т-распределении, чем при нормальном распределении.
Ограничения использования Т-распределения
Распределение T может искажать точность по сравнению с нормальным распределением. Его недостаток возникает только тогда, когда есть потребность в совершенной нормальности. Т-распределение следует использовать только в том случае, если стандартное отклонение популяции неизвестно. Если известно стандартное отклонение генеральной совокупности и размер выборки достаточно велик, для получения лучших результатов следует использовать нормальное распределение.
1.3.6.7.2. Критические значения распределения Стьюдента
1.3.6.7.2. Критические значения Стьюдента-t Распределение 1. Исследовательский анализ данных Исследовательский анализ данных 1.3. Методы ЭДА 1.3.6. Распределения вероятностей 1.3.6.7. Таблицы распределения вероятностей
| |||
| Как использовать эту таблицу | Эта таблица содержит критические значения
Студенческая т раздача
вычислено с использованием
кумулятивная функция распределения.
Распределение t симметрично, так что т 1- α,ν = -т α,ν . Стол т можно использовать как для одностороннего (нижнего, так и для верхний) и двусторонние тесты с использованием соответствующего значения α . Уровень значимости α показан на графике
ниже, где показано распределение t с 10
степени свободы. Учитывая указанное значение для α :
| ||
Критические значения распределения Стьюдента t с ν степенями свободы Вероятность меньше критического значения ( т 1- α , ν ) ν 0,90 0,95 0,975 0,99 0,995 0,999 | |||


 com/funkcii-excel/raspredeleniya-styudenta-styudraspobr
com/funkcii-excel/raspredeleniya-styudenta-styudraspobr Наиболее часто используемый уровень значимости α = 0,05. Для двустороннего теста вычисляем
1 — α /2, или 1 — 0,05/2 = 0,975, когда α = 0,05.
Если абсолютное значение тестовой статистики больше, чем
критическое значение (0,975), то мы отвергаем нулевую гипотезу. Из-за
симметрия t распределение, мы только табулируем
положительные критические значения в таблице ниже.
Наиболее часто используемый уровень значимости α = 0,05. Для двустороннего теста вычисляем
1 — α /2, или 1 — 0,05/2 = 0,975, когда α = 0,05.
Если абсолютное значение тестовой статистики больше, чем
критическое значение (0,975), то мы отвергаем нулевую гипотезу. Из-за
симметрия t распределение, мы только табулируем
положительные критические значения в таблице ниже.
 1,330 1,734 2,101 2,552 2,878 3,610
19. 1,328 1,729 2,093 2,539 2,861 3,579
20. 1,325 1,725 2,086 2,528 2,845 3,552
21. 1,323 1,721 2,080 2,518 2,831 3,527
22. 1,321 1,717 2,074 2,508 2,819 3,505
23. 1,319 1,714 2,069 2,500 2,807 3,485
24. 1,318 1,711 2,064 2,492 2,797 3,467
25. 1,316 1,708 2,060 2,485 2,787 3,450
26. 1,315 1,706 2,056 2,4792,779 3,435
27. 1,314 1,703 2,052 2,473 2,771 3,421
28. 1,313 1,701 2,048 2,467 2,763 3,408
29. 1,311 1,699 2,045 2,462 2,756 3,396
30. 1,310 1,697 2,042 2,457 2,750 3,385
31. 1,309 1,696 2,040 2,453 2,744 3,375
32. 1,309 1,694 2,037 2,449 2,738 3,365
33. 1,308 1,692 2,035 2,445 2,733 3,356
34. 1,307 1,691 2,032 2,441 2,728 3,348
35. 1,306 1,690 2,030 2,438 2,724 3,340
36. 1,306 1,688 2,028 2,434 2,7193.333
37. 1,305 1,687 2,026 2,431 2,715 3,326
38. 1,304 1,686 2,024 2,429 2,712 3,319
39. 1,304 1,685 2,023 2,426 2,708 3,313
40. 1,303 1,684 2,021 2,423 2,704 3,307
41. 1,303 1,683 2,020 2,421 2,701 3,301
42. 1,302 1,682 2,018 2,418 2,698 3,296
43.
1,330 1,734 2,101 2,552 2,878 3,610
19. 1,328 1,729 2,093 2,539 2,861 3,579
20. 1,325 1,725 2,086 2,528 2,845 3,552
21. 1,323 1,721 2,080 2,518 2,831 3,527
22. 1,321 1,717 2,074 2,508 2,819 3,505
23. 1,319 1,714 2,069 2,500 2,807 3,485
24. 1,318 1,711 2,064 2,492 2,797 3,467
25. 1,316 1,708 2,060 2,485 2,787 3,450
26. 1,315 1,706 2,056 2,4792,779 3,435
27. 1,314 1,703 2,052 2,473 2,771 3,421
28. 1,313 1,701 2,048 2,467 2,763 3,408
29. 1,311 1,699 2,045 2,462 2,756 3,396
30. 1,310 1,697 2,042 2,457 2,750 3,385
31. 1,309 1,696 2,040 2,453 2,744 3,375
32. 1,309 1,694 2,037 2,449 2,738 3,365
33. 1,308 1,692 2,035 2,445 2,733 3,356
34. 1,307 1,691 2,032 2,441 2,728 3,348
35. 1,306 1,690 2,030 2,438 2,724 3,340
36. 1,306 1,688 2,028 2,434 2,7193.333
37. 1,305 1,687 2,026 2,431 2,715 3,326
38. 1,304 1,686 2,024 2,429 2,712 3,319
39. 1,304 1,685 2,023 2,426 2,708 3,313
40. 1,303 1,684 2,021 2,423 2,704 3,307
41. 1,303 1,683 2,020 2,421 2,701 3,301
42. 1,302 1,682 2,018 2,418 2,698 3,296
43. 1,302 1,681 2,017 2,416 2,695 3,291
44. 1,301 1,680 2,015 2,414 2,692 3,286
45. 1,301 1,679 2,014 2,412 2,690 3,281
46. 1.300 1.679 2.013 2.410 2.687 3.277
47. 1.300 1.678 2.012 2.408 2.685 3.273
48. 1,299 1,677 2,011 2,407 2,682 3,269
49. 1,299 1,677 2,010 2,405 2,680 3,265
50. 1,299 1,676 2,009 2,403 2,678 3,261
51. 1,298 1,675 2,008 2,402 2,676 3,258
52. 1,298 1,675 2,007 2,400 2,674 3,255
53. 1,298 1,674 2,006 2,399 2,672 3,251
54. 1,297 1,674 2,005 2,397 2,670 3,248
55. 1,297 1,673 2,004 2,396 2,668 3,245
56. 1,297 1,673 2,003 2,395 2,667 3,242
57. 1,297 1,672 2,002 2,394 2,665 3,239
58. 1,296 1,672 2,002 2,392 2,663 3,237
59. 1,296 1,671 2,001 2,391 2,662 3,234
60. 1,296 1,671 2,000 2,390 2,660 3,232
61. 1,296 1,670 2,000 2,389 2,659 3,229
62. 1,295 1,670 1,999 2,388 2,657 3,227
63. 1,295 1,669 1,998 2,387 2,656 3,225
64. 1,295 1,669 1,998 2,386 2,655 3,223
65. 1,295 1,669 1,997 2,385 2,654 3,220
66. 1,295 1,668 1,997 2,384 2,652 3,218
67. 1,294 1,668 1,996 2,383 2,651 3,216
68.
1,302 1,681 2,017 2,416 2,695 3,291
44. 1,301 1,680 2,015 2,414 2,692 3,286
45. 1,301 1,679 2,014 2,412 2,690 3,281
46. 1.300 1.679 2.013 2.410 2.687 3.277
47. 1.300 1.678 2.012 2.408 2.685 3.273
48. 1,299 1,677 2,011 2,407 2,682 3,269
49. 1,299 1,677 2,010 2,405 2,680 3,265
50. 1,299 1,676 2,009 2,403 2,678 3,261
51. 1,298 1,675 2,008 2,402 2,676 3,258
52. 1,298 1,675 2,007 2,400 2,674 3,255
53. 1,298 1,674 2,006 2,399 2,672 3,251
54. 1,297 1,674 2,005 2,397 2,670 3,248
55. 1,297 1,673 2,004 2,396 2,668 3,245
56. 1,297 1,673 2,003 2,395 2,667 3,242
57. 1,297 1,672 2,002 2,394 2,665 3,239
58. 1,296 1,672 2,002 2,392 2,663 3,237
59. 1,296 1,671 2,001 2,391 2,662 3,234
60. 1,296 1,671 2,000 2,390 2,660 3,232
61. 1,296 1,670 2,000 2,389 2,659 3,229
62. 1,295 1,670 1,999 2,388 2,657 3,227
63. 1,295 1,669 1,998 2,387 2,656 3,225
64. 1,295 1,669 1,998 2,386 2,655 3,223
65. 1,295 1,669 1,997 2,385 2,654 3,220
66. 1,295 1,668 1,997 2,384 2,652 3,218
67. 1,294 1,668 1,996 2,383 2,651 3,216
68. 1,294 1,668 1,995 2,382 2,650 3,214
69. 1,294 1,667 1,995 2,382 2,649 3,213
70. 1,294 1,667 1,994 2,381 2,648 3,211
71. 1,294 1,667 1,994 2,380 2,647 3,209
72. 1,293 1,666 1,993 2,379 2,646 3,207
73. 1,293 1,666 1,993 2,379 2,645 3,206
74. 1,293 1,666 1,993 2,378 2,644 3,204
75. 1,293 1,665 1,992 2,377 2,643 3,202
76. 1,293 1,665 1,992 2,376 2,642 3,201
77. 1,293 1,665 1,991 2,376 2,641 3,199
78. 1,292 1,665 1,991 2,375 2,640 3,198
79. 1,292 1,664 1,990 2,374 2,640 3,197
80. 1,292 1,664 1,990 2,374 2,639 3,195
81. 1,292 1,664 1,990 2,373 2,638 3,194
82. 1,292 1,664 1,989 2,373 2,637 3,193
83. 1,292 1,663 1,989 2,372 2,636 3,191
84. 1,292 1,663 1,989 2,372 2,636 3,190
85. 1,292 1,663 1,988 2,371 2,635 3,189
86. 1,291 1,663 1,988 2,370 2,634 3,188
87. 1,291 1,663 1,988 2,370 2,634 3,187
88. 1,291 1,662 1,987 2,369 2,633 3,185
89. 1,291 1,662 1,987 2,369 2,632 3,184
90. 1,291 1,662 1,987 2,368 2,632 3,183
91. 1,291 1,662 1,986 2,368 2,631 3,182
92. 1,291 1,662 1,986 2,368 2,630 3,181
93.
1,294 1,668 1,995 2,382 2,650 3,214
69. 1,294 1,667 1,995 2,382 2,649 3,213
70. 1,294 1,667 1,994 2,381 2,648 3,211
71. 1,294 1,667 1,994 2,380 2,647 3,209
72. 1,293 1,666 1,993 2,379 2,646 3,207
73. 1,293 1,666 1,993 2,379 2,645 3,206
74. 1,293 1,666 1,993 2,378 2,644 3,204
75. 1,293 1,665 1,992 2,377 2,643 3,202
76. 1,293 1,665 1,992 2,376 2,642 3,201
77. 1,293 1,665 1,991 2,376 2,641 3,199
78. 1,292 1,665 1,991 2,375 2,640 3,198
79. 1,292 1,664 1,990 2,374 2,640 3,197
80. 1,292 1,664 1,990 2,374 2,639 3,195
81. 1,292 1,664 1,990 2,373 2,638 3,194
82. 1,292 1,664 1,989 2,373 2,637 3,193
83. 1,292 1,663 1,989 2,372 2,636 3,191
84. 1,292 1,663 1,989 2,372 2,636 3,190
85. 1,292 1,663 1,988 2,371 2,635 3,189
86. 1,291 1,663 1,988 2,370 2,634 3,188
87. 1,291 1,663 1,988 2,370 2,634 3,187
88. 1,291 1,662 1,987 2,369 2,633 3,185
89. 1,291 1,662 1,987 2,369 2,632 3,184
90. 1,291 1,662 1,987 2,368 2,632 3,183
91. 1,291 1,662 1,986 2,368 2,631 3,182
92. 1,291 1,662 1,986 2,368 2,630 3,181
93.