Примеры применения калькулятора масштабов · Как пользоваться Контрольная Работа РУ
Рассмотрим несколько примеров, как использовать калькулятор масштабов, чтобы переводить из различных размеров на местности и на чертеже при заданном масштабе.
Популярные масштабы:
|
|
|
|
|
Например, надо определить сколько метров местности в 1 см чертежа при масштабе 1:500
Выполните след. шаги:
- Перейдите на страницу калькулятора масштабов
- Для нашего примера введите значение 1 см на чертеже, масштаб — 1:500, так, как указано на рис. ниже:
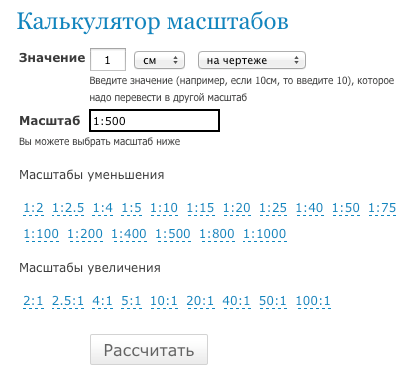
- Нажимаете кнопку рассчитать и получаете ответ:
- Масштаб 1:500 показывает, что 1.0 см на чертеже соответствует 5.0 м на местности.
Приятного вам черчения!
Менее популярные масштабы
|
м5 к 1 75 к 1 400 2500 20000 м2 как считать 1.5 к 1 |
3 к 1 2 к 1 60 метров 55 м 1 3000 1х20 1х2000 1х300 |
1х6 2 разделить на 1 2/600 28 мм 1/70 2х1 4х3 5мм 1м 60 дм к 2 см |
Использование в целях
Калькулятор можно использовать для изменения масштаба в следующих целях:
- Для измерения участка, квартиры, дома или комнаты
- Фасада здания, генплана и плана
- Понять размер объектов на карте (вычислить расстояние)
- Чтобы понять формулу вычисления
- Как будет выглядеть на листе a1, a2, a3, a4, а1, а2, а3, а4, а0 (большая бумага ватман)
- Можно понять сколько метров в 1 см при заданном масштабе
- Даже 1 к 1
- Определить численный линейный масштаб
- Применение к госту
- В учебных целях для школы 4 класса, 5 класса, 6 класса, 7 класса (по предмету: математика)
- Увидеть численный линейный масштаб
Масштаб
Всем здравствуйте! Решила рассмотреть несколько задачек на масштаб – оказалось, есть такая нужда у моих учеников. Может, и вам пригодится!
Всем нам знакомы карты местности – так или иначе, но каждый встречался с ними, в школе или по жизни. Понятно, что карта – лишь только изображение, и по сравнению с расстоянием на местности объекты на карте должны быть меньше (иначе зачем она нужна?). Масштаб – это как раз отношение, которое показывает, во сколько раз карта меньше, чем реальная местность, то есть во сколько раз расстояние на карте меньше, чем на местности.
Но масштаб призван также и увеличивать что-то маленькое так, чтобы можно было сделать подробный чертеж или внимательно рассмотреть что-то мелкое.
Первый, “уменьшающий”, масштаб, может быть записан, например, так: 1:5. Тогда расстояние на карте (или чертеже) в пять раз меньше, чем в реальности. Масштаб, записанный так: 1: 100 000 означает, что изображение меньше в сто тысяч раз.
“Увеличивающий” масштаб записывается: 100:1, или 1000:1. Это значит, что расстояние увеличили в сто или тысячу раз, чтобы его можно было изобразить.
В зависимости от конкретной задачи выбирают и масштаб: карта не должна быть слишком уж мелкой, а понятной и подробной, но в то же время не должна быть гигантской, а простую, но небольшую деталь вовсе необязательно увеличивать в десятки раз, когда может быть достаточно и пяти.
Когда работаешь с масштабом, очень важно уметь составлять отношения (пропорции). Давайте потренируемся в этом!
1. Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.
Чтобы определить масштаб, нужно узнать, во сколько раз расстояние на карте меньше, чем на местности. Для этого нужно расстояние на местности привести к тем же единицам, что и на плане:
20 м = 20*100 см=2000 см.
Тогда, если одному см на карте соответствуют 2000 см на местности, то и масштаб 1:2000, то есть на карте длина отрезка меньше в 2000 раз.
2. Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?
Так как масштаб показывает, во сколько раз карта или план меньше действительного расстояния, или, иначе говоря, во сколько дом больше своего изображения, то:

3. Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе: а) 1:10 000 000; б) 1:2 000 000?
Обозначим за  расстояние на карте. Переведем длину магистрали в сантиметры:
расстояние на карте. Переведем длину магистрали в сантиметры:
3140 км = 3 140 000 м = 314 000 000 см.
Тогда 

По правилу пропорции 
Изображение карты во втором масштабе – крупнее (2 миллиона меньше, чем 10). Так как отношение масштабов – 1:5, то и изображение будет крупнее в пять раз: 157 см. В этом можно убедиться, решив задачу “стандартным” способом.
4. Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?
Снова за  обозначим расстояние на карте. Тогда
обозначим расстояние на карте. Тогда


 см.
см.5. Длина железной дороги Москва – Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.
Переведем километры в сантиметры:
650 км = 650 000 м = 65 000 000 см.
Обозначаем расстояние на карте неизвестной и составляем пропорцию:


 см.
см.6. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте расстояние между ними 12,6 см?
Такую задачу можно решать длинным путем: определить масштаб карты и затем найти расстояние между городами, зная масштаб.
Тогда масштаб будет таким:

А второе расстояние найдем так:

Почему бы тогда не упростить себе задачу, не определяя масштаб, а составить пропорцию сразу:

Отсюда  см, или 25,2 км
см, или 25,2 км
7. Длина детали на чертеже, сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 2:1?
Нам не нужно знать, каковы реальные размеры детали – нас об этом не спрашивают. Поэтому мы и не будем их искать, а найдем новый размер чертежа через отношение масштабов:

 см
см
8. Площадь земельного участка изображается на плане, масштаб которого 1:250, в виде прямоугольника площадью 128 кв. см. Найдите действительную площадь этого земельного участка.
Хорошая задача. Не пугайтесь, что длина и ширина участка неизвестны – нам и не надо знать их. Однако для лучшего понимания все же обозначим их, например,  и
и  . Тогда на карте расстояние
. Тогда на карте расстояние  изображается отрезком
изображается отрезком  , а расстояние
, а расстояние  – отрезком
– отрезком  . Если перемножить длину и ширину изображения участка, то получим как раз 128 кв. см. Но тогда получается, что
. Если перемножить длину и ширину изображения участка, то получим как раз 128 кв. см. Но тогда получается, что  , или
, или  , то есть реальная площадь участка получится, если площадь изображения умножить на квадрат масштаба:
, то есть реальная площадь участка получится, если площадь изображения умножить на квадрат масштаба:  кв. см. Переведем это в кв. метры, для этого нужно разделить не на 100, а на
кв. см. Переведем это в кв. метры, для этого нужно разделить не на 100, а на  : 800 кв. м, а если нужны квадратные километры, тогда еще на
: 800 кв. м, а если нужны квадратные километры, тогда еще на  : 0,0008 кв. км.
: 0,0008 кв. км.
9. Площадь земельного участка прямоугольной формы 6 га. Найдите площадь прямоугольника, изображающего этот участок на плане, масштаб которого 1:5000.
Аналогичная задача. Вспомним, что такое га: это квадрат со стороной 100 м, то есть это 10 000 кв. м. Тогда в сантиметрах это (умножаем на  ) 100 000 000 кв. см. А у нас – 600 000 000 кв. см.Поделим на масштаб в квадрате, чтобы определить площадь этого прямоугольника на карте:
) 100 000 000 кв. см. А у нас – 600 000 000 кв. см.Поделим на масштаб в квадрате, чтобы определить площадь этого прямоугольника на карте:  кв.см.
кв.см.
Нетрудно догадаться, что, если бы речь шла об объеме, то масштаб пришлось бы возводить в куб: в данном случае масштаб – это коэффициент подобия. Площади относятся как квадрат коэффициента подобия, а объемы – как куб коэффициента подобия.
Как рассчитать масштаб | Сделай все сам
На всякий географической карте вы можете видеть приблизительно такую надпись: «Масштаб 1:100 000». Традиционно первое число – 1, а второе может меняться. Если надписи нет, то непременно есть крошечная линеечка, поделенная на равные отрезки, либо номограмма. Эти знаки обозначают отношение размера того либо другого объекта на карте либо плане к его реальному размеру.
Вам понадобится
- Рулетка либо землемерный циркуль
- Линейка
Инструкция
1. Если у вас есть план, на котором довольно верно нанесены разные объекты, и вам нужно узнать, в каком масштабе данный план сделан – начните с измерений. Выберите объект, тот, что находится неподалеку. Обмерьте его на плане и запишите итоги.
2. Измерьте собственно объект. Используйте для этого рулетку. Для того, дабы избежать ошибок, сделайте колышек и зацепите за него петельку рулетки. Вбейте колышек в землю так, дабы нулевая отметка рулетки оказалась на ярусе исходной точки длины либо ширины объекта.
3. Определите масштаб. Комфортнее каждого записать его цифрами. Запишите размер объекта на плане, после этого – тот, тот, что получился при измерении на территории. Скажем, у вас получилось, что сарай длиной 5 метров на плане занимает 2, 5 см. Переведите метры в сантиметры. То есть получается, что у вас в 2, 5 см содержится 500 см. Вычислите, сколько сантиметров территории содержится в 1 см на плане. Для этого большее число поделите на меньшее. Получится 2,5:500=1:200, то есть 1 см на плане соответствует 2 м на территории.
4. Для того, дабы определить масштаб больше верно, сделайте несколько измерений. Скажем, обмерьте сарай на участке и расстояние от ворот до пруда. Планы бывают различные, и размеры того либо другого объекта могут быть нанесены неудовлетворительно верно. Если есть расхождения, сделайте еще один застыл. Изображение объекта, тот, что не соответствует двум иным, откорректируйте на плане.
Масштаб это – численное обозначение параметров, имеющих отношение к реальным объектам, которые немыслимо изобразить в естественную величину. На рисунке применяются их макеты.
Инструкция
1. Записывается масштаб несколькими методами, скажем, численным – 1: 1000000. Соотношение размеров может быть указано и в таком виде: 1 см 10 км – это именованный масштаб. Линейный метод отображения показывается линией с делениями.
2. Если рассматривать масштаб касательно картографии, вид определенной карты будет зависеть от используемых соотношений. Чем он огромнее, тем подробней будет изображена местность. На подробность влияет и нрав территории, малообжитую, скажем, изобразить проще. Карты бывают большие, средние и мелкомасштабные. Крупномасштабные карты – это когда в 1 см от 100 до 2000 метров, среднемасштабные – в 1 см до 10 км, мелкомасштабные – в 1 см больше 10 км.
3. Масштаб значим и в фотографии. При помощи объективов фотографы изменяют размеры от дюже маленького, до дюже большого. Методология метаморфозы масштаба зависит от специфики съемок. Если это небольшие объекты, скажем, насекомые, масштаб возрастает, если огромные – уменьшается.
4. Представление применяется и во многих науках. В математике – это отношение чисел, в программировании – масштаб времени, в астрономии – масштаб вселенной. Значение слова применяется и в строительной сфере.
5. По масштабу деятельности отличают фирмы. Бывают, скажем территориальные организации, а есть и федерального яруса. Разны по масштабу и люди. Правда, не с физической точки зрения, есть психологическое представление “масштаб фигуры”. Под этим подразумеваются человеческие качества, поставленные цели и итоги деятельности.
Видео по теме
Обратите внимание!
Величина уменьшенного объекта относительна к его естественным размерам. Расстояние между объектами может быть изменено на несколько сантиметров, метров, километров. Масштаб действительности меняется дюже гораздо, но все параметры обязаны оставаться пропорциональными. Если не соблюдать пропорции, проанализировать расстояния и размеры объектов будет немыслимо.
С необходимостью представить настоящие размеры изображенного на чертеже предмета человек сталкивается теснее в школе. На уроке черчения бывает надобно начертит деталь в масштабе 1:2 либо 1:4, на уроке географии – сосчитать точное расстояние между двумя городами. Дабы совладать с заданием, надобно знать, как переводится масштаб.
Вам понадобится
- – географическая карта;
- – чертеж детали;
- – калькулятор;
- – чертежные принадлежности.
Инструкция
1. Если вам необходимо вычертить детали в масштабе 1:1, это значит, что 1 см поверхности будет соответствовать 1 см и на чертеже. Измерьте ту поверхность, которую вам необходимо изобразить, и начертите ее на бумаге в естественную величину.
2. В черчении используются и другие масштабы. 1:2 обозначает, что деталь на чертеже должна быть в два раза поменьше, чем в действительности. Если указан масштаб 1;4, это значит, что 1 см на чертеже равен 4 см детали. Бывает и напротив. Вовсе маленький объект дозволено вычертить, скажем, в масштабе 4:1, 10:1 и т.д. Если вы видите перед собой сходственное обозначение, оно значит, что на рисунке предмет в четыре либо десять раз огромнее, чем на самом деле.
3. В географии также требуется перевод масштаба. Разглядите географическую карту. В одном из нижних углов вы увидите либо линейку с цифрами, либо примитивно цифры – скажем, 1:50 000. Цифры, финально, огромнее, чем на чертеже, но правило перевода их верно такой же, то есть в приведенном примере на 1 см карты доводится 50 000 см земной поверхности, то есть 500 м. Это карта относительно огромного масштаба. Заглянув в атлас мира, вы увидите и куда больше внушительные цифры.
4. Достаточно зачастую бывает необходимо перевести масштаб не линейной меры, а квадратной, то есть определить, сколько квадратных сантиметров. Для этого измерьте необходимый вам участок любым комфортным методом. Скажем, с поддержкой палетки. Дабы узнать реальную площадь территории, нужно линейный масштаб перевести в квадратный, то есть построить число сантиметров, содержащихся в 1 см карты, в квадрат. Полученное число умножьте на площадь участка, изображенного на карте. Таким образом вы узнаете, сколько квадратных метров занимает волнующая вас территория.
5. Изредка появляется надобность перевести масштаб объемного предмета. Скажем, на уроке труда педагог может дать задание изготовить деталь, изображенную на техническом рисунке в определенном масштабе. Вам необходимо узнать, сколько материала для этого потребуется. Тезис перевода будет тем же самым. Вначале узнайте, скольким реальным сантиметрам соответствует та либо другая линия на чертеже. Определите объем детали по чертежу. Это простая математическая задача, метод ее решения зависит от формы определенной детали. Число, которым указан масштаб, возведите в куб, а после этого умножьте на объем детали, рассчитанный по данным чертежа.
Полезный совет
Вы можете испробовать самосильно начертить несложный план, задав себе определенный масштаб. Скажем, масштаб 1:10 для плана комнаты абсолютно сгодится. Замерьте длину стен и большие предметы, определите их взаимное расположение и начертите план в точном соответствии с полученными данными.
Обратите внимание!
Масштаб тем огромней, чем поменьше знаменатель дроби, которой он записан. 1:100 огромнее, чем 1:2 000.Измерять объект комфортнее с помощником. Если помощника нет, а колышка под рукой не оказалось, плотно прижимайте рулетку к стене объекта. Измерять комфортнее каждого по земле – скажем, по низу стены.
Конспект «Масштаб. Определение расстояний» — УчительPRO
Масштаб. Определение расстояний
Масштаб — это отношение длины линии на чертеже, плане или карте к длине соответствующей линии в действительности. Он показывает, во сколько раз расстояние на карте уменьшено относительно реального расстояния на местности. Если, например, масштаб географической карты 1 : 1 000 000, это значит, что 1 см на карте соответствует 1 000 000 см на местности, или 10 км.
Различают численный, линейный и именованный масштабы.
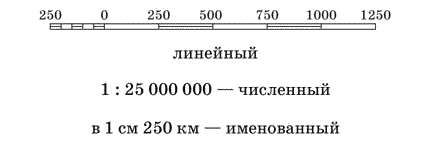
Численный масштаб изображается в виде дроби, у которой числитель равен единице, а знаменатель – число, показывающее, во сколько раз уменьшены линии на карте (плане) относительно линий на местности. Например, масштаб 1:100 000 показывает, что все линейные размеры на карте уменьшены в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем масштаб мельче, при меньшем знаменателе — крупнее. Численный масштаб – это дробь, поэтому числитель и знаменатель даются в одинаковых измерениях (сантиметрах).
Линейный масштаб представляет собой прямую линию, разделенную на равные отрезки. Эти отрезки соответствуют определенному расстоянию на изображаемой местности; деления обозначаются цифрами. Мера длины, по которой нанесены деления на масштабной линейке, называются основанием масштаба. В нашей стране основание масштаба принято равным 1 см. Количество метров или километров, соответствующее основанию масштаба, называют величиной масштаба. При построении линейного масштаба цифру 0, от которой начинается отсчет делений, обычно ставят не у самого конца масштабной линии, а отступив на одно деление (основание) вправо; на первом же отрезке налево от 0 наносят наименьшие деления линейного масштаба – миллиметры. Расстояние на местности, соответствующее одному наименьшему делению линейного масштаба, отвечает точности масштаба, а 0,1 мм – предельной точности масштаба. Линейный масштаб по сравнению с численным имеет то преимущество, что дает возможность без дополнительных вычислений определять действительное расстояние на плане и карте.
Именованный масштаб – масштаб, выраженный словами, например, в 1 см 32 км.
Измерение расстояний на карте и плане.
Измерение расстояний с помощью масштаба. Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е. на местности это расстояние составляет 1 * 5 = 5 (км). Измерять расстояние по карте можно и с помощью циркуля-измерителя. В этом случае удобно пользоваться линейным масштабом.
Измерение расстояний с помощью градусной сети. Для расчета расстояний по карте или глобусу можно использовать следующие величины: длина дуги 1° меридиана и 1° экватора равна приблизительно 111 км. Для меридианов это верно всегда, а длина дуги 1° по параллелям уменьшается к полюсам. На экваторе его можно тоже принять равному 111 км. А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.
Следующая тема:
Рельеф. Изображение неровностей
§ 11. Как правильно рассчитать расстояние на карте с использованием масштаба
Существует несколько способов определения расстояния на карте, плане или местности. Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.
Алгоритм определения расстояние между двумя объектами
Предположим, тебе необходимо по конкретной карте узнать реальное расстояние между селами А и В. При этом дан такой масштаб: в 1 см – 0,5 км (или 1:50000).
- Возьми обычную линейку и измерь расстояние между двумя пунктам по карте (рис. 1).
- Полученную величину (предположим это отрезок длиной 5 см) умножь на 0,5 км, соответственно масштабу карты.
- Переведи полученный ответ в наиболее рациональную единицу измерения расстояний (м или км). В данном случае ты получишь правильный ответ: расстояние между селом А и селом В составляет 2,5 километра.
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом. Для этого достаточно циркуль-измеритель, раствор (угол) которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рисунке измеренное расстояние равно 1070 м (рис. 2).
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки и циркуля-измерителя (рис. 3).
Раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
— Хорошие калькуляторы
Вы можете использовать этот онлайн-калькулятор преобразования масштаба, чтобы преобразовать размер реального объекта в масштабированный размер и наоборот.
Как пользоваться калькулятором преобразования шкалы
- 1. Выберите, какой метод преобразования вы хотите использовать:
- а. Преобразование реального (реального) размера в масштаб.
- г. Преобразование масштаба в реальный (реальный) размер.
- 2.Введите масштабный коэффициент; например, если вы хотите работать со шкалой 1/6, введите 6.
- 3. Введите размеры фактического объекта (или размеры масштабируемого объекта, если вы планируете преобразовать масштаб в фактический размер)
- 4. Выберите единицу измерения из раскрывающегося списка
- 5. Нажмите кнопку «Преобразовать», чтобы получить результаты.
Дополнительная информация
Масштабный коэффициент — это число, которое используется как множитель при масштабировании размера объекта.Его можно использовать для масштабирования объектов в 1, 2 или 3 измерениях, а также в виде дробей, соотношений, процентов или десятичных знаков. Когда применяется масштабный коэффициент, размер объекта увеличивается или уменьшается в соответствии с желаемым масштабом. Несмотря на то, что размер изображения был изменен, соотношения каждого измерения должны быть зеркальными.
Чтобы масштабировать объект до большего размера, вы просто умножаете каждое измерение на требуемый масштабный коэффициент. Например, если вы хотите применить масштабный коэффициент 1: 6, а длина предмета равна 5 см, вы просто умножаете 5 × 6 = 30 см, чтобы получить новое измерение.
Чтобы масштабировать объект до меньшего размера, вы просто делите каждое измерение на требуемый коэффициент масштабирования. Например, если вы хотите применить масштабный коэффициент 1: 6, а длина предмета составляет 60 см, вы просто разделите 60/6 = 10 см, чтобы получить новое измерение.
Методы масштабирования, описанные выше, работают в предположении, что коэффициент масштабирования принимает форму 1 / n или 1: n (где n — коэффициент). Однако, если это не так, может потребоваться дополнительная работа.Например, скажем, у нас есть соотношение 2: 5. Чтобы преобразовать соотношение в форму 1: n, вам нужно будет разделить каждую сторону на число, которое появляется слева. Например, если соотношение составляет 2: 5, вы разделите обе стороны на 2, что даст эквивалентное соотношение 1: 2,5. Кроме того, вы можете использовать наш онлайн-расчетчик соотношений.
.Калькулятор масштабного коэффициента— найдите коэффициент масштабирования 2-х длин
Ваш браузер не поддерживает элемент холста.
Этот калькулятор поможет нам найти масштабный коэффициент между двумя длинами, просто введите две длины, он автоматически рассчитает масштабный коэффициент, поддерживает различные единицы длины (мм, см, м, км, дюймы, футы, ярды, мили), в дополнение к соответствующему графическому изображению и формуле, легкое понимание процесса расчета и результата.
Как использовать измеритель масштабного коэффициента
- Введите длину A и B
- Число принимает десятичное или дробное число, например.6, 12, 4,7, 1/2, 5 3/8
- Если единицы длины разные, выберите подходящие
- Результат (масштабный коэффициент) будет рассчитан автоматически.
Как определить масштабный коэффициент?
В двух одинаковых геометрических фигурах, масштабный коэффициент — это отношение их соответствующих сторон, разделение двух соответствующих длин сторон даст соотношение, например
Какой масштабный коэффициент от 4 до 10 см?
4 и 10 делятся на 2
Длина A: 4 ÷ 2 = 2
Длина B: 10 ÷ 2 = 5
, поэтому коэффициент масштабирования от A до B равен 2: 5
Если 12 дюймов равны 3 дюймам, каков масштабный коэффициент?
12 и 3 делятся на 3
12 ÷ 3 = 4
3 ÷ 3 = 1
Упрощенное соотношение 12: 3 составляет 4: 1
, поэтому коэффициент масштабирования от 12 дюймов до 3 дюймов составляет 4: 1
Если 1/4 дюйма равняется 2 футам, каков масштабный коэффициент?
1⁄4 дюйма = 1 ÷ 4 = 0.25 дюймов
2 фута = 12 × 2 = 24 дюйма
1 ÷ 0,25 = 4
24 × 4 = 96
0,25: 24 упрощенное соотношение составляет 1:96
, поэтому масштабный коэффициент от 1⁄4 дюйма до 2 футов равен 1: 96
Если вы хотите знать, какая длина при конвертации в разных масштабах, попробуйте этот инструмент преобразования длины шкалы, это помогает нам быстро рассчитать длину.
Что вы думаете об этом калькуляторе масштабного коэффициента?
Попробуйте калькулятор масштабного коэффициента на своем смартфоне
Отсканируйте QR-код, чтобы открыть браузер
Онлайн линейки
Поделитесь с хорошими друзьями
Добро пожаловать, чтобы поделиться этим онлайн-калькулятором весов со своими друзьями, может быть, им он понравится.
.Калькулятор среднего балла
Scholaro
Страна:| Курс | Кредиты / часа * | Оценка * |
|---|
Количество добавляемых строк: Добавить Рассчитать GPA
Прозрачные марки
* Не теряйте свой средний балл.Получите отчет Premium, чтобы сохранить его в формате PDF, обновить, распечатать или поделиться с учебными заведениями и работодателями.
О калькуляторе Scholaro GPA
Этот международный калькулятор среднего балла предназначен для того, чтобы помочь вам рассчитать США. Средний балл (GPA) на основе оценок или баллов практически из любой страны Мир. Средний академический балл США рассчитывается по шкале 4,0.
Как рассчитывается средний балл?
1) Сначала оценки переводятся в U.Эквивалент S. для других стран, кроме США
| Китайский сорт | Сорт США |
|---|---|
| 90 | А |
| 85 | Б |
| 80 | B |
2) Конвертер GPA переводит каждую оценку в США в баллы по следующей шкале:
| U.S. Оценка | Баллы |
|---|---|
| А + | 4.0 |
| А | 4,0 |
| A- | 3,7 |
| Оценка США | Баллы |
|---|---|
| Б + | 3,3 |
| В | 3,0 |
| Б- | 2,7 |
| U.S. Оценка | Баллы |
|---|---|
| К + | 2.3 |
| С | 2,0 |
| К- | 1,7 |
| Оценка США | Баллы |
|---|---|
| Д + | 1,3 |
| D | 1.0 |
| Д- | 0,7 |
| U.S. Оценка | Баллы |
|---|---|
| Ф | 0,0 |
| – | |
| – |
3) Баллы за каждый класс умножаются на количество кредитов или часов для этого класса, складываются и делятся на общее количество кредитов или часов.
| Кредиты | Оценка США | Баллы |
|---|---|---|
| 3 | А | 4.0 |
| 3 | B | 3,0 |
| 2 | B | 3,0 |
| Всего баллов | |
|---|---|
| 3 x 4,0 = | 12,0 |
| 3 x 3,0 = | 9,0 |
| 2 x 3,0 = | 6,0 |
| 12.0 + 9,0 + 6,0 = | 27,0 |
| разделить на | |
| 3 + 3 + 2 = | 8 |
| Совокупный GPA = | 3,38 |
Другие весы для переоборудования
Приведенная выше шкала является наиболее распространенной шкалой пересчета среднего балла, используемой в средних школах и университетах США. Некоторые университеты используют.67 и 0,33 шага для большей точности, но это разница существенно не влияет на итоговый средний балл. Некоторые школы используют 0,5 шага. Например, и A-, и B + конвертируются в 3.5. Этот тип преобразования менее точен, потому что A- и B + редко считаются одной и той же оценкой. A + иногда конвертируется в 4,3 (или 4,33) балла, но многие университеты не имеют A +.
Старшие школы также часто дают дополнительный балл за классы AP (Advanced Placement), поэтому GPA может быть на уровне 5.0. Однако этот средний балл известен как взвешенный средний балл. Невзвешенный средний балл по-прежнему рассчитывается из 4 баллов и указывается в расшифровке стенограммы рядом с взвешенным средним баллом.
Является ли D в США проходным баллом?
D — это проходной балл в большинстве государственных школ (начальных и средних школ) в США, но обычно не в колледже. Курсы колледжа с оценкой D не могут быть переведены, но могут быть взяты повторно. Для получения высшего образования в большинстве средних школ требуется средний балл не ниже 1.0. Большинство программ бакалавриата требуют минимум 2.0 ГПД. Для большинства программ магистратуры требуется 3.0 или выше.
.Калькулятор соотношения
Укажите любые три значения ниже, чтобы вычислить четвертое в соотношении A: B = C: D .
Калькулятор масштабирования отношения
Связано: Калькулятор дробей
Что такое коэффициент?
Отношение — это количественное соотношение между двумя числами, которое описывает, сколько раз одно значение может содержать другое. Коэффициенты применяются повсеместно, а концепция коэффициентов интуитивно понятна. Вероятно, это можно продемонстрировать, если дать ребенку вдвое меньше печенья, чем его сестре.Хотя ребенок, возможно, не сможет озвучить несправедливость, используя коэффициенты, хриплые протесты, которые, скорее всего, последуют, должны сразу сделать очевидным, что он хорошо осведомлен о том, что получил 1: 2 столько печенья, сколько его сестра, концептуально, если не математически .
Как показано выше, отношения часто выражаются двумя числами, разделенными двоеточием. Их также можно записать как «от 1 до 2» или как дробь ½. Отношение представляет собой число, которое необходимо умножить на знаменатель, чтобы получить числитель.В этом случае ½. Это понятнее, если первое число больше второго, т.е. при соотношении 2: 1, 2 может содержать 1, 2 раза. Также возможно иметь отношения, содержащие более двух членов.
Соотношения распространены во многих повседневных приложениях, включая: соотношения сторон экранов, описание карт и моделей как уменьшенную версию их фактического размера, при выпечке и приготовлении пищи, при обсуждении вероятности того, что что-то произойдет, или для описания показателей, например, в финансы. Если, например, человек хотел испечь 5 пирожных, для каждого из которых требовалось соотношение масла: сахара: муки 1: 2: 3, и хотел определить общее количество масла, сахара и муки, которое необходимо, он было бы просто вычислить с учетом этого отношения.Увеличение соотношения в пять раз дает соотношение 5:10:15, и его можно умножить на любое количество сахара, муки и масла, которые используются в фактическом рецепте торта.
Типичные форматы и размеры экранов и видео
Соотношение сторон — это соотношение размеров геометрической фигуры в разных измерениях. В случае прямоугольника соотношение сторон — это соотношение его ширины к его высоте. Хотя соотношения сторон широко используются в таких приложениях, как калибровка шин, размер бумаги и стандартные размеры фотографий, некоторые из наиболее частых применений соотношений сторон включают размеры экрана компьютера, экраны мобильных телефонов и размеры видео.Таким образом, ниже приведен список типичных разрешений экрана / видео и соотношений сторон экрана компьютера.
| Имя | Соотношение сторон | Ширина (пиксель) | Высота (пиксель) |
| 480p | 3: 2 | 720 | 480 |
| 576p | 5: 4 | 720 | 576 |
| 720p | 16: 9 | 1280 | 720 |
| 1080p | 16: 9 | 1920 | 1080 |
| 2160p (4K UHD) | 16: 9 | 3840 | 2160 |
| 4320p (8K UHD) | 16: 9 | 7680 | 4320 |
| 8640p | 16: 9 | 15360 | 8640 |
| SVGA | 4: 3 | 800 | 600 |
| WSVGA | ~ 17: 10 | 1024 | 600 |
| XGA | 4: 3 | 1024 | 768 |
| XGA + | 4: 3 | 1152 | 864 |
| WXGA | 16: 9 | 1280 | 720 |
| WXGA | 5: 3 | 1280 | 768 |
| WXGA | 16:10 | 1280 | 800 |
| SXGA (UVGA) | 4: 3 | 1280 | 960 |
| SXGA | 5: 4 | 1280 | 1024 |
| HD | ~ 16: 9 | 1360 | 768 |
| HD | ~ 16: 9 | 1366 | 768 |
| SXGA + | 4: 3 | 1400 | 1050 |
| WXGA + | 16:10 | 1440 | 900 |
| HD + | 16: 9 | 1600 | 900 |
| UXGA | 4: 3 | 1600 | 1200 |
| WSXGA + | 16:10 | 1680 | 1050 |
| FHD | 16: 9 | 1920 | 1080 |
| WUXGA | 16:10 | 1920 | 1200 |
| QWXGA | 16: 9 | 2048 | 1152 |
| WQHD | 16: 9 | 2560 | 1440 |
| WQXGA | 16:10 | 2560 | 1600 |
