Расстояние между отрезком и точкой: Расстояние от точки до отрезка

Расстояние от точки до прямой. Что это такое? На плоскости и в пространстве

Если вам понадобится узнать расстояние от дома до пиццерии, то вы без труда справитесь с задачей, ведь расстояние между точками — это длина отрезка, который соединяет эти точки. А что если нужно вычислить расстояние от дома до проспекта или улицы? В такой ситуации поможет знание темы «Расстояние от точки до прямой на плоскости».

Что называется расстоянием от точки до прямой?

Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на прямую. Перпендикуляр — это кратчайшее расстояние от точки до прямой.

Доказать это очень просто. Из точки M на прямую f мы опустим перпендикуляр MN и произвольную прямую MP, которая также называется наклонной. А по свойству мы помним, что наклонная всегда больше перпендикуляра, что и требовалось доказать.

Расстояние между точкой M и прямой f на плоскости обозначают так:

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Расстояние между параллельными прямыми

А если нужно вычислить расстояние между двумя параллельными улицами — какое математическое понятие поможет в этом случае? Конечно, вы уже догадались, что это расстояние между параллельными прямыми.

Расстоянием между параллельными прямыми называется расстояние от какой-либо прямой до другой прямой на плоскости.

Убедимся в верности этого утверждения — рассмотрим параллельные прямые m и n. На прямой m выберем две точки E и F, опустим из них перпендикуляры на прямую n, точки пересечения перпендикуляров с прямой n обозначим буквами G и H, а также соединим E и H отрезком.

Рассмотрим треугольники GEH и EFH: сторона EH — общая, (как накрест лежащие углы). Следовательно, по гипотенузе и острому углу. А из свойства равных треугольников мы знаем, что будут равны и соответствующие элементы, например, EG = FH.

Делаем вывод, что расстоянием между параллельными прямыми на плоскости является длина их общего перпендикуляра, причем выбор перпендикуляра может быть произвольным.

Расстояние между двумя прямыми m и n обозначается так: .

Решение задач

Применим полученные знания, решив несколько задач.

Задача 1

На клетчатой бумаге с размером клетки отмечены точки K, M и N. Чему равно расстояние от точки K до прямой MN?

Как вы помните, чтобы найти расстояние от точки до прямой, нужно из точки на прямую опустить перпендикуляр и вычислить его длину.

Ответ: 4 см.

Задача 2

Найдите расстояние от точки Q до прямой PR, пользуясь данными с чертежа.

Из чертежа видно, что отрезок QR перпендикулярен прямой PR, а значит QR — расстояние от точки Q до прямой PR. В прямоугольном треугольнике PQR отрезок QR лежит против угла в , а значит, равен половине гипотенузы, то есть 14 см.

Ответ: 14 см.

Задача 3

В равностороннем треугольнике PQR проведена биссектриса QS, а ST — расстояние от точки S до прямой QR, равное 12 см. Чему равно расстояние от точки Q до прямой PR?

1. Поскольку — равносторонний, то , а так как по условию QS — биссектриса, то .

2. Рассмотрим , так как ST — расстояние от точки S до прямой QR, значит, — прямоугольный. А ST — катет, лежащий против угла в , следовательно, QS = 2ST = 24 см.

3. Так как — равносторонний, то QS не только биссектриса, но и высота , значит, .

Ответ: 24 см.

А если прямая на плоскости находится так далеко, что провести до нее перпендикуляр физически не получается — что делать в этом случае? Поможет формула расстояния от точки до прямой в координатах.

Пусть формула задана прямой f: ax + by + c = 0 и есть точка M с координатами , тогда формула расстояния от точки до прямой на плоскости выглядит следующим образом:

.

Задача 4

Найдите расстояние от точки M (36; 6) до прямой f: 6x + 2y − 12 = 0.

Нам не придется даже изображать прямую и точку, а тем более подбирать масштаб, чтобы поместился перпендикуляр, — достаточно воспользоваться формулой:

Конечно, без координат тоже можно вычислить, но вариант выше — самый рациональный и удобный.

На курсах по математике в онлайн-школе Skysmart мы всегда показываем разные способы решений, которые сохранят вам время на контрольной или экзамене. Выберите подходящий по уровню и цели обучения курс и начните заниматься в удовольствие!

Шпаргалки по математике родителей

Все формулы по математике под рукой

Графическое определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

Алгоритм

1. Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
2. Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
3. Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

Пример

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Решение

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П

4. В новой системе (П₁, П₄) точки C»₁, D»₁, M»₁ находятся на том же удалении от оси X₁, что и C», D», M» от оси X.

Выполняя вторую часть алгоритма, из M»₁ опускаем перпендикуляр M»₁N»₁ на прямую b»₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину.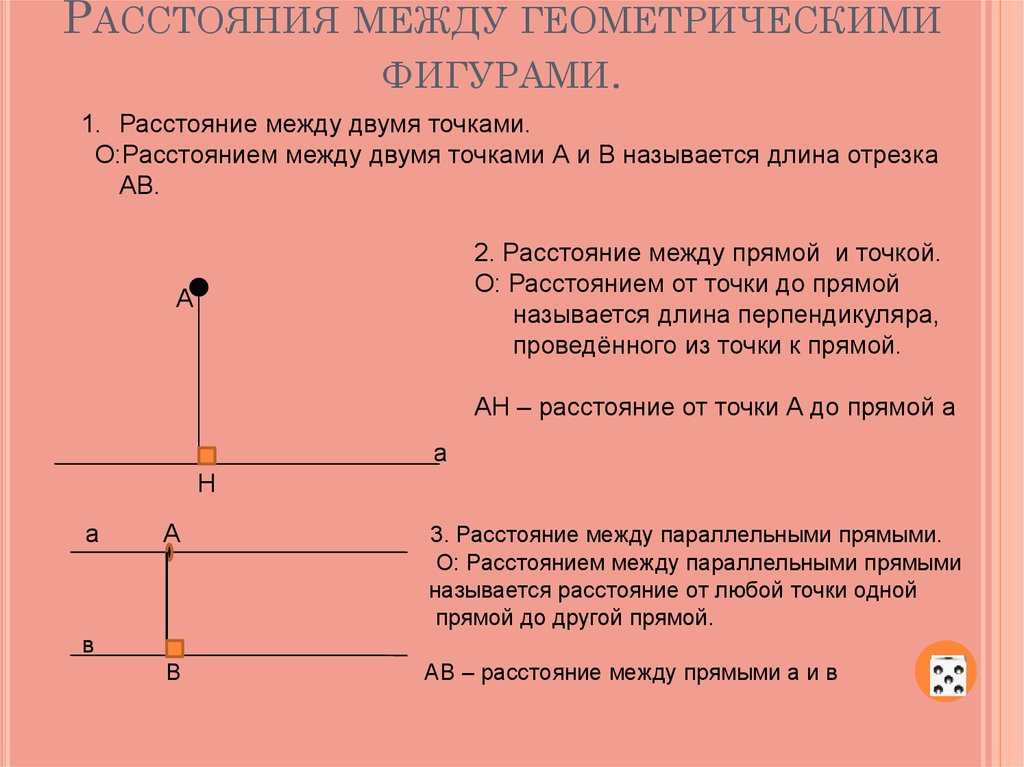 По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»₁N»₁. Для этого строим прямоугольный треугольник M»₁N»₁N₀, у которого катет N»₁N₀ равен разности (Y_M1

 – Y_N1) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M»₁N₀ треугольника M»₁N»₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

• Параллельно CD вводим новую фронтальную плоскость П₄. Она пересекает П₁ по оси X₁, причем X₁∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»₁, D»₁ и M»₁, как это изображено на рисунке.
• Перпендикулярно C»₁D»₁ строим дополнительную горизонтальную плоскость П₅, на которую прямая b проецируется в точку C’₂ = b’₂.
• Величина расстояния между точкой M и прямой b определяется длиной отрезка M’₂C’₂, обозначенного красным цветом.

Похожие задачи:

Заказать чертеж

Расстояние точки от линии

Согласно евклидовой геометрии, расстояние от точки до линии можно рассматривать как кратчайшее расстояние от данной точки до точки на бесконечной прямой линии. Длина отрезка, соединяющего точку с ближайшей точкой на линии, равна кратчайшему расстоянию от этой точки, то есть расстоянию по перпендикуляру от точки до линии. Формула для расчета расстояния от точки до линии может быть получена и выражена во многих формах. Знание расстояния от точки до линии может быть полезно в различных жизненных ситуациях, например, чтобы найти расстояние между двумя объектами, такими как два дерева.

В этой статье мы изучим, как найти расстояние точки от линии, используя вывод и решенные примеры.

1.	Определение расстояния точки от линии
2.	Определение расстояния точки от линии
3.	Решенные примеры
4.	Практические вопросы
5.	Часто задаваемые вопросы о расстоянии точки от линии

Определение расстояния точки от линии

Расстояние между точкой и линией — это кратчайшее расстояние между ними. Это минимальная длина, необходимая для перемещения от точки к точке на линии. Это расстояние минимальной длины может быть показано как отрезок, перпендикулярный линии. Рассмотрим прямую L и точку X, которая не лежит на L, как показано ниже:

Как измерить расстояние точки от прямой, если точка не лежит на прямой? Чтобы ответить на вопрос, вспомним уравнение прямой и формулу расстояния. Кроме того, рассмотрим треугольник ABC с прямым углом в точке B:

Обратите внимание, что, поскольку ∠B = 90°, это самый большой угол в треугольнике, а это означает, что AC (гипотенуза) является наибольшей стороной.

Это всегда будет правдой. Гипотенуза АС всегда больше перпендикуляра из А в ВС, то есть АВ. Возвращаясь к нашей точке и прямой, опустим перпендикуляр из X на L:

Y — основание этого перпендикуляра, а Z — любая другая точка на L. Обратите внимание, что XY всегда будет на меньше, чем XZ, независимо от того, где находится Z на линии. Другими словами: кратчайшее расстояние точки от прямой проходит по перпендикуляру, опущенному из точки на эту прямую. Таким образом, определение расстояния точки X от прямой L равно длине перпендикуляра, опущенного из X на L.

Определение расстояния точки от линии

Выведем формулу для измерения расстояния точки от прямой, используя формулу расстояния и формулу площади треугольника.

Рассмотрим прямую L в плоскости XY и K(\(x_{1}\),\(y_{1}\)) — любая точка на расстоянии d от прямой L. Эта линия представлена ​​Ax + By + C = 0. Расстояние точки от линии, ‘d’ — это длина перпендикуляра, проведенного из K в L.

Точки пересечения x и y могут быть указаны как (-C/A) и ( -С/В) соответственно.

Линия L пересекает оси x и y в точках B и A соответственно. KJ — перпендикулярное расстояние точки K, которая пересекает основание AB Δ KAB в точке J. Для трех заданных точек K, B и A координаты могут быть заданы как K(\(x_{1}\), \(y_{1}\)), B(\(x_{2}\),\(y_{2}\)) и A(\(x_{3}\),\(y_{3}\) ))

Здесь (\(x_{2}\),\(y_{2}\)) = ((-C/A), 0) и (\(x_{3}\),\(y_ {3}\)) = (0, (-С/В)).

Требуется найти перпендикулярное расстояние KJ = d

Площадь треугольника определяется по формуле: Площадь (Δ КАВ) = ½ основания × перпендикулярная высота

Площадь (Δ КАВ) = ½ АВ × КДж

⇒ КДж = 2 × площадь (Δ KAB) / AB -> (1)

В координатной геометрии площадь (Δ KAB) рассчитывается как:

Площадь A = ½ |\(x_{1}\)(\(y_{2}\ ) — \(y_{3}\)) + \(x_{2}\)(\(y_{3}\) — \(y_{1}\)) + \(x_{3}\)(\ (у_{1}\) — \(у_{2}\))|

= ½ | \(x_{1}\) (0 — (-C/B)) + (-C/A) ((-C/B) — \(y_{1}\)) +0 (\(y_{1 }\) − 0)|

= ½ |(C/B) × \(x_{1}\) — C/A ((−C/B) -\(y_{1}\)) + 0|

= ½ |(C/B) × \(x_{1}\) — C/A ((−C-B\(y_{1}\))/B)|

= ½ |(C/B) × \(x_{1}\) + C ² /AB + ((BC\(y_{1}\))/AB)|

= ½ |(C/B) × \(x_{1}\) + (C/A) × \(y_{1}\) + (C ² /AB)|

= ½ |C( \(x_{1}\)/B + \(y_{1}\)/A + C/AB)|

Умножаем и делим выражение на AB, получаем

= ½ |C(AB\(x_{1}\)/AB ² + (AB\(y_{1}\))/BA ² + (АВС ² )/(AB) ² |

= ½ |CA\(x_{1}\)/AB + CB\(y_{1}\)/AB + C ² /AB|

=½ |C/ (AB)|.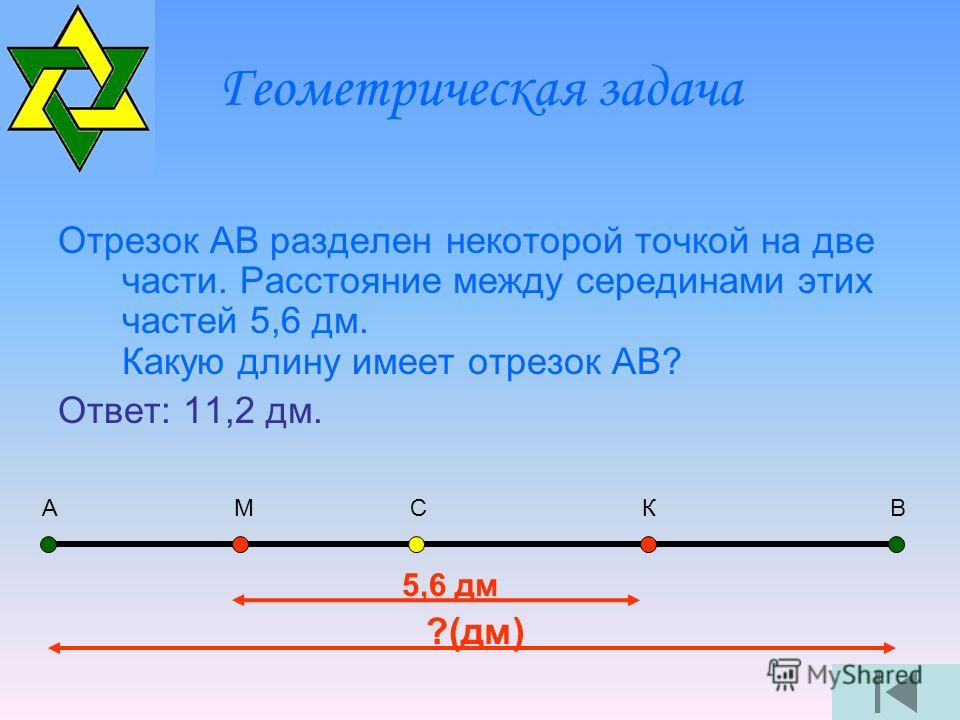

|A\(x_{1}\) + B\(y_{1}\) + C| ->(2)

Согласно формуле расстояния расстояние от линии AB с координатами A(\(x_{1}\),\(y_{1}\)), B(\(x_{2 }\),\(y_{2}\)) можно рассчитать как:

AB = ((\(x_{2}\) _{— \(x_{1}\)) ² + (\( y_{2}\) — \(y_{1}\)) ² ) ^½}

Здесь A(\(x_{1}\),\(y_{1}\)) = A (0, -C/B) и B(\(x_{2}\),\(y_{2}\)) = B(-C/A,0)

AB = (((-C/A) ² — 0) + (0 — (-C/B) ² )) ^½

= ((C/A) ² + ( C/B) ² ) ^½

Расстояние, AB = |C/AB| (A ² + B ² ) ^½ -> (3)

Подставляя (2) и (3) в (1), получаем

Расстояние перпендикуляра KJ = d = |A\ (x_{1}\) + B\(y_{1}\) + C| / (A ² + B ² ) ^½

Следовательно, расстояние от точки (\(x_{1}\),\(y_{1}\)) до прямой Ax + By + C = 0 определяется выражением = |A\(x_{1}\) + B\(y_{1}\) + C| / √(А ² + B ²⁾

Числитель в этой формуле должен быть заключен со знаком абсолютного значения, так как расстояние должно быть положительным значением, и некоторые комбинации A \(x_{1}\ ) , B\(y_{1}\) , C может дать отрицательное число.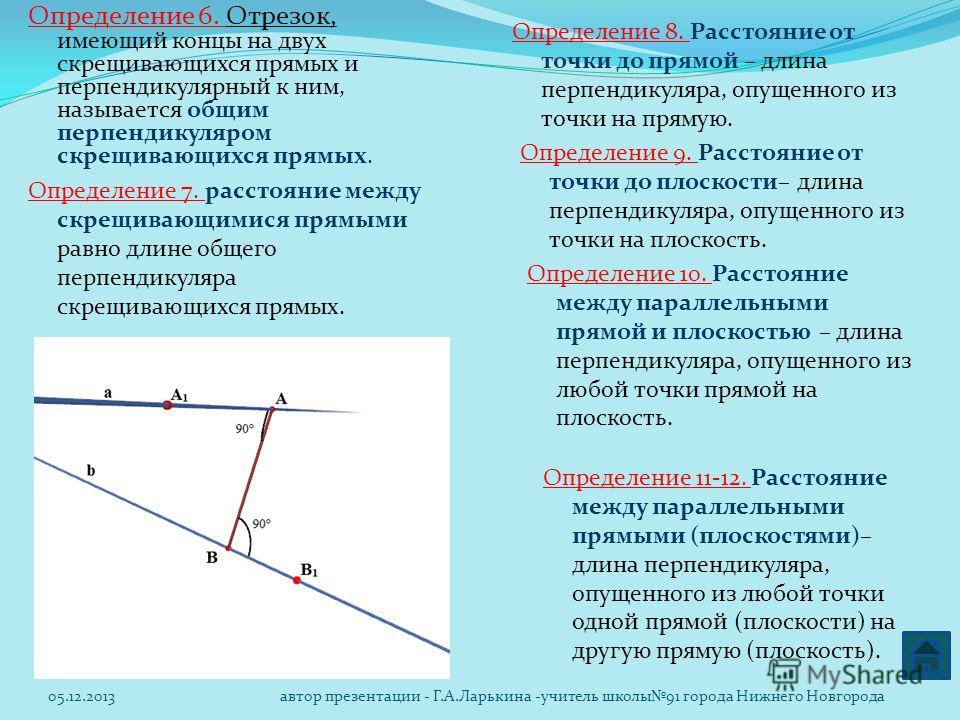

Похожие статьи о расстоянии точки от линии

Ознакомьтесь со следующими страницами, посвященными расстоянию точки от линии.

• Уголки
• Строки
• Линейный сегмент
• Перпендикуляр
• Геометрия

Важные примечания

Вот несколько точек, которые следует помнить при изучении расстояния точки от линии:

• Для получения формулы для измерения расстояния точки от линии мы используем формула расстояния и формула площади треугольника.
• Согласно евклидовой геометрии расстояние от точки до прямой можно рассматривать как кратчайшее расстояние от данной точки до любой точки на бесконечной прямой линии.
• Длина отрезка, соединяющего точку с ближайшей точкой на линии, равна кратчайшему расстоянию от этой точки, то есть расстоянию по перпендикуляру от точки до линии.

Часто задаваемые вопросы о расстоянии точки от линии

Как найти расстояние от точки до прямой?

Расстояние от точки (\(x_{1}\),\(y_{1}\)) до прямой Ax + By + C = 0 можно рассчитать по формуле |A\(x_{1 }\) + В\(у_{1}\) + С| / √(А ² + B ²⁾

Каково расстояние от точки до прямой?

В соответствии с евклидовой геометрией расстояние от точки до прямой можно рассматривать как кратчайшее расстояние от данной точки до любой точки на бесконечной прямой линии.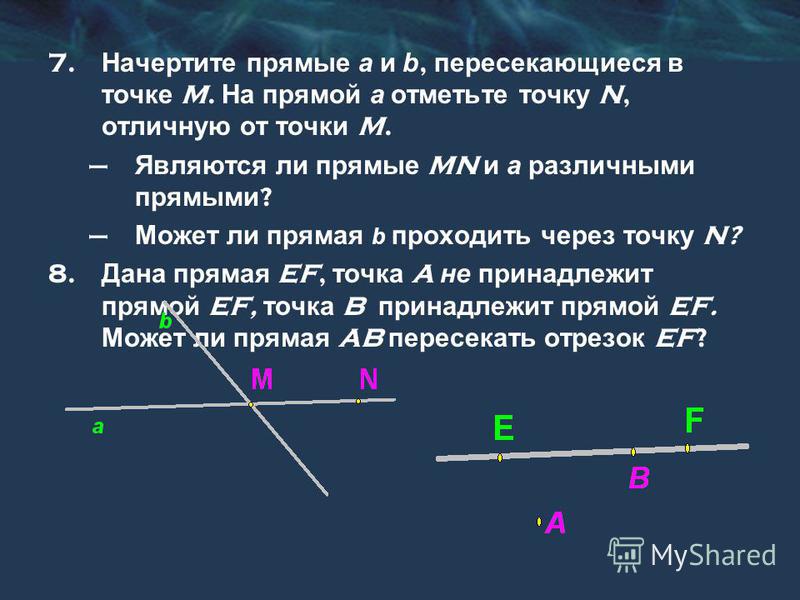 Длина отрезка, соединяющего точку с ближайшей точкой на линии, равна кратчайшему расстоянию от этой точки, то есть расстоянию по перпендикуляру от точки до линии.

Как найти перпендикулярное расстояние точки от прямой в декартовой форме?

Рассмотрим уравнение прямой DF как (x-\(x_{1}\))/a = (y-\(y_{1}\))/b = (z-\(z_{1}\) )/с. Пусть L — основание перпендикуляра из K (α, β, γ) на прямую DF. Пусть координаты L равны (\(x_{1}\) + aλ, \(y_{1}\) + bλ, \(z_{1}\) + cλ). Тогда отношения направлений KL равны (\(x_{1}\) + aλ – α, \(y_{1}\) + bλ – β, \(z_{1}\) + cλ – γ). Отношения направлений DF равны (a, b, c). Так как KL перпендикулярна DF, то a (\(x_{1}\)+ aλ – α) + b (\(y_{1}\) + bλ – β) + c (\(z_{1}\) + cλ – γ) = 0. Подставляя значение λ в (\(x_{1}\) + aλ, \(y_{1}\) + bλ, \(z_{1}\) + cλ), получаем подошва перпендикуляра. Теперь мы можем получить расстояние KL, используя формулу расстояния.

Как найти расстояние от точки до линии в 3D?

Таким образом можно найти расстояние от точки до линии в 3D. Если \(J_{0}\)(\(x_{0}\),\(y_{0}\),\(z_{0}\)) координаты точки, \begin{equation} \bar{s} =\{м; н; p\} \end{equation} направляющий вектор прямой l, \(J_{1}\)(\(x_{1}\),\(y_{1}\),\(z_{1}\)) — координаты точки на прямой l, затем расстояние между точкой \(J_{0}\)(\(x_{0}\),\(y_{0}\),\(z_{0}\)) и прямой l можно найти по следующей формуле: \begin{equation} d=\frac{\left|\overline{J_{0} J_{1}} \times \bar{s}\right|}{|\bar{ s}|} \end{уравнение} 92}$.

Пожалуйста, помогите

• геометрия
• аналитическая геометрия

$\endgroup$

4

$\begingroup$

Вот элементарный геометрический вывод формулы:

Любая (ст.)прямая, перпендикулярная прямой $$Ax+By+C=0\qquad\text{(1)}$$ задается $ $Bx-Ay+C’=0\qquad\text{(2)}$$ Поскольку (2) должно проходить через точку $(x_1,y_1)$ ( 92}}.$$

$\endgroup$

$\begingroup$

Для чего это стоит, вот план с использованием «производного подхода». 2}}. $$ 92 } $$

Теперь должно быть очевидно, что расстояние от точки $p$ на прямой до $(x_1,y_1)$ велико, если $p$ находится «на крайнем конце прямой». Итак, минимальное расстояние достигается в точке, где $P'(x)=0$.

Итак, вам нужно найти $P'(x)$, а затем решить $P'(x)=0$. Я оставлю это для вас…

Вы должны получить только одно решение $P'(x)=0$. Минимум $P$ и, следовательно, минимум $D$ должен был бы иметь место в этой точке. Если вы затем подставите это решение в (1), ваша формула будет получена после небольшого упрощения.

$\endgroup$

3

$\begingroup$

Расстояние $d$ между точкой $P_1(x_{1},y_{1})$ и прямой $r$, уравнение $Ax+By+C=0$ можно вывести алгебраически следующим образом:

i) Найдите уравнение прямой $s$, проходящей через $P_1$ и ортогональной к $r$. Назовем $P_2$ точкой пересечения $r$ и $s$.

ii) Найдите координаты $P_2(x_{2},y_{2})$.

iii) Найдите расстояние от $P_1$ до $P_2$. Это расстояние равно $d$.

$\endgroup$

4

$\begingroup$

Предположим, что $(x_0,y_0)$ находится на прямой, а $(x_1-x_0,y_1-y_0)$ ортогонален этой прямой. Пифагор говорит, что квадрат расстояния от $(x_1,y_1)$ до любого $(x,y)$ на прямой равен сумме квадратов расстояний от $(x_1,y_1)$ до $(x_0,y_0). )$ и от $(x_0,y_0)$ до $(x,y)$. Следовательно, это расстояние минимально, когда $(x,y)=(x_0,y_0)$. 92$, и я позволю тебе закончить отсюда.

$\endgroup$

$\begingroup$

Я не решаю, но даю шаги для этого. 1. Проведите перпендикуляр на заданную прямую из данной точки. 2. Поскольку у нас есть уравнение линии, мы можем узнать ее наклон (м). 3. Используйте соотношение, чтобы узнать наклон перпендикулярной линии m1 * m2 = -1 (m1 и m2 — наклоны перпендикулярных линий). Теперь у нас есть наклон перпендикулярной линии и 1 точка, из которой она проходит (данная точка (x1 , у1)). 4. узнать уравнение perpend.line. 5.найти точку пересечения нижней линии. 6.finally рассчитать расстояние между заданной точкой и точкой пересечения.

$\endgroup$

$\begingroup$

Рассмотрим прямую $\overleftrightarrow{l}$, уравнение которой равно $Ax+By+C=0$, и точку $P(x_1,y_1)$, как показано выше. Предположим, что $\overleftrightarrow{l}$ пересекает оси $x$ и $y$ в точках $M$ и $N$ соответственно.

Чтобы найти расстояние между $P$ и $\overleftrightarrow{l}$, давайте сначала найдем расстояние между пересечениями $x$ и y $\overleftrightarrow{l}$. 9{2}}}\справа| Область △PMN$$

Теперь снова рассмотрим приведенное выше △PMN; Мы знаем, что площадь треугольника с вершинами в точках $(x_1,y_1),(x_2,y_2)$ и $(x_3,y_3)$ определяется как

$$Area = \frac{1}{2}\ влево|x_{1}\влево(y_{2}-y_{3}\вправо)+x_{2}\влево(y_{3}-y_{1}\вправо)+x_{3}\влево(y_ {1}-y_{2}\right)\right|$$

Итак, используя приведенный выше результат, Area $\triangle{PMN}$ становится $\dfrac{1}{2}\left| \dfrac{C}{AB}\right| \cdot \влево| Ax_1 +By_1 +C\right|$ кв.