По какой формуле найти расстояние между двумя точками? – Обзоры Вики
Узнайте, как найти расстояние между двумя точками, используя формулу расстояния, которая является приложением теоремы Пифагора. Мы можем переписать теорему Пифагора в виде d=u221a((x_2-x_1)²+(y_2-y_1)²) чтобы найти расстояние между любыми двумя точками.
Отсюда, каково расстояние между двумя точками? Расстояние между двумя точками определяется как длина прямой, соединяющей эти точки в координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками.
Дополнительно Каково расстояние между точками A и B? Расстояние от А до В равно то же, что и расстояние от B до A. Чтобы вывести формулу расстояния между двумя точками на плоскости, рассмотрим две точки A(a,b) и B(c,d).
Мы можем построить прямоугольный треугольник ABC, как показано на следующей диаграмме, где точка C имеет координаты (a, d).
Каково расстояние между точками A и B quizlet? Члены этого набора (84) Расстояние между точками A и B, записанное как AB, равно абсолютное значение разности координат точек A и B. Мера ∠AOB, которую можно записать как m∠AOB, равна модулю разности между действительными числами, совпадающими с лучом OA и лучом OB на транспортире.
Для какой пары точек можно использовать числовую прямую, чтобы найти расстояние?
Каково расстояние между 8 — 3 и 4 — 7? Расстояние между (8, -3) и (4, -7) равно О 5.66.
Каково расстояние между точками P и Q?
Расстояние между двумя точками P (x1, y1) и Q (x2, y2) определяется как: d (P, Q) = √ (x2 — x1) 2 + (y2 — y1) 2 {Формула расстояния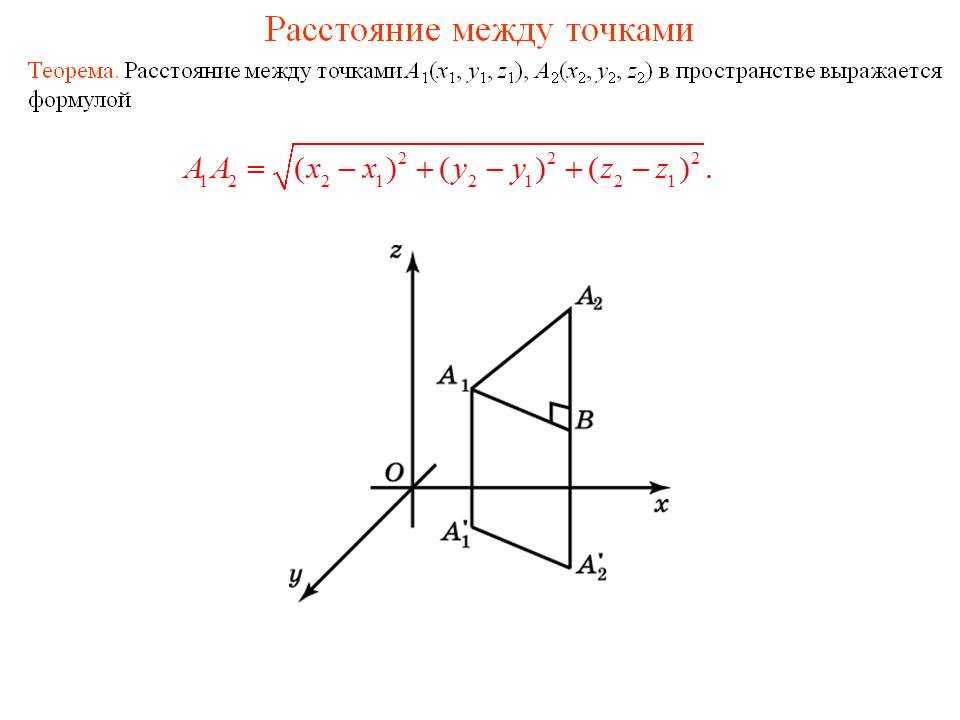} 2.
2)
Как найти расстояние между двумя точками на отрезке?
Как найти расстояние между двумя рациональными числами? Чтобы найти расстояние между двумя рациональными числами на числовой прямой, может посчитать количество единиц между числами. Используя формулу, расстояние между рациональными числами p и q равно |p – q|.
Каково расстояние между точками 4 7 и 2 2? Расстояние между (4, 7) и (2, 2) равно О 5.385 после округления.
Какова длина линии?
Ответ: Длина отрезка прямой может быть измеренным путем измерения расстояния между двумя его конечными точками. Это путь между двумя точками определенной длины, который можно измерить. Объяснение: На графике длину отрезка линии можно определить с помощью формулы расстояния между его конечными точками.
На каком расстоянии точка 6 8 от начала координат? ∴ Расстояние точки A(6, 8) от начала координат равно 10 см.
Каково расстояние точки (- 6 8 от начала координат?
Следовательно, расстояние точки P (–6, 8) от начала координат равно 10 единиц.
Каково расстояние между точками a B b C и AB CB? Следовательно, расстояние между точками (a + b, b + c) и (a – b, c – b) равно 2√2b единиц.
Какова координата точки А?
Координаты точки пара чисел, определяющая его точное местоположение на двумерной плоскости. Напомним, что координатная плоскость имеет две оси, расположенные под прямым углом друг к другу, называемые осью x и y.
Как найти единицы измерения на координатной плоскости?
Имеет и длину и ширину? В изучении искусства, форма представляет собой замкнутое пространство, ограниченную двумерную форму, имеющую как длину, так и ширину.
… Границы формы определяются другими элементами искусства, такими как линии, значения, цвета и текстуры; а добавляя ценность, вы можете превратить форму в иллюзию ее трехмерного кузена, формы.
Сколько точек на плоскости?
Таким образом, плоскость определяется три неколлинеарные точки.
Сколько точек на линии?
Линия (прямая линия) может рассматриваться как связное множество бесконечно многих точек. Он простирается бесконечно далеко в двух противоположных направлениях. Линия имеет бесконечную длину, нулевую ширину и нулевую высоту. Любой две точки в строке назовите это.
Расстояние между точками на плоскости и в пространстве Модуль вектора, его направляющие углы и косинусы. Координаты орта вектора. » Аналитическая геометрия f(x)dx.Ru
п.1. Расстояние между точками на плоскости и в пространстве.
Мы выведем формулу расстояния между любыми двумя точками в пространстве. Случай на плоскости будет следовать из общей формулы как частный случай.
Рассмотрим предварительно частный случай. Пусть вектор коллинеарный какой-нибудь координатной оси, например, Ох.
рис.1.
Расстояние между точками А и В равно:
. (1)
Ординаты и аппликаты точек А и В в этом случае равны:
, .
Формула, аналогичная формуле (1) имеет место и в случаях, когда или .
Рассмотрим теперь общий случай расположения точек А и В в пространстве относительно системы координат Охуz.
Пусть и – две произвольные точки пространства. Проведем через точки А и В плоскости параллельные координатным плоскостям. Эти 6 плоскостей высекают прямоугольный параллелепипед. См. рис.2.
рис.2.
Из прямоугольного треугольника ADC по теореме Пифагора , а из прямоугольного треугольника АВС:
.
Так как точки А, D, С лежат в плоскости перпендикулярной оси Оz, то , т.
к. , то .
Точки В, С, D лежат в плоскости перпендикулярной оси Оу, поэтому и , откуда следует, что .
Теперь, по формулам, аналогичным формуле (1), имеем:
,
,
,
откуда следует равенство:
.
Таким образом мы доказали следующую теорему.
Теорема. Пусть и . Тогда
. (2)
Следствие. Пусть и . Тогда
.
п.2. Модуль вектора, его направляющие углы и косинусы. Координаты орта вектора.
Теорема. (О модуле вектора.)
Модуль вектора равен корню квадратному из суммы квадратов его координат.
Иначе, если , то
. (3)
Доказательство. Пусть . Тогда равны их модули и их декартовые координаты: и
, , .
Подставляя в формулу (2), получаем (3), ч.т.д.
Теорема доказана.
Обозначим углы между вектором и координатными осями: , , .
Определение. Углы между вектором и координатными осями называются направляющими углами вектора.
рис.3.
Пусть . По теореме о вычислении проекции вектора на ось, имеем: , , . Отсюда следует:
, , , (4)
. (5)
Из последнего равенства следует, что орт вектора , т.е. вектор единичной длины и сонаправленный с имеет декартовые координаты:
. (6)
А т.к. , то по теореме о модуле вектора, получаем:
, откуда следует
. (7)
Расстояние между точкой и плоскостью
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, мы можем сказать, что расстояние между точкой и плоскостью — это длина вектора нормали, опущенного из данной точки на данную плоскость.
Если мы хотим определить расстояние между точкой P с координатами (x o , y o , z o ) и данной плоскостью уравнением Ax + By + Cz = D, то расстояние между точкой P и данная плоскость задается |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
| 1. | Что такое расстояние между точкой и плоскостью? |
| 2. | Формула расстояния между точкой и плоскостью |
| 3. | Расстояние между точкой и плоскостью Доказательство |
| 4. | Как применить формулу расстояния между точкой и плоскостью? |
| 5. | Часто задаваемые вопросы о расстоянии между точкой и плоскостью |
Что такое расстояние между точкой и плоскостью?
Расстояние между точкой и плоскостью — это кратчайшее перпендикулярное расстояние от точки до данной плоскости.
Проще говоря, кратчайшее расстояние от точки до плоскости — это длина перпендикуляра, параллельного вектору нормали, опущенного из данной точки на данную плоскость. Давайте теперь посмотрим формулу для расстояния между точкой и плоскостью.
Расстояние между точкой и плоскостью Формула
Кратчайшее расстояние между точкой и плоскостью равно длине вектора нормали, который начинается в данной точке и касается плоскости. Рассмотрим точку P с координатами (x o , y o
, z o ) и данную плоскость π с уравнением Ax + By + Cz = D. Тогда расстояние между точкой P и плоскостью π равно определяется |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).Расстояние между точкой и плоскостью Доказательство
Теперь, когда мы знаем формулу расстояния между точкой и плоскостью, выведем ее формулу, используя различные формулы трехмерной геометрии.
Рассмотрим точку P с координатами (x o , y o , z o ) в трехмерном пространстве и плоскость с вектором нормали, скажем, v = (A, B, C) и точку Q с координатами (x 1 , у 1 , з 1 ) на самолете. Тогда уравнение плоскости задается как A(x — x 1 ) + B(y — y 1 ) + C(z — z 1 ) = 0. Это уравнение можно переписать как Ax + By + Cz + (- Ax 1 — By 1
- Уравнение плоскости: Ax + By + Cz + D = 0
- Точка P: (x или , у или , я или )
- Нормальный вектор: Ai + Bj + Ck
Пусть w вектор, соединяющий точки P(x o , y o , z o ) и Q(x 1 , y 1 , z 1 ). Тогда w = (x o — x 1 , y o — y 1 , z o — z 1 ).
Теперь давайте вычислим единичный вектор нормали, т. Е. Вектор нормали с величиной, равной 1, который определяется делением вектора нормали v на его величину. Единичный вектор нормали определяется выражением
n = v/||v||
= (A, B, C)/√(A 2 + B 2 + C 2
)Теперь расстояние между точкой P и данной плоскостью есть не что иное, как длина проекции вектор w на единичный вектор нормали n. Как мы знаем, длина вектора n равна единице, расстояние от точки P до плоскости есть модуль скалярного произведения векторов w и n, т. е.
Расстояние, d = |w.n|
= | (х о — х 1 , у o — у 1 , z o — z 1 ). [(A, B, C)/√(A 2 + B 2 + C 2 )] |
= |A(x o — x 1 ) + B(y o — y 1 ) + C(z o — z 1 7 )|/0 + В 2 + С 2 )
= | Ax o + By o + Cz o — (Ax 1 + By 1 + Cz 1 ) |/√(A 2 + В 2 + С 2 )
= | Ax o + By o + Cz o + D |/√(A 2 + B 2
Так как точка Q с координатами (x 1 , y 1 , z 1 ) является произвольной точкой на данной плоскости и D = — (Ax 1 + By 1 + Cz 1 ), поэтому формула остается той же для любой точки Q на плоскости и, следовательно, не зависит от точки Q, т.
е. где бы точка Q ни лежала на плоскости, формула для расстояния между точкой и плоскостью остается прежним. Следовательно, расстояние между точкой P(x o , y o , z o ) и плоскость π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz o + D |/√(А 2 + В 2 + С 2 )
Как применить формулу расстояния от точки до плоскости?
Мы вывели формулу расстояния от точки до плоскости, решим пример с помощью формулы, чтобы понять ее применение и определить расстояние между точкой и плоскостью.
Пример: Определить расстояние между точкой P = (1, 2, 5) и плоскостью π: 3x + 4y + z + 7 = 0
Решение: Мы знаем, что формула для расстояния между точкой и плоскость: d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
,, Здесь B = 4, C = 1, D = 7, x o = 1, y o = 2, z o = 5
Подставляя значения в формулу, имеем
d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 + 3 × 3 ×
) | 2 + 1 × 5 + 7|/√(3 2 + 4 2 + 1 2 )= |3 + 8 + 5|/√(9 + 16 + 1)
= |16 |/√26
= 8√26/13 ед.
Темы, связанные с расстоянием между точкой и плоскостью
- Формула расстояния
- Расстояние между двумя точками
- Формула Евклидова расстояния
Часто задаваемые вопросы о расстоянии между точкой и плоскостью
Что такое расстояние между точкой и плоскостью в геометрии?
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, расстояние между точкой и плоскостью есть кратчайшее перпендикулярное расстояние от точки до данной плоскости.
Какая формула для расстояния между точкой и плоскостью?
Расстояние между точкой P(x o , y o , z o ) и плоскость π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
Как найти кратчайшее расстояние между точкой и плоскостью?
Чтобы найти кратчайшее расстояние между точкой и плоскостью, воспользуемся формулой 2 ), где (х o , у o , z o ) — заданная точка, а Ax + By + Cz + D = 0 — уравнение данной плоскости.
Какое расстояние между точкой и плоскостью x-z?
Расстояние между точкой (x o , y o , z o ) и плоскостью x-z определяется координатой y, т. е. y o
Как найти кратчайшее расстояние точка к плоскости?
Чтобы вычислить кратчайшее расстояние от точки до плоскости, мы рассматриваем длину вектора, параллельного вектору нормали к плоскости, которая опускается из данной точки на данную плоскость.
Каково расстояние между точкой и плоскостью, когда точка лежит на данной плоскости?
Расстояние между точкой и плоскостью равно нулю, если данная точка лежит на данной плоскости.
Расстояние от точки до плоскости
Вот краткий набросок того, как рассчитать расстояние от точки
$P=(x_1,y_1,z_1)$ в плоскость, определяемую вектором нормали
$\vc{N}=(A,B,C)$ и точка $Q=(x_0,y_0,z_0)$. Уравнение для
плоскость, определяемая $\vc{N}$, и $Q$ есть $A(x-x_0)+B(y-y_0) +C(z-z_0) =
0$, что можно записать как $Ax+By+Cz+D=0$, где
$D=-Ax_0-By_0-Cz_0$.
Этот апплет демонстрирует настройку задачи и метод, который мы будем использовать для вывода формулы расстояния от плоскости до точка $P$.
Загрузка апплета
Расстояние от точки до плоскости. Набросок способа расчета расстояния от точки $\color{red}{P}$ (выделена красным) до плоскости. Вектор $\color{green}{\vc{n}}$ (выделен зеленым цветом) является единичным вектором нормали к плоскости. Вы можете перетаскивать точку $\color{red}{P}$, а также вторую точку $\vc{Q}$ (желтого цвета), которая ограничена плоскостью. Хотя вектор $\color{green}{\vc{n}}$ не меняется (поскольку плоскость фиксирована), он перемещается вместе с $\color{red}{P}$, чтобы всегда находиться в конце серого цвета. отрезок прямой из $\color{red}{P}$, перпендикулярный плоскости. Это расстояние от $\color{red}{P}$ до плоскости равно длине этого сегмента серой линии. Это расстояние является длиной проекции вектора из $Q$ в $P$ (фиолетового цвета) на вектор нормали $\color{green}{\vc{n}}$.